Simulating Sediment Erosion in a Small Kaplan Turbine
Abstract
1. Introduction
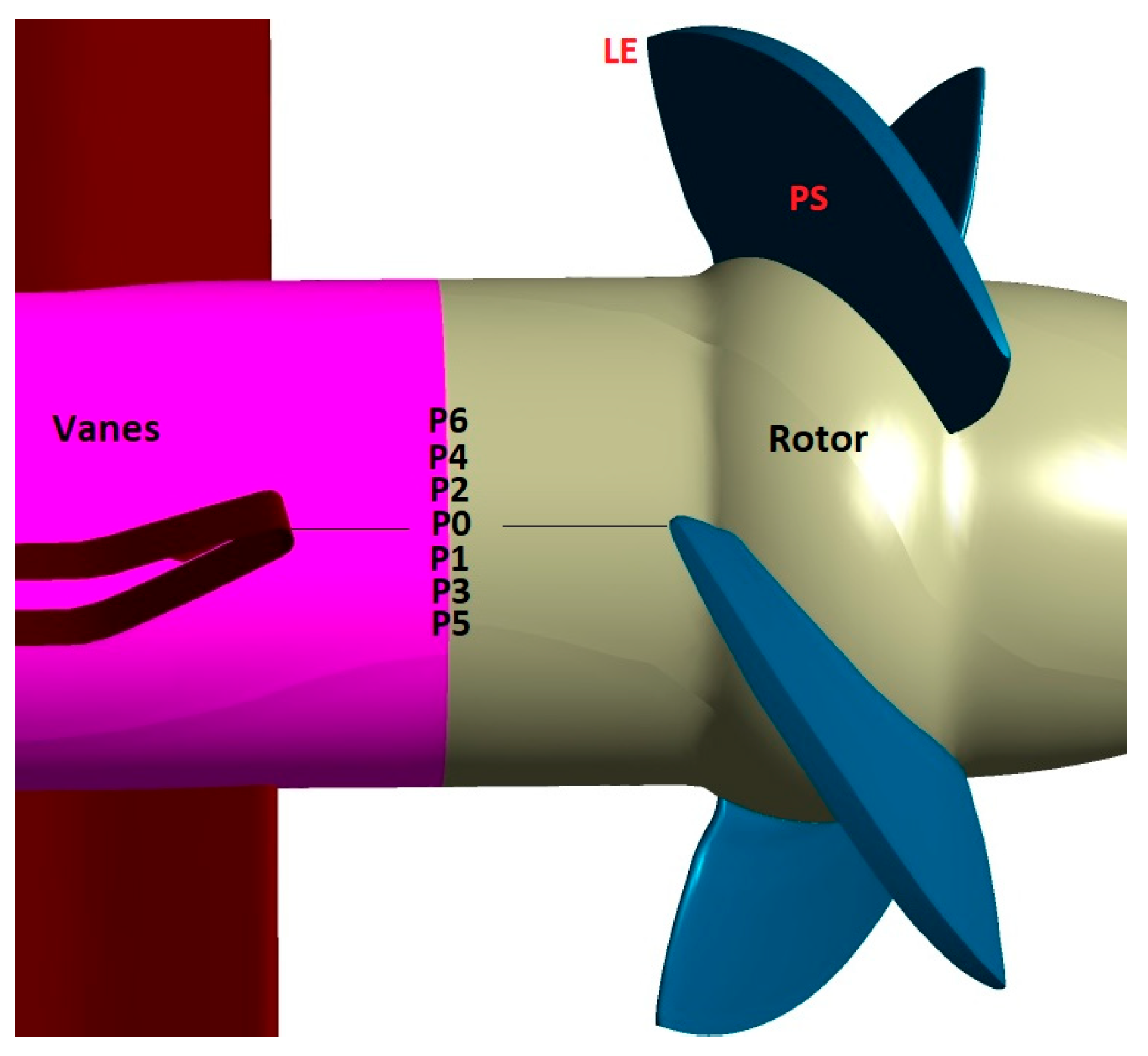
2. Kaplan Turbine Model
3. Flow Computation
3.1. Mesh Generation
3.2. Flow Results
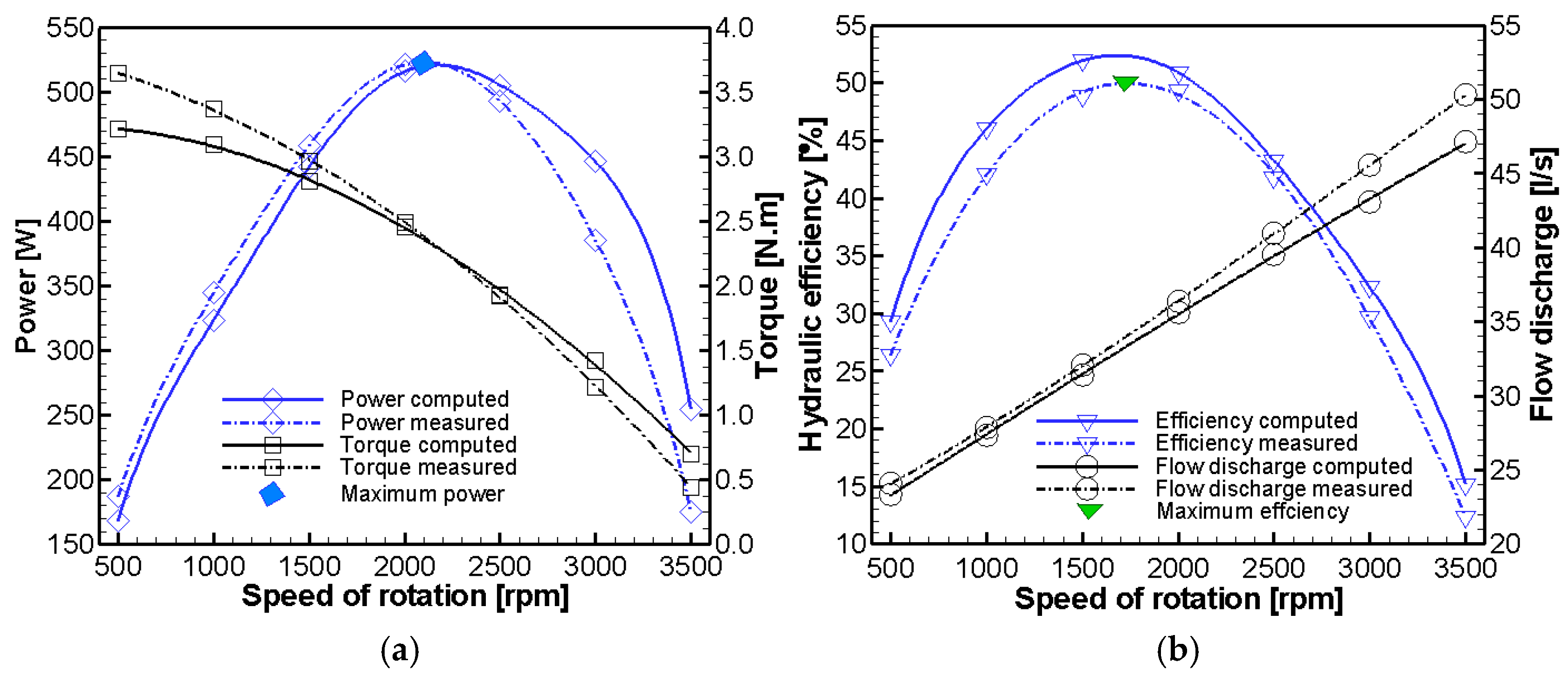
3.2.1. Turbine Performance Validation
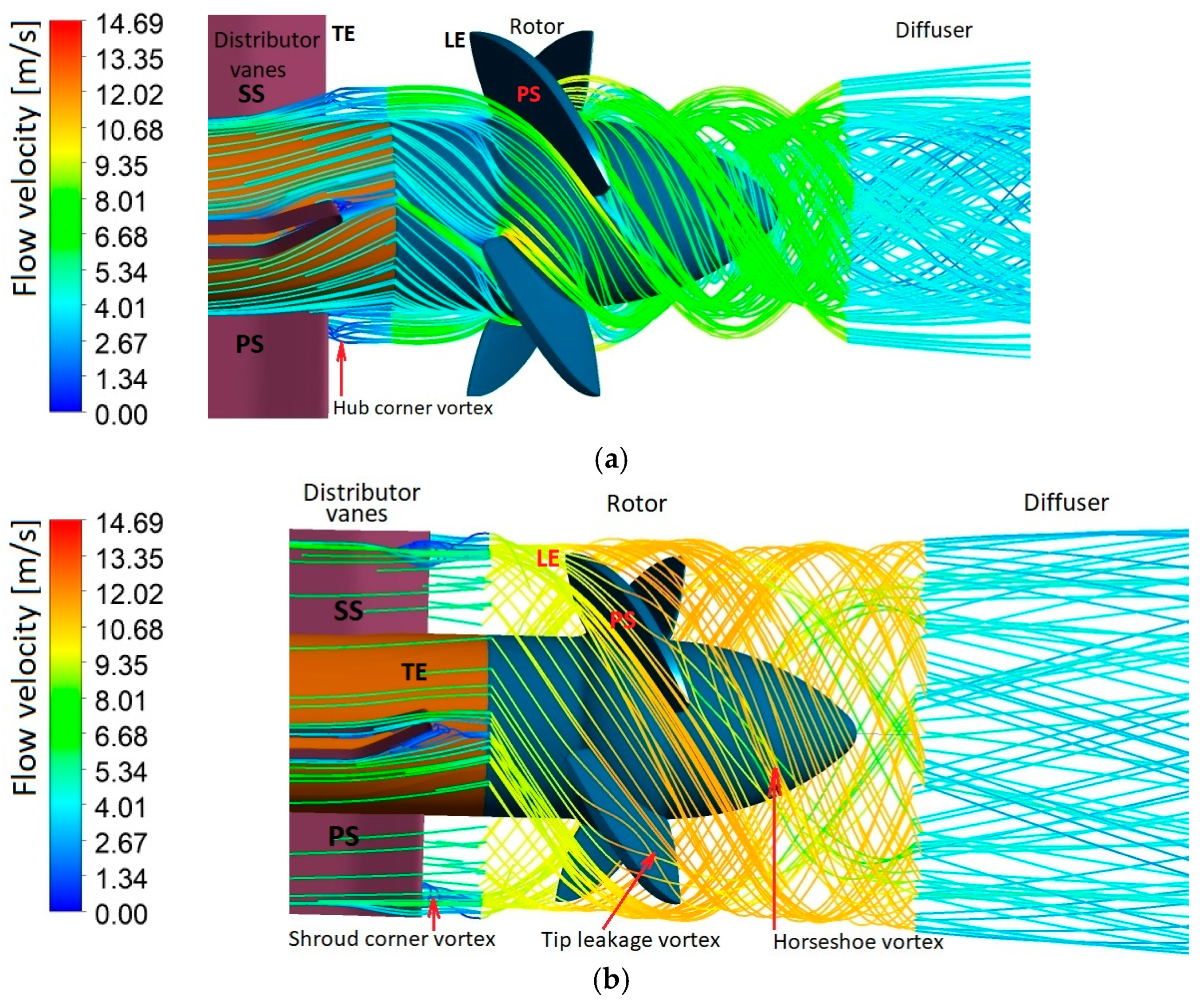
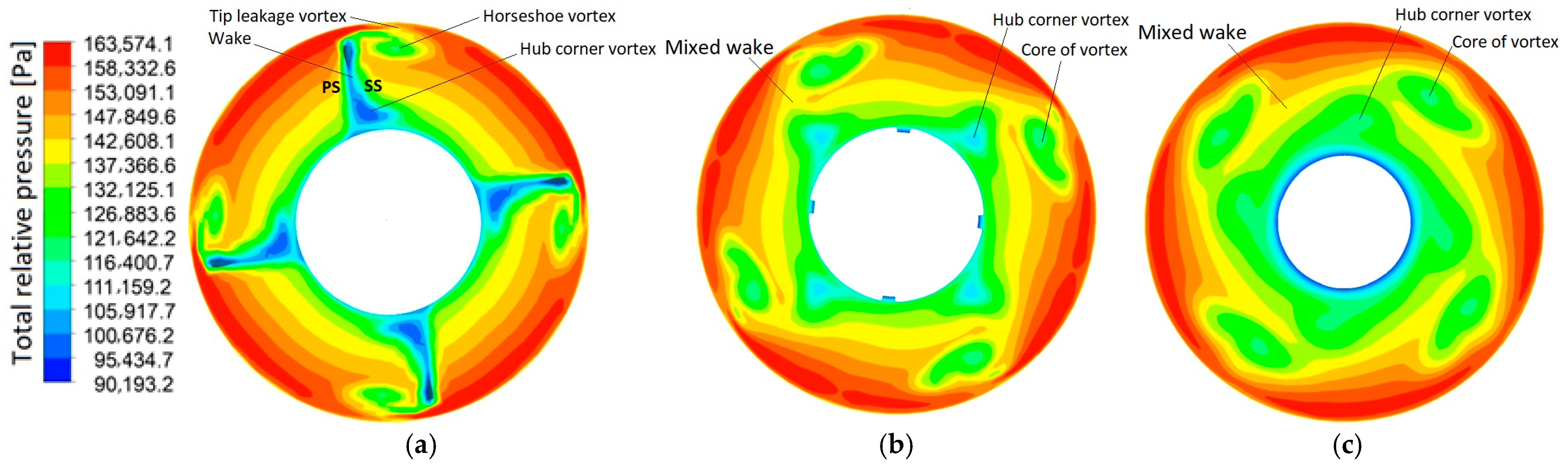
3.2.2. Flow Structures
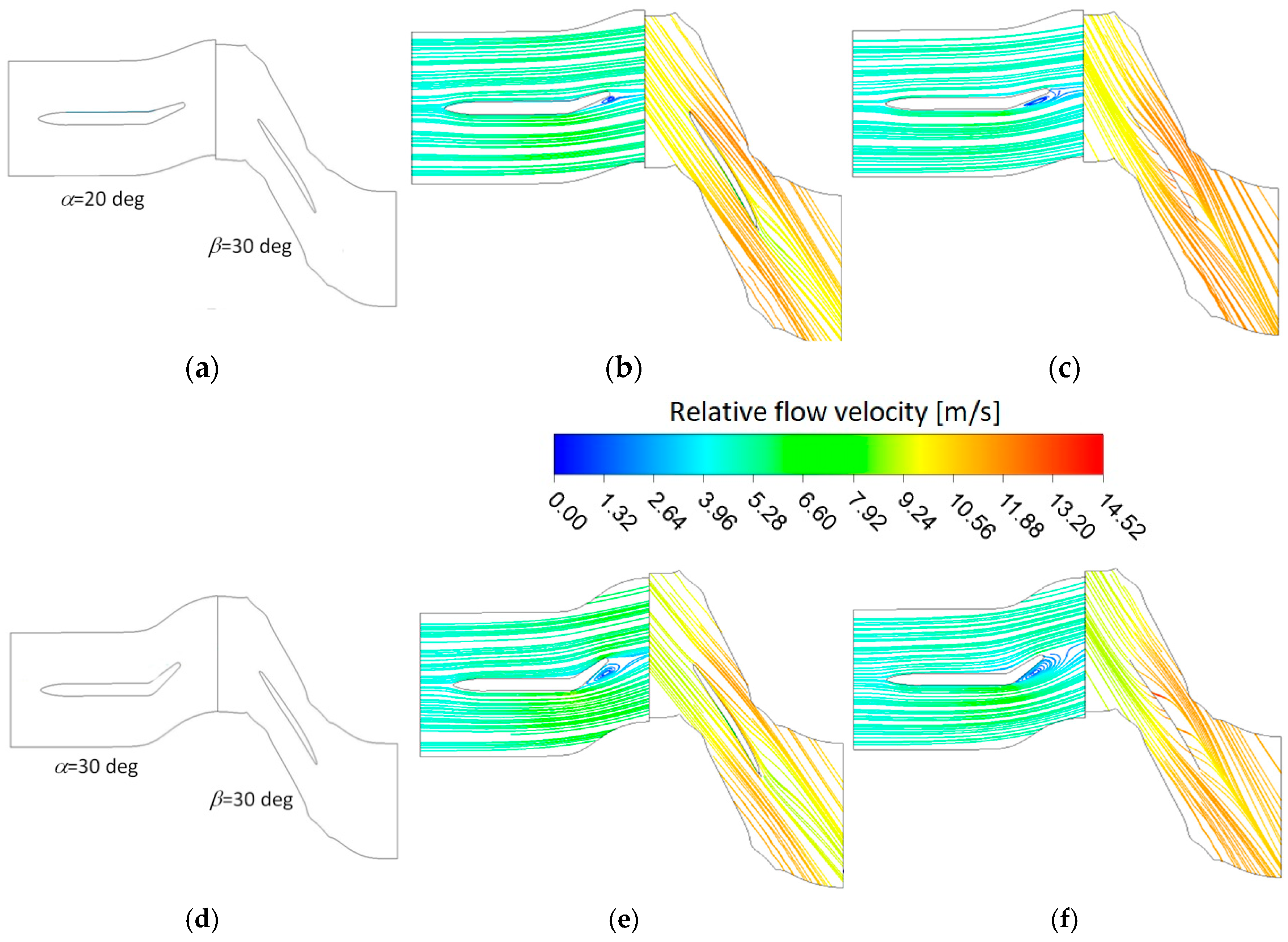
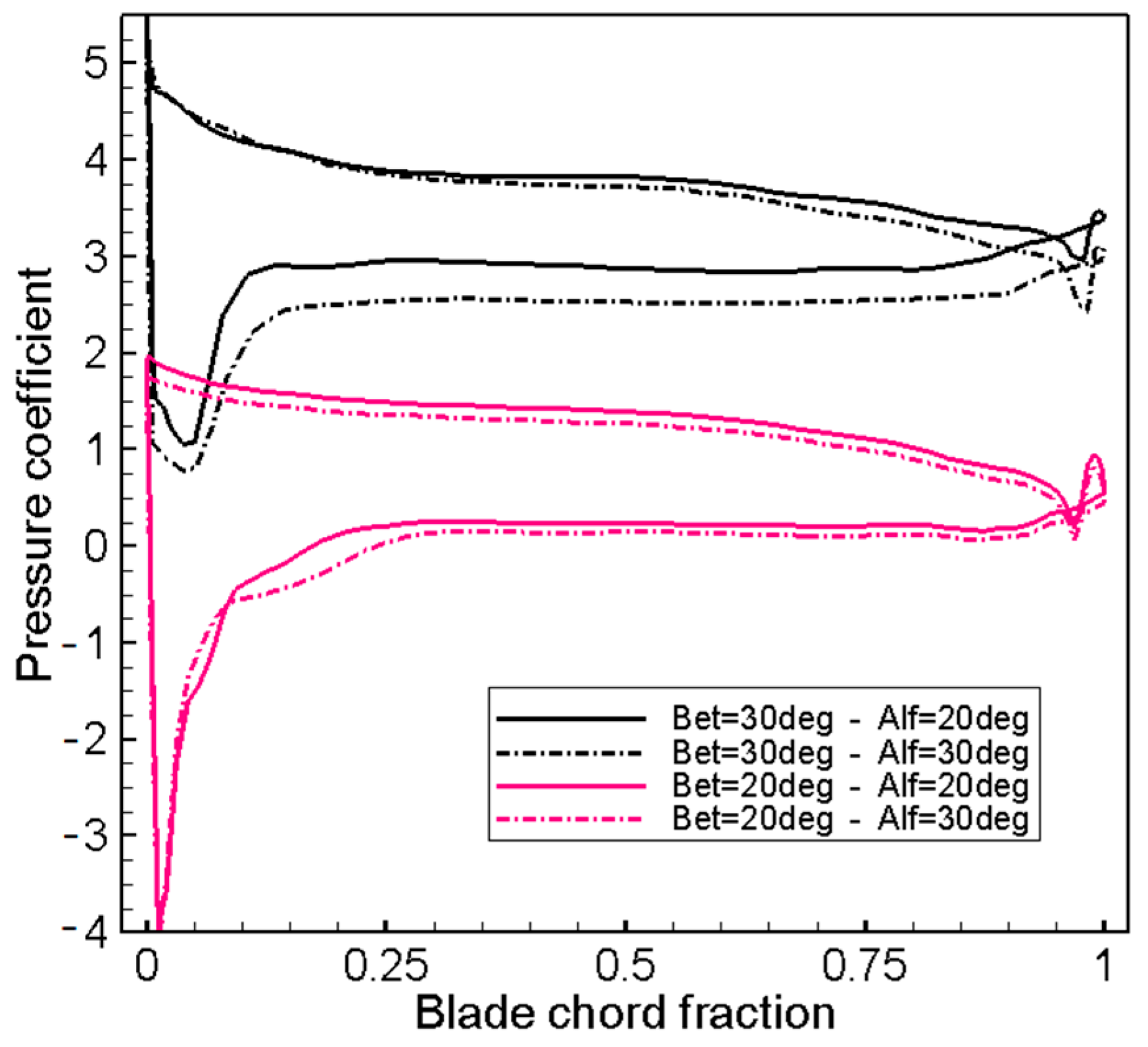
3.2.3. Effect of Blade Setting Angle and Vane Opening
4. Particle Trajectory Calculation
4.1. Turbulence Effect
4.2. Particle Tracking
4.3. Boundary Conditions
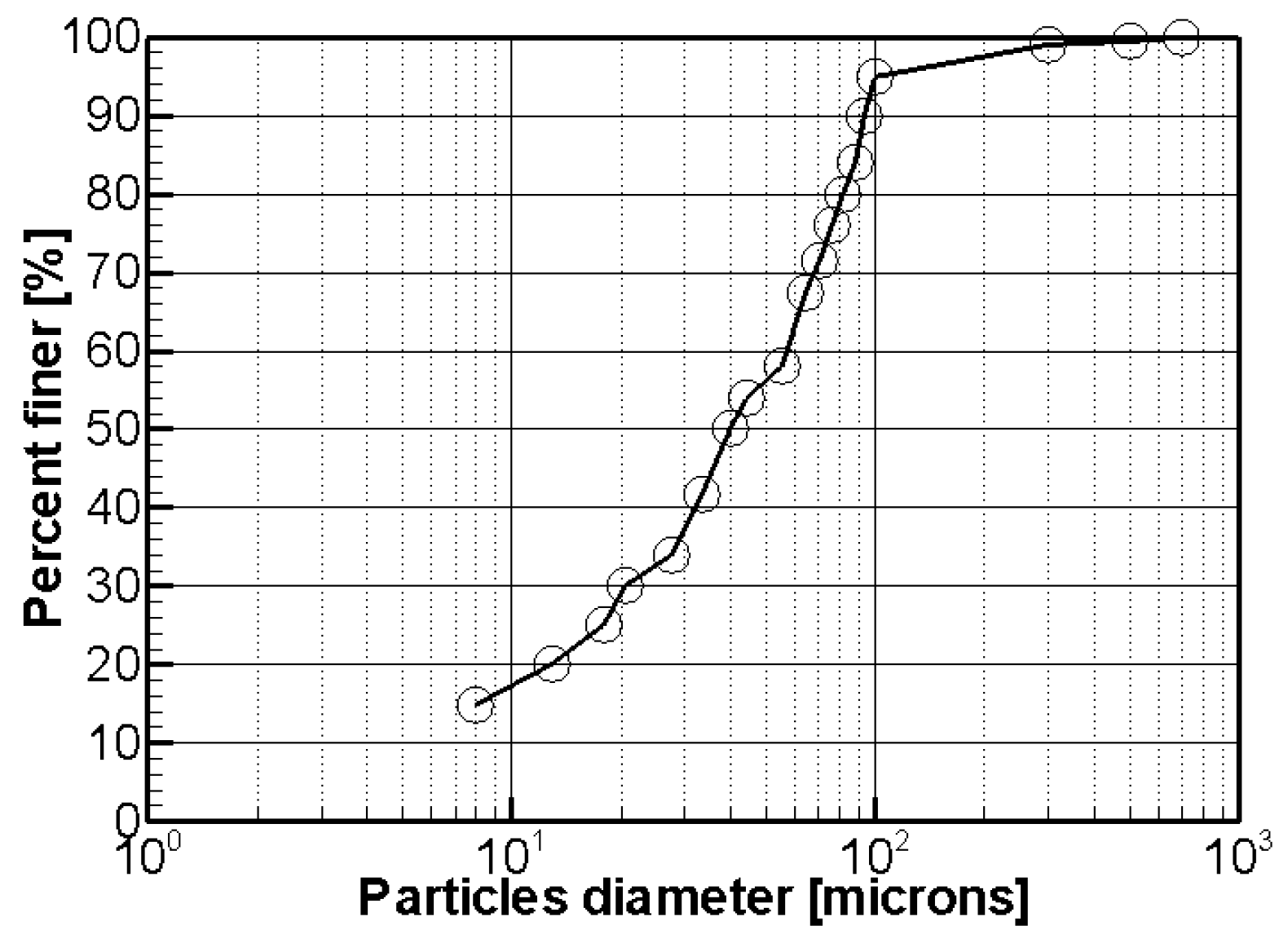
4.4. Particle Seeding
5. Erosion Assessment
6. Results and Discussions
6.1. Particle Trajectories
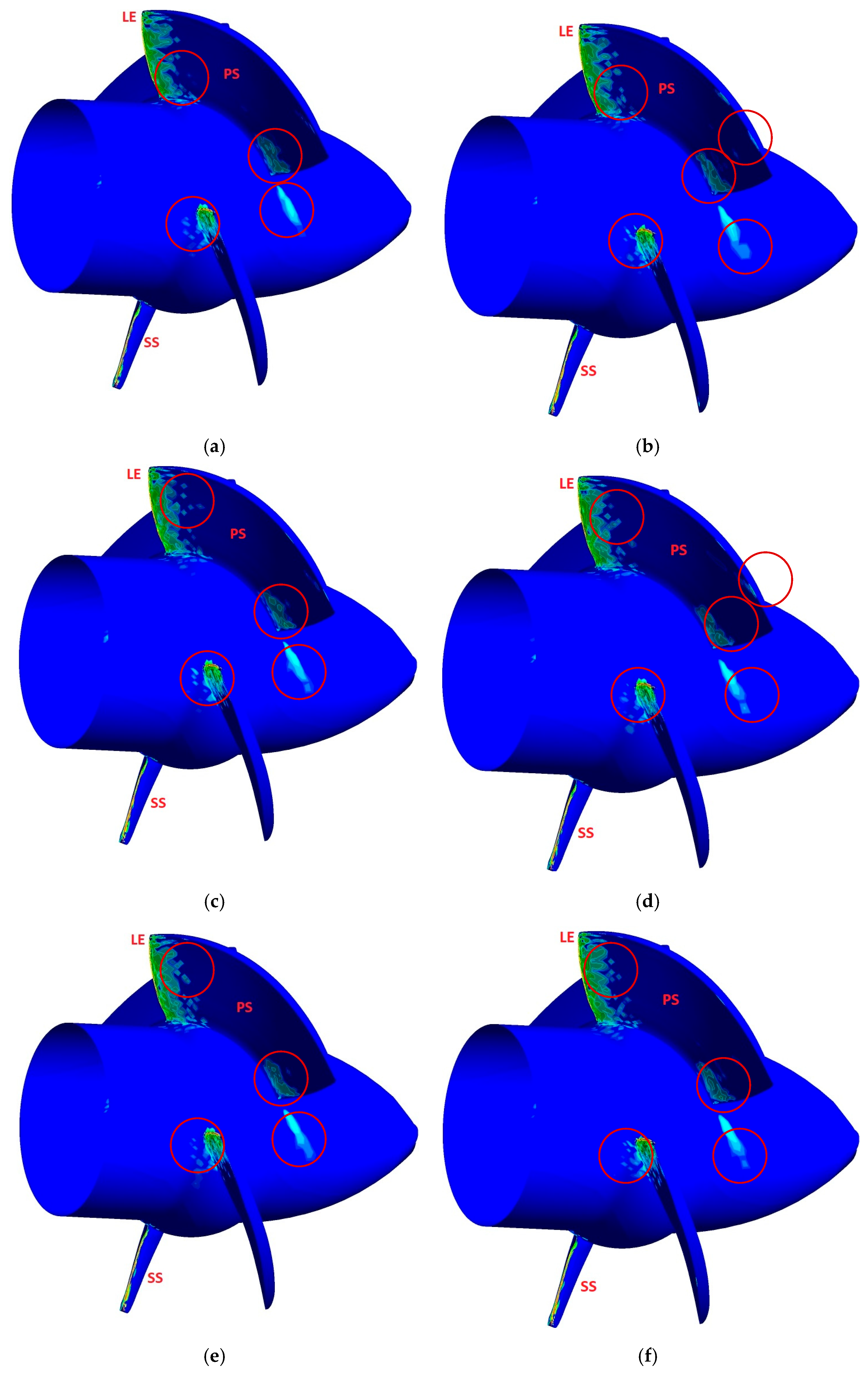
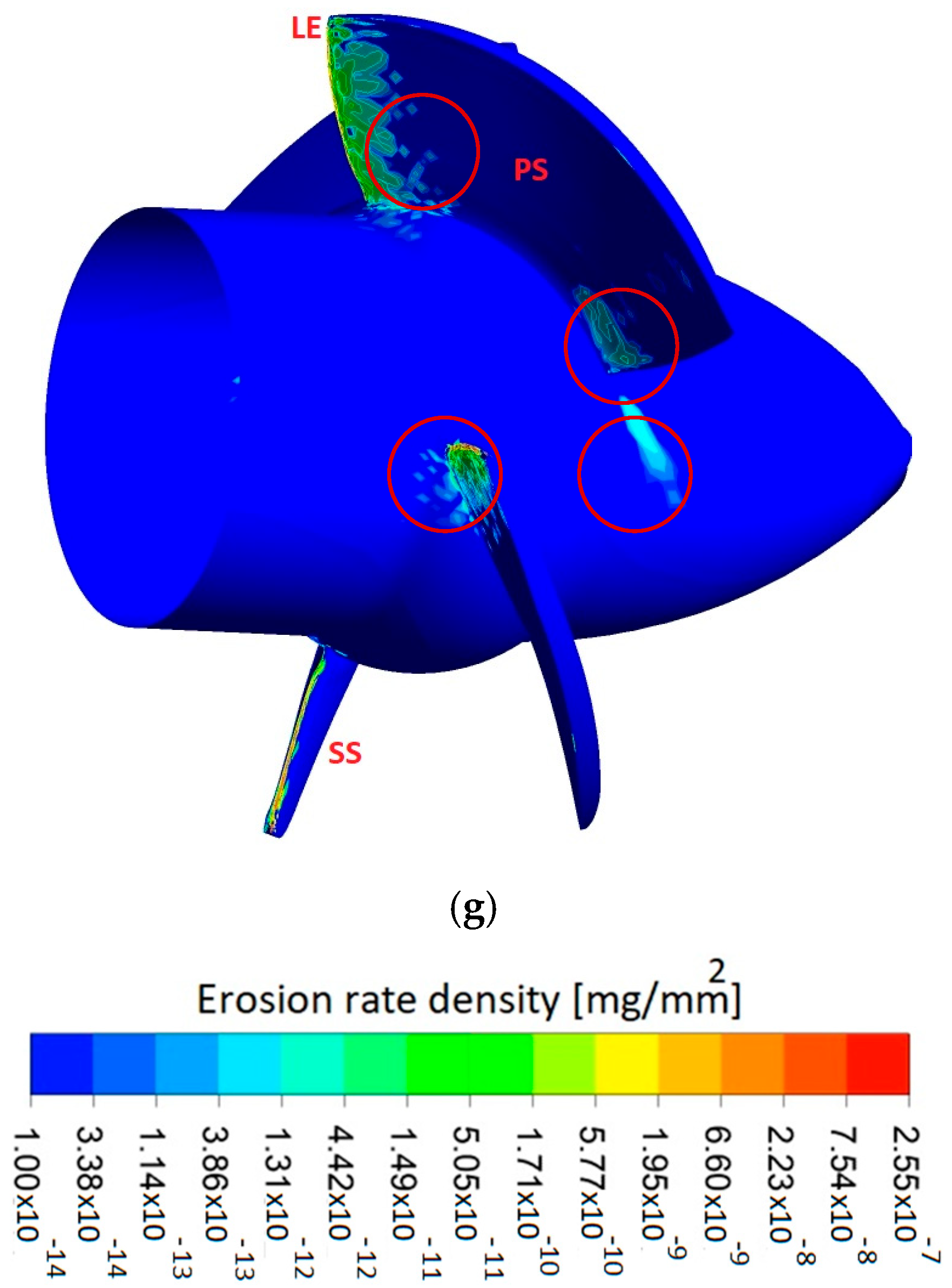
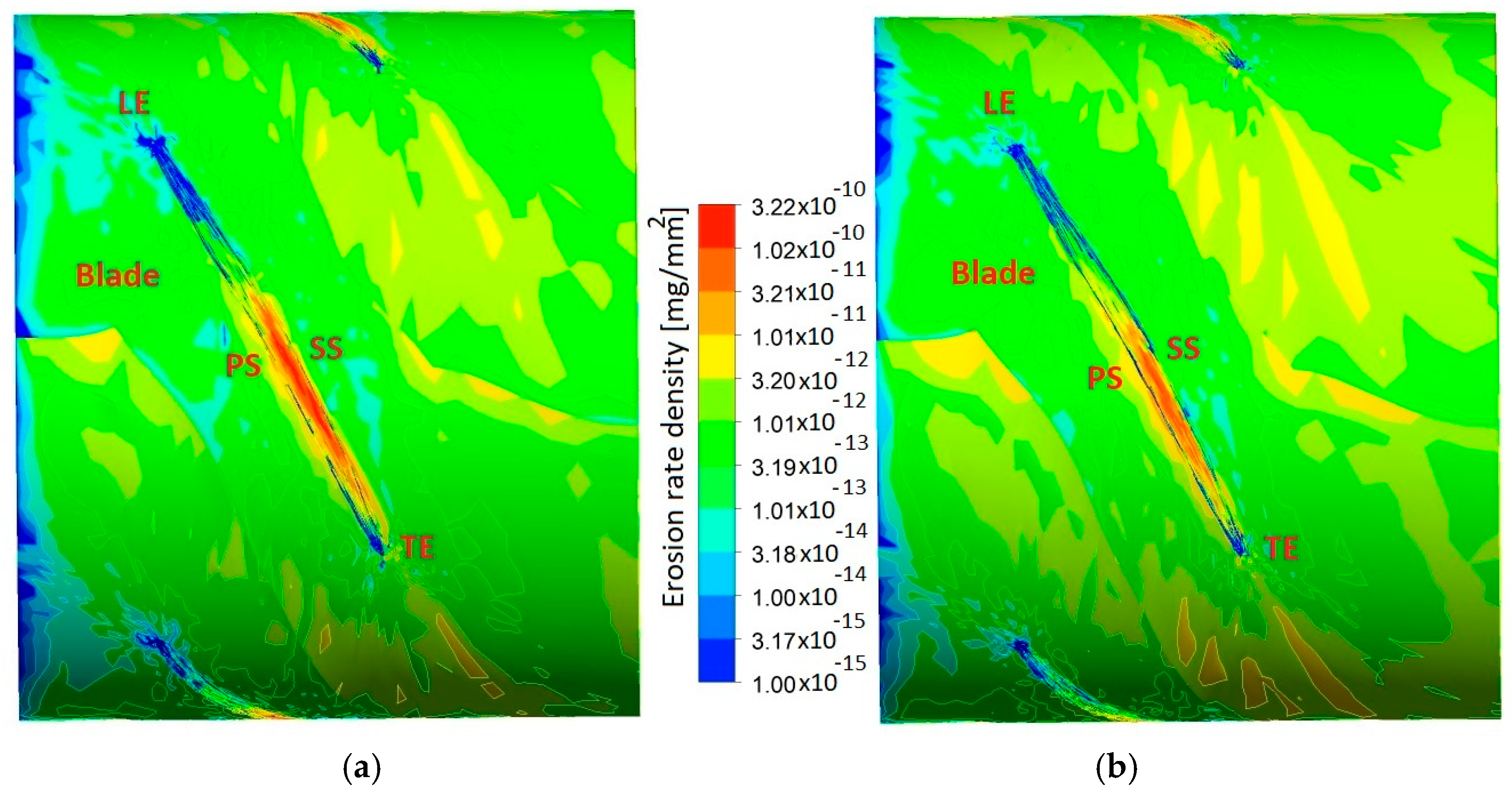
6.2. Effect of Vane/Blade Position on Erosion Development
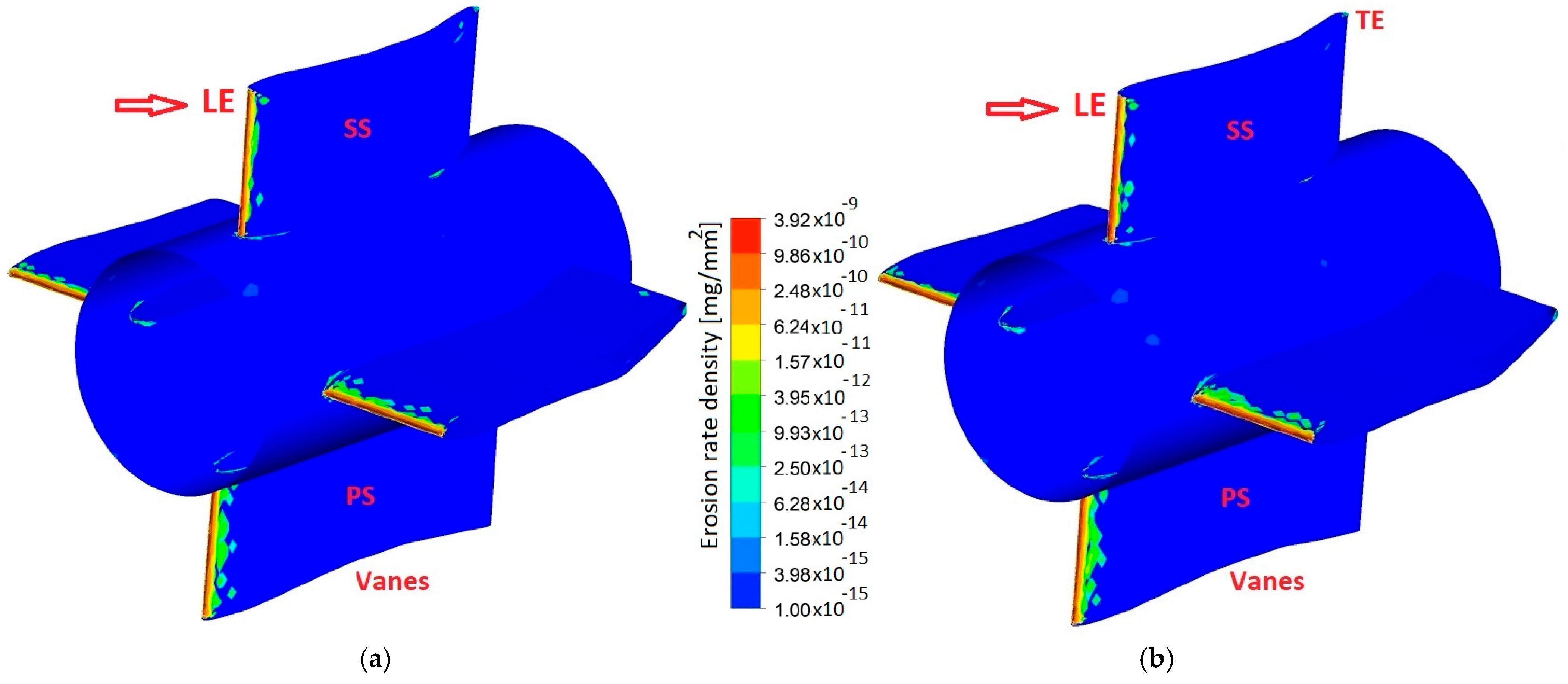
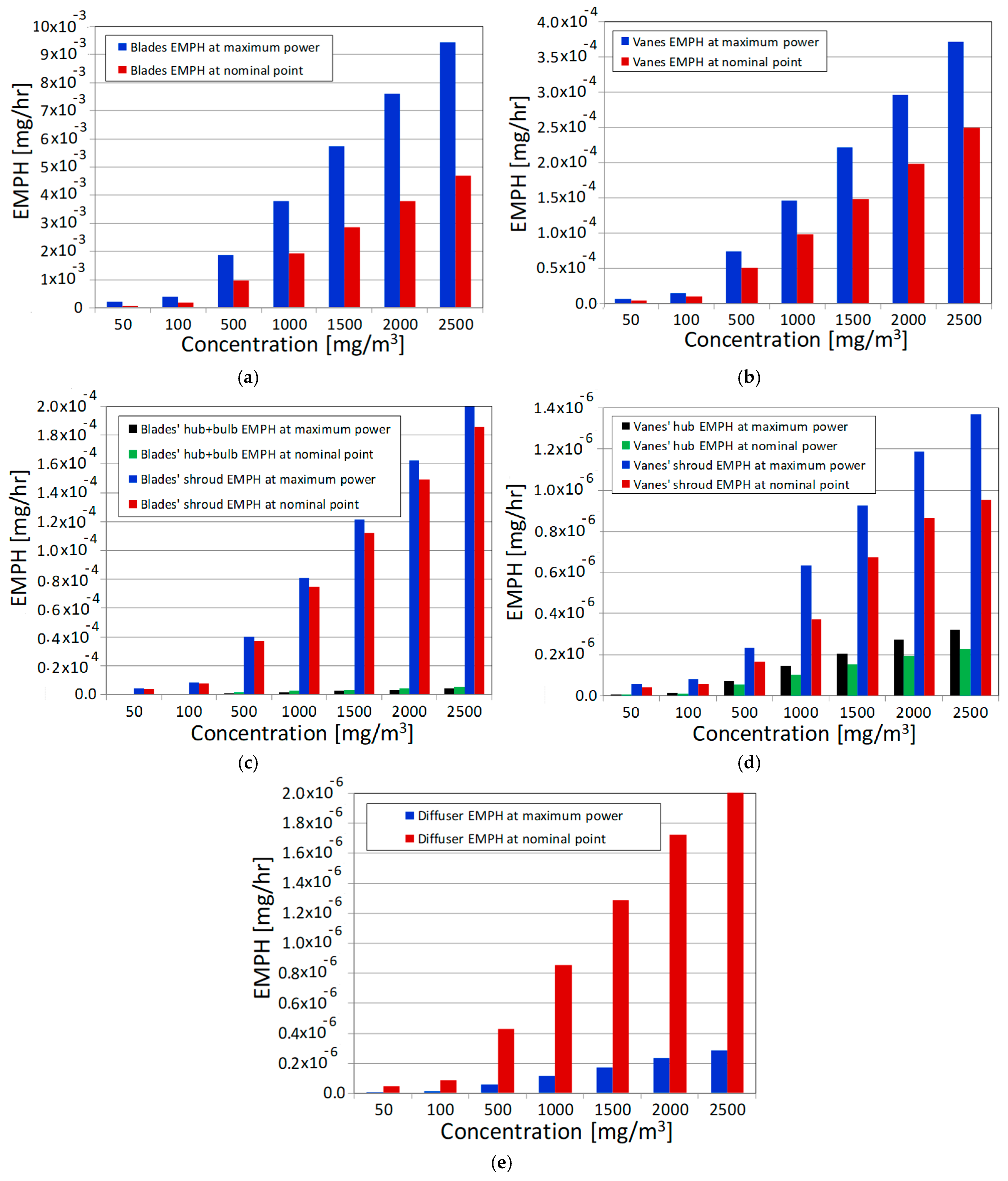
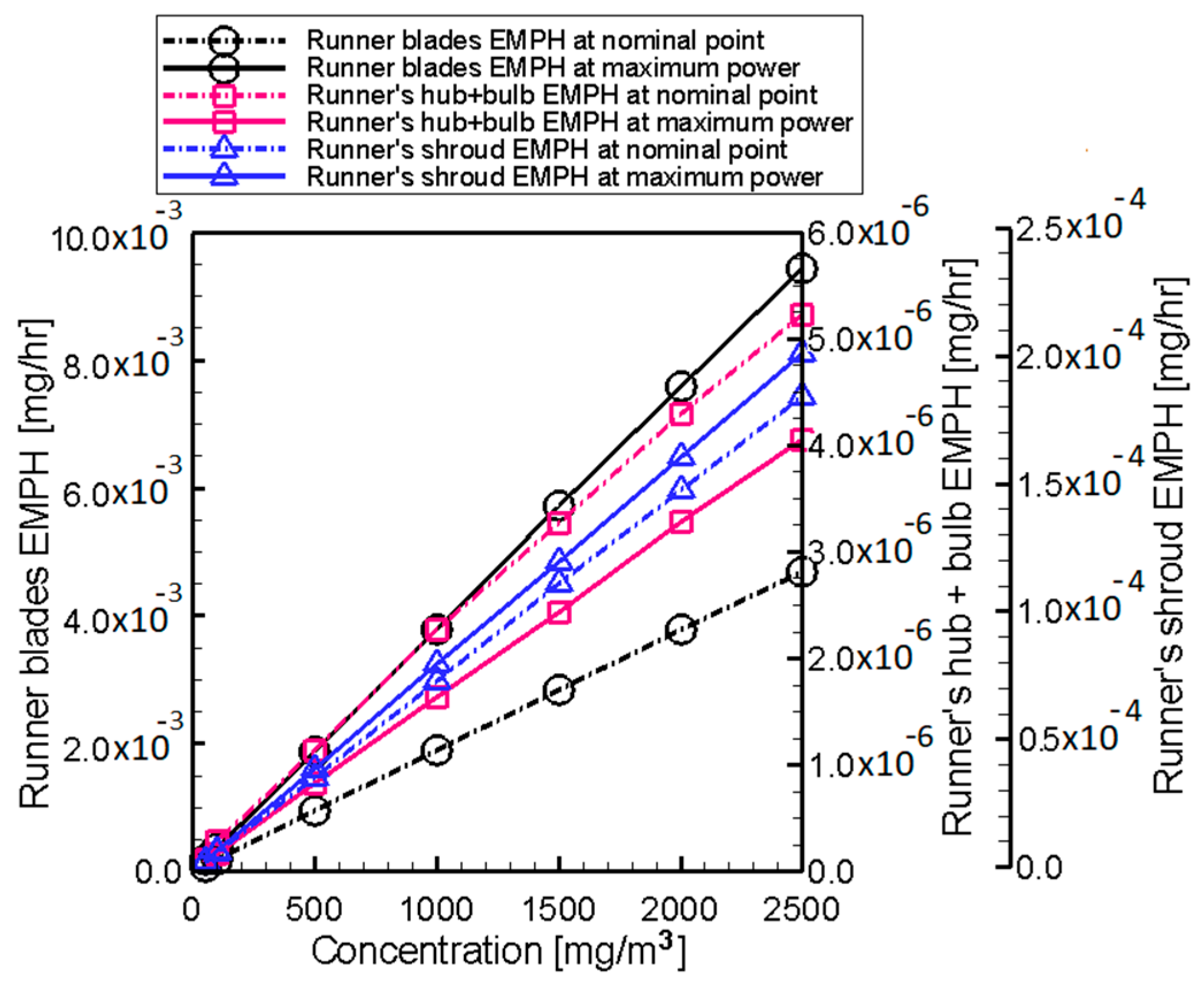
6.3. Erosion of Kaplan Turbine Components at Different Operating Conditions
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| area (m2) | |
| AERD | average erosion rate density (mg/s·mm2) |
| c | chord (m) |
| drag coefficient | |
| shear lift force coefficient | |
| d | diameter of particle (m) |
| D | diameter of runner (m) |
| EMPH | eroded mass per hour (mg/hr) |
| ERD | erosion rate density (mg/s·mm2) |
| F | force (N) |
| f | force reduced by mass (N/kg) |
| g | gravity (m/s2) |
| H | Water head (m) |
| k | turbulent kinetic energy (m2/s2) |
| k1, k2, k3 | material constants |
| m | mass (kg) |
| normal vector | |
| p | pressure (Pa) |
| P | power (W) |
| Q | Volume flow rate (m3/s) or (l/s) |
| r | radius, radial co-ordinate (m) |
| Re | Reynolds number |
| Stk | Stokes number |
| time (s) | |
| tangential vector | |
| torque (n·m) | |
| velocity (m/s) | |
| Greek Symbols | |
| β | impact angle (deg) |
| local erosion rate (mg/g) | |
| η | efficiency |
| ρ | density (kg/m3) |
| μ | dynamic viscosity (kg/m·s) |
| ν | Kinematic viscosity(m2/s) |
| blade speed of rotation (rad/s) | |
| fluid rotation (1/s) | |
| Subscripts | |
| f | fluid |
| p | particle |
| r | radial |
| θ | tangential component |
| z | axial direction |
| 1, 2 | impact/rebound |
| Abbreviation | |
| LE | leading edge |
| PS | pressure side |
| SS | suction side |
| TE | trailing edge |
References
- Rai, A.K.; Kumar, A.; Staubli, T. Effect of concentration and size of sediments on hydro-abrasive erosion of Pelton turbine, Renew. Energy 2020, 145, 893–902. [Google Scholar]
- Felix, D.; Albayrak, I.; Abgottspon, A.; Boes, R.M. Hydro-abrasive erosion of hydraulic turbines caused by sediment—A century of research and development. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 122001. [Google Scholar] [CrossRef]
- Pradhan, P.M.S.; Dahlhaug, O.G.; Joshi, P.N.; Støl, H. Sediment and Efficiency Measurements at Jhimruk Hydropower Plant—Monsoon 2003; Hydro Lab: Kathmandu, Nepal, 2004. [Google Scholar]
- Noon, A.A.; Kim, M.H. Erosion wear on Francis turbine components due to sediment flow. Wear 2017, 378–379, 126–135. [Google Scholar] [CrossRef]
- Singh, M.; Banerjee, J.; Patel, P.L.; Tiwari, H. Effect of silt erosion on francis turbine: A case study of Maneri Bhalistage-II, Uttarakhand, India. ISH J. Hydraul. Eng. 2013, 19, 1–10. [Google Scholar] [CrossRef]
- Eltvik, M.; Dahlhaug, O.G.; Neopane, H.P. Prediction of sediment erosion in Francis turbines. In Proceedings of the 4th International Meeting on Cavitation and Dynamic Problems in Hydraulic Machinery and Systems, Belgrade, Serbia, 26–28 October 2011. [Google Scholar]
- Koirala, R.; Thapa, B.; Neopane, H.P.; Zhu, B.; Chhetry, B. Sediment erosion in guide vanes of Francis turbine: A case study of Kaligandaki Hydropower Plant, Nepal. Wear 2016, 362–363, 53–60. [Google Scholar] [CrossRef]
- Truscott, G.F. Literature survey of abrasive wear in hydraulic machinery. Wear 1972, 20, 29–50. [Google Scholar] [CrossRef]
- Brekke, H. Design of hydraulic machinery working in sand laden water. In Abrasive Erosion and Corrosion of Hydraulic Machinery; Duan, C.G., Karelin, V.Y., Eds.; Imperial College Press: London, UK, 2002; pp. 155–181. [Google Scholar]
- Padhy, M.K.; Saini, R.P. A review on silt erosion in hydro turbines. Renew. Sustain. Energy Rev. 2008, 12, 1974–1987. [Google Scholar] [CrossRef]
- Padhy, M.K.; Saini, R.P. Study of silt erosion on performance of a Pelton turbine. Energy 2011, 36, 141–147. [Google Scholar] [CrossRef]
- Padhy, M.K.; Saini, R.P. Study of silt erosion mechanism in Pelton turbine buckets. Energy 2012, 39, 286–293. [Google Scholar] [CrossRef]
- Thapa, B.S.; Dahlhaug, O.G.; Thapa, B. Sediment erosion in hydro turbines and its effect on the flow around guide vanes of Francis Turbine. Renew. Sustain. Energy Rev. 2015, 49, 1100–1113. [Google Scholar] [CrossRef]
- Thapa, B.S.; Dahlhaug, O.G.; Thapa, B. Effects of sediment erosion in guide vanesof Francis turbine. Wear 2017, 390–391, 104–112. [Google Scholar] [CrossRef]
- Rai, A.K.; Kumar, A. Analyzing hydro abrasive erosion in Kaplan turbine: A Case Study from India. J. Hydrodyn. 2016, 28, 863–872. [Google Scholar] [CrossRef]
- Thapa, B.S.; Thapa, B.; Dahlhaug, O.G. Empirical modelling of sediment erosion in Francis turbines. Energy 2012, 41, 386–391. [Google Scholar] [CrossRef]
- Dinesh, K.; Bhingole, P.P. CFD based analysis of combined effect of cavitation and silt erosion on Kaplan turbine. Mater. Today Proc. 2015, 2, 2314–2322. [Google Scholar] [CrossRef]
- Leguizamón, S.; Jahanbakhsh, E.; Alimirzazadeh, S.; Maertens, A.; Avellan, F. Multiscale simulation of the hydroabrasive erosion of a Pelton bucket: Bridging scales to improve the accuracy. Int. J. Turbomach. Propuls. Power 2019, 4, 9. [Google Scholar] [CrossRef]
- Shen, Z.; Chu, W.; Li, X.; Dong, W. Sediment erosion in the impeller of a double-suction centrifugal pump—A case study of the Jingtai Yellow River Irrigation Project, China. Wear 2019, 422–423, 269–279. [Google Scholar] [CrossRef]
- Ghenaiet, A. Computation of erosion in a hydro turbine. Eng. Comput. 2022, 39, 1317–1347. [Google Scholar] [CrossRef]
- Bajracharya, T.R.; Acharya, B.; Joshi, C.B.; Saini, R.P.; Dahlhaug, O.G. Sand erosion of Pelton turbine nozzles and buckets: A case study of Chilime Hydropower Plant. Wear 2008, 264, 177–184. [Google Scholar] [CrossRef]
- Abgottspon, A.; Staubli, T.; Felix, D. Hydro-abrasive erosion of Pelton buckets and suspended sediment monitoring. In Proceedings of the Hydro Vision International, Denver, CO, USA, 23–26 July 2013. [Google Scholar]
- Rai, A.K.; Kumar, A.; Staubli, T. Analytical modelling and mechanism of hydro-abrasive erosion in pelton buckets. Wear 2019, 436–437, 203003. [Google Scholar] [CrossRef]
- Rai, A.K.; Kumar, A.; Staubli, T.; Yexiang, X. Interpretation and application of the hydro-abrasive erosion model from IEC 62364 (2013) for Pelton turbines. Renew. Energy 2020, 160, 396–408. [Google Scholar] [CrossRef]
- Xiao, Y.; Guo, B.; Rai, A.K.; Liu, J.; Liang, Q.; Zhang, J. Analysis of hydro-abrasive erosion in Pelton buckets using a Eulerian-Lagrangian approach. Renew. Energy 2022, 197, 472–485. [Google Scholar] [CrossRef]
- Li, L.; Lu, J.; Gong, Y.; Zhao, H.; Liu, X.; Zhu, B. Sediment erosion characteristics of Pelton turbine runner: Effects of sediment concentration and diameter. Renew. Energy 2024, 220, 119679. [Google Scholar] [CrossRef]
- Sangal, S.; Singhal, M.K.; Saini, R.P.; Tomar, G.S. Hydro-abrasive erosion modelling in Francis turbine at different silt conditions. Sustain.Vol. Oct. 2022, 53, 102616. [Google Scholar] [CrossRef]
- Sharma, S.; Gandhi, B.K. Assessment of erosion wear in low specific speed Francis turbine due to particulate flow. Adv. Powder Technol. 2023, 34, 104065. [Google Scholar] [CrossRef]
- Wei, X.-Y.; Pei, J.; Wang, W.-Q.; Yu, Z.-F. Numerical study on sediment erosion characteristics of Francis turbine runner. Eng. Fail. Anal. 2024, 161, 108270. [Google Scholar] [CrossRef]
- Ghenaiet, A.; Tan, S.C.; Elder, R.L. Experimental investigation of an axial fan erosion and performance degradation. Proc. Inst. Mech. Eng. Part A J. Power Energy 2004, 218, 437–450. [Google Scholar] [CrossRef]
- Ghenaiet, A.; Tan, S.C.; Elder, R.L. Prediction of axial turbomachine performance degradation. Proc. Inst. Mech. Eng. Part A J. Power Energy 2005, 219, 273–287. [Google Scholar] [CrossRef]
- Ghenaiet, A. Study of sand particle trajectories and erosion into the first compression stage af a turbofan. J. Turbomach. 2012, 134, 051025. [Google Scholar] [CrossRef]
- Ghenaiet, A. Simulation of particle trajectories and erosion in a centrifugal compressor. J. Turbomach. 2012, 134, 051022. [Google Scholar] [CrossRef]
- Ghenaiet, A. Effects of solid particle ingestion through an hp turbine. In Proceedings of theASME TurboExpo, Glasgow, UK, 14–18 June 2020; Paper No. GT2012-69875. pp. 1583–1595. 13p. [Google Scholar] [CrossRef]
- Ghenaiet, A. Prediction of erosion in radial turbine components. In Proceedings of the ASME TurboExpo, Glasgow, UK, 14–18 June 2020; Paper No. GT2010-22419. pp. 1831–1846. 16p. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Mossinger, P.; Jester-Zuerker, R.; Jung, A. Investigation of different simulation approaches on a high-head Francis turbine and comparison with model test data: Francis-99. J. Phys. Conf. 2015, 579, 012005. [Google Scholar] [CrossRef]
- Fluent Theory, General Multiphase Models; Fluent Inc.: New York, NY, USA, 28 November 2001; Chapter 20.
- CFX-Pre User’s Guide, CFX-Solver Manager User’s Guide, Theory Guide; release R.16; Ansys Inc.: Canonsburg, PA, USA, 2015.
- Patankar, S.V.; Spalding, D.B.A. Calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transf. 1972, 15, 1778–1806. [Google Scholar] [CrossRef]
- Rhie, C.M.; Chow, W.L.A. Numerical study of the turbulent flow past an isolated airfoil with trailing edge separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
- White, F.M. Fluid Mechanics, 5th ed.; McGraw-Hill: Blacklick, OH, USA, 2003; p. 467. [Google Scholar]
- Elghobashi, S. On the Predicting Particle-Laden Turbulent Flows. Appl. Sci. Res. 1994, 52, 309–329. [Google Scholar] [CrossRef]
- Haider, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and non spherical particles. J. Powder Technol. 1989, 58, 63. [Google Scholar] [CrossRef]
- Thompson, T.L.; Clark, N.N. A holistic approach to particle drag prediction. Powder Technol. 1991, 67, 57–66. [Google Scholar] [CrossRef]
- Saffman, P. The lift on a small sphere in a slow shear flow. J. Fluid Mech. 1965, 22, 385–400. [Google Scholar] [CrossRef]
- Mei, R. An approximated Expression for the shear lift force on a spherical particle at finite Reynolds number. Int. J. Multiph. Flows 1992, 18, 145–147. [Google Scholar] [CrossRef]
- Gosman, A.D.; Ionnides, E. Aspects of computer simulation of liquid fuelled combustors. In Proceedings of the 19th Aerospace Science Meeting, St. Louis, MO, USA, 12–15 January 1981. Paper AIAA 81-0323. [Google Scholar]
- Brown, D.J.; Hutchinson, P. The interaction of solid or liquid and turbulent fluid flow fields—A numerical simulation. J. Fluids Eng. 1979, 101, 265–269. [Google Scholar] [CrossRef]
- Shirolkar, J.S.; Coimbra, C.F.M.; Queiroz, M.Q. Fundamental aspects of modeling turbulent particle dispersion in dilute flows. Prog. Energy Combust. Sci. 1996, 22, 363–399. [Google Scholar] [CrossRef]
- Tabakoff, W.; Hamed, A.; Murugan, D.M. Effect of target materials on the particle restitution characteristics for turbomachinery application. J. Propuls. Power 1996, 12, 260–266. [Google Scholar] [CrossRef]
- Grant, G.; Tabakoff, W. Erosion prediction in turbomachinery due to environmental solid particles. In Proceedings of the AIAA 12th Aerospace Sciences Meeting, Washington, DC, USA, 30 January–1 February 1974. AIAA Paper No 74-16. [Google Scholar]
- Ball, R.; Tabakoff, W. An Experimental Investigation of the Erosive Characteristics of 410 Stainless Steel and 6AL-4V Titanium. Report No 73-40, AD774325, December 1973. Available online: https://apps.dtic.mil/sti/citations/AD0774325 (accessed on 15 August 2025).
- Sangal, S.; Singhal, M.K.; Saini, R.P. CFD based analysis of silt erosion in Kaplan hydraulic turbine. In Proceedings of the International Conference on Signal Processing, Communication, Power and Embedded System, SCOPES 2016—Proceedings, Paralakhemundi, India, 3–5 October 2016; pp. 1765–1770. [Google Scholar] [CrossRef]
- Arora, N.; Kumar, A.; Singal, S.K. Hydro-abrasive erosion in Kaplan turbines: A case study. J. Hydroinform. 2024, 26, 2251. [Google Scholar] [CrossRef]
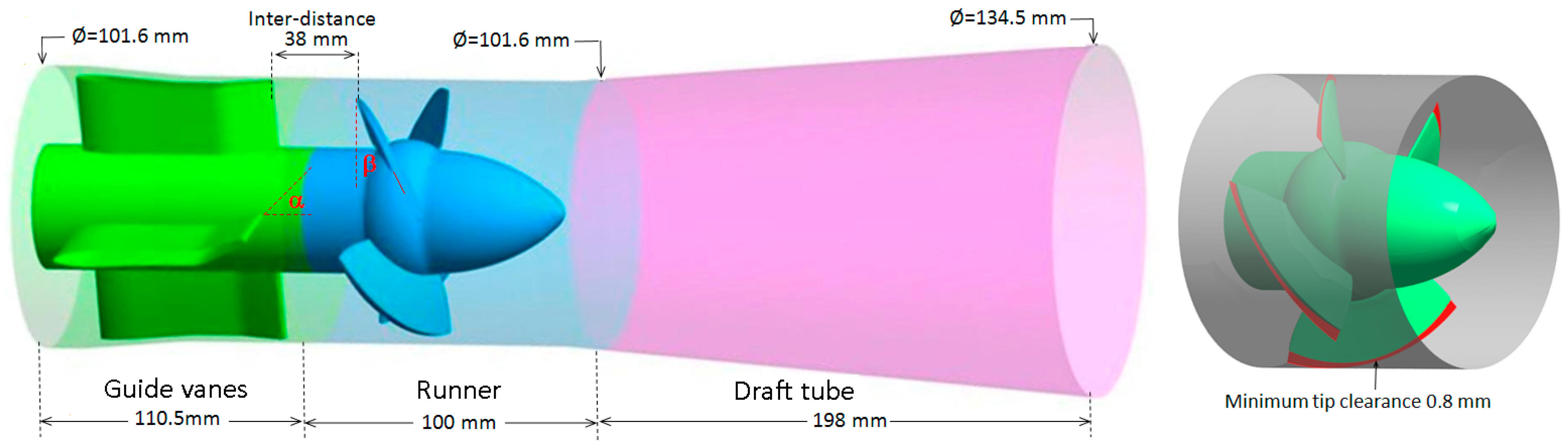
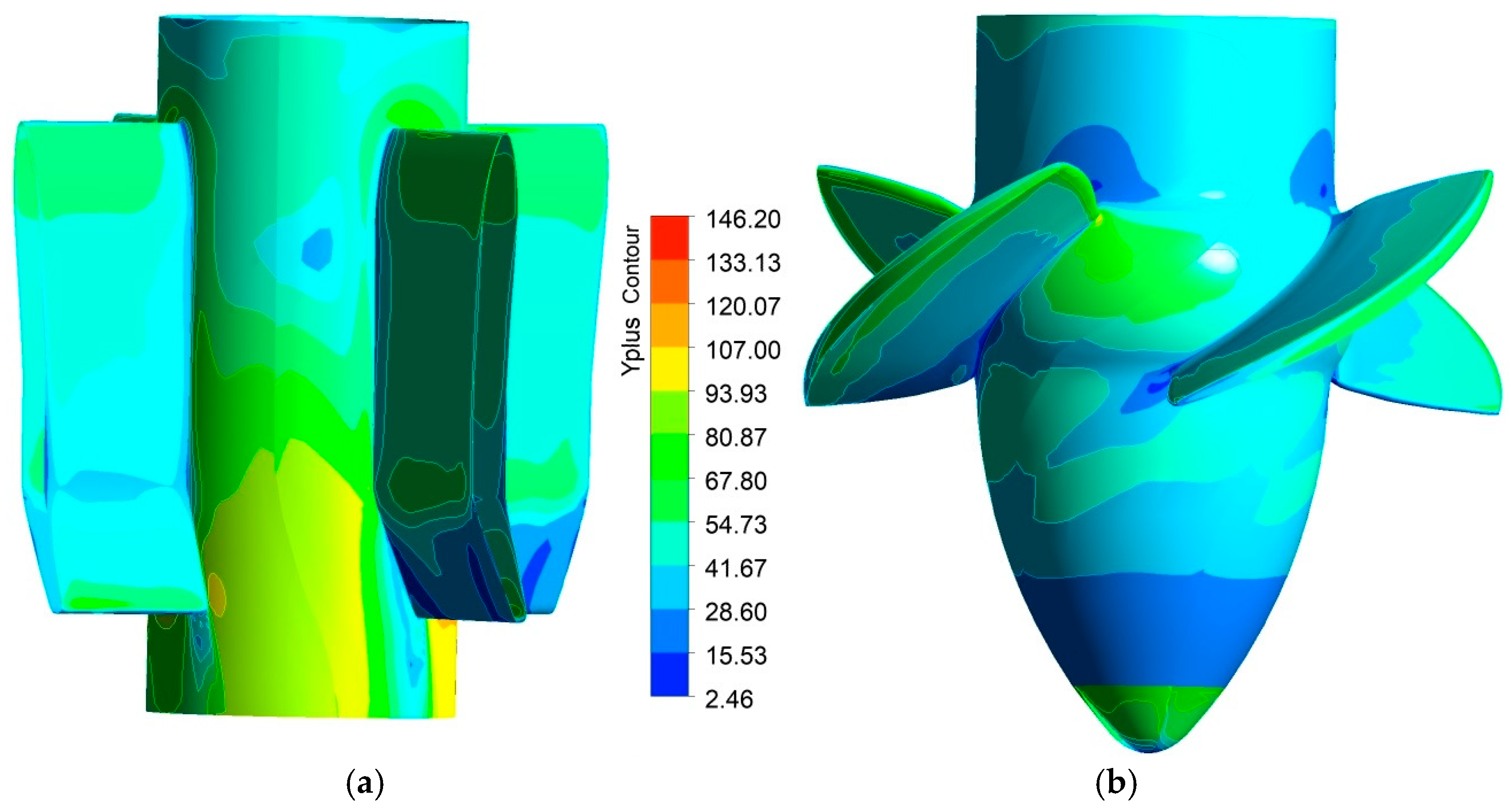
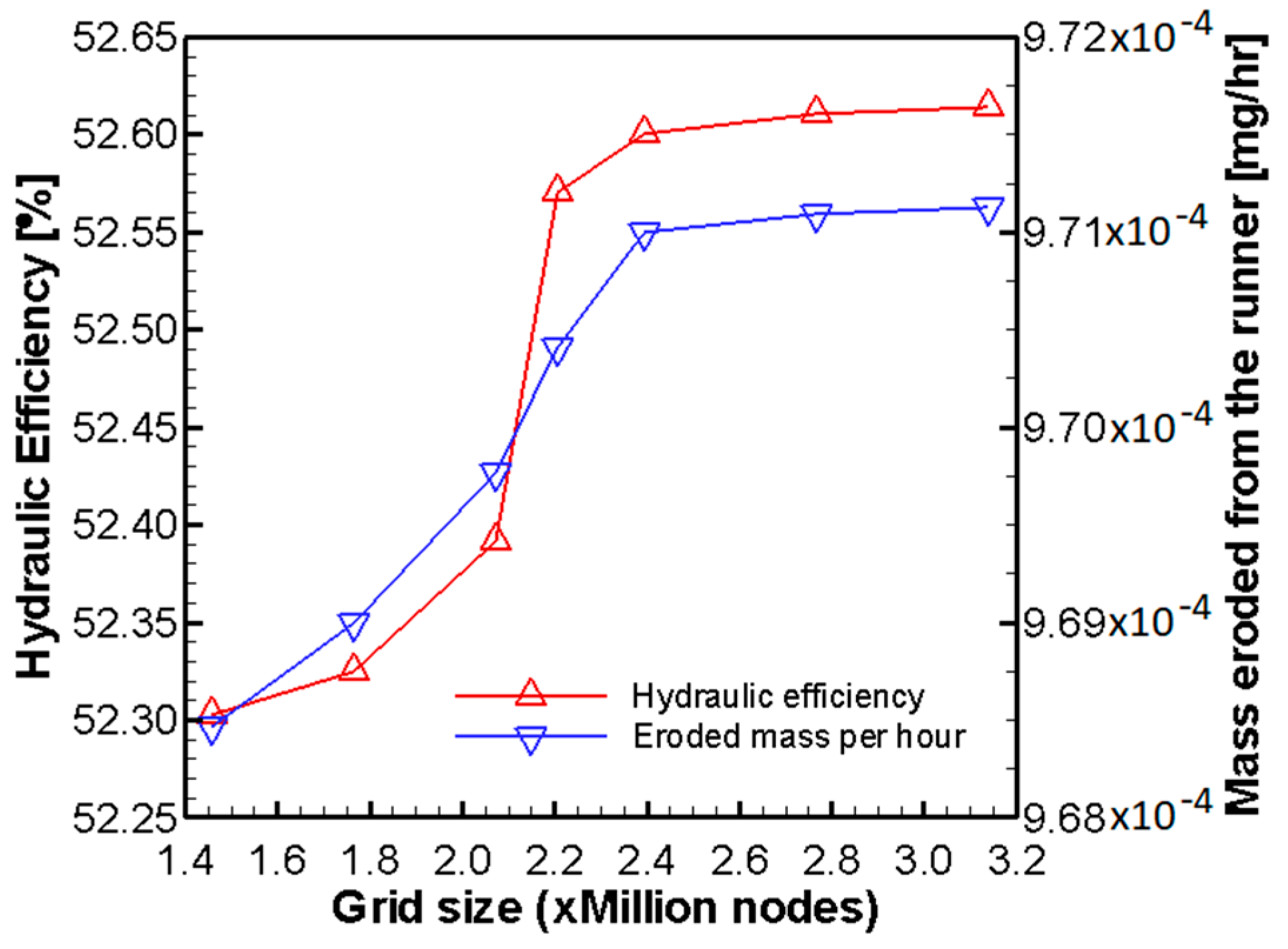





| Parameter | Value |
|---|---|
| Maximum speed (rpm) | 3680 |
| Nominal speed (rpm) | 2000 |
| Maximum power (kW) | 0.52 @ 2000 rpm |
| Maximum head (m) | 3.05 |
| Maximum flow rate (l/s) | 10–30 |
| Component | Parameter | Value |
|---|---|---|
| Distributor | Number of vanes | 4 |
| Hub/shroud diameter (mm) | 50/105.6 | |
| Chord (mm) | 78.3 | |
| Vane opening angle (deg) | 0–30 | |
| Rotor | Number of blades | 4 |
| Hub/tip diameter (mm) | 50/100 | |
| Tip clearance (mm) | 0.8 | |
| Mid span chord (mm) | 52.2 | |
| Blade setting angle (deg) | 10–30 |
| AERD (mg/s·mm2) EMPH (mg/hr) | Sediment concentration (mg/m3) | ||||||
| 50 | 100 | 500 | 1000 | 1500 | 2000 | 2500 | |
| Distributor vanes | |||||||
| AERD of vanes × 10−12 | 0.0687 | 0.1511 | 0.7692 | 1.5034 | 2.2652 | 3.0358 | 3.8148 |
| EMPH of vanes × 10−4 | 0.0449 | 0.0988 | 0.5031 | 0.9834 | 1.4817 | 1.9858 | 2.4953 |
| AERD of hub × 10−15 | 0.0998 | 0.2139 | 0.9592 | 1.8811 | 2.8152 | 3.5847 | 4.2055 |
| EMPH of hub × 10−7 | 0.0540 | 0.1158 | 0.5190 | 1.0178 | 1.5232 | 1.9396 | 2.2755 |
| AERD of shroud × 10−15 | 0.3496 | 0.4604 | 1.3284 | 2.9737 | 5.3967 | 6.9217 | 7.6279 |
| EMPH of shroud × 10−7 | 0.4367 | 0.5751 | 1.6595 | 3.7147 | 6.7416 | 8.6466 | 9.5288 |
| Runner | |||||||
| AERD of blades × 10−10 | 0.0173 | 0.0466 | 0.2442 | 0.4894 | 0.7309 | 0.9735 | 1.2008 |
| EMPH of blades × 10−3 | 0.0674 | 0.1814 | 0.9503 | 1.9048 | 2.8447 | 3.7887 | 4.6732 |
| AERD of hub+bulb × 10−14 | 0.1917 | 0.5901 | 2.3107 | 4.6344 | 6.6761 | 8.7632 | 10.6691 |
| EMPH of hub+bulb × 10−6 | 0.0938 | 0.2888 | 1.1310 | 2.2684 | 3.2678 | 4.2894 | 5.2223 |
| AERD of shroud × 10−12 | 0.0273 | 0.0553 | 0.2681 | 0.5445 | 0.8212 | 1.0891 | 1.3566 |
| EMPH of shroud × 10−4 | 0.0374 | 0.0758 | 0.3670 | 0.7455 | 1.1243 | 1.4911 | 1.8573 |
| Draft tube | |||||||
| AERD of draft tube × 10−15 | 0.1708 | 0.3170 | 1.5367 | 3.0859 | 4.6556 | 6.2267 | 7.7867 |
| EMPH of draft tube × 10−6 | 0.0473 | 0.0877 | 0.4254 | 0.8542 | 1.2887 | 1.7236 | 2.1554 |
| AERD (mg/s·mm2) EMPH (mg/hr) | Sediment concentration (mg/m3) | ||||||
| 50 | 100 | 500 | 1000 | 1500 | 2000 | 2500 | |
| Distributor vanes | |||||||
| AERD of vanes × 10−12 | 0.1064 | 0.2283 | 1.1350 | 2.2385 | 3.3817 | 4.5191 | 5.6864 |
| EMPH of vanes × 10−4 | 0.0696 | 0.1494 | 0.7426 | 1.4646 | 2.2126 | 2.9568 | 3.7205 |
| AERD of hub × 10−15 | 0.1293 | 0.2820 | 1.3214 | 2.7244 | 3.8186 | 5.0623 | 5.9313 |
| EMPH of hub × 10−7 | 0.0699 | 0.1526 | 0.7149 | 1.4740 | 2.0660 | 2.7388 | 3.2090 |
| AERD of shroud × 10−15 | 0.4740 | 0.6560 | 1.8829 | 5.0866 | 7.4208 | 9.5085 | 10.9766 |
| EMPH of shroud × 10−7 | 0.5921 | 0.8194 | 2.3520 | 6.3541 | 9.2699 | 11.8780 | 13.7120 |
| Runner | |||||||
| AERD of blades × 10−10 | 0.0495 | 0.0950 | 0.4796 | 0.9695 | 1.4717 | 1.9485 | 2.4206 |
| EMPH of blades × 10−3 | 0.1928 | 0.3699 | 1.8673 | 3.7739 | 5.7290 | 7.5849 | 9.4229 |
| AERD of hub+bulb × 10−14 | 0.2296 | 0.3308 | 1.7005 | 3.3369 | 4.9793 | 6.6979 | 8.2757 |
| EMPH of hub+bulb × 10−6 | 0.1124 | 0.1619 | 0.8324 | 1.6334 | 2.4374 | 3.2786 | 4.0509 |
| AERD of shroud × 10−12 | 0.0297 | 0.0580 | 0.2937 | 0.5924 | 0.8843 | 1.1851 | 1.4795 |
| EMPH of shroud × 10−4 | 0.0406 | 0.0794 | 0.4021 | 0.8111 | 1.2107 | 1.6225 | 2.0256 |
| Draft tube | |||||||
| AERD of draft tube × 10−15 | 0.0208 | 0.0433 | 0.2015 | 0.4110 | 0.6230 | 0.8386 | 1.0250 |
| EMPH of draft tube × 10−7 | 0.0576 | 0.1199 | 0.5579 | 1.1377 | 1.7246 | 2.3213 | 2.8372 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Published by MDPI on behalf of the EUROTURBO. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Ghenaiet, A. Simulating Sediment Erosion in a Small Kaplan Turbine. Int. J. Turbomach. Propuls. Power 2025, 10, 44. https://doi.org/10.3390/ijtpp10040044
Ghenaiet A. Simulating Sediment Erosion in a Small Kaplan Turbine. International Journal of Turbomachinery, Propulsion and Power. 2025; 10(4):44. https://doi.org/10.3390/ijtpp10040044
Chicago/Turabian StyleGhenaiet, Adel. 2025. "Simulating Sediment Erosion in a Small Kaplan Turbine" International Journal of Turbomachinery, Propulsion and Power 10, no. 4: 44. https://doi.org/10.3390/ijtpp10040044
APA StyleGhenaiet, A. (2025). Simulating Sediment Erosion in a Small Kaplan Turbine. International Journal of Turbomachinery, Propulsion and Power, 10(4), 44. https://doi.org/10.3390/ijtpp10040044





