Assessment of Large-Eddy Simulations to Simulate a High-Speed Low-Pressure Turbine Cascade †
Abstract
1. Introduction
2. SPLEEN Cascade Configuration
3. Numerical Methodology
3.1. Numerical Solver
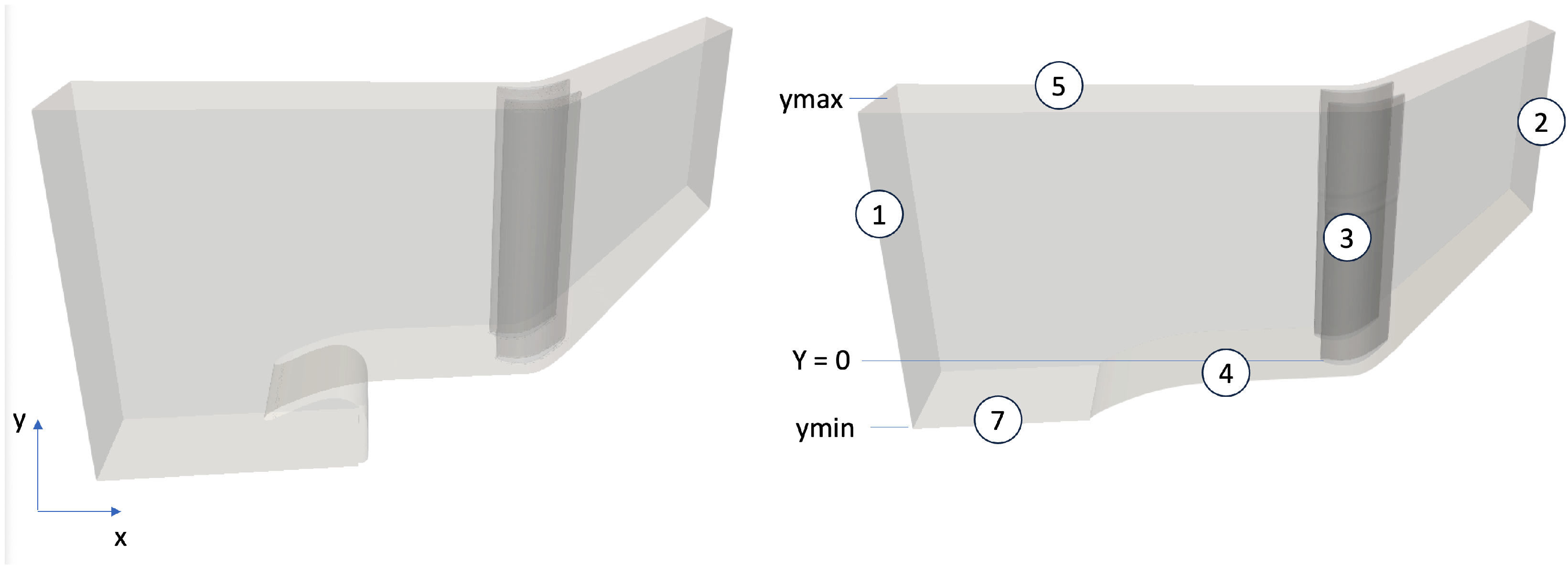
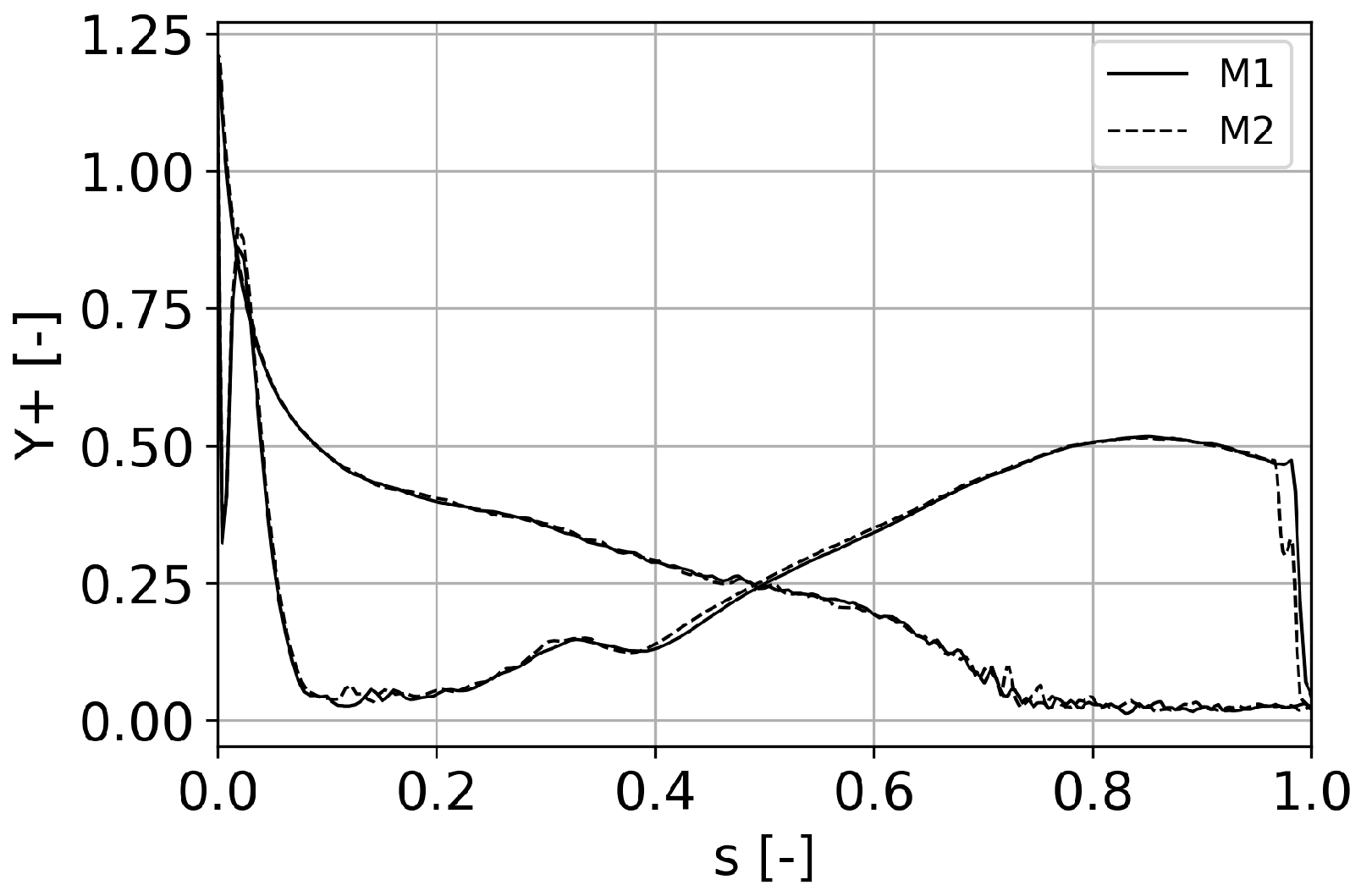
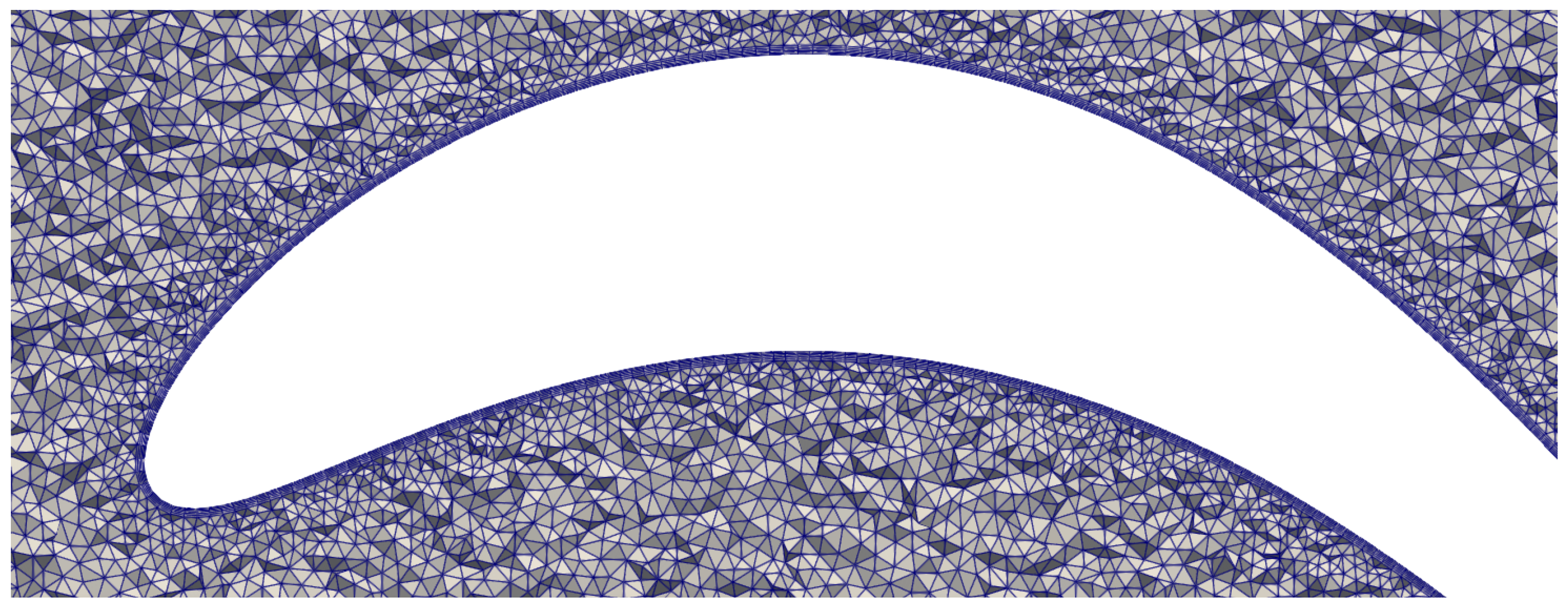
3.2. Computational Domain, Meshes, and Boundary Conditions
4. Results
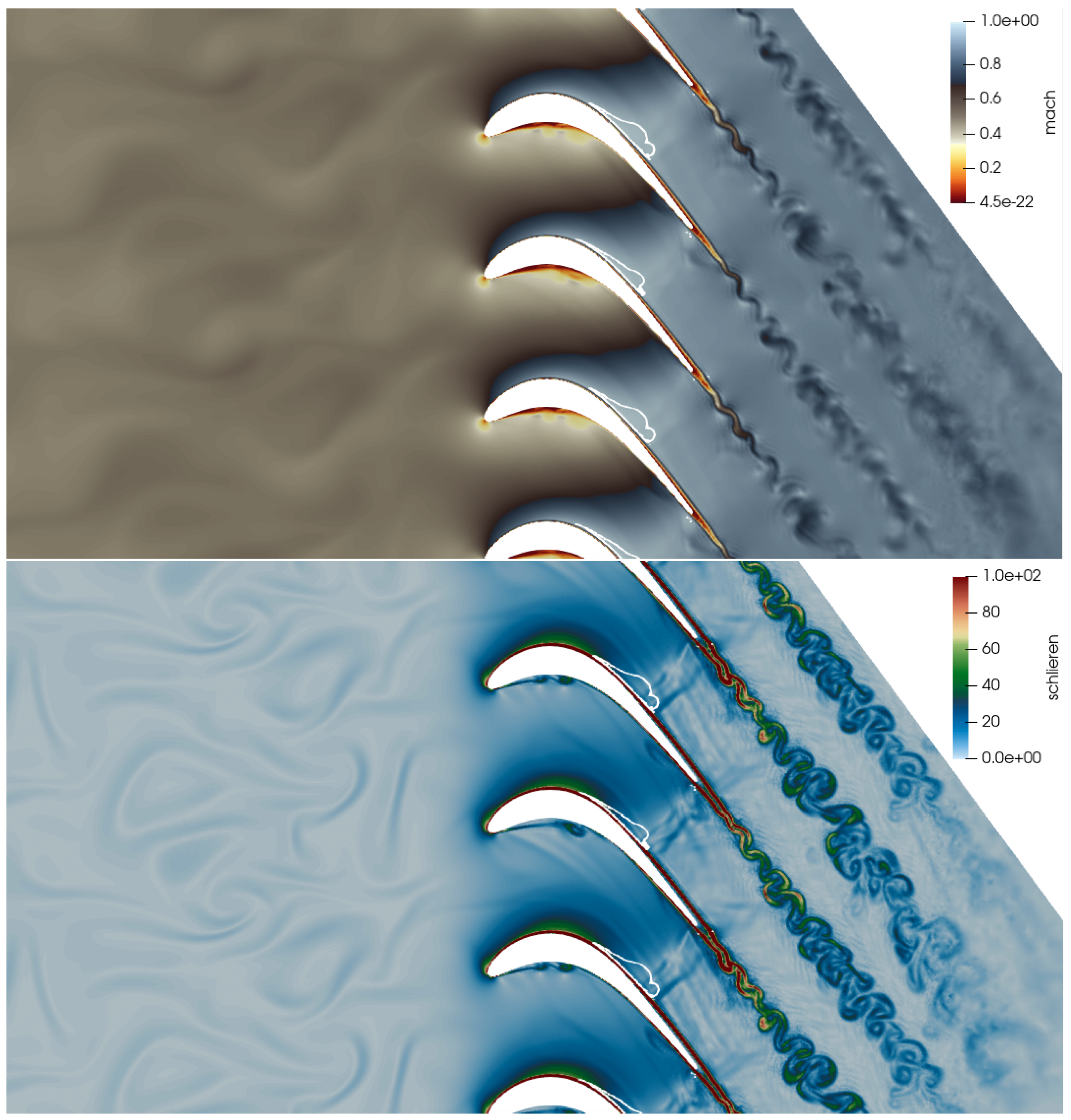
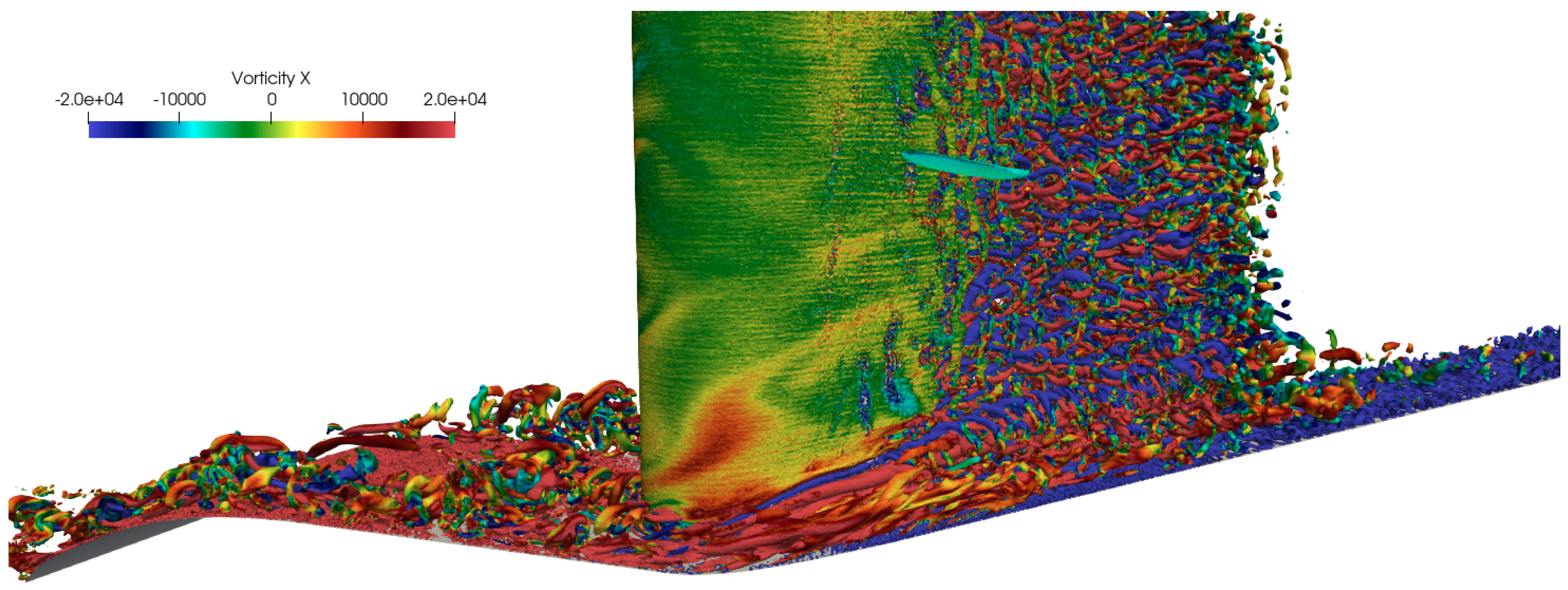
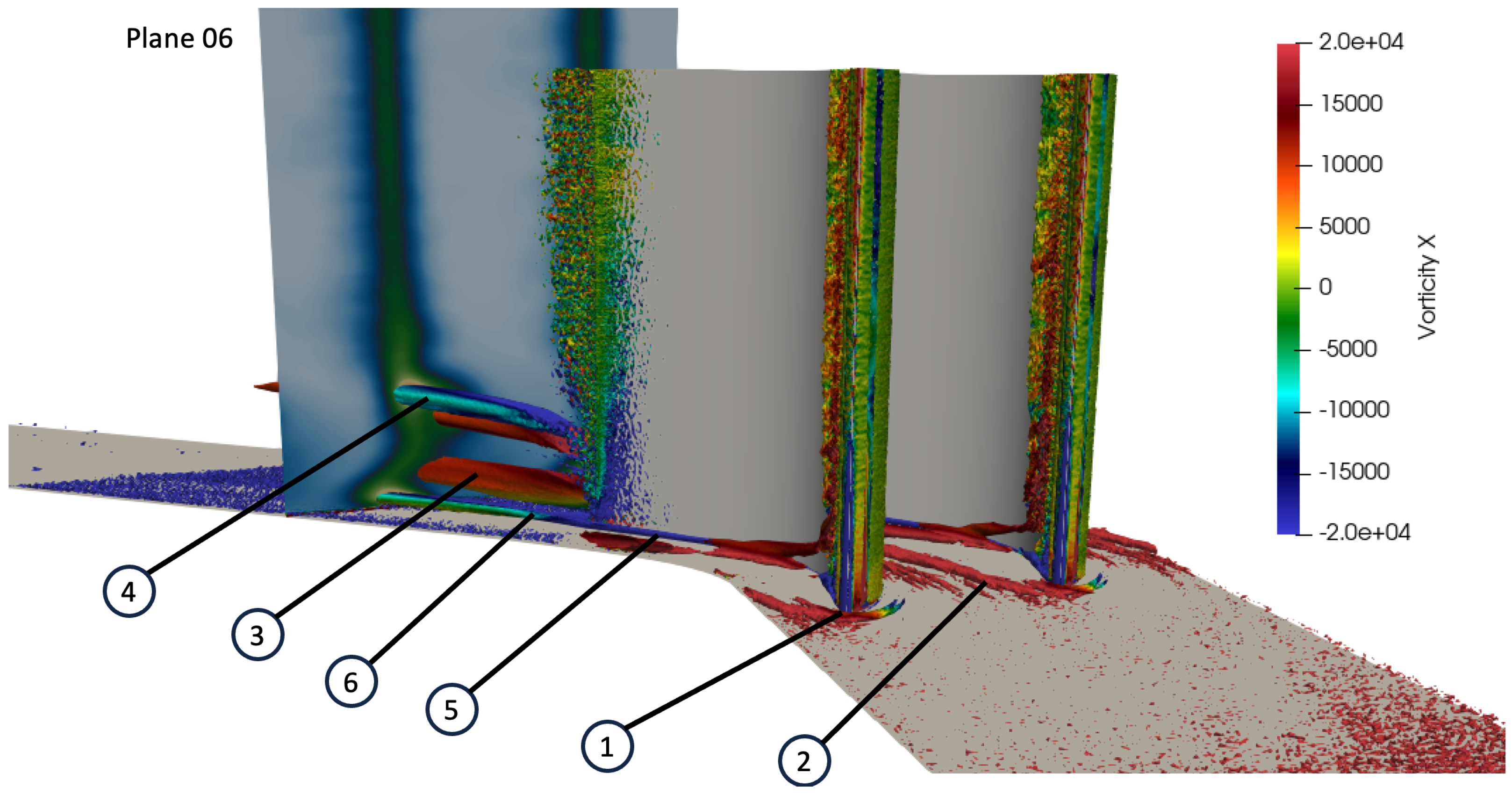
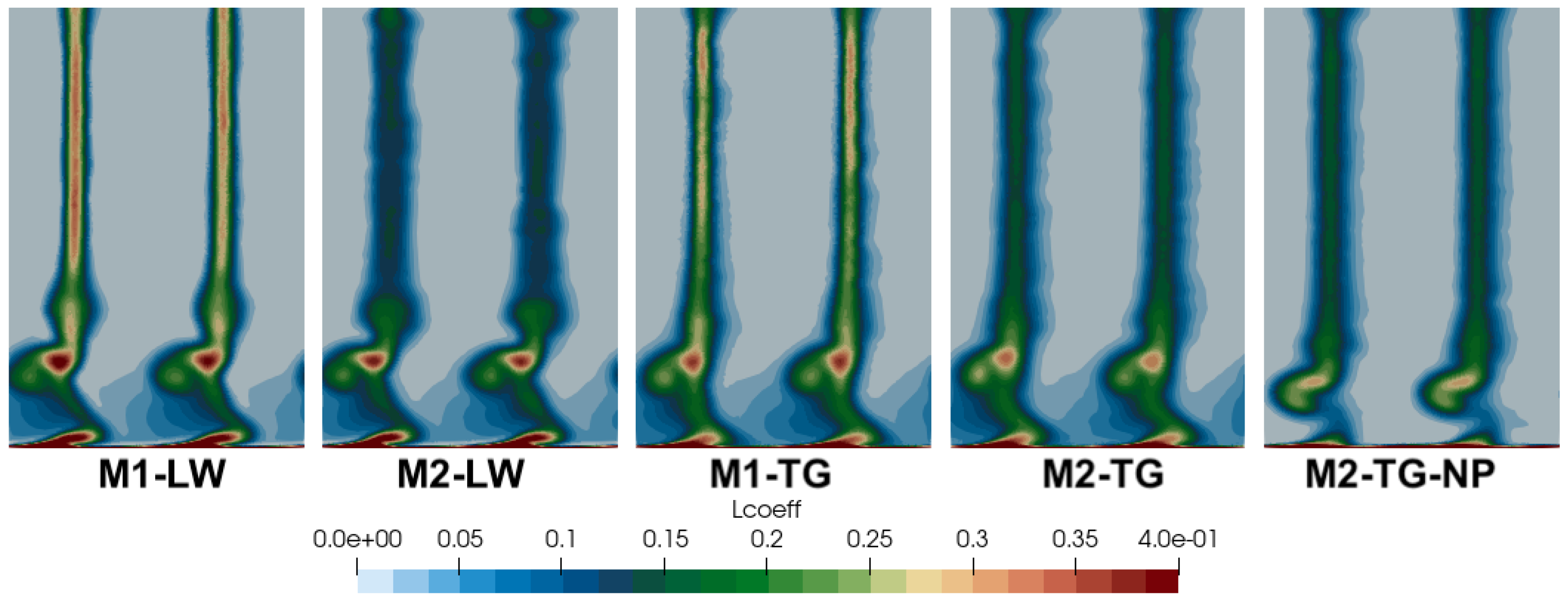
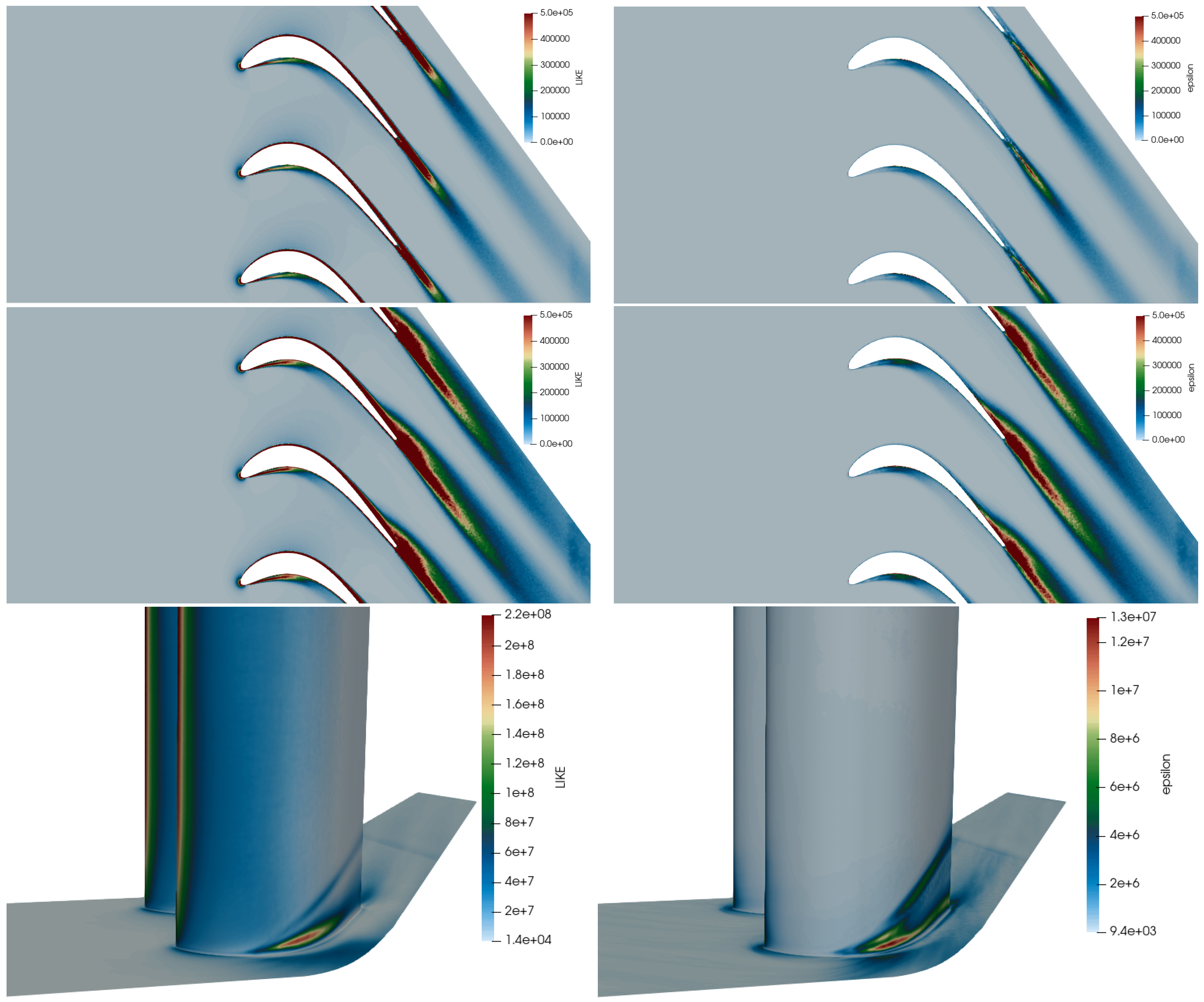
4.1. General Instantaneous Flow Organization
4.2. Time-Averaged Flow Features
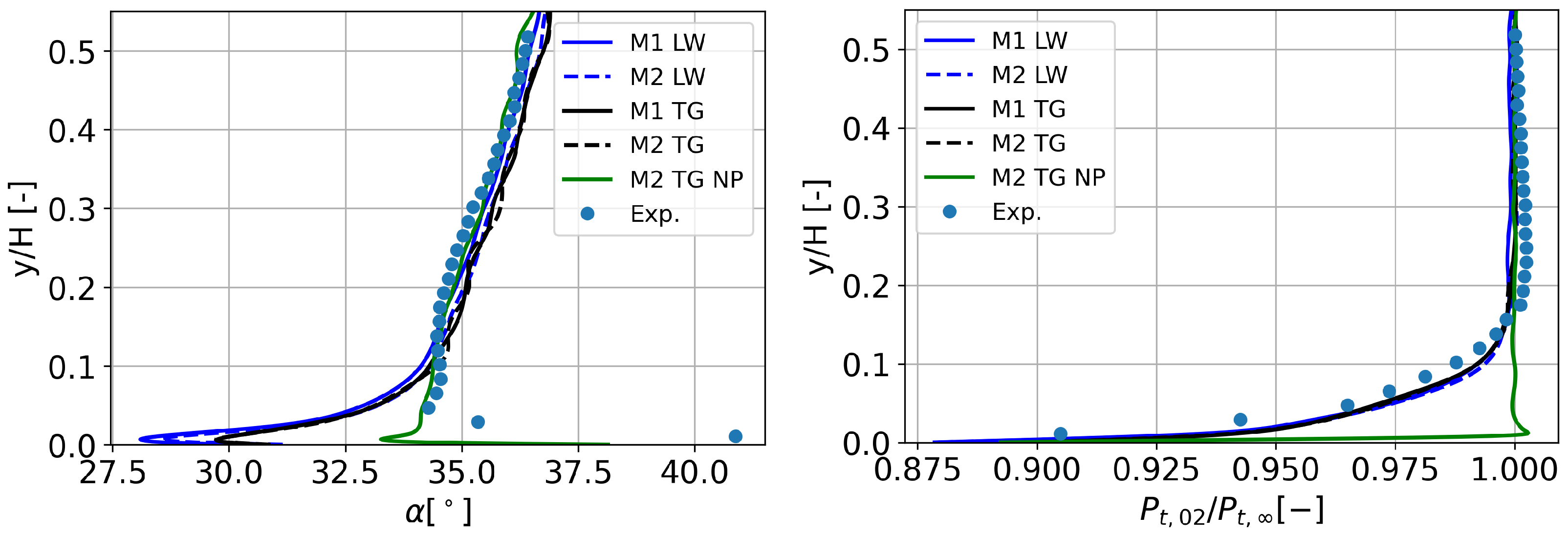
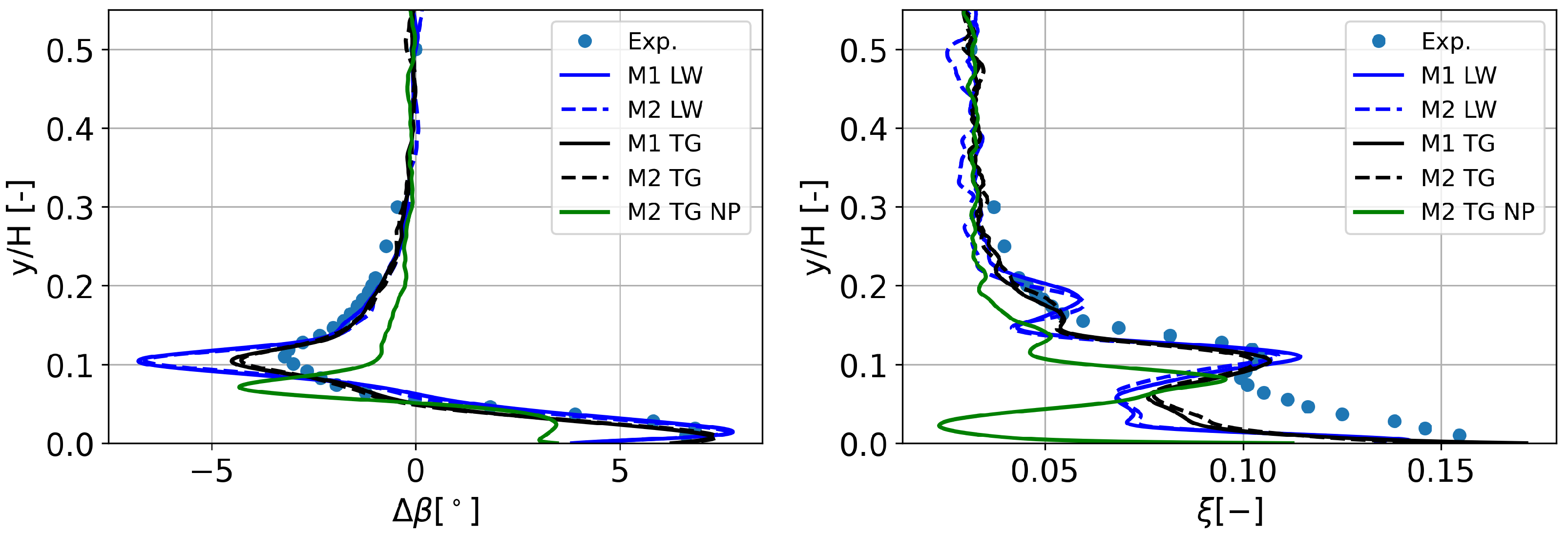
4.2.1. Flow Prediction at the Inlet of the Cascade
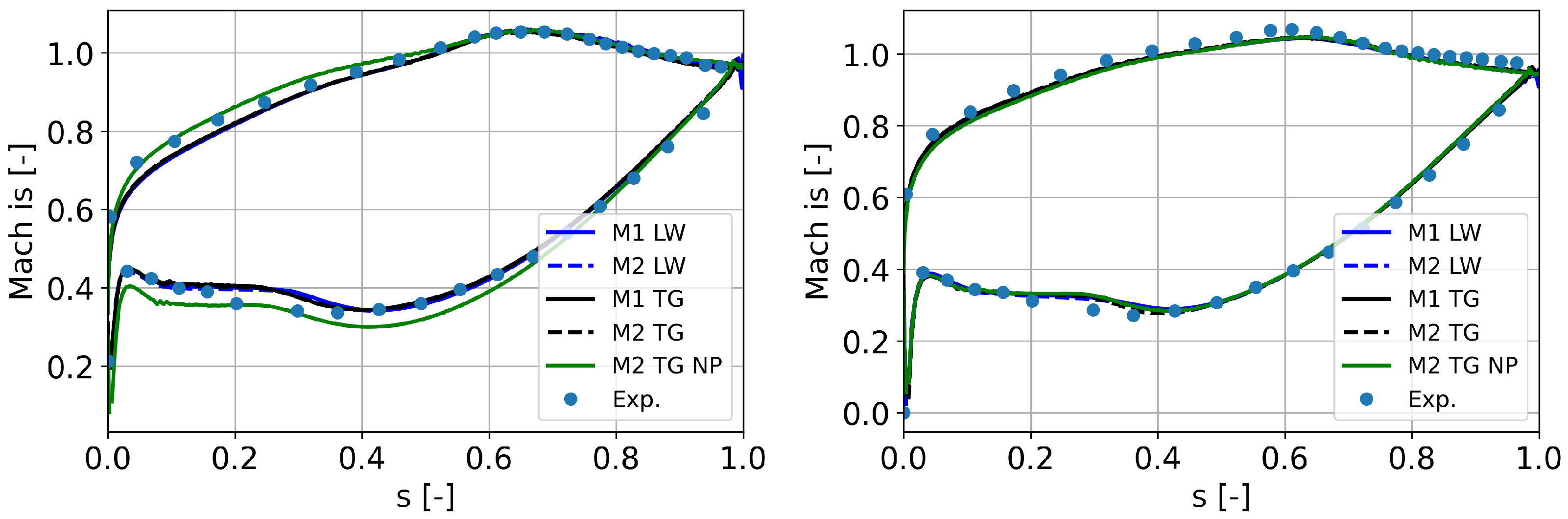
4.2.2. Flow Prediction in the Cascade Passage
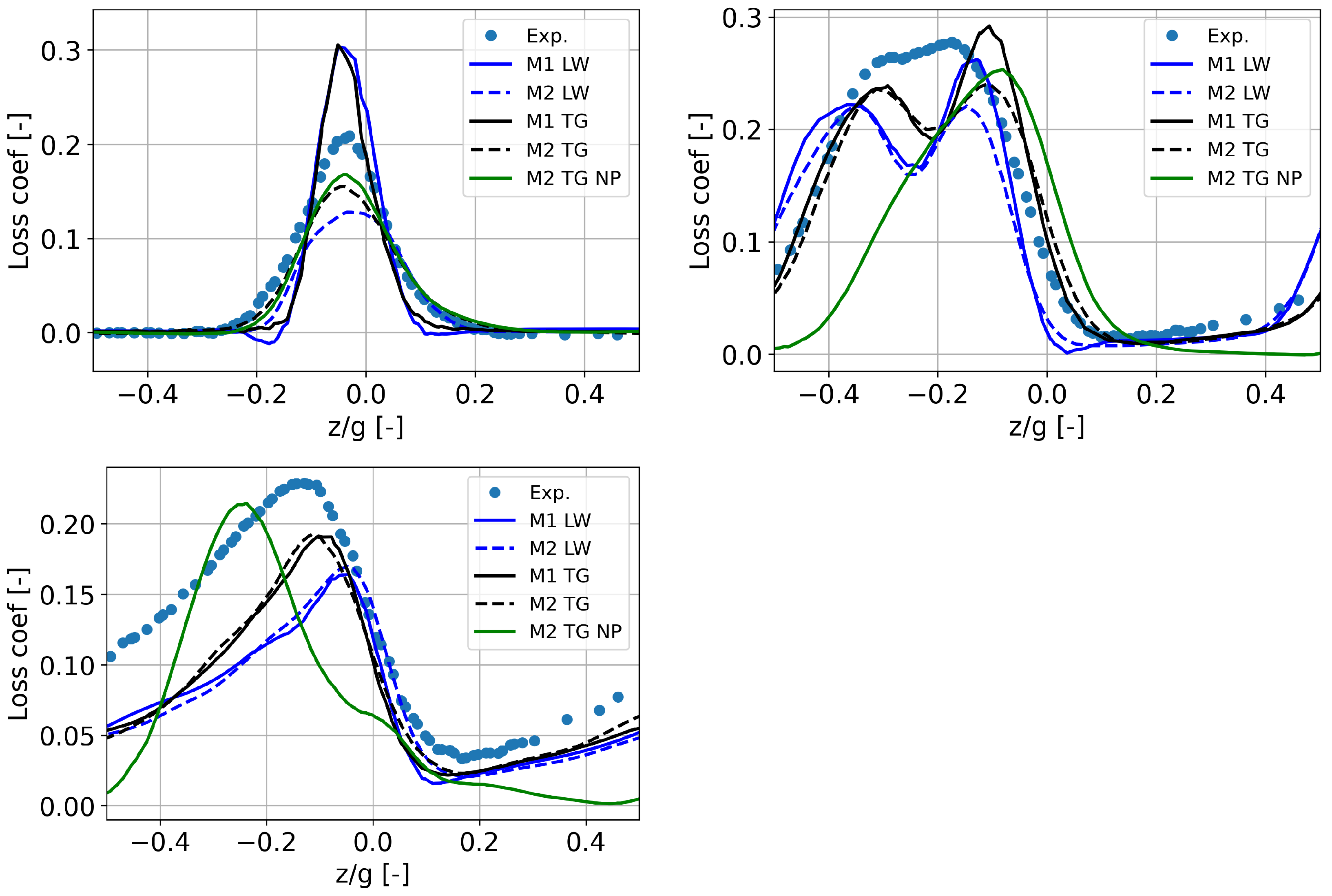
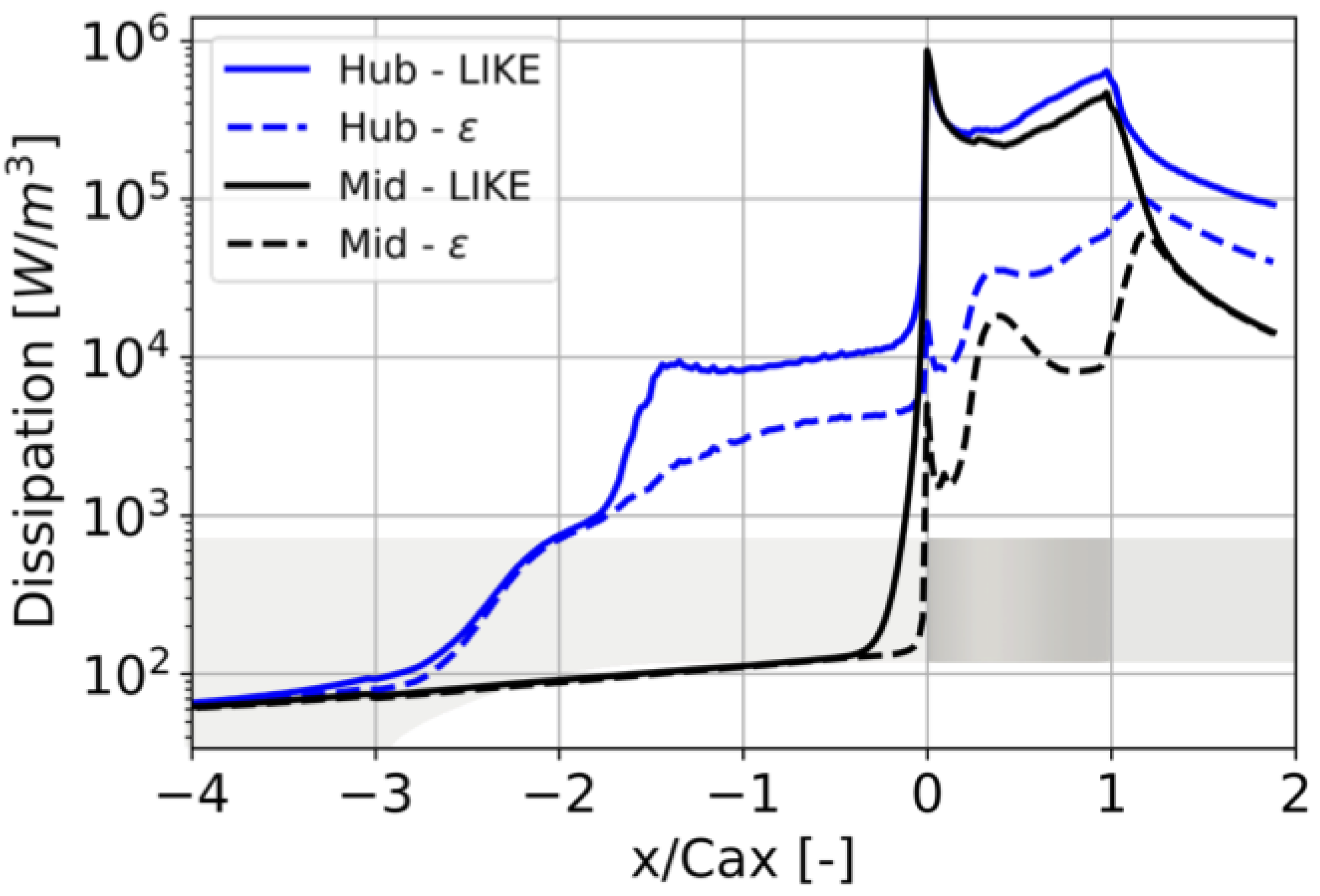
4.3. Loss Quantification in the Flow Passage
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duchaine, F.; Delon, X. Assessment of Large-Eddy Simulations to simulate a high-speed low-pressure turbine cascade. In Proceedings of the 16th European Conference on Turbomachinery Fluid dynamics & Thermodynamics, Hannover, Germany, 24–28 March 2025. Number ETC2025-292. [Google Scholar]
- Kurzke, J. Fundamental Differences Between Conventional and Geared Turbofans. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2009; Volume 1, pp. 145–153. [Google Scholar] [CrossRef]
- Kestner, B.K.; Schutte, J.S.; Gladin, J.C.; Mavris, D.N. Ultra High Bypass Ratio Engine Sizing and Cycle Selection Study for a Subsonic Commercial Aircraft in the N+2 Timeframe. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2011; Volume 1, pp. 127–137. [Google Scholar] [CrossRef]
- Johnson, B.V. Internal Air and Lubrication Systems. In Encyclopedia of Aerospace Engineering; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Steiner, M.; Zerobin, S.; Bauinger, S.; Heitmeir, F.; Göttlich, E. Development and Commissioning of a Purge Flow System in a Two Spool Test Facility. In Proceedings of the 12th European Conference on Turbomachinery Fluid Dynamics & Thermodynamics, Stockholm, Sweden, 3–7 April 2017; pp. 3–7. [Google Scholar]
- Moore, A. Gas Turbine Engine Internal Air Systems: A Review of the Requirements and the Problems. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 1975; p. V001T01A001. [Google Scholar] [CrossRef]
- Giovannini, M.; Rubechini, F.; Marconcini, M.; Arnone, A.; Bertini, F. Analysis of a LPT Rotor Blade for a Geared Engine: Part I — Aero-Mechanical Design and Validation. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2016; Volume 2B, p. V02BT38A053. [Google Scholar] [CrossRef]
- Pau, M.; Paniagua, G.; Delhaye, D.; de la Loma, A.; Ginibre, P. Aerothermal Impact of Stator-Rim Purge Flow and Rotor-Platform Film Cooling on a Transonic Turbine Stage. J. Turbomach. 2010, 132, 021006. [Google Scholar] [CrossRef]
- Léonard, T.; Gicquel, L.; Gourdain, N.; Duchaine, F. Steady/Unsteady Reynolds-Averaged Navier–Stokes and Large Eddy Simulations of a Turbine Blade at High Subsonic Outlet Mach Number. J. Turbomach. 2014, 137, 041001. [Google Scholar] [CrossRef]
- Troth, L.M.S. Multiphysics Coupled Simulations of Gas Turbines. Ph.D. Thesis, Institut National Polytechnique de Toulouse, Toulouse, France, 2017. [Google Scholar]
- Fiore, M.; Gourdain, N.; Boussuge, J.; Lippinois, E. Delineating Loss Sources Within a Linear Cascade With Upstream Cavity and Purge Flow. J. Turbomach. 2019, 141, 091008. [Google Scholar] [CrossRef]
- Denton, J.D. Loss Mechanisms in Turbomachines. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 1993; Volume 2, p. V002T14A001. [Google Scholar] [CrossRef]
- Gallier, K.D.; Lawless, P.B.; Fleeter, S. Development of the Unsteady Flow on a Turbine Rotor Platform Downstream of a Rim Seal. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2004; Volume 5, pp. 939–947. [Google Scholar] [CrossRef]
- Schäflein, L.; Janssen, J.; Brandies, H.; Jeschke, P.; Behre, S. Influence of Purge Flow Injection on the Performance of an Axial Turbine With Three-Dimensional Airfoils and Non-Axisymmetric Endwall Contouring. J. Turbomach. 2022, 145, 061004. [Google Scholar] [CrossRef]
- Hodson, H.P.; Howell, R.J. Bladerow Interactions, Transition, and High-Lift Aerofoils in Low-Pressure Turbines. Annu. Rev. Fluid Mech. 2005, 37, 71–98. [Google Scholar] [CrossRef]
- Fard Afshar, N.; Kozulovic, D.; Henninger, S.; Deutsch, J.; Bechlars, P. Turbulence Anisotropy Analysis at the Middle Section of a Highly Loaded 3D Linear Turbine Cascade Using Large Eddy Simulation. J. Glob. Power Propuls. Soc. 2023, 7, 71–84. [Google Scholar] [CrossRef] [PubMed]
- Boudin, A.; Dombard, J.; Duchaine, F.; Gicquel, L.; Odier, N.; Lavagnoli, S.; Lopes, G.; Simonassi, L. Analysis of rotor/stator interactions in a high-speed low-pressure turbine cascade using Large-Eddy Simulations. In Proceedings of the 15th European Conference on Turbomachinery Fluid dynamics & Thermodynamics, Budapest, Hungary, 24–28 April 2023. Number ETC2023-257. [Google Scholar]
- Hullin, L.; Gonzalez-Martino, I.; Bonnal, B. Unsteady Flow Simulations of a Transonic Low-Pressure Turbine Cascade. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2024; Volume 12B. [Google Scholar]
- Tene Hedje, P.; Bechane, Y.; Lavagnoli, S.; Bricteux, L. Wall Resolved Large-Eddy Simulations of High-Speed Low-Pressure Turbine Cascades. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2023; Volume 13B, p. V13BT30A005. [Google Scholar]
- Tene Hedje, P.; Bricteux, L.; Bechane, Y.; Lavagnoli, S. Large Eddy Simulations of a High-Speed Low-Pressure Turbine Cascade at Subsonic and Transonic Mach Numbers. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2024; Volume 12C. [Google Scholar]
- Perkins, D.W.; Duchaine, F. Large-Eddy Simulations of a High-Speed Low-Pressure Turbine Cascade With Purge Flow. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2024; Volume 12C. [Google Scholar]
- Lavagnoli, S.; Lopes, G.; Simonassi, L.; Torre, A.F.M. SPLEEN-High Speed Turbine Cascade—Test Case Database; Zenodo: Geneva, Switzerland, 2023. [Google Scholar] [CrossRef]
- Okada, M.; Simonassi, L.; Lopes, G.; Lavagnoli, S. PIV Measurements in a High-Speed Low-Reynolds Low-Pressure Turbine Cascade. In Proceedings of the ASME Turbo Expo 2023: Turbomachinery Technical Conference and Exposition, Boston, MA, USA, 26–30 June 2023. GT2023-102156. [Google Scholar]
- Pastorino, G.; Simonassi, L.; Lopes, G.; Boufidi, E.; Fontaneto, F.; Lavagnoli, S. Measurements of Turbulence in compressible Low-Density Flows at the Inlet of a Transonic Linear Cascade with and without Unsteady Wakes. J. Turbomach. 2024, 146, 071002. [Google Scholar] [CrossRef]
- Lopes, G.; Simonassi, L.; Lavagnoli, S. Time-Averaged Aerodynamics of a High-Speed Low-Pressure Turbine Cascade with Cavity Purge Flow and Unsteady Wakes. J. Turbomach. 2024, 146, 021008. [Google Scholar] [CrossRef]
- Lax, P.; Wendroff, B. Systems of Conservation Laws. Commun. Pure Appl. Math. 1960, 13, 217–237. [Google Scholar] [CrossRef]
- Quartapelle, L.; Selmin, V. High-order Taylor-Galerkin methods for nonlinear multidimensional problems. Finite Elem. Fluids 1993, 76, 46. [Google Scholar]
- Colin, O.; Benkenida, A.; Angelberger, C. 3d Modeling of Mixing, Ignition and Combustion Phenomena in Highly Stratified Gasoline Engines. Oil Gas Sci. Technol.-Rev. IFP 2003, 58, 47–62. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Dupuy, D.; Gicquel, L.; Odier, N.; Duchaine, F.; Arts, T. Analysis of the effect of intermittency in a high-pressure turbine blade. Phys. Fluids 2020, 32, 095101. [Google Scholar] [CrossRef]
- Poinsot, T. Boundary Conditions for Direct Simulations of Compressible Viscous Flows. J. Comput. Phys. 1992, 101, 104–129. [Google Scholar] [CrossRef]
- Granet, V.; Vermorel, O.; Léonard, T.; Gicquel, L.; Poinsot, T. Comparison of Nonreflecting Outlet Boundary Conditions for Compressible Solvers on Unstructured Grids. AIAA J. 2010, 48, 2348–2364. [Google Scholar] [CrossRef]
- Odier, N.; Sanjosé, M.; Gicquel, L.; Poinsot, T.; Moreau, S.; Duchaine, F. A Characteristic Inlet Boundary Condition for Compressible, Turbulent, Multispecies Turbomachinery Flows. Comput. Fluids 2019, 178, 41–55. [Google Scholar] [CrossRef]
- Roach, P. The Generation of Nearly Isotropic Turbulence by Means of Grids. Int. J. Heat Fluid Flow 1987, 8, 82–92. [Google Scholar] [CrossRef]
- Boudin, A. Turbulence Injection Methods for Large-Eddy Simulations; Working Note; Cerfacs-ISAE SUPAERO: Toulouse, France, 2021. [Google Scholar]
- Passot, T.; Pouquet, A. Numerical Simulation of Compressible Homogeneous Flows in the Turbulent Regime. J. Fluid Mech. 1987, 181, 441–466. [Google Scholar] [CrossRef]
- Langston, L.S. Secondary Flows in Axial Turbines—A Review. Ann. N. Y. Acad. Sci. 2001, 934, 11–26. [Google Scholar] [CrossRef] [PubMed]



| Boundary Condition | Flow Quantity Imposed | Values |
|---|---|---|
| Inlet | Total pressure | 9000 Pa |
| Total temperature | 300 K | |
| Inlet yaw angle | 40.2° | |
| Outlet | Static pressure | 5323.3 Pa |
| Left | Periodicity | – |
| Right | Periodicity | – |
| Shroud Wall | Slip adiabatic wall | – |
| Hub Wall | No-slip adiabatic wall | – |
| Blades | No-slip adiabatic wall | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the EUROTURBO. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Duchaine, F.; Delon, X. Assessment of Large-Eddy Simulations to Simulate a High-Speed Low-Pressure Turbine Cascade. Int. J. Turbomach. Propuls. Power 2025, 10, 21. https://doi.org/10.3390/ijtpp10030021
Duchaine F, Delon X. Assessment of Large-Eddy Simulations to Simulate a High-Speed Low-Pressure Turbine Cascade. International Journal of Turbomachinery, Propulsion and Power. 2025; 10(3):21. https://doi.org/10.3390/ijtpp10030021
Chicago/Turabian StyleDuchaine, Florent, and Xavier Delon. 2025. "Assessment of Large-Eddy Simulations to Simulate a High-Speed Low-Pressure Turbine Cascade" International Journal of Turbomachinery, Propulsion and Power 10, no. 3: 21. https://doi.org/10.3390/ijtpp10030021
APA StyleDuchaine, F., & Delon, X. (2025). Assessment of Large-Eddy Simulations to Simulate a High-Speed Low-Pressure Turbine Cascade. International Journal of Turbomachinery, Propulsion and Power, 10(3), 21. https://doi.org/10.3390/ijtpp10030021






