An Automated Load Restoration Approach for Improving Load Serving Capabilities in Smart Urban Networks
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Contributions
- Proposing a fast and accurate MIQCP model for load restoration for distribution networks with multiple DGs;
- Optimal network reconfiguration to maximize critical load restoration by assigning the grid-forming units for each islanded MG;
- Improving the functionality of the EMS for both grid-connected and islanded mode operation by optimal network reconfiguration with minimum switching actions in the network.
1.4. Paper Organization
2. Multi-Purpose Model for Optimal Operation of MGs
3. MG Operation Problem Formulation
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Indices: | |
| Index for scenarios | |
| Indexes for buses | |
| Index for branches | |
| Sets: | |
| Set of distributed generators | |
| Set of scenarios | |
| Set of branches | |
| Set of buses | |
| Set of substation buses | |
| Parameters: | |
| Hourly cost of distributed generator | |
| Hourly cost at substation bus | |
| Resistance of branch | |
| Reactance of branch | |
| Impedance magnitude of the branch | |
| Current capacity limit of the branch | |
| , | Minimum/maximum of node voltage magnitude |
| Reference voltage of grid-forming unit | |
| Active/reactive power demand at bus | |
| Active/reactive power limit of the branch | |
| Active/apparent power limit of unit | |
| Minimum/maximum reactive power limit of unit | |
| Load curtailment cost for active power | |
| Load curtailment cost for reactive power | |
| Load serving/restoration priority | |
| Probability of scenario | |
| Continuous variables: | |
| Current magnitude of branch | |
| , | Active/reactive power flows through branch |
| , | Active/reactive power generations of unit |
| , | Active/reactive power load shedding at bus |
| Active/reactive power loss of branch | |
| Voltage magnitude at bus | |
| Slack voltage variable for grid-forming unit | |
| Binary variables: | |
| Status of the load shedding at bus | |
| Status of the unit | |
| Status of the link | |
| Auxiliary variable representing the flow direction | |
References
- Javadi, M.S.; Nezhad, A.E.; Gough, M.; Lotfi, M.; Anvari-Moghaddam, A.; Nardelli, P.H.J.; Sahoo, S.; Catalão, J.P.S. Conditional Value-at-Risk Model for Smart Home Energy Management Systems. e-Prime—Adv. Electr. Eng. Electron. Energy 2021, 1, 100006. [Google Scholar] [CrossRef]
- Rao, R.S.; Ravindra, K.; Satish, K.; Narasimham, S.V.L. Power Loss Minimization in Distribution System Using Network Reconfiguration in the Presence of Distributed Generation. IEEE Trans. Power Syst. 2013, 28, 317–325. [Google Scholar] [CrossRef]
- Salau, A.O.; Gebru, Y.W.; Bitew, D. Optimal Network Reconfiguration for Power Loss Minimization and Voltage Profile Enhancement in Distribution Systems. Heliyon 2020, 6, e04233. [Google Scholar] [CrossRef]
- Agarwal, U.; Jain, N. Reconfiguration of Radial Distribution Network for Reliability Enhancement Considering Renewal Energy Sources. In Proceedings of the International Conference on Electrical and Electronics Engineering, ICE3 2020, Gorakhpur, India, 14–15 February 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 162–167. [Google Scholar]
- Li, X.; Xia, Q. Stochastic Optimal Power Flow with Network Reconfiguration: Congestion Management and Facilitating Grid Integration of Renewables. In Proceedings of the 2020 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Chicago, IL, USA, 12–15 October 2020. [Google Scholar]
- Noruzi Azghandi, M.; Shojaei, A.A.; Toosi, S.; Lotfi, H. Optimal Reconfiguration of Distribution Network Feeders Considering Electrical Vehicles and Distributed Generators. Evol. Intell. 2021, 16, 49–66. [Google Scholar] [CrossRef]
- Kianmehr, E.; Nikkhah, S.; Vahidinasab, V.; Giaouris, D.; Taylor, P.C. A Resilience-Based Architecture for Joint Distributed Energy Resources Allocation and Hourly Network Reconfiguration. IEEE Trans. Ind. Inform. 2019, 15, 5444–5455. [Google Scholar] [CrossRef]
- Gutiérrez-Alcaraz, G.; Galván, E.; González-Cabrera, N.; Javadi, M.S. Renewable Energy Resources Short-Term Scheduling and Dynamic Network Reconfiguration for Sustainable Energy Consumption. Renew. Sustain. Energy Rev. 2015, 52, 256–264. [Google Scholar] [CrossRef]
- Gazijahani, F.S.; Salehi, J. Robust Design of Microgrids with Reconfigurable Topology under Severe Uncertainty. IEEE Trans. Sustain. Energy 2018, 9, 559–569. [Google Scholar] [CrossRef]
- Hamidpour, H.; Pirouzi, S.; Safaee, S.; Norouzi, M.; Lehtonen, M. Multi-Objective Resilient-Constrained Generation and Transmission Expansion Planning against Natural Disasters. Int. J. Electr. Power Energy Syst. 2021, 132, 107193. [Google Scholar] [CrossRef]
- Cicilio, P.; Swartz, L.; Vaagensmith, B.; Rieger, C.; Gentle, J.; McJunkin, T.; Cotilla-Sanchez, E. Electrical Grid Resilience Framework with Uncertainty. Electr. Power Syst. Res. 2020, 189, 106801. [Google Scholar] [CrossRef]
- Hossain, E.; Roy, S.; Mohammad, N.; Nawar, N.; Dipta, D.R. Metrics and Enhancement Strategies for Grid Resilience and Reliability during Natural Disasters. Appl. Energy 2021, 290, 116709. [Google Scholar] [CrossRef]
- Beyza, J.; Yusta, J.M. The Effects of the High Penetration of Renewable Energies on the Reliability and Vulnerability of Interconnected Electric Power Systems. Reliab. Eng. Syst. Saf. 2021, 215, 107881. [Google Scholar] [CrossRef]
- Niu, G.; Wei, X.; Wu, M.; Kou, L.; Lin, J.; Li, Y. Dynamic Power Service Restoration Method for Distribution Network with Distributed Generation Penetration. Energy Rep. 2020, 6, 792–796. [Google Scholar] [CrossRef]
- Liu, W.; Chen, Y.; Ding, F. Distributed Generator-Based Distribution System Service Restoration Strategy and Model-Free Control Methods. Glob. Energy Interconnect. 2021, 4, 126–135. [Google Scholar] [CrossRef]
- Faria, W.R.; Carvalho, E.O.P.; Dantas, L.B.; Maciel, C.D.; Alberto, L.F.C.; London, J.B.A.; Pereira, B.R. Service Restoration in Modern Distribution Systems Addressing Grid-Connected and Islanded Operations. Electr. Power Syst. Res. 2021, 196, 107238. [Google Scholar] [CrossRef]
- Huang, G.; Wang, J.; Chen, C.; Qi, J.; Guo, C. Integration of Preventive and Emergency Responses for Power Grid Resilience Enhancement. IEEE Trans. Power Syst. 2017, 32, 4451–4463. [Google Scholar] [CrossRef]
- Zhang, B.; Dehghanian, P.; Kezunovic, M. Optimal Allocation of PV Generation and Battery Storage for Enhanced Resilience. IEEE Trans. Smart Grid 2019, 10, 535–545. [Google Scholar] [CrossRef]
- Prakash, K.; Islam, F.R.; Mamun, K.A.; Pota, H.R. Configurations of Aromatic Networks for Power Distribution System. Sustainability 2020, 12, 4317. [Google Scholar] [CrossRef]
- Abessi, A.; Shirazi, E.; Jadid, S.; Shafie-Khah, M. Sustainable and Resilient Smart House Using the Internal Combustion Engine of Plug-in Hybrid Electric Vehicles. Sustainability 2020, 12, 6046. [Google Scholar] [CrossRef]
- Zahraoui, Y.; Alhamrouni, I.; Mekhilef, S.; Reyasudin Basir Khan, M.; Seyedmahmoudian, M.; Stojcevski, A.; Horan, B. Energy Management System in Microgrids: A Comprehensive Review. Sustainability 2021, 13, 10492. [Google Scholar] [CrossRef]
- Khan, S.N.; Kazmi, S.A.A.; Altamimi, A.; Khan, Z.A.; Alghassab, M.A. Smart Distribution Mechanisms—Part I: From the Perspectives of Planning. Sustainability 2022, 14, 16308. [Google Scholar] [CrossRef]
- Vita, V.; Fotis, G.; Pavlatos, C.; Mladenov, V. A New Restoration Strategy in Microgrids after a Blackout with Priority in Critical Loads. Sustainability 2023, 15, 1974. [Google Scholar] [CrossRef]
- Garcia, E.; Águila, A.; Ortiz, L.; Carrión, D. Optimal Resource Assignment in Hybrid Microgrids Based on Demand Response Proposals. Sustainability 2024, 16, 1797. [Google Scholar] [CrossRef]
- Kasimalla, S.R.; Park, K.; Zaboli, A.; Hong, Y.; Choi, S.L.; Hong, J. An Evaluation of Sustainable Power System Resilience in the Face of Severe Weather Conditions and Climate Changes: A Comprehensive Review of Current Advances. Sustainability 2024, 16, 3047. [Google Scholar] [CrossRef]
- Lotfi, H.; Hajiabadi, M.E.; Parsadust, H. Power Distribution Network Reconfiguration Techniques: A Thorough Review. Sustainability 2024, 16, 10307. [Google Scholar] [CrossRef]
- Hassan, K.; Trireksani, T.; Hussain, A.; Kim, H.-M. A Rule-Based Modular Energy Management System for AC/DC Hybrid Microgrids. Sustainability 2025, 17, 867. [Google Scholar] [CrossRef]
- Kanchana, K.; Murali Krishna, T.; Yuvaraj, T.; Sudhakar Babu, T. Enhancing Smart Microgrid Resilience Under Natural Disaster Conditions: Virtual Power Plant Allocation Using the Jellyfish Search Algorithm. Sustainability 2025, 17, 1043. [Google Scholar] [CrossRef]
- Li, B.; Chen, Y.; Wei, W.; Huang, S.; Mei, S. Resilient Restoration of Distribution Systems in Coordination with Electric Bus Scheduling. IEEE Trans. Smart Grid 2021, 12, 3314–3325. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, C.C.; Schneider, K.P.; Tuffner, F.K.; Ton, D.T. Microgrids for Service Restoration to Critical Load in a Resilient Distribution System. IEEE Trans. Smart Grid 2018, 9, 426–437. [Google Scholar] [CrossRef]
- Oboudi, M.H.; Mohammadi, M.; Rastegar, M. Resilience-Oriented Intentional Islanding of Reconfigurable Distribution Power Systems. J. Mod. Power Syst. Clean Energy 2019, 7, 741–752. [Google Scholar] [CrossRef]
- Sedgh, S.A.; Doostizadeh, M.; Aminifar, F.; Shahidehpour, M. Resilient-Enhancing Critical Load Restoration Using Mobile Power Sources with Incomplete Information. Sustain. Energy Grids Netw. 2021, 26, 100418. [Google Scholar] [CrossRef]
- Home Ortiz, J.M.; Melgar-Dominguez, O.D.; Javadi, M.S.; Santos, S.F.; Mantovani, J.R.S.; Catalão, J.P.S. Distribution Systems Resilience Improvement Utilizing Multiple Operational Resources. In Proceedings of the 21st IEEE International Conference on Environment and Electrical Engineering and 2021 5th IEEE Industrial and Commercial Power System Europe, EEEIC/I and CPS Europe, Bari, Italy, 7–10 September 2021. [Google Scholar] [CrossRef]
- Mishra, S.; Das, D.; Paul, S. A Comprehensive Review on Power Distribution Network Reconfiguration. Energy Syst. 2016, 8, 227–284. [Google Scholar] [CrossRef]
- Shakeri Kahnamouei, A.; Lotfifard, S. Enhancing Resilience of Distribution Networks by Coordinating Microgrids and Demand Response Programs in Service Restoration. IEEE Syst. J. 2021, 16, 3048–3059. [Google Scholar] [CrossRef]
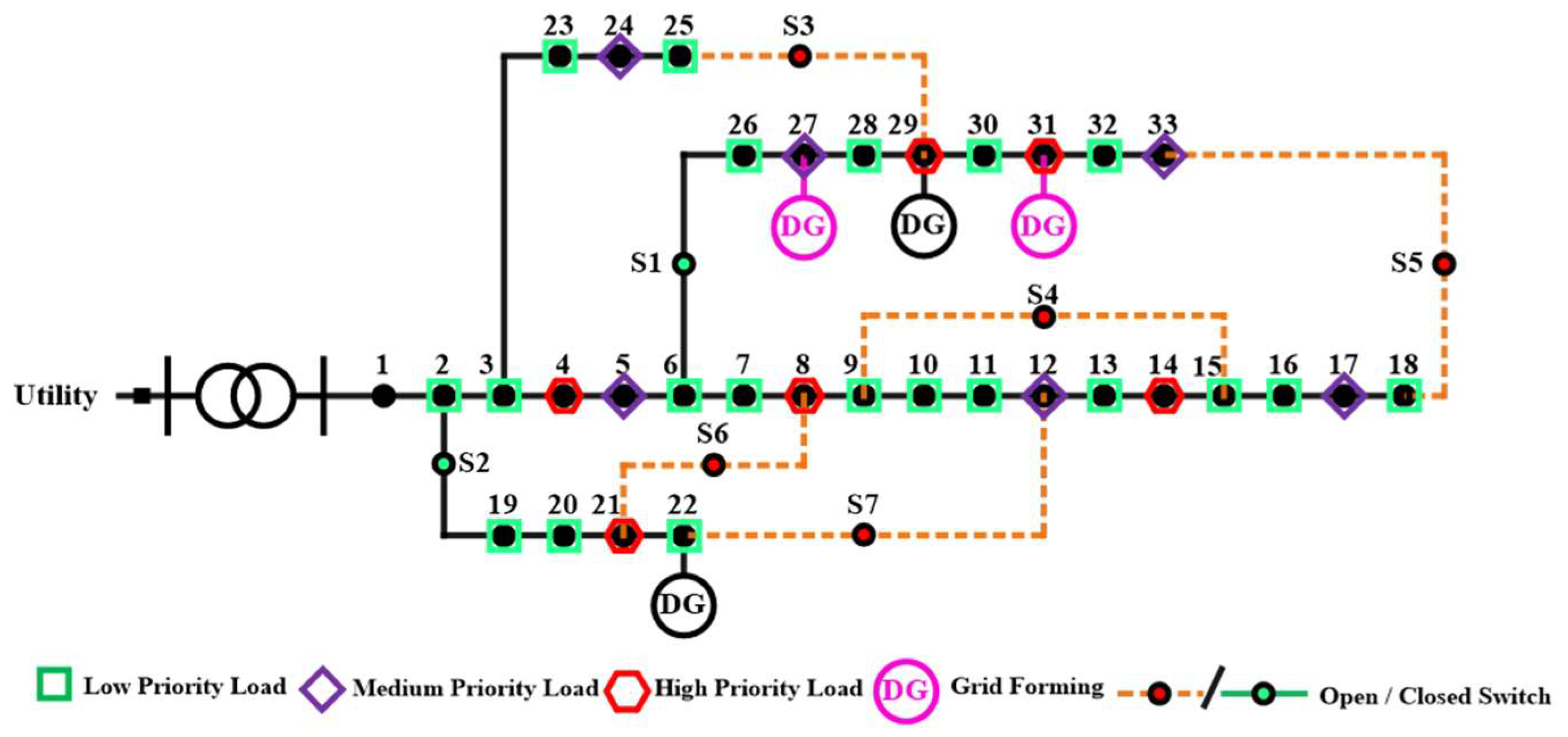
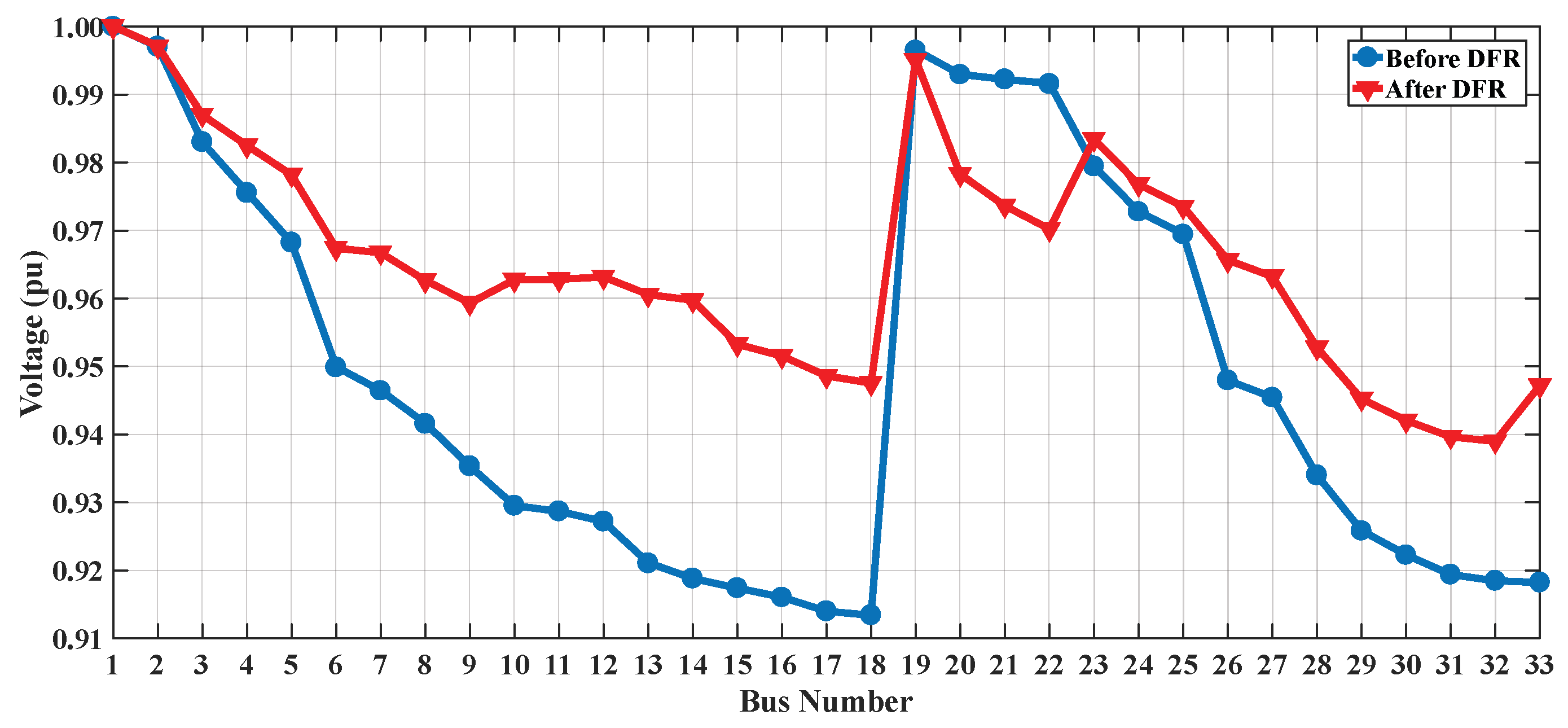
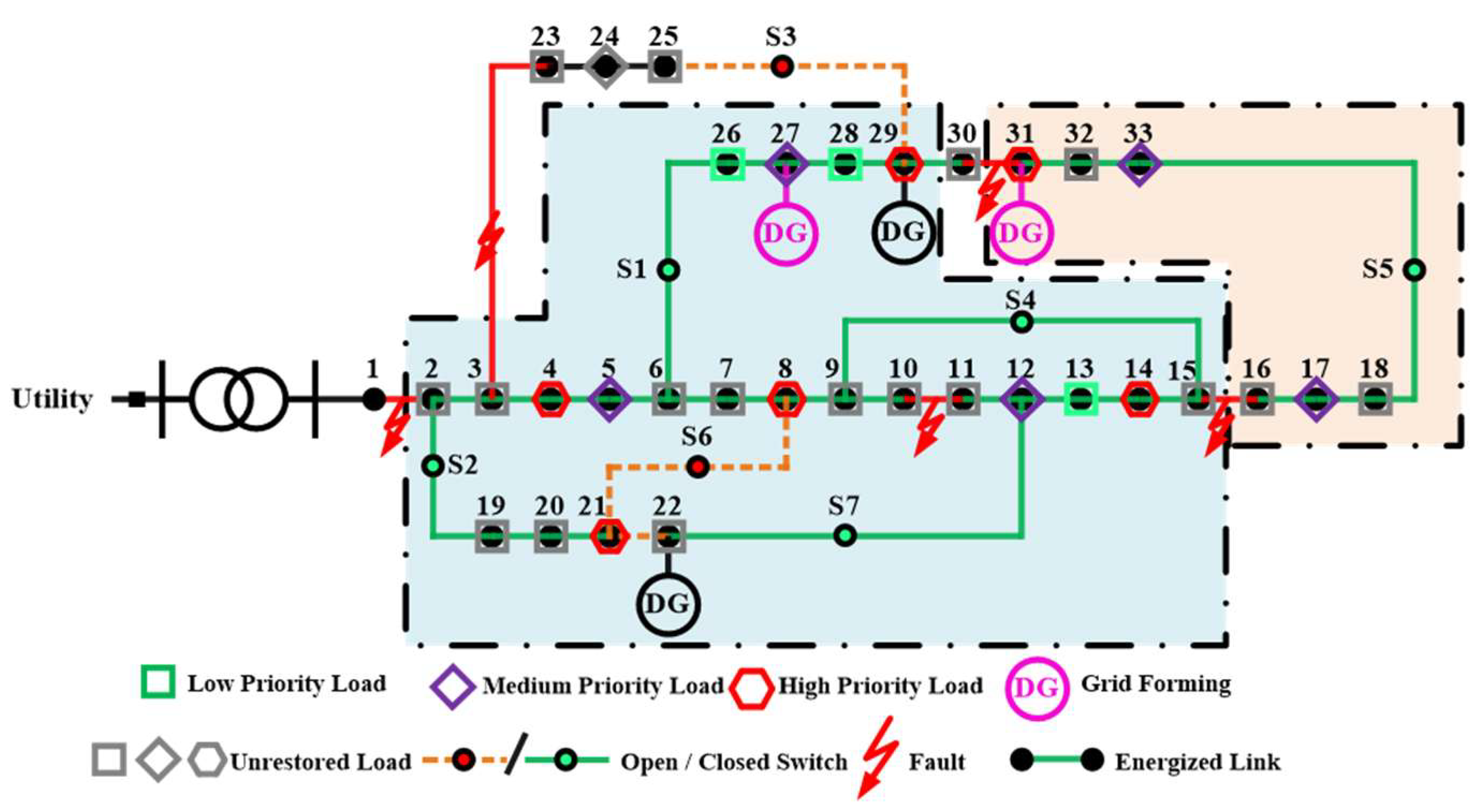
| Unit | Bus | (kW) | (kVAr) | (kVAr) | (kVA) | ($/kWh) |
|---|---|---|---|---|---|---|
| Utility | 1 | 4000 | −3000 | +3000 | 5000 | 0.010 |
| DG 1 | 22 | 100 | −50 | 50 | 100 | 0.005 |
| DG 2 | 27 | 630 | −450 | 450 | 630 | 0.005 |
| DG 3 | 29 | 425 | −300 | 300 | 425 | 0.005 |
| DG 4 | 31 | 300 | −220 | 220 | 300 | 0.005 |
| Unit | MG | (kW) | (kVAr) | Loading (%) | (kW) | (kVAr) |
|---|---|---|---|---|---|---|
| DG 1 | 1 | 86.690 | 49.836 | 100 | 1010 | 540 |
| DG 2 | 555.956 | 296.300 | 100 | |||
| DG 3 | 372.501 | 197.771 | 99.2 | |||
| DG 4 | 2 | 270.104 | 130.128 | 99.9 | 270 | 130 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esmaeel Nezhad, A.; Javadi, M.S.; Ghanavati, F.; Tavakkoli Sabour, T. An Automated Load Restoration Approach for Improving Load Serving Capabilities in Smart Urban Networks. Urban Sci. 2025, 9, 255. https://doi.org/10.3390/urbansci9070255
Esmaeel Nezhad A, Javadi MS, Ghanavati F, Tavakkoli Sabour T. An Automated Load Restoration Approach for Improving Load Serving Capabilities in Smart Urban Networks. Urban Science. 2025; 9(7):255. https://doi.org/10.3390/urbansci9070255
Chicago/Turabian StyleEsmaeel Nezhad, Ali, Mohammad Sadegh Javadi, Farideh Ghanavati, and Toktam Tavakkoli Sabour. 2025. "An Automated Load Restoration Approach for Improving Load Serving Capabilities in Smart Urban Networks" Urban Science 9, no. 7: 255. https://doi.org/10.3390/urbansci9070255
APA StyleEsmaeel Nezhad, A., Javadi, M. S., Ghanavati, F., & Tavakkoli Sabour, T. (2025). An Automated Load Restoration Approach for Improving Load Serving Capabilities in Smart Urban Networks. Urban Science, 9(7), 255. https://doi.org/10.3390/urbansci9070255







