1. Introduction
Reinforced concrete (RC) churches built in Italy throughout the 20th century represent a significant portion of the nation’s cultural infrastructure. While these structures were initially conceived with modern materials and architectural ambitions, their seismic performance has become a growing concern due to aging, design irregularities, and lack of detailed structural documentation. Historically, churches also serve a dual function, not only as places of worship but also as community anchors during post-disaster recovery. This dual role underscores the necessity of ensuring seismic resilience, not just for structural preservation but for maintaining societal continuity.
While several studies have addressed the vulnerability of masonry churches, simplified evaluation frameworks for RC churches remain scarce. Conventional methods, such as nonlinear time-history analysis or finite element modeling, are often impractical due to missing construction data and computational demands. Recent literature [
1,
2,
3] has highlighted the need for low-data assessment tools. This study addresses this gap by adapting classical mechanics and limit state theory into a unified, simplified methodology tailored to RC churches with cathedral portal frames.
The innovation lies not only in the simplification of mechanics but also in its application at the community scale, where traditional tools are too resource-intensive. This dual-scale applicability both at building and community level, represents a key innovation of the proposed approach.
Italy’s high seismicity, evidenced in regions such as Irpinia, L’Aquila, and Emilia Romagna, has highlighted the vulnerability of both masonry and RC churches) [
4,
5]. Unlike masonry structures, RC churches—especially those with basilica plans—often exhibit irregular geometries, tall naves, and non-ductile detailing. One recurring structural configuration is the “cathedral portal” frame, a simple yet widely used design consisting of inclined beams and repeated portal frames in the transverse direction. Despite its prevalence, this configuration introduces specific seismic vulnerabilities, particularly in the absence of rigid diaphragms and in the presence of high center-of-mass conditions. Masi [
6] performed a seismic vulnerability assessment of gravity-load-designed RC frames typical of mid-20th century Italian buildings, highlighting the high risk associated with structures and the influence of infill configuration on overall seismic performance.
Conventional seismic assessment methods, such as Finite Element Modeling (FEM) or nonlinear time-history analysis, require extensive data and computational expertise, limiting their applicability for large-scale assessments. Several researchers have proposed performance-based methods and local failure mechanisms for masonry churches [
1,
2,
3], but relatively fewer studies address RC churches with simplified, data-efficient models. This gap is particularly relevant for heritage inventories lacking structural drawings or material records.
To address this challenge, the present study proposes a simplified methodology for evaluating the seismic vulnerability of RC churches characterized by the cathedral portal frame. The approach combines linear and nonlinear static analysis, plastic limit theory, and capacity spectrum methods to generate a vulnerability index using minimal input data. The framework is calibrated with a real-world case study (Reggio Calabria Cathedral) and validated with an application to a typical church in Naples. Designed for rapid deployment, especially in data-scarce conditions, the model serves as a screening tool to prioritize retrofitting and risk mitigation efforts.
Beyond their architectural and historical significance, reinforced concrete churches also serve as critical community landmarks. In the aftermath of seismic events, these buildings often act as informal gathering spaces or aid distribution centers, further underscoring the need to assess their seismic safety not only as isolated structures but as essential components of community-level resilience [
7,
8].
In practice, churches are frequently used as emergency shelters and community hubs following seismic events. Therefore, their seismic resilience is closely tied to the strength of the surrounding population. This dual role, as cultural artifacts and functional infrastructure, requires a tailored approach to vulnerability assessment that goes beyond conventional engineering practices [
9].
One of the central challenges in assessing seismic risk for heritage buildings lies in the lack of detailed structural documentation, particularly for older RC churches. This makes traditional FEM-based approaches resource-intensive and impractical for large-scale applications. The proposed methodology addresses this gap by offering a low-data, high-impact alternative for preliminary vulnerability screening. In doing so, it contributes to a broader urban resilience strategy, where safeguarding cultural infrastructure also means supporting social continuity during crises [
10,
11,
12].
The PERPETUATE guidelines provide a performance-based framework for assessing seismic vulnerability of heritage masonry structures through displacement-based methods and appropriate modeling strategies for complex architectural forms [
10].
This paper also discusses the potential integration of AI and machine learning techniques as a future development to extend the model’s scalability and predictive power. By focusing on a typologically recurrent structural form, the methodology offers a replicable and practical solution for assessing the seismic safety of RC churches, an area where traditional analysis methods fall short due to resource and data constraints.
Recent studies on seismic assessment and retrofitting of cultural heritage structures, including masonry and reinforced concrete (RC) churches, have significantly contributed to advancing our understanding of their seismic behavior and vulnerability. Investigations such as those by Tzanakis et al. [
13], Hadzima-Nyarko et al. [
14], and Almassri and Safiyeh [
15] have highlighted the critical role of numerical modeling in evaluating structural performance and retrofitting interventions. Research on seismic retrofitting techniques, including grout injection and RC jacketing, has proven effective in mitigating structural vulnerabilities while preserving architectural integrity.
Moreover, contributions like Sferrazza Papa et al. [
16] focus on the role of roofing interventions in seismic performance, emphasizing the trade-offs between timber and reinforced concrete roofs. Davis et al. [
17] provide practical insights into meso-scale seismic collapse analyses for historic masonry churches, addressing challenges posed by low-magnitude seismicity. Similarly, pragmatic approaches proposed by researchers like Amarantidou et al. [
18] and Cianchino et al. [
19] integrate soil–structure interaction (SSI) effects and address the complex interplay between original construction methods and modern retrofitting measures. These works collectively shed light on optimizing interventions for seismic safety and cultural preservation [
20].
2. Reinforced Concrete Churches
2.1. General
Between the end of the nineteenth century and the first half of the twentieth century, the architecture of churches proposed new themes essentially linked to the innovations of building techniques and the use of modern construction materials (reinforced concrete, steel, glass, etc.) and in-depth study of technical solutions (visibility, lighting, acoustics, etc.). Even the construction of churches is in abundance in Italy; nevertheless, there is no specific style or configuration. Architects still lack nostalgic forms, uselessly pursued with simplifications, and the contributions of contemporary architecture. The first twenty years of the twentieth century saw the birth of modern architecture based on the explicit use of reinforced concrete structures. The expressive and technical significance of this material marked the most significant architectural achievements of the twentieth century. It allows you to create objects of any shape and size, allowing one to overcome nature’s limits [
21,
22].
2.2. Classification Proposal
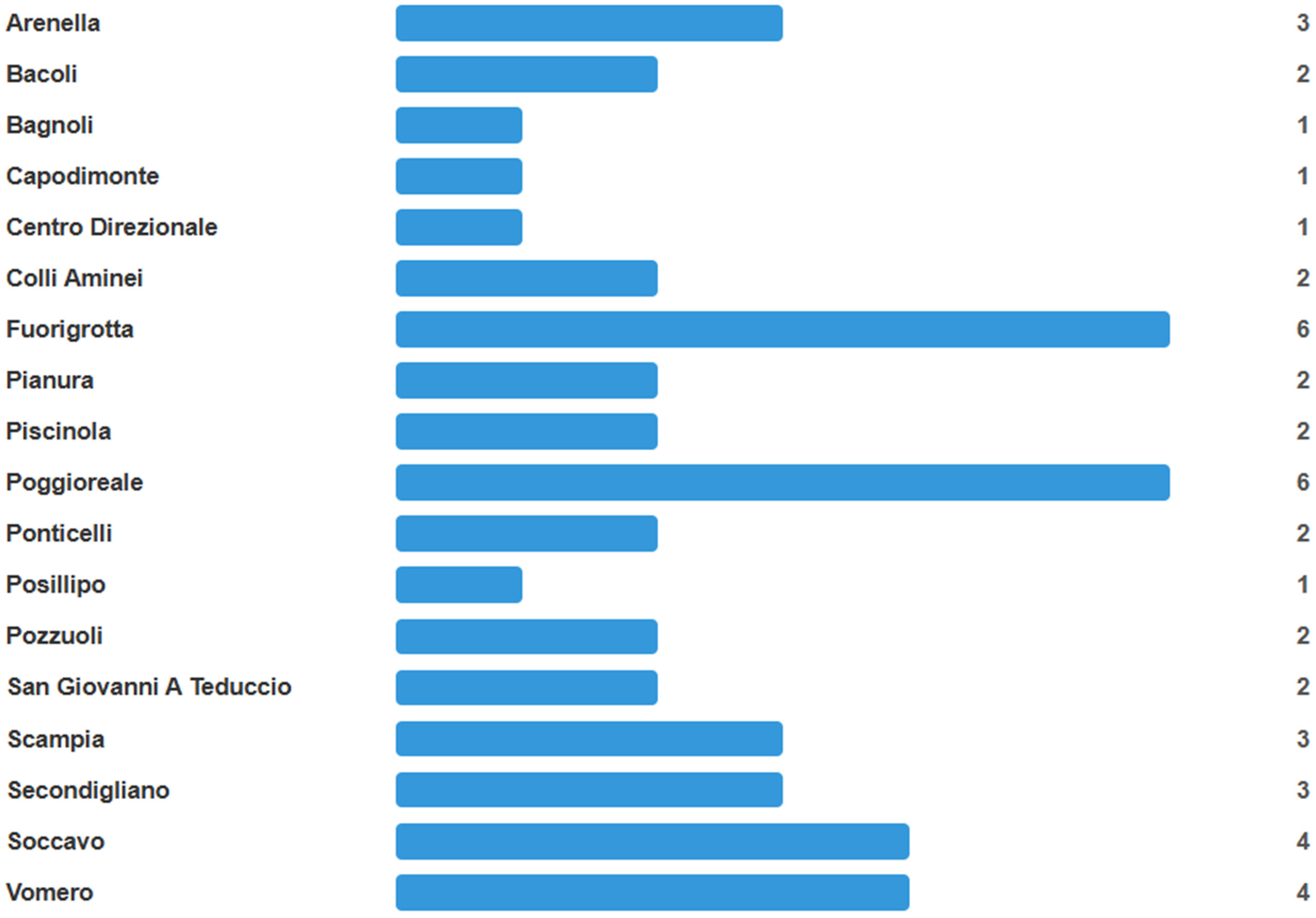
The first step in the present work is to identify a possible recurring structural pattern concerning reinforced concrete churches. Therefore, the churches located in Naples were first identified, considering both inside and outside in the historic center. About 534 churches have been identified, with 54 in reinforced concrete. It should be noted that the generic term “churches” includes major churches, small churches, and basilicas inside and outside the historic center. The reinforced concrete churches identified (
Figure 1) were classified according to the type of plan (
Figure 2) and the position of the bell tower (
Figure 3). Classifying churches by structural typology and layout is useful for technical modeling and provides a framework for prioritizing retrofitting efforts at the city or regional level. This approach enables stakeholders to evaluate vulnerability patterns and focus limited resources on the most at-risk structures, especially in urban centers with dense cultural heritage like Naples [
23]. This typological mapping also facilitates comparative risk assessment across cities with similar architectural heritage.
This classification provides the basis for modeling across multiple churches and supports the development of a regional vulnerability index.
A frequent approach immediately emerges from a preliminary analysis in 20 of the 54 churches studied. This simple portal pitch roof is known in the literature as the “cathedral portal,” a simple scheme, but of great interest in the present work. Therefore, the frequent type of reinforced concrete church has a rectangular plan, a detached bell tower, and a structural calculation scheme of the cathedral portal type. In this work, bell tower-structure interaction is neglected as their analysis is considered beyond the scope of the current paper [
24].
2.3. Typological Applicability and Boundaries
The proposed methodology is applicable primarily to RC churches that exhibit a repetitive transverse portal frame system commonly referred to as the “cathedral portal” configuration. These buildings typically possess a rectangular layout, lack rigid diaphragms, and were constructed between the 1930s and 1970s using early reinforced concrete technologies. The model assumes regular spacing of frames in the transverse direction and minimal plan irregularity.
Table 1 summarizes the key typological features that define the domain of applicability. Structures falling outside of these boundaries such as those with complex plans, irregular diaphragms, or later construction detailing may require adaptation or alternative assessment methods.
The development of a structural typology for RC churches provides not only a basis for engineering analysis but also a replicable framework for other historic cities with dense church inventories, enabling comparative vulnerability assessments across regions.
2.4. The Cathedral Portal
The plane frame represents a particular structure consisting of elements loaded in a 2D plane. The members are commonly assembled in polygonal meshes with vertices representing the intersection of the members’ axes that converge at the joints. The connection of the frames with the ground is realized with constraints in such a way that makes the system externally isostatic or hyperstatic. The nodes are rigid, and relative rotation at the ends of the members is not allowed. The load condition on a frame consists of several actions acting on the members and nodes. As a result of this load condition, a system of displacements (translations and rotations) is determined in the frame. The most important ones are at the nodes. From literature and in the hypothesis of linear behavior of structure and the possibility of using the principle of superposition, it is possible to calculate both stresses and deformations of all elements that constitute the frame.
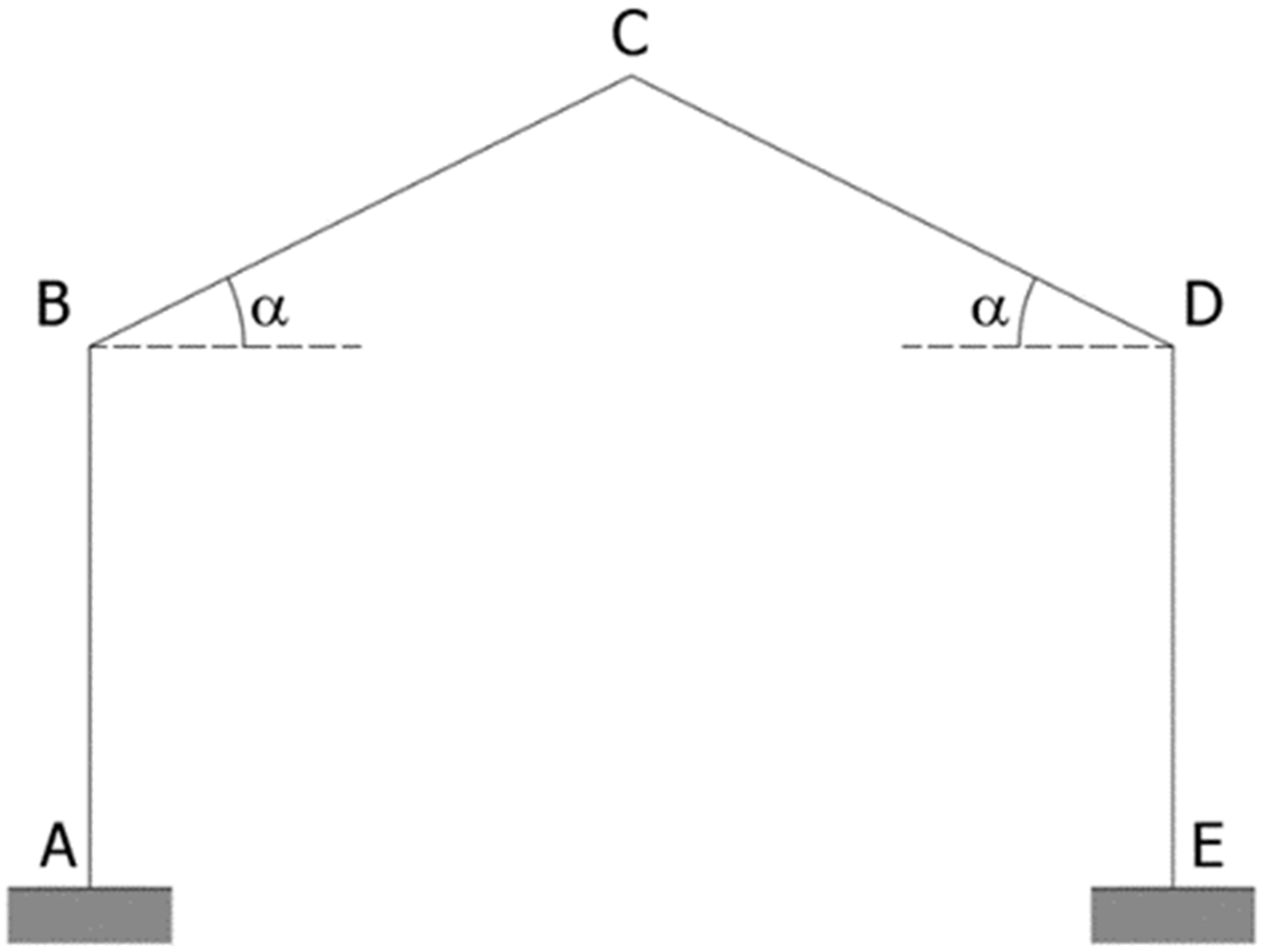
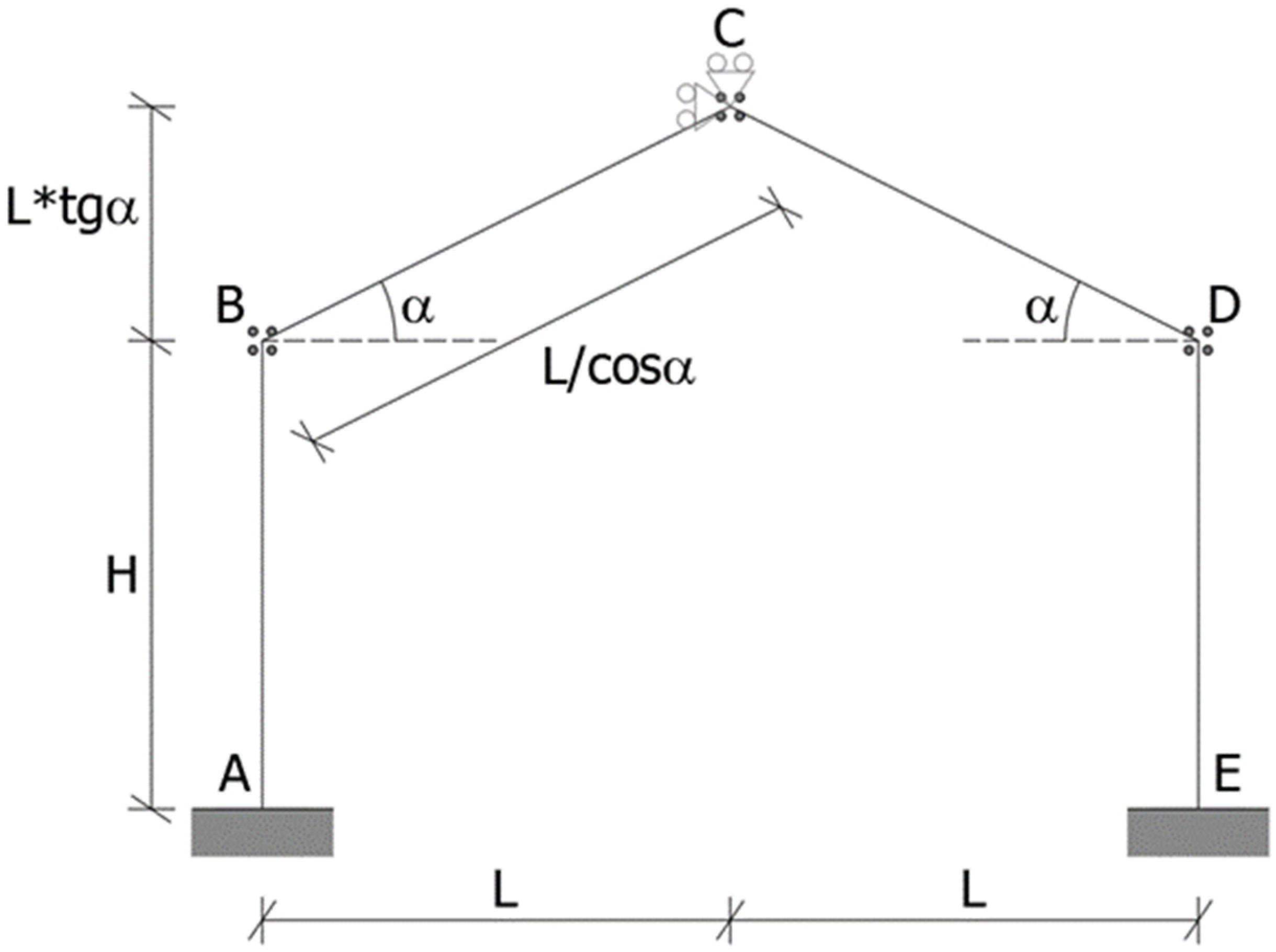
Figure 4 shows a simple portal frame fixed at the base at A and E with pitches inclined by an angle α. It is possible to calculate both stresses and deformations of all the members of the frame [
24].
Since the end of each member has 3 degrees of freedom, the number of variables in such a scheme is given by the product of the number of nodes and the degrees of freedom. Therefore, in total, there are fifteen unknowns. The unknowns are reduced to nine by considering the external constraint conditions (fixed at nodes A and E). The axial stiffness of the members then provides four conditions. Two of these immediately turn into constraint conditions, canceling two other degrees of freedom for the embedded members (v
A = v
B; v
E = v
D). On the other hand, the other two conditions link the movements together. The seven remaining variables are divided into three rotational (
;
;
) and four translational (
;
;
;
) unknowns. Internal relationships link translational unknowns; hence, two are dependent, and two are independent. Five unknowns are obtained by considering only the independent displacements: two translational and three rotational, translating into five additional constraints. The choice of the displacements is not unique. Still, the structure must have fixed nodes for the displacements to be considered independent (
Figure 5).
Once the stiffness matrix has been calculated and the force F is known, it is possible to calculate the displacement vector δ using Equation (1).
Once the displacement vector has been defined, the actual stresses in the frame nodes are calculated. To quickly verify the results, refer to the Handbook of Reinforced Concrete (Santarella) [
6], which provides the results in closed form for calculating the stresses of various types of frames.
This typological classification is not only a convenient structural modeling tool but also a practical tool for city authorities. By mapping churches with shared vulnerabilities, stakeholders can plan targeted retrofitting efforts and allocate limited resources more effectively, particularly in densely built historic urban centers like Naples.
3. Seismic Analysis
3.1. General
The Ministerial Decree of 17 January 2018 allows us to apply various analyses to evaluate the seismic capacity of RC buildings, such as (a) Linear static analysis, (b) Linear dynamic analysis, (c) Nonlinear static analysis, and (d) Nonlinear dynamic analysis. It is well known that modeling and verification requirements indicated for ordinary buildings cannot always be applied to structures with architectural heritage. However, it is necessary to evaluate the building’s overall seismic behavior with appropriate models. This evaluation can be made by considering the entire church (global model) or limiting the analysis to the parts that constitute it (local model). In the study of seismic behavior of masonry churches, the use of local models appears to be the most appropriate. Hence, it is valuable to do member analysis or divide the church into portions characterized by a substantially independent seismic response and analyze them using local models. However, it is sometimes possible for churches in reinforced concrete to consider either or both global (full church) and local (frame only) models.
Furthermore, a fundamental problem distinguishing churches from other buildings is the absence of a rigid diaphragm, which leads to the difficult choice of the control point to consider. In general, for dissipative systems, the linear analysis methods are very restrictive, as they underestimate the resistance and deformation capacities of the materials. The most suitable methods of analysis are nonlinear ones. Plasticity in the linear elastic behavior approach has often been emphasized based on experimental investigations and surveys on actual structures [
25]. It is well known that the elastic material is characterized by a natural state, such that under the action of external forces, it deforms and returns to its original position once the forces have been removed, regardless of the deformation it experienced. Therefore, the elastic material exhibits reversible deformations, accumulating the effort performed by external actions in the form of elastic potential energy, an energy that it returns ultimately during the unloading phase. However, it is well established that in a structure, loads induce local failures in various points (due to concentrated loads, residual stresses in steel profiles, eccentricity in assembly, local stresses, constraint failures in hyperstatic structures, thermal effects, shrinkage, manufacturing, and assembly imperfections) that exceed the permissible values. Although many of the causes listed above are not included in the structural analysis, there is no resulting failure [
26].
The focus on transversal analysis is justified by the structural configuration of many RC churches, where portal frames are aligned in the transverse direction and often repeated. Past seismic events have shown that damage tends to concentrate along this axis due to geometric irregularities and lack of diaphragms. This transversal vulnerability is further exacerbated by the absence of rigid diaphragm, which reduces the structure’s capacity to redistribute seismic forces in plan. Moreover, this directional focus aligns with observed damage patterns in recent Italian earthquakes, where lateral instability was often concentrated along the transverse axis due to repetitive portal frame configurations.
Unlike standard residential or office buildings, churches often lack rigid diaphragms and regular geometry, making traditional seismic analysis less directly applicable. These architectural idiosyncrasies underscore the need for simplified, yet robust, models that can be adapted to a wide variety of church typologies across Italy.
Given their irregular geometry, lack of diaphragms, and functionally critical role, churches require nonlinear assessment strategies that can capture failure mechanisms not evident in linear approximations [
27].
3.2. Plastic Behavior and Theory of Plasticity
Thanks to numerous researchers due to their theoretical and experimental studies in the first half of the 20th century, the so-called theory of plasticity was developed (Heyman et al.) [
9]. To easily understand the fundamental aspects of this theory, think of a simple single-axis load test. Considering a steel bar and carrying out a tensile test on it, it is possible to highlight some noticeable features:
Deformations result instantaneously upon application of the load.
The σ-ε plot is linear and reversible until a certain strain value εy is achieved, which corresponds to the yield stress σy.
For deformation values greater than εy, the material has a profoundly different behavior: a slight increase in stress is associated with a generic load increase, whereas high deformations are mostly permanent. Some of them are recovered with a small amount of unloading.
It is evident that, in general, the elastic behavior is characterized by a σ-ε curve that is not necessarily linear but reversible, where the deformations are recovered at unloading. The action depends only on the final value of the deformation. Several materials behave elastically, at least in the first phase of the loading process. Many of them exhibit behavior that can be considered linear with an excellent approximation. On the other hand, plastic behavior is characterized by permanent deformations that occur after the elastic phase. Upon unloading from a plastic phase, the material returns to behave elastically in a specific interval. From these reflections, it can be said that a deformable solid, when subjected to actions, exhibits elastic behavior if the stress is less than the yield stress. By increasing the forces, some parts of the member were plasticized. However, it might still be able to increase loads further in the presence of some portion that still behaves elastically and, therefore, supports the plasticized portion of the member. However, there is a limit to which the elastic part can no longer carry out this beneficial function; therefore, the body comes to “spread,” and its deformation reaches the state of collapse [
28,
29].
3.3. Limit Analysis
The limit analysis, or collapse state, is that part of the plastic theory that allows for the direct evaluation of the collapse load (or limit load) of the structure, i.e., the value of the external load that leads to the loss of bearing capacity [
16,
30]. It is based on three fundamental assumptions: (a) perfectly plastic elastic material, (b) Small displacements until collapse, and (c) monotonously increasing loads.
This analysis is immediately interpretable and is substantially independent of the numerical parameters on which the calculation procedure depends. The general methods of finding the limit load are based on two fundamental theorems: the static theorem and the kinematic theorem. Based on these two theorems, it can be stated that the collapse multiplier represents the element of separation between two classes: the static ones and the kinematic ones. Therefore, in general, the limit analysis derives from the simple consideration that collapse occurs when the number of plastic hinges causes the structure to fail. The plastic hinges appear during the progressive increase in loads and therefore fall into a kinematic collapse mechanism. Once the failure configuration with the relative set of plastic hinges has been identified, the structure’s analysis is reduced to equilibrium conditions. However, this quick and straightforward way of proceeding requires the failure of some counterparts. The section does not collapse from the hypothesis where the first hinge is formed in a section, and the section does not collapse. Due to the increase in loads, subsequent hinges are formed, and the structure becomes a mechanism (any rotation at the plastic hinges is accepted). In this regard, consider the frame shown in
Figure 6, loaded with an equal vertical and horizontal force. All the members are prismatic and have the same section; consequently, they have the exact plastic moment M
p. We can find the limit multiplier λL if the two loads increase proportionally. The system is three times hyperstatic. It follows that complete collapse requires the formation of 4 plastic hinges. The sections indicated that the shear stress is constant. At the same time, the bending moment varies linearly since the members are not loaded [
31,
32,
33,
34].
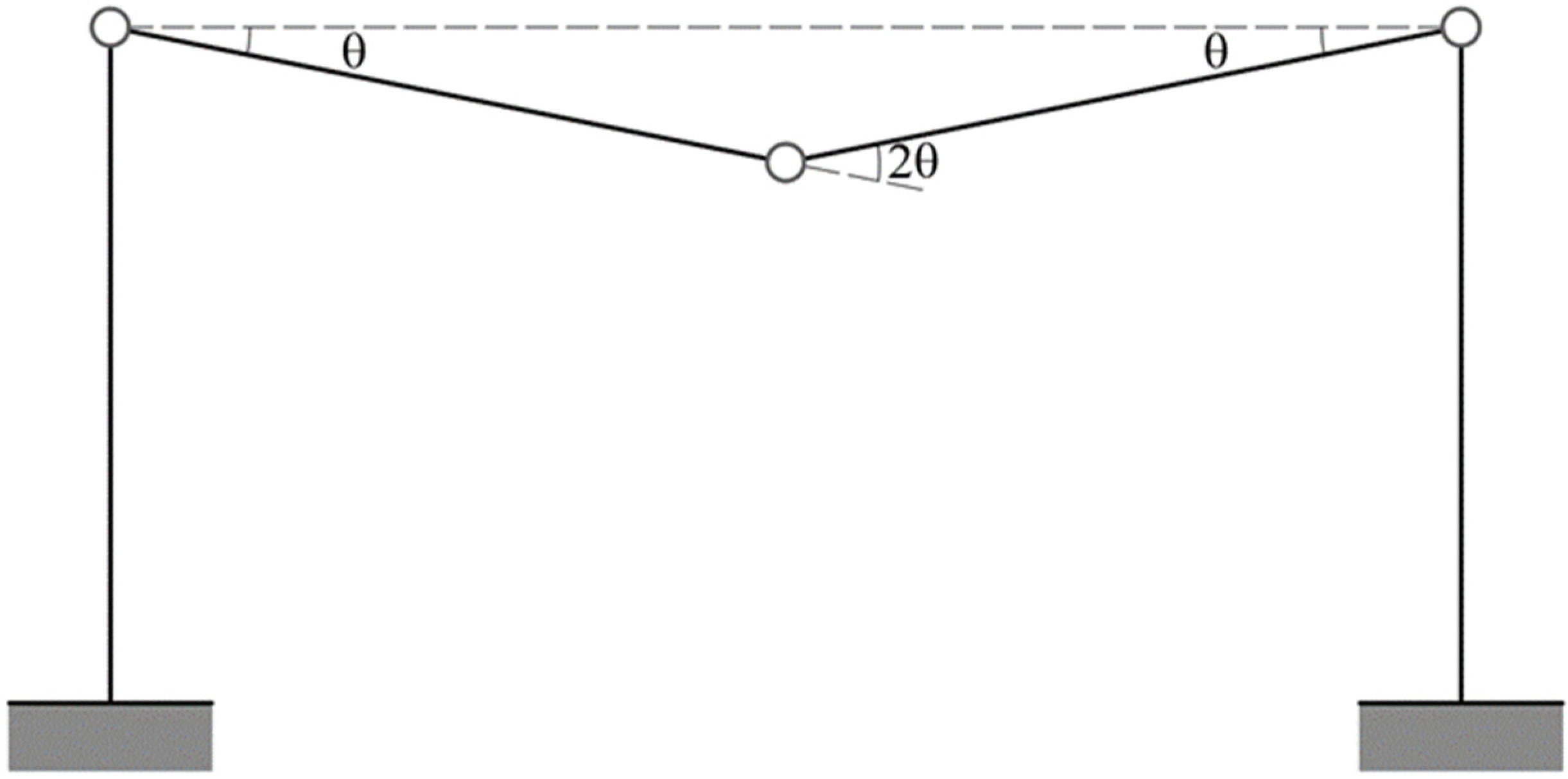
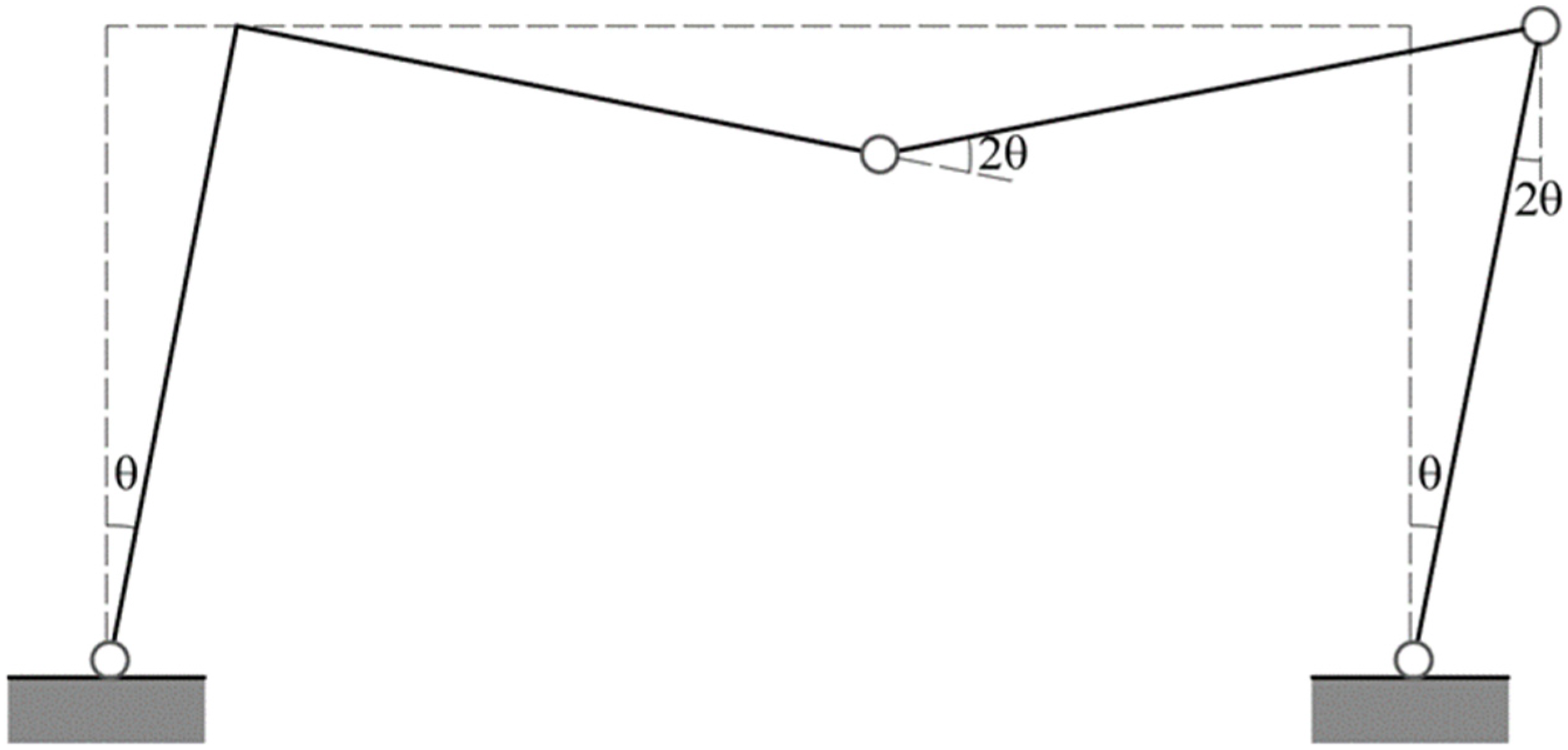
Plastic hinges can, therefore, only form in A, B, C, D, E. Specifically, a first possible mechanism is represented in
Figure 7 and is called the “beam mechanism.” This mechanism contains only three plastic hinges and is, therefore, a partial mechanism, as it leaves the columns of the portal undeformed. Instead, the mechanism that has the hinges in A, B, D, E (
Figure 8) takes the name of the “Storey mechanism.” Finally, the mechanism that presents the hinges in A, C, D, and E is represented in
Figure 9 and is known as a “mixed mechanism.” [
6,
35,
36,
37].
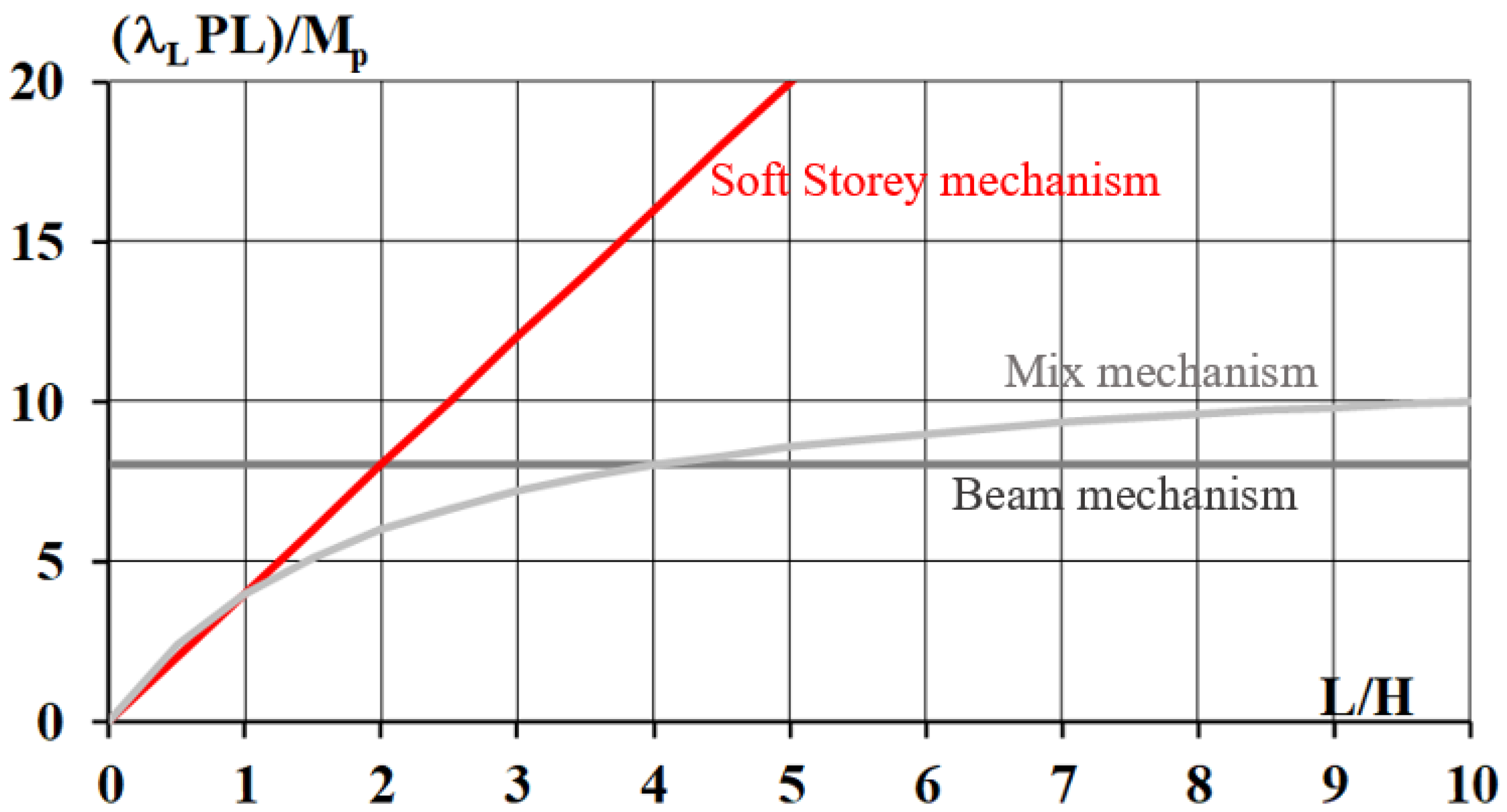
From this, the kinematic theorem gives the following equations:
Beam Mechanism (Equation (2)).
Soft Storey Mechanism Equation (3).
Hybrid mechanism Equation (4).
from which
.
If we report on a Cartesian diagram with L/H in the abscissa and
Ordinate, we obtain the graph in
Figure 10 [
25].
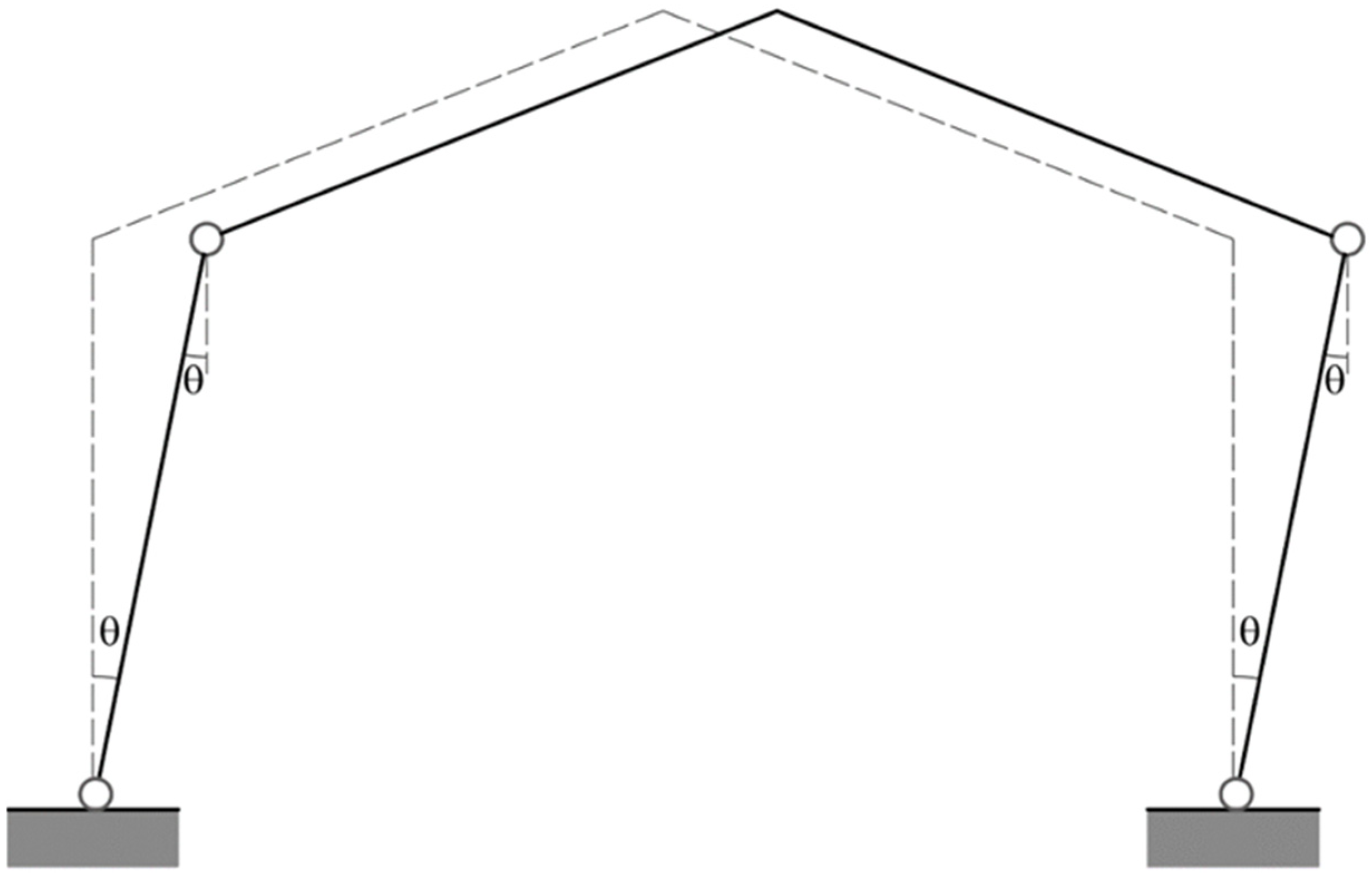
For a given L/H value, it is sufficient to estimate the vertical and determine the intersection points with the three curves represented. In this way, the portal collapses indifferently for L/H = 1 according to the Soft Storey and mixed mechanism. If L/H = 2, the collapse occurs according to the mixed mechanism. According to the beam and the mixed mechanism, the portal collapses indifferently if L/H = 4. Finally, if L/H > 4, the collapse occurs according to the beam mechanism (partial collapse). In this case, the determination of various rigid parts making up the rupture mechanism is immediate and straightforward. In the case of pitched portals, such as those present in the church buildings under consideration, the kinematics of the collapse mechanism is more complex. It is often helpful to use mechanics techniques to find the center of rotation of different parts of the mechanism, which can be suitably combined. In the present paper, the rigorous procedure for calculating the collapse mechanisms of pitched portals is omitted since only the Soft Storey mechanism is considered in a simplified way (See
Figure 11), which is identical to that analyzed for the simple frame fixed at the base.
Building upon the theoretical framework and failure mechanisms discussed, the following section presents a simplified modeling approach tailored to the typological characteristics of RC churches.
4. Proposed Methodology
In this section, a simplified approach that allows the evaluation of the seismic vulnerability of reinforced concrete churches with the cathedral portal as a structural element by analyzing the geometry of the structural complexity is proposed and applied. This approach can be used for large-scale church vulnerability analysis or a general assessment of the seismic safety of the individual church after the evaluation of the Cathedral of Reggio Calabria. It is ascertained that the critical element for certain types of church buildings is the transverse frame, which can be traced back with a good approximation to the cathedral portal analyzed in this work.
The proposed methodology is intended for preliminary screening purposes only and is not a substitute for code-compliant design or detailed assessment. The methodology is therefore aligned with the scope of preliminary screening assessments under NTC 2018, ensuring that safety margins are maintained while enabling evaluations.
In accordance with the Italian NTC 2018, the use of nonlinear analysis under low documentation conditions (FC = 1.35) is interpreted as acceptable only in the context of vulnerability ranking and prioritization, not for final retrofit design. The method is suitable for both pre-earthquake prevention planning and post-earthquake rapid condition screening of RC churches. Safety margins are preserved, and assumptions are clearly defined to avoid misuse.
The following section presents the simplified model in detail, emphasizing its applicability even with limited input data, making it ideal for rapid assessments at the community scale.
4.1. Description of the Proposed Model
One key advantage of this model is its applicability, even in the absence of detailed structural documentation, which is common in older churches. By relying on basic geometric and material properties, it offers a practical, alternative to full-scale FEM or nonlinear time-history analysis.
First, the frame’s geometry is defined by entering its geometric dimensions and sections (
Figure 12).
Then, the materials of the frame under consideration are defined (concrete and steel). Finally, the Confidence Factor is entered, which is based on the accuracy of the data available. Since this is a simplified analysis and does not have detailed information, FC = 1.35 is used, corresponding to a Knowledge Level equal to 1 (
Figure 13).
The longitudinal reinforcements (the number of bars and their diameter in each section) and the stirrups (the diameter and pitch of bars) are incorporated. Finally, the concrete cover used in the calculations is specified (
Figure 14).
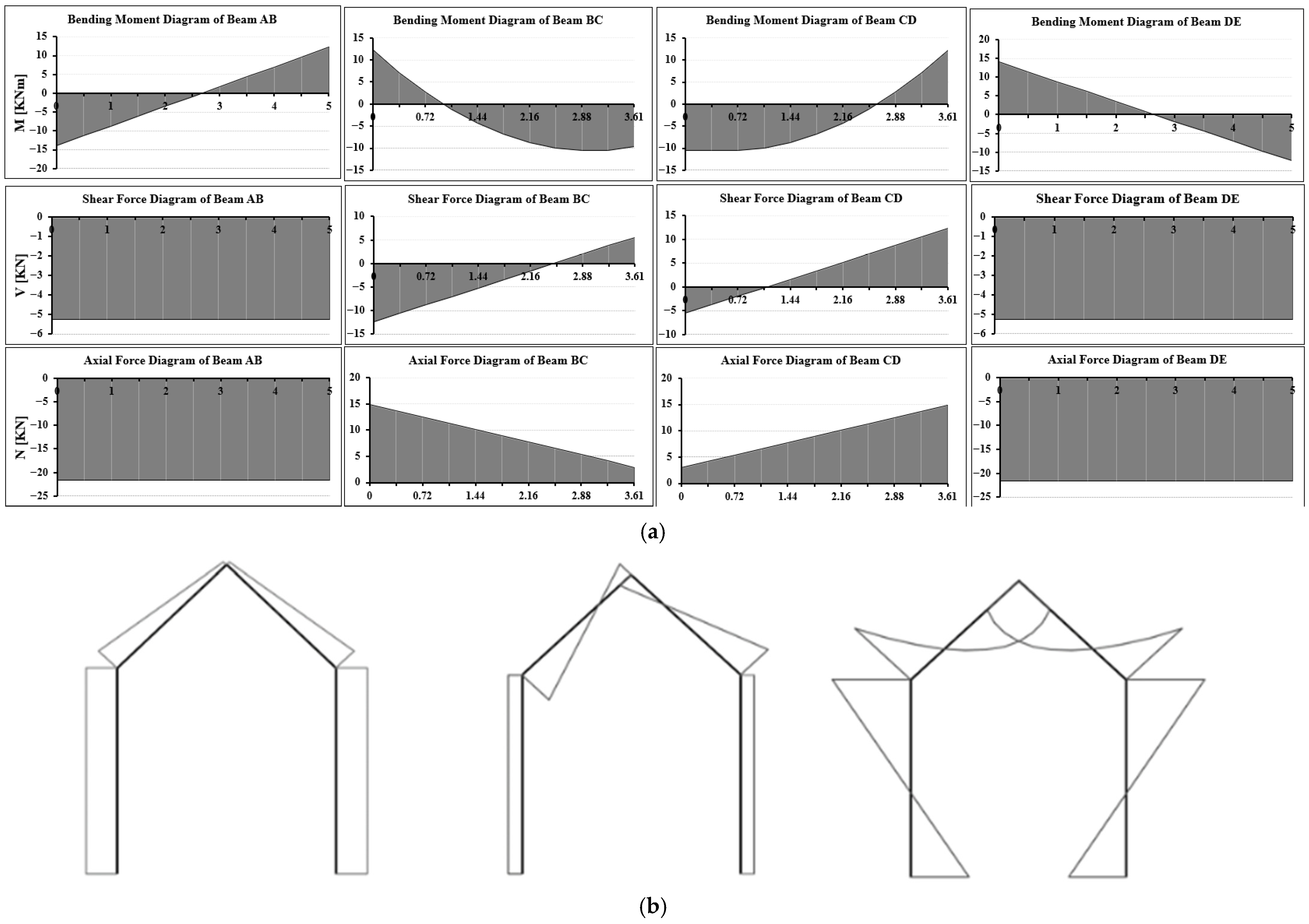
Once the input data has been defined, it is possible to conduct linear analysis. Then, the load acting on the roof has been entered, and bending moment, shear, and normal stress diagrams are automatically drawn for the individual members and the overall structure (
Figure 15a,b).
The simplified tool automatically generates a simplified resistance domain, as shown in
Figure 16.
Finally, a fundamental pushover analysis is performed on the considered frame by referring to point C8.7.2.3 of the Circular of the new NTCs approved with DM 17/01/2018. In general, in the verification of a framed structure, it can be assumed that the collapse of a column occurs when the limit value
θu (SLC) of the chord rotation is reached, which can be calculated with an analytical formulation provided by the standard. In the verifications of the Life Safety Limit State, the limit value of rotation at the chord
θu (SLV) is obtained using Equation (5) equal to 75% of the collapse rotation is assumed:
At the Collapse Prevention Limit State, the capacity in terms of total rotation concerning the beam can be evaluated alternatively using numerical models that consider the contributions of concrete, steel, and steel-concrete interaction or employing proven formulas’ validity (point C8.7.2.3.2). Multiplying this value by the column’s height, it is possible to obtain approximately the final displacement δu of the element. For completion, it is necessary to know the capacity θy in terms of total rotation concerning the chord when the yield stress is reached, which can be evaluated using the case of beams and columns C8.7.2.7a and C8.7.2.7b. By multiplying the value thus obtained by the height of the element, it is possible to obtain the displacement δy.
Assuming the activation of the soft story collapse mechanism, as seen in
Figure 11, it is possible to obtain the value of
Fu with the simplified formulas of the limit analysis. Finally, by dividing the value of
Fu thus obtained by the frame’s weight, it is possible to represent the in-plane
F/
W −
δ. The capacity curve can then be represented in the AD plane by modeling the cathedral frame as a one-degree-of-freedom system, compared with the Acceleration Displacement Response Spectrum of the location considered and the seismic risk index calculated (
Figure 17) [
13,
14,
15].
4.2. Application of the Proposed Model
4.2.1. Case Study Overview
The proposed model is applied to the Church of San Giovanni Battista dei Fiorentini in Naples, a typical example of mid-20th century RC church architecture. The structure follows a basilical layout with a repetitive cathedral portal frame in the transverse direction. Given the absence of detailed design drawings, reinforcement and material values are estimated based on historical construction practices and regulatory provisions in place at the time.
4.2.2. Input Parameters and Assumptions
Table 2 summarizes the key input parameters used in the analysis. These reflect typical construction assumptions for RC churches built in the 1950s, including longitudinal reinforcement estimates and concrete class.
4.2.3. Capacity Curve and Risk Index Derivation
The capacity curve is derived using a simplified pushover analysis of the cathedral portal frame, assuming a soft-storey failure mechanism. The bilinear curve captures both elastic and plastic deformation stages. The ultimate displacement (δu) is estimated using chord rotation limits from NTC 2018 (θu), while the yield displacement (δy) is calculated using simplified formulations for RC columns.
The seismic risk index (ζE) is computed as the ratio of spectral capacity to demand at the Life Safety Limit State. A comparison with the ADRS spectrum is used to assess performance. The values obtained for the case study ζE = 1.13 and δu/δmax = 1.37 suggest that the structure meets minimum performance thresholds but may require further investigation for retrofit prioritization.
While tailored to a specific church, the process used here can be replicated across a broad inventory of similar structures, laying the groundwork for a city-wide vulnerability index that supports strategic retrofitting and emergency planning. This section is related to the proposed calculation model applied to the Church of San Giovanni Battista dei Fiorentini, as shown in
Figure 18, built in 1952 in Piazza degli Artisti in Vomero, Naples.
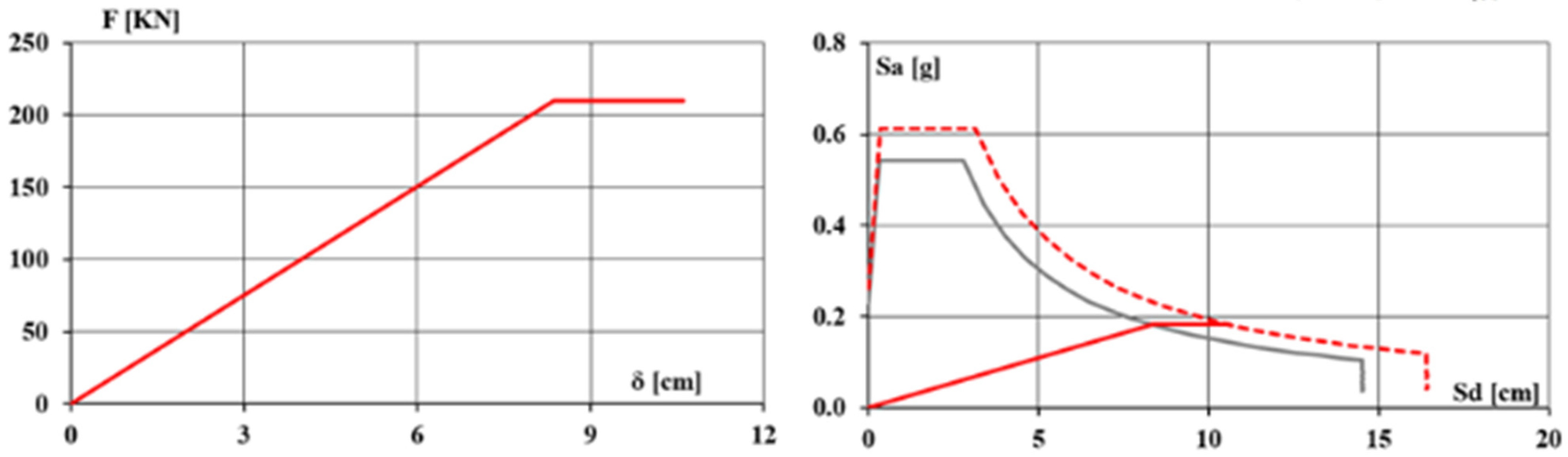
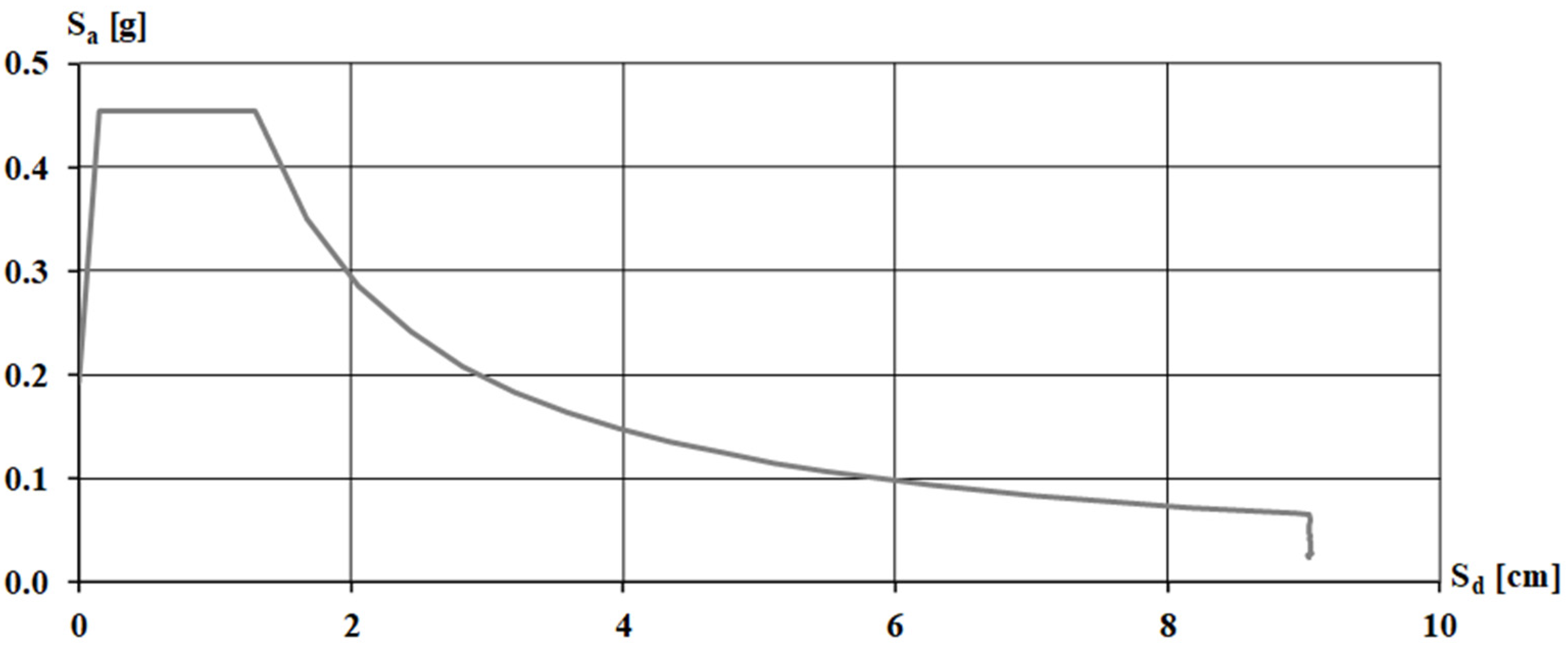
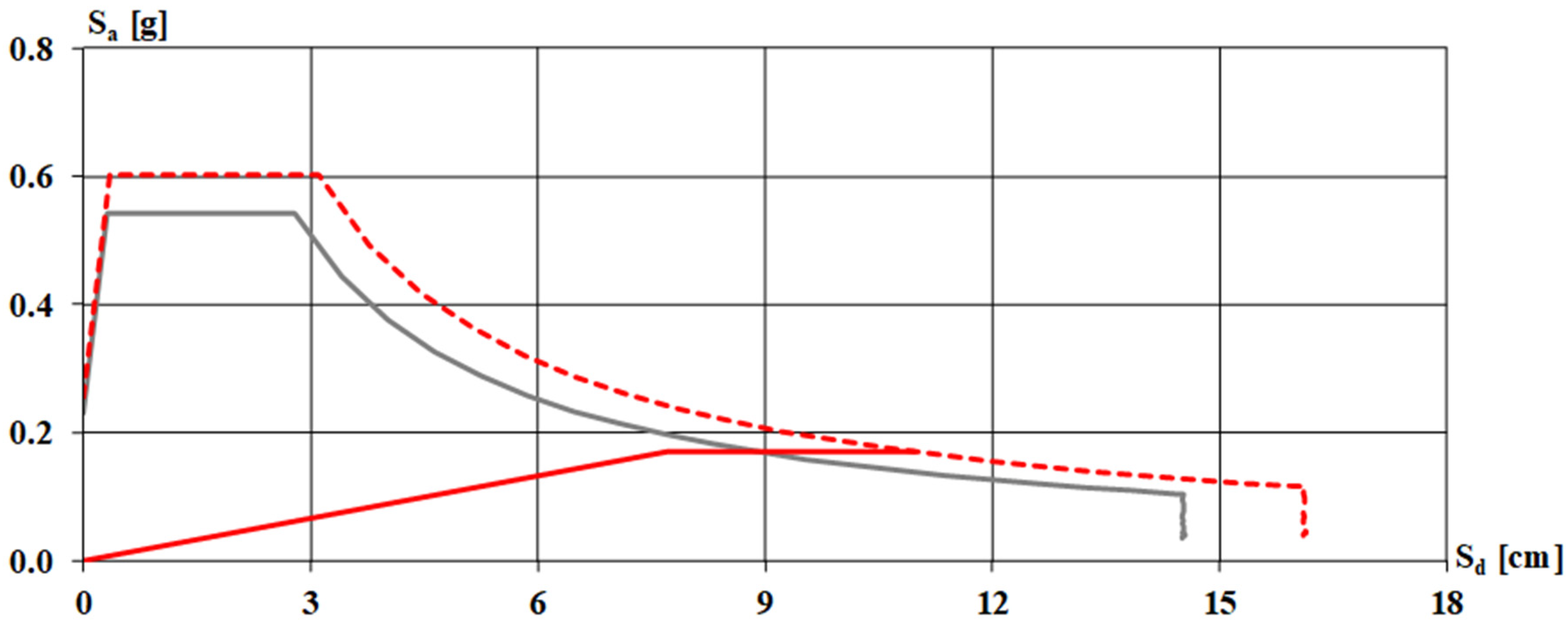
For this purpose, a simplified analysis is carried out based on available information, assuming sections and reinforcements compatible with the state-of-the-art rules and the regulatory provisions at construction. The first step is to define the city of Naples’s seismic hazard parameters. The elastic spectra are determined based on these parameters in terms of accelerations and displacements; therefore, the ADRS spectrum (
Figure 19). The Comparison with ADRS is shown in
Figure 20.
Once the geometric dimensions have been entered, it is possible to note that at the time of construction, the RD 16/11/1939 was in force, which requires providing a minimum longitudinal reinforcement of 0.8% Ac (if Ac < 2000 cm
2) and 0.5 Ac (if Ac > 8000 cm
2) for the columns. The pitch had to be at least 1/2 of the column area, and the concrete cover was 2 cm. No specific information regarding the size and minimum reinforcement of the beams is reported. In the 1950s, the most widely used steel was AQ 42 type [
16]. Inserting the above data results in the diagrams of the characteristics stress and the simplified resistance domain, which can be used for preliminary and quick verification.
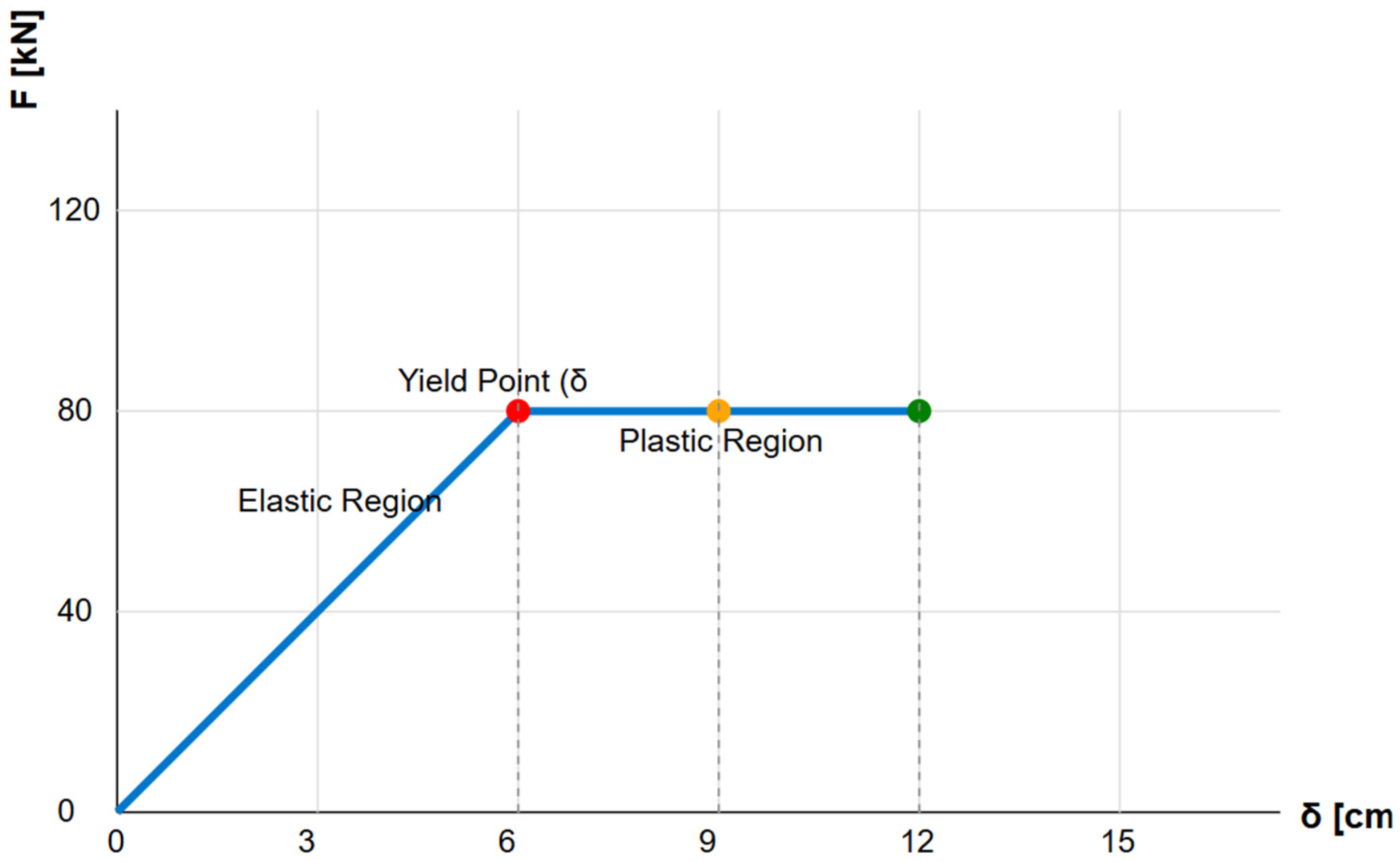
Figure 21 presents an idealized force–displacement (F–δ) curve representing the lateral seismic response of a reinforced concrete (RC) cathedral portal frame. The bilinear shape captures both the initial elastic stiffness and the post-yield plastic behavior of the structure. Key performance points are identified: the Yield Point (red), where the frame transitions from elastic to inelastic behavior; Life Safety (LS) (orange), indicating the deformation level at which significant structural damage is expected but collapse is avoided; and Collapse Prevention (CP) (green), marking the ultimate deformation capacity before instability. These thresholds are crucial for nonlinear static (pushover) analysis and are used to derive the seismic risk index and performance level of RC churches. The diagram also delineates the Elastic and Plastic regions, providing a simplified but informative visualization of structural capacity under increasing seismic demand.
The results obtained provide the following values: umax/dmax = 10.97/8.00 = 1.37, and ζE = 0.26/0.23 = 1.13
While this study focuses on a detailed case, the proposed framework can be extended to a larger inventory of RC churches to support urban-scale seismic risk mapping. By applying the model across a dataset of similar structures, local authorities could develop a city-wide vulnerability index, aiding emergency planning and heritage conservation strategies.
While based on a single structure, the methodology used here is transferable to a wide range of similar buildings. The ability to generate capacity curves and risk indices with minimal input makes this an ideal tool for regional-scale assessments.
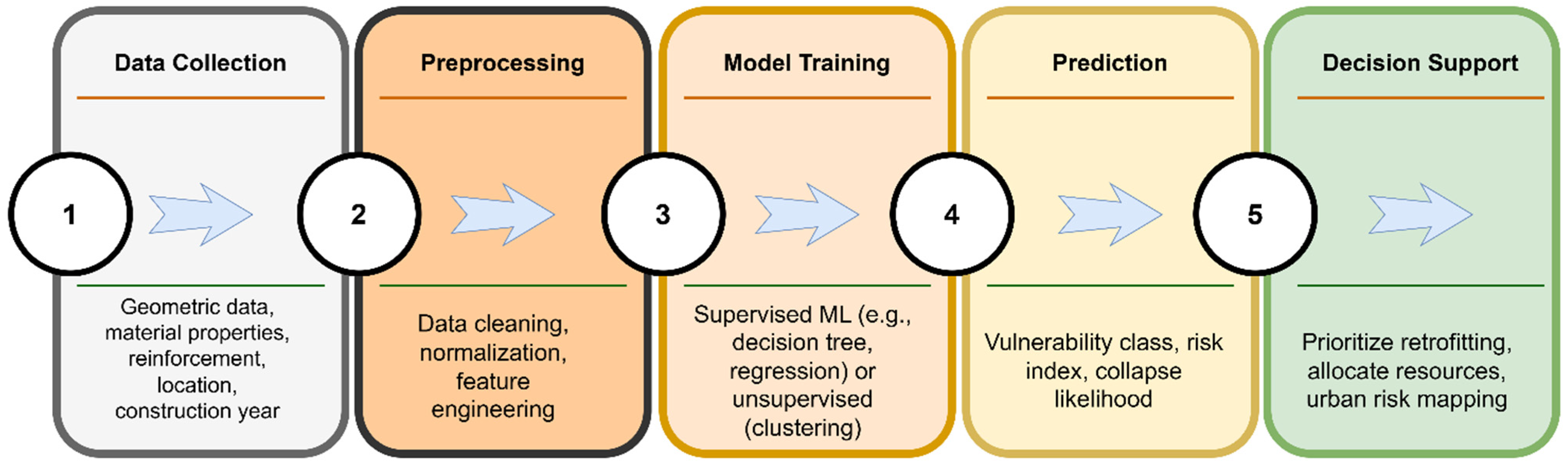
4.3. Potential Integration with AI/ML Frameworks
Artificial Intelligence (AI) and Machine Learning (ML) are emerging as powerful tools in structural engineering and disaster risk reduction. While the present study focuses on a simplified, mechanics-based assessment model, future extensions could adopt AI/ML methods to enhance scalability and automate vulnerability classification.
A conceptual AI/ML workflow for seismic vulnerability assessment of reinforced concrete (RC) churches is presented in
Figure 22. The process begins with the collection of structural and material data, such as geometric dimensions, reinforcement details, and construction age, followed by preprocessing steps like normalization and feature selection. These inputs can then be used to train supervised models (e.g., decision trees, regression algorithms) to predict a structure’s seismic vulnerability index. Alternatively, unsupervised learning (e.g., clustering) could identify typological groups with similar vulnerability patterns.
The AI/ML-driven predictions could support decision-making by enabling rapid screening of extensive church inventories at the city or regional scale. This would be particularly valuable for local authorities or heritage conservation agencies that must prioritize retrofitting under limited resources. While this approach is not implemented in the current study, it represents a promising direction for future research integrating data science with structural safety and cultural resilience. By combining domain knowledge with data-driven pattern recognition, future systems could classify structural risk and recommend retrofit strategies based on typological and contextual similarities.
Future work could also explore integrating satellite data, GIS layers, or archival construction records to enrich AI/ML feature sets, potentially enabling vulnerability predictions even before on-site inspections.
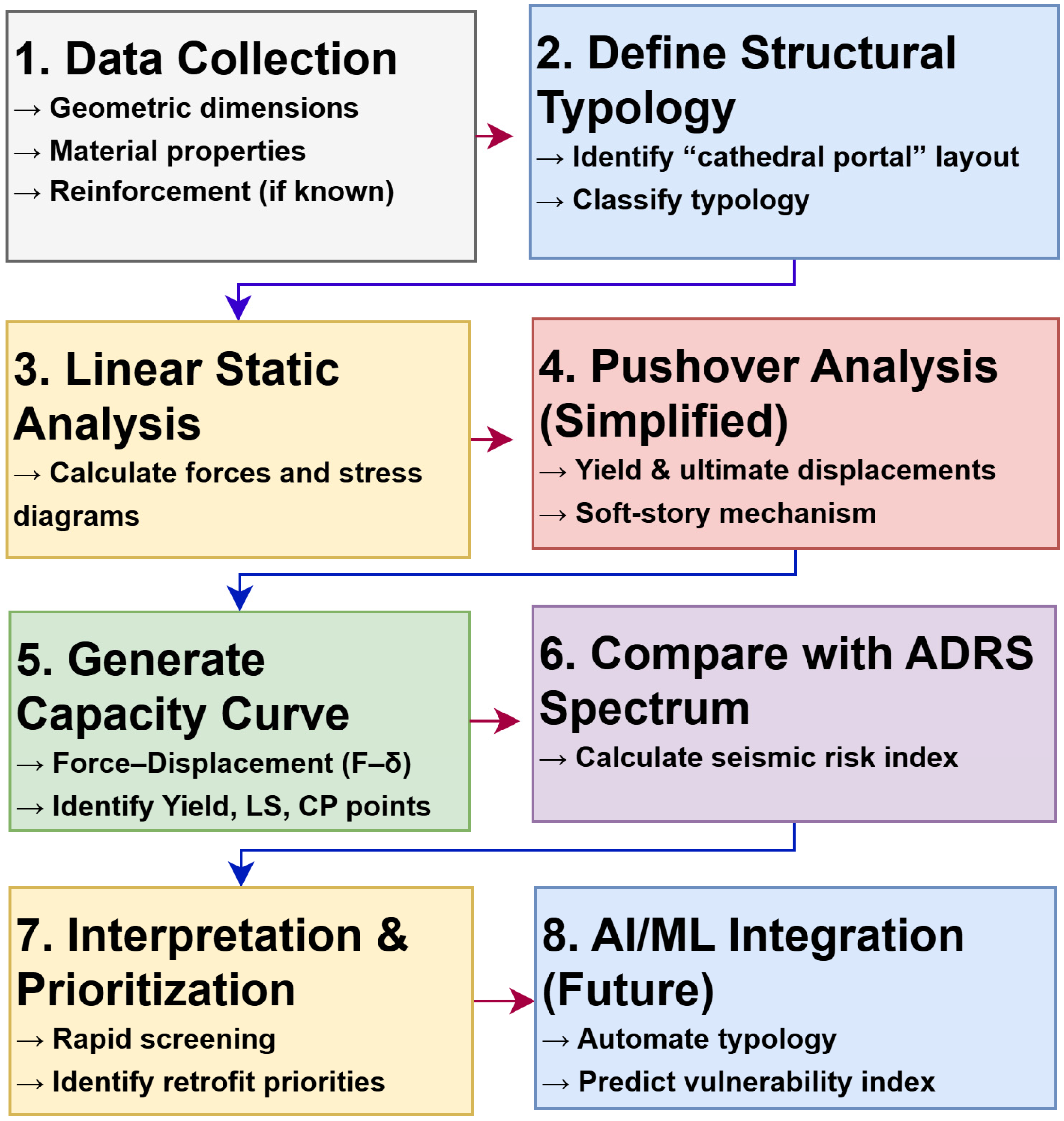
The complete workflow of the proposed methodology is illustrated in
Figure 23, where each stage from geometric input to risk index estimation is streamlined for rapid application in data-scarce environments.
5. Discussion of Contributions and Limitations
The methodology presented in this study addresses a critical gap in seismic vulnerability assessment for RC churches, namely the lack of accessible tools that can be applied in the absence of detailed structural documentation. The proposed approach contributes to the field by introducing a framework based on simplified mechanics, which allows for rapid vulnerability screening at the community level. Its novelty lies in adapting classical limit analysis and pushover methods typically used in high-data contexts into a low-data, typology-driven model suitable for heritage infrastructure.
One of the key strengths of this method is its minimal input requirement, relying only on basic dimensions, reinforcement assumptions, and material properties. This makes it a viable tool for preliminary evaluations in regions where archival data are incomplete or missing. Additionally, the typological focus on the “cathedral portal” (refers to a repetitive inclined-beam portal frame) allows for replicability across a broad inventory of RC churches sharing similar structural characteristics. Moreover, the model’s low computational demand makes it suitable for integration into mobile apps or web-based dashboards for use by non-experts in emergency situations.
However, the model also presents several limitations. The use of a high Confidence Factor (FC = 1.35) reflects the uncertainty in input data, and while the tool is useful for screening, it is not intended to replace detailed analysis for final design or retrofitting.
The method’s flexibility also allows for potential integration with rapid post-earthquake assessment frameworks using mobile or web-based platforms in future implementations. Furthermore, the reliance on simplified collapse mechanisms does not capture the full complexity of irregular geometries or dynamic interactions, such as tower-church interaction, which were excluded from this study.
Finally, the potential integration of AI/ML frameworks remains conceptual at this stage. Future work should focus on developing a data pipeline and training models capable of automatically classifying structural typologies and predicting seismic risk, especially when combined with GIS and remote sensing data.
Limitations of the Proposed Model
The proposed model is intended as a rapid, low-data screening tool and is not intended to replace detailed numerical simulations. A key limitation is the lack of validation against advanced Finite Element Method (FEM) models. This was not feasible due to insufficient structural documentation for the case studies, which reflects the real-world conditions the method is designed to address. However, this also limits the ability to quantify the model’s accuracy compared to more detailed approaches.
Additionally, the simplified mechanics-based approach does not account for dynamic effects such as torsional response, soil-structure interaction, or the influence of bell towers. These simplifications are acceptable at the screening stage but must be addressed in detailed assessment phases.
The current model is calibrated and applied to a single case study, and while it is based on a recurrent structural typology, broader application requires careful typological matching. AI/ML integration remains a proposed direction and is not implemented in the current version.
Despite these limitations, the model provides a practical compromise between reliability and data availability, particularly for heritage inventories where detailed modeling is impractical.
6. Limitations and Future Directions
The simplified methodology presented in this study offers a reliable and accessible tool for preliminary screening of seismic vulnerability in reinforced concrete (RC) churches. However, its application is limited to initial assessments and does not replace detailed numerical simulations. The reliance on high confidence factors (e.g., FC = 1.35) reflects uncertainties in input data, and the exclusion of dynamic effects such as soil-structure interaction, torsional response, and tower-structure interaction constrains its scope. Additionally, the study’s findings are based on a single case study, which necessitates broader validation across diverse typologies and geographic contexts to generalize its applicability.
Future research should focus on extending the methodology’s scalability and precision through the integration of Artificial Intelligence (AI) and Machine Learning (ML). These technologies have the potential to automate typological classification and vulnerability prediction, enabling rapid assessments across large inventories of RC churches. A structured dataset comprising geometric dimensions, construction typologies, and historical performance data could serve as the foundation for supervised learning models, improving predictive accuracy. Furthermore, incorporating Geographic Information System (GIS) layers or satellite imagery into the framework may facilitate region-wide vulnerability screening without requiring extensive on-site surveys, making the methodology more accessible and practical for heritage conservation agencies.
By emphasizing specific quantitative findings, such as the seismic risk index (ζE = 1.13) and displacement ratio (δu/δmax = 1.37), this study demonstrates the utility of simplified mechanics-based tools in identifying critical vulnerabilities and prioritizing retrofitting efforts. These results lay the groundwork for integrating advanced data-driven techniques into the framework, supporting a more robust and scalable approach to cultural infrastructure resilience.
7. Outlook
The simplified, mechanics-based methodology developed in this study addresses a critical gap in seismic vulnerability assessment for RC churches in low-data scenarios. While effective for initial screening, future advancements should aim to enhance the model’s scalability, accuracy, and automation. The integration of AI and ML techniques represents a promising direction, enabling rapid and automated vulnerability assessments across extensive inventories of heritage structures.
Developing structured datasets that include geometric attributes, construction typologies, and historical performance records will be essential for training supervised learning models capable of predicting seismic vulnerability indices with greater precision. Combining these datasets with GIS layers and remote sensing technologies could facilitate region-wide assessments, reducing reliance on resource-intensive on-site inspections.
Although AI integration remains conceptual in this study, it holds significant potential for complementing the mechanics-based framework. By automating typological classification and vulnerability estimation, future iterations of this methodology could support city-wide and regional-scale resilience strategies. These advancements would empower local authorities, civil protection agencies, and heritage conservation organizations to make informed decisions, prioritize interventions, and allocate resources effectively in seismically active regions.
8. Conclusions
This study presents a simplified methodology for assessing the seismic vulnerability of reinforced concrete (RC) churches characterized by cathedral portal frames. Designed for use in low-data scenarios, the proposed approach integrates classical mechanics, limit state theory, and pushover analysis to derive capacity curves and seismic risk indices for preliminary screening. The methodology was calibrated using the Cathedral of Reggio Calabria and validated on the Church of San Giovanni Battista dei Fiorentini in Naples, yielding specific quantitative findings that underscore its practical applicability.
Key findings from the analysis include the following quantitative results:
Seismic Risk Index (ζE): The computed seismic risk index for the case study was 1.13, indicating that the structure meets the minimum safety thresholds for the Life Safety Limit State (LS) but requires further investigation to confirm its performance under higher seismic demands.
Displacement Ratio (δu/δmax): The ultimate displacement-to-demand ratio was found to be 1.37, demonstrating that the structure retains sufficient deformation capacity beyond the expected seismic demand.
Capacity Curve Performance: The simplified pushover analysis produced an idealized bilinear force–displacement curve, clearly delineating the elastic and plastic deformation regions. Critical performance points, such as the yield point, life safety limit, and collapse prevention limit, were identified and aligned with regulatory standards (NTC 2018).
Failure Mechanism: The soft-story collapse mechanism was identified as the dominant failure mode, confirming the vulnerability of the transverse cathedral portal frame configuration under seismic loading conditions.
These findings highlight the effectiveness of the proposed methodology in producing actionable insights with minimal input data. By focusing on geometric and material properties, as well as simplified structural mechanics, the approach enables rapid assessments of seismic vulnerability, particularly for older RC churches with limited structural documentation.
The study’s contributions extend beyond methodological innovation to practical implications for urban-scale applications. Specifically, the ability to generate capacity curves and risk indices with minimal computational resources supports city-wide vulnerability mapping, aiding stakeholders in prioritizing retrofitting efforts for heritage structures. The results for the Church of San Giovanni Battista dei Fiorentini demonstrate the scalability of the methodology to similar RC churches across Italy’s seismic-prone regions.