Abstract
A finite difference model of a heat exchanger (HX) considered maldistribution, axial conduction, heat leak, and the edge effect, all of which are needed to model a high effectiveness HX. An HX prototype was developed, and channel height data were obtained using a computerized tomography (CT) scan from previous work along with experimental results. This study used the core geometry data to model results with the finite difference model, and compared the modeled and experimental results to help improve the expanded microchannel HX (EMHX) prototype design. The root mean square (RMS) error was 3.8%. Manifold geometries were not put into the model because the data were not available, so impacts of the manifold were investigated by varying the temperature conditions at the inlet and exit of the core. Previous studies have not considered the influence of heat transfer in the manifold on the HX effectiveness when maldistribution is present. With no flow maldistribution, manifold heat transfer increases overall effectiveness roughly as would be expected by the greater heat transfer area in the manifolds. Manifold heat transfer coupled with flow maldistribution for the prototype, however, causes a decrease in the effectiveness at high flow rate, and an increase in effectiveness at low flow rate.
1. Introduction
Heat exchangers (HXs) are ubiquitous in modern life [1] and have a market size predicted to reach over $20 billion U.S. dollars by 2024 [2]. There has been substantial interest in improving heat exchanger performance by utilizing microchannel-based HX [3,4,5,6]. Even with improved performance, minimizing economic costs are a core driver of specific applications. For example, an emerging application, solar water pasteurization, demands low-cost HX and has the potential to save the lives of thousands of children a day [7,8,9]. Another important application can be found in absorption cycles, which can utilize waste heat from diesel engines, such as those found on ships [10].
One of the ways gaining prominence for reducing the costs of products is applying the open-source paradigm of technical development to hardware [11,12,13,14]. An open-source polymer laser welder has been developed [15], heat transfer in polymer HX using it was studied [16] and recent work [17] has also provided a low-cost method of making a polymer-based expanded microchannel HX (EMHX). EMHX modeling is more complicated than conventional microchannel HX [18]. A study performed a computed tomography (CT) scan to examine a prototype polymer-based EMHX such as this, and it indicates significant flow maldistribution due to channel height variations [19]. There have been significant improvements in the modeling of micro-channel HX, which can be used to drive the development of EMHX [4,20,21,22,23,24,25,26,27,28,29,30,31]. Recently, a paper [32] developed a finite difference model that can be applied to this EMHX that was scanned, allowing for a comparison between modeled and experimental heat transfer characteristics when maldistribution is present.
The performance of a HX is characterized by its effectiveness, η, defined as the ratio of the actual heat transfer rate to the maximum heat transfer rate.
Here we use effectiveness to mean the approach to the ideal temperature, which can be applied to the HX as a whole, or individual channels. The actual heat transfer rate is:
where the heat capacity rates, CH and CC, are defined using mass flow rate and specific heat.
The maximum heat transfer rate is:
where Cmin is the minimum heat capacity rate between the hot and cold side.
The number of transfer units or NTU is defined as the ratio of the heat transfer rate between the fluids to the minimum heat capacity rate. NTU represents the heat transfer ability of a heat exchanger normalized by heat transfer area. A high NTU value indicates a low flow rate.
Here A is the heat transfer area and U is the overall heat transfer coefficient. If channels in an HX vary in size, then fluid velocity will be greater in some channels. The channels with greater fluid velocity will have a smaller NTU, which means the fluid in these channels will not cool down as much. The mechanisms producing channel irregularity include non-uniform fouling [33], two phase flow [34], thermally induced maldistribution caused by unequal thermal expansion coefficients [35], and non-uniform spacing of fins [36].
To understand the way that fluid travels through the channels of the HX, a few definitions are required. Consider a cross section of the core of the HX in Figure 1.
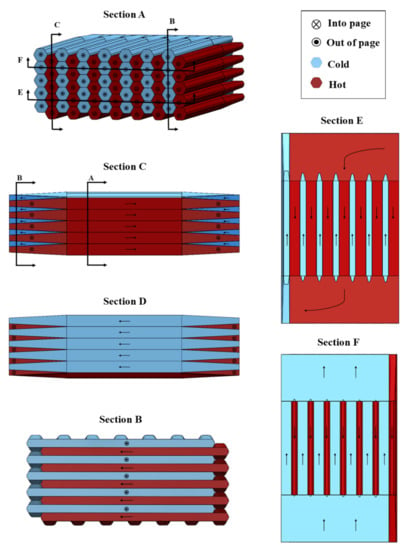
Figure 1.
HX cross section and manifold flow patterns.
When the flow is uniform, the flow rate is the same for each channel (hot and cold alike because it is balanced flow). Now, consider the cold and hot channels of a cross section as separate groups. Positive correlation is defined as a group of cold and hot channels having the same flow maldistribution, e.g., the right-side channels have lower flow rate for both cold and hot. Negative or anti-correlation is defined by hot channels having the opposite flow rate trend as the cold channels, e.g., the cold channels on the right side having lower flow rate than the cold channels on the left, but the hot channels on the left side having lower flow rate than the hot channels on the right. Uncorrelated flow occurs when the flow rates of the hot and cold channels show neither positive nor negative correlation, which could mean that one temperature of channels has constant flow rate and the other temperature of channels could have any pattern.
Microchannels (<1 mm hydraulic diameter) that are smooth and contain a liquid with negligible viscous heat generation have the same physics as traditional laminar correlations [37,38,39,40,41]. Therefore, traditional laminar correlations are used for this paper.
Axial conduction is the conduction of heat in the direction of fluid flow, by both the fluid and the HX material [42,43]. This can be a significant source of ineffectiveness for high effectiveness HXs. The ineffectiveness due to axial conduction can be added as post-processing for a large range of configurations [44].
The heat leak is the gain or loss of heat from the environment. As a first approximation, the heat leak ineffectiveness can be added as a linear term to the other ineffectivenesses [45].
Edge effects are considered in that the channels near the edge have fewer neighbors and thus do not transfer as much heat, giving those channels a lower NTU. This edge effect actually penetrates to channels not on the exterior as well and can be important even for 80 layers [46].
Large temperature variations in the HX can significantly change the properties of the fluid and the wall [47]. However, the prototype HX for this paper has small temperature variations, so these effects are not considered.
A number of papers discussed flow maldistribution due to the manifold [48,49,50,51]. Different paths of the fluid in the manifold (see Figure 1) have different flow resistances, so channels have varying flow rates in the HX core. The problem of manifold heat transfer not being the same for all fluid paths has not been analyzed [52]. The present paper addresses this analysis by varying the boundary conditions at the HX core based on different manifold heat transfer characteristics to examine the effect on each fluid path in the core. With improvement to the model using the conclusions of the analysis, better fit between the modeled and experimental results can be achieved and design of microchannel heat exchangers can be improved by taking into account manifold heat transfer with maldistribution.
2. Materials and Methods
2.1. The Advanced Model
The advanced model is a finite difference model that calculates the flow in each channel of the HX based on the height of each channel as a function of its length. The advanced model takes into account edge effects, heat transfer between all neighboring channels, axial conduction, and heat leak. Edge effects and heat transfer between neighboring channels are considered with a transverse heat flux term, see Figure 2 and Equation (6):
where AHT is the total heat transfer area shared with one neighbor, U is the overall heat transfer coefficient, and the temperature difference between the example cold channel and a transverse neighbor k is Ttran,k − Tc,i,j. While two of the transverse channel neighbors are cold channels, the potential for similar fluid heat transfer means the temperature difference is evaluated the same as the hot channels and is summed into a single term. The m in the denominator is the number of discretized steps of the heat exchanger core length. The expanded channels have a rough hexagon shape, which means there are four heat flux terms from neighboring hot channels, and two heat flux terms from neighboring cold channels. Similar fluid heat transfer between cold channels could be in either direction depending on their temperature, and is generally lower in value than the heat transfer with neighboring hot channels.
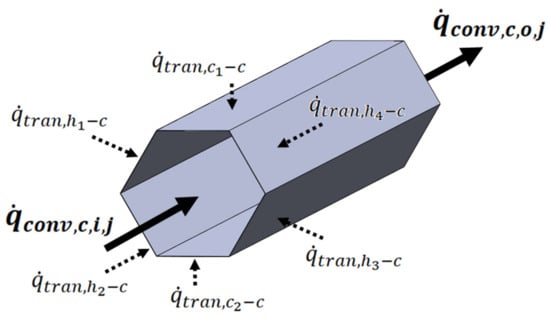
Figure 2.
Cold channel control volume and heat fluxes.
Axial conduction is included in the advanced model with the parameter λax, which is a ratio of axial conduction to fluid convection heat transfer.
Aw is the cross-sectional area of the HX wall, kw is the thermal conductivity of the HX wall, Af is the cross-sectional area of the HX fluid channel, kf is the thermal conductivity of the fluid, and LHX is the length of the HX core. A factor of half of this is included in the axial conduction term because only one half of the heat conducted in the axial direction enters a channel, since it is conducted through HX walls which have a channel on each side.
Heat leak is included in the advanced model with the parameter λleak, which is the ratio of external heat leak to the heat transferred within the HX.
The subscript “ins” stands for insulation, which describes the surface area (A), thermal conductivity (k), and thickness (L) of the insulation covering the HX. To derive the factor of ¼, consider if the cold inlet temperature of the HX is at environmental temperature. Then the difference between the average HX temperature and the environment is one half of the difference driving heat transfer between fluids, resulting in the factor of ¼.
Using the overall heat balance:
where the flux of each convective side is:
The average velocity of fluid is V, the cross-sectional area is A, the fluid density is , the fluid specific heat is Cp, and T is fluid temperature.
These equations are solved using MATLAB (The MathWorks, Inc, Natick, MA, USA) for multiple cases, which validate the model. A case with only two channels (no maldistribution or edge effect) compared the advanced model to a simple NTU model, shown in Equation (12):
The advanced model exactly reached the NTU result when the number of cells in the model approached infinity. A case with edge effect but no maldistribution was compared to results from a plate heat exchanger by Shah and Focke [53]. Results extrapolated from the advanced model for comparison with a plate heat exchanger were within 0.1% of Shah and Focke. Last, cases with maldistribution and axial conduction compared the advanced model to analytical results using the Peclet number (Pe) and the irregularity parameter (ε):
where the Peclet number is the ratio of convective heat transfer to transverse heat transfer as previously defined, and ±a is the channel diameter variation. The advanced model results shared good agreement with this analytical method. Table 1 and Table 2 show the default input and output of the MATLAB calculations. See [32] for more details on validation.

Table 1.
Default MATLAB Input.

Table 2.
Default MATLAB Output.
2.2. Heat Exchanger Prototype
The prototype HX was fabricated out of low-density polyethylene (LDPE) sheets that were 28 µm thick [17] on an open-source polymer laser welding system [15]. The sheets were laser welded together in a pattern that would create both the core and the manifolds of the HX. The HX was expanded with air and fixed into shape. The channels were nominally smooth hexagons with a hydraulic diameter of 2.1 mm in a pattern similar to a honeycomb, shown in Figure 3. The HX was tested with water-to-water flow at a variety of flow rates driven by a water head. The expansion process was not perfect, so a CT scan was used to ascertain the core channel heights as a function of their length [19].
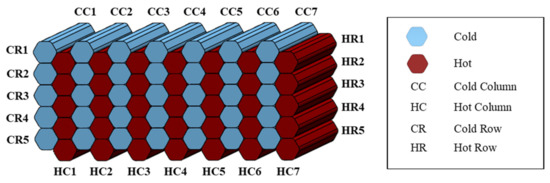
Figure 3.
A 70-channel model with 14 columns and 5 rows.
The present paper applies the advanced model to the prototype and discusses the results against experimental data. The conclusions note that this model can be applied to other HXs.
2.3. Heat Exchanger Manifold
The manifold was not included in the discretized model because of a lack of CT scan data. The monotonically varying flow rates across the HX in the flow correlation studies [32] could be thought to be due to manifold maldistribution, although the manifold is not explicitly modeled. This section reviews other possible impacts of the manifold for an idealized HX to extract the concepts with the goal of improving the advanced model’s fit to the experimental data.
One impact of the manifold is the heat transfer that occurs in it. For the prototype, the heat transfer area in the manifold is approximately 70% the size of the heat transfer area in the core. Therefore, the boundary condition at the core of the cold-water inlet could be significantly hotter, and the hot water inlet could be significantly colder due to heat transfer in the manifold.
For the ideal case of no flow maldistribution, the temperatures of the inlet boundary conditions to the core were varied linearly between two values. Since the cold is entering in the side tube, the first channel will have nearly the same temperature as the tube (see Figure 4).
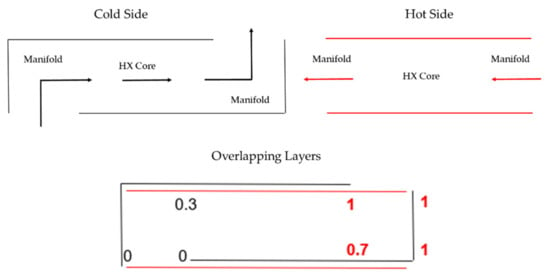
Figure 4.
Manifold heat transfer, symmetric temperature boundary conditions (numbers are normalized temperatures, red lines and bold numbers correspond to the hot side).
However, the water that goes to the far channel will warm up as it goes through the manifold. The hot inlet is not so straightforward. The path length for the hot flow in the manifold is the same for each channel. However, the side of the HX where the cold flow entered directly into the core will be cooler than the other side of the HX. Therefore, on the cooler side of the HX, the hot flow will cool down more. The extreme case would be the hot flow cooling down as much as the maximum that the cold flow warmed up (symmetric temperature boundary conditions) (see Figure 4). The other extreme case is the hot flows all warming up the same (asymmetric temperature boundary conditions) (see Figure 5).

Figure 5.
Manifold heat transfer, asymmetric temperature boundary conditions (numbers are normalized temperatures, red lines and bold numbers correspond to the hot side).
These boundary conditions were used in additional effectiveness trials on an idealized prototype with no channel height variation.
When flow maldistribution is added due to real channel height variations, the situation becomes more complex. The average deviation in temperature from the two boundary inlet conditions is no longer guaranteed to be the same. This is a small problem for randomly generated flow deviations, which were used in previous work for theoretical manifold investigation [32]. However, for the actual prototype channel height, there is some monotonic flow maldistribution. For instance, in order to conserve energy (with equal heat transfer in each manifold), with hot boundary conditions of 0.8 and 0.9, cold boundary conditions of 0 and 0.3 would be expected, but 0 and 0.46 was required.
This is not physically realistic, so the solution is to sum up the heat flux of pre-heating the cold water in the manifold and applying that same flux to the hot for post-cooling. Similarly, the heat flux of pre-cooling the hot flow in the other manifold is applied to the cold flow for post-heating.
3. Results
3.1. Flow Maldistribution with Measured Height Data
The measured height of the core of the prototype is shown in Figure 6, split into discretized cells (CT scan data were not available for the manifold). There are 26 cells for each channel in the prototype, and there are 70 channels. The data are organized such that the first 26 cells represent the channel in Cold Row 1–Cold Column 1 (see also Figure 3), the next 26 represent Cold Row 1–Cold Column 2, to the end of Cold Row 1. Then the next channel is Hot Row 1–Hot Column 1, to the end of Hot Row 1 and so on. Starting from Cold Row 1–Column 1, the first cold row ends at cell number 182, which can be seen on Figure 6 as the first sharp decrease in cell height because of the pinched sides on the layer. The next layer starting with Hot Row 1–Hot Column 1 goes from cell 183 to 365, and each layer following in increments of 182 cells. Note the lowest cell height is 0.115 mm which is the pinch height (minimum height required for modeling, see [32]). From these data, the change is more rapid at the top and bottom of the HX (left and right of the figure).
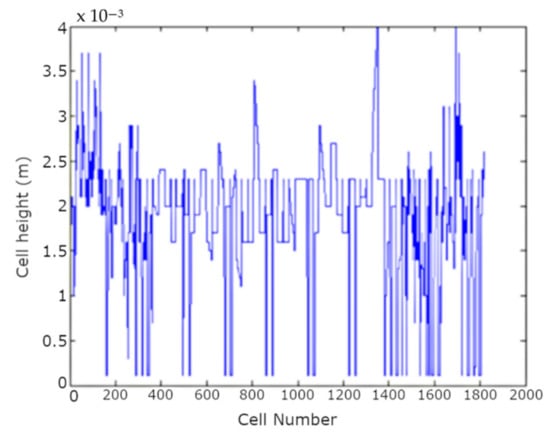
Figure 6.
Cell height for prototype.
The flow predicted by the advanced model in the actual HX based on channel heights in the core is shown in Figure 7, which shows the positive correlation between the hot and cold flows. The irregularity parameter, ε, characterizes the channel flow maldistribution with 1 being no maldistribution [52]. At high NTU, the effectiveness approaches the irregularity parameter. Based on the channel height geometry, the cold ε = 0.591, and the hot ε = 0.540. The sixth and seventh column channels are nearly all pinched off for both cold and hot flow. There is also less flow in the first column than in the center columns. This makes sense because gluing the layers on the sides of the HX pinched the side columns together.
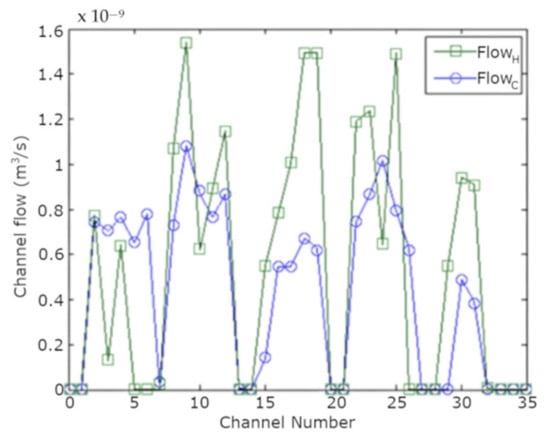
Figure 7.
Channel flow for the prototype with NTU = 100, showing positive correlation.
The effectiveness results at high NTU are very sensitive to the assumed insulation value for the supply tubes. A combination of fiberglass wrap and foam that was designed to enclose tubes was used, as was feasible for the shape at different points. Results are shown for the reasonable estimate of 1 cm of foam equivalent on average over the tubes.
The 10 experimental trials were simulated in the advanced model. The averaged results of the advanced model are compared with the experimental data in Figure 8. The overall root mean square (RMS) effectiveness error of 3.8% is larger than expected with the effectiveness expected experimental error of 0.7% and the flow rate experimental error of 1–2% (small effectiveness impact).
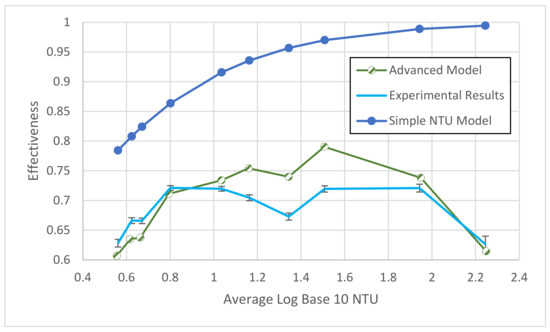
Figure 8.
Advanced model, experimental results with error bars, and simple NTU model average effectiveness as a function of average NTU.
The experimental case had ε = 0.54 and 0.59, but this irregularity parameter increased as high NTU allowed thermal coupling between the channels. A reasonable fit to the data was achieved with rigorous handling of the heat leak. This means that the internal effectiveness of the HX was high (>80%), but the heat leak brought effectiveness down.
3.2. Manifold Heat Transfer with Idealized HX
The error between the advanced model and experimental results suggests an unaccounted influence from the manifold. These next sections introduce the results of effectiveness trials at varying inlet temperatures that mimic specific conditions in the manifold, first without channel height variation in the HX.
The cases of NTU = 5 and NTU = 100 correspond to an advanced model effectiveness of 79% and 98%. Since the manifold takes up about 40% of the total heat transfer area, but part of it produces cross flow, which is not as effective, each manifold effectiveness was assumed to be 15%. Therefore, the cold effectiveness in the entry manifold would be 0% and 30% for all cases. The hot effectiveness in the entry manifold would be 0% and 30% for the symmetric case. For the asymmetric case, the hot effectiveness would be 15% and 15%.
The case of NTU = 5 was run first in the advanced model. The case of cold effectiveness in the entry manifold at 15% and 15% and hot effectiveness in the entry manifold at 15% and 15% is not physically realistic for the expanded HX (“equal case”), but it provides an interesting starting point. The overall η = 85.3%, which is consistent with η = 79% from the advanced model between the modified boundary conditions (not shown in graphs).
Figure 9, Figure 10, Figure 11 and Figure 12 show the effectiveness of each channel. The points are connected because the effectivenesses of nearby channels are correlated due to thermal coupling, similar boundary conditions, and similar expansion. Figure 9 and Figure 10 have identical channels (no flow maldistribution). The cold effectivenesses for the symmetric case are shown in Figure 10 (the hot is a mirror image). The cold effectiveness can approach the hot end boundary condition of 70% on the left side and 100% on the right. These graphs correspond to η = 0.679, with an extrapolated value of 0.688. By conservation of energy, if the cold flow was preheated in the manifold 15%, then since these are balanced flow cases, the hot flow would have to be cooled by 15% in the manifold. Therefore, the overall extrapolated η = 0.838. For the asymmetric case the overall extrapolated η = 0.845.
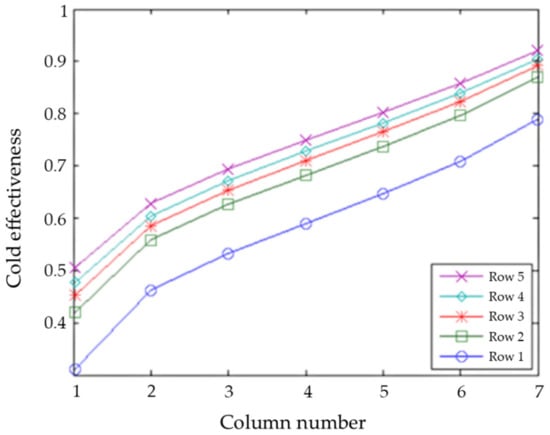
Figure 9.
Cold effectiveness with uniform flow, symmetric boundary temperatures, and NTU = 5 (the hot side is a mirror image).
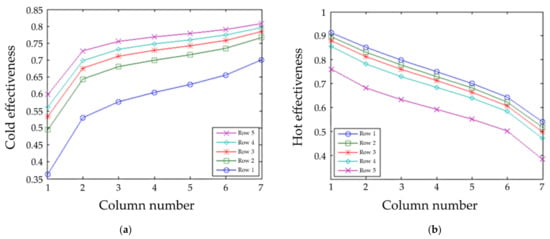
Figure 10.
Effectiveness with uniform flow, asymmetric boundary temperatures, and NTU = 5. (a) Cold side; (b) hot side.
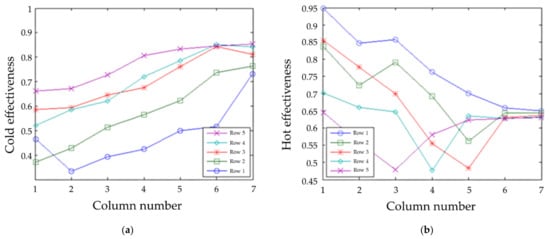
Figure 11.
Effectiveness with symmetric temperature boundary conditions and NTU = 5. (a) Cold side; (b) hot side.
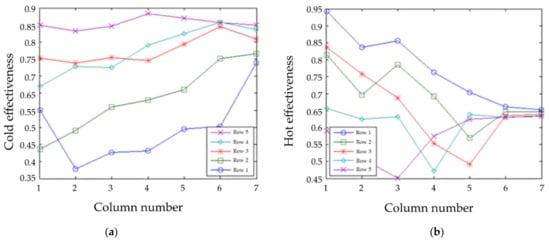
Figure 12.
Effectiveness with asymmetric boundary temperatures and NTU = 5. (a) Cold side; (b) hot Side.
Next the case of NTU = 100 was run. The symmetric case was again mirror images, see Figure 13. The temperature variation between the rows was much less than the NTU = 5 case because there is much stronger thermal coupling in the NTU = 100 case.
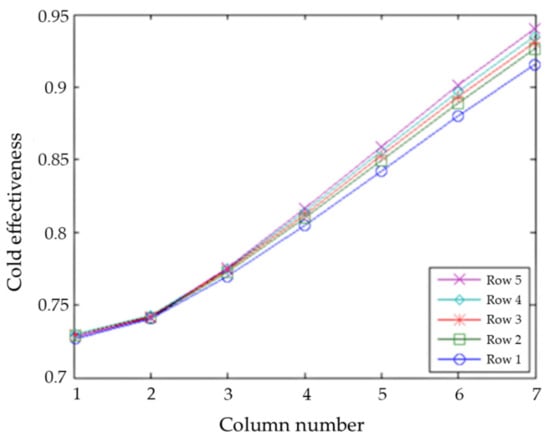
Figure 13.
Cold effectiveness with uniform flow, symmetric boundary temperatures, and NTU = 100 (hot side is mirror image).
As in the NTU = 5 case, the cold effectivenesses for uniform and symmetric flow were approaching the hot boundary conditions of 70% and 100%. The overall extrapolated η = 98.4%.
The NTU = 100 asymmetric case had temperatures that were again not mirror images, and this time the difference was extreme (see Figure 14).
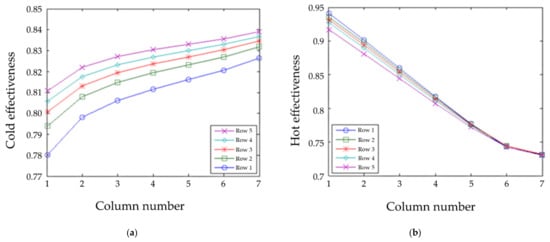
Figure 14.
Effectiveness with uniform flow, asymmetric boundary temperatures, and NTU = 100. (a) Cold side; (b) hot side.
The hot side behaved similarly to both sides of the symmetric case above. There was significant heat transfer from the left to the right side of the HX. The overall extrapolated effectiveness for the asymmetric case is 98.5%, which again is slightly higher than the symmetric effectiveness, again due to lower entropy production.
3.3. Manifold Heat Transfer with Measured Geometry
With channel variations from the HX measured geometry, the results from trials with NTU = 100 and symmetric temperature boundary conditions are shown in Figure 15. The extrapolated cold η = 76.8% the extrapolated hot η = 86.0%. However, different amounts of heat transfer occurred in the two manifolds, so the extrapolated overall η = 97.4% for both hot and cold. This is higher than the value of 96.2% without manifold heat transfer, so the manifold heat transfer was still beneficial despite flow maldistribution.
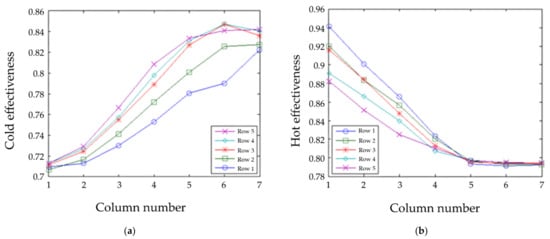
Figure 15.
Effectiveness with symmetric boundary temperatures and NTU = 100. (a) Cold side; (b) hot side.
For the prototype with NTU = 100 and asymmetric temperature boundary conditions, the cold and hot effectivenesses are shown in Figure 16. The extrapolated cold η = 82.2% and the extrapolated hot η = 85.8%.
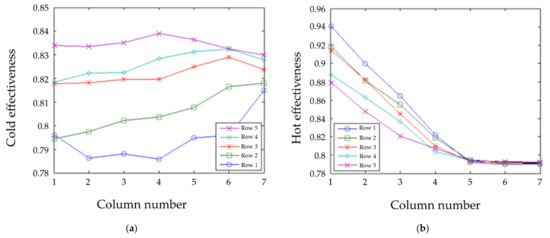
Figure 16.
Effectiveness with asymmetric boundary temperatures and NTU = 100. (a) Cold side; (b) hot side.
Again, different amounts of heat transfer occurred in the two manifolds, so the extrapolated overall η = 97.2% for both hot and cold. This is lower than the value of 97.4% for correlated, which is surprising. Perhaps this is due to this specific maldistribution producing more entropy for the uncorrelated case.
For the prototype with NTU = 5 and symmetric temperature boundary conditions, the cold and hot effectivenesses are shown in Figure 11. The extrapolated cold η = 56.2% and the extrapolated hot η = 65.5%. However, different amounts of heat transfer occurred in the two manifolds, so the extrapolated overall η = 76.8% for both hot and cold. This is lower than the value of 79.0% without manifold heat transfer, so surprisingly the manifold heat transfer was detrimental with maldistribution.
For the prototype with NTU = 5 and asymmetric temperature boundary conditions, the cold and hot effectivenesses are shown in Figure 12. The extrapolated cold η = 59.9% and the extrapolated hot η = 63.6%. Again, different amounts of heat transfer occurred in the two manifolds, so the extrapolated overall η = 75.2% for both hot and cold. As for NTU = 100, this is lower than the value of 76.8% for correlated. Manifold heat transfer decreased the overall effectiveness even more in this case.
The conclusion for manifold heat transfer coupled with flow maldistribution for the prototype is that the manifold heat transfer increases effectiveness at high NTU and decreases effectiveness at low NTU.
4. Discussion
Examining the trials with uniform flow and NTU = 5, Figure 9 and Figure 10, the effectiveness is significantly higher than the similar case with no manifold heat transfer, but lower than the “equal case.” This is reasonable because heat transfer between the columns would produce entropy, and the outlet temperatures not being equal cause mixing, producing more entropy. For the asymmetric case, the temperatures are not mirror images, as expected (Figure 10). The effectiveness is also greater than the symmetric case, which makes sense because there is less entropy production. It is reasonable that the highest effectiveness achieved is the hot left because it is approaching the most extreme temperature of the cold inlet. The cold effectivenesses on both the left and the right are approaching 85% (hot inlet), but the right approaches are closer because it is already preheated in the manifold.
As for the symmetric NTU = 100 cases (Figure 13 and Figure 15), one would expect an approach within 1% of the boundary conditions because of the very high NTU. However, only 93% was achieved on the hot side, but 73% was achieved on the cold side, which is higher than the boundary condition. This means that heat was actually flowing from the "cold" channels to the "hot" channels. That is to say, the flow did not violate the laws of thermodynamics but due to maldistribution the “cold” channels actually became warmer than the “hot” channels. This also explains the very small temperature deviation between rows where this occurred. This is because there is a very small temperature difference between the hot and cold channels, so it did not matter as much that row 1 for cold flow and row 5 for hot flow only have half as many neighbors, because less heat is being transferred regardless of the number of neighbors.
On the cold side of the asymmetric NTU = 100 cases (Figure 14 and Figure 16), one would expect a very close approach (within 1%) to the boundary condition with high NTU, thus yielding near η = 85%. This was true on the right side, but not for the left. The left started out at a colder temperature, but still one could think that the approach should have been closer. This can be explained by the transfer of heat from the left side to the right side of the HX.
The overall conclusion for varying the temperature boundary conditions with no flow maldistribution is that manifold heat transfer increases overall effectiveness roughly what would be expected by the greater heat transfer area in the manifolds.
Another impact of the manifold in addition to altering boundary conditions is the much higher flow resistance for the bent channels. The bent channels are those that enter one side of the HX, turn 90° to flow axially, and then exit the other side of the HX in a Z type pattern. The straight channels enter one end of the HX and exit the other end of the HX without turning. The relative impact of some of the core channels being pinched would be smaller in this case of bent flow. Therefore, the flow maldistribution on the bent side would be decreased. The current maldistribution on the hot and cold sides is correlated because of the significant pinching on the edges of the HX for both hot and cold. Reducing the flow variation on the bent side would still maintain positive correlation, but it would be less positively correlated. This would reduce the effectiveness somewhat.
A further impact of the manifold is flow maldistribution to the channels. With the Z-type flow, the flow resistance of each channel should be similar. However, there could be significant variations in the flow resistance for different channels in the manifold. This could occur in a uniform way, for instance by having significantly higher flow on one side of the HX than the other. In this case, the heat would have to conduct a much greater distance to smooth out the temperature differences. The Peclet number Pe is the ratio of convective heat transfer to diffusive heat transfer; in this case the latter is the transverse heat transfer. Therefore, the equivalent Pe would be significantly greater with this increased conduction distance.
If heat is conducted from the neighbor of a channel to the neighbor on the opposite side, the Nusselt number should be one (laminar flow). This is about one fourth the case of heating or cooling from all sides of one channel. Therefore, the thermal coupling between channels on opposite sides of the HX would be significantly less. This further reduces the gradient in effectiveness from NTU = 5 to NTU = 100.
It could be possible that the amount of maldistribution changed with flow rate. If maldistribution were significantly higher at high NTU, then the effectiveness could saturate more. A reason for this is the changing pressure experienced by the HX at different flow rates. At 0.01 atm., most of the 100 mm water driving pressure drop at high flow occurred in the manifold for the bent flow. It takes approximately 0.02 atm to inflate the channels to 1 mm high. With some assumptions about the width and length of the pinches, the average height for the bent flow in the manifold was estimated to be approximately 0.2 mm. This is consistent with the observation that the manifold did not contract in a measurable way in the axial direction. Since the pinches in the manifold are only ~0.2 mm, a 0.01 atm change in pressure due to flow rate could have significant effects on the maldistribution.
5. Conclusions
A finite difference model of a HX considered the edge effect, maldistribution, axial conduction, and heat leak. This advanced model is discretized so that it modeled the effects of maldistribution from the first principles, and it has been validated for multiple cases. Data for the channel height as a function of length in the core of the HX were obtained via CT scan. The results run on this core geometry were compared to the experimental results on an expanded microchannel HX. The RMS error was 3.8%.
Though the manifold geometries were not put into the model (because the data were not available), manifold heat transfer was approximated by varying the temperature boundary conditions on the core for the advanced model. With no flow maldistribution, manifold heat transfer increases the overall effectiveness roughly what would be expected by the greater heat transfer area in the manifolds.
However, manifold heat transfer coupled with flow maldistribution for the prototype causes a decrease in the effectiveness at low NTU, and an increase in effectiveness at high NTU.
Another impact of the manifold is the much higher flow resistance for the bent channels. This would reduce the effectiveness somewhat. A further impact of the manifold is flow maldistribution to the channels. The equivalent Pe would be significantly greater, so the effectiveness would saturate more at high NTU.
If heat is conducting from the neighbor of a channel to the neighbor on the opposite side, the Nusselt number should be one if the channels were square. This is approximately one fourth the case of heating or cooling from all sides of one channel. Thus, the thermal coupling between channels on opposite sides of the HX would be significantly less. This further reduces the increase in effectiveness from NTU = 5 to NTU = 100.
It could be possible that the amount of maldistribution changed with flow rate. If maldistribution were significantly higher at high NTU, then the effectiveness could saturate more.
Therefore, with further refinements of the advanced model, a better fit to the experimental data may be achieved. If manifold geometry could be obtained, improvements to microchannel heat exchanger modelling could be made by computing manifold heat transfer.
Author Contributions
Conceptualization, D.D.; methodology, D.D., J.M.P., M.B. and J.Z.; software, D.D.; validation, D.D.; formal analysis, D.D.; data curation, D.D.; writing—original draft preparation, D.D.; writing—review and editing, J.M.P., M.B., M.A., and J.Z.; visualization, D.D. and M.A.; supervision, J.M.P., M.B., and J.Z.; project administration, J.M.P., M.B., and J.Z.; funding acquisition, D.D., J.M.P., M.B., and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
Support for this project was received from the American Society of Heating, Refrigeration, and Air Conditioning Engineers Graduate Research Fellowship, the Office of Naval Research, the M.J. Murdock Charitable Trust, and the University of Colorado at Boulder Technology Transfer Office Proof of Concept Grant. J.P would like to acknowledge support from the Thompson Endowment. These funding sources had negligible influence on the research and publication process.
Acknowledgments
Ray Radebaugh, Ben Goebel, Kyle Jones, Joshua Klina and Moncef Krarti provided valuable feedback.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
| a | Channel diameter, m |
| A | Area, m2 |
| ax | Axial, subscript |
| C | Heat capacity rate, J/K |
| C | Cold, subscript |
| conv | Convection, subscript |
| cs | Cross section, subscript |
| Cp | Specific heat, J/kg-K |
| EMHX | Expanded microchannel heat exchanger |
| f | Fluid, subscript |
| h | Convective heat transfer coefficient, W/m2-K |
| H | Hot, subscript |
| HT | Heat transfer, subscript |
| HX | Heat exchanger |
| i | In, subscript |
| ins | Insulation, subscript |
| j | Axial direction, subscript |
| k | Thermal conductivity, W/m-K |
| k | Series index variable, subscript |
| L | Length, m |
| leak | Environmental leak, subscript |
| m | Number of discretized steps |
| Mass flow rate, kg/s | |
| max | Maximum, subscript |
| min | Minimum, subscript |
| NTU | Number of transfer units |
| o | Out, subscript |
| Pe | Peclet number |
| Re | Reynold’s number |
| Heat transfer rate, W | |
| T | Temperature, °C |
| tran | Transverse direction, subscript |
| U | Overall heat transfer coefficient, W/m2-K |
| V | Velocity, m/s |
| w | Wall, subscript |
| Δx | Cell step size, m |
| Effectiveness | |
| Axial conduction | |
| Heat leak | |
| Density, kg/m3 | |
| Irregularity |
References
- Master, B.I.; Chunangad, K.S.; Boxma, A.J.; Kral, D.; Stehlík, P. Most Frequently Used Heat Exchangers from Pioneering Research to Worldwide Applications. Heat Transf. Eng. 2006, 27, 4–11. [Google Scholar] [CrossRef]
- Markets and Markets. Available online: https://www.marketsandmarkets.com/Market-Reports/heat-exchanger-market-750.html (accessed on 18 January 2021).
- Jiang, P.-X.; Fan, M.-H.; Si, G.-S.; Ren, Z.-P. Thermal–Hydraulic Performance of Small Scale Micro-Channel and Porous-Media Heat-Exchangers. Int. J. Heat Mass Transf. 2001, 44, 1039–1051. [Google Scholar] [CrossRef]
- Dixit, T.; Ghosh, I. Review of Micro- and Mini-Channel Heat Sinks and Heat Exchangers for Single Phase Fluids. Renew. Sustain. Energy Rev. 2015, 41, 1298–1311. [Google Scholar] [CrossRef]
- Bhutta, A.; Mahmood, M.; Hayat, N.; Bashir, M.H.; Khan, A.R.; Ahmad, K.N.; Khan, S. CFD Applications in Various Heat Exchangers Design: A Review. Appl. Therm. Eng. 2012, 32, 1–12. [Google Scholar] [CrossRef]
- Ramesh, K.N.; Sharma, T.K.; Rao, G.A.P. Latest Advancements in Heat Transfer Enhancement in the Micro-Channel Heat Sinks: A Review. Arch. Comput. Methods Eng 2020, 28, 1–31. [Google Scholar] [CrossRef]
- UNICEF. The State of the World’s Children: Excluded and Invisible; UNICEF: New York, NY, USA, 2005. [Google Scholar]
- Pearce, J.M.; Denkenberger, D. Numerical Simulation of the Direct Application of Compound Parabolic Concentrators to a Single Effect Basin Solar Still. In Proceedings of the Solar Cookers and Food Processing 2006 International Conference, Granada, Spain, 12–16 July 2006; Volume 118, p. 7. [Google Scholar]
- Denkenberger, D.C.; Pearce, J.M. Design Optimization of Polymer Heat Exchanger for Automated Household-Scale Solar Water Pasteurizer. Designs 2018, 2, 11. [Google Scholar] [CrossRef] [Green Version]
- Tao, C.; Lee, H.; Hwang, Y.; Radermacher, R.; Chun, H. Performance Investigation of Engine Waste Heat Powered Absorption Cycle Cooling System for Shipboard Applications. Appl. Therm. Eng. 2015, 90, 820–830. [Google Scholar] [CrossRef]
- Daniel, K.F.; Peter, J.G. Open-Source Hardware Is a Low-Cost Alternative for Scientific Instrumentation and Research. Mod. Instrum. 2012, 1, 2. [Google Scholar] [CrossRef] [Green Version]
- Pearce, J.M. Cut Costs with Open-Source Hardware. Nature 2014, 505, 618. [Google Scholar] [CrossRef] [Green Version]
- Pearce, J.M. Quantifying the Value of Open Source Hardware Development. Mod. Econ. 2015, 6, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Pearce, J.M. Open-Source Lab: How to Build Your Own Hardware and Reduce Research Costs; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Laureto, J.J.; Dessiatoun, S.V.; Ohadi, M.M.; Pearce, J.M. Open Source Laser Polymer Welding System: Design and Characterization of Linear Low-Density Polyethylene Multilayer Welds. Machines 2016, 4, 14. [Google Scholar] [CrossRef] [Green Version]
- Arie, M.A.; Shooshtari, A.H.; Tiwari, R.; Dessiatoun, S.V.; Ohadi, M.M.; Pearce, J.M. Experimental Characterization of Heat Transfer in an Additively Manufactured Polymer Heat Exchanger. Appl. Therm. Eng. 2017, 113, 575–584. [Google Scholar] [CrossRef] [Green Version]
- Denkenberger, D.C.; Brandemuehl, M.J.; Pearce, J.M.; Zhai, J. Expanded Microchannel Heat Exchanger: Design, Fabrication, and Preliminary Experimental Test. Proc. Inst. Mech. Eng. Part. A J. Power Energy 2012, 226, 532–544. [Google Scholar] [CrossRef] [Green Version]
- Balasubramanian, K.; Lee, P.S.; Jin, L.W.; Chou, S.K.; Teo, C.J.; Gao, S. Experimental Investigations of Flow Boiling Heat Transfer and Pressure Drop in Straight and Expanding Microchannels—A Comparative Study. Int. J. Therm. Sci. 2011, 50, 2413–2421. [Google Scholar] [CrossRef]
- Denkenberger, D.C.; Brandemuehl, M.J.; Pearce, J.M.; Zhai, J. Expanded Microchannel Heat Exchanger: Nondestructive Evaluation. Heat Transf. Eng. 2019, 40, 1671–1679. [Google Scholar] [CrossRef] [Green Version]
- Harpole, G.M.; Eninger, J.E. Micro-Channel Heat Exchanger Optimization. In Proceedings of the Seventh IEEE Semiconductor Thermal Measurement and Management Symposium, Phoenix, AZ, USA, 12–14 February 1991; pp. 59–63. [Google Scholar] [CrossRef]
- Kawano, K.; Sekimura, M.; Minakami, K.; Iwasaki, H.; Ishizuka, M. Development of Micro Channel Heat Exchanging. JSME Int. J. Ser. B Fluids Therm. Eng. 2001, 44, 592–598. [Google Scholar] [CrossRef] [Green Version]
- Harris, C.; Kelly, K.; Wang, T.; McCandless, A.; Motakef, S. Fabrication, Modeling, and Testing of Micro-Cross-Flow Heat Exchangers. J. Microelectromechanical Syst. 2002, 11, 726–735. [Google Scholar] [CrossRef]
- Shaoi, B.; Wang, L.; Li, J.; Sun, Z. Application of Thermal Resistance Network Model in Optimization Design of Micro-channel Cooling Heat Sink. Int. J. Numer. Methods Heat Fluid Flow 2009, 19, 535–545. [Google Scholar] [CrossRef]
- Majnis, M.F.; Fung, C.K. Computational Fluid Dynamic Simulation Analysis of Effect of Microchannel Geometry on Thermal and Hydraulic Performances of Micro Channel Heat Exchanger. ARFMTS 2019, 62, 198–208. [Google Scholar]
- Gomse, D.; Kochenburger, T.M.; Grohmann, S. Modeling of Two-Phase Heat Exchangers with Zeotropic Fluid Mixtures. J. Heat Transf. 2018, 140, 5. [Google Scholar] [CrossRef]
- Hegde, P.; Seetharamu, K.N.; Quadir, G.A.; Aswathanarayana, P.A.; Abdullah, M.Z.; Zainal, Z.A. Thermal Analysis of Micro-channel Heat Exchangers with Two-phase Flow Using FEM. Int. J. Numer. Methods Heat Fluid Flow 2005, 15, 43–60. [Google Scholar] [CrossRef] [Green Version]
- Raghuraman, D.R.S.; Thundil Karuppa Raj, R.; Nagarajan, P.K.; Rao, B.V.A. Influence of Aspect Ratio on the Thermal Performance of Rectangular Shaped Micro Channel Heat Sink Using CFD Code. Alex. Eng. J. 2017, 56, 43–54. [Google Scholar] [CrossRef] [Green Version]
- Nonino, C.; Savino, S.; Giudice, S.D. FEM for the 3-D Analysis of Conjugate Conduction-Convection Heat Transfer in Cross-Flow Micro Heat Exchangers. J. Numer. Methods Heat Fluid Flow 2015, 25, 1322–1339. [Google Scholar] [CrossRef]
- Nonino, C.; Savino, S. Numerical Investigation on the Performance of Cross-Flow Micro Heat Exchangers. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 745–766. [Google Scholar] [CrossRef]
- Ariyo, D.O.; Bello-Ochende, T. Constructal Design of Two-Phase Stacked Microchannel Heat Exchangers for Cooling at High Heat Flux. Int. Commun. Heat Mass Transf. 2021, 125, 105294. [Google Scholar] [CrossRef]
- Hasan, M.I.; Hasan, H.M.; Abid, G.A. Study of the Axial Heat Conduction in Parallel Flow Microchannel Heat Exchanger. J. King Saud Univ. Eng. Sci. 2014, 26, 122–131. [Google Scholar] [CrossRef] [Green Version]
- Denkenberger, D.C.; Brandemuehl, M.J.; Zhai, J.; Pearce, J.M. Finite Difference Heat Exchanger Model: Flow Maldistribution with Thermal Coupling. Heat Transf. Eng. 2021, 42, 889–903. [Google Scholar] [CrossRef]
- Bossan, D.; Grillot, J.M.; Thonon, B.; Grandgeorge, S. Experimental Study of Particulate Fouling in an Industrial Plate Heat Exchanger. JEH(T) 1995, 2, 167–175. [Google Scholar] [CrossRef]
- Hoysall, D.C.; Keniar, K.; Garimella, S. Addressing Two-Phase Flow Maldistribution in Microchannel Heat and Mass Exchangers. J. Heat Transf. 2018, 140, 11. [Google Scholar] [CrossRef]
- Haseler, L.E. Layer Pattern Effects in Plate-Fin Heat Exchangers. Am. Soc. Mech. Eng. Heat Transf. Div. 1987, 75, 119–125. [Google Scholar]
- Mondt, J. Effects of Nonuniform Passages on Deepfold Heat Exchanger Performance. J. Eng. Gas. Turbines Power 1977, 99, 657–663. [Google Scholar] [CrossRef]
- Papautsky, I.; Ameel, T.; Frazier, A.B. A Review of Laminar Single-Phase Flow in Microchannels. In Proceedings of the 2001 ASME International Mechanical Engineering Congress and Exposition, New York, NY, USA, 11–16 November 2001; Volume 2, pp. 3067–3075. [Google Scholar]
- Rostami, A.; Mujumdar, A.; Saniei, N. Flow and Heat Transfer for Gas Flowing in Microchannels: A Review. Heat Mass Transf. 2002, 38, 359–367. [Google Scholar] [CrossRef]
- Kandlikar, S.G. History, Advances, and Challenges in Liquid Flow and Flow Boiling Heat Transfer in Microchannels: A Critical Review. J. Heat Transf. 2012, 134, 3. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Colin, S.; Peles, Y.; Garimella, S.; Pease, R.F.; Brandner, J.J.; Tuckerman, D.B. Heat Transfer in Microchannels—2012 Status and Research Needs. J. Heat Transf. 2013, 135, 9. [Google Scholar] [CrossRef] [Green Version]
- Morini, G.L. Single-Phase Convective Heat Transfer in Microchannels: A Review of Experimental Results. Int. J. Therm. Sci. 2004, 43, 631–651. [Google Scholar] [CrossRef]
- Chiou, J. The Advancement of Compact Heat Exchanger Theory Considering the Effects of Longitudinal Heat Conduction and Flow Nonuniformity. In Proceedings of the Symposium on Compact Heat Exchangers, New York, NY, USA; 1980; Volume 10, pp. 101–121. [Google Scholar]
- Radebaugh, R. Heat Transfer Issues in Cryogenic Catheters. In Microscale Heat Transfer Fundamentals and Applications; Springer: New York, NY, USA, 2005; pp. 445–464. [Google Scholar]
- Chowdhury, K.; Sarangi, S. Performance of Cryogenic Heat Exchangers with Heat Leak from the Surroundings. In Advances in Cryogenic Engineering; Springer: New York, NY, USA, 1984; pp. 273–280. [Google Scholar]
- Polley, G.T.; Abu-Khader, M.M. Compensating for End Effects in Plate-and-Frame Heat Exchangers. Heat Transf. Eng. 2005, 26, 3–7. [Google Scholar] [CrossRef]
- Heggs, P.J.; Scheidat, H.-J. Thermal Performance of Plate Heat Exchangers with Flow Maldistribution; ASME: New York, NY, USA, 1992; Volume 201, pp. 87–93. [Google Scholar]
- Wen, J.; Li, Y. Study of Flow Distribution and Its Improvement on the Header of Plate-Fin Heat Exchanger. Cryogenics 2004, 44, 823–831. [Google Scholar] [CrossRef]
- Selimovic, F.; Bruun, T.; Sundén, B. Computational Analysis of Gas Flow and Heat Transport Phenomena. In Monolithic Structures for High Temperature Processes; American Society of Mechanical Engineers: New York, NY, USA, 2005; pp. 87–96. [Google Scholar]
- Smith, E.M. Advances in Thermal Design of Heat Exchangers: A Numerical Approach: Direct-Sizing, Step-Wise Rating, and Transients, 1st ed.; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Zou, Y.; Tuo, H.; Hrnjak, P.S. Modeling Refrigerant Maldistribution in Microchannel Heat Exchangers with Vertical Headers Based on Experimentally Developed Distribution Results. Appl. Therm. Eng. 2014, 64, 172–181. [Google Scholar] [CrossRef]
- Nellis, G. A Heat Exchanger Model That Includes Axial Conduction, Parasitic Heat Loads, and Property Variations. Cryogenics 2003, 43, 523–538. [Google Scholar] [CrossRef]
- Gotovsky, M.; Fedorovich, E.; Firsova, E.; Blagoveshchensky, A.; Mizonov, N.; Piskunov, V.; Vinokurov, V. Thermal Effectiveness of Heat Exchangers: Effect of Manufacturing Inaccuracies and Deformation of Tube Bundles. Heat Transf. Eng. 1985, 6, 52–57. [Google Scholar] [CrossRef]
- Shah, R.; Focke, W. Plate heat exchangers and their design theory. Heat Transf. Equip. Des. 1988, 227. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).