Abstract
This paper presents the effect of grinding wheel contact stiffness on the plunge grinding cycle. First, it proposes a novel model of the generalized plunge grinding system. The model is applicable to all plunge grinding operations including cylindrical, centerless, shoe-centerless, internal, and shoe-internal grinding. The analysis of the model explicitly describes transient behaviors during the ramp infeed and the spark-out in the plunge grinding cycle. Clarification is provided regarding the premise that the system stiffness is composed of machine stiffness and wheel contact stiffness, and these stiffnesses significantly affect productivity and grinding accuracy. The elastic deflection of the grinding wheel is accurately measured and formulas for representing the deflection nature under various contact loads are derived. The deflection model allows us to find the non-linear contact stiffness with respect to the normal load. The contact stiffnesses of four kinds of grinding wheels with different grades and bond materials are presented. Both cylindrical grinding and centerless grinding tests are carried out, and it is experimentally revealed that the time constant at ramp infeed and spark-out is significantly prolonged by reducing the grinding force. It is verified that a simulation of the grinding tests using the proposed model can accurately predict critical parameters like forces and machine deflection during plunge grinding operations. Finally, this paper provides a guideline for grinding cycle design in order to achieve the required productivity and grinding accuracy.
1. Introduction
In the plunge grinding of cylindrical components, the grinding performance is assessed by productivity and grinding accuracy. The productivity in the number of finished parts per unit time is determined by the grinding cycle time consisting of the plunge-infeed time and the spark-out time. As the actual infeed to the CNC command has a time delay, the required cycle time is largely affected by the system stiffness. On the other hand, the grinding accuracy is significantly governed by the system stiffness. In fact, the actual depth of cut always lower than the command value due to the elastic deflections of the grinding system. These deflections become the root cause of geometrical errors such as size error, profile error, roundness error, etc., in the ground products.
The system stiffness is composed of the grinding machine stiffness and the contact stiffness of grinding wheel. The machine stiffness has a linear characteristic under general grinding conditions, and it is relatively easy to integrate it to the grinding system. However, it is well known that the contact deflection in wheel-workpiece interactions shows a non-linear characteristic. As the result, the process parameters like grinding forces in the grinding cycle exhibit complicated behaviors and the phenomena make it difficult to design a proper grinding cycle. Thus, it is crucial to take the influence of contact stiffness on the grinding processes into account in order to achieve the required productivity and accuracy.
There are many publications related to the wheel contact stiffness. However, no published paper has described the effect of wheel contact stiffness on the plunge grinding cycle. Much research has been done in the area of grinding wheel deflection. Hahn [1] first suggested that the deflection of the wheel surface could explain the differences in material removal rates arising from the conformity difference between internal and external grinding. Peklenik [2] proposed the use of the thermocouple method to measure grinding temperature and contact length. He showed a difference in the effective number of cutting points with the wheel grade which attributed to differences in wheel elasticity. Snoeys and Wang [3] carried out static loading tests to verify their model of grain mounted on springs and concluded that the model provided more realistic values for the deflection of the wheel.
Brown, Saito, and Shaw [4] analyzed the influence of elastic deflection on contact length and established a contact length model using Hertzian theory. Kumar and Shaw [5] analyzed the deflection of the grinding wheel and workpiece separately and concluded that the predominant deflection was due to the grinding wheel, not the workpiece. Krug and Honcia [6] estimated the amount of local wheel deflection and found that it would be on the order of 1 μm for a vitrified wheel and 2.5 μm for a resinoid wheel.
Nakayama, Brecker, and Shaw [7] conducted experiments to measure the deflection associated with an individual grain and showed that the local elastic deformation of the grain was the same order of magnitude as the undeformed chip thickness. Nakayama [8] observed deflection of the grains that behaved as if the grains on the wheel were supported by non-linear springs. Zhou and Lutterwelt [9] presented a measuring method to identify the maximum contact length and local length at the wheel-work contact zone. Rowe et al. [10] proposed a model based on the theory of cylinders in contact, including the effect of grains, and explained why measured contact length can be 50% to 200% greater than geometric contact length.
Hucker, Farris, and Chandrasekar [11] conducted grinding tests to measure machine and wheel deflection under various grinding loads and concluded that the contact stiffness of CBN wheels is about three times greater than that of Al2O3 wheels. Yamada et al. [12,13] proposed a model of a wheel consisting of rigid body and spring elements and measured the contact stiffness of the wheel under both stationary conditions and grinding operations. Papanikolaou and Salonitis [14] applied a three-dimensional molecular dynamics simulation to investigate the effect of contact stiffness on grinding processes under various grinding speeds.
Self-excited regenerative chatter vibrations are another aspect of the contact stiffness of the wheel that havet been extensively investigated. Chatter vibrations are generally associated with the dynamic compliances of the grinding machine, and a great deal of research has been devoted to understanding these instabilities [15,16,17,18,19]. Snoeys and Brown [20] proposed a model representing work-regenerative and wheel-regenerative chatter vibrations in cylindrical grinding. The model was represented by a block diagram with feedback loops of machine compliances, including the contact stiffness of the wheel.
Inasaki [21] experimentally investigated wheel contact stiffness with hard-spring characteristics and pointed out that it changed with grinding conditions such as speed ratio, depth of cut, etc. He discussed the effects of contact stiffness on the stability of the chatter vibrations. Miyashita, Hashimoto, and Kanai [22] analyzed the dynamic stability of a centerless grinding system and proposed a new setup index for suppressing work-regenerative chatter vibrations. Their model indicated that the contact stiffnesses of both the grinding wheel and regulating wheel had significant influence on chatter vibrations. Hashimoto, Kanai, and Miyashita [23] investigated the growing mechanism of chatter vibrations in cylindrical grinding and proposed a stabilization index related to the wheel contact stiffness for selecting the grinding wheel specifications. A parameter related to the dynamic time constant was introduced and discussed the in-process measurement of the time constant to predict the stability of the chatter vibrations.
In the field of grinding cycle investigations, King and Hahn [24] analyzed a cylindrical grinding system and introduced a concept of time constant which was applicable to the cylindrical grinding, but not to centerless grinding. Malkin and Koren [25] investigated the plunge grinding cycle and proposed accelerated spark-out to reduce the cycle time. Chiu and Malkin [26] presented a simulation of the grinding parameters specific to infeed cylindrical grinding.
The aforementioned research concentrated primarily on the modeling and measurement of real contact length and the deflection characteristics at the local contact zone of the wheel. This literature revealed the nature of wheel elastic deflection and provided valuable evidence about contact stiffness with hard-spring characteristics. However, the extensive knowledge gleaned about wheel deflection has been little used in practical applications. Current practices for determining the operational grinding conditions of the grinding cycle still largely rely on a cut-and-try method. One reason for this may be the disconnection between the scientific parameters used in past research and the practical parameters required for real-world grinding operations.
It is necessary to establish practical procedures for setting up the proper grinding conditions including grinding stocks, infeed rates, spark-out time, and the selection of the grinding wheel. Furthermore, clear guidelines for designing the grinding cycle that take the effect of contact stiffness on grinding performance into account are indispensable.
This paper presents the effect of grinding wheel contact stiffness on the plunge grinding cycle. It also provides guidelines for the design of the grinding cycle. First, the generalized plunge grinding system including cylindrical, centerless, shoe-centerless, internal, and shoe-internal grinding is explicitly described and analyzed in terms of system outputs corresponding to the inputs of the plunge grinding conditions. The analysis describes the influence of system stiffness on the time constant that governs the transient behaviors of the process parameters such as forces, power, and machine elastic deflection. Additionally, it clarifies that system stiffness is composed of machine stiffness and wheel contact stiffness. These stiffnesses significantly affect the grinding performance indicators such as productivity and grinding accuracy.
The elastic deflection of the grinding wheel is accurately measured and a function for representing the deflection nature under various contact loads is derived. The function allows us to find the non-linear contact stiffness with respect to the normal load. The contact stiffnesses of four kinds of grinding wheels with different grades and bond materials are presented, and the changes in contact stiffness after dressing are discussed.
Experimental tests for both cylindrical grinding and centerless grinding are conducted, and it is experimentally confirmed that the time constant at ramp infeed and spark-out is significantly prolonged by reducing the grinding force. It is verified that a simulation of the grinding tests using the proposed model can accurately predict critical parameters like forces, machine deflection, and system stiffness during plunge grinding operations. Finally, this paper emphasizes that it is vital to take the effect of wheel contact stiffness into consideration during the design of the plunge grinding cycle.
2. Plunge Grinding System and the Grinding Cycle
2.1. Plunge Grinding System
In order to investigate the effect of the grinding wheel’s elastic contact deflection on the plunge grinding process, it is necessary to clarify the relationship between the operational setup parameters and the machine characteristics (including the abrasive tools). There are several methods of plunge internal and external grinding, as shown in Figure 1. The grinding method parameter c is used to identify the influence of the amount of infeed on the size reduction of the workpieces. In the centerless grinding and shoe centerless grinding methods (Figure 1d,e), the amount of infeed becomes the diameter reduction of the workpieces and c = 0.5 is denoted. On the other hand, in Figure 1a–c,f, the amount of infeed gives the radial reduction on the external or internal ground surface of the workpieces, and c = 1.0 is assigned for these methods.
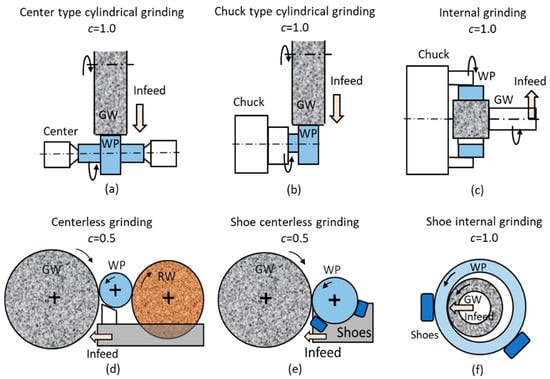
Figure 1.
Plunge grinding operations and the method parameter c. (a) Center type cylindrical grinding; (b) Chuck type cylindrical grinding; (c) Internal grinding; (d) Centerless grinding; (e) Shoe centerless grinding; (f) Shoe internal grinding.
In plunge grinding, as shown in Figure 1, the grinding wheel mounted on the infeed slide is fed into the workpiece as a command infeed If. The actual infeed can be expressed by:
where t is the grinding time and is the elastic deflection of the grinding system including the contact deflection of grinding wheel. The actual infeed rate is:
The SMRR (specific material removal rate) is expressed by:
where is the internal or external diameter of the workpiece. The MRR (material removal rate) is:
where b is the grinding width. The normal grinding force can be written as follows:
where η is the force ratio of Fn to tangential force Ft, is the grinding speed, and u is the specific energy. The elastic deflection of the grinding system in the infeed direction can be expressed by:
where is the equivalent system stiffness.
Equivalent system stiffness consists of the stiffness of each machine structure involved in the grinding system and the stiffness of the grinding wheel. The main components of equivalent stiffness are shown in Figure 2. Material removal by grinding generates a normal grinding force as described in Equation (5). The force gives the elastic deflection , which is determined by the system stiffness . Figure 2a,b illustrate the stiffnesses of the grinding wheel support system and the workpiece support system, respectively. Figure 2c shows the stiffness of workpiece itself, which cannot be ignored when is low (as in the case of thin-wall rings). Figure 2d shows the local deflection at the contact area between the grinding wheel and the workpiece, and is the contact stiffness of the grinding wheel.
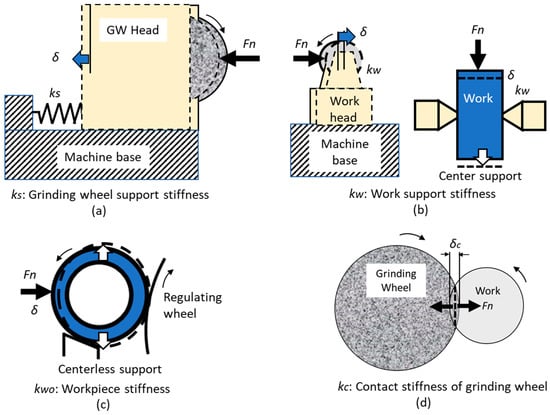
Figure 2.
Components of equivalent system stiffness in plunge grinding system. (a) Stiffness of grinding wheel head; (b) Stiffness of work head; (c) Stiffness of workpiece; (d) Contact stiffness of grinding wheel.
The equivalent system stiffness is expressed by:
where is the mechanical stiffness represented by the stiffness of each mechanical structure related to the grinding system:
where is the i-th stiffness of the mechanical structure relevant to the grinding system and n is the degrees of freedom. Since each component of mechanical stiffness has a linear spring characteristic, remains a constant during the plunge grinding process. On the other hand, the wheel contact stiffness has the non-linear characteristics referred to as “hard-spring.” As a result, the equivalent system stiffness behaves as a non-linear spring, which changes in stiffness value depending on the grinding conditions. As such, it is crucial to take the spring characteristics at the contact area of the grinding wheel into account in the design of the plunge grinding cycle.
The deflection given by Equation (6) is fed back to Equation (1). Thus, the plunge grinding process can be described as a closed-loop system repeating Equations (1)–(6). By using Equations (3)–(5), Equation (6) can be rewritten as follows:
where T is the time constant of the grinding system.
The time constant T is one of the most critical parameters in the plunge grinding system.
The Laplace transformation of Equations (1)–(6) leads to the following equations:
where s is the Laplace operator. Actual infeed , actual infeed rate , SMMR normal grinding force and elastic deflection are Laplace functions.
Figure 3 shows a block diagram of the plunge grinding system representing the transfer functions given by Equations (11)–(16). The plunge grinding system can be expressed by a closed-loop feedback system. The transfer function G(s) of the system is represented by:
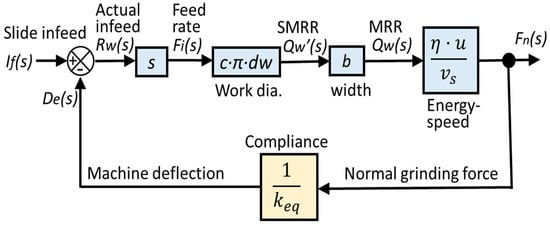
Figure 3.
Block diagram of the plunge grinding system.
Thus, plunge grinding can be represented by a first-order lag system with the time constant T given by Equation (10). The cut-off frequency (Hz) of the plunge grinding system is represented by:
2.2. Analysis of Plunge Grinding Cycle
The plunge grinding cycle starts with a rapid forward infeed of the slide from the home position. Typically, the slide feed rate is then changed for rough, semi-finish or finish grinding. After infeed grinding, spark-out grinding is performed in order to reduce the elastic deflection of the grinding system, followed by the rapid retraction of the slide to the home position. To study the effect of the wheel’s contact stiffness on the plunge grinding process, this paper focuses on a primary grinding cycle consisting of plunge grinding with a constant infeed rate followed by spark-out grinding.
The diagram in Figure 4a depicts the plunge grinding operation. The infeed slide is rapidly fed forward to position P from the home position H. Then, the infeed rate is changed to a constant infeed rate at point P. At some point O, which is determined by the size of the incoming workpiece, the grinding wheel mounted on the slide contacts the workpiece at the infeed rate and plunge grinding starts. At position A, the slide infeed is stopped and spark-out grinding starts. At point B, the slide is rapidly retracted to the home position H. Figure 4b shows the primary cycle with plunge grinding time and spark-out time
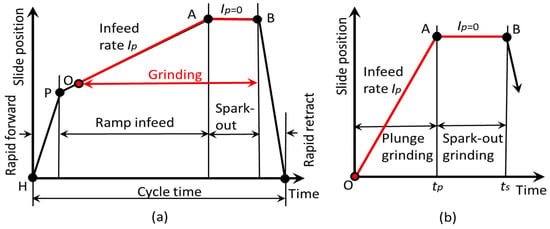
Figure 4.
Plunge grinding cycle. (a) Diagram of plunge grinding operations; (b) Primary cycle of plunge grinding.
During plunge grinding , the actual feed rate can be obtained by the following equations [27]:
The actual infeed position is:
The normal grinding force is:
The grinding power is:
The deflection causing the size and roundness error is obtained by:
When plunge grinding time is long enough compared to time constant T, the above Equations (20), (22), (24), and (26) for spark-out grinding can be approximately represented by the following equations:
Figure 5 is an example simulation of the plunge grinding process. The actual slide position (Figure 5a) is calculated by Equations (21) and (22). The actual slide position delays the command and gradually catches up. Eventually, it attains the same slope as the command feed. The asymptote of the actual infeed curve intersects at time T on the horizontal axis. The position difference between the command feed and the actual feed represents the system deflection and is also the size error. The deflection is reduced with increased spark-out time. The grinding power found by Equations (25) and (26) is the response to the ramp infeed command with a constant rate and the no-infeed command for the spark-out.
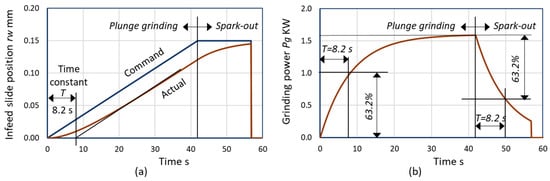
Figure 5.
Simulation of plunge grinding processes (conditions: c = 1.0, dw = 177.8 mm, b = 30 mm, vs. = 45 m/s, η = 2.0, keq = 2421 N/mm, u = 26.7 J/mm3, S = 0.3 mm, Qw′ = 2.0 mm3/mm·s, Ip = 3.58 μm/s, tp = 41.9 s, ts = 56.9 s). (a) Infeed slide position; (b) Grinding power.
The power is gradually increased and finally reaches a constant value. The time constant T is defined as the time when the power reaches 63.2% ( of the final value. The definition of T can be applied to the spark-out grinding shown in Figure 5b. The transient curves of other parameters, including the actual infeed rate , the normal grinding force and the deflection , follow the curve of Figure 5b.
2.3. The Effect of Grinding Wheel Contact Stiffness on the Plunge Grinding Process
As mentioned above, system stiffness consists of a constant mechanical stiffness and contact stiffness of the grinding wheel with non-linear characteristics. In this section, the effect of system stiffness (particularly wheel contact stiffness ) on the plunge grinding process is discussed.
Figure 6 shows the effect of system stiffness on the plunge grinding process. The response of the grinding power is increased with increased system stiffness. Accordingly, the greater the system stiffness , the shorter the time constant T. In the design of a plunge grinding cycle, the spark-out time can be reduced by increasing system stiffness.
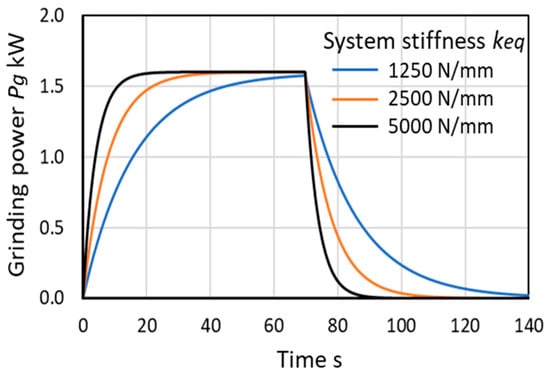
Figure 6.
The effect of system stiffness on the plunge grinding process.
Figure 7 presents the effect of system stiffness on the time constant T. T becomes longer where becomes smaller. By using Equations (7) and (10), the time constant T can be rewritten as follows:
where F is the ratio of normal grinding force to infeed rate fi.
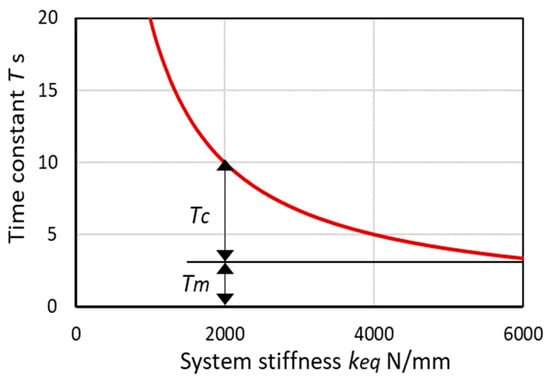
Figure 7.
The effect of system stiffness on the time constant.
Given that machine stiffness is a constant, the machine time constant also becomes a constant determined by the grinding machine. On the other hand, wheel contact stiffness has a non-linear characteristic and is dependent on the applied load. In a grinder with a constant machine stiffness , the time constant T is composed of machine time constant and contact time constant , as shown in Figure 7.
3. Measurement of Contact Stiffness of Grinding Wheel
3.1. Experimental Setup
In order to measure the contact stiffness, various grinding wheels were mounted on a center-type cylindrical grinder. A workpiece was supported by the centers of the main work head and tailstock head. The machine and workpiece specifications are shown in Table 1. The specifications of four kinds of grinding wheels are shown in Table 2.

Table 1.
Specifications of applied grinding machine and workpiece.

Table 2.
Specifications of grinding wheels tested.
The experimental setup is illustrated in Figure 8. The main shaft and the tailstock shaft were supported by hydrostatic bearings. Pressure gauges were installed to measure the pocket pressures of the hydrostatic bearings. So, the normal load L acting on the contact area between the workpiece and the wheel can be measured by detecting the pressure differences of the pockets in the hydrostatic bearings. Also, a load compensator [28] was attached to the machine. The compensator provided the same force as the detected load L to the workpiece. Therefore, the effective radial stiffness of the workpiece was significantly increased from 10.4 kN/mm to 200 kN/mm by the load compensator. The contact deflection of the grinding wheel can be found by measuring the deflection at the flange of the grinding wheel and the workpiece deflection . The deflections and are measured with cantilever type electric micrometers. The estimated measurement error is which is accurate enough compared with the amounts of deflections and . The micrometers are mounted on the base of the grinding machine. The difference ( − ) corresponds to the wheel deflection .
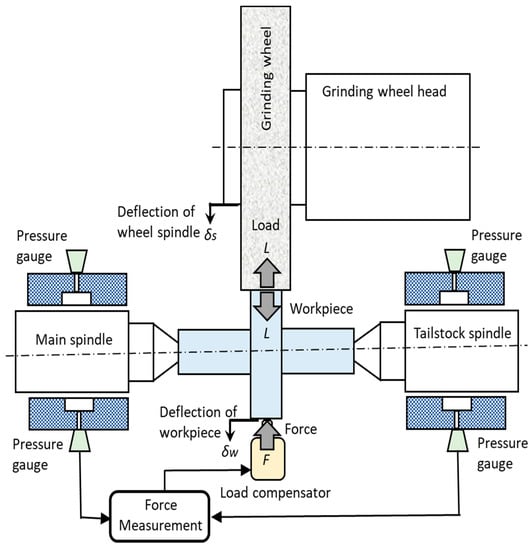
Figure 8.
Experimental setup.
3.2. Footprint Method
The workpieces painted black were pressed with a normal load L to the grinding wheel as shown in Figure 8. Both shafts of the workpiece and the wheel were locked in rotation. The contact footprints of the wheel were left on the surface of the workpiece, and the contact length was measured with a microscope. This paper names the method “footprint method”.
Figure 9a,b describe the contact length and the contact deflection for external grinding and internal grinding, respectively. Contact deflection is approximately expressed by:
where is the equivalent wheel diameter represented by:
where and are the diameters of grinding wheel and workpiece, respectively. The + sign is used for external grinding and the − sign for internal grinding.
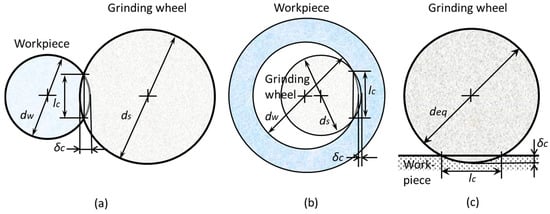
Figure 9.
Contact length and deflection. (a) External grinding; (b) Internal grinding; (c) Equivalent wheel diameter.
In the external grinding shown in Figure 9a, is always less than both and . In the internal grinding shown in Figure 9b, is always bigger than and . Typically, the contact length for internal grinding is much longer than that of external grinding. The contact situation can be considered equivalent to one in which a flat-plate workpiece is ground by a surface grinder with the grinding wheel (diameter ), as shown in Figure 9c.
Figure 10 shows microscopic images of the footprints when the grinding wheel (WA60J8V) was pressed to the workpiece with a varying specific load L’. Increasing load L’ increases not only the band width corresponding to contact length , but also the number of contact marks corresponding to the number of abrasive grains. As the contact boundary was unclear sometimes, the measurement of the contact length by the microscope does not have high accuracy. The estimated error is mm. The measurement results of the contact length are discussed in the next section.

Figure 10.
Contact footprint of grinding wheel WA60J8V, . (a) 1 N/mm; (b) 2.5 N/mm; (c) 5 N/mm; (d) 10 N/mm.
3.3. Deflection Method
The deflections of and were directly measured under loading and unloading conditions. This paper names this method “deflection method”. Figure 11a shows the measurement results without the load compensator. When the specific load L’ was increased from zero to 22 N/mm, deflection increased from zero to point B via point A. At point B, L’ gradually reduced to zero via C. During measurement, the deflection changes O-A’-B’-C’-O. There are small differences in the deflection values between loading and unloading.
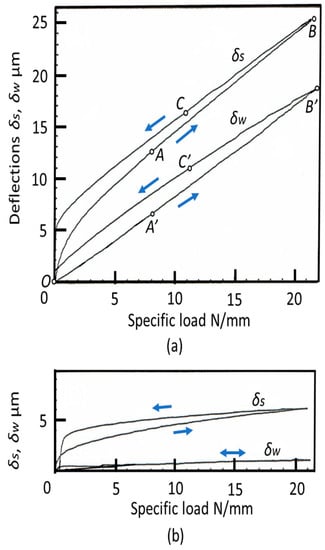
Figure 11.
Deflections of wheel and workpiece under loading and unloading with grinding wheel WA60J8V. (a) Without load compensator; (b) With load compensator.
Figure 11b is the result of the deflection measurements after implementing the load compensator. The deflection of the workpiece was drastically reduced by the compensator, which also created an improvement in measuring accuracy. In both cases (Figure 11a,b), the hard-spring characteristics were clearly observed in the changes to especially at the lower load L’, while linearly changed with load L’. The contact deflection at load L’ is found by under loading or unloading conditions. It was also observed that the grinding wheel elastically deflected with the load; it behaved like a hard spring at the lower load and like a linear spring at the higher load.
Figure 12a shows the repeatability of the measurement of . The specific load L’ was increased from O to B via A, then L’ was reduced to O via C. Then, L’ was increased from O to B via D again and was reduced to O via E. The tests were repeated four times. Although there was a difference in between the first loading and unloading, there was no difference after the second loading. The deflection patterns with the load were repeated and the good repeatability was confirmed. Figure 12b shows the difference in between the first loading and unloading at the different maximum loads R1, R2, R3, and R4. The difference was seen only at the first loading. After the second loading, there was no difference, as shown in Figure 11b.
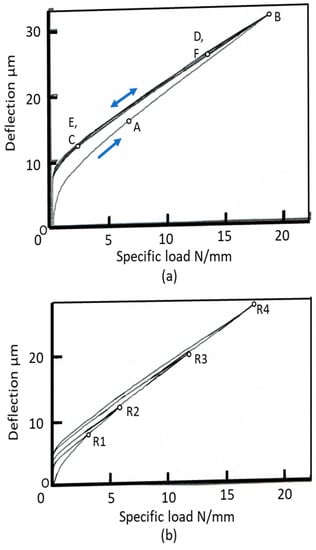
Figure 12.
Repeatability of the measurements of wheel deflection, grinding wheel WA60J8V. (a) Same load cycle; (b) Incremental load cycle.
3.4. Modeling of Grinding Wheel Contact Deflection
Figure 13 compares the measurement results of wheel contact deflection obtained by the deflection method with the load compensator and the footprint method. The deflections found by the deflection method are greater than the footprint values at each specific load L′. Although the deflection method has much higher measurement accuracy than the footprint method, the difference is obvious. It can be considered that the footprint method’s results reflect only the deflection of the local contact area, while the deflection method’s results contain the deflections of both the local contact area and the wheel body from the contact point to the bore with wheel flange. Both methods reveal that wheel deflection is composed of non-linear characteristics at the lower range of the load and linear spring characteristics at the higher range of the load. In this case, the critical specific load is about 3 N/mm.
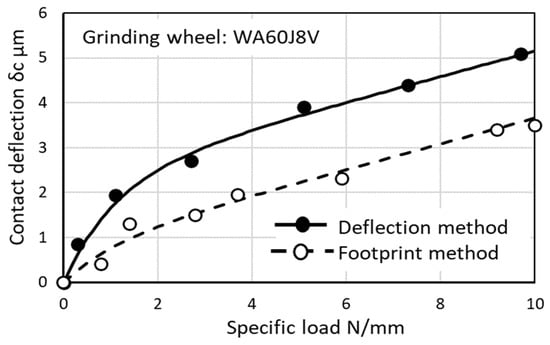
Figure 13.
Comparison of wheel deflections obtained by the deflection method and the footprint method.
From the experimental observations, it is assumed that the contact stiffness of the grinding wheel is composed of a non-linear spring and a liner spring. Figure 14a illustrates the wheel-workpiece inference with the equivalent wheel diameter . The contact deflection under the normal load L is represented by a hard spring shown in Figure 14b. It is assumed that the hard spring can be replaced with the series connection of two springs shown in Figure 14c. One has the non-linear spring constant , which represents the local stiffness of the contact area. The other has the linear spring constant , which represents the body stiffness of the grinding wheel itself.
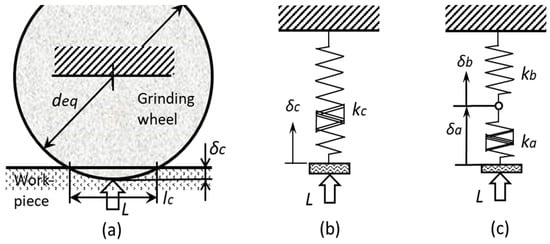
Figure 14.
Modeling of the contact stiffness of the grinding wheel. (a) Contact of wheel with workpiece; (b) Model of contact stiffness; (c) Series connection of linear and non-linear springs.
In Figure 14c, contact deflection is expressed by:
where is the deflection of the non-linear spring with and is the deflection of the linear spring with . As represents the non-linear deflection with load L, it is assumed that deflection can be represented by:
where A and S are constants and is the specific load per unit contact width. It is also assumed that the body of the grinding wheel has a spring constant of So, deflection is expressed by:
where is the specific spring stiffness per unit width. Therefore, contact deflection can be rewritten as follows:
Differentiating both sides of Equation (41) provides the specific compliance of the grinding wheel.
Therefore, specific contact stiffness per unit width can be expressed by:
Also, the non-linear contact stiffness of local area per unit width is:
In Figure 13, the best fit curves for both methods were found by using Equation (41). The solid line is for the deflection method and the dotted line is for the footprint method. The parameters shown in Table 3 were used for the calculations of . represents the wheel body stiffness and parameter A shows the degree of local deflection . Parameter S expresses the degree of raising curve at the lower specific load L′.

Table 3.
Parameters for representing the contact deflection of the grinding wheel WA60J8V.
The specific contact stiffnesses for both methods were calculated by using Equation (43), as shown in Figure 15. At L′ > 6 N/mm·mm, both methods provide the same contact stiffness. At L′ < 6 N/ mm·mm, the deflection method provides lower contact stiffness than the footprint method. The specific contact stiffness was 3.5 kN/mm·mm at L′ > 6 kN/mm. At L′ = 2 kN/mm, 1.5 kN/mm·mm and 2.5 kN/mm·mm were obtained by the deflection method and the footprint method, respectively.
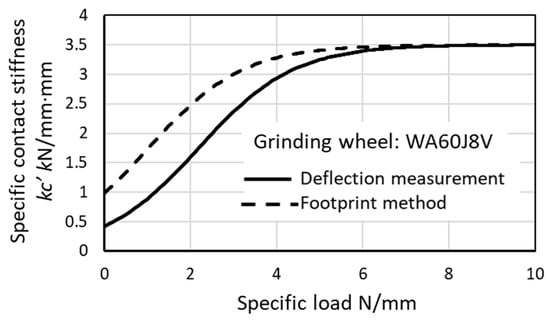
Figure 15.
Specific contact stiffness of grinding wheel.
Based on the contact stiffness model, the specific contact stiffness is composed of two components, for local deflection and for wheel body deflection. Figure 16 shows the specific contact stiffness obtained by the deflection method, where was found by Equation (44) and was set to 3.5 kN/mm·mm. The specific local area stiffness shows heavy hard-spring characteristics such as lower stiffness at L′ < 2 kN/mm and higher stiffness at L′ > 3 kN/mm. The dominant component of is at the lower load L′ < 2 kN/mm and at the higher load L′ > 4 kN/mm.
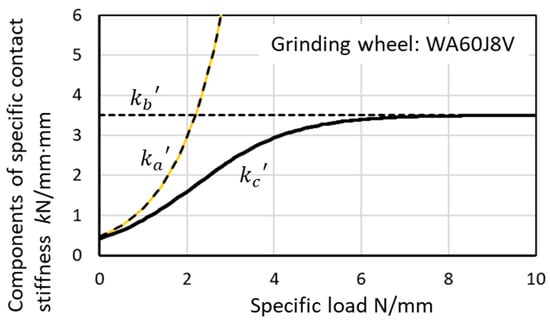
Figure 16.
Components of specific contact stiffness.
3.5. Measurement Results of Grinding Wheel Contact Stiffness
The contact deflections of four kinds of grinding wheels shown in Table 2 were measured by the deflection method with the load compensator. Figure 17 shows the measurement results. The best fit curves were found by using the parameters shown in Table 4. As seen in Figure 17, all grinding wheels exhibited heavy hard-spring behavior at the lower load and a liner spring nature at the higher load. The resinoid bond wheel WA60L8B exhibited the greatest deflection among the tested wheels and the vitrified bond wheel WA60L8V gave the smallest. In wheels WA60M8V and WA60L8B, the reduction of the deflection appeared at L’> 8 kN/mm. It seems that a structural change in the grinding wheels occurred at the higher load. These phenomena should be investigated in the future.
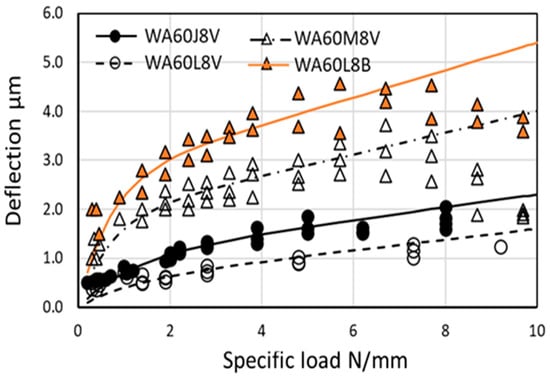
Figure 17.
Contact deflection of various grinding wheels.

Table 4.
Parameters of various grinding wheels obtained by the deflection measurements.
The contact stiffnesses were found by Equation (43) from the deflection curves shown in Figure 17. Figure 18 shows the specific contact stiffness of various #60 grinding wheels. The WA60L8V wheel had the highest contact stiffness, followed by the WA60J8V and WA60M8V wheels. The resinoid bond WA60J8B wheel had the lowest stiffness among them. At the specific load L′ < 2 kN/mm, all grinding wheels exhibited very low contact stiffness at the range of 0 < L′ < 4 N/mm. At the higher load L′ > 4 N/mm, the contact stiffness reached a constant level.
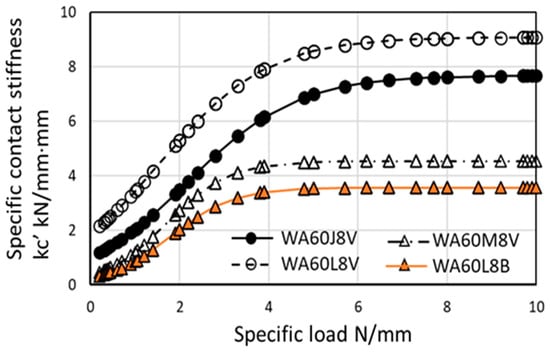
Figure 18.
Contact stiffness of various #60 grinding wheels.
Figure 19 shows the influence of accumulative SMR (specific material removal) on the deflection of the WA60M8V wheel. The dressing conditions are single point dresser, dressing lead 0.1 mm/rev., and adress depth of cut 20 μm. The best fit curves are drawn in the figure. The deflection after dressing was reduced and the deflection curve changed with increased SMR. No clear trend was observed. After dressing, the deflection curves gradually changed up and down according to the accumulative SMR progression. The G-ratio (grinding ratio) for monitoring the wear progress was not investigated in this study.
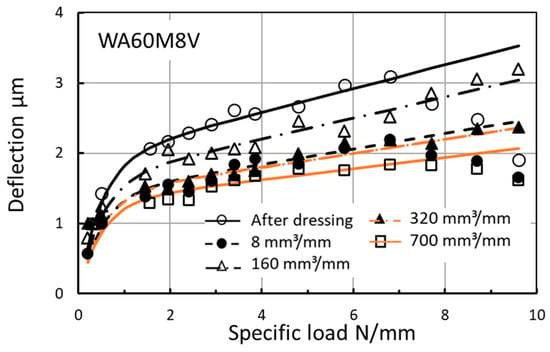
Figure 19.
The effect of accumulative specific material removal on contact deflection.
Figure 20 shows the changes in contact stiffness after dressing. The contact stiffness was found by applying the parameters shown in Table 5 to Equation (43). The contact stiffness at the lower range of load (L′ < 1.5 kN/mm) was very low and no corresponding change occurred. But, at the higher range (L′ > 4 kN/mm), the contact stiffness increased significantly by 20–50% after dressing.
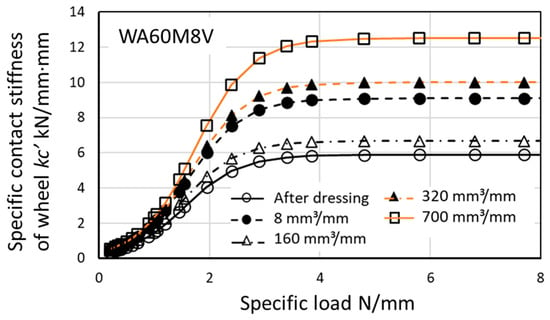
Figure 20.
The effect of accumulative specific material removal on contact stiffness.

Table 5.
Parameters of wheel deflection taken during specific material removal (SMR) progression.
4. Results of Plunge Cylindrical and Centerless Grinding Tests
4.1. Test Results of Plunge Cylindrical Grinding
Given that the contact stiffness of the grinding wheel largely relies on the specific normal load L′, it is expected that the normal grinding force affects the time constant T in the plunge grinding system because T is a function of (see Equation (34)). Plunge cylindrical grinding (c = 1.0) tests were carried out with various infeed rates and grinding power was measured during the grinding process. The grinding conditions are shown in Table 6.

Table 6.
Grinding conditions of plunge cylindrical grinding.
Figure 21 shows the ramping up of the grinding power from start to steady state during the plunge grinding process. At SMRR = 0.25 mm3/mm·s, which was very low (Figure 21a), the grinding power slowly built up and finally reached a steady state power of 0.31 kW. From the power curve, the time constant T of 17 s was measured. The time constant became shorter with increased SMRR . At mm3/mm·s, the time constant T was shortened and T = 8.2 s was obtained.
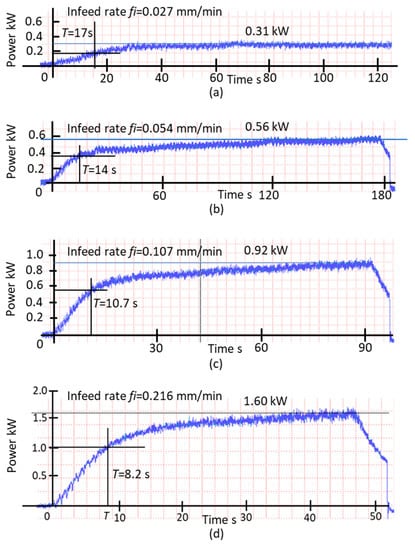
Figure 21.
Experimental results of plunge cylindrical grinding and the time constant. (a) = 0.25 mm3/mm·s; (b) = 0.5 mm3/mm·s; (c) = 1.0 mm3/mm·s; (d) = 2.0 mm3/mm·s.
The reason the time constant gets shorter with increased is that contact stiffness becomes greater at the higher normal grinding force . The estimated range of the specific normal grinding force is 0.46~2.36 N/mm, which can be considered as the lower specific load . In the load range, contact stiffness clearly exhibits a hard-spring nature and the contact time constant Tc of Equation (34) significantly changes.
4.2. Test Results of Plunge Centerless Grinding
Table 7 delineates the grinding conditions for plunge centerless grinding (c = 0.5) of glass workpieces. The regulating wheel spindle of the grinding machine was supported by hydrostatic bearings and the grinding forces were measured by detecting the pocket pressures of the bearings [29].

Table 7.
Grinding conditions of plunge centerless grinding.
Figure 22 shows test results of plunge centerless grinding with different infeed rates. The periodic fluctuations observed on the force curves were due to the radial runout of the regulation wheel rotation. Taking the average of the fluctuations, the time constant T was measured for each plunge grinding operation. The time constant was prolonged when the specific material removal rate was reduced.
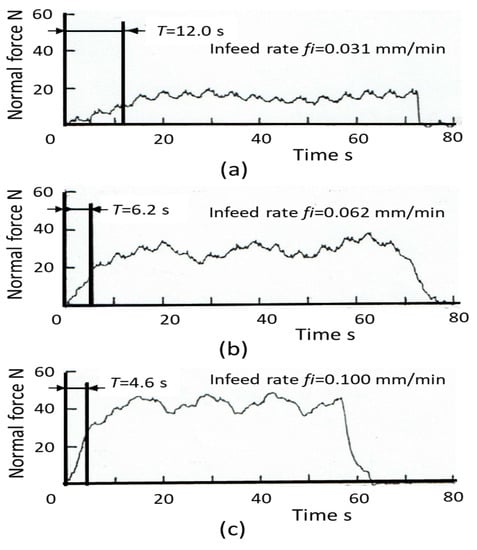
Figure 22.
Experimental results of plunge centerless grinding and the time constant. (a) mm3/mm·s; (b) mm3/mm·s; (c) mm3/mm·s.
The grinding tests were repeated many times with a specific normal load range of = 0.06~0.7 N/mm (which is considered a very light load). The results are summarized in Figure 23. The time constant T converges at about 4 s at SMRR > 0.03 mm3/mm·s. The converged time (about 4 s) corresponds to the machine time constant described in Figure 7. By contrast, the time constant was rapidly prolonged where the SMRR was reduced. It reaches 28 s at SMRR = 0.002 mm3/mm·s. In this case, the contact time constant becomes 24 s. The increased comes from the reduced contact stiffness created by the reduced contact load. This result clearly reveals that the time constant T is significantly increased with reduced SMRR .
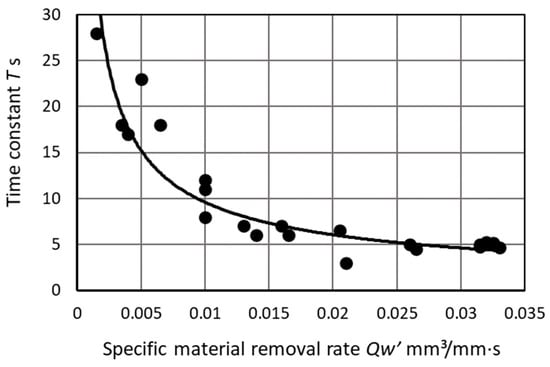
Figure 23.
The effect of specific material removal rate on the time constant in plunge centerless grinding.
5. Validation and Discussion
The plunge cylindrical grinding (c = 1.0) test results shown in Figure 21a–d were simulated using Equations (19)–(28) for the primary grinding cycle shown in Figure 4b. The simulation results are shown in Figure 24a–d. Also, Figure 25a–c show the simulations of experimental results obtained by plunge centerless grinding (c = 0.5) shown in Figure 22a–c. In all simulations of plunge grinding operations, the transient behaviors in build-up during ramp infeed and the reduction during spark-out are almost identical to the experimental results, and the levels in steady state and the time constant are excellent matches to the experimental results. These correlations indicate that the proposed model can accurately predict critical parameters such as forces and , power , machine deflection de, equivalent system stiffness keq, and time constant T during both plunge cylindrical grinding and centerless grinding.
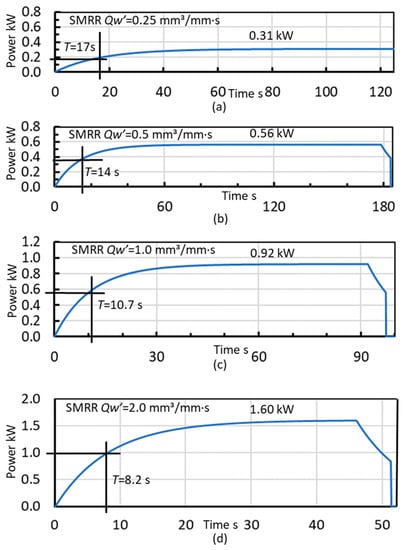
Figure 24.
Simulations of plunge cylindrical grinding processes. (a) = 0.25 mm3/mm·s; (b) = 0.5 mm3/mm·s; (c) = 1.0 mm3/mm·s; (d) = 2.0 mm3/mm·s.
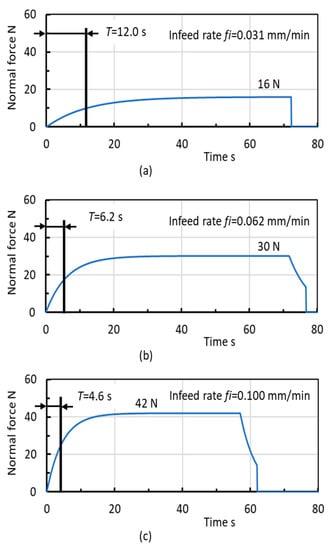
Figure 25.
Simulations of plunge centerless grinding. (a) mm3/mm·s; (b) mm3/mm·s; (c) mm3/mm·s.
Table 8 lists the critical parameters obtained by the simulations in Figure 24a–d. The specific energy u for each plunge grinding operation was found, and it was observed that u increased with increased SMRR . These phenomena are well known in grinding [30]. The equivalent chip thickness (defined as the ratio of SMRR to grinding speed ) is a key parameter that affects energy u and the finished surface quality [31]. The system stiffness obtained by the simulation decreased with the decrease in specific normal grinding force .

Table 8.
Critical parameters obtained by the simulations in Figure 23.
From the system stiffness analysis, the machine stiffness of the applied grinder was estimated to = 2.47 kN/mm as a constant value. Then, the specific contact stiffness of the grinding wheel was calculated. = 4.0 kN/mm·mm was obtained when the infeed rate was highest (Figure 24d). When the infeed rate was slowest (Figure 24a), the specific contact stiffness was significantly reduced to = 0.29 kN/mm·mm and hard-spring characteristics were clearly exhibited, as expected.
As the result of the reduced system stiffness due to the reduction of contact stiffness , the time constant T drastically increased by over 200% from 8.2 s to 17 s, as predicted by Equation (10). So, when a grinding cycle is designed, the plunge infeed time and spark-out time should be determined by taking into account the influence of the infeed rate on the time constant T.
It is clear that the time constant T significantly changes by 2–2.6 times, as seen in Figure 24 and Figure 25. The amount of change depends on the contact stiffness of the grinding wheel, which relies on contact load L; that is, normal grinding force in this case. When a plunge grinding cycle with a lower infeed rate fi is set up, a long-time constant will be found due to the lower contact stiffness at the lower grinding force Fn. On the other hand, the effect of contact stiffness on the time constant can be ignored when high stock removal conditions with high SMRR and high normal grinding force are set up.
In general, the ramp infeed time of the plunge grinding cycle requires at least five times T (5T). This setting provides sufficient time for reaching 99.3% of the target level of the steady state (). The spark-out time requires at least three times T (3T) in order to reduce the system deflection de by 95% (). Setting the spark-out time to 3T affords the grinding operation not only improved size error, but also improved roundness of the finished products. In the plunge grinding operations using grinding wheels, the time constant T can be reasonably estimated by using the data of wheel contact stiffness shown in Figure 18 and Figure 20. It allows process engineers to determine the spark-out time and the proper grinding cycle for achieving the required size error and roundness. The design procedures are described in [27].
For high-efficiency and high-precision plunge grinding, it is vital to take the effect of contact stiffness on the plunge grinding process into consideration during the design of the grinding cycle.
6. Conclusions
This paper presented the effect of grinding wheel contact stiffness on the plunge grinding cycle and provided guidelines for the design of the grinding cycle. First, the generalized plunge grinding system (including cylindrical, centerless, shoe-centerless, internal, and shoe-internal grinding) was explicitly described and analyzed in terms of system outputs corresponding to the inputs of the plunge grinding conditions. The analysis discussed the influence of system stiffness on the time constant that governs the transient behaviors of process parameters such as forces, power, and machine deflection. Also, it clarified that system stiffness is composed of machine stiffness and wheel contact stiffness, and these stiffnesses significantly affect grinding performance indicators such as productivity and grinding accuracy.
The elastic deflection of the grinding wheel was accurately measured and a function for representing the deflection nature under various contact loads was derived. The function provides the non-linear contact stiffness with respect to the normal load. The contact stiffnesses of four kinds of grinding wheels with different grades and bond materials were presented, and changes in the contact stiffness after dressing were discussed.
Experimental tests for both cylindrical grinding and centerless grinding were carried out, and it was experimentally confirmed that the time constant at ramp infeed and spark-out is significantly prolonged by reducing the grinding force. It was verified that a simulation of the grinding tests using the proposed model can accurately predict critical parameters like forces, machine deflection, and system stiffness during plunge operations. Finally, this paper emphasized that it is vital to take the effect of wheel contact stiffness into consideration during the design of the plunge grinding cycle.
The study provides the following conclusions.
- (1)
- The equivalent stiffness of the plunge grinding system is composed of machine stiffness and wheel contact stiffness. The contact stiffness greatly depends on the normal contact load. It is confirmed by the measurement of wheel deflection and the plunge grinding tests with various infeed rates.
- (2)
- The contact deflection of the grinding wheel behaves like a non-linear spring representing a local contact deflection at lower load and a linear spring expressing the elasticity of the wheel body itself at a higher load. Formulas representing the wheel deflection behaviors are presented.
- (3)
- The contact stiffness significantly affects the time constant T that governs the transient behaviors in ramp infeed and spark-out grinding.
- (4)
- The time constant T is drastically prolonged with reduced normal grinding force due to the reduction of contact stiffness at lower contact loads. The grinding tests revealed that the time constant T significantly changes by 2–2.6 times.
- (5)
- All measured Al2O3 wheels exhibit very low contact stiffness at a specific load less than 3 N/mm. At a higher load greater than 4 N/mm, contact stiffness reaches a constant.
- (6)
- Plunge grinding tests applying both cylindrical grinding and centerless grinding methods with various infeed rates experimentally verified the effect of wheel contact stiffness on the time constant T.
- (7)
- As guidelines for plunge grinding cycle, the ramp infeed grinding time should be set to at least five times T and at least three times T for spark-out grinding.
Author Contributions
Conceptualization, F.H.; methodology, F.H. and H.I.; software, F.H.; validation, F.H. and H.I.; formal analysis, F.H.; investigation, F.H.; resources, F.H. and H.I.; data curation, F.H. and H.I.; writing—original draft preparation, F.H.; writing—review and editing, F.H. and H.I.; visualization, F.H. and H.I.; supervision, F.H.; project administration, F.H.; funding acquisition, F.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest. F.H. is a founder of Advanced Finishing Technology Ltd., in which he holds shares. H.I. is a founder of Toba Engineering, in which he holds shares. The sponsors of both companies had no role in the design, collection, analysis, or interpretation of data, the writing of this article, or the decision to submit it for publication.
Nomenclature
| s | Laplace operator | Equivalent wheel diameter | |
| Deflection of machine in s-domain | Diameter of grinding wheel | ||
| Actual infeed rate in s-domain | Diameter of workpiece | ||
| Normal grinding force in s-domain | Cut-off frequency | ||
| Transfer function in s-domain | Actual infeed rate | ||
| (s) | Command infeed in s-domain | Equivalent chip thickness | |
| MRR in s-domain | Stiffness of wheel contact area | ||
| SMRR in s-domain | Specific stiffness of wheel contact area | ||
| Actual infeed in s-domain | Stiffness of wheel body | ||
| A | Constant | Specific stiffness of wheel body | |
| F | Ratio of Fn to fi | Contact stiffness of grinding wheel | |
| Normal grinding force | Specific contact stiffness of grinding wheel | ||
| Tangential grinding force | Equivalent system stiffness | ||
| Specific normal grinding force | Machine stiffness of grinding system | ||
| Specific tangential grinding force | Stiffness of i-th. mechanical structure | ||
| GW | Grinding wheel | Estimated machine stiffness | |
| Command infeed | Stiffness of wheel support system | ||
| Constant infeed rate | Stiffness of work support system | ||
| L | Contact load | Stiffness of workpiece itself | |
| L′ | Specific contact load | Contact length | |
| MRR | Material removal rate | n | Degrees of freedom |
| Grinding power | Actual infeed | ||
| Material removal rate | t | Time | |
| Specific material removal rate | Plunge grinding time | ||
| RW | Regulating wheel | Time at end of grinding | |
| S | Constant | u | Specific energy |
| SMR | Specific material removal | Grinding speed | |
| SMRR | Specific material removal rate | Deflection | |
| T | Time constant | Deflection of wheel contact area | |
| Contact time constant | Deflection of grinding wheel body | ||
| Machine time constant | Contact deflection of grinding wheel | ||
| WP | Workpiece | Deflection at flange of grinding wheel | |
| b | Width of workpiece | Deflection of workpiece | |
| c | Grinding method parameter | η | Force ratio (Fn/Ft) |
| Deflection of grinding machine |
References
- Hahn, R.S. The Effect of Wheel-Work Conformity in Precision Grinding. Trans. ASME 1955, 77, 1325–1329. [Google Scholar]
- Peklenik, J. Ermittlung von Geometrschen und Physikalischen Kenngröβenfür die Grundlagenforschung des Schleifens. Ph.D. Dissertation, Aachen Technical University, Aachen, Germany, 1957. [Google Scholar]
- Snoeys, R.; Wang, I.-C. Analysis of the Static and Dynamic Stiffness of the Grinding Surface. In Proceedings of the 9th International MTDR Conference, Manchester, UK; 1968; p. 1133. [Google Scholar]
- Brown, R.H.; Saito, K.; Shaw, M.C. Local Elastic Deflections in Grinding. CIRP Ann. 1970, 19, 105–113. [Google Scholar]
- Kumar, K.V.; Shaw, M.C. The Role of Wheel-Work Deflection in Grinding Operations. J. Eng. Ind. 1981, 103, 73–78. [Google Scholar] [CrossRef]
- Krug, H.; Honcia, G. Die Elastische Verformung bei Schleifwerkzeugen. Werkstattstech 1964, 54, 53. [Google Scholar]
- Nakayama, K.; Brecker, J.; Shaw, M.C. Grinding Wheel Elasticity. J. Eng. Ind. 1971, 93, 609–613. [Google Scholar] [CrossRef]
- Nakayama, K. Elastic Deformation of Contact Zone in Grinding. Bull. Jpn. Soc. Prec. Eng. 1971, 5, 93. [Google Scholar]
- Zhou, Z.; Van Lutterwelt, C. The Real Contact Length between Grinding Wheel and Workpiece—A New Concept and a New Measuring Method. CIRP Ann. 1992, 41, 387–391. [Google Scholar] [CrossRef]
- Rowe, W.B.; Morgan, M.N.; Qi, H.S.; Zheng, H.W. The Effect of Deformation on the Contact Area in Grinding. CIRP Ann. 1993, 42, 409–412. [Google Scholar] [CrossRef]
- Hucker, S.A.; Farris, T.N.; Chandrasekar, S. Estimation of Contact Stiffness for Grinding of Hardened Steel. In Proceedings of the 1993 ASME Winter Annual Meeting, New Orleans, LA, USA, 28 November–3 December 1993; pp. 191–198. [Google Scholar]
- Yamada, T.; Lee, H.S.; Matsushita, H. A Study on the Contact Stiffness of Grinding Wheels. Key Eng. Mater. 2004, 257, 263–266. [Google Scholar] [CrossRef]
- Yamada, T.; Morgan, M.N.; Lee, H.S.; Miura, K. Calculation of the Contact Stiffness of Grinding Wheel. Adv. Mater. Res. 2011, 325, 54–59. [Google Scholar] [CrossRef]
- Papanikolaou, M.; Salonitis, K. Contact stiffness effects on nanoscale high-speed grinding: A molecular dynamics approach. Appl. Surf. Sci. 2019, 493, 212–224. [Google Scholar] [CrossRef]
- Hahn, R.S. On the Theory of Regenerative Chatter in Precision Grinding Operations. Trans. ASME 1954, 76, 563. [Google Scholar]
- Furukawa, Y.; Miyashita, M.; Shiozaki, S. Vibration analysis and work-rounding mechanism in centerless grinding. Int. J. Mach. Tool Des. Res. 1971, 11, 145–175. [Google Scholar] [CrossRef]
- Gurney, J.P. An Analysis of Surface Wave Instability in Grinding. J. Mech. Eng. Sci. 1965, 7, 198–209. [Google Scholar] [CrossRef]
- Thompson, R.A. The Character of Regenerative Chatter in Cylindrical Grinding. J. Eng. Ind. 1973, 95, 858–864. [Google Scholar] [CrossRef]
- Inasaki, I.; Karpuschewski, B.; Lee, H.-S. Grinding Chatter—Origin and Suppression. CIRP Ann. 2001, 50, 515–534. [Google Scholar] [CrossRef]
- Snoeys, R.; Brown, D. Dominating Parameters in Grinding Wheel and Workpiece Regenerative Chatter. Proc. MTDR 1969, 325–348. [Google Scholar]
- Inasaki, I. Regenerative Chatter in Grinding. Proc. MTDR 1977, 423–429. [Google Scholar]
- Miyashita, M.; Hashimoto, F.; Kanai, A. Diagram for Selecting Chatter Free Conditions of Centerless Grinding. CIRP Ann. 1982, 31, 221–223. [Google Scholar] [CrossRef]
- Hashimoto, F.; Kanai, A.; Miyashita, M. Growing Mechanism of Chatter Vibrations in Grinding Processes and Chatter Stabilization Index of Grinding Wheel. CIRP Ann. 1984, 33, 259–263. [Google Scholar] [CrossRef]
- King, R.I.; Hahn, R.S. Handbook of Modern Grinding Technology; Service Network Incorporated: Princeton, MA, USA, 1998; pp. 3–29. [Google Scholar]
- Malkin, S.; Koren, Y. Optimal Infeed Control for Accelerated Spark-Out in Plunge Grinding. J. Eng. Ind. 1984, 106, 70–74. [Google Scholar] [CrossRef]
- Chiu, N.; Malkin, S. Computer Simulation for Cylindrical Plunge Grinding. CIRP Ann. 1993, 42, 383–387. [Google Scholar] [CrossRef]
- Hashimoto, F. The Design of an Infeed Cylindrical Grinding Cycle. Inventions 2020, 5, 46. [Google Scholar] [CrossRef]
- Kanai, A.; Suzuki, N.; Toriumi, M.; Miyashita, M. The Development of the “Load Compensator” for Cylindrical Grinding Machines. CIRP Ann. 1976, 25, 313–318. [Google Scholar]
- Hashimoto, F.; Kanai, A.; Miyashita, M. High Precision Trueing Method of Regulating Wheel and Effect on Grinding Accuracy. CIRP Ann. 1983, 32, 237–239. [Google Scholar] [CrossRef]
- Hashimoto, F.; Yamaguchi, H.; Krajnik, P.; Wegner, K.; Chaudhari, R.; Hoffmeister, H.-W.; Kuster, F. Abrasive Fine-Finishing Technology. CIRP Ann. 2016, 65, 597–620. [Google Scholar] [CrossRef]
- Snoeys, R.; Peters, J. The Significance of Chip Thickness in Grinding. CIRP Ann. 1974, 23, 227–237. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).