Abstract
First-principles calculations for underdoped La2−xSrxCuO4 (LSCO) have revealed a Fermi surface consisting of spin-triplet (KS) particles at the antinodal Fermi-pockets and spin-singlet (SS) particles at the nodal Fermi-arcs in the presence of AF local order. By performing a unique method of calculating the electronic-spin state of overdoped LSCO and by measurement of the spin-correlation length by neutron inelastic scattering, the origin of the phase-diagram, including the pseudogap phase in the high temperature superconductor, Sr-doped copper-oxide LSCO, has been elucidated. We have theoretically solved the long-term problem as to why the angle-resolved photoemission spectroscopy (ARPES) has not been able to observe Fermi pockets in the Fermi surface of LSCO. As a result, we show that the pseudogap region is bounded below the characteristic temperature T*(x) and above the superconducting transition temperature Tc(x) in the T vs. x phase diagram, where both the AF order and the KS particles in the Fermi pockets vanish at T*(x), whilst KS particles contribute to d-wave superconductivity below Tc. We also show that the relationship T*(xc) = Tc(xc) holds at xc = 0.30, which is consistent with ARPES experiments. At T*(x), a phase transition occurs from the pseudogap phase to an unusual metallic phase in which only the SS particles exist.
1. Introduction
Since the discovery of high temperature superconductivity (HTS) in cuprates by Bednorz and Müller [1], more than thirty years have passed. However, a consensus on its origin has not yet been reached. Copper oxide (cuprate) superconductors differ from ordinary metallic superconductors in their production process of carriers. In La2CuO4, for example, which is an antiferromagnetic insulator [2], carriers are generated by doping with chemical elements or by creating oxygen deficiencies, by replacing 3+ cations (La3+) by 2+ (Sr2+) ions. Thus, the electronic structures of cuprate superconductors vary drastically with doping, due to the special feature of the ionic crystal in cuprates.
In this context, we have recently performed first-principles calculations for underdoped La2−xSrxCuO4 (LSCO) [3] and have revealed the appearance of a spin-polarized band occupied by doped holes within the energy gap of the antiferromagnetic (AF) insulator La2CuO4. The tight binding parameterization of the first principles calculation for the underdoped LSCO clarified that doped holes in the spin-polarized band correspond to KS particles. Furthermore, when extra holes are doped, the apical O2− ions in the elongated CuO6 octahedrons in LSCO tend to approach the central Cu2+ ions to gain attractive electrostatic energy. This backward deformation is called the anti-JT effect [4,5,6]. This effect, due to the apical oxygen in cuprates, was supported experimentally by neutron scattering [7] and polarization-dependent spectroscopy measurements [8,9].
As regards the electronic-spin state of LSCO, one view is based on the single-component theory, in which only orbitals extended in a CuO2 plane are considered. Since a doped hole moves within a CuO2 plane, this model is irrelevant to the anti-JT effect. A typical model which takes this view is the t-J model [10,11]. An alternative view is based on the two-component theory initiated by Kamimura and Suwa [12,13], in which the two kinds of orbitals of each CuO6 octahedron, both parallel and perpendicular to a CuO2 plane, are considered.
By means of the anti-JT effect, the energy separation between two JT-split levels at each Cu2+ ion becomes smaller with increasing hole concentration x, i.e., they become pseudo-degenerate. These pseudo-degenerate states are represented by antibonding molecular orbitals (MOs) and bonding MOs , as shown in Figure 1.
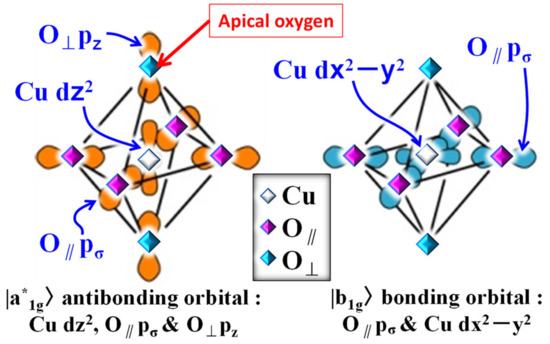
Figure 1.
Relevant electronic orbitals for a doped hole: a1g antibonding molecular orbital (MO) (left side) and b1g bonding MO (right side).
Paying attention to the pseudo-degenerate states and at each Cu site, Kamimura and Suwa [12] showed that, in the presence of the local AF order, a doped hole with up (or down) spin can itinerate by taking, alternately, a Hund’s coupling spin-triplet with a localized up (or down) spin at a Cu site and a spin-singlet with a localized down (or up) spin in a neighboring Cu site without destroying the AF order, as shown in Figure 2. Later, this model was named the Kamimura–Suwa (K–S) model when published in Physical Review B [13]. A feature of the K–S model is the coexistence of a metallic state and the AF order, as shown in Figure 2.
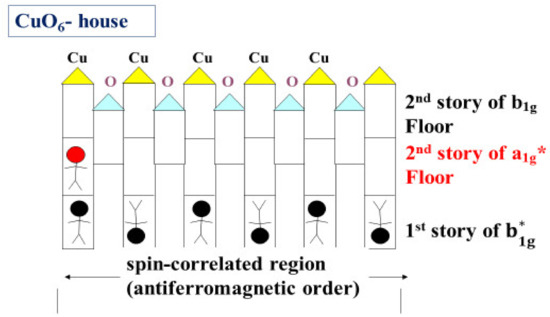
Figure 2.
Heuristic explanation of the K–S model using a two-story house model [13,14].
In Figure 2, the first story of the Cu house (CuO6-house) is occupied by localized spins (black arrows), which form the AF order by means of the superexchange interaction via intervening O2− ions. The second story in the copper house consists of two floors, due to the anti-JT effect; the lower a*1g floor and the upper b1g floor. In the second story, a doped hole with an up spin (red arrow) enters the a*1g floor of the left-side Cu house owing to the Hund’s coupling spin-triplet exchange interaction with a Cu localized up spin in the first story. By means of the transfer interaction, the doped hole with up or down spin is transferred into the b1g (or a*1g) floor in the neighboring Cu house through the oxygen rooms, and thus forms a metallic state in the presence of the AF order by alternately taking Hund’s coupling spin-triplet and spin-singlet states without destroying the AF order. The doped hole with an up spin (red arrow) shown in Figure 2 has been named a “KS particle” [3]. Below Tc, the KS particles contribute to the d-wave superconductivity [15,16]. As seen in Figure 2, these KS particles can itinerate under the coexistence of the AF order.
In our previous paper [3], first-principles calculations showed that a feature of the KS particles in the underdoped LSCO is the coexistence with AF order. Here, the underdoped regime in LSCO corresponds to the doping concentration range from the metal-insulator transition, x = 0.05 (≡xo), to the optimum doping x = 0.15 (≡xp), at which a vale of Tc takes the highest value of about 40 K [17] while the overdoped regime corresponds to the doping concentration beyond xp, where the AF order vanishes at x = 0.30 (≡xc) [18].
Following on from the previous paper for underdoped LSCO [3], the purpose of this contribution is to clarify the electronic-spin state of LSCO in the overdoped regime. Then, combining the results obtained in the previous paper and the present paper, we establish a new phase diagram leading to the origin of the so-called pseudogap [19] in LSCO.
2. How to Clarify the Electronic-Spin State of Overdoped LSCO
In the previous paper [3], we adopted the first-principles SCAN method [20] to calculate the electronic-spin state of underdoped LSCO following the method of Furness et al. [21]. However, in the overdoped regime we face a great difficulty, as explained below: With increasing Sr concentration x, doped holes tend to occupy the p orbitals in O2− ions between Cu2+ ions in LSCO. As a result, some of the O2− ions in CuO2 planes change to O1− ions, so that the superexchange interactions, in the K–S Hamiltonian (see Equations (1) and (2) in Ref. [3]), are gradually destroyed with increasing x in the overdoped regime. Thus, the spin direction in the overdoped regime changes from the AF order to a spin-disordered phase, and finally the AF order vanishes at xc = 0.30 [18]. We call this spin-disordered phase a spin-glass phase. In the spin-glass phase, the number of KS particles which coexist with the AF order decreases with increasing doping with holes or temperature, and finally vanishes.
3. Comparison with Neutron Scattering Experimental Results of the Magnetic Excitations in the Underdoped to Overdoped Regimes of LSCO
Detailed neutron scattering studies have been reported in [22,23,24]. In particular, Figure 5 in [24] by Aeppli et al. reports the doping dependence of the dynamic spin-correlation in LSCO to be from xo = 0.05 in the underdoped regime to x = 0.30 in the overdoped regime. It should be noted that a similar trend has been reported in a wide doping dependence in [22]. Later, Wakimoto et al. [18] reported that AF correlation disappears at x = 0.30. In order for readers to understand these experimental results quantitatively, we put them together in Figure 3.
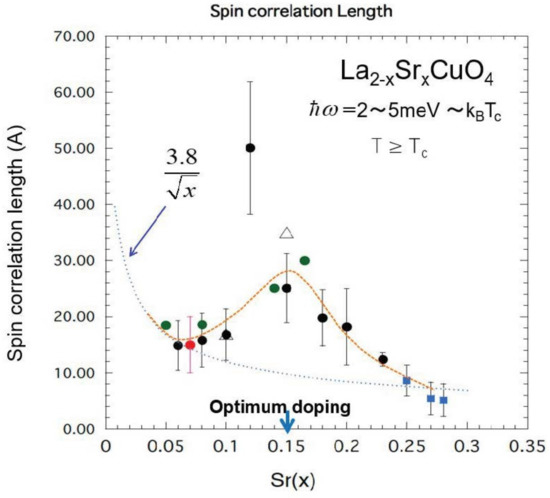
Figure 3.
Experimental results by various groups [22,23,24] on the doping dependence of the spin-correlation length in underdoped to overdoped regimes of La2−xSrxCuO4.
The dotted thin line (blue) in Figure 3 is expressed as the function nm, which is just the average separation between the holes introduced by Sr2+ doping [25].
From Figure 3, we notice qualitatively that the spin-correlation length begins to increase with increasing x from the metal-insulator transition at xo (=0.05) to the optimum doping at xp (=0.15) in the underdoped regime, and then decreases in the overdoped regime. In order to clarify a reason why the spin-correlation length begins to increase with increasing x from xo up to xp in the underdoped regime, the K–S Hamiltonian for model systems in a two-dimensional (2D) square lattice with 16 (=4 × 4) localized spins was solved [26]. The calculated results have clarified that the AF correlation grows from the metal-insulator transition at xo up to the optimum doping xp so as for the kinetic energy of a doped hole not to increase. We call this characteristic feature the “kinetic energy lowering mechanism”.
Concerning the spin-ordering, Tranquada et al. [27] suggested the possibility of a spin-stripe order in connection with an anomalous suppression of the superconductivity in LaBaCO in a very narrow region around x = 1/8. In the case of LSCO, however, the first principles calculations [3] did not show such an anomaly. Thus, we think that the appearance of a spin-stripe order might depend on the cuprate’s family.
As regards the Fermi surface (FS), the first principles calculations for underdoped LSCO [3] have shown the coexistence of Fermi pockets at the antinodal G1 point (π, 0) and three equivalent points, and Fermi arcs at the Δ point (π/2, π/2) and three equivalent points in the square Brillouin zone (BZ) in the kx–ky plane in k space, as shown in Figure 4.
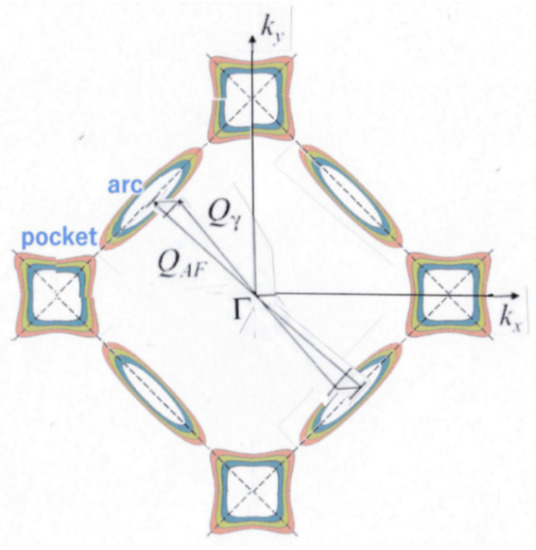
Figure 4.
Fermi surface (FS) of LSCO in the underdoped to overdoped regimes.
When x increases from the underdoped to overdoped regime, the two arcs separated with the magnetic ordering vector QAF(π, π) move to the incommensurate positions Qγ(π ∓ γ, π ± γ). As a result, Fermi surface nesting occurs, as shown in Figure 4. In fact, this FS nesting has already been pointed out by the neutron inelastic scattering experiments [28]. As regards the Fermi surface nesting, we can make further comments: the hour-glass-shaped magnetic excitation spectrum reported in cuprates [29] may be related to the Fermi surface nesting behavior.
4. Angle-Resolved Photoemission Spectroscopy (ARPES) Experiments and a Reason Why ARPES Is Not Able to Observe Fermi Pockets
Concerning the coexistence of the Fermi pockets and the Fermi arcs, ARPES experiments have reported only on the existence of Fermi arcs, but not on the Fermi pockets (see Yoshida et al. [30]). Here, we suggest a reason why ARPES is not able to observe Fermi pockets. As shown in Figure 1, the KS particles in the Fermi-pockets occupy MO (mainly Cu dz2 orbital), while the SS particles in the Fermi arcs occupy MO (mainly Cu dx2−y2 orbital). Thus, the wavefunction of the KS particle is perpendicular to the CuO2 plane (the crystal surface), while that of the SS particle is parallel to the CuO2 plane. As a result, we can say that, for most of the ARPES experiments in which the electric vector of incident photon is parallel to the CuO2 plane, we can mainly observe the Fermi arcs, even though FS consists of pockets and arcs.
Another reason for why Fermi pockets cannot be observed could be that the mean free path of an SS particle (mainly Cu dx2−y2 orbital) in the metallic phase is considerably longer than the spin-correlation length, while that of a KS particle (mainly Cu dz2 orbital) is slightly longer than the spin-correlation length [14]; on the boundary of a spin-correlated region, localized spins on the boundary are frustrated. The spin flip time on the boundary is estimated from τs = h/J, where h is the Planck constant and J is the superexchange constant (0.1 eV), while the travelling time of an SS particle over a spin-correlated region λ is estimated from τss = λ/vF(ss), where vF(ss) is the Fermi velocity of an SS particle [3]. Thus, τs and τss are estimated, respectively, to be 10−14 s and 10−13 s. Hence, the spin-flip time is shorter than the travelling time of an SS particle over λ, so that an SS particle can move coherently beyond the spin-correlated region. In fact, the mean free path of an SS particle is 30 nm, so that ARPES could observe Fermi arcs clearly. On the other hand, the travelling time of a KS particle is estimated from τks = λ/vF(ks), where vF(ks) is the Fermi velocity of a KS particle The band calculation of the spin-polarized band [3] shows that vF(ks) is 10 times faster than vF(ss), and thus the mean free path of a KS particle is estimated as 3nm. From this estimate, we conclude that, for ARPES measurements, it is difficult to observe Fermi pockets.
Since the KS particles in the Fermi pockets coexist with AF order, the number of the KS particles decreases with increasing x in the overdoped regime due to the diminution of the AF order. This behavior is consistent with the experimental results shown in Figure 3. On the other hand, the number of the SS particles in Fermi arcs increases with increasing x, because the SS particles do not depend on the AF order. Here, we remark that the present definition of SS particles is similar to the Zhang–Rice singlet in the t-J model [10,11].
5. New Phase Diagram
Finally, we propose a new phase diagram for LSCO, as shown in Figure 5a. By increasing x and/or T, both the AF correlation and the number of KS particles decrease together and finally disappear at the characteristic temperature T*(x), while the number of SS particles increases across T*(x). In addition, the wavefunctions of a KS particle with up and down spins, Ψk,↑(r) and Ψk,↓(r), have the unique phase relation [15]
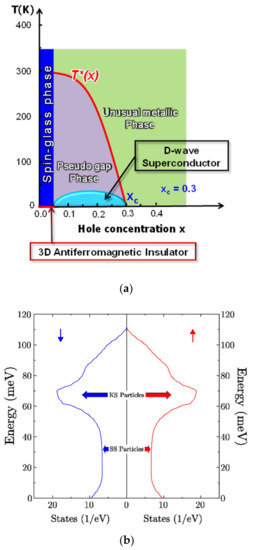
Figure 5.
(a) New Phase diagram. The pseudogap phase consisting of KS and SS particles appears below the characteristic temperature T*(x) and above Tc(x). When x and/or temperature T increase, the number of KS particles decreases and disappears at T*(x). At T*(xc), both the AF order and the d-wave superconductivity disappear. Thus, the relation T*(xc) = Tc(xc) = 0 holds. Below Tc, the KS particles with up and down spins form a Cooper pair, contributing to d-wave superconductivity. The SS particles form the unusual metallic phase above T*(x). (b) The first-principles calculated density of states (DOS) for the pseudogap phase in underdoped LSCO with x = 0.125. This area is occupied by holes (above EF (=energy 0)).
Thus, below Tc the KS particles on the Fermi pockets contribute to the d-wave superconductivity in the phonon mechanism due to apical oxygen modes [31].
Thus, a “mixed phase” consisting of both KS and SS particles appears below the characteristic temperature T*(x) and above Tc(x) in the T vs. x phase diagram. We define this mixed phase as the pseudogap phase. Since the number of SS particles increases across T*(x), the SS particles form a unique phase above T*(x), where the AF correlation vanishes at T*(x).
The wavefunction of the SS particle, ΨAA(r1σ1, r2σ2), takes the following entanglement form. This causes the emergence of a new particle called an SS particle. Then, the wave function of an SS particle at a site A, Ψss,A(r1σ1, r2σ2) has an entangled form, given by
where ϕ(r) and χ(r) represent the wavefunctions of the upper bonding b1g orbital and lower antibonding b*1g localized orbitals, respectively.
Thus, the itinerant behavior of SS particles is different from that of a single particle in a metallic state. In this context, we call a new metallic phase beyond T*(x) “Unusual Metallic phase”. Thus, the characteristic temperature T*(x) in the phase diagram represents a phase boundary between the pseudogap phase and the Unusual Metallic phase, and a phase transition occurs at T*(x), at which the AF correlation vanishes. The order parameter in this phase transition may be the spin-correlation length in the AF correlation.
In order to calculate the x dependence of T*(x), we introduce a quantity defining the difference between the free energy of the pseudogap phase FPS (T, x) and that of the UnusualMetallic phases FST(T, x), following Ref. [32]:
ΔF(T, x) ≡ FPS(T, x) − FST(T, x),
Then, T*(x) is defined by the equation
ΔF(T*(x), x) = 0
Since both the calculated electronic entropy [13] and measured electronic entropy [33] coincide well in both the pseudogap phase and the unusual metallic phase in LSCO without introducing any adjustable parameter [13], we calculated T*(x) as a function of x by taking T*(xo = 0.05) = 300 K [32] and T*(xc = 0.30) = 0, where T*(xc = 0.30) indicates the disappearance of both the AF order and the KS particles at xc = 0.30. Since the d-wave superconductivity also disappear at x = 0.30 [17], the relation T*(xc) = Tc(xc) = 0 holds. This theoretical prediction is consistent with ARPES experiments [34]. The calculated results of T*(x) are shown (red curve) in the phase diagram in Figure 5a.
6. Discussion
The doping dependence of T*(x) is consistent with the result of T*(x) obtained from ARPES experiments on Pb-Bi2201 [34]. The appearance of the superconducting gap much lower than the pseudogap is consistent with the results of the tunneling spectroscopy experiment [35].
Figure 5b shows the first-principles calculated density of states (DOS) for the pseudogap phase in the underdoped LSCO. The predicted key feature of the pseudogap phase is the appearance of a broad peak around +70 meV, which is due to the flat nature of the spin-polarized band. Through accurate parametrizations of the first-principles spin-polarized band to the K-S model in the underdoped LSCO, we have shown that a doped hole in the spin-polarized band corresponds to a KS particle with the Hund’s coupling spin triplet [14]. The KS particles with up or down spin occupy the antibonding a1g orbital () around a Fermi pocket at the antinodal point (π, 0) in the 2D BZ, and thus may cause the circulating orbital motion, including the apical oxygen around the up or down localized spin. This circulating orbital motion due to the spin-triplet Hund’s coupling of a KS particle may be compared with recent inelastic neutron scattering results in Hg-cuprates [36]. Thus, the present theory has clearly shown that the magnetic effect appears in the pseudogap phase in LSCO, although the magnetic order and superconductivity have been said to be mutually exclusive.
Since the calculated DOS of the pseudogap in Figure 5b predicts the spontaneous breaking of time-reversal symmetry, we may say that the calculated result in Figure 5b is consistent with the experimental result of left- or right-circular polarized photons by Kaminski et al. [37]. In addition to those already mentioned, we would also like to point out that the phase diagram proposed in Figure 5a is also consistent with the polar-Kerr experiment [38], in which the Kerr rotation angle is zero above Tk while non-zero below Tk. Since Tk is below T*(x), and thus the magnetic order exists at Tk, the polar-Kerr effect may occur in the pseudogap phase in Figure 5a.
In conclusion, we have shown that the present new theory born from the anti-JT effect due to apical oxygen is consistent with a considerable number of experimental results on LSCO and similar oxide superconductors.
Author Contributions
Conceptualization, H.K. and J.-S.T.; Methodology, H.S. and K.Y.; Validation, K.S. (Kenji Sasaoka); Formal analysis, M.A., K.I., S.M., K.S. (Kenji Shiraishi) and O.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research funding is due to Tokyo University of Science.
Data Availability Statement
Not applicable.
Acknowledgments
We thank Robert J. Birgeneau, Shuichi Wakimoto, Atsushi Fujimori, Teppei Yoshida, Masaki Fujita and Chul-Ho Lee for helpful discussions. This work was supported by Tokyo University of Science. The computations were carried out in part using the computer resource offered under the category of General Projects by the Research Institute of Information Technology Kyushu University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bednorz, J.G.; Müller, K.A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. B 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Anderson, P.W. Resonating valence bond state in La2CuO4 and superconductivity. Science 1987, 235, 1196–1198. [Google Scholar] [CrossRef] [PubMed]
- Kamimura, H.; Araidai, M.; Ishida, K.; Matsuno, S.; Sakata, H.; Shiraishi, K.; Sugino, O.; Tsai, J.S. First-Principles Calculation of copper oxide superconductors that supports the Kamimura-Suwa model. Condens. Matter 2020, 5, 69. [Google Scholar] [CrossRef]
- Shima, N.; Shiraishi, K.; Nakayama, T.; Oshiyama, A.; Kamimura, H. Electronic structures of doped (La(1-x)Srx)2CuO4 in tetragonal phase. In Proceedings of First International Conference on Electronic Materials “New Materials and New Physical Phenomena for Electronics of the 21st Century; Sugano, T., Chang, R.P.H., Kamimura, H., Hayashi, I., Kamiya, T., Eds.; Material Research Society: Pittsburgh, PA, USA, 1989; pp. 51–54. [Google Scholar]
- Anisimov, V.L.; Ezhov, S.Y.; Rice, T.H. Singlet and triplet hole-doped configuration in La2Cu0.5Li0.5O4. Phys. Rev. B 1997, 55, 12829–12832. [Google Scholar] [CrossRef]
- Kamimura, H.; Matsuno, S.; Mizokawa, T.; Sasaoka, K.; Shiraishi, K.; Ushio, H. On the important role of the anti-Jahn-Teller effect in underdoped cuprate superconductors. J. Phys. Conf. Ser. 2013, 428, 012043. [Google Scholar] [CrossRef]
- Cava, R.J.; Batlogg, B.; Sunshine, S.A.; Siegrist, T.; Fleming, R.M.; Rabe, K.; Schneemeyer, L.F.; Murphy, D.W.; van Dover, R.B.; Gallagher, P.K.; et al. Studies of oxygen-deficient Ba2YCu3O7-δ and superconductivity Bi(Pb)-Sr-Ca-Cu-O. Phys. C 1988, 153–155, 560–565. [Google Scholar] [CrossRef]
- Chen, C.T.; Tjeng, L.H.; Kwo, H.; Kao, L.; Rudolf, P.; Sette, P.; Fleming, R.M. Out-of-plane orbital characteristics of intrinsic and doped holes in La2−xSrxCuO4. Phys. Rev. Lett. 1992, 68, 2543–2546. [Google Scholar] [CrossRef]
- Pellegrin, E.; Nücker, N.; Fink, J.; Molodtsov, S.L.; Gutierre, A.; Navas, E.; Sterebel, O.; Hu, Z.; Domke, M.; Kaindl, G.; et al. Orbital character of states at the Fermi level in La2−xSrxCuO4 and R2-xCexCuO4 (R = Nd2Sm). Phys. Rev. B 1993, 47, 3354–3367. [Google Scholar] [CrossRef]
- Zhang, F.C.; Rice, T.M. Effective Hamiltonian for the superconducting Cu oxides. Phys. Rev. B 1988, 37, 3759–3761. [Google Scholar] [CrossRef]
- Norman, M.R.; Kanigel, A.; Randeria, M.; Chtterjee, U.; Campuzano, J.C. Modeling the Fermi arc in underdoped cuprates. Phys. Rev. B 2007, 76, 174501. [Google Scholar] [CrossRef]
- Kamimura, H.; Suwa, Y. New theoretical view for high temperature superconductivity. J. Phys. Soc. Jpn. 1993, 62, 3368–3371. [Google Scholar] [CrossRef]
- Kamimura, H.; Hamada, T.; Ushio, H. Theoretical exploration of electronic structure in cuprates from electronic entropy. Phys. Rev. B 2002, 66, 054504. [Google Scholar] [CrossRef]
- Kamimura, H.; Ushio, H. On the interplay of Jahn-Teller physics and Mott physics leading to the occurrence of Fermi pockets without pseudogap hypothesis and d-wave high Tc superconductivity in underdoped cuprate superconductors. J. Supercond. Nov. Magn. 2012, 25, 677–690. [Google Scholar] [CrossRef]
- Kamimura, H.; Matsuno, S.; Suwa, Y.; Ushio, H. Occurrence of d-wave pairing in the phonon-mediated mechanism of high temperature superconductivity in cuprates. Phys. Rev. Lett. 1996, 77, 723–726. [Google Scholar] [CrossRef]
- Tsuei, C.C.; Kirtley, J.R. Pairing symmetry in cuprate superconductors. Rev. Mod. Phys. 2000, 72, 969–1016. [Google Scholar] [CrossRef]
- Takagi, H.; Ido, T.; Ishibashi, S.; Uota, M.; Uchida, S.; Tokura, Y.; Millis, A.J. Effect of a nonzero temperature on quantum critical points in itinerant fermion systems. Phys. Rev. B 1989, 40, 2254. [Google Scholar] [CrossRef]
- Wakimoto, S.; Yamada, K.; Tranquada, J.M.; Frost, C.D.; Birgeneau, R.J.; Zhang, H. Disappearance of antiferromagnetic spin excitations in overdoped La2−xSrxCuO4. Phys. Rev. Lett. 2007, 98, 247003. [Google Scholar] [CrossRef]
- Norman, M.R.; Pines, D.; Kalin, C. The pseudogap: Friend or foe of high Tc. Adv. Phy. 2005, 54, 715–733. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly correlated and approximately normed semilocal density functional. Phys. Rev. lett. 2015, 115, 036402. [Google Scholar] [CrossRef]
- Furness, J.W.; Zhang, Y.; Lane, C.; Buda, I.G.; Barbielini, B.; Markiewicz, R.S.; Bansil, A.; Sun, J. An accurate first-principles treatment of doping-dependent electronic structure of high-temperature cuprate superconductors. Commun. Phys. 2018, 1, 11. [Google Scholar] [CrossRef]
- Yamada, K.; Lee, C.H.; Kurahashi, K.; Wada, J.; Wakimoto, S.; Ueli, S.; Kimura, H.; Endoh, T.; Hosoya, S.; Shirane, G.; et al. Doping dependence of the spatially modulated dynamical spin correlations and sperconducting-transition temperature in La2−xSrxCuO4. Phys. Rev. B 1998, 57, 6165. [Google Scholar] [CrossRef]
- Wakimoto, S.; Zhang, H.; Yamada, K.; Swainson, I.; Hyunkyung, K.; Birgeneau, R.J. Direct Relation between the low-energy spin excitation and superconductivity of overdoped high-Tc supeconductors. Phys. Rev. Lett. 2004, 92, 217004. [Google Scholar] [CrossRef] [PubMed]
- Aeppli, G.; Bishop, D.J.; Brohom, C.; Bucher, E.; Cheong, S.-W.; Dai, P.; Fisk, Z.; Hayden, S.M.; Kleiman, R.; Mason, T.E.; et al. Neutron scattering and the search for mechanism of superconductivity. Physica C 1999, 317–318, 9–17. [Google Scholar] [CrossRef]
- Birgeneau, R.J.; Endoh, Y.; Hidaka, K.; Katarai, K.; Kastner, M.A.; Murakami, T.; Shirane, G.; Thurston, T.R.; Yamada, K. Quasaielastic and inelastic spin fluctuations in superconducting La2−xSrxCuO4. In Mechanisms of High Temperature Supercondcutivity; Kamimura, H., Oshiyama, A., Eds.; Springer: Berlin/Heidelberg, Germany, 1989; pp. 120–128. [Google Scholar]
- Hamada, T.; Ishida, K.; Kamimura, H.; Suwa, Y. Computational study on the ground state of a doped hole in a two-dimensional quantum spin systems. J. Phys. Soc. Jpn. 2001, 70, 2033–2037. [Google Scholar] [CrossRef]
- Tranquada, J.M.; Woo, H.; Perring, T.G.; Goka, H.; Gu, G.D.; Xu, G.; Fujita, M.; Yamada, K. Quantum magnetic excitations from stripes in copper oxide superconductors. Nature 2004, 429, 534–538. [Google Scholar] [CrossRef]
- Mason, Y.E.; Schröder, A.; Aeppli, G.; Mook, H.A.; Haydon, S.M. New magnetic coherence effect in superconducting La2−xSrxCuO4. Phys. Rev. Lett. 1996, 77, 1604–1607. [Google Scholar] [CrossRef]
- Drees, Y.; Lamago, D.; Piovano, A.; Komarek, A.C. Hour-glass magnetice spectrum in stripeless insulating transition metal oxide. Nature Comm. 2013, 4, 2449. [Google Scholar] [CrossRef]
- Yoshida, T.; Zhou, X.J.; Tanaka, K.; Yang, W.L.; Hussain Shen, Z.-X.; Fujimori, A.; Sahrakorpi, S.; Lindroos, M.; Markiewicz, R.S.; Bansil, A.; et al. Systematic doping evolution off underlying Fermi surface of La2−xSrxCuO4. Phys. Rev. B 2006, 74, 224510. [Google Scholar] [CrossRef]
- Kamimura, H.; Sugino, O.; Tsai, J.S.; Ushio, H. High-Tc Copper Oxide Superconductors and Related Novel Materials; Bussmann-Holder, A., Keller, H., Bianconi, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Chapter 11; pp. 129–150. [Google Scholar]
- Kamimura, H.; Sasaoka, K.; Ushio, H. Occurrence of Fermi pockets without pseudogap hypothesis and clarification of the energy distribution of angle-resolved photoemission spectroscopy in underdoped cuprate superconductors. J. Phys. Soc. Jpn. 2011, 80, 114715. [Google Scholar] [CrossRef]
- Lorama, J.; Mirza, K.; Cooper, J.; Tallon, J. Specific heat evidence on the normal state pseudogap. J. Phys. Chem. Solids 1998, 59, 2091–2094. [Google Scholar] [CrossRef]
- Nakayama, K.; Sato, T.; Sekiba, Y.; Richard, P.; Takahashi, T.; Kudo, K.; Okumura, N.; Sasaki, Y.; Kobayashi, N. Evolution of a pairing-induced pseudogap from the superconducting gap of (Bi, Pb)2Sr2CuO6. Phys. Rev. Lett. 2009, 102, 227006. [Google Scholar] [CrossRef]
- Suzuki, M.; Watanabe, T. Discriminating the superconducting gap from the pseudogap in Bi2Sr2CaCu2O8+δ by interlayer tunneling spectroscopy. Phys. Rev. Lett. 2000, 85, 4787–4790. [Google Scholar] [CrossRef]
- Li, Y.; Balédent, V.; Yu, G.; Barišić, N.; Hradil, K.; Mole, R.A.; Sidis, Y.; Steffens, P.; Zhao, X.; Bourges, P.; et al. Hidden magnetic excitation in the pseudogap phase of a high-Tc superconductor. Nature 2010, 468, 283–285. [Google Scholar] [CrossRef]
- Kaminski, A.; Rosenkranz, E.; Freswell, H.M.; Campzano, J.C.C.; Li, Z.; Raffy, H.; Cullen, W.G.; You, H.; Olsen, C.G.; Varma, C.M.; et al. Spontaneous time reversal symmetry breaking in the pseudogap state of high-Tc uperconductors. Nature 2002, 416, 610–613. [Google Scholar] [CrossRef]
- Hosur, P.; Kapitulnik, A.; Kiverlson, S.A.; Orenstein, J.; Raghu, S. Kerr effect as evidence of gyrotropic order in the cuprates. Phys. Rev. B 2013, 87, 115116. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).