Abstract
In contrast to the network security that relies on upper-layer encryption for the confidentiality and authenticity of communications, physical layer security (PLS) exploits the uniqueness and randomness of the physical channel to encrypt information and enhance the security of the system. In this paper, we study the PLS of a polar-coded wireless communication system. To be more specific, we leverage the unique properties in polar code construction and propose a channel quality indicator (CQI)-based frozen-bit pattern generation scheme. The transmitter employs the Gaussian approximation algorithm to generate the corresponding frozen bit pattern according to the instantaneous CQI of the legitimate link. At the receiver, by leveraging the full channel reciprocity in the time-division duplex (TDD) mode, we can map the CQI to the corresponding frozen bit pattern and correctly decode the received bits. By contrast, the eavesdropper was unable to have the knowledge of the legal channel, and hence cannot determine the frozen bit pattern of the polar-coded bit sequence. Our simulation results demonstrate that by adopting the proposed PLS key generation scheme, Eve was hardly able to correctly decode a complete frame, leading to a high block error rate (BLER), while Bob was able to attain a BLER.
1. Introduction
With the continued deployment of digital devices, wireless communications are experiencing rapid evolutions. However, due to the inherent broadcast nature of wireless communications, security has become a significant problem during wireless transmissions. To prevent eavesdropping and to ensure the security of transmitted data, traditional security relies on upper-layer encryption. However, the higher-layer secret key exchange requires extra communication resources, reducing the throughput. Fortunately, this can be addressed by employing physical layer security (PLS) techniques [1,2] that utilize the inherent randomness of wireless channels.
PLS has been widely studied as a technique to protect the confidentiality of wireless communications, which uses the uniqueness and reciprocity of the physical channel to encrypt information and enhance the security of the system. There are now two main categories of PLS techniques: the first uses the public channel to generate keys [3]; the second uses link signatures to generate physical layer keys [4]. Due to the reciprocity of uplink and downlink transmissions in time-division duplex (TDD) systems, legitimate users have access to identical channel characteristics, which is the basis for legitimate user-generated keys [5,6]. In addition, to reduce the resource consumption associated with the sharing and management of keys in wireless networks by exploiting the reciprocity of wireless channels with mutual information (MI) from channel measurements between legitimate users [7], researchers have proposed a number of PLS methods to generate cryptographic keys using channel state information (CSI) to ensure the security of communication systems [8,9,10].
In addition, PLS techniques for visible light communication (VLC) systems were investigated by many researchers as well [11]. A highly accurate and low computational burden noncoherent detection algorithm was proposed in [12]. The use of high-dimensional (HD) constructions of ultraviolet signal geometrical features that are insensitive to intersymbol interference (ISI) contamination provides better detection performance. Additionally, [13] proposed a spatial constellation design method based on generalized spatial shift keying for the PLS of multiuser (MU) multiple-input multiple-output (MIMO) VLC systems, where the transmit power of randomly selected light-emitting diodes is adjusted by using the CSI of the user at the transmitter. Interuser security is ensured while providing minimum bit error rate (BER) for legitimate users.
However, the disadvantage of using CSI to generate keys is that when the wireless channel changes slowly, the rate of key generation becomes small as well [14]. In addition, most key generation schemes assume that the eavesdropper’s channel is independent of the legitimate channel, ignoring the influence of the eavesdropper. However, when the eavesdropper’s channel is correlated with the legitimate channel, the eavesdropper may be able to extract enough information to generate the same key as the legitimate user, resulting in the disclosure of confidential information [14]. To further ensure communication security, artificial noise and beamforming techniques have been proposed in existing research, which have been demonstrated to be effective in increasing the secrecy capacity between legitimate users [15,16]. Furthermore, in relay communication scenarios, cooperative jamming and cooperative forwarding are proposed in [17] to ensure the security of the communication systems.
The use of artificial noise to improve physical layer security was first proposed by R. Negi et al. [18]. Specifically, the transmitter splits a fraction of the transmit power to send artificial noise that is directed at the eavesdropper and aimed at the zero space of the legitimate receiver, artificially increasing the gap in noise levels between the legitimate user and the eavesdropping user.
When the transmitter has the perfect knowledge of the CSI of the eavesdropping channel, joint optimization of information and artificial noise covariance can be performed [19], which better achieves secure communications. However, in practical engineering applications, obtaining a complete and accurate CSI is difficult due to limitations such as time delay, Doppler offset and the finite length of feedback information. A power allocation scheme for artificial noise injection is proposed in [20], in which the transmitter does not need to know the CSI of the eavesdropping channel. The work of [21] developed a new layered PLS model to protect confidential information and proposed an artificial noise-assisted PLS scheme to maximize information security while maintaining low information confidentiality.
Furthermore, artificial noise can also be generated in a cooperative manner, that is, other nodes in the communication system assist in sending noise to interfere with the eavesdropper while sending information by a single antenna node [22], where the system security is ensured by adding spatial artificial noise to the relay forwarding signal in a collaborative manner. Although the design scheme based on artificial noise improves the security communication rate of the system, it also inevitably increases the peak average power ratio.
In addition to artificial noise techniques, more practical PLS designs were proposed over the past years. For example, by encoding the source message, PLS secure encoding not only eliminates the need for a key but also avoids the resource overhead associated with multiple interactions between the communicating parties. A spatial modulation scheme for channel-quality indicator (CQI) mapping was proposed in [4], which changes the spatial modulation mapping pattern for generating physical layer keys based on the instantaneous CQI in the legitimate channel and shares the spatial modulation pattern with the legitimate receiver, which not only improves the data rate of the legitimate channel but also reduces the detection performance of the eavesdropper. Because the eavesdropper is not aware of the CQI-based spatial modulation mapping pattern, the correct demodulation method cannot be obtained.
Due to the advantages of channel coding with high decoding performance, the combination of high-performance codes with the characteristics of the wireless system itself has become a hot spot for the exploration of secure coding. Ref. [23] proposed a secrecy coding based on the randomness of the wireless channel, which can guarantee the security and reliability of the communication system at the same time. Ref. [24] proposed a coding design guideline for Rayleigh fading eavesdropping channels, using lattice codes to achieve confidential communication. In [25], a new wired eavesdropping channel code construction with security and error correction guarantees was proposed to protect important confidential messages while protecting legitimate users from errors when receiving them. Ref. [26] used discrete-time fully analog joint source-channel coding over wireless channels to prevent eavesdropping. These secrecy coding schemes have theoretically proven to be close to the secrecy capacity. However, the design of more practical secrecy coding schemes remains to be addressed.
Polar code [27] has been studied for decades and has been used in Enhanced Mobile Bandwidth (EMBB) control channels for 5G communication systems. Corresponding decoding algorithms such as successive cancellation (SC) [28], successive cancellation list (SCL) and cyclic redundancy check-aided (CRC) SCL [29] algorithms perform recursive decoding based on the concatenated structure of polarized codes, which greatly improves decoding accuracy. The characteristics of the channel polarization make it suitable for PLS, and hence attract numerous researchers’ attention. For instance, the authors in [30] designed a PLS key generation scheme by selecting a frozen bits mapping pattern according to instantaneous CQI. Additionally, the strong and weak secrecy limits of PLS polarization codes are studied in [31,32], respectively.
To the best of our knowledge, there are currently no designs based on frozen bit constructions of polar codes in PLS. Against this background, in this paper, we propose a polar code construction scheme based on the CQI for wireless communication systems operating on the TDD mode, where the construction of the frozen bits in this scheme is determined by the instantaneous gain in the legal link. Due to the reciprocity of TDD systems, the transmitter and the legitimate receiver can obtain the same CSI of the legitimate channel without using the feedback channel, so the legitimate receiver always knows the instantaneous gain of the legitimate channel and its mapped frozen bit pattern, which ensures that the legitimate receiver can perform accurate decoding using a low-complexity decoding algorithm. At the same time, the eavesdropper does not have access to the instantaneous gain of the legitimate channel and therefore is not able to determine the frozen bit construction used by the transmitter, and thus the eavesdropper is not be able to decode in the correct way, which greatly reduces the accuracy of the eavesdropper’s decoding. We provide a bold and clear comparison with the literature in Table 1, and our novel contributions are summarized below:

Table 1.
Contrasting our contributions to the state of the art.
- We introduce a frozen bit construction scheme that is determined by the instantaneous channel gain of the legitimate link. The range of instantaneous channel gain is first divided into multiple nonrepeating continuous intervals. Due to the adaptive nature of polar codes, different channel gain intervals generate different frozen bit construction patterns as a way to match the reliability of the channel. Since the eavesdropper does not know the frozen bit pattern selected by the transmitter, he/she is not able to complete the decoding of the legitimate link information. Therefore, this scheme improves the decoding performance of legitimate receivers, degrades the performance of eavesdroppers and breaks the condition of the single construction pattern.
- In contrast to the work in [30], which considers the 0-1 mapping patterns of the frozen bits, we investigate the frozen bit generation by adopting the Gaussian approximation (GA). Specifically, we employ the GA construction algorithm to generate different frozen bit patterns depending on the instantaneous CQI of the legal channel. We demonstrate that different channel gains have relatively large differences in the frozen bit structure constructed by the GA algorithm. The eavesdropper decodes the information propagated by the transmitter according to a different frozen bit pattern, which leads to a higher bit error rate (BER) performance.
- Assuming that the eavesdropper has strong computational power, the eavesdropper can rely on the brute force search of the frozen bit construction used by the transmitter for strong detection capabilities to obtain confidential information transmitted over the legitimate link. Simulation results demonstrate that as the signal-to-noise ratio (SNR) increases, the chances of the eavesdropper relying on powerful computational power to find the correct frozen bits location information do not show much prominence, confirming that the PLS scheme proposed in this paper shows strong stability against powerful eavesdroppers.
The remainder of this paper consists of the following sections. Section 2 describes the system model and the compiled code for the transmitter and receiver. Section 3 details the proposed CQI-based PLS design scheme, and Section 4 presents simulation results and evaluates the performance of the scheme. Finally, the paper is concluded in Section 5.
2. System Model
In this section, we describe the channel model, transmitter and receiver model of the polar-coded communication system in Section 2.1, Section 2.2 and Section 2.3, respectively.
2.1. Channel Model
Consider a point-to-point communication system operating in the TDD mode, as in many scenarios where passive attacks exist, that has a single-antenna wiretap channel, as shown in Figure 1, where Alice passes information to Bob, the legitimate receiver, while Eve, the eavesdropper, is eavesdropping on the information transmitted by the legitimate link. Alice, Bob and Eve are all single-antenna devices. The legitimate link and the wiretapping link are independently and identically distributed block Rayleigh fading channels, denoted by and , respectively, where and are complex Gaussian distributions obeying zero-mean, unit-variance constant over a block length S.
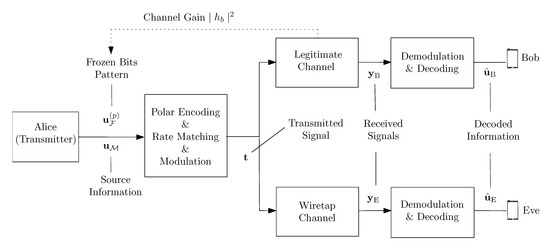
Figure 1.
Overview of the system model.
Alice transmits an arbitrary block with S symbols and defines the symbols received by Bob and Eve in terms of vectors and , which are expressed as
and
where and obey complex Gaussian distribution containing ; denotes the zero-valued vector and denotes the identity matrix. represents the additive white Gaussian noise (AWGN) component.
2.2. Transmitter
As shown in Figure 2, Alice encodes the information bits, performs rate matching and M-ary quadrature amplitude modulation (MQAM) to transmit the signal over the wireless channel.
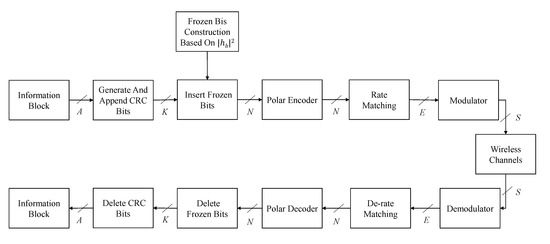
Figure 2.
The transmitter and receiver structure of a point-to-point polar-coded communication system.
Alice’s polar encoding process through the modulo-2 matrix can be expressed as
where represents the encoded bit vector, and the original sequence of information bits and frozen bits is collected in ; represents the generating matrix and denotes the power Kronecker product of the Kernel matrix , which is given by
The encoding process can be implemented using the polar code graph in Figure 3, where the input core information block is on the left side of the graph and the core encoded block is output on the right side of the graph after successive exclusive OR (XOR) operations.
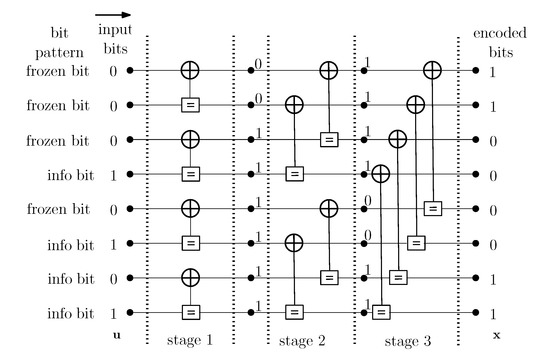
Figure 3.
An example of polar code graph, which converts information bits [1101] into encoded bits [11000011].
Alice takes the encoded N bits and rate matches them to E bits according to the actual transmission capacity. Typical rate matching approaches include puncturing, shortening and repetition [33]. MQAM is then performed to obtain symbols for transmission.
2.3. Receiver
Alice transmits the information to Bob, while Eve steals confidential information. When Bob receives the signal and Eve steals the signal, they demodulate and derate match to obtain the N-bit demodulated sequence. Then, the SCL polar decoding first calculates the log likelihood ratio (LLR) of the bit by
where y denotes the received signal and , denotes the bit transmitted by Alice.
Combining these LLRs, the decoding mechanism is shown in Figure 4a, where the two connections on the right-hand side of the particular XOR both provide an LLR, and respectively. This enables the XOR to mod-2 sum of the and LLRs at the level, , , which can be expressed as
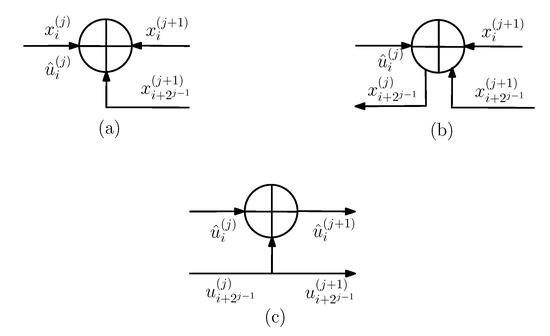
Figure 4.
The SC decoding process for the mod-2 sum of the and the bits at the level: (a) the f function, (b) the g function and (c) partial sum calculation.
Note that by performing the f function, for the left-most XORs in the polar code graph, the corresponding hard bit decision can be expressed as
Then, as shown in Figure 4b, the hard bit decision may be combined with the LLRs and in order to compute a new LLR for the second connection on the left-hand side, according to the g function of
As shown in Figure 4c, is provided on the second of the connections on the left-hand side of the XOR. Together with , we can perform the partial sum computation of the bits and for the first and second connections on the right-hand side of the XOR, where we have
Performing the three types of XOR calculations above in a given SC algorithm scheduling [27], an LLR may be obtained for each of the N connections on the left-hand edge of the polar code graph; one at a time in a sequential order from top to bottom. The SC decoding algorithm is decoded one bit by one in the decoding process, and there is a phenomenon of error transmission. Therefore, its error correction performance is not very ideal. Ref. [28] further solves this problem. When the LLR in this sequence is obtained, a path metric (PM) may be updated for the decoding candidate, which can be expressed as
The PM quantifies the likelihood of decoding candidates. The SCL algorithm is divided into three main steps, starting with initialization. The candidate path list is initialized to an empty path, corresponding to a PM .
The second step performs the extension operation. For each node in the list, two sequences of length i can be generated, corresponding to decoded estimates of 0 or 1, respectively, and then the PM value of each candidate path is changed for each line.
The third step is the competition operation. After the expansion step, if the number of candidate paths does not reach the list size L, this step is skipped. Otherwise, the L paths with the smallest PM among the current candidate paths are kept and the rest of the paths are trimmed.
Repeat the second and third steps until all decoding is completed. Select the path with the lowest PM value as the decoding result. If the CRC-SCL algorithm is used, the final output of L candidate paths is sorted from the smallest to the largest metric value and CRC-checked in turn. The first path that passes the CRC check is the output decoded result. Note that if no path passes the CRC check, the polar decoder chooses the path taken as the decoding result.
3. Physical Layer Secret Key Generation
In this section, we introduce the proposed CQI-based PLS scheme for polar-coded systems.
3.1. Polar Encoding at Alice
At Alice, an -bit vector can be encoded into an N-bit encoded vector , where contains K information bits and frozen bits, and the location of the frozen bits is defined in terms of , while the complementary set of is representing the information bit position. Accordingly, represents the information bit locations.
Due to the channel reciprocity in the TDD systems, both Alice and Bob are able to obtain the channel gain . However, Eve cannot obtain any information about the legitimate link between Alice and Bob by eavesdropping. Therefore, Alice uses the random channel gain and performs the GA algorithm to determine the number and the positions of frozen bits. The range of the channel gain is , which is divided into P consecutive intervals , where . In order to make the probability of the channel gain be in each interval the same , the probability density function (pdf) of the channel gain is set to . Then, we have
Thus, the range of channel gain is divided into P nonoverlapping consecutive intervals according to (11); therefore, Alice has P candidate constructions for frozen bits, denoted as . Alice selects the frozen bit pattern corresponding to the interval for polar encoding. In this case, the frozen bits construction is used to match the reliability of the channel using the GA algorithm to achieve the current channel capacity, as shown in Algorithm 1. Different channel intervals correspond to different frozen bits patterns, as shown in Table 2. Here, we list the situation of when and and represent the frozen bit patterns as hexadecimal. Furthermore, to prevent Eve from observing the modulation and thus obtaining the gain level of the legitimate channel, Alice takes the same MQAM, thus using bits per channel, where is the energy of each quadrature amplitude modulation (QAM) symbol and is the noise power.
| Algorithm 1 Generate frozen bits patterns |
|

Table 2.
Examples of frozen bit construction for P = 4 and P = 8.
Alice then encodes the original sequence to by XOR operation through (3),(4) and modulates the encoded with MQAM to obtain symbols for transmission; Bob receives the signal and decodes it successfully. However, Eve is not able to decode the message in the correct way because she does not know the frozen bit pattern used by Alice. This greatly enhances the security of the information transmitted over the legitimate channel.
3.2. Polar Decoding at Bob
Due to the reciprocity of TDD systems, Bob is already fully aware of the channel gain in each block of the legitimate channel, and therefore Bob also knows the frozen bits construction chosen by Alice. According to (12), when Bob receives the signal, he/she can decode it using the SC [28], SCL or CRC-SCL [29] decoding algorithms to obtain the information bits. For any polar-coded bit sequence , Bob calculates the LLR of the bit by
where is the signal received by Bob and represents Alice’s transmitted bit, where .
Through these LLRs, Bob’s SC decoding process depends on (6), (7) and (8). As shown in Figure 4, can be completely estimated, and the confidential information transmitted by Alice can be successfully obtained.
In addition, Bob can also use the SCL algorithm to decode, which can further improve the decoding performance of legitimate links. Furthermore, by adding a CRC check code to the transmitted source signal, after the SCL decoding obtains a variety of decoding results, the CRC check is performed on these decoding results. The decoding results with the minimum PM value are the actual output decoding results through CRC check. In this way, the decoding performance is improved.
3.3. Polar Decoding at Eve
Eve tries to eavesdrop on confidential information from a legitimate link, according to (2) received the signal , and uses SC algorithm to decode the same as Bob, as shown in Figure 4; the LLRs on the right side of its XOR is represented as
where is the signal received by Eve.
Eve combines these LLRs and performs three different XOR operations like Bob, and finally successfully estimates information bits transmitted by Alice . Furthermore, Eve can also decode by adding candidate decoding paths and a CRC check, using SCL and CRC-SCL. However, the biggest difference from Bob is that Eve determines the construction of frozen bits in the signal according to the gain of eavesdropping channel , and then estimates the bits transmitted by Alice through (7), which cannot obtain the legitimate channel gain . Therefore, Eve adopts the wrong frozen bit construction for decoding.
4. Simulation Results
In this section, the design of the proposed PLS scheme is verified by comparing the error correction capability of Bob and Eve. Considering the worst-case security performance evaluation of our scheme, Eve is assumed to have strong eavesdropping capability and full knowledge of the eavesdropping channel gain. In addition, in the TDD system, we assume that Alice and Bob also have full knowledge of the legitimate channel gain . Under this condition, simulations are carried out. The simulation parameters are summarized in Table 3.

Table 3.
Simulation parameters.
The BER and block error rate (BLER) are compared in Figure 5 and Figure 6 for Bob and Eve, respectively, where Alice uses quadrature phase-shift keying (QPSK) with a polar code length of and a code rate of , and the channel gain is divided into consecutive nonrepeating intervals. Under this condition, Bob and Eve may adopt SC, SCL or CRC-SCL decoding algorithms, where the candidate list size is in the SCL decoder and a 24-bit CRC is employed in the CRC-SCL decoder. As shown in Figure 5, through the design of our proposed PLS scheme, under the same condition, as the SNR increases, the BER of the eavesdropper Eve differs from that of Bob. The difference between Eve’s BER and Bob’s BER is over 9 dB at the BER of . The difference is even more significant in terms BLERs, as shown in Figure 6, which verifies the reliability of the proposed PLS scheme. Note also that by comparing the case of Bob with only a single frozen bit pattern versus multiple frozen bit patterns, we can observe that our proposed PLS scheme improves the decoding performance of legitimate receivers; degrades the performance of eavesdroppers, and breaks the condition of the single construction pattern.
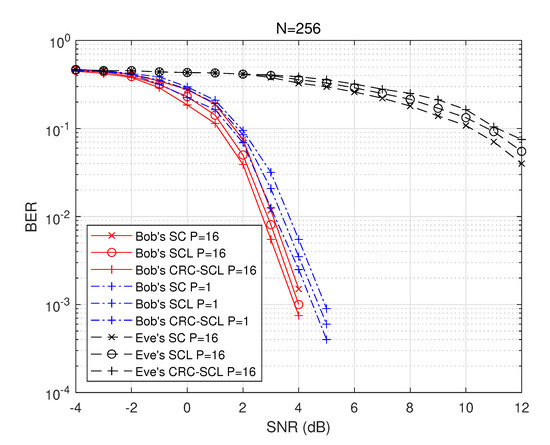
Figure 5.
BER performance at Bob and Eve, where , and QPSK is employed.
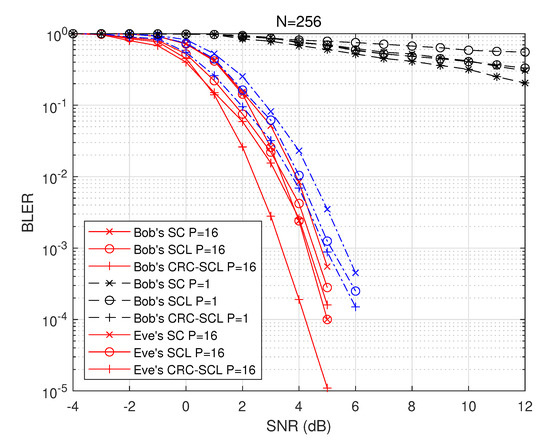
Figure 6.
BLER performance at Bob and Eve, where , and QPSK is employed.
As expected, Bob was able to obtain better decoding performance using the SCL and CRC-SCL decoding algorithms than Eve, who was unable to determine the frozen bit construction selected by Alice due to its inability to obtain the legitimate channel gain . He/she could only guess the frozen bit construction based on the eavesdropping channel parameters , and thus achieved worse performance when Eve used the SCL and CRC-SCL decoders. The main reason for this is that Eve does not know the correct , resulting in an incorrect candidate path for the SCL decoder, and adding check bits to this results in a higher error rate. We can see that in BLER, Eve’s SCL decoder has almost the same performance as CRC-SCL decoding, which is consistent with the intuition that Eve will pick the shortest path decoding result when the CRC checksum does not pass. Similarly, in terms of BLER, our proposed PLS solution not only reduces Eve’s performance but also improves Bob’s performance.
Figure 7 and Figure 8 further investigate the PLS scheme proposed in this paper, using a longer polar code length . By comparing Figure 5 with Figure 7, we find that as the code length N increases, Bob’s decoding performance improves, however, Eve’s performance decreases, with their BER performance differing from Bob by more than 10 dB. Similar conclusions can be drawn by comparing Figure 6 with Figure 8.
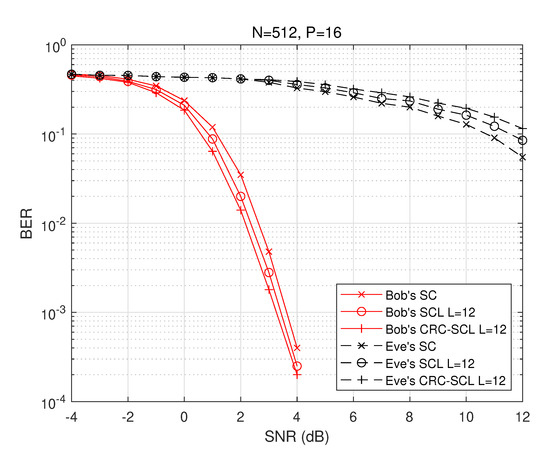
Figure 7.
BER performance at Bob and Eve, where , and QPSK is employed.
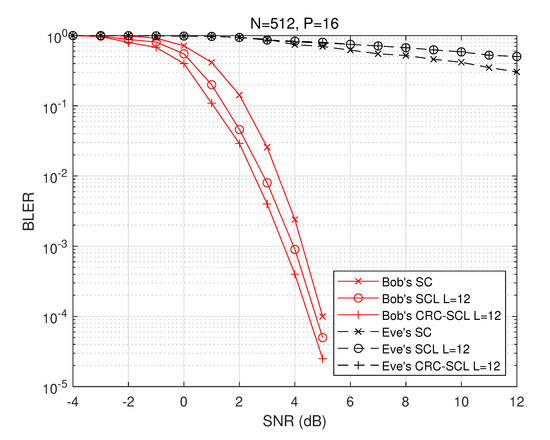
Figure 8.
BLER performance at Bob and Eve, where , and QPSK is employed.
By definition, the physical layer secrecy capacity is the channel capacity difference between the legitimate channel and the eavesdropping channel. In the proposed scheme, Bob is able to reach a BLER of , while Eve can barely decode a complete frame correctly, so the mutual information between Eve and Alice is almost zero, which makes the capacity capacity of the system asymptotically close to the legitimate channel capacity, thus verifying that this scheme achieves superior performance in terms of the secrecy capacity.
Furthermore, the number of channel gain intervals P and the possible effect of the code rate R on this scheme are investigated in Figure 9. The formula (11) and Table 2 give details of the different frozen bit constructions at different intervals of P. As shown in Figure 9, there is almost no difference between the BLER of Bob using and intervals. This is because Bob knows clearly about the corresponding frozen bit construction pattern of the interval every time. The only performance difference results from the GA construction at different SNRs. By contrast, by comparing Eve’s decoding performance at and , it can be seen that Eve’s decoding performance decreases as P increases because as the interval of channel gain becomes larger, Alice has more different frozen bit constructions, which leads to a lower probability that Eve’s perceived frozen bit construction is the same as the one used by Alice, thus leading to a worse decoding performance. On the other hand, when we lower the code rate R, we can find that Bob’s performance improves at compared with . The reason for this is that as the code rate decreases, there are fewer locations to transmit confidential information, and thus Bob’s performance improves somewhat. Eve also has the same effect. Overall, Eve’s performance is well-suppressed and Bob’s performance is slightly improved as the number of channel gain intervals increases without changing the code rate.
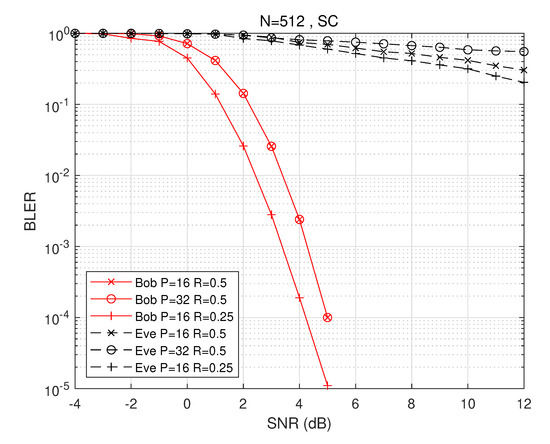
Figure 9.
In the QPSK modulation system with , the number of channel gain intervals P and the code rate R affect the performance of this scheme.
5. Conclusions
5.1. Summary
In this paper, the design scheme of coding frozen bit construction based on channel gain mapping not only reduces the decoding performance of the eavesdropper Eve but also improves the error correction performance of the legitimate receiver Bob. Furthermore, this scheme breaks the conditions of the single structure model. The idea is to map the multiple constructions of frozen bits based on the instantaneous gain of the legitimate channel obtained by Alice as the physical layer key. Since Eve does not have access to the gain of the legitimate channel, she does not have access to this key, resulting in her inability to decode it in an appropriate way to obtain confidential information. Alice does not need to know the CSI of the eavesdropping channel, which ensures authenticity and flexibility. In addition, this paper verifies the performance of the proposed scheme under Eve’s powerful eavesdropping capabilities. Simulation results show that the proposed scheme still performs well under these conditions, demonstrating its wide applicability.
5.2. Future Work
So far, we only considered a single-antenna eavesdropping channel model, and in order to have better application scenarios while increasing security, we may extend this work to MIMO systems to consider more complex scenarios, and other advanced decoding algorithms can be considered. Additionally, in practice, a completely known CSI is difficult to achieve, and in order to improve the randomness of PLS and guarantee the performance of legitimate users, the polarization code can be considered in the presence of CSI estimation errors.
Furthermore, in order to validate the effectiveness of our proposed scheme, we will dedicate ourselves to building a demonstration prototype.
Author Contributions
Investigation, Y.T.; Writing—original draft, Y.Z.; Writing—review & editing, L.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data were presented in main text.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zou, Y.; Zhu, J.; Wang, X.; Hanzo, L. A Survey on Wireless Security: Technical Challenges, Recent Advances, and Future Trends. Proc. IEEE 2016, 104, 1727–1765. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Ng, D.W.K.; Gerstacker, W.H.; Chen, H.H. A Survey on Multiple-Antenna Techniques for Physical Layer Security. IEEE Commun. Surv. Tutorials 2017, 19, 1027–1053. [Google Scholar] [CrossRef]
- Zhang, J.; Duong, T.Q.; Marshall, A.; Woods, R. Key Generation From Wireless Channels: A Review. IEEE Access 2016, 4, 614–626. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Yang, Y.; Yang, L.L.; Hanzo, L. Physical Layer Security of Spatially Modulated Sparse-Code Multiple Access in Aeronautical Ad-hoc Networking. IEEE Trans. Veh. Technol. 2021, 70, 2436–2447. [Google Scholar] [CrossRef]
- Zhang, S.; Jin, L.; Lou, Y.; Zhong, Z. Secret key generation based on two-way randomness for TDD-SISO system. China Commun. 2018, 15, 202–216. [Google Scholar] [CrossRef]
- Da Silva, J.M.B.; Wikström, G.; Mungara, R.K.; Fischione, C. Full Duplex and Dynamic TDD: Pushing the Limits of Spectrum Reuse in Multi-Cell Communications. IEEE Wirel. Commun. 2021, 28, 44–50. [Google Scholar] [CrossRef]
- Aldaghri, N.; Mahdavifar, H. Physical Layer Secret Key Generation in Static Environments. IEEE Trans. Inf. Forensics Secur. 2019, 18, 3104–3112. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; He, B.; Duong, T.Q.; Woods, R. On the key generation from correlated wireless channels. IEEE Commun. Lett. 2017, 21, 961–964. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Woods, R.; Marshall, A.; Duong, T.Q. An effective key generation system using improved channel reciprocity. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, 19–24 April 2015; pp. 1727–1731. [Google Scholar]
- Jin, H.; Huang, K.; Jin, L.; Zhong, Z.; Chen, Y. Physical-layer secret key generation with correlated eavesdropping channel. In Proceedings of the 2018 IEEE 4th International Conference on Computer and Communications (ICCC), Chengdu, China, 7–10 December 2018; pp. 226–231. [Google Scholar]
- Arfaoui, M.A.; Soltani, M.D.; Tavakkolnia, I.; Ghrayeb, A.; Safari, M.; Assi, C.M.; Haas, H. Physical Layer Security for Visible Light Communication Systems: A Survey. IEEE Commun. Surv. Tutorials 2020, 22, 1887–1908. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Zhang, M.; Li, Z.; Popov, S.; Leeson, M.; Xu, T. High-Dimensional Feature Based Non-Coherent Detection for Multi-Intensity Modulated Ultraviolet Communications. J. Light. Technol. 2022, 40, 1879–1887. [Google Scholar] [CrossRef]
- Su, N.; Panayirci, E.; Koca, M.; Yesilkaya, A.; Poor, H.V.; Haas, H. Physical Layer Security for Multi-User MIMO Visible Light Communication Systems With Generalized Space Shift Keying. IEEE Trans. Commun. 2021, 69, 2585–2598. [Google Scholar] [CrossRef]
- Bakşi, S.; Popescu, D.C. Secret key generation with precoding and role reversal in MIMO wireless systems. IEEE Trans. Wirel. Commun. 2019, 18, 3104–3112. [Google Scholar] [CrossRef]
- Ji, X.; Kang, X.; Huang, K.; Li, N.; Yi, M. The full-duplex artificial noise scheme for security of a cellular system. China Commun. 2015, 12, 150–156. [Google Scholar] [CrossRef]
- Lai, S.H.; Lin, P.H.; Lin, S.C.; Su, H.J. On optimal artificial-noise assisted secure beamforming for the multiple-input multiple-output fading eavesdropper channel. In Proceedings of the 2012 IEEE Wireless Communications and Networking Conference (WCNC), Paris, France, 1–4 April 2012; pp. 513–517. [Google Scholar]
- Zou, Y.; Zhu, J.; Wang, X.; Leung, V.C. Improving physical-layer security in wireless communications using diversity techniques. IEEE Netw. 2015, 29, 42–48. [Google Scholar] [CrossRef] [Green Version]
- Negi, R.; Goel, S. Secret communication using artificial noise. In VTC-2005-Fall. In Proceedings of the 2005 IEEE 62nd Vehicular Technology Conference, Dallas, TX, USA, 25–28 September 2005; pp. 1906–1910. [Google Scholar]
- Li, G.; Hu, A. MISO secrecy transmission via designing artificial noise by receiver under perfect and imperfect CSI. In Proceedings of the 2016 2nd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 14–17 October 2016; pp. 2664–2668. [Google Scholar]
- Mukherjee, A.; Swindlehurst, A.L. Robust beamforming for security in MIMO wiretap channels with imperfect CSI. IEEE Trans. Signal Process. 2010, 59, 351–361. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Chen, J.; Kuo, Y.; Zhou, Y. Artificial-noise-aided optimal beamforming in layered physical layer security. IEEE Commun. Lett. 2018, 23, 72–75. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, C.; Zhao, H.; Long, H.; Wang, W. Algorithms for secrecy guarantee with null space beamforming in two-way relay networks. IEEE Trans. Signal Process. 2014, 62, 2111–2126. [Google Scholar] [CrossRef]
- Nafea, M.; Yener, A. A new wiretap channel model and its strong secrecy capacity. IEEE Trans. Inf. Theory 2017, 64, 2077–2092. [Google Scholar] [CrossRef]
- Belfiore, J.C.; Oggier, F. Lattice code design for the Rayleigh fading wiretap channel. In Proceedings of the 2011 IEEE International Conference on Communications Workshops (ICC), Kyoto, Japan 5–9 June 2011; pp. 1–5. [Google Scholar]
- Cassuto, Y.; Bandic, Z. Low-complexity wire-tap codes with security and error-correction guarantees. In Proceedings of the 2010 IEEE Information Theory Workshop, Cairo, Egypt, 6–8 January 2010; pp. 1–5. [Google Scholar]
- Hodgson, E.; Brante, G.; Souza, R.D.; Rebelatto, J.L. On the physical layer security of analog joint source channel coding schemes. In Proceedings of the 2015 IEEE 16th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Stockholm, Sweden, 28 June–1 July 2015; pp. 585–589. [Google Scholar]
- Arikan, E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Muramatsu, J. Successive-cancellation decoding of binary polar codes based on symmetric parametrization. In Proceedings of the 2021 IEEE International Symposium on Information Theory (ISIT), Virtual, 12–20 July 2021; pp. 2364–2368. [Google Scholar]
- Raj, A.A.; Pooranasankari, M.; Abinayaa, S.S. Design of successive cancellation list decoding of polar codes. In Proceedings of the 2021 6th International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 8–10 July 2021; pp. 21–25. [Google Scholar]
- Yang, Y.; Li, W. Security-Oriented Polar Coding Based on Channel-Gain-Mapped Frozen Bits. IEEE Trans. Wirel. Commun. 2022, 1. [Google Scholar] [CrossRef]
- Wang, H.; Tao, X.; Li, N.; Han, Z. Polar coding for the wiretap channel with shared key. IEEE Trans. Inf. Forensics Secur. 2017, 13, 1351–1360. [Google Scholar] [CrossRef]
- Song, L.; Xie, L.; Chen, H.; Wang, K. A feedback-based secrecy coding scheme using polar code over wiretap channels. In Proceedings of the 2014 Sixth International Conference on Wireless Communications and Signal Processing (WCSP), Hefei, China, 23–25 October 2014; pp. 1–6. [Google Scholar]
- Jang, M.; Ahn, S.K.; Jeong, H.; Kim, K.J.; Myung, S.; Kim, S.H.; Yang, K. Rate matching for polar codes based on binary domination. IEEE Trans. Commun. 2019, 67, 6668–6681. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).