3.1. Homomorphic Encryption
The definition of the homomorphic encryption (HE) scheme is given in [
21] as follows:
Definition 1 (Homomorphic Encryption). A family of schemes is said to be homomorphic with respect to an operator ∘ if there exist decryption algorithms such that for any two ciphertexts , the following equality is satisfied:where are the corresponding randomness. A homomorphic encryption scheme is a pair of algorithms, and , with the following properties:
takes as input a plaintext , and outputs a ciphertext c such that c is a homomorphic image of m, i.e., ;
takes as input a ciphertext c, and outputs a plaintext m such that m is a homomorphic image of c;
and are computationally efficient.
There are two types of homomorphic encryption: additively homomorphic and multiplicatively homomorphic.
Additively homomorphic encryptionconsists of a pair of algorithms and such that, for all , ,, and , we have .
Multiplicatively homomorphic encryption consists of a pair of algorithms and such that, for all , ,, and , we have .
Partially homomorphic encryption is a variant of homomorphic encryption where homomorphism is only partially supported, i.e., the encryption scheme is homomorphic for some operations while not homomorphic for others.
Somewhat homomorphic encryption is a variant of fully homomorphic encryption where homomorphism is only limited supported, i.e., the encryption scheme is homomorphic for all operations for a limited number of operations.
Fully homomorphic encryption (FHE) is a variant of homomorphic encryption which allows for homomorphism over all functions, i.e., the encryption scheme is homomorphic for all operations. In other words, an FHE scheme consists of a pair of algorithms and such that, for all , ,, and , we have .
Table 1 shows a summary of the major homomorphic encryption schemes.
3.2. Brakerski–Fan–Vercauteren (BFV) Scheme
Since the work of Brakerski, Fan, and Vercauteren (BFV), the somewhat homomorphic encryption (SHE) scheme has become one of the most important research topics in cryptography. In this section, we give the definition of this scheme.
Definition 2 (BFV scheme).
An SHE scheme is said to be in the BFV family of schemes if it consists of the following three algorithms: Key generation algorithm: It takes the security parameter k as input, and outputs a public key and a secret key .
Encryption algorithm: It takes the message , a public key , and a randomness as inputs, and outputs a ciphertext .
Decryption algorithm: It takes a ciphertext , a secret key , and an integer as inputs, and outputs a message .
Remark 1. In the above definition, the integer i is called the decryption index. It is introduced to allow for efficient decryption of ciphertexts that are the result of homomorphic operations. For example, when the ciphertext is the result of homomorphic operations on ciphertexts and , that is, , then can be decrypted by taking the decryption index .
In the following, we give a brief description of the BFV scheme.
The key generation algorithm of the BFV scheme consists of the following two steps.
- 1.
Let t be the security parameter. For a positive integer t, define a number and a positive integer p where is a polynomial, and p is a prime number satisfying .
- 2.
Let d be a positive integer such that . Choose a monic polynomial of degree d with for some . Let . Choose a quadratic nonresidue b of , and let .
Let . The secret key is chosen to be a nonnegative integer s less than q. The public key is chosen to be the sequence .
The encryption algorithm of the BFV scheme consists of the following three steps.
- 1.
Let be the public key. Choose a random polynomial of degree less than d.
- 2.
Given a message , compute .
- 3.
Choose a random integer , and output the ciphertext .
The decryption algorithm of the BFV scheme consists of the following two steps.
- 1.
Let be the secret key. Compute .
- 2.
Given a ciphertext , compute .
Remark 2. In the BFV scheme, the message space is .
3.2.1. Homomorphic Operations
Additive Homomorphism
In the BFV scheme, the additive homomorphism is defined as follows:
Definition 3 (Additive homomorphism). Let and be two ciphertexts. The additive homomorphism is defined to be the ciphertext .
Remark 3. In the BFV scheme, the standard polynomial addition algorithm implements the additive homomorphism.
Multiplicative Homomorphism
In the BFV scheme, the multiplicative homomorphism is defined as follows:
Definition 4 (Multiplicative homomorphism). Let be a ciphertext and be a message. The multiplicative homomorphism is defined to be the ciphertext .
Remark 4. In the BFV scheme, the standard polynomial multiplication algorithm implements the multiplicative homomorphism.
Remark 5. The multiplicative homomorphism is sometimes called the “plaintext multiplication” or the “scalar multiplication”.
3.2.2. Relinearization
Relinearization is a homomorphic operation used in the BFV scheme to reduce the number of ciphertexts generated by homomorphic operations. In the following, we give the definition of this operation.
Definition 5 (Relinearization). Let and be two ciphertexts. The relinearization homomorphism is defined to be the ciphertext .
Remark 6. In the BFV scheme, the relinearization homomorphism is implemented by the standard polynomial addition and multiplication algorithms.
3.2.3. Rotation
Rotation is a homomorphic operation used in the BFV scheme to implement the power operation efficiently. It can be used to implement a large class of homomorphic operations on encrypted data. In the following, we give the definition of this operation.
Definition 6 (Rotation). Let be a ciphertext. The rotation homomorphism is defined to be the ciphertext , where r is an integer.
Remark 7. In the BFV scheme, the rotation homomorphism is implemented by the standard polynomial multiplication algorithm.
Remark 8. The rotation is sometimes called the “power operation”.
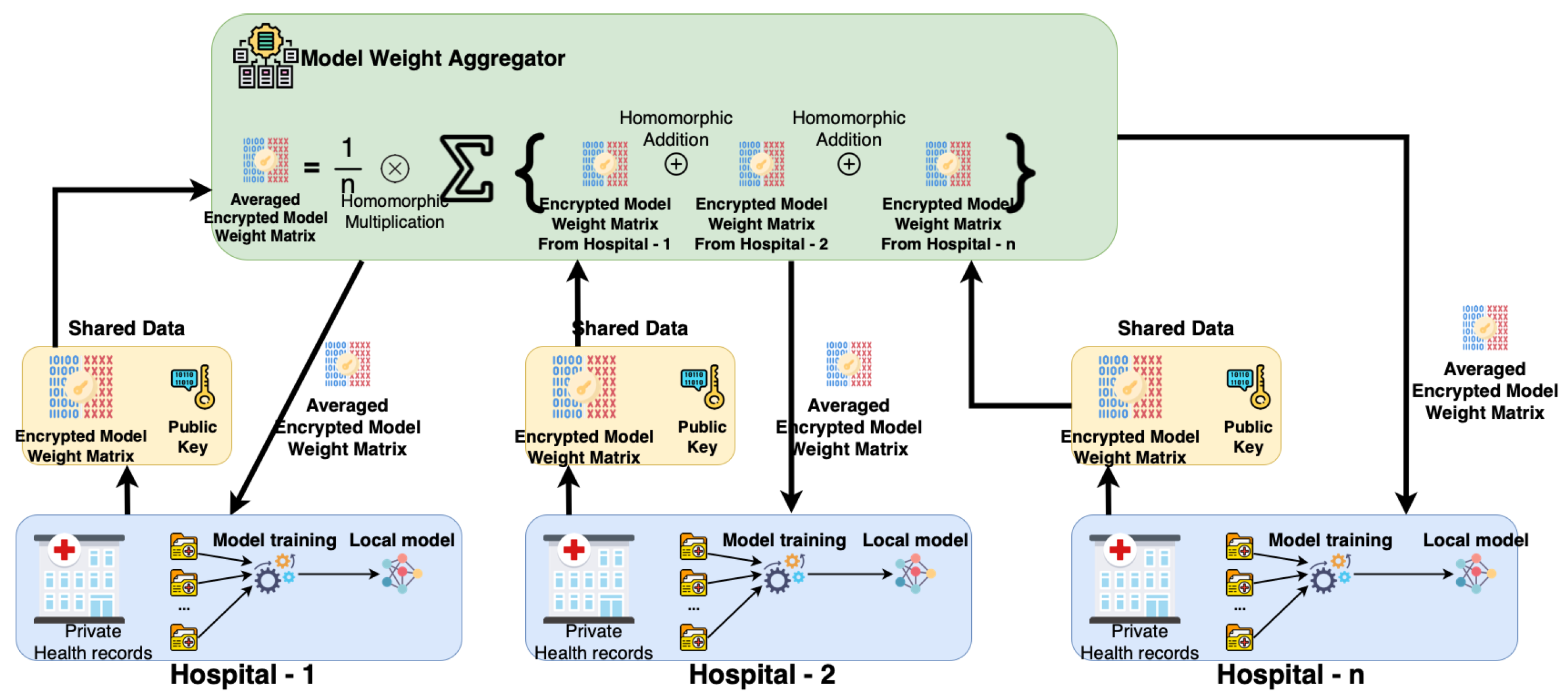
3.3. Federated Learning
In this section, we briefly describe the federated learning (FL) framework. We refer to [
22,
23] for more details.
Definition 7(FL model).Let N be a positive integer, and be a probability space. Let m be a positive integer such that , and be a collection of random variables on with for . The FL model consists of the following four algorithms: Initialization algorithm: It takes the security parameter k as input, and outputs the global model , where n is the number of free parameters in .
Local training algorithm: It takes the global model , a local dataset , and a positive integer t as inputs, and outputs a local model .
Upload algorithm: It takes the local model , and a positive integer t as inputs, and outputs a vector .
Aggregation algorithm: It takes a set of vectors , and a positive integer t as inputs, and outputs the global model .
In the above definition, the integer t is called the training round. The global model is a function of the training round t. The global model is trained by the local models , which are trained on the local datasets . The global model is trained on the aggregated dataset . The global model is initialized to be the global model .
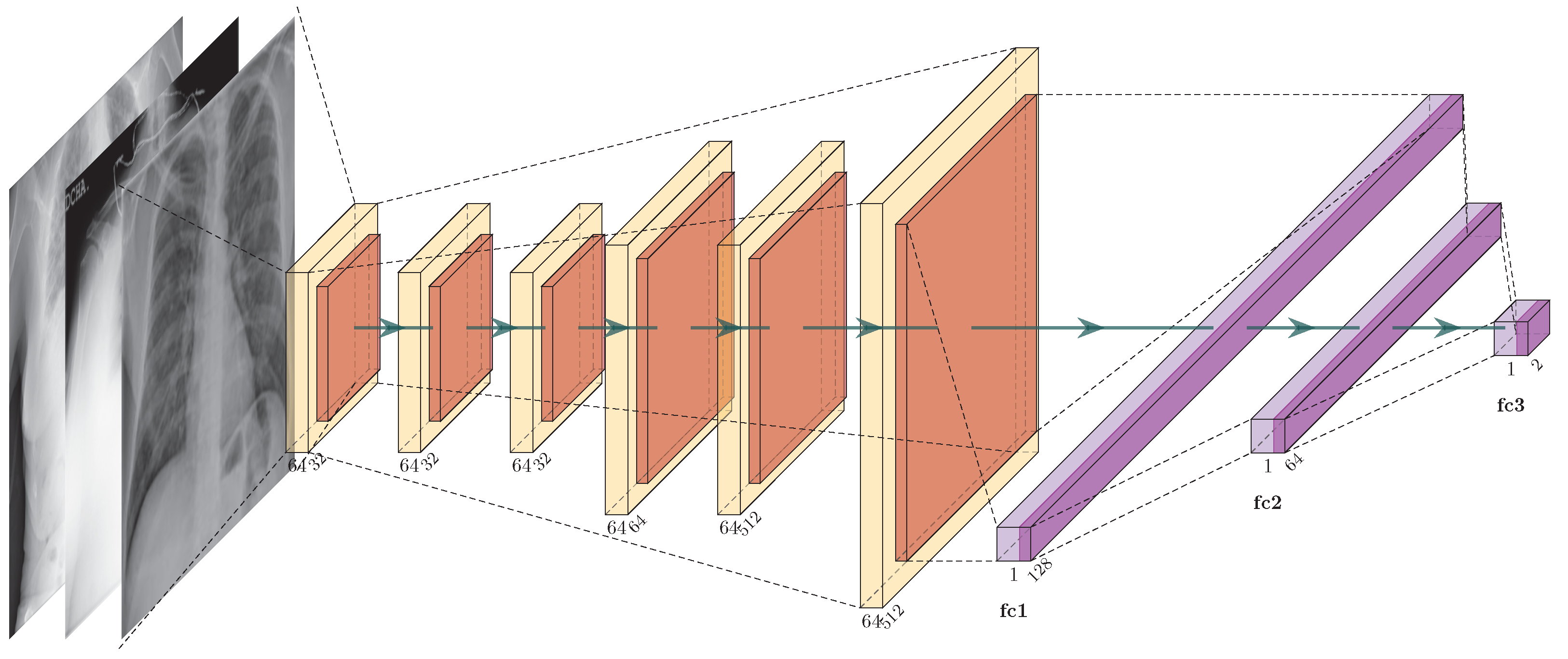
Remark 9. In the FL model, the local training algorithm, upload algorithm, and aggregation algorithm can be implemented by any machine learning algorithm.
Remark 10. The global model can be trained on the aggregated dataset using any machine learning algorithm.
Remark 11. In the FL model, the global model is shared among all the participating clients, and the local models are not shared among the clients.