Abstract
Weak Supplementation (WSP) is the view that if a thing x has a part y with which x is not identical, then x has a part z that does not overlap y. I note that there is a slightly weaker principle, Quasi-Supplementation (QS), which says that that if a thing x has a part y with which x is not identical, then x has at least two parts, z and w, that do not overlap each other. I then argue that QS has WSP’s main virtues while avoiding its main vices. That is the primary aim of this paper. A secondary aim is to explore some potential applications of QS. I note that QS can be used in (i) an argument from a plenitudinous form of coincidentalism to the non-existence of simples and the ‘strong gunkiness’ of all things, (ii) an argument in the other direction—from the possibility of simples to the conclusion that plenitudinous coincidentalism is not necessary, and (iii) arguments for and against certain constituent ontologies, according to which ordinary concrete particulars have formal components.
1. Introduction
Much in mereology is controversial. Is parthood governed by a uniqueness of composition principle? By principle of unrestricted composition? Reasonable people disagree.
But there are areas of relative consensus. Nearly everyone on both sides of these controversies agrees that parthood (the being a proper-or-improper part of a relation) obeys a reflexivity principle and a transitivity principle.1 These principles are neutral with respect to the debates over uniqueness and unrestricted composition. They belong to what we might think of, rather loosely, as ‘the non-negotiable core’ of principles governing parthood. Are there other principles that have this status?
One principle to which the status is often attributed is Weak Supplementation (WSP). It says that if a thing x has a proper part y, then x has a part z that does not overlap y.2 I think that WSP is overrated. But there is a slightly weaker principle, which Gilmore [] calls Quasi-Supplementation (QS), that deserves the high ratings typically given to WSP. Here, I show (in Section 2) that QS has what I take to be WSP’s main virtues while avoiding what I take to be its main vices. This is the primary purpose of this paper.
A secondary purpose is to explore (without accepting or rejecting) some potential uses of QS. I note that it can be used in (i) an argument from an appealing ‘plenitudinous’ form of coincidentalism to the non-existence of simples (and the ‘strong gunkiness’ of all actual things), (ii) an argument in the other direction—from the possibility of simples to the conclusion that plenitudinous coincidentalism is not necessary, and (iii) arguments for and against certain ‘constituent ontologies’, according to which ordinary concrete particulars have ‘formal components’. Section 3 and Section 4 take up these tasks.
2. Core Mereology
2.1. Reflexivity and Transitivity
For the time being, I will adopt two fairly common policies. I will treat the proper-or-improper-parthood predicate, ‘P’, as primitive, and I will assume that it is reflexive and transitive:
- ∀xP(x, x) ReflexivityEach thing is a part of itself.
- ∀x∀y∀z[(P(x, y) & P(y, z)) → P(x, z)] TransitivityIf x is a part of y and y is a part of z, then x is a part of z.
These are typically seen as unobjectionable (and as not especially interesting).3 In this respect, they contrast with two very controversial and very interesting principles, namely, the Uniqueness of Composition and Unrestricted Composition. To state these latter principles, we need some definitions:
- (D1)
- O(x, y) = df. ∃z[P(z, x) & P(z, y)] Overlap‘x overlaps y’ means ‘x and y have a common part’.
- (D2)
- F(x, s) = df. ∀y[y∈s → P(y, x)] & Fusion∀y[P(y, x) → ∃z[z∈s & O(y, z)]‘x fuses s’ (or ‘x is a fusion of s’) means ‘s is non-empty, each of s’s members is a part of x, and each part of x overlaps some member of s’.
With these definitions in place, we can state the controversial principles as follows:
- 3.
- ∀x∀y∀s[(F(x, s) & F(y, s)) → x = y] UniquenessA set of things has at most one fusion.
- 4.
- ∀s[∃x(x∈s) → ∃yF(y, s)] UNREach non-empty set of things has at least one fusion.
Uniqueness and UNR are both popular, and they both have a range of powerful considerations working in their favor (Sider []). But they both face serious opposition, as well. Here is the standard case against Uniqueness. A statue, Goliath, and the lump of clay of which it is made, Lump1, are each fusions of the same set of sub-atomic particles (or temporal parts of such particles),4 but they have different modal profiles (Lump1 but not Goliath could survive being squashed, e.g.) and so are not identical. Here is a standard argument against UNR. There is a set whose members are just my nose and the Eiffel Tower, but nothing fuses this set. After all, if this set had a fusion, the fusion would be an ‘unfamiliar’ object, an object not recognized by common sense and not posited by any science.
Of course, Uniqueness and UNR are not a package deal. Some philosophers accept them both, and some reject them both; but others accept Uniqueness while rejecting UNR, and still others accept UNR while rejecting Uniqueness (see the chart below). The controversies over these principles are separate and independent.
| Accept Uniqueness | Reject Uniqueness | |
| Accept UNR | Lewis [], Sider [] | Thomson [] |
| Reject UNR | van Inwagen [], Koslicki [] | Korman [], Simons []5 |
Let me recap. Reflexivity and Transitivity belong to a common core of mereological principles, where the principles in this core have two key features: (i) they are neutral with respect to the two main controversies in mereology, and (ii) they have seemed especially obvious and unobjectionable to nearly all participants in these controversies, even to the extent that doubting them is a sign of failing to grasp the meaning of ‘part’. (It is hard to know how one might go about arguing for Reflexivity or Transitivity; they seem more plausible than any premise that might be used to support them. By contrast, arguments for Uniqueness and UNR abound.) So far, so good. But Reflexivity and Transitivity are quite weak. Surely there is more we can say about the behavior of parthood without taking a stand on the debates over Uniqueness and UNR. What further principles might reasonably be thought to belong to the ‘non-negotiable core’ of mereology?
2.2. Anti-Symmetry?
One standard suggestion here is:
- 5.
- ∀x∀y[(P(x, y) & P(y, x)) → x = y] Anti-SymmetryNo two things are parts of each other.
According to this suggestion, parthood is governed at a minimum by Reflexivity, Transitivity, and Anti-Symmetry and hence is a partial order.
I find Anti-Symmetry fairly plausible. I think that, other things being equal, we should keep it. It is prima facie odd to think of two different things each being a part of the other. But I do not find Anti-Symmetry nearly so obvious as Reflexivity or Transitivity. Moreover, it seems to me that Anti-Symmetry is not sufficiently neutral vis-à-vis Uniqueness to be considered a ‘core’ principle. Specifically, Anti-Symmetry has a pro-Uniqueness bias that should make Uniqueness-deniers (‘Coincidentalists’) a bit leery of it.6
To explain why, I need to discuss Strong Supplementation. It will be convenient to begin by defining a predicate for disjointness:
- (D3)
- D(x, y) = df. ~O(x, y) Disjointness‘x is disjoint from y’ means ‘x does not overlap y’.
This lets us state Strong Supplementation as:
- 6.
- ∀x∀y[~P(x, y) → ∃z(P(z, x) & D(z, y))] Strong SupplementationIf x is not a part of y, then x has a part that is disjoint from y.
I find Strong Supplementation roughly as plausible as Anti-Symmetry. If x does not have any parts that are disjoint or ‘mereologically separate’ from y, then x is in some sense ‘entirely mereologically within’ y, and it is natural to think that this entails that x is a part of y. As was the case for Anti-Symmetry, we should keep Strong Supplementation if we can do it without too much cost. Uniqueness-deniers, no less than Uniqueness-supporters, should admit this.
But it turns out that (given Transitivity, which I take to be untouchable), Uniqueness-deniers cannot accept both Anti-Symmetry and Strong Supplementation: Transitivity, Anti-Symmetry, Strong Supplementation, and the negation of Uniqueness form a logically inconsistent set.7 (Van Inwagen [] (p. 53) makes a very similar point, though he thinks that Anti-Symmetry is non-negotiable.)
This sets up an interesting choice-point for Uniqueness-deniers, i.e., for Coincidentalists. They can embrace Anti-Symmetry and reject Strong Supplementation. Alternatively, they can embrace Strong Supplementation and reject Anti-Symmetry. (Of course, they can reject both principles if they wish, but I do not see why they would.) Let us use A-Coincidentalism as a name for the conjunction of Anti-Symmetry with the negation of Uniqueness, and let us use S-Coincidentalism as a name for the conjunction of Strong Supplementation with the negation of Uniqueness. We can expect the A-Coincidentalist to say things like this:
- Lump1 and Goliath both fuse s but are not identical. It is not the case that Goliath is a part of Lump1 and Lump1 is a part of Goliath. Goliath’s head is a part of Goliath but not a part of Lump1.8
We can expect the S-Coincidentalist, by contrast, to say things like this:
- Lump1 and Goliath both fuse s but are not identical. They are parts of each other. Goliath’s head is a part of both Goliath and Lump1.9
I think that these are both respectable forms of Coincidentalism. It would be nice for the Coincidentalist if they could keep both Anti-Symmetry and Strong Supplementation, but they cannot. S-Coincidentalism and A-Coincidentalism are their best options.
The key point, however, is the following: since Anti-Symmetry, when combined with other plausible assumptions (Strong Supplementation and Transitivity), entails Uniqueness, Anti-Symmetry has a pro-Uniqueness bias. Likewise, since Strong Supplementation, when combined with other plausible assumptions (Anti-Symmetry and Transitivity), entails Uniqueness, Strong Supplementation has a similar bias. Neither principle is sufficiently neutral with respect to the debate over Uniqueness to be placed alongside Reflexivity and Transitivity in our core mereology.
2.3. Weak Supplementation?
Among those who take this core to contain Reflexivity, Transitivity, and Anti-Symmetry, a popular suggestion is that it also contains the Weak Supplementation Principle (WSP). Although I think that these philosophers are wrong about Anti-Symmetry, perhaps they are right about WSP. To this question I now turn.
First, we need to state WSP. Unfortunately, this is a vexed issue, for WSP is almost universally framed in terms of a predicate for proper parthood (by contrast with proper-or-improper parthood), and treatments of this predicate differ. So, eventually it will be necessary to consider a variety of WSP-like principles, each associated with a different treatment of proper parthood. To keep things simple, however, I will focus primarily on the option that I find most natural. It involves the following definition:
- (D4)
- PPNI(x, y) = df. P(x, y) & x≠y ProperNI Parthood‘x is a properNI part of y’ means ‘x is a part of but not identical to y’.
The WSP-like principle associated with (D4) is:
- 7.
- ∀x∀y[PPNI(x, y) → ∃z(P(z, y) & D(z, x))] WSPNIIf x is a properNI part of y, then y has somepart z that is disjoint from x.
We will consider some variants of WSPNI later. (As I explain toward the end of Section 2.4, the Weak Supplementation principle WSPNI does not follow from Strong Supplementation alone, so the names are a bit misleading.)
2.4. Virtues and Vices of WSPNI
What I want to do now is list some virtues of this principle. These count in favor of granting WSPNI ‘core’ status along with Reflexivity and Transitivity. I will then point out some vices of WSPNI. In Section 2.5, I will show that Quasi-Supplementation retains the given virtues while avoiding the vices. I will also discuss some alternative principles that attempt to do the same.
Virtue 1: It is strong enough to rule out Models 1–3. Following Simons [] (pp. 26–28) and Varzi [], I assume that our core mereology should rule out models like the following three:10
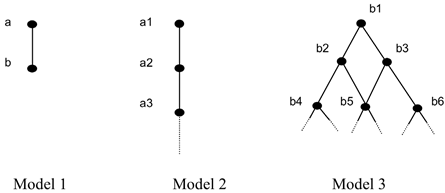
In Model 1, we have an object with just a single properNI part; in the second, we have an infinitely descending chain of objects, each of which is a properNI part of all and only the objects above it; and in the third, we have an infinitely descending ‘pyramid’—a situation in which each pair of objects overlap, though there are pairs of non-identical objects (any two in the same row), neither of which is a part of the other. The first model, but neither the second nor the third, is ruled out by:
- 8.
- ∀x∀y[PPNI(x, y) → ∃z(PPNI(z, y) & z≠x)] Weak CompanyNIIf a thing has a properNI part, then it hasat least two properNI parts.
The first and second models, but not the third, are ruled out by:
- 9.
- ∀x∀y[PPNI(x, y) → ∃z(PPNI(z, y) & ~P(z, x))] Strong CompanyNIIf a thing y has a properNI part x, then y has a properNI part z that is not a part of x.11
Finally, all three models are ruled out by WSPNI. In each of these models, we can find a properNI part x of the ‘top’ object y such that y does not have any parts that are disjoint from x. (In fact, for any properNI part of the top object that we pick, it will turn out that the top object does not have any parts that are disjoint from the chosen properNI part.)
Virtue 2: It is weak enough to be consistent with Uniqueness and with Coincidentalism. WSPNI is consistent with Uniqueness. Classical mereology (on which, see Hovda []) includes them both, and it is consistent. But, more interestingly, WSPNI is also consistent with Coincidentalism (the negation of Uniqueness), as can be seen by considering the following model:
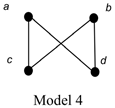
In this model, Uniqueness fails, since a and b are not identical, but each of them fuses the set {c, d}. (UNR also fails, since nothing fuses {a, b}.) WSPNI is satisfied, however. There are only two things in the model that have properNI parts, a and b, and each of them has exactly two properNI parts, c and d, which are disjoint from each other. So each properNI part of a is disjoint from some part of a, and each properNI part of b is disjoint from some part of b.
Virtue 3: It is weak enough to permit Model 5 and avoid a bias in favor of arbitrary undetached parts. WSPNI is consistent with Unrestricted Composition (UNR); classical mereology includes them both. But it is also worth pointing out that WSPNI, unlike certain neighboring principles, harmonizes with forms of Restricted Composition that reject ‘arbitrary undetached parts’. Let me explain.
Initially, one might be tempted to articulate the intuition behind WSPNI as follows: if a thing x is a proper part of a thing y, then there is a thing z that is ‘the rest of y’—i.e., that is disjoint from x and that, together with x, makes up the whole of y. Here is a more formal statement of such a thesis—call it Moderate SupplementationNI:
- 10.
- ∀x∀y[PPNI(x, y) → ∃z(P(z, y) & D(z, x) & MSPNI∀w(P(w, y) → (O(w, x) v O(w, z)))]If x is a properNI part of y, then y has a part z disjoint from x such that y fuses {x, z}.
MSPNI shares the two previous virtues of WSPNI. Since MSPNI is logically stronger than WSPNI, it is equally effective at ruling out Models 1–3.12 And it is easy to see that MSPNI is satisfied by Model 4 and so is consistent with Coincidentalism. MSPNI has a lot going for it.
One main problem for MSPNI, however, is that it rules out certain models that most opponents of UNR will want to permit. Suppose that I am a fusion of a certain set s of simple particles, where s = {p1, p2, . . . , pn}. Now consider a proper subset s* of s, viz., {p2, . . ., pn}. Does s* have a fusion? Many friends of Restricted Composition (e.g., van Inwagen [], Olson [], Merricks []) would say ‘No’ on something like the following grounds: such a fusion would be a mere ‘arbitrary undetached part’ of me—it would be neither a living organism in its own right nor a thing posited by any science, nor an artifact or other common-sense object. It would be an ‘unfamiliar’ object.
These philosophers will reject MSPNI. In their view, p1 is a properNI part of me, but there is no such thing as ‘the rest of me’: I do not have a part z such that (i) z is disjoint from p1, and (ii) each of my parts overlaps either p1 or z. More generally, these philosophers will not want to rule out models such as:
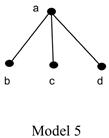
Model 5 satisfies WSPNI (which is easy to see) but not MSPNI: b is a properNI part of a, but, since {c, d} has no fusion, there is no part z of a such that (i) z is disjoint from b and (ii) each part of a overlaps b or z.
Virtue 4: It is weak enough to permit Model 6 and so can be accepted even by Coincidentalists who reject arbitrary undetached parts. So far, I have shown that WSPNI (i) rules out Models 1–3, (ii) permits Model 4, and (iii) permits Model 5. (Moreover, of the principles I have considered, it is the only one that does all this.) The fact that WSPNI permits Model 4 shows that it can be accepted by Coincidentalists, and the fact that it permits Model 5 shows that it can be accepted by opponents of arbitrary undetached parts. However, nothing that we have said so far guarantees that WSPNI can be accepted by Coincidentalists who reject arbitrary undetached parts. To see that it can be, consider:
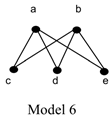
In this model, Uniqueness fails, since a and b are not identical, but each of them fuses {c, d, e}. Moreover, UNR fails since neither {a, b}, {c, d}, {d, e}, nor {c, e} have fusions. Finally, MSPNI fails, since (e.g.) c is a proper part1 of a, but a does not have a part z disjoint from c such that each part of a overlaps c or z. WSPNI, however, is satisfied by Model 6. So much for the virtues of WSPNI. I turn now to its vices.13
Vice 1: In the presence of Transitivity, it is inconsistent with S-Coincidentalism. The most obvious problem for WSPNI is that, like Anti-Symmetry, it conflicts with a respectable form of Coincidentalism—namely, S-Coincidentalism. WSPNI, Transitivity, and S-Coincidentalism form a logically inconsistent set.14 To obtain a feel for this problem in an informal way, it may help to consider an example. Let s be a set of clay particles and suppose that (i) Lump1 fuses s, (ii) Goliath fuses s, and (iii) Lump1≠ Goliath. Since Lump1 and Goliath are both fusions of a common set, neither of them has a part that is disjoint from the other. In particular, Lump1 does not have any parts that are disjoint from Goliath. So, the S-Coincidentalist, as someone who accepts Strong Supplementation, will say that Lump1 is a part of Goliath. And since Lump1≠Goliath, the S-Coincidentalist will need to say that Lump1 is a properNI part of Goliath. But, once again, since Lump1 and Goliath fuse a common set, Goliath does not have any parts that are disjoint from Lump1. So the S-Coincidentalist will be forced to reject WSPNI. It may also be worthwhile to frame the basic point in terms of a model that WSPNI rules out but that our core mereology intuitively ought to leave open. One such model is specified by the directed graph below.15 (Arrows represent a relation we can think of as ‘immediate proper parthood’. So, e.g., b is an immediate proper part of G. We can assume that x is a part of y just in case either x = y or x stands in the transitive closure of immediate proper parthood to y. This guarantees that parthood is reflexive and transitive.)
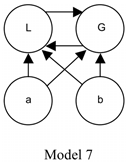
In Model 7, Uniqueness fails since L and G are non-identical, but each of them fuses {a, b}, among other sets. Strong Supplementation is satisfied (as can be easily verified, and as I will explain in more detail when I return to this model in Section 2.5). But WSPNI is not satisfied.16 L is a properNI part of G, but G does not have any parts that are disjoint from L. (Hence, the names of these supplementation principles are misleading: Strong Supplementation is not by itself logically stronger than Weak SupplementationNI.)
Vice 2: Together with UNR and Transitivity, it entails Extensionalism. Many philosophers who reject Uniqueness will also want to reject a somewhat weaker doctrine, namely, Extensionalism:
- 11.
- ∀x∀y[∃z[PPNI(z, x)] → (E)[∀w[PPNI(w, x) ↔ PPNI(w, y)] → x = y]]‘No two things have exactly the same proper[NI] parts (unless they are atomic, i.e., have no proper[NI] parts at all)’ (Varzi []).
To see how Uniqueness and Extensionalism can come apart, consider the following model (from Varzi [], who uses it to make the same point):
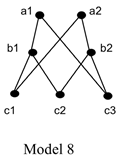
In Model 8, Uniqueness fails, since a1 and a2 are not identical but they each fuse {c1, c2, c3}. Extensionalism, however, is satisfied, since, of the four composite objects in the model, no two of them have exactly the same properNI parts. (WSPNI is also satisfied in this model.)17
So, there is logical space to reject Uniqueness while retaining Extensionalism. But they are similar in spirit, and many Coincidentalists will presumably want to reject them both. Recently, however, Varzi [] has shown that Extensionalism (E) follows from Unrestricted Composition, Transitivity, and WSPNI:18
[A]ll that is needed, to get (E), is finitary Universalism [(U)], i.e., the assumption that any pair of objects has a fusion. For suppose that x and y are distinct non-atomic objects. There are two possibilities:(a) One object, say x, is part of the other, y. Then, obviously x and y don’t have the same proper parts. For x must be a proper part of y, though it cannot be a proper part of itself (on pain of being non-self-identical).(b) Neither x nor y is part of the other. Then let z be a fusion of x and y, whose existence follows from (U). By definition of ‘fusion’, x must be part of z, in fact, a proper part. (If x were identical to z, then y, which must also be part of z, would be part of x, contrary to what we are assuming.) Thus, by [WSPNI], z has a part, z1, that is disjoint from x. By definition of ‘fusion’, again, z1 cannot be also disjoint from y, which is to say that it must have a part, z2, in common with y. Now, either z2 is a proper part of y, or z2 is y. In the first case, it is clear that z2 cannot be part of x, let alone a proper part, since x is disjoint from z1. In the second case, let z3 be a proper part of y (which is not atomic). By [Transitivity], z3 must be part of z1, hence, again, it cannot be part of x, let alone a proper part. It follows that in both cases, x does not have the same proper parts as y.Since (a)–(b) are the only possibilities, this shows that the non-identity of x and y is reflected in their different mereological composition. (E) now follows by generalization (Varzi [] (p. 600)).
Prima facie, one would have thought that the controversies over doctrines like Uniqueness and Extensionalism were independent of the controversies over UNR. Suppose that one decides that Lump1 and Goliath are not identical but that they fuse the same set and indeed have exactly the same properNI parts. Why should this force one to take a stand on the apparently separate question about whether every non-empty set has a fusion? Why should one’s views about ‘coinciding objects’ constrain one’s views about ‘scattered objects’ in this way? It seems to me that anti-Extensionalists should remain free to reject UNR and free to accept it. At the very least, it would be preferable, other things being equal, if our core mereology did not force them to reject UNR. But if our core mereology includes both Transitivity and WSPNI, then it does force them to reject UNR. And our core mereology does include Transitivity. Hence, other things being equal, it would be preferable if our core mereology did not include WSPNI.
Vice 3: It goes beyond Simons’s informal gloss. A principle going by the name ‘Weak Supplementation’ was first highlighted by Peter Simons [] (p. 28). He originally motivated such a principle by noting the intuitive impossibility of Models 1–3 and by pointing out that both Weak and Strong CompanyNI are too weak to rule out all three models [] (p. 27).19 In connection with Model 3, he writes:
What we have here is a universe all of whose parts overlap. But surely if a universe is complex (i.e., has proper parts at all) then at least two of these parts will be disjoint. To express this we first define overlapping and disjointness [via the definitions that are here labeled ‘(D1)’ and ‘(D3)’—CG]. . . . We then have:SA3 PP(x, y) → ∃z[PP(z, y) & D(z, x)] (WSP)This axiom will be known as the Weak Supplementation Principle. It says that if an individual has a proper part, then it has a proper part disjoint from the first [] (pp. 27–28).20
It seems to me that Simons is right when he says: ‘[S]urely if a [thing] is complex (i.e., has proper parts at all) then at least two of these will be disjoint.’ This is a key insight. But I deny that it is best expressed in formal terms by his SA3 or my WSPNI. After all, unlike the formal theses, the informal statement does not say that if a thing x has a proper part y, then x has a proper part that is disjoint from that first proper part, namely, y. Rather, the informal statement says merely that if a thing x has a proper part y, then x has at least two proper parts that are disjoint from each other (but not necessarily from y). Other things being equal, the closer we stay to Simons’s informal statement, the better.
2.5. Quasi-Supplementation
Here is a principle that does the job:
- 12.
- ∀x∀y[(P(x, y) & x≠y) → Quasi-Supplementation∃z∃w(P(z, y) & P(w, y) & D(z, w))]Anything that has a distinct part has disjoint parts.
Quasi-Supplementation (QS) avoids the three vices of WSPNI noted above while retaining the four virtues. I will start with Vice 3.
Avoiding Vice 3. Given Reflexivity together with the relevant definitions, QS is equivalent to the following principle:
- 13.
- ∀x∀y[PPNI(x, y) → QS *∃z∃w[z≠w & D(z, w) & PPNI(z, y) & PPNI(w, y)]]If a thing has a properNI part, then it has at least two disjoint properNI parts.
(Proof omitted.) And I assume that QS * is as close as we can get using our mereological vocabulary (which contains no primitive predicate for proper parthood) to a formal expression of Simons’s informal statement. Clearly, QS is much closer to the informal statement than is WSPNI, and this is all that matters for present purposes.
Avoiding Vice 2. Varzi has shown that WSPNI has the following property: in conjunction with Transitivity and UNR, it entails Extensionalism. As I see it, this property is not one we want in a ‘core’ mereological principle.
Fortunately, QS does not have the property. (This may come as a surprise given how well QS captures Simons’s informal statement of the idea behind WSP-like principles.) To see that QS lacks the property in question, consider:
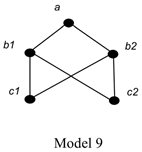
In Model 9, UNR is satisfied, since each non-empty set (of subsets of {a, b1, b2, c1, c2}) has a fusion. (This is easy to check.) Likewise, Quasi-Supplementation is satisfied, since each thing that has a properNI part (namely, a, b1, and b2) has disjoint parts (the simples c1 and c2). And of course Transitivity is satisfied (as is Reflexivity). But Extensionalism is not, for b1 and b2 are non-identical, and each of them has the same two things as its only properNI parts, namely, c1 and c2.
It is worth pausing to see why WSPNI fails in Model 9. WSPNI tells us that since a has b1 as a properNI part, a must have some part that is disjoint from b1. But a has no such part: its only parts are a itself, b1, b2, c1, and c2, none of which is disjoint from b1. So, in shifting from WSPNI to QS, we open up the possibility of models like Model 9, which satisfy both UNR and the negation of Extensionalism.
The fact that QS is so much closer than WSPNI to Simons’s informal statement already gave us one reason to replace the latter with the former in our core mereology. (It may be a weak reason, but it still carries some weight.) Now, we see that when this substitution is made, we avoid the unwelcome result that ‘Universalism entails Extensionalism’. This gives us a second, independent reason to make the switch.
Avoiding Vice 1. Here is a third independent reason. WSPNI has Vice 1: in the presence of Transitivity, it rules out a respectable form of Coincidentalism, namely, S-Coincidentalism. (Other things being equal, our core mereology should be consistent with all respectable forms of Coincidentalism.) QS lacks this vice. This follows from the fact that Model 7 satisfies QS, Transitivity, and S-Coincidentalism (i.e., the conjunction of Strong Supplementation with the negation of Uniqueness).
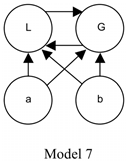
Transitivity is satisfied for the reasons noted earlier. (Likewise for Reflexivity.) The negation of Uniqueness is satisfied because L and G are non-identical but both fuse {a, b}, among other sets.
To see that Strong Supplementation (‘if x is not a part of y, then x has a part disjoint from y’) is satisfied, note that there are exactly six ordered pairs of objects in the model, such that the first member of the pair is not a part of the second member: (i), (ii), (iii), (iv), (v), (vi). For each of these pairs, we can see that the first member has a part that is disjoint from the second member: (i) a is a part of a and disjoint from b, (ii) b is a part of b and disjoint from a, (iii) b is a part of L and disjoint from a, (iv) b is a part of G and disjoint from a, (v) a is a part of L and disjoint from b, and (vi) a is a part of G and disjoint from b.
Finally, to see that QS is satisfied, note that there are exactly two objects in the model that are composite (i.e., that have a part with which they are not identical): L and G. And each of them has parts—namely, a and b—that are disjoint from each other.21
So far, I have shown that QS lacks Vices 1–3.22 Now I will show that it retains Virtues 1—4. I will take them in order.
Retaining Virtue 1. I agree with Simons and Varzi that our core mereology should be strong enough to rule out Models 1–3. Hence, I agree that it is a virtue of WSPNI that it does this. But WSPNI is not the only principle that has this virtue. QS also has it, for QS fails in all three models. In Model 1, b is part of and not identical to a, but a does not have disjoint parts. Its only parts are itself and b, which are not disjoint. (Their common part is b.) In Model 2, a2 is a part of and not identical to a1, but a1 does not have disjoint parts: for any objects x and y in the model, we can find an object z in the model that is a part of both x and y. To do this, just pick any object that is below both of the dots representing x and y. This will show that x and y overlap and hence are not disjoint. Finally, in Model 3, b2 is a part of and not identical to b1, but b1 does not have disjoint parts. Again, for any parts x and y of b1, we can find an object z that is a part of both x and y—just by ‘looking far enough down the pyramid’.
Retaining Virtues 2–4. These virtues do not require separate discussion. They are all of the form being weak enough to permit so-and-so or being weak enough to be consistent with such-and-such. Since QS is weaker than WSPNI,23 anything that WSPNI permits will be permitted by QS, as well. It retains Virtues 2–4.
2.6. Alternatives?
We have seen that QS avoids the given vices of WSPNI while retaining the given virtues. Are there any other principles that do all this? In this section, I will take a brief look at two candidates. I will touch upon a third candidate in Section 3.
2.6.1. WSPNM
To state our first candidate, it will be helpful to define a different notion of proper parthood—viz.:
- (D4)
- PPNM(x, y) =df. P(x, y) & ~P(y, x) ProperNM Parthood‘x is a properNM part of y’ means ‘x is a part of y but not vice versa’.
In other words, ‘x is a properNM part of y’ means ‘x is a part of y but the relationship is not mutual’ (hence, the ‘NM’ subscript). The associated WSP-like principle is:
- 14.
- ∀x∀y[PPNM(x, y) → ∃z(P(z, y) & D(z, x))] WSPNMIf x is a properNM part of y, then y has apart z that is disjoint from x.
Since ‘properNM part’ is more demanding than ‘properNI part’, WSPNM is weaker than WSPNI. It follows immediately that WSPNM retains Virtues 2–4. But it also retains Virtue 1, as is easily checked. In those models, properNM parthood never comes apart from properNI parthood.
Moreover, WSPNM avoids Vice 1. To see this, return to Model 7 and note that, although it does not satisfy WSPNI, it does satisfy WSPNM. The only objects in the model that have properNM parts at all are L and G. These each have exactly two properNM parts, namely, a and b, which are disjoint from each other. True, L and G count as properNI parts of each other (which dooms WSPNI, since neither has a part disjoint from the other), but neither L nor G counts as a properNM part of the other (since they are mutual parts).
However, WSPNM does not avoid Vices 2 or 3. With regard to Vice 3, I take it to be obvious that (for what it is worth) QS is a much better translation of Simons’s informal statement than is WSPNM. The situation with Vice 2 is more complicated. Varzi proved that WSPNI has the following (to my mind undesirable) property: in the presence of Transitivity and UNR, it entails Extensionalism. Call this the Varzi property. I then showed that QS does not have the Varzi property. What about WSPNM?
There are really two questions we might want to ask here. The first question concerns the Varzi property itself: does WSPNM have it? The second question concerns an analogue of the Varzi property. This analogous property can be specified as follows. In our formulation of Extensionalism, replace each occurrence of the predicate ‘PPNI’ with an occurrence of the predicate ‘PPNM’ and call the resulting doctrine Extensionalism *. Further, say that a given doctrine has the Varzi * property just in case in the presence of Transitivity and UNR, that doctrine entails Extensionalism *. Then we can pose the second question as follows: does WSPNM have the Varzi * property?
It does not—and neither does QS. To see that QS does not have it, we can reflect on Model 9. QS, Transitivity, and UNR hold there (as we have seen), but Extensionalism * fails. Objects b1 and b2 each have properNM parts, and they have exactly the same properNM parts (c1 and c2), but they are not identical. But WSPNM does have the Varzi * property. Now, to see that WSPNM does not have the Varzi * property, return to Model 7. WSPNM, Transitivity, and UNR all hold there, but Extensionalism * does not. L and G each have properNM parts, and they have exactly the same properNM parts (namely, a and b), but they are not identical. So, now let us turn to the first question: does WSPNM have the Varzi property itself? It does, as we can see by considering a slight modification of Varzi’s proof. In what follows, the bold-face type inside square brackets has been added by me; the rest of the text is Varzi’s:
[A]ll that is needed, to get (E), is finitary Universalism [(U)], i.e., the assumption that any pair of objects has a fusion. For suppose that x and y are distinct non-atomic objects [i.e., that each of these objects has at least one properNI part, so that the antecedent of (E) is satisfied]. There are two possibilities:(a) One object, say x, is part of the other, y. Then obviously x and y don’t have the same proper[NI] parts. For x must be a proper[NI] part of y, though it cannot be a proper[NI] part of itself (on pain of being non-self-identical).(b) Neither x nor y is part of the other. Then let z be a fusion of x and y, whose existence follows from (U). By definition of ‘fusion’, x must be part of z, in fact a proper[NM] part. (If [z were a part of x], then y, which must also be part of z, would [by Transitivity] be part of x, contrary to what we are assuming.) Thus, by [WSPNM], z has a part, z1, that is disjoint from x. By definition of ‘fusion’, again, z1 cannot be also disjoint from y, which is to say that it must have a part, z2, in common with y. Now, either z2 is a proper[NI] part of y, or z2 is y. In the first case, it is clear that z2 cannot be part of x, let alone a proper part, since x is disjoint from z1. In the second case, let z3 be a proper[NI] part of y (which is not atomic, [i.e., which has at least one properNI part]). By [Transitivity], z3 must be part of z1, hence again it cannot be part of x, let alone a proper[NI] part. It follows that in both cases x does not have the same proper[NI] parts as y.Since (a)–(b) are the only possibilities, this shows that the non-identity of x and y is reflected in their different mereological composition [i.e., in the fact that they have different proper[NI] parts, as (E) requires, given their compositeness]. (E) now follows by generalization [] (p. 600).
The only significant change occurs in the fourth sentence of the third paragraph, which is enclosed in parentheses. In order to make WSPNM ‘kick in’ as applied to the case of x and z, we need to show not merely that x is a properNI part of z, but that it is a properNM part of z, as well. Once this is accomplished, the rest of the proof goes through as before. To its discredit, then, WSPNM does have the Varzi property. This strikes me as a significant reason for preferring QS. We can make a similar point in much simpler terms. WSPNM is too strong: it rules out certain models that intuitively ought to be left open by our core mereology. The simplest example is:
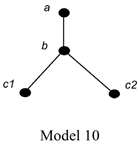
This approximates the following view, which I regard as a respectable thing for a Coincidentalist to endorse: the statue and the lump are not identical; they both fuse the same set of simple particles; and the lump is a part of the statue, but the statue is not a part of the lump. I do not know whether anyone has actually endorsed such a view, but it would not surprise me if someone had. (One might think that the lump is a part of the statue and not vice versa for a variety of reasons—e.g., because the statue is ontologically dependent on the lump but not vice versa, or because the statue’s primary kind somehow dominates the lump’s primary kind.)
In any event, it is easy to see that WSPNM fails in this model: b is a properNM part of a but does not have a part that is disjoint from b. QS, of course, is satisfied. The only things in the model that have parts with which they are not identical are a and b, and each of them has disjoint parts (c1 and c2).
On the whole, then, I take QS to be clearly superior to WSPNM as a candidate for inclusion in our core mereology.
2.6.2. WSPS
So far, we have been working with a primitive predicate, ‘P’, for proper-or-improper parthood. But one might instead invoke a primitive predicate, ‘PPS’, for proper parthood and use it to define a parthood predicate, ‘PS(x, y)’, as ‘PPS(x, y) v x = y’. One could then define a predicate for overlapping, ‘OS(x, y)’, in the standard way, as ‘∃z[PS(z, x) & PS(z, y)]’, and a predicate for disjointness, ‘DS(x, y)’, as ‘~OS(x, y)’. One might then state a WSP-like principle as:
- 15.
- ∀x∀y[PPS(x, y) → ∃z(PS(z, y) & DS(z, x))] WSPSIf x is a properS part of y, then y has a parts that is disjointS from x.
It is easy to confirm that this enjoys Virtues 1–4 and that it suffers from Vices 2 and 3. The situation with respect to Vice 1 is somewhat less clear and would require a detailed discussion that is probably not worth our while in the present context. Suffice it to say that Vices 2 and 3 make WSPS less attractive as a core principle than QS. Moreover, even if WSPS were just as attractive as QS with respect to Virtues 1–4 and Vices 1–3 (which it is not), the mere fact that it depends upon the tendentious decision to treat proper parthood as primitive shows that it is less than optimally neutral.
So much for alternatives to QS. There are, of course, many candidates that I have not considered. But space is limited, and these strike me as the two most natural. Moreover, a third candidate will be discussed briefly in Section 3.2.2.
In any event, this completes my case for enshrining QS, rather than any version of WSP, alongside Reflexivity and Transitivity in our core mereology. For the remainder of the paper I will work under the (perhaps hazardous) assumption that these three principles are non-negotiable, and I will explore some uses to which they can be put.
3. Plenitudinous Coincidentalism, Simples, and Gunk
Let us say that things coincide just in case they overlap exactly the same things:
- (D5)
- CO(x, y) =df. ∀z[O(x, z) ↔ O(y, z)] Coincidence
In the presence of Transitivity and Reflexivity, the view that there are coinciding objects that are not identical is equivalent to the negation of Uniqueness, i.e., to Coincidentalism.24
The standard example of distinct coinciding objects, of course, is the case of the statue Goliath and the lump of clay Lump1. They coincide (arguably) but seem to have different modal profiles (Lump1 but not Goliath could keep existing after having been flattened, e.g.) and so seem not to be identical.
For ease of exposition, I will adopt a standard package of views that includes (i) the B-theory of time (where this is understood as entailing eternalism), (ii) spacetime substantivalism, (iii) perdurantism, and, as I mention in note 1, (iv) the view there is exactly one fundamental part–whole relation, viz., the two-place relation expressed by ‘x is a part simpliciter of y’. Given this package, it is plausible that objects will count as coinciding only if they are spatially co-located throughout their careers, i.e., only if they trace out exactly the same total ‘spacetime path’.25
Coincidentalism leaves open a number of questions about the extent of this sort of coincidence. Which objects are involved in this sort of career-long coincidence with another object? Given an object that is so involved, how many other objects does it coincide with in the relevant way? Just one other object? Two? Millions?
Plenitude, roughly stated, is the view that necessarily, every matter-filled26 spacetime region contains a great many objects that coincide in this way—specifically, a different object for each different modal profile that is, in some minimal sense, ‘eligible’ to be instantiated in the region.
Consider the region, R, that we would ordinarily describe as the spacetime path of Goliath and of Lump1. How many material objects have R as their path? Those who deny the existence of composite objects such as lumps of clay and statues will say: none (Dorr []). Those who accept lumps and/or statues but who reject Coincidentalism will say: exactly one (Rea []). Most Coincidentalists will say: more than one. A friend of a moderate, non-plenitudinous form of Coincidentalism might say: exactly two—specifically, a lump of clay that could survive being squashed but could not survive the loss of a significant portion of its matter, and a statue that could not survive being squashed but could survive the loss of a significant portion of its matter. (Such a view is in the spirit of Korman []).
A friend of Plenitude will say: a vast abundance (probably continuum-many or more)—specifically, an object that could survive being squashed but could not survive the loss of a significant portion of its matter; an object that could not survive being squashed but could survive the loss of a significant portion of its matter; an object that both could survive being squashed and could survive the loss of a significant portion of its matter but could not have existed for more than 4.732 days and could not have survived being taken into a different time zone, and so on.
Recently, Karen Bennett [] and John Hawthorne [] have argued that Plenitude is more plausible than non-plenitudinous versions of Coincidentalism.27 Bennett thinks that adopting Plenitude is the coincidentalist’s best response to the grounding problem—“what grounds the modal differences between coinciding objects, given that these objects are otherwise so similar?”
If only some of the possible modal profiles are instantiated in a region, we can always ask why those are so special—which, given the view about objects just described, is just to ask why the things that exist there have the modal properties they do. An answer of ‘they just do’ sounds decidedly mysterious and obfuscatory. But if all of the possible modal profiles are instantiated, the question simply does not arise. Thus the fullness of each spatiotemporal region explains—or at least explains away—the primitiveness of the de re modal facts [] (p. 355).
Hawthorne suggests that adopting Plenitude is the best way to take one’s modal intuitions at face value without exposing oneself to charges of arbitrariness or anthropocentrism:
Even setting aside possible cases where objects spatiotemporally coincide without mereologically coinciding, we must still decide whether pairs of distinct objects ever mereologically coincide for the entirety of their careers. . . . I explore a more unbridled plenitude that recognizes a multitude of coinciding objects for any given filled region. . . . Having allowed for multiple coinciding objects with matching spatiotemporal boundaries, one is naturally led to wonder just how many objects inhabit a given boundary. Here again, it seems arbitrary to suggest anything but the modally plenitudinous answer: for any function from possible worlds to filled regions, there is an object whose modal profile is given by that function [] (p. viii).
Although I will not discuss their arguments in detail here, it seems to me that considerations in this vicinity do carry real weight.28 Plenitude is a contender. So, it is interesting to see what consequences it generates when it is combined with our core mereology (which I take to be held fixed).
In Section 2.1, I show that this combination yields a (more-or-less a priori) argument for the view that there are no simples, i.e., that every object is, in a sense, to be specified ‘strongly gunky’. This may come as a surprise, since the question of whether there are simples in the actual world is usually taken to be an empirical question. In Section 3.2, I briefly consider running the argument in the opposite direction: specifically, I consider arguing from the possibility of simples to the conclusion that Plenitude is not a necessary truth.
Finally, in Section 3, I explore some ways in which the foregoing considerations might bear on the question of whether material objects (a.k.a. ‘physical substances’, a.k.a. ‘ordinary concrete particulars’) have formal components. Specifically, I sketch two new arguments—one in favor of formal components, one against.
3.1. From Plenitude to the Actual Gunkiness of All Things?
Here is the main argument for gunk:
Argument A
- (AP1)
- Plenitude is true.
- (AP2)
- If Plenitude is true, then everything has disjoint parts.
- (AP3)
- If everything has disjoint parts, then everything is strongly gunky.
- (AC1)
- So, everything is strongly gunky.
Of course, all the action comes in the arguments for the premises. In particular, the bulk of our time will be spent on (AP2). But first I want to say a few words about the other two premises, starting with (AP1). It is useful to see this premise as being motivated by the following sub-argument:
Argument B
- (BP1)
- Coincidentalism is true. (Carry out the Lump1/Goliath case; reflect on the mereological content and modal profiles of the resulting objects.)
- (BP2)
- If Coincidentalism is true, then Plenitude is true. (Appeal to Bennett/Hawthorne-style considerations.)
- (AP1)
- So, Plenitude is true.
One thing to notice about this argument is that its premises are supported almost exclusively by ‘armchair methods’. True, (BP1) depends on the claim there is some matter out there in reality that undergoes the relevant sorts of processes, and the justification for that claim is at least partly empirical. But, presumably, that does not require any detailed scientific investigation, and the rest of the argument is supported purely from the armchair.
Now, we can turn to premise (AP3) from the main argument. This employs the expression ‘strongly gunky’, which requires explication. We can start with the standard definition of the more familiar term ‘gunky’:
- (D6)
- G(x) = df. ∀y[P(y, x) → ∃z(PPNI(z, y))] Gunkiness‘x is gunky’ means ‘each of x’s parts has properNI parts’.
To illustrate, suppose that object x is gunky. Then, each of its parts (which, given Reflexivity, includes x itself) has properNI parts. So, in the presence of Reflexivity, being gunky entails having properNI parts. In the presence of Transitivity, it entails being such that each of its parts is gunky. And if we define ‘x is simple’ as ‘x does not have any properNI parts’, then being gunky is equivalent to having no simple parts. All this is familiar.
Less frequently noted is that, given (D6), the objects in Models 2 and 3 all count as gunky, as do those in
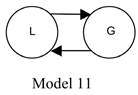
Ordinarily, when philosophers call an object gunky, they take this to mean that the object has disjoint properNI parts, as does each properNI part of that object, and so on ad infinitum. But none of the objects in the given models has disjoint properNI parts. We already know this about Models 2 and 3. But it is also true of Model 11. G overlaps itself and L, and L overlaps itself and G. And yet L and G both count as gunky. L has exactly two parts, itself and G, and each of these things has a properNI part: L has G as a properNI part, and G has L as a properNI part.
Of course, QS rules out all these models. But it will be useful to have a stronger gunkiness predicate. This lets us capture something closer to what philosophers ordinarily have in mind when they call an object gunky (without presupposing QS). The relevant definition goes as follows:
- (D7)
- SG(x) = df. ∀y[P(y, x) → Strong Gunkiness∃z∃w(PPNI(z, y) & PPNI(w, y) & D(z, w))]‘x is strongly gunky’ means ‘each of x’s parts has disjoint properNI parts’.
None of the objects in Models 2, 3, or 11 counts as strongly gunky, as is easily seen. With this notion in hand, we can motivate premise (AP3) from the main argument by noting that it follows from Reflexivity plus the relevant definitions.29
Finally, we can turn to premise (AP2); this is where things become interesting. It turns out that, as weak and innocuous as our core mereology is, it yields (AP2) as a logical consequence. I assume that, whatever our official formulation of Plenitude ultimately comes to, it will entail at the very least that:
- 16.
- ∀x∃y[CO(x, y) & x≠y] No SolitudeEverything coincides with something other than itself.
Although we do not have a formal statement of Plenitude, we can be sure that it is much stronger than No Solitude. No Solitude says that each thing coincides with at least one other thing, whereas Plenitude says that each thing coincides with a vast abundance of other things. (Plenitude also seems to build in UNR—on which No Solitude is silent—but nothing turns on this here.) This lets us argue for (AP2) by proving the following result—call it Result 1: it follows from No Solitude, QS, and Reflexivity that:
- 17.
- ∀x∃y∃z[P(y, x) & P(z, x) & D(y, z)] Disjoint PartsEverything has disjoint parts.
Transitivity is not needed, which I found surprising. The proof is in a note.30 Moreover, we have already seen that given Reflexivity:
- 18.
- ∀xSG(x) The Strong Gunk ThesisEverything is strongly gunky.
This follows from Disjoint Parts. Putting these last two points together, we obtain the result that the Strong Gunk Thesis is a logical consequence of Reflexivity, QS, and No Solitude. In case there is any doubt as to whether the Strong Gunk Thesis is consistent with those three latter claims, or with those claims together with Transitivity and/or Anti-Symmetry, consider Model 12:
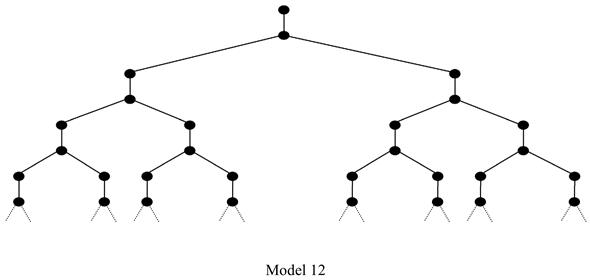
This satisfies Reflexivity (and Transitivity and Anti-Symmetry), for obvious reasons. To see that it satisfies the Strong Gunk Thesis and QS, note that each object has disjoint properNI parts. For any object x, either x is the bottom member of a ‘vertically aligned pair’, or x is the top member of such a pair. If x is the bottom member of such a pair, then its immediate properNI parts are disjoint from each other (since the downward running lines never converge). If x is the top member of such a pair, then the immediate properNI parts of the object that it is paired with are disjoint properNI parts of x. To see that the model satisfies No Solitude, note once again that each object is a member of a vertically aligned pair, where (i) the top member of such a pair is not identical with the bottom member of such a pair, and (ii) the top and bottom members coincide with each other (overlap exactly the same things).
We have seen that the Strong Gunk Thesis is a logical consequence of Reflexivity, QS, and No Solitude (and that it is consistent with those claims, together with Transitivity and Anti-Symmetry). This is a novel route to the Strong Gunk Thesis, and it strikes me as carrying some real weight. It certainly cannot be accused of begging any questions against the friend of simples. None of the premises derives its plausibility from some sort of pre-existing hostility to simples. Indeed, each of the premises is motivated by considerations that are completely orthogonal to questions about the existence of simples. And yet, together, these premises entail that there are not any simples.
It would be interesting to compare this pro-gunk argument to those of Leibniz, McTaggart, and, more recently, Zimmerman [] and Arntzenius [] and others, though this is not the place for it.31 In any event, I think that the gunk-lover will find it encouraging that Coincidentalism, which is prima facie quite independent from questions about gunk, can be marshaled against simples (via the Bennett/Hawthorne arguments against moderate Coincidentalism, together with the core mereology defended in Section 2).32
3.2. From the Possibility of Simples to the Thesis That Plenitude Is Not Necessary?
Still, that is an odd way to learn that there are no simples. Some will find it incredible that we could make such a discovery without doing any detailed empirical investigation. Indeed, many will be convinced (a priori?) that simple objects are at least possible. It will be natural for them to deny that we could know, from the armchair, that there are no simples.
Given their belief in the possibility of simples, they may also want to ‘run the argument in the opposite direction’, so to speak, and treat it as a case against the necessity of Plenitude. Here is a first approximation of that argument:
Argument C
- (CP1)
- Possibly, something is simple.
- (CP2)
- Necessarily, if a thing is simple, it does not coincide with any other thing.
- (CC1)
- So, possibly, there is a thing that does not coincide with any other thing.
- (CP3)
- Necessarily, if Plenitude is true, then each thing coincides with some other thing.
- (CC2)
- So, possibly, Plenitude is not true.
(CP1) is extremely popular and highly plausible on its face. And as we will see, (CP2) follows from the necessitations of Reflexivity and QS. Finally, I expect (CP3) to meet no resistance. So, initially, the argument looks like a good one. But it is worth considering three responses that the friend of Plenitude might be tempted to give.
3.2.1. First Response: (CP1) Begs the Question Against the Plenitude Theorist
Unfortunately, one might think that it, and specifically (CP1), begs an important question against the Plenitude theorist. Hawthorne anticipates the worry in the following passage:
[A]ssume that in every possible world everything is composed of simples without proper parts . . . Note that the notion of ‘proper part’ needs to be treated with care by someone who believes Plenitude. If a proper part of x is a part of x that is not identical to x, then there are no simples (according to the Plenitude Lover), since every purported simple will be mereologically coincident with sundry objects that differ in their modal profiles. For current purposes, think of a proper part of x as some y that is part of x and is such that there is some z that is part of x that does not overlap y [] (p. 55).
In line with this suggestion, let us set out some new definitions:
- (D8)
- SS(x) = df. ~∃yPPNI(y, x) Strong Simplicity‘x is a strong (s-)simple’ means ‘x does not have any properNI parts (any parts with which x is not identical)’.
- (D9)
- PPH(x, y) = df. P(x, y) & ∃z[P(z, y) & D(z, x)] ProperH Parthood‘x is a properH part of y’ means ‘x is a part of y and some part of y is disjoint from x’.
- (D10)
- HS(x) = df. ~∃yPPH(y, x) Hawthorne Simplicity‘x is a Hawthorne (h-)simple’ means ‘x does not have any properH parts’.
A strong simple has no distinct parts (no parts from which it is distinct); an h-simple has no disjoint parts (no parts disjoint from each other). Given Reflexivity, all strong simples are h-simples, as well.33 When I wish to speak of h-simples that are not strong simples, I will use the term ‘mere h-simple’. The unmodified phrase ‘h-simple’ has a broad meaning and applies to strong simples (if such there be), as well as to mere h-simples.
In the passage above, Hawthorne suggests that Plenitude theorists are free to accept h-simples but must deny the existence of strong simples. If he is right about this, then one might suspect that premise (CP1), which asserts the possibility of simples (i.e., strong simples), somehow begs the question against those who take Plenitude to be a necessary truth.
Reply. Two questions arise here. First, is Hawthorne right? Must the Plenitude theorist deny the existence of strong simples? This is unclear, at least absent further argument. As support for the claim that Plenitude rules out strong simples, Hawthorne notes that, given Plenitude, every object coincides with some other object. But does it follow from this that every object has some properNI part, i.e., some part with which it is not identical? Not in the absence of some substantive assumptions about how parthood behaves. After all, in Model 1, objects a and b coincide with each other and are not identical. But b does not have any properNI parts. Transitivity, Reflexivity, and Anti-Symmetry fail to rule this out. So, in the absence of something like WSPNI or QS, the Plenitude theorist is apparently free to accept the existence of strong simples. It is not obvious, then, that (CP2) begs any questions.
This matters little, however, since we need not rely on that claim, for the following, weaker premise will serve our purposes equally well: possibly, something is an h-simple. And this premise, in addition to being plausible, obviously does not beg the question against the Plenitude theorist. After all, Hawthorne himself seems to think that the Plenitude theorist ought to accept it. When the rest of Argument C is restated accordingly, we obtain:
Argument D
- (DP1)
- Possibly, something is an h-simple.
- (DP2)
- Necessarily, if a thing is an h-simple, then it does not coincide with any other thing.
- (DC1)
- So, possibly, there is a thing that does not coincide with any other thing.
- (DP3)
- Necessarily, if Plenitude is true, then each thing coincides with some other thing.
- (DC2)
- So, possibly, Plenitude is not true.
The only changes are the following: the first premise has been weakened, and the second premise has been strengthened. The second change has no real effect, however, since (DP2) still follows from the necessitations of Reflexivity and QS.34 Call this Result 2.
This is a significant fact. A number of philosophers have wondered about the possibility of a simple that mereologically coincides with some other object.35 I think that such things are impossible, and I think that Result 2 provides the fundamental reason why. If an object coincides with some other thing, then—on pain of violating Reflexivity or QS—it has disjoint parts and hence is neither a strong simple nor even a Hawthorne simple. (And Reflexivity and QS are necessary.)
3.2.2. Second Response: QS Should Be Replaced with WSPH
At this point I anticipate the following objection: to undermine the argument for (DP2), QS should be rejected in favor of:
- 19.
- ∀x∀y[PPH(x, y) → ∃z(P(z, y) & D(z, x))] WSPHIf x is a properH part of y, then y has a part z that is disjoint from x.
This is our long-promised third alternative to QS (in addition to WSPNM and WSPS). Does this principle retain Virtues 1–4 from Section 1 while avoiding Vices 1–3? If so, then there is little incentive to keep QS. And once QS is replaced with WSPH, the argument for (DP2) no longer goes through.
Reply. It should be clear that WSPH does not retain Virtue 1. After all, it is a mere truth of logic. When ‘properH part’ is replaced with its definiens, the principle says: if x is a part of y that is disjoint from some part z of y, then there is a part z of y that is disjoint from x. This is satisfied by every model. Hence, it does nothing to rule out the problematic Models 1—3. Our core mereology requires something stronger. (If WSPH was all that Simons had in mind when he wrote ‘surely if a [thing] is complex (i.e., has proper parts at all) then at least two of these will be disjoint’ [] (p. 27), he would not have needed the ‘surely’!)
3.2.3. Third Response: Conceding Argument D and Restricting Plenitude
I think that the Plenitude theorist’s best response is this: admit that Argument D is sound and retreat, but only slightly. A minimally restricted version of Plenitude would entail that necessarily, if an object has disjoint parts (i.e., if it is ‘strongly composite’), then it coincides with a vast number of other objects fitting all manner of modal profiles; but if an object is an h-simple, then it does not coincide with any other object at all. In short: Plenitude holds for composites but not for simples.
How does this square with the original motivations for Plenitude? To answer this question, I want to distinguish three versions of Restricted Plenitude. Each implements the basic idea in a different way.
Version 1. This says that each simple is spatiotemporally co-located with a great many nonmodally indiscernible simples fitting all manner of modal profiles, but none of them coincides (mereologically) with any of the others. It has two main virtues. First, like any version of Restricted Plenitude, it avoids the problematic commitment to coinciding simples. Second, like the original unrestricted Plenitude, it posits an abundance of simples, fitting all manner of modal profiles, in any region that is exactly occupied by a simple at all. It thus avoids a commitment to a potentially arbitrary or anthropocentric distinction between the modal profiles that are instantiated at the location of a simple and those that are not.
The main problem with Version 1 concerns properties like masses. Version 1 tells us that in any region that exactly contains a simple, there are vast numbers of nonmodally exactly similar simples, each disjoint from all the rest. Thus—on the assumption that mass properties are nonmodal—in any region that contains a simple with a mass of 1 unit, there are vast numbers of disjoint simples each with a mass of 1 unit. But do not the masses of these objects add? If I put n pennies on a scale, and if each of them has a mass of m units, the scale will indicate they have a mass of n x m units. Presumably, co-located simples will behave differently. There will be cases in which, if I were to put n (co-located) simples on a scale, and each of these were to have a mass of 1 unit, the scale would indicate that they have a mass of just 1 unit, not n units, as we might naively expect. What explains this? The standard answer—roughly, that co-located objects are not disjoint, and that the masses of non-disjoint objects ‘do not add’—does not work here, since the simples on the scale are disjoint. (Johannson [] makes a similar point in a slightly different context.)
Version 2. The second version of Restricted Plenitude tells us that simples are typically not spatiotemporally co-located with other things: if a region is exactly occupied by a simple, typically it is exactly occupied by only one simple.36 Version 2 avoids the problem about mass for Version 1. But by cutting down so drastically on the number of simples in a region, Version 2 loses a virtue of Version 1: it commits itself to a potentially worrisome distinction between the modal profiles that are instantiated in a simple’s location and those that are not. This may seem to undermine much of the original motivation for any form of Plenitude. After all, if one can tolerate the existence of such a distinction with respect to regions occupied by simples, why cannot one also tolerate the existence of such a distinction with respect to other regions, regions occupied by composite objects? Two points are worth making here.
(1) The first point concerns the grounding problem and Bennett’s suggestion that it is best dealt with by embracing Plenitude. Could it be dealt with equally well by embracing the second version of Restricted Plenitude instead? I think so. For the grounding problem arises only when we have two different objects in the same region that are just alike non-modally but different modally. According to the second version of Restricted Plenitude, simples are typically not involved in such situations, and so the grounding problem will not arise for them. The things that the problem arises for are composite objects, and the present view gives the same account of them as does the original, full-strength Plenitude. When a thing does not coincide with any other object (as in the case of simples), then the possibility remains open that we can ground its modal properties in its nonmodal ones. When a thing does coincide with some other object, then the thing will be composite, and we can ‘demystify’ the ungroundedness of its modal properties in the manner Bennett suggests—by noting that every modal profile minimally eligible to be instantiated in the given region is in fact instantiated there.
(2) The second point concerns Hawthorne-style worries about arbitrariness and anthropocentrism. Hawthorne suggests that if one is led by reflection on the Lump1/Goliath case to accept Coincidentalism, then one might be moved to embrace Plenitude, for fear that any other answer to the question ‘Which modal profiles are instantiated in this region?’ would be objectionably arbitrary or anthropocentric. But would Restricted Plenitude, version 2, suffer from either of these vices? I think not. It is not anthropocentric to say that if a thing is composite, then it coincides with an abundance of other objects fitting an abundance of other modal profiles, whereas if a thing is simple, it does not coincide with anything else and is probably the sole occupant of its region. This does not take ‘common-sense modal profiles’ to be somehow objectively privileged. (Whether or not the relevant sort of ‘anthropocentrism’ is really a vice is a question on which I take no stand in this paper.) To be sure, distinctions will need to be drawn in the case of simples. Let R be a region exactly occupied by exactly one object, o, a simple. Then there will be a great many modal profiles that are ‘minimally eligible’ to be instantiated in R, but one and only one of them will in fact be instantiated there. Which one? Here are two kinds of answer:
Extreme: the ‘hyperessentialist’ modal profile that takes all of o’s properties (intrinsic and extrinsic alike) to be essential to o, andModerate: a modal profile that picks one or more of the following families:
- ○
- ○
- ○
- ○
Neither kind of answer is objectionably arbitrary.37
To see this, suppose that I point to a region apparently occupied by a dollar bill and say, “that region contains exactly one thing, a thing that has its original legal status essentially but its current precise temperature accidentally. It does not contain a thing that has its current precise temperature essentially while having its original legal status accidentally.” To say this would be much more arbitrary and/or anthropocentric than to point to a region occupied by a simple and to say, “that region contains a thing that has its intrinsic properties essentially but its distance from San Francisco accidentally; it does not contain a thing that has its distance from San Francisco essentially and its intrinsic properties accidentally.” So, it seems to me that someone who adopts a moderate answer to the question about the modal profiles of simples can still, in perfectly good conscience, appeal to common sense and considerations of arbitrariness avoidance to motivate Restricted Plenitude (about composite objects).
4. Formal Components?
4.1. From Restricted Plenitude to a ‘Constituent Ontology’
Nevertheless, there is a lingering problem for Restricted Plenitude, version 2. It stems from considerations of uniformity. The problem is simply that Version 2 posits an unaesthetic asymmetry within the category of material objects: composite material objects coincide with vast numbers of other composite material objects fitting a wide variety of modal profiles, whereas simple material objects do not coincide with anything aside from themselves. Is it really plausible that simple material objects are so different from composite ones? After all, they are all material objects; they all belong to the same ontological category. Would not it be preferable, other things being equal, to give a more uniform picture of things within this category rather than giving such a dramatically bifurcated one? I think so.
Version 3. This leads to the third version of Restricted Plenitude. It pushes the distinction between simples and composites out of the category of material objects38 and thus permits a more uniform treatment of material objects. The idea is to hold that, as a matter of necessity, all material objects are composite and have, among their properNI parts, formal components (either tropes or universals). Specifically, Version 3 says that even if a material object has no other material objects as parts, it is still composite, since it has at least one formal component as a properNI part. As such, Restricted Plenitude applies to the thing and entails that it coincides with an abundance of other things, as does any material object. If there are simples, according to Version 3, they fall outside the category of material objects. Some or all of an object’s formal components might be simple. And there might be such things as ‘substrata’, ‘thin particulars’, or ‘portions of matter’, in which case some or all of them might be simple. But no material object is simple.39
Thus we obtain a new route to a constituent ontology.40 Whereas formal components have in the past been invoked as a way of accommodating Uniqueness (McDaniel []), Paul [], Koslicki []) while still granting the non-identity of Lump1 and Goliath, they are here invoked as a way of reconciling Reflexivity and QS with the extreme anti-Uniqueness view that as a matter of necessity, every material object mereologically coincides with a vast abundance of others.
4.2. An Abductive, QS-Based Argument Against Formal Components
For what it is worth, my own attitude toward constituent ontologies is that they involve a category mistake. Material objects instantiate properties and relations. They do not have properties or relations or tropes as parts (or as ‘constituents’, whatever exactly that might mean). This seems obvious to me, but it is not clear what can be said by way of argument for it.
Perhaps the best that can be done is to appeal to some facts about the nature of properties and relations. They are just unsaturated cousins of propositions:41 they are abundant, hyperintensionally individuated, non-spatiotemporal, intrinsically unchanging things, many of which are uninstantiated. They are not well suited to be parts of material objects. (Essentially these same points are made by van Inwagen [].)
But here is a very different line of thought. Say that a thing is an m-simple, just in case the thing is a material object and does not have any other material objects as parts. Say that a thing is an m-composite, just in case the thing is a material object and does have other material objects as parts. Both friends and foes of constituent ontologies are free to accept the existence of m-composites and, more significantly, m-simples. Philosophers on both sides of this dispute can agree, for example, that an electron (or an instantaneous temporal part of an electron, if electrons have temporal parts) is an m-simple. What they will disagree about is whether the thing in question is a simple, full stop.42 Foes of constituent ontologies will say that it is; friends of constituent ontologies will say that it is not.
Now, set aside (as far as possible) any prior views one might have with regard to formal components, and consider the following questions:
- (Q1)
- Can an artist cause it to happen that an m-composite mereologically coincides with some other object?
- (Q2)
- Can an artist cause it to happen that an m-simple mereologically coincides with some other object?
One might take it as basic data that the correct answers are ‘Yes’ and ‘No’, respectively, and one might then wonder what explains the fact that the answer to (Q2) is ‘No’. Here are three potential explanations:
- (E1)
- It is impossible for two different material objects to coincide.
- (E2)
- As a matter of necessity, m-simples are too small and/or too short-lived to coincide with an artwork (which must be large enough and long-enough lived for a human being to perceive).
- (E3)
- Genuine coincidence requires career-long spatial co-location. Hence, in order to cause it to happen that an object x coincides with object y, an artist must cause both x and y to begin to exist. Artists may be able to cause m-composites to begin to exist—say, by bringing smaller material objects together. But an artist cannot cause an m-simple to begin to exist.
These are all very poor. (E1) obviously conflicts with another relevant piece of data, namely, that the answer to (Q1) is ‘Yes’. (E2) is implausible. I strongly suspect that artworks that are visible only through microscopes are possible, perhaps even actual. (E3) is equally implausible. Surely (if m-simples are possible at all) there is nothing impossible about a causal process that results in the creation of an m-simple. If so, it would be odd if an artist could not deploy such a process to their own ends. And yet, despite the low quality of (E1)–(E3), I can think of only one better explanation—namely:
- (E4)
- It is necessary that: (i) Reflexivity is true, (ii) QS is true, and (iii) any part of a material object is itself a material object.
(E4) entails that it is impossible for an m-simple to coincide with another object. Hence, it entails that the correct answer to (Q2) is ‘No’. And it harmonizes with the fact that the correct answer to (Q1) is ‘Yes’. But of course it entails that, necessarily, material objects do not have formal components—at least not as parts. (I assume that no formal component of a material object is itself a material object.) Thus, we have an inference-to-the-best-explanation argument against the relevant sorts of constituent ontology. They are inconsistent with the best explanation of the fact that m-simples cannot coincide with other things.
Now, those who are antecedently attracted to formal components will feel relatively little pressure to accept the data. And even among the foes of formal components (and among the fence-sitters), there is of course a widespread attraction to Uniqueness that will generate pressure to reject the data. But I also think that there is a sizeable group of philosophers who will feel the pull of the data, and not because of any prior hostility toward formal components. These philosophers make up the target audience of the argument, and I see no reason why it should not carry some weight for them.
5. Conclusions
In this paper I have explored arguments: (i) from Plenitude, Reflexivity, and QS to the Strong Gunk Thesis; (ii) from the possibility of simples and necessitations of Reflexivity and QS to the conclusion that Plenitude is not necessary; (iii) from Restricted Plenitude and considerations of uniformity to a constituent ontology; and (iv) from the impossibility of distinct, coinciding m-simples, together with the necessitations of Reflexivity and QS, to the impossibility of a certain kind of constituent ontology. My main ambition, however, has been to focus attention on the superiority of Quasi-Supplementation to Weak Supplementation as a candidate for inclusion in a core mereology.
Throughout the paper, I have worked under the simplifying assumption that there is just one parthood relation and that it is a two-place relation. But, as I mention in note 1, these are controversial, so it is worthwhile to see what survives when these simplifying assumptions are dropped. I suggest that it is something like this: any fundamental parthood relation must be governed by the necessitations of Reflexivity, Transitivity, and QS, at least if it is a two-place relation; and, if it is not two-place, it must be governed by ‘adicity-appropriate analogues’ of these principles.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
For helpful comments, I would like to thank Joshua Earlenbaugh, Michael Glanzberg, Brendan Jackson, Dan Korman, John Malcolm, Bernard Molyneux, Adam Sennet, Peter Simons, Paul Teller, Achille Varzi, Pekka Väyrynen, and especially Maureen Donnelly, Robert Garcia, Dana Goswick, Kris McDaniel, Joshua Spencer, and two anonymous referees for this journal.
Conflicts of Interest
The author declares no conflict of interest.
Notes
| 1 | Though see Johnston [] for dissent. And, strictly speaking, what is almost universally accepted is not that parthood is reflexive and transitive, but that, if it is two-place, then it is reflexive and transitive, and if it is three-place (and time-relative, say), then it has ‘adicity-appropriate analogues’ of reflexivity and transitivity, and so on. Many philosophers deny that parthood is two-place. See, e.g., Thomson [], van Inwagen [], Hudson [], McDaniel [], and Koslicki []. Gilmore [] argues that parthood might be a four-place relation and formulates analogues of reflexivity and transitivity principles that it plausibly obeys in such a case. Similar ideas are independently developed, and ultimately rejected, in Kleinschmidt []. Further, there is a dispute about how many fundamental parthood relations there are. (See McDaniel [] on this.) Since these complications are not relevant here, I assume that there is exactly one fundamental parthood relation and that it is two-place. |
| 2 | Among those who attribute a special status to WSP are Simons [], Oppy [] (pp. 213–215), Effingham and Robson [], Koslicki [], Varzi [], Bynoe [], and van Inwagen []. Van Inwagen distinguishes between those mereological principles that ‘we shall presuppose’ and those that ‘we shall not presuppose’ (even though he ultimately endorses some in this second category). Among the principles that van Inwagen accepts but does not ‘presuppose’ are a version of Uniqueness and the claim that some things have simple parts. Among those that he ‘presupposes’ are the transitivity of parthood and WSPPVI: “if x is a proper part of y, there are zs (none of which is x) such that x and the zs compose y” [] (p. 55). His definition of “compose” entails that if x and the zs compose y, then x and all of the zs are parts of y, and none of the zs overlaps x or any of the other zs. So WSPPVI entails that if x is a proper part of y, then y has some part disjoint from x. For further discussion of WSP and additional references, see Koslicki [], Russell [], Donnelly [], Smith [], Caplan, Tillman, and Reeder [], and Gilmore [] and []. |
| 3 | For a defense of Transitivity against a recent challenge, see Varzi []. |
| 4 | This has been denied by McDaniel [], Paul [], and Koslicki [], who claim that at least one of the given objects has, as a part, at least one ‘formal component’ (trope or property or relation) that is disjoint from the other object. |
| 5 | Korman [] rejects UNR but is silent on Uniqueness. In personal communication he has confirmed that he is a Uniqueness-denier. Simons [] rejects Uniqueness and repeatedly expresses strong doubts about UNR but does not, as far as I am aware, explicitly reject it. |
| 6 | For very different reasons for doubting Anti-Symmetry, see Tillman and Fowler []. |
| 7 | We can derive a contradiction from this set of claims. From the negation of Uniqueness we obtain the result that there are non-identical objects, call them a and b, that both fuse a common set of things, call it s. So, (i) a fuses s, (ii) b fuses s, and (iii) a≠b. Together with Transitivity, (i) and (ii) guarantee that neither a nor b has any part that is disjoint from the other. To see this, suppose (for reductio) that (iv) a has a part that is disjoint from b. Let c be such a part. This gives us (v) c is a part of a, and (vi) c is disjoint from b. From (v), (i), and the definition of ‘fuses’, we obtain (vii) c overlaps some member of s. Let d be such a thing. Then we have (viii) d is a member of s, and (ix) c overlaps d. From (ix) and definition of ‘overlaps’ we obtain (x) something is a part of both c and d. If we let e be such a thing, we have (xi) e is a part of c, and (xii) e is a part of d. Now recall that (viii) d is a member of s and that (ii) b fuses s. Together with the definition of ‘fuses’, these entail that (xiii) d is part of b. So, (xii) e is a part of d, and (xiii) d is a part of b. Given Transitivity, these yield (xiv) e is a part of b. But, as we already know, (xi) e is a part of c. So, (xv) something is a part of both c and b. Given the definition of ‘overlap’, this entails that (xvi) c overlaps b, which, given the definition of ‘disjoint’, entails that (xvii) c is not disjoint from b. This contradicts (vi), which lets us conclude that (xviii) a does not have a part that is disjoint from b. A parallel argument obtains the result that (xix) b does not have a part that is disjoint from a. (More generally, if there a set that x and y both fuse then, given Transitivity, neither x nor y has a part that is disjoint from the other. This is a useful point to keep in mind.) Now, in the presence of Strong Supplementation, (xviii) entails that (xx) a is a part of b, and (xix) entails that (xxi) b is a part of a. But, given Anti-Symmetry, (xx) and (xxi) entail that (xxii) a = b, which contradicts (iii). |
| 8 | Similar claims are made by Doepke [] and Lowe []. Van Inwagen [] (p. 53) rejects coincidentalism but advises coincidentalists to be, in my terminology, A-Coincidentalists. |
| 9 | Similar claims are made by Thomson []. Sider [] (p. 155) rejects coincidentalism but advises coincidentalists to be, in my terminology, S-Coincidentalists. |
| 10 | Upward-running lines stand for properNI parthood. |
| 11 | In the presence of Reflexivity, (i) Weak CompanyNI follows from Strong CompanyNI (but not vice versa), (ii) both principles follow from WSPNI (but it follows from neither), and (iii) none of the three follow from Strong Supplementation (nor does it follow from any of them). |
| 12 | As with WSPNI, neither MSPNI nor Strong Supplementation follows from the other. |
| 13 | Smith [] rejects WSP on the basis of cases described by Effingham and Robson []. Gilmore [] shows that if parthood is a four-place relation (expressed by ‘x at y is a part of z at w’), the cases in question do not threaten the ‘four-place counterpart’ of WSP, and argues that there are independent reasons to take parthood to be four-place. (Kleinschmidt [] develops similar ideas independently.) See Forrest [], Russell [] and Caplan, Tillman, and Reeder [] for a discussion of certain other pressures against WSP that lie beyond the scope of this paper. |
| 14 | Suppose for reduction that these claims are all true. Given S-Coincidentalism (Strong Supplementation + the negation of Uniqueness), we obtain the result that there are non-identical objects, call them a and b, that fuse a common set, call it s. This gives us (i) a fuses s, (ii) b fuses s, and (iii) a≠b. Earlier, we saw that (i) and (ii), together with Transitivity, yield the following consequences: (xviii) a does not have a part that is disjoint from b, and (xix) b does not have a part that is disjoint from a. In the presence of Strong Supplementation, (xviii) entails that (xx) a is a part of b, which, together with (iii) and the definition of ‘properNI part’, entails that (xxi) a is a properNI part of b. Together with WSPNI, (xxi) entails that (xxii) b has a part that is disjoint from a, which contradicts (xix). |
| 15 | See Cotnoir [] (p. 399) on the use of directed graphs (as opposed to Hasse diagrams) to specify models in which parthood fails to be anti-symmetric. |
| 16 | Neither is Strong CompanyNI. L is a properNI part of G, but G does not have any properNI parts that are not parts of L. (G’s properNI parts are L, a, and b, and they are all parts of L). |
| 17 | Extensionality and Uniqueness both fail in Models 4 and 6. In Model 7, Extensionality is satisfied but Uniqueness is not. |
| 18 | See Rea [] for a response to Varzi’s argument. |
| 19 | Although his versions of those principles employ a primitive notion of proper parthood, whereas ours employ the defined notion properNI parthood. See the next note. |
| 20 | I have replaced Simons’s notation with my own. (E.g., I have replaced Simons’s ‘⊃’ with my ‘→’ and his ‘<<’ with my ‘PP’.) He treats ‘proper part’ as primitive, and he defines ‘x is a part of y’ as ‘either x is a proper part of y or x = y’. |
| 21 | The fact that Model 7 satisfies QS but not Strong CompanyNI (see note 14) shows that QS is not logically stronger than Strong Company. This may come as a surprise, given that Strong CompanyNI fails to rule out all of Models 1–3, whereas QS succeeds in ruling these out (as I show in the main text below). |
| 22 | For further defenses of QS (and its adicity-appropriate analogues), see Gilmore [], where a four-place counterpart of QS is shown to harmonize with endurantist interpretations of certain puzzling time travel cases (Effingham and Robson []), and Gilmore [], where a four-place counterpart of QS is shown to harmonize with Russellian theories of propositions, contrary to what one might think on the basis of the arguments in Bynoe []. |
| 23 | To see that QS is weaker than WSPNI, note two points. First, WSPNI is not a logical consequence of QS. This is shown by the fact that there are models (e.g., Models 7 and 9) in which QS is satisfied but WSPNI fails. Second, QS is a logical consequence of WSPNI. To see this, suppose that WSPNI is true. Then either (i) there are some things that satisfy its antecedent or (ii) there are not. Either way, QS comes out true too. Given (ii), nothing is a properNI part of anything and, hence, given the definition of ‘properNI part’, there is no pair such that x is a part of but not identical to y. In that case, there are not any things that satisfy the antecedent of QS either, which makes QS true (vacuously). On the other hand, suppose that (i) is true, and in particular, suppose that (iii) a is a properNI part of b. Then, given WSPNI, we obtain the result there is a part of b, call it c, that is disjoint from a. So, now we know that (iv) c is a part of b and (v) c is disjoint from a. But a is a properNI part of b and, hence, (given the definition of ‘properNI part’) a part of b. So, b has parts, namely, a and c, that are disjoint from each other, and hence, the consequent of QS is satisfied too. |
| 24 | To see this, first note that the failure of Uniqueness entails the existence of distinct coinciding objects. (This direction is easy.) For suppose that x and y fuse the same set, s, but are not identical. Now suppose for reductio that they do not overlap exactly the same things. Then, there will be an object z that overlaps one them, say x, but not the other, y. By the definition of ‘overlaps’, there is a thing z1 that is a part of both z and x; and by the definition of ‘fuses’, z1 overlaps some member m1 of s. So, by the definition of ‘overlaps’ again, there is a thing z2 that is a part of both z1 and m1. Now, since z2 is a part of z1 and z1 is a part of z, Transitivity lets us conclude that z2 is a part of z. And since z2 is a part of m1 and m1 (by the definition of ‘fuses’) is a part of y, Transitivity also lets us conclude that z2 is a part of y. So, since z2 is a part of both z and y, we can conclude (by the definition of ‘overlap’) that z overlaps y, which contradicts what we said earlier. This shows that if two objects fuse the same set, then (given Transitivity) they overlap exactly the same things, i.e., they coincide. Now, for the other direction: the existence of distinct coinciding objects entails the failure of Uniqueness. (This is harder, at least for me.) Suppose that x and y coincide but are not identical. By Reflexivity, x is a part of, and hence overlaps, itself. Mutatis mutandis for y. So, by the definition of ‘coincide’, x and y overlap each other. Hence, there is a thing z that is a part of both x and y. Now, let s be the set of things that are parts of both x and y, i.e., let s = {w: w is a part of x and w is a part of y}. We now show that x and y both fuse s. We know that (i) s has at least one member, z. And we know that (ii) each member of s is a part of x and is a part of y. So, all that remains is to show that (iii) each part of x overlaps at least one member of s and (iv) each part of y overlaps at least one member of s. Start with (iii). Assume for reductio that x has a part x1 that does not overlap any member of s. Now, x1 is a part of itself (given Reflexivity) and of x, hence, given the definition of ‘overlap’, x overlaps x1. So, by the definition of ‘coincide’, y overlaps x1 too. So, there is a thing y1 that is a part of both x1 and y. Since y1 is a part of x1 and x1 is a part of x, Transitivity lets us conclude that y1 is a part of x. But it is also a part of y. So, y1 is a member of s, the set of those things that are parts of both x and y. But y1 is a part of both itself (given Reflexivity) and x1. So, by the definition of ‘overlaps’, x1 overlaps y1, a member of s. This contradicts our assumption, which lets us conclude that (iii) is true. The case for (iv) is exactly parallel. Given (i)—(iv), it follows by the definition of ‘fuses’ that x and y both fuse s even though they are not identical. Uniqueness fails. |
| 25 | As is emphasized, e.g., by Heller []. |
| 26 | Region R is matter-filled just in case each subregion of R spatiotemporally overlaps the path of some material object. The path of an object is the sum or union of spacetime regions at which the object is exactly located. These definitions leave open the possibility of a region that is matter-filled but not the path of any material object. Such a region might, e.g., be the sum of the paths of two distant particles that do not themselves compose any larger object. |
| 27 | Similar views are discussed by Sosa [], Yablo [], and, in the context of a trope bundle theory, McDaniel []. Hawthorne also expresses sympathy for extensions of Plenitude that make no distinction between regions that are ‘matter-filled’ and those that are not [] (p. viii, p. 118). Such views posit a great many objects for every region, bar none. As Hawthorne notes, one might think of such objects as not merely occupying, but mereologically coinciding with, the regions at which they are located. For further relevant discussion, see Schaffer []. |
| 28 | Though see Korman [] for resistance. |
| 29 | To see this, assume for reductio that the antecedent (‘everything has disjoint parts’) is true and that the consequent (‘everything is strongly gunky’) is false, hence, that there is some object, call it x, that is not strongly gunky. By the definition of ‘strongly gunky’, it follows that there is a part x1 of x that does not have disjoint properNI parts. But given the antecedent, x1 does have disjoint parts, call them x2 and x3. Since x1 does not have disjoint properNI parts, it follows by the definition of ‘properNI part’ that at least one of x2 or x3, say x2, is identical to x1. So, since x3 is part of x1, and since x2 is identical to x1, it follows that x3 is a part of x2. And since, given Reflexivity, x3 is a part of itself, it follows that x3 and x2 have a common part (namely, x3) and hence, by the definitions of ‘overlap’ and ‘disjoint’, that they are not disjoint, which contradicts what we said earlier. This yields the desired conclusion. |
| 30 | Assume for reductio that (A) No Solitude, Reflexivity, QS the negation of Disjoint Parts are all true. From the negation of Disjoint Parts and the definition of ‘disjoint’, it follows that there is an object, call it x, such that any parts a and b of x overlap. Given No Solitude, there is an object, call it y, that coincides with but is not identical to x. Given Reflexivity, x is a part of itself and hence has a part in common with itself (namely, x), from which it follows, by the definition of ‘overlap’ that x overlaps itself. Now, since x coincides with y, and since x overlaps x, by the definition of ‘coincides’ it follows that y overlaps x. So, given the definition of ‘overlap’, there is a thing z that is a part of both x and y. Since x≠y, it follows that z is identical to at most one of x and y. Thus we have only three possibilities: (i) z is identical neither to x nor to y, (ii) z is identical to y but not x, and (iii) z is identical to x but not y. In each case we obtain a contradiction. First suppose that (i) is true. Then, since z is a part of x but not identical to x, QS kicks in and yields the result that x has parts x1 and x2 that are disjoint from each other and hence (given the definition of ‘disjoint’) do not overlap each other. This contradicts our initial claim about x in the previous paragraph. So suppose that (ii) is true. Then, once again, since z is a part of x but not identical to x, QS yields the result that x has parts that are disjoint and hence do not overlap, which contradicts that same initial claim about x. Finally, suppose that (iii) is true. Then, since z is a part of but not identical to y, QS yields the result that y has parts y1 and y2 that are disjoint. Now y1 is a part of y and (by Reflexivity) of y1, which means that y and y1 have a common part (namely, y1). Hence, (by the definition of ‘overlaps’) y overlaps y1. A parallel argument shows that y overlaps y2. So, by the definition of ‘coincides’, x overlaps y1 and x overlaps y2. So, there is a thing z1 that is a part of both x and y1, and there is a thing z2 that is a part of both x and y2. Now, we have two sub-cases: either (iii.1) z1 = z2 or (iii.2) z1≠z2. Each one leads to a contradiction. Suppose that (iii.1) is true. Then, since z2 is a part of y2, it follows that z1 is a part of y2. But we already know that z1 is a part of y1. So y1 and y2 have a common part (namely, z1). Hence, by the definitions of ‘overlap’ and ‘disjoint’, y1 is not disjoint from y2, which contradicts our initial claim about them in the second sentence of the previous paragraph. So, suppose instead that (iii.2) is true, and z1≠z2. Then, by Leibniz’s law, at least one of them, say z1, fails to be identical to x. So, z1 is a part of and not identical to x. Given QS, it follows from this that x has parts, call them a1 and b1, that are disjoint and hence (by the definition of ‘disjoint) do not overlap. But this contradicts our initial claim about x. Since there were only three possibilities—(i), (ii), and (iii)—and since each of them yields a contradiction, our initial assumption, (A), must be false. Disjoint parts is a logical consequence of No Solitude, Reflexivity, and QS. |
| 31 | On Leibniz’s views, see McDonough []; on McTaggart’s, see McDaniel []. |
| 32 | Why not take these considerations to cast doubt on QS’s status as a core principle? After all, WSPNI was called into question on the basis of the fact that it was in tension with ‘a respectable form of coincidentalism’, namely S-Coincidentalism. Why cannot we, with equal justice, call QS into question on the basis of the fact that it is in tension with another respectable form of coincidentalism—one we might call Plenitudinous-Coincidentalism-with-Simples? (Thanks to Dana Goswick and Maureen Donnelly for pressing me on this.) In reply, I want to make three points. (1) I am just assuming that Simons’s point (that our core mereology should include some principle that rules out Models 1—3) is true and non-negotiable. Personally, I find the point compelling (far more compelling than the claim that Plenitudinous-Coincidentalism-with-Simples is a respectable view that our core mereology should not rule out) and I think that, all things considered, QS is the best candidate for the given job. (2) Even if one insists that our core mereology should not rule out Plenitudinous-Coincidentalism-with-Simples, it is not clear that QS is the principle to blame. Why not blame Reflexivity instead? (3) If one finds Simons’s point less compelling than I do and if one insists that our core mereology must include Reflexivity, then of course one is free to use the above considerations as a reason for denying ‘core status’ to QS. In light of the fact that QS has so much going for it (and avoids so many of the vices of WSPNI), this would seem to be a surprising and significant result in its own right. |
| 33 | A strong simple has at most one part. Since, by Reflexivity, each thing is a part of and hence overlaps itself, we can conclude that if a thing x is a strong simple, then if y and z are parts of x, y and z are identical and hence overlap and hence fail to be disjoint. |
| 34 | Modal operators aside, this was established in our proof of Result 1. We assumed that x coincides with some distinct object y, and we were able to prove, by appeal to just Reflexivity and QS, that x has disjoint parts (and hence is not an h-simple). I assume that those who find Reflexivity, Transitivity, and QS especially obvious will find their necessitations roughly equally obvious. |
| 35 | Sider [] (p. 179), Wasserman [], Hawthorne [] (p. 55), Hudson [], Johansson []. |
| 36 | I say ‘typically’ because there might be cases in which two fundamental particles happen to interpenetrate for a while, in which case one might think that there are simple temporal parts of one and simple temporal parts of another that are distinct and co-located. For a defense of such things, see McDaniel []; for a criticism, see Schaffer []. Schaffer does think, however, that simple tropes can be co-located. See also Schaffer []. |
| 37 | The hyperessentialist answer, though, has consequences that are so counterintuitive that they seem to undermine the arguments that motivated Coincidentalism in the first place. For example, the hyperessentialist answer entails that for any object x, if there are some simples, the Ys, such that it is essential to x that at least one of the Ys is a part of x, then x has all of its properties essentially. So, for example, if Lump1 never in fact was squashed, and if there are some simple ‘clay particles’, the cs, such that it is essential to Lump1 that at least one of the cs is a part of Lump1, then Lump1 could not have survived being squashed. |
| 38 | What I am calling ‘material objects’, others might call ‘concrete material particulars’ or ‘physical substances’. I have in mind things like planets, tables, trees, cats, perhaps quarks and electrons, temporal parts of things like these (if they have temporal parts), and any fusions of sets of things like these. |
| 39 | Some philosophers seem to hold that there are properties, relations, or tropes that are both (i) simple and (ii) material objects in their own right. (David Robb [], e.g., claims that there are simple objects, and that each of them is identical to a simple trope.) This view is inconsistent with Restricted Plenitude, Version 3, since it entails that some material objects are simple. Thus it seems that Restricted Plenitude, Version 3 works best under the assumption that no property, relation, or trope is itself a material object. Thanks to Robert Garcia for this point. For a discussion of ‘object-like’ and ‘non-object-like’ conceptions of tropes, see Garcia []. |
| 40 | I take a constituent ontology to be a view according to which material objects have formal components as parts or constituents. I take bundle theories and hylomorphic theories to be constituent ontologies. |
| 41 | But it is not obvious that all unsaturated ‘cousins’ (or parts) of propositions are properties or relations. For one might think, e.g., that the sentential connective ‘and’ expresses an unsaturated entity, CONJ, that is a part of various propositions but that is neither a property nor a relation. See Gilmore []. |
| 42 | A qualification is required. Some friends of constituent ontologies will say that material objects have their formal components as constituents but not as parts (or as partsf but not as partsm, where these two predicates are taken to express different fundamental parthood relations). See McDaniel [] on ‘compositional pluralist’ views like these. The argument that I give in this section does not apply to such views. |
References
- Johnston, M. Parts and Principles: False Axioms in Mereology. Philos. Top. 2002, 30, 129–166. [Google Scholar] [CrossRef]
- Thomson, J.J. Parthood and Identity Across Time. J. Philos. 1983, 80, 201–220. [Google Scholar] [CrossRef]
- van Inwagen, P. Material Beings; Cornell University Press: Ithaca, NY, USA, 1990. [Google Scholar]
- Hudson, H. A Materialist Metaphysics of the Human Person; Cornell University Press: Ithaca, NY, USA, 2001. [Google Scholar]
- McDaniel, K. Modal Realism with Overlap. Australas. J. Philos. 2004, 82, 137–152. [Google Scholar] [CrossRef]
- Koslicki, K. The Structure of Objects; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Gilmore, C. Why Parthood Might Be a Four-Place Relation, and How It Behaves If It Is. In Unity and Time in Metaphysics; Honnefelder, L., Runggaldier, E., Schick, B., Eds.; de Gruyter: Berlin, Germany, 2009; pp. 83–133. [Google Scholar][Green Version]
- Kleinschmidt, S. Multilocation and Mereology. Philos. Perspect. 2011, 25, 253–276. [Google Scholar] [CrossRef]
- McDaniel, K. Structure-Making. Australas. J. Philos. 2009, 87, 251–274. [Google Scholar] [CrossRef]
- Simons, P. Parts: A Study in Ontology; Oxford University Press: Oxford, UK, 1987. [Google Scholar][Green Version]
- Oppy, G. Philosophical Perspectives on Infinity; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar][Green Version]
- Effingham, N.; Robson, J. A Mereological Challenge to Endurantism. Australas. J. Philos. 2007, 85, 633–640. [Google Scholar] [CrossRef]
- Varzi, A. Mereology. In The Stanford Encyclopedia of Philosophy (Spring 2011 Edition); Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2011; Available online: https://plato.stanford.edu/archives/spr2011/entries/mereology/ (accessed on 1 July 2025).[Green Version]
- Bynoe, W. Against the Compositional View of Facts. Australas. J. Philos. 2011, 89, 91–100. [Google Scholar] [CrossRef]
- Russell, J. The Structure of Gunk: Adventures in the Ontology of Space. In Oxford Studies in Metaphysics; Zimmerman, D.W., Ed.; Oxford University Press: Oxford, UK, 2009; Volume 4, pp. 248–274. [Google Scholar]
- Donnelly, M. Using Mereological Principles to Support Metaphysics. Philos. Q. 2011, 61, 225–246. [Google Scholar] [CrossRef]
- Smith, D. Mereology without Weak Supplementation. Australas. J. Philos. 2009, 87, 505–511. [Google Scholar] [CrossRef]
- Caplan, B.; Tillman, C.; Reeder, P. Parts of Singletons. J. Philos. 2010, 107, 501–533. [Google Scholar] [CrossRef]
- Gilmore, C. Parts of Propositions. In Mereology and Location; Kleinschmidt, S., Ed.; Oxford University Press: Oxford, UK, 2014; pp. 156–208. [Google Scholar][Green Version]
- Varzi, A. A Note on the Transitivity of Parthood. Appl. Ontol. 2006, 1, 141–146. [Google Scholar] [CrossRef]
- Sider, T. Four Dimensionalism: An Ontology of Persistence and Time; Oxford University Press: Oxford, UK, 2001. [Google Scholar][Green Version]
- McDaniel, K. Tropes and Ordinary Physical Objects. Philos. Stud. 2001, 104, 269–290. [Google Scholar] [CrossRef]
- Paul, L.A. Coincidence as Overlap. Noûs 2006, 40, 623–659. [Google Scholar] [CrossRef]
- Lewis, D. Parts of Classes; Blackwell: Oxford, UK, 1991. [Google Scholar][Green Version]
- Thomson, J.J. The Statue and the Clay. Noûs 1998, 32, 149–173. [Google Scholar] [CrossRef]
- Korman, D.Z. Strange Kinds, Familiar Kinds, and the Charge of Arbitrariness. In Oxford Studies in Metaphysics; Zimmerman, D.W., Ed.; Oxford University Press: Oxford, UK, 2010; Volume 5, pp. 119–144. [Google Scholar]
- Tillman, C.; Fowler, G. Propositions and Parthood: The Universe and Anti-Symmetry. Australas. J. Philos. 2012, 90, 525–539. [Google Scholar] [CrossRef]
- Doepke, F. Spatially Coinciding Objects. Ratio 1982, 24, 45–60. [Google Scholar]
- Lowe, E.J. Substantial Change and Spatiotemporal Coincidence. Ratio 2003, 16, 140–160. [Google Scholar] [CrossRef]
- Hovda, P. What is Classical Mereology? J. Philos. Log. 2009, 38, 55–82. [Google Scholar] [CrossRef]
- Olson, E. Why I Have No Hands. Theoria 1995, 61, 182–197. [Google Scholar] [CrossRef]
- Merricks, T. Objects and Persons; Oxford University Press: Oxford, UK, 2001. [Google Scholar][Green Version]
- Forrest, P. Nonclassical Mereology and Its Application to Sets. Notre Dame J. Form. Log. 2002, 43, 79–94. [Google Scholar] [CrossRef]
- Cotnoir, A. Anti-symmetry and non-extensional mereology. Philos. Q. 2010, 60, 396–405. [Google Scholar] [CrossRef]
- Varzi, A. Universalism Entails Extensionalism. Analysis 2009, 69, 599–604. [Google Scholar] [CrossRef]
- Varzi, A. The Extensionality of Parthood and Composition. Philos. Q. 2008, 58, 108–133. [Google Scholar] [CrossRef]
- Rea, M. Universalism and Extensionalism: A Reply to Varzi. Analysis 2010, 70, 490–496. [Google Scholar] [CrossRef]
- Heller, M. Temporal Overlap is Not Coincidence. Monist 2000, 83, 362–380. [Google Scholar] [CrossRef]
- Dorr, C. What We Disagree about When We Disagree about Ontology. In Fictionalist Approaches to Metaphysics; Kalderon, M.E., Ed.; Oxford University Press: Oxford, UK, 2005. [Google Scholar][Green Version]
- Rea, M. Constitution and Kind Membership. Philos. Stud. 2000, 97, 169–193. [Google Scholar] [CrossRef]
- Bennett, K. Spatiotemporal Coincidence and the Grounding Problem. Philos. Stud. 2004, 118, 339–371. [Google Scholar] [CrossRef]
- Hawthorne, J. Metaphysical Essays; Oxford University Press: Oxford, UK, 2006. [Google Scholar][Green Version]
- Sosa, E. Subjects Among Other Things. Philos. Perspect. 1987, 1, 155–187. [Google Scholar] [CrossRef]
- Yablo, S. Identity, Essence, and Indiscernibility. J. Philos. 1987, 84, 293–314. [Google Scholar] [CrossRef]
- McDaniel, K. Modal Realisms. Philos. Perspect. 2006, 20, 303–331. [Google Scholar] [CrossRef]
- Schaffer, J. Spacetime the One Substance. Philos. Stud. 2009, 145, 131–148. [Google Scholar] [CrossRef]
- Zimmerman, D. Could Extended Objects Be Made Out of Simple Parts? An Argument for “Atomless Gunk”. Philos. Phenomenol. Res. 1996, 56, 1–29. [Google Scholar] [CrossRef]
- Arntzenius, F. Gunk, Topology, and Measure. In Oxford Studies in Metaphysics; Zimmerman, D.W., Ed.; Oxford University Press: Oxford, UK, 2009; Volume 4, pp. 225–247. [Google Scholar]
- McDonough, J. Leibniz’s Philosophy of Physics. In The Stanford Encyclopedia of Philosophy; Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2007; Available online: https://plato.stanford.edu/archives/win2007/entries/leibniz-physics/ (accessed on 1 July 2025).[Green Version]
- McDaniel, K. John M. E. McTaggart. In The Stanford Encyclopedia of Philosophy; Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2009; Available online: https://plato.stanford.edu/archives/win2009/entries/mctaggart/ (accessed on 1 July 2025).[Green Version]
- Wasserman, R. The Constitution Question. Noûs 2004, 38, 693–710. [Google Scholar] [CrossRef]
- Hudson, H. Simple Statues. Philo 2006, 9, 40–46. [Google Scholar] [CrossRef]
- Johansson, J. Constituted Simples? Philosophia 2009, 37, 87–89. [Google Scholar] [CrossRef]
- McDaniel, K. Brutal Simples. In Oxford Studies in Metaphysics; Zimmerman, D.W., Ed.; Oxford University Press: Oxford, UK, 2007; Volume 3, pp. 233–256. [Google Scholar]
- Schaffer, J. The Individuation of Tropes. Aust. J. Philos. 2003, 79, 247–257. [Google Scholar] [CrossRef]
- Robb, D. Qualitative Unity and the Bundle Theory. Monist 2005, 88, 466–492. [Google Scholar] [CrossRef]
- Garcia, R. Is Trope Theory a Divided House? In The Problem of Universals in Contemporary Philosophy; Loux, M., Galluzzo, G., Eds.; Cambridge University Press: Cambridge, UK, 2015; pp. 133–155. [Google Scholar][Green Version]
- van Inwagen, P. A Theory of Properties. In Oxford Studies in Metaphysics; Zimmerman, D.W., Ed.; Oxford University Press: Oxford, UK, 2004; Volume 1, pp. 107–138. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).