Abstract
This study presents a multiphysics simulation approach to optimize graphite-buffered bilayer anodes for enhanced energy density in lithium-ion batteries, assessing the electrochemical impact of diverse inner-layer materials, including silicon, hard carbon, lithium titanate (LTO), and metallic lithium, in pure and graphite-composite forms. A coupled finite-element model implemented in COMSOL Multiphysics 6.2 was used to integrate spherical lithium diffusion, charge conservation, and the solid electrolyte interphase (SEI) formation kinetics. The evaluated anode structure consisted of a 60 µm-thick bilayer: a 30 µm graphite surface layer coupled with a 30 µm inner layer of alternative active materials. Simulations were performed using an NMC622 cathode, LiPF6 in EC:EMC electrolyte, at room temperature, under a charge rate of 1 C, considering realistic particle sizes (graphite: 2.5 µm; Si: 0.1 µm; hard carbon: 2.5 µm; LTO: 0.2 µm; Li metal: 0.5 µm), and evaluated over 2000 cycles. The hard carbon/graphite configuration exhibited a capacity fade of 5.8% compared with 7.1% in pure graphite. Additionally, the SEI thickness decreased to 0.20 µm (from 0.25 µm), the overpotential dropped to −17 mV (from −59 mV), and the electrolyte consumption was reduced to 20.8% (from 42.9%). The analysis highlights hard carbon and LTO inner layers as optimal trade-offs between capacity and cycle stability, whereas silicon and lithium metal significantly increased the initial capacity but accelerated SEI formation and impedance growth. These findings demonstrate the graphite-buffered bilayer’s potential to decouple interfacial degradation from high-capacity materials, providing valuable guidelines for the design of advanced lithium-ion battery anodes.
1. Introduction
Lithium-ion batteries are the dominant energy storage technology for consumer electronics, electric vehicles, and renewable energy systems due to their high energy density and long service life [1]. Benchmark Mineral Intelligence (London, UK) projects that annual demand will exceed 3 TWh by 2030, more than twice today’s installed manufacturing capacity [2]. First, it drives the need to increase the energy density and cycle life to reduce the levelized cost of storage. Second, it requires securing sustainable and traceable supply chains for anode-critical materials (natural graphite, lithium, battery-grade silicon) while minimizing the mining impacts. Third, it necessitates efficient recycling routes and safe end-of-life disposal to close the materials loop and curb long-term ecological risks.
Layered-oxide cathodes are nearing their redox limits, and liquid electrolytes have largely been optimized. However, the anode still offers considerable room for improvement and remains a key factor in achieving higher energy density [2]. Commercial anodes are still dominated by graphite due to its low intercalation potential, robust cycling behavior, and well-documented stability [3]. However, graphite’s theoretical capacity limit of 372 mAh/g now constrains long-range electric vehicles, fast-charging applications, and high-demand stationary systems. The geographic concentration of natural graphite mining also raises sustainability and geopolitical concerns [4]. These pressures are accelerating research into alternative materials capable of storing more lithium without incurring prohibitive costs or durability issues.
Silicon remains the prime contender to replace graphite, with a theoretical capacity of about 3579 mAh/g, almost an order of magnitude higher [5]. Its nearly 300% volume expansion during lithiation fractures the particles, consumes electrolytes, and thickens the solid electrolyte interphase (SEI), leading to rapid capacity fade [6,7]. Nanoscale design strategies such as nanostructuring, protective coatings, and hollow or yolk-shell structures slow this degradation. Conductive Si/C hybrids with graphite, graphene, or carbon nanotubes improve electronic pathways and buffer stress. However, these approaches still suffer from progressive SEI growth and capacity fade [8,9,10]. External commercial prototypes illustrate both the promise and the remaining hurdles. NanoGraf (Chicago, IL, USA)’s SiOx–graphene anode targets a roughly 20% extra range but at a higher cost [11]. ProLogium (Taoyuan, Taiwan) embeds SiOx in solid-state ceramic cells, though this incurs high ceramic costs and poor conductivity at sub-zero temperatures [11]. Amprius (Fremont, CA, USA) reports nanowire-silicon cells near 450 Wh/kg that fast-charge in minutes, although the fabrication cost and swelling constrain scale-up [12,13].
Other anode options trade capacity for stability. Metallic lithium exemplifies this challenge: despite offering superior capacity (3860 mAh/g) and the lowest anode potential, dendrite formation and unstable SEI behavior have prevented its commercial adoption [14]. Li4Ti5O12 provides excellent safety and a long cycle life, but at the expense of energy density [5]. Hard carbon offers a capacity of around 250–350 mAh/g and performs better at low temperatures and high rates than graphite. Advanced carbon nanostructures can exceed a 700 mAh/g capacity, but complex synthesis routes and high cost limit scale-up [15]. These anode alternatives demonstrate that performance optimization in one parameter typically results in compromises across other critical metrics including structural integrity, electrochemical stability, manufacturing costs, and first-cycle efficiency.
Building on the above discussion of the physicochemical advantages of graphite, silicon, LTO, graphene-derived carbons, and other hosts, the following narrative provides a year-by-year account of how researchers have progressively combined these constituents into vertically stacked multilayer anodes (Figure 1). In 2014, Choi et al. [16] provided a proof of concept by confining nano-LTO between a graphene current collector and an outer SWCNT film. This architecture sustained 109 mAh/g at 100 C for 1000 cycles, revealing that a carbon cladding could buffer oxide expansion while maintaining electronic pathways.
By 2016, the research focus had shifted to lithium metal systems. Lin et al. [17] showed that layered reduced-graphene-oxide (rGO) with sub-10 nm gaps guided uniform Li deposition for over 1000 cycles at 3–5 mA/cm2. Also in 2016, Ming et al. [4] stacked a sulfur/graphite/LTO tri-layer that delivered 572 mAh/g with 82% retained capacity after 100 cycles using a water-based binder. In 2018, Bai et al. [18] extended the rGO strategy by spray-coating graphene oxide sheets that spontaneously reduced to a ~330 nm film, an optimum thickness that suppresses dendrites but preserves ionic resistance.
In 2017, Guo et al. [19] explored layer-structured materials such as graphite and metal oxides using techniques like chemical/mechanical exfoliation, host molecule intercalation, and hydro/solvothermal synthesis to enhance the reactivity, ion accessibility, and structural stability. In the same year, Sharma et al. [20] illustrated a cost-aware alternative, physically mixing hard carbon with LTO cut lithium inventory by ~80% but preserved 500 full-cell cycles, underscoring that power-energy trade-offs can be tuned even without precise layering.
In 2018, Su et al. [6] encapsulated each Si particle inside a 4–5 nm pyrolytic-carbon shell and an outer rGO skin, curbing ~300% volume expansion and sustaining >2000 mAh/g for 200 cycles, though the initial coulombic efficiency remained <80%. To achieve greater control over the electrode architecture, Wang et al. [7] adopted electrostatic layer-by-layer self-assembly, sequentially depositing conductive carbon and Li-intercalating oxide nano-bilayers. The resulting electrodes showed a 28% lower charge-transfer resistance than the slurry-cast controls, confirming that ordered stacks can outperform mixed slurries when interfacial coherence is critical.
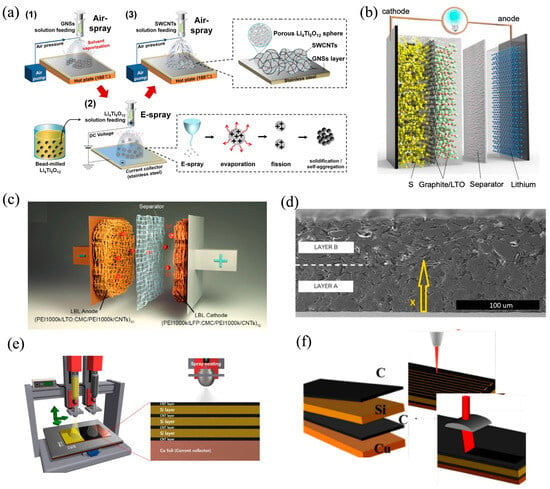
Figure 1.
Representative multilayer electrode architectures explored in recent studies including (a) nano-LTO aggregates confined between graphene and SWCNT networks [16]; (b) a hybrid lithium-sulfur battery where a sulfur-rich electrode (90 wt% S-10 wt% Super P) is covered by graphite and LTO layers [4]; (c) a full lithium-ion cell integrating multilayered anode and cathode architectures self-assembled via electrostatic interactions within a 3D porous melamine foam substrate [6]; (d) a multilayer anode with vertically graded porosity dense near the current collector and open near the separator developed by EnPower Inc. (Indianapolis, IN, USA) [21]; (e) a multilayer Si/CNT anode fabricated via ultrasonic spray-coating with alternating conductive and active layers [22]; and (f) a graphite/Si-rich multilayer anode featuring femtosecond-laser-engraved micro-channels to enhance electrolyte access and cycling stability [23]. Note: Panels (a–f) are reproduced from Refs. [4,6,16,21,22,23], respectively, and are distributed under the Creative Commons Attribution (CC BY 4.0) license (https://creativecommons.org/licenses/by/4.0/, accessed on 24 August 2025).
In 2023, Hamedi et al. [21] implemented graded porosity vertically, dense near the current collector and open near the separator, to enable 5 C charging without Li plating, a design commercialized by EnPower Inc., which retained a >80% capacity after 500 cycles. Complementary laser-printed laminates from Gottschalk et al. [24] exposed the danger of under-engineered binders; the graphite/Si (12 wt%)/graphite stacks failed prematurely when PVDF could not absorb the Si swelling. At the same time, Gottschalk mapped how Si content and particle size governed the calendaring response, providing a quantifiable window for multilayer thickness optimization.
Ko et al. [22] alternated three Si sheets with CNT networks via ultrasonic spray-coating; the laminated cell retained 157.6 mAh/g after 500 cycles at 2 A/g while reducing the charge-transfer resistance and boosting the Li+ diffusion coefficient to 1.19 × 10−13 cm2/s, but the MWCNT cost still clouds industrial feasibility. Finally, Yuan et al. [23] demonstrated graphite/Si-rich composite graphite sandwiches whose top layer was micro-channeled with a femtosecond laser. After 300 cycles, this cell was still 1350 mAh/g, 40% above a nano-Si benchmark, supporting the dual strategy of graphite-buffered SEI formation and inner-Si high capacity.
Recent studies have traced a progression from early carbon-buffer concepts to porosity-graded and micro-machined stacks. Three principles recur: an outer carbon layer that stabilizes the SEI; a high-capacity inner layer shielded from direct electrolyte contact; and mechanical/porosity gradients that tolerate fast-charge stress. The simulation framework developed in this work adopted that same approach by placing a pure graphite surface layer over a second layer (either pure or composite) next to the current collector to leverage the high capacity or stability offered by the second-layer material.
Additionally, three specific gaps remain that hinder the systematic design of multilayer anodes. First, prior studies have rarely compared candidate inner layers under identical cathode, electrolyte, geometry, and operating conditions. As a result, material rankings and trade-offs are often confounded by inconsistent test protocols. Second, most models do not couple SEI formation to transport within a single framework that predicts the retained capacity, SEI thickness growth, electrolyte consumption, and impedance evolution over extended cycling. Third, despite innovative demonstrations of multilayer stacks, clear design rules indicating when a graphite interlayer enhances or impairs performance remain elusive. To address these gaps, this work introduces a unified multiphysics framework for graphite-buffered bilayer anodes that isolates the role of the outer graphite layer and enables systematic screening of the inner materials (silicon, hard carbon, lithium titanate, and metallic lithium) as well as their graphite-based composites, under consistent baseline conditions.
The model couples ion transport, charge balance, porous-electrode kinetics, and SEI growth using experimentally validated parameters, together with a calibrated time-compression approach to assess long-horizon behavior; it generates quantitative projections of retained capacity, SEI thickness, resistance growth, electrolyte consumption, and impedance spectra over 2000-cycle horizons. From these controlled comparisons, several design rules have emerged. (i) The graphite interlayer confines SEI formation to the outer surface and mitigates electrolyte loss. (ii) The inner layer dictates the trade-off between energy and stability. (iii) Thickness and porosity allocations determine the rate capability. (iv) Metallic lithium and silicon maximize energy but incur the steepest penalties in stability and impedance, which restricts their practical use to narrow operating regimes. These contributions transform a diverse set of case studies into a coherent, predictive framework for engineering next-generation anodes that increase the energy density without sacrificing durability or safety.
2. Methodology
The long-term performance of lithium-ion anodes depends critically on both the active-material composition and the interfacial reactions that occur during cycling. The initial hypothesis suggests that adding an outer carbonaceous layer in direct contact with the electrolyte will act as both a mechanical and electrochemical buffer, protecting the inner composite or alternative material layer [6,16,17,23]. As a result, graphite was adopted as the baseline outer carbon layer because its parasitic reactions with carbonate electrolytes are well-characterized and comparatively limited [25]. Additionally, it delivers chemically stable operation over a broad particle-size and porosity window and forms a reproducible, passivating SEI, which simplifies parameterization and reinforces its practical role as a buffer layer [26,27,28].
To probe these effects, five multilayer anode configurations were simulated in COMSOL Multiphysics using an NMC cathode [29], LiPF6 in EC:EMC (3:7) liquid electrolyte [30], copper and aluminum current collectors [31], at room temperature and a 1 C charge rate, over 2000 cycles (Figure 2). Additionally, a graphite particle diameter of 2.5 µm [24,32,33] and an equal layer ratio (50:50) were represented as two 30 µm-thick layers [34]. Particle sizes for the other materials were chosen according to the bibliographic recommendations (hard carbon: 2.5 µm [35,36]; lithium titanate (LTO): 0.2 µm [37]; metallic lithium: 0.5 µm [38,39]; and silicon: 0.1 µm) to ensure realistic diffusion and interfacial behavior in each layer [40,41].
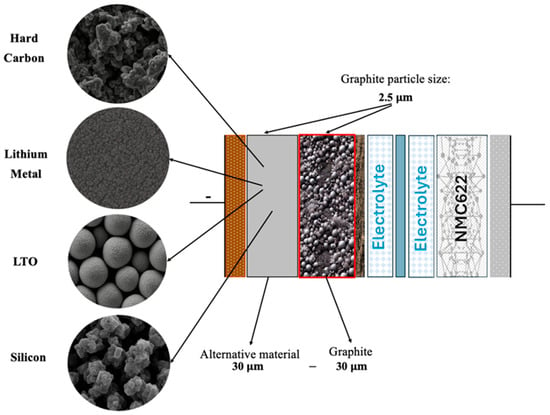
Figure 2.
Schematic representation of the simulated battery showing the layer thicknesses, graphite particle sizes, and the alternative materials considered for the second layer.
For lithium metal, sub-micron spherical domains (0.5 µm) were modeled within the inner layer rather than a free-standing foil. This choice maintained geometric consistency across all inner-layer materials, matched the spherical-diffusion formulation (Baker–Verbrugge) with the Butler–Volmer kinetics and charge/mass conservation, and ensured numerical stability and realistic interfacial areas for like-for-like comparisons.
Once these parameters were determined, the graphite–Si composite was replaced by three active phases: hard carbon (H), lithium titanate (LTO), and lithium metal (ML). Each phase was tested in its pure form (100%) and as 10/20/30 wt% composites with graphite (Figure 2). In the bilayer architecture, only the outer graphite layer is in direct contact with the electrolyte; the inner layer contributes capacity and transport without additional electrolyte exposure, which is essential for isolating the buffer effect of graphite in the simulations.
The identical 2000-cycle protocol yielded directly comparable electrochemical and impedance metrics. Upon the completion of all simulation runs (including twelve additional cases for hard carbon, LTO, and lithium-metal composites), the three highest-performing configurations were identified, together with the top silicon configuration from Phase I and the 100% graphite reference. For each of these five cells, the same response metrics were compared: SEI overpotential drop (mV), capacity fade (%), SEI thickness (µm), and electrolyte consumption (%).
Electrochemical impedance spectroscopy (EIS) was performed in COMSOL. Nyquist plots (−Z″ vs. Z′) isolated the electrolyte/contact resistance (Rs) at high frequency and combined SEI plus charge-transfer resistance (RSEI + Rct) in the mid-frequency semicircles, while Bode plots of Z′ vs. frequency showed the shift from electrolyte-dominated to diffusion-limited regimes at low frequency. Plots of −Z″ vs. frequency separated capacitive from diffusive phenomena; a mid-frequency peak indicated double-layer/SEI capacitance, and the characteristic −45° slope at low frequency confirmed Warburg-type diffusion [42]. Extracted Rct, RSEI, and the Warburg coefficient revealed which laminate best balanced the kinetics, mechanical resilience, and long-term capacity retention.
Conclusions were drawn from the configurations that exhibited the most favorable results and were compared with reported composites/multilayers and where appropriate with commercial cells, supporting the hypothesis of a protective graphite buffer for integrating high-capacity phases without sacrificing stability.
3. Mathematical Model
The five cells share a single coupled system comprising spherical diffusion, charge conservation, and ionic transport. Table 1 compactly lists the full algebraic form; the text below explains how each block operates and why it matters for contrasts between architectures [43].

Table 1.
Governing equations for electrochemical transport, charge balance, and SEI formation.
Modeling begins with Bruggeman’s effective conductivity law, which reduces the liquid electrolyte’s intrinsic ionic conductivity by a layer-specific porosity–tortuosity factor. This apparently modest adjustment already pulls the designs apart: dense hard carbon throttles Li+ flow, whereas the Li metal composite provides highly conductive electronic pathways and modifies porosity, allowing Li+ to access the back of the electrode more efficiently.
Within the active particles, lithium transport obeys the Baker–Verbrugge spherical-diffusion equation in both the front-layer graphite and the back-layer material. Its radial term captures the nonlinear filling of nano-silicon while preserving the near-constant behavior of graphite and LTO. Coupled to the global Li balance, it determines how fast the graphite face saturates and how fully the backing layer participates during discharge [44,45].
At each particle surface, boundary conditions knit diffusion to surface kinetics: the Butler–Volmer law translates local overpotential into interfacial current density, and the stoichiometry-dependent exchange current scales that kinetics with both solid lithiation and surrounding Li+ concentration. Together they explain, for instance, why the Si layer reacts briskly at low state-of-charge (ample vacant sites) and self-moderates as it nears saturation.
All numerical values used in the SEI side-reaction and film-resistance model were taken from the COMSOL Battery Design Module documentation and the associated “Capacity Fade of a Lithium-Ion Battery” application example. In that example, the SEI kinetics follow the framework of Ekström and Lindbergh, which models diffusion-limited growth through an evolving SEI and incorporates crack-accelerated aging due to graphite expansion. The lumped parameters are pre-calibrated in the COMSOL example against cycling and calendar-aging data for a graphite/LFP cell at 45 °C. This study adopted those documented values and the module’s standard couplings without further modification, thereby isolating the architectural effects on capacity fade. The contribution lies in leveraging this established submodel as a validated foundation for architecture-driven predictive screening of graphite-buffered bilayer anodes, enabling the evidence-based selection of inner-layer materials and thicknesses prior to experimental fabrication [43,46].
At the electrode scale, charge conservation in the solid phase forces electrons drawn by the copper current-collector to redistribute according to microstructure. In the Li metal/graphite cell, the conductivity jump between layers diverts part of the electronic load directly into the Li sheet, relieving Ohmic drop in the front layer. An analogous balance in the electrolyte built on the migration–diffusion relation without convection ensures that the Li+ flux mirrors the electronic current, preserving electroneutrality [47].
External boundary conditions close the system: a zero-potential reference on the copper collector, a uniform galvanostatic draw at the aluminum collector, and electrically insulating lateral edges that collapse the geometry to one dimension through the stack thickness. This simplification halves the mesh size without sacrificing fidelity for the pouch-style layout.
Auxiliary variables, vacant-site fraction, and normalized state of charge update algebraically after every time step and are exported as global probes. The equations in the table remain unchanged while the conductivities, porosities, particle radii, and equilibrium potentials shift. The result is a unified framework that compares, with identical numerical rigor, how hard carbon curbs diffusive polarization, how LTO dampens current spikes, how Li metal cuts internal electronic resistance, and how silicon supplies extra capacity at the cost of higher mechanical stress.
Table 1 summarizes the physical basis of each equation block including the spherical diffusion, surface kinetics, charge and mass balances, and boundary conditions. Together, these relations form a coherent framework for the electrochemical dynamics of the five anode designs studied.
While the previous section focused on transport, charge balance, and the kinetics that move lithium into the active particles, this second branch concentrates on the solid-electrolyte interphase (SEI) and on the distinct charge-storage reactions that differentiate each bilayer architecture from the graphite baseline.
Equation (12) represents the SEI kinetic expression, modeling diffusion-limited growth through an evolving film and incorporating crack-accelerated aging under particle expansion. As summarized in Table 1, three material-sensitive parameters vary with the inner layer: (i) the expansion factor capturing stress-induced rate amplification; (ii) the exchange current density J for the solvent-reduction pathway; and (iii) a lumped film constant representing SEI porosity and ionic leakage. Within the rate expression, the SEI overpotential provides the electrochemical driving force, while , J, and act as mechanical, kinetic, and transport coefficients that scale the reaction rate, mapping local conditions to a parasitic reduction current that competes with intercalation or alloying. is negligible for the hard carbon and LTO back layers, increases modestly in the Li-metal composite, and rises sharply once the Si fraction exceeds ~10%, consistent with the large volume change of nano-Si [48].
Electrolyte additives, such as vinylene carbonate (VC) or fluoroethylene carbonate (FEC), are widely used to stabilize the SEI. Recent studies have shown that small amounts of these additives reduce the SEI thickness and improve the retained capacity in cells with graphite and with silicon [49]. Within the model, these improvements could be reflected as a reduction in the parasitic current , a smaller initial thickness , and a higher film conductivity , the trends described later in Section 4 toward thinner SEI layers and smaller potential drops without changing the relative ranking of the configurations.
In addition, the repeated expansion and contraction of Si induced mechanical stresses that fractured the SEI and exposed reactive areas. The literature indicates that Si can expand up to 300%, generating stresses that cause cracking, loss of electrical contact, and recurrent destruction of the SEI [50]. This process accelerates lithium and electrolyte consumption. In the bilayer anodes, the graphite layer acts as a mechanical buffer, reducing stresses on the outer surface. However, the factor increases with the Si fraction, which explains the higher overpotential discussed later in Section 4. A detailed thermo-mechanical study will be conducted when more experimental data from the constructed prototypes become available including heat generation and crack propagation measurements. Current trends suggest that the incorporation of electrolyte additives, such as vinylene carbonate (VC) and fluoroethylene carbonate (FEC), along with the selection of low-expansion materials (e.g., lithium titanate oxide or hard carbon), could significantly enhance the stability of bilayer anodes.
Because the anode can host more than one active phase, Equation (13) builds the total parasitic current as a simple volumetric blend of graphite-only and composites. This linear superposition is numerically inexpensive but captures the experimentally observed trend: adding even 20% Si pulls a disproportionate fraction of the SEI-forming current away from graphite during early cycles.
Once the parasitic current is known, Equation (14) integrates it into SEI concentration in mol/m3 using the appropriate stoichiometry and electron count. A direct algebraic map (Equation (15)) then converts that concentration into film thickness; the initial thickness comes from the formation-cycle data, while the molar mass and density follow the literature values for a mixed Li2CO3/Li-alkyl-carbonate layer. Finally, Equation (16) translates the thickness into film resistance , which appears in the Butler–Volmer overpotential of each active particle, closing the electrochemical feedback loop: the thicker the SEI, the larger the Ohmic drop and the smaller the useful current.
To accelerate aging sweeps without running thousands of real-time cycles, every SEI reaction was multiplied by a time-compression factor . This heuristic, validated against long-term calendar-life tests, collapses 250 physical cycles into one simulated cycle while preserving the asymptotic growth trend of both and .
A time-acceleration factor was applied to the SEI-formation reactions, consistent with the time-compression approach demonstrated in COMSOL’s Battery Design Module [43,48,51]. Under this assumption, each simulated charge–discharge cycle represents the average effect of approximately 250 real cycles, which expedites the emergence of degradation within practical compute times. The factor is used solely as an exploratory device to enable relative comparisons across anode architectures under identical accelerated-aging conditions. No claim is made that provides an exact mapping to physical cycles or an absolute lifetime prediction.
Beyond the SEI, each architecture is defined by the primary charge-storage reaction operative in its second layer. Graphite intercalation is common to all; hard carbon stores Li+ in nanopores at slightly lower potential; LTO undergoes its symmetrical zero-strain redox; Li metal plates and strips at a nearly flat potential; and Si alloys up to Li4.4Si, delivering the highest capacity but also the strongest stress–SEI coupling. These reactions, together with the most prevalent solvent-reduction and impurity pathways, are summarized in Table 2; only the charge-storage reactions are activated in the finite-element solve.

Table 2.
Summary of electrochemical reactions.
By chaining Equations (12)–(16) to the transport block, the model reproduces the intertwined phenomena that govern real pouch cells: capacity fade via SEI thickening, impedance rise via film resistance, and the shifting share of current between graphite and the alternative back-layer. In turn, this integrated framework explains why the hard carbon variant best restrains SEI growth under low-rate cycling, why the Li metal composite minimizes electronic drop but suffers early electrolyte starvation, why the LTO blend remains voltage-stable but capacity-limited, and why the Si-rich layer offers surge capacity at the expense of rapid initial aging.
4. Results and Discussion
The study ran sixteen simulations, varying the second layer across the pure materials (100%) and 10/20/30 wt% graphite composites (Figure 3). This approach aimed to evaluate four key response variables: capacity fade (%), SEI layer thickness (µm), potential drop over the SEI layer (mV), and electrolyte consumed (%).
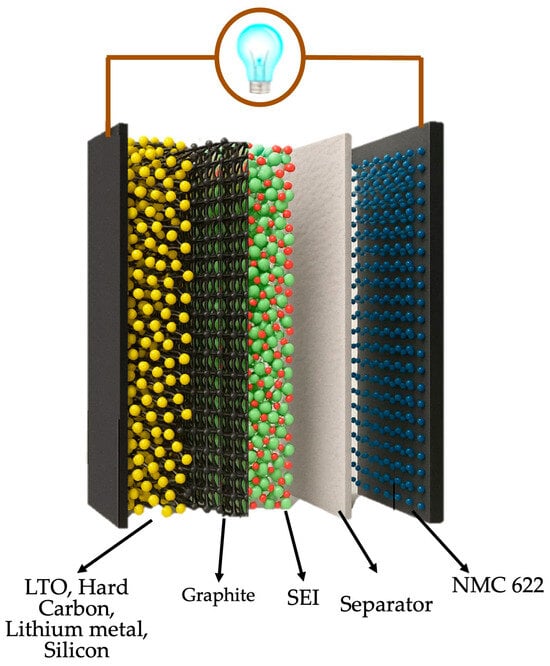
Figure 3.
3D schematic of a Li-ion battery with bilayer anode architecture and NMC622 cathode.
The four configurations that exhibited the most favorable or boundary values were selected for further analysis and are reported in Table 3. These boundary values were defined based on a reference point using pure graphite and data reported in the literature. For example, the maximum acceptable capacity fade was set at 20% after 2000 cycles, a value consistently reported as a typical upper limit in previous studies [52,53].

Table 3.
Simulation results by battery configuration using multiple materials.
Because the simulations used accelerated SEI aging, the reported values for retained capacity, SEI thickness, and SEI overpotential are comparative. These rank the architectures by relative resistance to SEI growth and capacity fade and are not intended to predict an exact number of physical cycles.
All response variables were weighted equally when determining the optimal configurations. This selection enabled a direct comparison between the best-performing simulations and the graphite-based reference, providing a robust evaluation framework for material performance in multilayer anode architectures.
Figure 4a summarizes four key metrics. The dotted blue line for the graphite anode showed a steady decline in retained capacity with cycling. Although the initial capacity was high, each cycle irreversibly consumed a small fraction of lithium through SEI formation, which reduced the usable capacity. After 2000 cycles, the retained capacity was ~94%. Introducing 20% silicon in the bilayer design increased the initial capacity while keeping the capacity fade within the ≤20% threshold defined in this work. The bilayer Si/graphite anode retained around 83% of its capacity after 2000 cycles. This retention contrasts with the pure-Si rear layer, which showed severe fading (≈83% fade, Table 3). The improved durability arises because the outer graphite layer localizes most SEI formation, while the inner silicon stores additional Li without direct electrolyte exposure, mitigating deep lithiation stress. In conventional mixed-blend graphite-Si electrodes, the SEI can propagate uncontrollably over silicon surfaces, hastening failure, a problem avoided in this bilayer architecture [54].
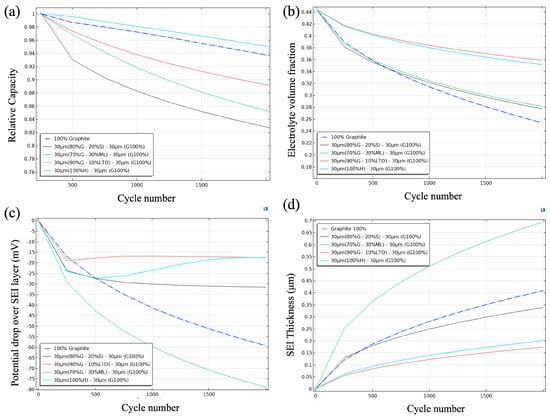
Figure 4.
Comparative evolution of capacity (a), electrolyte volume fraction (b), potential drop over the SEI (c), and SEI thickness (d) in four different bilayer anode configurations.
With hard carbon as the inner layer, the retained capacity reached ~95%. Hard carbon operates at a higher potential than graphite and forms a porous SEI that quickly saturates, which suppresses further solvent reduction and deep graphite lithiation. After the first-cycle loss, once the micropores were passivated, the capacity fade remained modest over hundreds of cycles [55].
The Li metal/graphite hybrid showed a steeper decline, retaining ~85% after 2000 cycles. Published hybrid cells often fade rapidly when plated lithium becomes electrically isolated as ‘dead Li’, with the usable capacity dropping below 80% in fewer than 15 cycles [56]. The simulation reproduced this failure mode when the Li metal fraction exceeded 30 wt% or in single-layer Li metal cases, where the detachment of plated Li reduced the contact area. At 30 wt% Li metal, the higher initial capacity offset early losses, and with the graphite buffer, kept the simulated retained capacity above 80% at 2000 cycles. This outcome is an upper-bound screening result. Practical applicability in liquid-electrolyte Li-ion cells remains limited and requires experimental validation with robust protective interphases or solid-electrolyte architectures.
Adding 10% LTO improved structural stability but slightly reduced the retained capacity. Although LTO’s zero-strain framework formed virtually no SEI, replacing 10 wt% graphite (372 mAh/g) with lower-capacity LTO (175 mAh/g) reduced reversible Li-host sites. Continuous SEI growth on the remaining graphite therefore consumed a comparable absolute lithium amount, which appeared as a steeper relative fade after normalization by the smaller initial capacity. Jung et al. [57] also reported a lithium-shuttle loss during open-circuit rests—from ~0.1 V graphite to 1.55 V LTO, which explains ~5% extra fade after 1000 cycles compared with graphite alone.
All five curves in Figure 4b started from the same electrolyte volume fraction (0.44 at cycle 1) and diverged by cycle 2000. Because only the outer 30 µm graphite layer was in direct contact with the liquid electrolyte, differences arose from how the inner layer modified solvent consumption at the graphite surface. In the reference cell, the anode surface reduced LiPF6 continuously; carbonate fragments diffused through a progressively porous SEI and converted to Li2CO3/LiF, so the fraction declined almost linearly to ~0.25, consistent with commercial graphite electrodes [58].
Substituting the inner half of the anode with hard carbon reduced the charge that the graphite must host at extreme low potentials; the outer layer therefore remained slightly less lithiated, generated fewer radicals, and once the highly porous hard carbon matrix was passivated, the solvent attack slowed, leveling off near ≈0.35. With LTO, a slightly better preservation was achieved ≈0.36. LTO intercalates Li well above the carbonate reduction window, so that fraction of the anode never forms a classical SEI; in addition, its zero-strain lattice dampens stress in the overlying graphite, limiting crack-induced SEI renewal.
The Li metal/graphite composite ended near 0.28, even though metallic Li is extremely reactive. The key is chronology: during formation, the sacrificial Li donates electrons that rapidly convert a portion of the solvent into a dense, LiF-rich SEI; once that compact layer is complete, solvent transport is kinetically hindered, and the slope flattens. Because only 30 µm of graphite remained exposed, half the area of the 60 µm reference, the ongoing consumption rate was lower than in the neat-graphite electrode, so the green trace ultimately sat above the blue one, despite the violent early reaction. This outcome is consistent with the bilayer strategy, since previous studies such as that developed by Zhang et al. [59] reported that the utilization of the lithium reserve falls to values below the typical 65% with similar solvents such as EC:DMC.
In the 20% Si/graphite configuration, the electrolyte volume fraction remained above the 60 µm graphite baseline near 0.25. Two concurrent mechanisms explain this behavior. First, halving the graphite thickness halves the area that can keep reducing solvent; the absolute amount of solvent consumed each cycle therefore drops, even if the rate per unit area remains unchanged. Second, ≈15% of the charge now enters the Si phase, so the graphite operates at a slightly higher average potential and generates fewer solvent-reduction radicals.
More electrolyte decomposition does not necessarily lead to a thicker SEI on graphite. Even though the bilayer cells with hard carbon or LTO consume less solvent, SEI growth on graphite is self-limiting once a passivating film forms, and further deposition is suppressed [60]. In situ spectroscopy and XPS analyses show that porous SEI contains trapped solvent and LiPF6 and that many decomposition products remain soluble [61]; therefore, some consumed electrolyte does not contribute to the solid film. Finally, the native SEI undergoes dynamic dissolution and re-formation during cycling, meaning that electrolyte consumption includes film regeneration rather than net growth [62]. These factors explain why the hard carbon/graphite bilayer consumes less electrolyte while producing an SEI thickness comparable to that of neat graphite.
Figure 4c (potential drop across the SEI) and Figure 4d (final SEI thickness) illustrate how each bilayer anode modified the response of the outer graphite, even though the underlying kinetic expression was identical for all. The parasitic-current equation (Equation (12)) includes three parameters that here varied with the second layer: the expansion factor Hk, which amplifies the reaction rate when the graphite expands or cracks; the exchange current density J, which measures how fast the electrolyte is reduced at the surface; and the transfer coefficient α, which determines the sensitivity of that reduction to the overpotential.
With these adjustments, each architecture generated an SEI of different thickness and resistivity. For example, for the 60 µm graphite layer, solid graphite exhibited moderate expansion and a constant J; its SEI grew quasi-linearly up to ~0.40 µm and ~60 mV after 2000 cycles. For the Li metal/graphite, at the beginning, the sacrificial Li triggered a very high J and rapidly formed a dense LiF/Li2O whose thickness exceeded 0.7 µm, with an ~80 mV polarization drop across the SEI. For hard carbon/graphite, the porous hard carbon absorbed part of the expansion, reducing Hk, and diverted a fraction of the current to slightly higher potentials. J and α remained in a middle range; the SEI stabilized around 0.20 µm. The resulting resistance was low, hence the second-smallest polarization ~17 mV observed.
The LTO did not expand but the parasitic current was not eliminated; the graphite continued to operate very close to 0 V, so J was maintained and with a relatively high α, yielding a thin film of ~0.18 µm. However, its resistivity did not dominate; the polarization drop was ~18 mV. Finally, in the configuration containing 20% Si/graphite, the internal Si expanded ~300%, raising Hk and cyclically cracking the graphite SEI. Even so, the time that the graphite spent in the most reducing regime was reduced, the film reached ~0.40 µm, and the polarization settled at ~32 mV, an intermediate between hard carbon and solid graphite. This demonstrates that the strategy of using a graphite buffer improves the behavior of silicon.
The multilayer anode (30 µm 90% G + 10% LTO/30 µm graphite) exhibited a discharge profile ≈ 100–120 mV lower than the 60 µm graphite reference throughout the 1600–2600 s interval (Figure 5a). The offset originated from the intrinsic electrochemical potentials of the two active hosts. The layered NMC622 cathode remained near 4.2 V vs. Li/Li+ at full charge, while fully lithiated graphite lay at ≈0.10 V vs. Li/Li+. LTO, in contrast, intercalated Li+ at 1.55 V vs. Li/Li+, roughly 1.4 V higher than graphite. Incorporating only 10 wt% LTO into the outer layer therefore raised the mass-weighted average anode potential to ≈0.20–0.25 V. Because the cell voltage is simply V = Vcathode − Vanode, this ~0.10–0.15 V increase in anode potential subtracts the same amount from the cell output, explaining the vertical gap observed in the mid-SOC plateau.
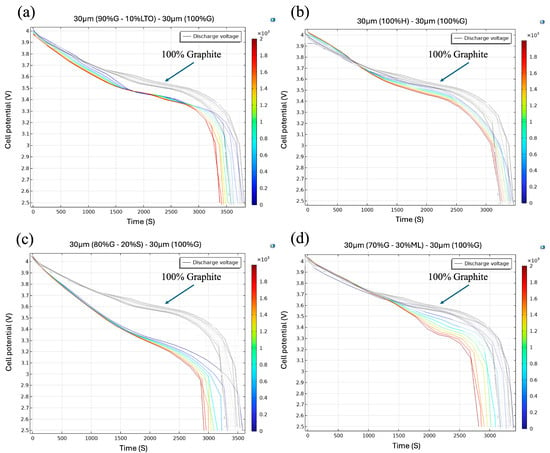
Figure 5.
Cell potential evolution during discharge for (a) 30 µm (90%G–10%LTO) − 30 µm (100%G), (b) 30 µm (100% H) + 30 µm (100% G), (c) 30 µm (80%G–20%S) − 30 µm (100%G), and (d) 30 µm (70%G–30%ML) − 30 µm (100%G).
Independent three-electrode tests and physics-based simulations confirmed that even ≤10 wt% LTO was sufficient to lift the anode potential and shorten the constant-current plateau by 80–150 mV at comparable rates [63]. The charge that pristine graphite would deliver below about 3.45 V (full-cell voltage) is now supplied by the LTO sub-phase at its higher equilibrium potential; the cell therefore enters the 3.40 V region sooner and maintains the 100–120 mV separation between the two voltage families throughout the 1500–3000 s window.
Beyond 2600 s, a second trend emerged: the hybrid-anode curves fell more steeply than those of pure graphite. Once most of the graphite staging transitions were complete, the small LTO fraction became the kinetic bottleneck, its lower lithium diffusivity and larger activation overpotential increased the electrode polarization so the voltage dropped faster, and the cycle-to-cycle spread widened. In short, the hybrid design traded a modest slice of energy density during the 1600–2600 s segment for greater mechanical stability and presented an additional polarization once the LTO phase governed the rate.
Figure 5b demonstrates that the multilayer anode with hard carbon provided a complementary Li storage mechanism to graphite. In the voltage window of 3.7–3.0 V (≈1000–3000 s), the hard carbon/graphite bilayer exhibited a discharge profile consistently ~50–80 mV lower than the 60 µm graphite benchmark. This offset is because hard carbon stores Li+ over a broad sloping region that begins near 0.2–0.5 V vs. Li/Li+. Substituting 50 wt% of the active layer with hard carbon therefore raises the mass-weighted anode potential by ≈0.10 V, reproducing the slight offset observed in Figure 5b. Farhan et al. [64] showed similar results, where mixed graphite/hard carbon anodes raised the average anode potential relative to pure graphite, which in turn lowered the mid-SOC cell voltage. This suggests that the hybrid anode potential is ~60–80 mV higher than that of pure graphite at 0.5 C, which translates into an equivalent drop in cell voltage.
Both graphite and hard carbon are forms of carbon and thus have relatively small volume changes on cycling, graphite ~10% expansion, and hard carbon often <5%. Unlike silicon or metallic lithium additions, hard carbon does not introduce acute expansion stress or massive SEI formation beyond the initial cycles. The primary degradation mechanism is gradual SEI growth on the large surface area of hard carbon pores, which can slowly increase the internal resistance; however, in the bilayer configuration, the graphite buffer limits this effect. In fact, some studies have shown composite hard carbon/graphite anodes to be highly stable over long cycling, with minimal capacity fade per cycle [65]. Consequently, their discharge voltage curves stay tightly clustered with cycling, and expansion of the curves is minor. Indeed, the voltage profiles evolve only slightly with a small increase in polarization, because neither component suffers severe active material loss.
The hard carbon’s sloping voltage contribution can even help maintain cell voltage in later cycles: as the graphite capacity fades a bit, the hard carbon can still uptake/discharge lithium over a broad potential range, sustaining the cell’s voltage output. Thus, divergence in the discharge curves tends to begin late in the discharge, often near the end of discharge around ~3.0 V and remains minimal. The combination of robust graphite and resilient hard carbon yields an anode with high retained capacity with limited impedance growth, explaining why its voltage profiles change very little, even after extensive cycling.
In Figure 5c, the Si/graphite bilayer discharged ~150–200 mV below the 60 µm graphite reference from the very start of the run ≈ 0–2500 s. This downward offset is expected, because the Si domains begin alloying at ~0.40 V vs. Li/Li+, significantly higher than the 0.10 V plateau of graphite. The graphite “buffer” layer keeps the silicon physically isolated from the electrolyte during the first half of the discharge, so the cell retains the smooth, single-phase slope typical of graphite; in full-Si or silicon/graphite blended electrodes that face the electrolyte directly, a voltage dip and large impedance rise usually appear within the first few cycles [66].
In the Si-rich multilayer, the Li-induced volumetric expansion slows down solid-state diffusion and increases reaction overpotential. Multiphysics models of Si/graphite composites show that simply adding diffusion-induced stress to the reaction kinetics reproduces the sharp rise in polarization that occurs once silicon carries most of the current, without invoking particle cracking or extra SEI growth [51,67]. The graphite buffer delays this kinetic bottleneck, hence the stable segment up to 2500 s, but cannot prevent it once the Si capacity becomes dominant.
Since the Si plateau is at a higher anode potential, the cell offers greater capacity per unit cell voltage drop below 3.3 V in the 2000 s (useful for applications that prioritize gravimetric energy over nominal voltage), but the faster polarization growth means it will reach its cut-off voltage sooner at high current rates. Whether that is advantageous depends on the duty cycle: for devices that exploit the extra Si capacity at modest C-rates such as portable electronics, the trade-off can be worthwhile, whereas for high-rate power tools, the earlier voltage could be a problem.
The configuration of Figure 5d with metallic lithium traced the 60 µm-graphite baseline up to 3.5 V (0–1300 s), confirming that the graphite buffer effectively shields the metallic-Li domains during the early part of discharge. Once the graphite in the upper layer is largely delithiated, Li stripping begins in the layer containing 30% Li-rich domains. Because metallic Li has virtually zero Li-diffusion resistance but a higher interfacial overpotential than graphite, the anode potential rises more steeply; the full-cell voltage therefore bends downward by an extra 120–150 mV, and the colored bundle widens between 3.5 V and 2.5 V.
Below 3.0 V, the curves maintained separation without notable drift, even after 2000 simulated cycles. This numerical stability can be attributed to two factors: the limited Li fraction (~30%) and the presence of graphite. Experimental studies on Li metal/graphite hybrid anodes indicate that maintaining the plated Li inventory below approximately 35% of the total capacity significantly enhances reversibility and mitigates short-circuit events. Cells with a 25–30% Li overlay retained 96% of their initial capacity after 120 cycles at 1 C, whereas full Li-foil anodes failed within 30 cycles [67]. A similar capacity-buffer concept was demonstrated by Martin et al. [56], where cycling Li on graphite delivered a 20% energy boost and >100 stable cycles without dendritic shorting.
The layer with 30% Li/70%G offered extra specific capacity with only a modest penalty in mid-SOC voltage. For applications that value gravimetric energy over constant-power output, for example, lightweight UAV packs, the trade-off could be advantageous, whereas high-rate tools might suffer from the earlier voltage sag [68].
Figure 6 compares the state of charge (SOC) evolution during the 2000th charge of five pouch cells that shared an identical cathode/electrolyte setup but differed in the architecture of a 60 µm anode. The blue trace represents the reference electrode, a monolithic 60 µm layer of graphite. Its curve showed the familiar profile of graphite with a rapid rise during the initial stage’s transitions, followed by a pronounced inflection after ≈500 s as the material approached full lithiation.
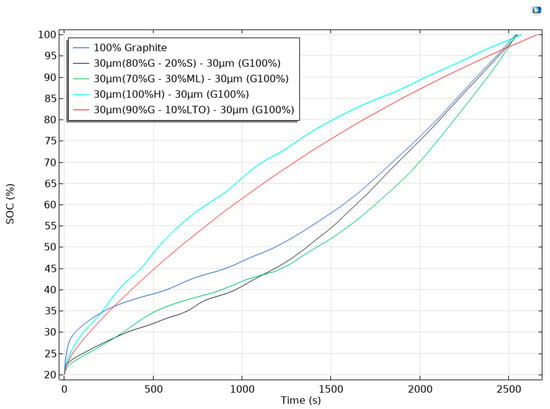
Figure 6.
Voltage profiles during charging for different anode configurations with multiple materials, simulated in a 3D pouch cell.
Introducing a bilayer design altered that behavior; when the rear 30 µm was replaced by hard carbon (cyan curve), the cell reached 50% SOC in barely 500 s, almost twice as fast as the reference. The disordered porosity of hard carbon accepts Li+ at higher potentials (~0.1–0.2 V) and with lower diffusion resistance, so the outer graphite never sinks into the Li-plating regime; the graphite therefore retains a larger active surface area, and the overall impedance remains low throughout the charge. A similar but slightly less pronounced acceleration was observed for the red curve, where 10% LTO was blended into the rear layer. LTO intercalates at 1.55 V and behaves as a kinetic buffer, taking up the initial current pulse, mitigating graphite polarization, and shortening the constant-voltage segment by roughly 15–20%. This behavior was evident in the turquoise trace (90% G + 10% LTO).
In contrast, replacing the rear layer with 20% Si (black) or 30% Li metal (green) delayed the rise in SOC. Silicon and plated lithium added substantial capacity, but their interfacial kinetics were slower under a 1 C rate: Si suffers from sluggish solid-state diffusion, whereas Li plating must overcome a nucleation overpotential. Consequently, both curves lagged until ≈1200 s, when the front graphite saturated and the current density across the rear layer dropped to a level that these materials could sustain. Once that threshold was crossed, the black and green traces steepened and all cells finally converged near full charge at ≈2600 s, indicating that the ultimate capacity is fixed by the total active mass while the anode architecture dictates how quickly that capacity can be accessed.
Overall, the plot showed that a thin graphite front coupled with a fast-kinetics rear layer (hard carbon or modest LTO) delivered the most balanced outcome: energy density of graphite, steeper SOC ascent, and mitigated Li-plating risk. Designs that instead prioritized extra capacity through Si or Li metal could match the final SOC but incurred an early-stage kinetic penalty that lengthened the charge time under identical current constraints. These observations underline the practical advantage of multilayer anodes that decouple kinetic buffering from capacity storage, offering a clear pathway toward faster and safer charging protocols without sacrificing gravimetric energy.
Figure 7a presents the Nyquist response of the five simulated pouch-cells and shows how the inner layer governs the overall electrochemical footprint once the outer 30 µm graphite buffer is fixed. The diameter of each semicircle diverges in proportion to the transport penalties introduced by the second layer.
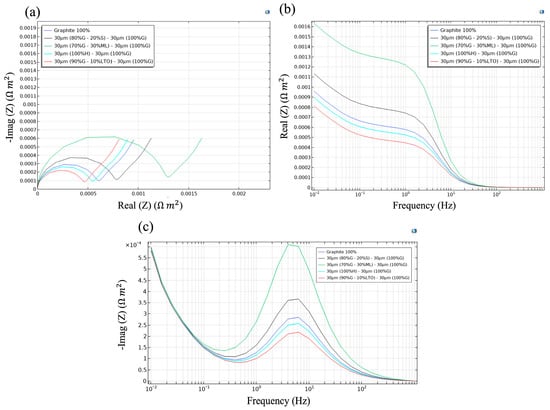
Figure 7.
Electrochemical impedance response of multilayer anodes with various material combinations: (a) Nyquist plot, (b) Bode magnitude plot, and (c) imaginary impedance vs. frequency.
The monolithic 60 µm graphite reference defines the baseline; inserting 20% Si behind the buffer (black trace) widens the arc because the lithiation of Si lowers the electronic conductivity and produces elastic mismatch at the silicon/graphite interface. However, this behavior is expected; an impedance study on cells with different contents of SiOx/graphite demonstrated that with >10 wt% SiOx, the progressive fracture of silicon particles and the continuous formation of SEI cause drastic increases in Rohm, RSEI, and Rct, correlated with rapid capacity degradation. Exceeding ~5–10% Si leads to an accelerated loss of cyclability, suggesting a practical threshold for Si content in order not to compromise the conductivity of the percolation network [69]. It is important to highlight that in this simulation and under this strategy, values up to 20 wt% of pure silicon were achieved.
Substituting a 30% Li metal domain (green) nearly doubled the diameter, a consequence of Li-ion starvation inside the plated layer that manifested as an additional Warburg component. Wang et al. [70] observed similar trends in Li metal/graphite hybrid anodes: the accumulation of dendritic Li deposits rapidly increases impedance and consumes active lithium, accelerating capacity fade unless a robust artificial SEI is implemented through coating strategies and careful electrolyte selection. In contrast, a 100% hard carbon backing increases resistance only marginally; anodes with hard carbon as the inner layer tend to behave more similarly to graphite in terms of resistance as they do not undergo abrupt phase transitions during Li+ insertion, resulting in a more gradual change in charge-transfer resistance [71].
With 10% LTO, the composite narrowed the arc, leveraging LTO’s zero-strain lithiation and three-dimensional Li-ion pathways to preserve electronic percolation across the laminate. Lee et al. [72] reported that spherical graphite coated with LTO showed better fast-charging capacity and longer cycle life at 25 °C and 55 °C compared with uncoated graphite, mainly because the LTO coating helped maintain low surface resistance during cycling. Zhao et al. [73] presented an expanded graphite/LTO composite with a retained capacity rate of 98.4%, even higher than that of hard carbons tested under the same conditions, which was attributed to the rapid Li+ diffusion facilitated by the porosity of the expanded graphite/LTO structure, reducing the interfacial resistance. In summary, an electrochemically benign inner layer such as LTO minimizes the generation of additional resistance during fast charge/discharge, overcoming the kinetic limitations of conventional graphite.
In Figure 7b, the differences between configurations became more evident at low frequencies, where each trace reflected the total system resistance, consistent with the arcs observed in the Nyquist plot. The Li metal laminate maintained the highest resistance across this band, indicating that ionic access to the plated domain is restricted to slow leakage through the outer graphite. The graphite-Si laminate exhibited a slightly higher impedance than the baseline, but it was moderate, and because slower ionic diffusion in the lithiated Si phase and minor electronic network discontinuities slow down internal charge transfer. Hard carbon was below the single-graphite baseline because its additional micro-porosity partially compensates for its poorer electronic conductivity, whereas the LTO-containing electrode persistently exhibited the lowest resistive, consistent with rapid transport within the structure.
Figure 7c shows the imaginary part of the impedance (-Imag(Z)) as a function of frequency, providing insight into the dominant electrochemical time constants of each configuration. Unlike the Nyquist plot (Figure 7a), which focuses on the resistive and capacitive behavior in the complex plane, or the real part of the impedance in Figure 7b, this representation highlights the frequency at which the system stores the most energy before dissipating it. This is particularly useful for identifying how internal diffusion and interfacial kinetics affect the relaxation dynamics of each multilayer design.
All configurations displayed a main peak around 10 Hz, although with different magnitudes. The lithium-metal architecture (green line) reached the highest peak, indicating greater charge accumulation and slower relaxation. The inclusion of 20% silicon (black line) also raised the peak height above the graphite reference, reflecting limited solid-state diffusivity and internal electronic bottlenecks. In contrast, the hard carbon laminate and the monolithic graphite (red and blue lines) clustered near the same frequency, with only a modest increase in peak height for hard carbon. The LTO-containing cell showed the lowest peak, consistent with its fast ionic transport and stable internal structure that maintains an unperturbed interfacial response.
The five impedance projections indicated a clear hierarchy. Because SEI growth is confined to the outer graphite layer, interfacial side reactions decouple from the high-capacity inner phases. Performance is driven by electronic percolation and Li-ion diffusivity rather than extra SEI resistance. Materials with low strain and fast transport (LTO, hard carbon) matched or surpassed monolithic graphite, while Si and Li metal added resistive penalties despite extra capacity. This section highlights a practical design rule: pair the graphite buffer with an inner layer that is mechanically benign and intrinsically fast for Li transport to outperform graphite while preserving interface stability.
5. Conclusions and Perspectives
The optimization study of graphite-buffered bilayer anodes provides a quantitative ranking of inner-layer choices under a consistent 2000-cycle protocol. Replacing half of a 60 µm graphite anode with a 30 µm hard carbon inner layer (E1) delivered the best balance: 5.9% capacity fade, 0.20 µm SEI thickness, ~17.5 mV SEI overpotential, and 20.8% electrolyte consumption after 2000 cycles. The monolithic graphite control (E17) showed higher fade (7.1%), a thicker SEI (0.25 µm), a more negative overpotential (~59 mV), and greater electrolyte use (42.9%). These side-by-side metrics indicate that modest hard carbon loadings stabilize the graphite–electrolyte interface and outperform the monolithic baseline across stability indicators.
For stability-focused designs, a 10 wt% LTO inner layer (E8) trades some energy density for durability, with 11.0% capacity fade, a thin 0.17 µm SEI, the lowest electrolyte consumption (19.2%), and a more negative overpotential (~79 mV). Electrochemical-impedance trends (Nyquist/Bode) corroborated the ranking: LTO showed the lowest low-frequency resistance; hard carbon remained close to graphite; 20% Si enlarged the mid-frequency semicircle; and 30% Li metal added a large arc with a Warburg tail. A practical design rule emerged: pair the graphite buffer with an inner layer that is mechanically benign and intrinsically fast for Li transport (e.g., LTO or hard carbon) to preserve interface stability while matching or surpassing graphite.
High-energy options introduce penalties. The Si composite (E15) increased the initial capacity but raised the capacity fade to 18.4%, with a 0.34 µm SEI and a ~31.6 mV overpotential. The Li-metal composite (E13) retained 83.2% capacity (16.8% fade) but formed the thickest SEI (0.70 µm) and showed pronounced impedance growth. The graphite buffer enabled higher Si or Li-metal fractions than single-layer electrodes, but practical deployment will depend on the further mitigation of transport and interphase limitations.
Interpretation should consider the model scope. Simulations assumed isothermal operation at 25 °C, a fixed NMC622 cathode, and an EC/EMC electrolyte. Stresses from silicon expansion were treated via the expansion factor ; additive effects were discussed qualitatively rather than fitted. Secondary SEI chemistry, gas evolution, binder fatigue, and full solid-mechanics coupling were not included. The study focused on 60 µm total anode thicknesses; scale-up to thicker electrodes or high-pressure calendaring may introduce additional failure modes.
Next steps are to fabricate coin-cell prototypes of the four best variants to validate the SEI thickness, impedance, and fade, followed by migration to pouch cells to optimize the electrolyte volume, stack pressure, and thermal management. Application-specific tailoring follows directly from the ranking: hard carbon or LTO cores for fast-charge, long-life systems, and Si or Li-rich cores where gravimetric energy is prioritized. Data-driven optimization of particle morphology and porosity, along with graded or tri-layer laminates, can further translate these insights into commercially viable high-energy cells.
Author Contributions
J.C.R.: Writing—original draft, Investigation, Formal analysis, Data curation, Conceptualization. M.B.: Writing—review and editing, Resources, Validation, Project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The simulation datasets that support the findings of this study are openly available in the Open Science Framework (OSF) at https://doi.org/10.17605/OSF.IO/MEV27. The repository includes COMSOL Multiphysics 6.2 exports of capacity fade and impedance simulations, along with processed files and documentation.
Acknowledgments
During the preparation of this manuscript, the authors used Rabbit Research databases, SOFIA (Université du Québec à Trois-Rivières), and Google Scholar for the literature search and filtering of publications. These tools were employed exclusively to support bibliographic compilation and reference management. The authors have reviewed and curated the retrieved material and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Al | Aluminum |
| C | Carbon/graphite |
| CH4 | Methane |
| CNT | Carbon nanotube |
| CO2 | Carbon dioxide |
| Cu | Copper |
| C2H4 | Ethylene |
| C2H6 | Ethane |
| DMC | Dimethyl carbonate |
| EC | Ethylene carbonate |
| EIS | Electrochemical impedance spectroscopy |
| EMC | Ethyl methyl carbonate |
| FEC | Fluoroethylene carbonate |
| HF | Hydrogen fluoride |
| H2 | Hydrogen gas |
| H2O | Water |
| LFP | Lithium iron phosphate |
| LTO | Lithium titanate (li4ti5o12) |
| Li | Lithium |
| LiF | Lithium fluoride |
| LiOH | Lithium hydroxide |
| LiPF6 | Lithium hexafluorophosphate |
| Li2CO3 | Lithium carbonate |
| MWCNT | Multi-walled carbon nanotube |
| NMC | Nickel manganese cobalt |
| NMC622 | Nickel manganese cobalt (LiNi0.6Mn0.2Co0.2O2) |
| OH− | Hydroxide ion |
| PF6− | Hexafluorophosphate anion |
| POF3 | Phosphorus oxyfluoride |
| PVDF | Polyvinylidene fluoride |
| RT | Room temperature |
| SEI | Solid electrolyte interphase |
| SOC | State of charge |
| SWCNT | Single-walled carbon nanotube |
| Si | Silicon |
| SiOx | Silicon oxide |
| TWh | Terawatt-hour |
| UAV | Unmanned aerial vehicle |
| VC | Vinylene carbonate |
| XPS | X-ray photoelectron spectroscopy |
| rGO | Reduced graphene oxide |
References
- Goodenough, J.B.; Park, K.-S. The Li-Ion Rechargeable Battery: A Perspective. J. Am. Chem. Soc. 2013, 135, 1167–1176. [Google Scholar] [CrossRef]
- Korthauer, R. Lithium-Ion Batteries: Basics and Applications. In Lithium-Ion Batteries: Basics and Applications; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–413. [Google Scholar] [CrossRef]
- Nitta, N.; Wu, F.; Lee, J.T.; Yushin, G. Li-Ion Battery Materials: Present and Future. Mater. Today 2015, 18, 252–264. [Google Scholar] [CrossRef]
- Ming, J.; Li, M.; Kumar, P.; Li, L.J. Multilayer Approach for Advanced Hybrid Lithium Battery. ACS Nano 2016, 10, 6037–6044. [Google Scholar] [CrossRef]
- Ezhyeh, Z.N.; Khodaei, M.; Torabi, F. Review on Doping Strategy in Li4Ti5O12 as an Anode Material for Lithium-Ion Batteries. Ceram. Int. 2023, 49, 7105–7141. [Google Scholar] [CrossRef]
- Su, M.; Wan, H.; Liu, Y.; Xiao, W.; Dou, A.; Wang, Z.; Guo, H. Multi-Layered Carbon Coated Si-Based Composite as Anode for Lithium-Ion Batteries. Powder Technol. 2018, 323, 294–300. [Google Scholar] [CrossRef]
- Wang, Z.; VahidMohammadi, A.; Ouyang, L.; Erlandsson, J.; Tai, C.W.; Wågberg, L.; Hamedi, M.M. Layer-by-Layer Self-Assembled Nanostructured Electrodes for Lithium-Ion Batteries. Small 2021, 17, 2006434. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Hanai, K.; Yang, J.; Imanishi, N.; Hirano, A.; Takeda, Y. Silicon/Carbon Composites as Anode Materials for Li-Ion Batteries. Electrochem. Solid-State Lett. 2004, 7, A369. [Google Scholar] [CrossRef]
- Kim, H.; Seo, M.; Park, M.; Cho, J. A Critical Size of Silicon Nano-Anodes for Lithium Rechargeable Batteries. Angew. Chem. Int. Ed. 2010, 49, 2146–2149. [Google Scholar] [CrossRef]
- Evanoff, K.; Magasinski, A.; Yang, J.; Yushin, G. Nanosilicon-Coated Graphene Granules as Anodes for Li-Ion Batteries. Adv. Energy Mater. 2011, 1, 495–498. [Google Scholar] [CrossRef]
- Karkar, Z.; Houache, M.S.E.; Yim, C.H.; Abu-Lebdeh, Y. An Industrial Perspective and Intellectual Property Landscape on Solid-State Battery Technology with a Focus on Solid-State Electrolyte Chemistries. Batteries 2024, 10, 24. [Google Scholar] [CrossRef]
- Tang, J. Progress in the Application of Silicon-Based Anode Nanotechnology in Lithium Batteries. E3S Web Conf. 2024, 553, 01007. [Google Scholar] [CrossRef]
- Chan, C.K.; Peng, H.; Liu, G.; McIlwrath, K.; Zhang, X.F.; Huggins, R.A.; Cui, Y. High-Performance Lithium Battery Anodes Using Silicon Nanowires. Nat. Nanotechnol. 2008, 3, 31–35. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.H.; Bai, Z.; Li, M.; Yu, A.; Luo, D.; Liu, W.; Yang, L.; Lu, J.; Amine, K.; Chen, Z. Developing High Safety Li-Metal Anodes for Future High-Energy Li-Metal Batteries: Strategies and Perspectives. Chem. Soc. Rev. 2020, 49, 5407–5445. [Google Scholar] [CrossRef]
- Xie, L.; Tang, C.; Bi, Z.; Song, M.; Fan, Y.; Yan, C.; Li, X.; Su, F.; Zhang, Q.; Chen, C. Hard Carbon Anodes for Next-Generation Li-Ion Batteries: Review and Perspective. Adv. Energy Mater. 2021, 11, 2101650. [Google Scholar] [CrossRef]
- Choi, J.H.; Ryu, W.H.; Park, K.; Jo, J.D.; Jo, S.M.; Lim, D.S.; Kim, I.D. Multi-Layer Electrode with Nano-Li4Ti5O12 Aggregates Sandwiched Between Carbon Nanotube and Graphene Networks for High Power Li-Ion Batteries. Sci. Rep. 2014, 4, 7334. [Google Scholar] [CrossRef]
- Lin, D.; Liu, Y.; Liang, Z.; Lee, H.W.; Sun, J.; Wang, H.; Yan, K.; Xie, J.; Cui, Y. Layered Reduced Graphene Oxide with Nanoscale Interlayer Gaps as a Stable Host for Lithium Metal Anodes. Nat. Nanotechnol. 2016, 11, 626–632. [Google Scholar] [CrossRef]
- Bai, M.; Xie, K.; Yuan, K.; Zhang, K.; Li, N.; Shen, C.; Lai, Y.; Vajtai, R.; Ajayan, P.; Wei, B. A Scalable Approach to Dendrite-Free Lithium Anodes via Spontaneous Reduction of Spray-Coated Graphene Oxide Layers. Adv. Mater. 2018, 30, 1801213. [Google Scholar] [CrossRef]
- Guo, Y.; Wei, Y.; Li, H.; Zhai, T. Layer Structured Materials for Advanced Energy Storage and Conversion. Small 2017, 13, 1701649. [Google Scholar] [CrossRef]
- Sharma, N.; Puthusseri, D.; Thotiyl, M.O.; Ogale, S. Hard Carbon and Li4Ti5O12-Based Physically Mixed Anodes for Superior Li-Battery Performance with Significantly Reduced Li Content: A Case of Synergistic Materials Cooperation. ACS Omega 2017, 2, 8818–8824. [Google Scholar] [CrossRef] [PubMed]
- Hamedi, A.S.; Yao, A.; Martin, R.; Roig, R.; Valadez, M.R.; Pile, D.; Shellikeri, A.; Liu, B.; Wheeler, D.R. Multi-Layer Anodes for High-Current Applications. Electrochim. Acta 2023, 439, 141649. [Google Scholar] [CrossRef]
- Ko, K.Y.; Sung, K.W.; Ahn, H.J. Layer-by-Layer-Structured Silicon-Based Electrode Design for Ultrafast Lithium-Ion Batteries. Korean J. Chem. Eng. 2024, 42, 1045–1053. [Google Scholar] [CrossRef]
- Yuan, Y.; Hu, R.; Wang, W.; Wang, Y.; Zhang, T.; Wang, Z. Design and Fabrication of High-Performance Multilayer Silicon-Carbon Composite Anodes for Lithium-Ion Batteries via Femtosecond Laser. J. Energy Storage 2025, 110, 115362. [Google Scholar] [CrossRef]
- Gottschalk, L.; Müller, J.; Schoo, A.; Baasch, E.; Kwade, A. Spherical Graphite Anodes: Influence of Particle Size Distribution and Multilayer Structuring in Lithium-Ion Battery Cells. Batteries 2024, 10, 40. [Google Scholar] [CrossRef]
- Zhang, Z.; Smith, K.; Jervis, R.; Shearing, P.R.; Miller, T.S.; Brett, D.J.L. Operando Electrochemical Atomic Force Microscopy of Solid–Electrolyte Interphase Formation on Graphite Anodes: The Evolution of SEI Morphology and Mechanical Properties. ACS Appl. Mater. Interfaces 2020, 12, 35132–35141. [Google Scholar] [CrossRef]
- Choi, Y.J.; Lee, Y.S.; Kim, J.H.; Im, J.S. Optimization of Pore Characteristics of Graphite-Based Anode for Li-Ion Batteries by Control of the Particle Size Distribution. Materials 2023, 16, 6896. [Google Scholar] [CrossRef]
- An, S.J.; Li, J.; Daniel, C.; Mohanty, D.; Nagpure, S.; Wood, D.L. The State of Understanding of the Lithium-Ion-Battery Graphite Solid Electrolyte Interphase (SEI) and Its Relationship to Formation Cycling. Carbon 2016, 105, 52–76. [Google Scholar] [CrossRef]
- Shi, J.; Ehteshami, N.; Ma, J.; Zhang, H.; Liu, H.; Zhang, X.; Li, J.; Paillard, E. Improving the Graphite/Electrolyte Interface in Lithium-Ion Battery for Fast Charging and Low Temperature Operation: Fluorosulfonyl Isocyanate as Electrolyte Additive. J. Power Sources 2019, 429, 67–74. [Google Scholar] [CrossRef]
- Nasajpour-Esfahani, N.; Garmestani, H.; Bagheritabar, M.; Jasim, D.J.; Toghraie, D.; Dadkhah, S.; Firoozeh, H. Comprehensive Review of Lithium-Ion Battery Materials and Development Challenges. Renew. Sustain. Energy Rev. 2024, 203, 114783. [Google Scholar] [CrossRef]
- Xiao, P.; Yun, X.; Chen, Y.; Guo, X.; Gao, P.; Zhou, G.; Zheng, C. Insights into the Solvation Chemistry in Liquid Electrolytes for Lithium-Based Rechargeable Batteries. Chem. Soc. Rev. 2023, 52, 5255–5316. [Google Scholar] [CrossRef]
- Nitta, N.; Yushin, G. High-Capacity Anode Materials for Lithium-Ion Batteries: Choice of Elements and Structures for Active Particles. Part. Part. Syst. Charact. 2014, 31, 317–336. [Google Scholar] [CrossRef]
- Bläubaum, L.; Röder, F.; Nowak, C.; Chan, H.S.; Kwade, A.; Krewer, U. Impact of Particle Size Distribution on Performance of Lithium-Ion Batteries. ChemElectroChem 2020, 7, 4755–4766. [Google Scholar] [CrossRef]
- Luo, M.; Mijailovic, A.S.; Wang, G.; Wu, Q.; Sheldon, B.W.; Lu, W. Understanding Particle Size Effect on Fast-Charging Behavior of Graphite Anode Using Ultra-Thin-Layer Electrodes. J. Energy Storage 2024, 104, 114521. [Google Scholar] [CrossRef]
- Geng, S.; Zhou, J.; Tan, B.; Zheng, B.; Zhang, K. Impact of Thickness and Charge Rate on the Electrochemical Performance of Si-Based Electrodes. Cell Rep. Phys. Sci. 2024, 5, 102305. [Google Scholar] [CrossRef]
- Alvira, D.; Antorán, D.; Darjazi, H.; Elia, G.A.; Gerbaldi, C.; Sebastian, V.; Manyà, J.J. High Performing and Sustainable Hard Carbons for Na-Ion Batteries Through Acid-Catalysed Hydrothermal Carbonisation of Vine Shoots. J. Mater. Chem. A 2025, 13, 2730–2741. [Google Scholar] [CrossRef]
- Lochab, S.; Bharathraj, S.; Mayya, K.S.; Barpanda, P.; Adiga, S.P. Unveiling the Degradation Mechanism of Sodium Ion Batteries Based on Na4Fe3(PO4)2P2O7 Cathode and Hard Carbon Anode Suggests Anode Particle Size Reduction for Cycling Stability. Batter. Supercaps 2024, 7, e202400025. [Google Scholar] [CrossRef]
- Pan, W.; Cheng, R.; Zhang, Y.; Hu, Z.; Julien, C.M.; Mauger, A. Fabrication of Li4Ti5O12 (LTO) as Anode Material for Li-Ion Batteries. Micromachines 2024, 15, 310. [Google Scholar] [CrossRef]
- Acebedo, B.; Cid, R.; de Lasen-Tejada, M.; Morant-Miñana, M.C.; Fallarino, L.; Goikolea, E.; Rikarte, J.; Gonzalo, E.; Ruiz de Larramendi, I. On the Role of Ultrathin Lithium Metal Anodes Produced by Thermal Evaporation. J. Power Sources 2024, 618, 235218. [Google Scholar] [CrossRef]
- Refino, A.D.; Adhitama, E.; Bela, M.M.; Sadhujan, S.; Harilal, S.; Eldona, C.; Bremers, H.; Bashouti, M.Y.; Sumboja, A.; Stan, M.C.; et al. Impact of Exposing Lithium Metal to Monocrystalline Vertical Silicon Nanowires for Lithium-Ion Microbatteries. Commun. Mater. 2023, 4, 58. [Google Scholar] [CrossRef]
- He, W.; Xu, W.; Li, Z.; Hu, Z.; Yang, J.; Qin, G.; Teng, W.; Zhang, T.; Zhang, W.; Sun, Z.; et al. Structural Design and Challenges of Micron-Scale Silicon-Based Lithium-Ion Batteries. Adv. Sci. 2025, 12, 2407540. [Google Scholar] [CrossRef]
- Patil, R.; Phadatare, M.; Blomquist, N.; Örtegren, J.; Hummelgård, M.; Meshram, J.; Dubal, D.; Olin, H. Highly Stable Cycling of Silicon-Nanographite Aerogel-Based Anode for Lithium-Ion Batteries. ACS Omega 2021, 6, 6600–6606. [Google Scholar] [CrossRef]
- Lazanas, A.C.; Prodromidis, M.I. Electrochemical Impedance Spectroscopy—A Tutorial. ACS Meas. Sci. Au 2023, 3, 162–193. [Google Scholar] [CrossRef]
- COMSOL. The Battery Design Module User’s Guide; COMSOL AB: Stockholm, Sweden, 2020. [Google Scholar]
- Li, D.; Danilov, D.; Zhang, Z.; Chen, H.; Yang, Y.; Notten, P.H.L. Modeling the SEI-Formation on Graphite Electrodes in LiFePO4 Batteries. J. Electrochem. Soc. 2015, 162, A858–A869. [Google Scholar] [CrossRef]
- Cai, L.; White, R.E. Mathematical Modeling of a Lithium Ion Battery; COMSOL AB: Stockholm, Sweden, 2009. [Google Scholar]
- Ekström, H.; Lindbergh, G. A Model for Predicting Capacity Fade Due to SEI Formation in a Commercial Graphite/LiFePO4 Cell. J. Electrochem. Soc. 2015, 162, A1003–A1007. [Google Scholar] [CrossRef]
- Wang, A.; Kadam, S.; Li, H.; Shi, S.; Qi, Y. Review on Modeling of the Anode Solid Electrolyte Interphase (SEI) for Lithium-Ion Batteries. npj Comput. Mater. 2018, 4, 15. [Google Scholar] [CrossRef]
- COMSOL. D Lithium-Ion Battery Model for the Capacity Fade Tutorial; COMSOL AB: Stockholm, Sweden, 2021. [Google Scholar]
- Geuder, K.; Klick, S.; Finster, P.; Graff, K.M.; Winter, M.; Nowak, S.; Seifert, H.J.; Ziebert, C. Influence of Vinylene Carbonate and Fluoroethylene Carbonate on Open Circuit and Floating SoC Calendar Aging of Lithium-Ion Batteries. Batteries 2024, 10, 275. [Google Scholar] [CrossRef]
- Nam, J.; Lee, H.; Chae, O.B. Overcoming Challenges in Silicon Anodes: The Role of Electrolyte Additives and Solid-State Electrolytes. Micromachines 2025, 16, 800. [Google Scholar] [CrossRef]
- Dhillon, S.; Hernández, G.; Wagner, N.P.; Svensson, A.M.; Brandell, D. Modelling Capacity Fade in Silicon-Graphite Composite Electrodes for Lithium-Ion Batteries. Electrochim. Acta 2021, 377, 138067. [Google Scholar] [CrossRef]
- Saxena, S.; Hendricks, C.; Pecht, M. Cycle Life Testing and Modeling of Graphite/LiCoO2 Cells under Different State of Charge Ranges. J. Power Sources 2016, 327, 394–400. [Google Scholar] [CrossRef]
- Rikka, V.R.; Sahu, S.R.; Chatterjee, A.; Prakash, R.; Sundararajan, G.; Gopalan, R. Enhancing Cycle Life and Usable Energy Density of Fast Charging LiFePO4-Graphite Cell by Regulating Electrodes’ Lithium Level. iScience 2022, 25, 104831. [Google Scholar] [CrossRef] [PubMed]
- Farhan, G.; Toki, I.; Khalid Hossain, M.; Rehman, W.U.; Zafar, R.; Manj, A.; Wang, L.; Yang, J. Recent Progress and Challenges in Silicon-Based Anode Materials for Lithium-Ion Batteries. Ind. Chem. Mater. 2024, 2, 226–269. [Google Scholar] [CrossRef]
- Liao, X.; Hu, D.; Yu, L.; Li, B.; Xiao, F.; Wang, S. Spherical Hard Carbon/Graphite Anode for High Performance Lithium Ion Batteries. PLoS ONE 2024, 19, e0311943. [Google Scholar] [CrossRef]
- Martin, C.; Genovese, M.; Louli, A.J.; Weber, R.; Dahn, J.R. Cycling Lithium Metal on Graphite to Form Hybrid Lithium-Ion/Lithium Metal Cells. Joule 2020, 4, 1296–1310. [Google Scholar] [CrossRef]
- Jung, H.G.; Kim, J.; Scrosati, B.; Sun, Y.K. Micron-Sized, Carbon-Coated Li4Ti5O12 as High Power Anode Material for Advanced Lithium Batteries. J. Power Sources 2011, 196, 7763–7766. [Google Scholar] [CrossRef]
- Asenbauer, J.; Eisenmann, T.; Kuenzel, M.; Kazzazi, A.; Chen, Z.; Bresser, D. The Success Story of Graphite as a Lithium-Ion Anode Material—Fundamentals, Remaining Challenges, and Recent Developments Including Silicon (Oxide) Composites. Sustain. Energy Fuels 2020, 4, 5387–5416. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, H.; Li, Y.; Hu, Y.; Li, Y. Prelithiation Strategies for Enhancing the Performance of Lithium-Ion Batteries. RSC Adv. 2025, 15, 1249–1274. [Google Scholar] [CrossRef]
- Xu, Y.; Jia, H.; Gao, P.; Galvez-Aranda, D.E.; Beltran, S.P.; Cao, X.; Le, P.M.L.; Liu, J.; Engelhard, M.H.; Li, S.; et al. Direct in Situ Measurements of Electrical Properties of Solid–Electrolyte Interphase on Lithium Metal Anodes. Nat. Energy 2023, 8, 1345–1354. [Google Scholar] [CrossRef]
- Dopilka, A.; Gu, Y.; Larson, J.M.; Zorba, V.; Kostecki, R. Nano-FTIR Spectroscopy of the Solid Electrolyte Interphase Layer on a Thin-Film Silicon Li-Ion Anode. ACS Appl. Mater. Interfaces 2023, 15, 6755–6767. [Google Scholar] [CrossRef]
- Jin, C.; Huang, Y.; Li, L.; Wei, G.; Li, H.; Shang, Q.; Ju, Z.; Lu, G.; Zheng, J.; Sheng, O.; et al. A Corrosion Inhibiting Layer to Tackle the Irreversible Lithium Loss in Lithium Metal Batteries. Nat. Commun. 2023, 14, 8269. [Google Scholar] [CrossRef]
- Fu, R.; Zhou, X.; Fan, H.; Blaisdell, D.; Jagadale, A.; Zhang, X.; Xiong, R. Comparison of Lithium-Ion Anode Materials Using an Experimentally Verified Physics-Based Electrochemical Model. Energies 2017, 10, 2174. [Google Scholar] [CrossRef]
- Chen, K.H.; Goel, V.; Namkoong, M.J.; Wied, M.; Müller, S.; Wood, V.; Sakamoto, J.; Thornton, K.; Dasgupta, N.P. Enabling 6C Fast Charging of Li-Ion Batteries with Graphite/Hard Carbon Hybrid Anodes. Adv. Energy Mater. 2021, 11, 2003336. [Google Scholar] [CrossRef]
- Yin, Y.; Shen, C.; Yturriaga, S.; Zheng, J.P.; Yin, Y.; Shen, C.; Yturriaga, S.; Zheng, J.P. The Power-Energy Coupling Effect of Mixed Hard-Carbon/Graphite Anode. J. Mater. Sci. Chem. Eng. 2021, 9, 16–31. [Google Scholar] [CrossRef]
- Durdel, A.; Friedrich, S.; Hüsken, L.; Jossen, A. Modeling Silicon-Dominant Anodes: Parametrization, Discussion, and Validation of a Newman-Type Model. Batteries 2023, 9, 558. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Z.; Zhang, J.; Bai, Z.; Zhao, L.; Li, R.; Yang, Z.; Bai, Y.; Sun, K. Decline Mechanism of Graphite/Lithium Metal Hybrid Anode and Its Stabilization by Inorganic-Rich Solid Electrolyte Interface. ACS Appl. Mater. Interfaces 2023, 15, 34922–34930. [Google Scholar] [CrossRef]
- Xiao, C.; Wang, B.; Zhao, D.; Wang, C. Comprehensive Investigation on Lithium Batteries for Electric and Hybrid-Electric Unmanned Aerial Vehicle Applications. Therm. Sci. Eng. Prog. 2023, 38, 101677. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, J.; Dai, H.; Yu, C.; Wei, X. Impedance Investigation of Silicon/Graphite Anode during Cycling. Batteries 2023, 9, 242. [Google Scholar] [CrossRef]
- Wang, S.; Liu, D.; Cai, X.; Zhang, L.; Liu, Y.; Qin, X.; Zhao, R.; Zeng, X.; Han, C.; Zhan, C.; et al. Promoting the Reversibility of Lithium Ion/Lithium Metal Hybrid Graphite Anode by Regulating Solid Electrolyte Interface. Nano Energy 2021, 90, 106510. [Google Scholar] [CrossRef]
- Goel, V.; Masel, K.; Chen, K.H.; Safdari, A.; Dasgupta, N.P.; Thornton, K. The Origin of the Superior Fast-Charging Performance of Hybrid Graphite/Hard Carbon Anodes for Li-Ion Batteries. Energy Storage Mater. 2025, 76, 104053. [Google Scholar] [CrossRef]
- Lee, M.L.; Li, Y.H.; Liao, S.C.; Chen, J.M.; Yeh, J.W.; Shih, H.C. Li4Ti5O12-Coated Graphite Anode Materials for Lithium-Ion Batteries. Electrochim. Acta 2013, 112, 529–534. [Google Scholar] [CrossRef]
- Zhao, J.; Zhu, X.; Zhang, W.; Qiu, J.; Zhai, F.; Zhang, H.; Cao, G.; Gao, S.; Ding, F.; Xiang, Y. Expanded Graphite Incorporated with Li4Ti5O12 Nanoparticles as a High-Rate Lithium-Ion Battery Anode. RSC Adv. 2024, 14, 11276–11283. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).