Abstract
Periodic systems of magnetic nanoparticles are now of interest as they support GHz spin waves. Their equilibrium configurations, switchable with the external magnetic field, are crucial for such applications. We study infinite and finite chains of particles of two shapes (i) ellipsoidal and (ii) rectangular stripes with long axes perpendicular to the chain axis. A variable magnetic field is applied parallel to the long axes. Micromagnetic simulations are compared with the corresponding discrete spin models (Stoner-Wohlfarth model, S-W). An antiferromagnetic configuration is the ground state for all the systems at vanishing field but a ferromagnetic configuration occurs when the field is strong enough. The switching of the infinite chains to the reversed ferromagnetic configuration proceeds directly for the ellipsoids and by an intermediate configuration, in which the magnetization within the particle is non-uniform, in the case of the stripes. The non-uniform configurations are well represented by tilted states in S-W model. Important differences are found in the finite analogs: the switching of ellipsoids becomes multistage and starts from the innermost particles relatively well reproduced with S-W model, whereas the reversal of the stripes, starts from the outermost particles and has no analog in S-W model. Practical consequences of the findings are discussed.
1. Introduction
Nanoparticle arrays are now patterned more and more precisely with various methods, such as sub-micron sphere self-assembly lithography techniques [1,2,3,4,5], selective ion irradiation [6,7,8,9] and film growth technologies [10,11]. Ferromagnetic nanomaterials are of special interest due to their potential application in magnetic data storage and spintronic devices, such as MRAM, microwave oscillators, magnetic nanosensors [12,13,14,15,16,17,18,19,20,21].
When formed into elongated shapes the ferromagnetic nanoparticles behave in many instances like single spins, called macrospins [22], due to the shape anisotropy that favors the magnetization orientation along the particles’ long axes. The organization of the individual spins in our macrospins is somewhat analogous to the parallel arrangement of the individual spins in some molecular magnets [23,24,25]. Monodomain ferromagnetic particles, tractable as macrospins, are particularly precious in the area of spintronics because the eigenfrequencies of such particles lie in the GHz region. Periodic arrangements of such particles constitute waveguides for the spin waves propagating in the same frequency range [26,27]. A separate research area concerns magnonic structures [28,29], characterized with one or more stop bands, in analogy to photonics [30].
The spin waves are in fact small deviations from equilibrium configurations. The latter are stable, i.e., are ground states, or metastable, when they correspond to local minima of energy. The equilibrium configurations can be controlled with external stimuli, the magnetic field being the most natural one.
In this paper we present the evolution of configurations of the most representative one-dimensional waveguide systems, infinite and finite, of ferromagnetic particles under a variable magnetic field. The main effect is the switching of the magnetization. The systems considered: elongated stripes and ellipsoids, consist of nanoparticles that favor the magnetization perpendicular to the chain due to their shape anisotropy. The shapes are, thus, elongated perpendicular to the chains. A common property of all such systems is that their most stable configuration is an antiferromagnetic (AF) one. This follows from the fact that the interparticle forces are dipolar, favoring antiparallel alignment of the nearest neighboring moments. However, when subjected to external magnetic field the systems transit to a ferromagnetic (FM) order. The recovery of the stable AF configuration then is rather improbable [26]. Instead a number of rather complex configurations is observed in some analogy to magnetic ice in spite of the fact that no geometric frustration is imposed by the system geometry [31,32,33].
We compare reliable but time consuming micromagnetic simulations with the simplest possible models. The simplest approximation of a macrospin is to replace it with a point-like dipole and to put it in a local potential constructed so as to reflect the shape anisotropy of the particle being modelled. This is an extended discrete dipole approximation [34,35]. The addition of the shape anisotropy to the discrete dipole approximation transform it into Stoner-Wohlfarth model [36,37].
In Section 2 we present the models and the approximations adopted. Section 3 gathers the results obtained for the infinite chains and analogous chains with seven and eight macrospins. A qualitative difference, a better adequacy of the S-W model in the case of ellipsoids and prospects for the simplest models for arbitrary shapes are discussed in Section 4.
2. The Models
2.1. Different Shapes with the Same Shape Anisotropy
The systems under study are depicted in Figure 1. Figure 1a,b illustrate a sequence of elongated macrospins adsorbed on a flat nonmagnetic substrate. Two different shapes are considered: rectangular stripes Figure 1a and ellipsoids Figure 1b. The sizes of the particles are selected so that the shape anisotropies be identical in the quadrupolar approximation. The linear dimensions of the stripes are 350, 5000 and 30 nm (width x, length y, thickness z), whereas the semi axes of the ellipsoids are 175, 2500 and 15 nm. Thus, every ellipsoid is the maximum-volume ellipsoid inscribed in the rectangular parallelepiped of the stripe. The separations of the stripes and ellipsoids along the chain are 100 nm.
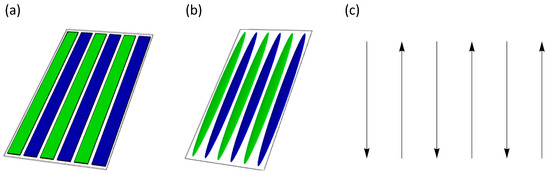
Figure 1.
Schematic of the models used: (a) stripes, (b) ellipsoids and (c) S-W discrete approximation. Green and blue colors in (a,b) correspond to the magnetization upwards and downwards, respectively.
The magnetic parameters correspond to permalloy Ni80Fe20 material: saturation magnetization and exchange stiffness parameter [38]. The material being magnetically isotropic (no magnetocrystalline anisotropy [39,40,41]) the only source of anisotropy here is the shape anisotropy. Consequently, the ground state of a single isolated macrospin corresponds to the magnetization being preferentially oriented along the longest axis of the shape. When arranged into the chains the macrospins exhibit the ground state in which the magnetizations of the neighboring particles are opposite. This configuration is legitimately called antiferromagnetic (AF) and is represented in Figure 1a,b by the green (up) and blue (down) colors. A magnetic field is assumed to be applied to the chains in the y-direction, i.e., parallel to the long axes of the shapes. The appropriate equilibrium configuration at every given field intensity is found by minimization of the magnetic energy with the use of the software MuMax3 [42,43]. It includes the isotropic exchange interactions between all the 5 nm × 5 nm × 5 nm voxels within every particle and the dipolar interactions between all the voxels of the system.
2.2. Point-Dipole Reduced Model
The reduction of the shapes to the point like-dipoles is known as the Stoner-Wohlfarth model [36,37]. In this approximation the whole dipole moment of a macrospin is concentrated at one point. This is schematized in Figure 1c. The total energy in the S-W model reads:
where the one-particle terms and correspond to the anisotropy and Zeeman contributions:
and:
with the particle volume being , the particle’s saturation magnetization . The unit vector indicates the spatial orientation of the dipole moment of the particle.
The only two-particle contribution originates from interparticle dipole-dipole interactions:
where is the separation of the dipoles, and is the vacuum permeability. To represent the shapes described in Section 2.1. we take the demagnetizing factors of Equation (2) as:
The anisotropy parameters are, thus, the same as for the stripes and ellipsoids. In fact, in this approach the difference between stripes and ellipsoids reduces to a difference in the net dipole moment of the point-like dipole.
In modelling of the infinite chains, the question of the long-range nature of the dipole-dipole interactions (Equation (4)) should be tackled. In the present calculations the largest range included is up to the 7th nearest neighbor. Thus, the finite systems, counting up to eight members are treated with the machine accuracy and the infinite show an error not exceeding . This is comparable to the accuracy defined in MuMax.
3. Results
3.1. Infinite Systems
In the discrete S-W model the sequence of configurations crucially depends on the ratio of the anisotropy parameters to the dipolar moment involved in the interparticle interactions.
In Figure 2a,b one can see the evolution of the magnetization in infinite chains under the external applied field B in the S-W model. The evolution starts from the ground state, i.e., AF configuration at B = 0 mT. With increasing field, the system switches abruptly to the FM configuration. With subsequently decreasing the field the behavior differs qualitatively for both systems. There is a direct switching to the reverse FM for the ellipsoid case and a progressive switching in the stripe case. The sequence is illustrated in Figure 2c. A particularity of the sequence is the occurrence of a tilted configuration in which the dipoles subtend an acute angle with the chain axis. The passage from the FM configuration (A) to the tilted one goes through a continuous phase transition or spontaneous symmetry breaking. The passage recovering the AF configuration at point (B) is, on the contrary, discontinuous, i.e., the tilted configuration loses its stability at the presence of a deeper minimum of energy as it is shown in Figure 3a. The tilted configuration has been reported in [35], without however the discontinuous transitions, the deficiency being a result of the neglect of the anisotropy terms.
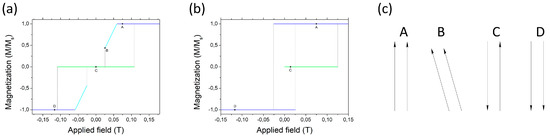
Figure 2.
Magnetization sequence under the applied magnetic field in a S-W model of (a) stripes, (b) ellipsoids. The starting configuration for B = 0 is antiferromagnetic. Panel (c) represents the stages of magnetization switching in the case of the stripes marked with the letters A, B, C, D.
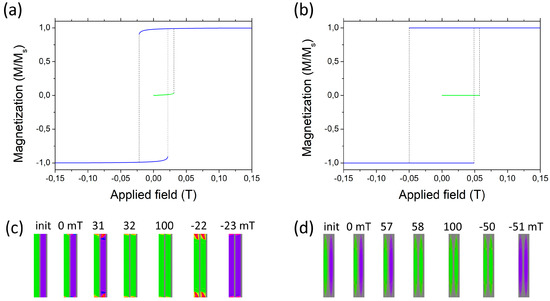
Figure 3.
Magnetization sequence under the applied magnetic field in infinite chains of (a) stripes, (b) ellipsoids treated with micromagnetic simulations. Panels (c,d) illustrate magnetization maps for stripes and ellipsoids, respectively.
For comparison we show in Figure 3 the magnetization sequence for more realistic micromagnetic counterparts of the stripes and ellipsoids. In spite of the differences some features of the behavior are similar. The ellipsoids switch directly between opposite FM configurations whereas the stripes exhibit an intermediate state marked with a smoothly decreasing magnetization, without, however recovery of the antiferromagnetic configuration. The decreasing magnetization corresponds here to a non-uniform magnetization as it is seen in Figure 3c. In fact, the net magnetization of every stripe is tilted as a result of an S-shaped inhomogeneity. An S-shape is best visible in panel Figure 3c at −22 mT; the magnetization is subsequently directed counting from below: right, upwards, right. Compared with that the magnetization of the ellipsoids remains visibly uniform even close to the switching points. In the Figure 3c,d the color code is the following: green up, violet down, red right and cyan left in accordance with Hue Color Wheel.
Interesting evolution of magnetization is also visible in the passage from AF to FM for stripes. Noteworthy is that the inhomogeneity then occurs at the stripe to-be reversed in contrast with the stripe already in the “right” direction. The end “tongues” grow in volume and intensity when approaching the instabilities.
The energies corresponding to the sequences from Figure 2 and Figure 3 are compared in Figure 4. One can see the continuous passage from FM to tilted configuration Figure 4a: a straight blue line transforms into a curved cyan line. The corresponding part of Figure 4c is in fact also curved, although to a very tiny extent. Additionally, no passage is visible from a straight line to the curved line behavior indicating that the “tongues” at the extremities subsist until very strong external fields and the saturation occurs but in infinity.
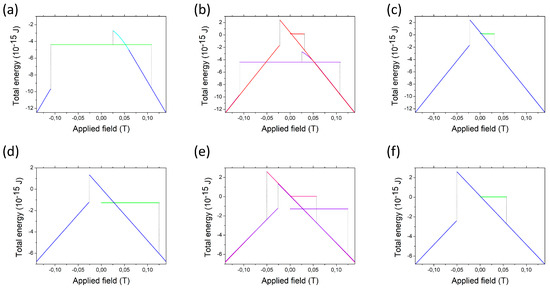
Figure 4.
Energies of the subsequent configurations of the models discussed in this section, upper panel: stripes, lower panel: ellipsoids. The leftmost (a,d) S-W model, the rightmost (c,f) micromagnetic calculations, the central parts (b,e) comparison of both.
3.2. Finite Chains
In practice all the nanoparticle systems are finite. We have studied two examples with even and odd number of particles, N = 7 and N = 8. The numbers have been selected to visualize how symmetry affects the end effects.
3.2.1. System of Seven Macrospins
The switching sequence turns out more involved than for infinite chain. Noteworthy is that for an odd number of particles there are two antiferromagnetic configurations with the net magnetization upwards (AF-u) and downwards (AF-d). As it is seen in Figure 5a,b the AF-u subsists to higher fields than AF-d. This may reflect an easier reversal of the end macrospins as compared with the internal ones. When starting from the ferromagnetic configuration, B > 0, an analog of the tilted configuration occurs (Figure 5c configuration (C)) in the case of stripes. This time, however, the tilt angle grows symmetrically from each end to the center of the chain. The reason for that is that the innermost macrospin has the largest number of interacting neighbors so its behavior is closest to that in the infinite chain in contrast with the end macrospin having only neighbors at one side. The most tilted macrospin eventually initiates the reversal that leads to the configuration D with one reversed macrospin.
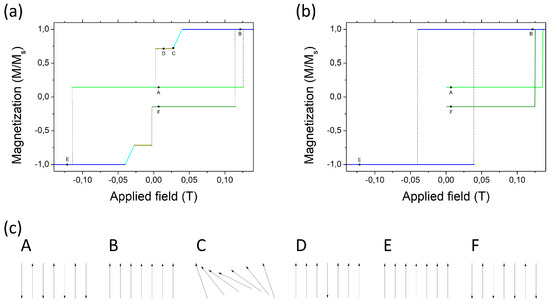
Figure 5.
Magnetization sequence under the applied magnetic field in a S-W model of (a) 7 stripes, (b) 7 ellipsoids. The starting configuration for H = 0 is antiferromagnetic. Panel (c) represents the stages of magnetization switching in the case of the stripes marked with the letters A, B, C, D, E and F. Mind that configurations A and F are two variants of AF configuration with the net magnetization upwards (AF-u) and downwards (AF-d), respectively.
We have studied the conditions for the tilted configuration as a function of the number of particles in the chain for the parameters used here. The shortest chain showing a tilt is 5.
The switching of the ellipsoids in S-W approximation is much simpler with no intermediate stages nor tilted configurations. The hysteresis loop then is squared Figure 5b.
Figure 6 illustrates analogous evolution of the system of seven stripes as modeled in micromagnetic simulations. The switching of the AF-d configuration is slightly ahead of the AF-u as it is seen in Figure 6b,c. The switching is two-stage and starts form the outermost unswitched macrospins.
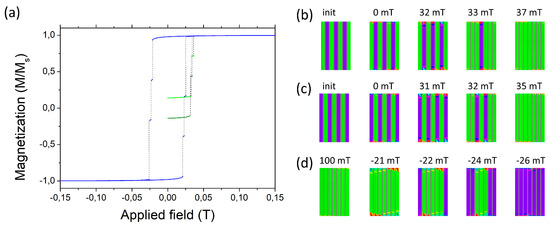
Figure 6.
(a) Hysteresis loop for the system of seven stripes. The configuration sequence when starting from (b) AFu and (c) AFd. (d) the sequence in the reversal of the FM configuration.
In contrast to the S-W model the same rule holds for the switching from the FM configuration. The evolution is shown in Figure 6d. With decreasing field oriented upwards end “tongues” of tilted spins appear on the generally parallel regions (green). The tongues grow when the field changes sign, but they do not represent a tilt of the net magnetization (compare Figure 3c and Figure 6d). They rather resemble a C-shape (right from the central stripe) and inverted C (left). The C-shapes are most intense at the extremities of the chain that explains the reversal sequence starting from the chain extremities.
The C-shaped inhomogeneity of magnetization does not produce a net deviation from the particle axis (mind that red and blue regions compensate). Its lowest effect is of the second order and consist of a reduction of the axial magnetization. This can be modelled assuming a macrospin magnetization being distensible around an equilibrium value lower than the uniform magnetization of the whole particle. In the FM configuration the neighborhood of particles magnetized parallelwise tends to reduce the magnetization, which tendency is the strongest in the center of the chain. The application of a reverse field will preserve this tendency as long as the distensibility of the magnetization remains linear, similar to the Hooke’s law. The question whether it is at all possible to model the real behavior of the finite system of stripes with a one-spin S-W-like model with an appropriate nonlinearity is open. Works are in progress on the minimal model of the phenomenon an alternative being a bi-spin model discussed in [44]. The problem is simpler in the case of the ellipsoids, Figure 7. Only the AFd configuration exhibits a two-stage reversal starting from the outermost macrospins (Figure 7a,c). The configuration AFu, on the contrary, occurs in a single leap. The switching of the FM configuration starts, like for seven stripes, from the innermost macrospins but no signs of inhomogeneity is seen in the magnetization map (Figure 7d). The hysteresis loop (Figure 7a) is, consequently, square-like (not rounded) similar to the S-W model.
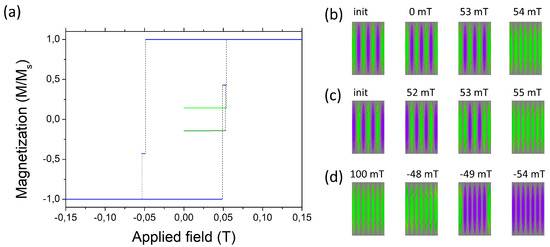
Figure 7.
(a) Hysteresis loop for the system of seven ellipsoids. The configuration sequence when starting from (b) AFu and (c) AFd. (d) the sequence in the reversal of the FM configuration.
The energies of the particular configurations in the systems of seven macrospins treated with the S-W model and in micromagnetic simulations are compared in Figure 8. One can appreciate a relatively good adequacy of the S-W model in the case of the ellipsoids. Larger discrepancies occur for the stripes, the most important being that the discrete spins show much broader range of the AF configuration and transit from the FM configuration to the AF one at a still positive external field. This indicates that the tilted configuration is less stable than the corresponding inhomogeneously deformed configuration of the stripes.
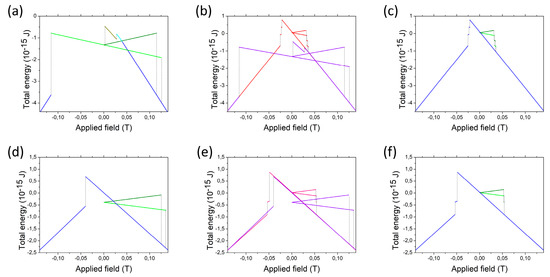
Figure 8.
Energies of the subsequent configurations of the models of seven stripes and ellipsoids discussed in this section, upper panel: stripes, lower panel: ellipsoids. The leftmost (a,d) S-W model, the rightmost (c,f) micromagnetic calculations, the central parts (b,e) comparison of both.
3.2.2. System of Eight Macrospins
Whereas the odd number of particles ensures a symmetry between the left and right terminations of the chain in the AF configuration, an even number always results in opposite orientations of the first and the last macrospin of the finite chain. Additionally, there is no central particle in the case of an even number. To study the consequences of that we present here our results for the chain of eight macrospins.
Figure 9, Figure 10 and Figure 11 are analogous to Figure 6, Figure 7 and Figure 8 but obtained for the system with eight particles. The fact that the system is no more symmetric with respect to the central particle is best reflected in the AF→FM switching. Interestingly, the switching starts from the outermost to-be-reversed macrospin but its nearest parallel neighbor remains unreversed as the last one no matter at which end the extreme to-be-reversed macrospin lies. In Figure 10b we show the case of the rightmost macrospin being reversed first. The reversal sequence breaks the translational periodicity. The observation of the C-shaped precursor inhomogeneities remains similar to the case of seven stripes (see Figure 10c).
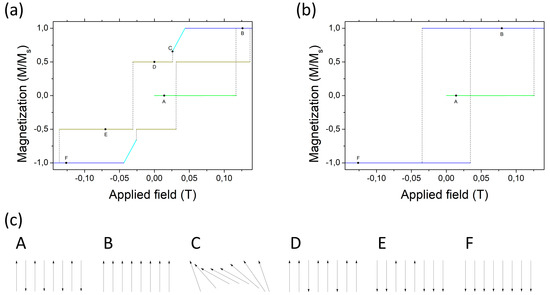
Figure 9.
Magnetization sequence under the applied magnetic field in a S-W model of (a) eight stripes, (b) eight ellipsoids. The starting configuration for H = 0 is antiferromagnetic. Panel (c) represents the stages of magnetization switching in the case of the stripes marked with the letters A, B, C, D, E and F.
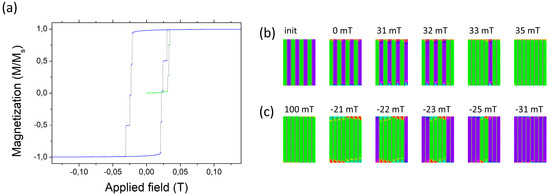
Figure 10.
(a) Hysteresis loop for the system of eight stripes. (b) The configuration sequence when starting from AF and (c) the configuration sequence when starting from FM. The AF configurations are equivalent, no distinction AFu and AFd.
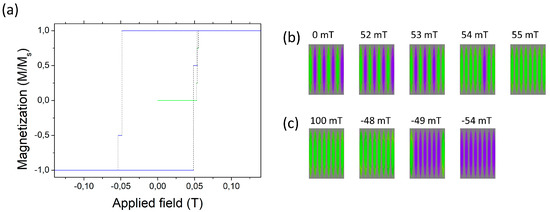
Figure 11.
(a) Hysteresis loop for the system of eight ellipsoids. The configuration sequence when starting (b) from AF and (c) from FM configuration.
The switching that starts from the AF configuration green-violet reversed with respect to Figure 10b is entirely analogous; the first reversed macrospin is the leftmost one, and the third-left remains as the last non-reversed. The reversal of the FM configuration involves more stages. One can see three intermediate configurations in Figure 10c preserving the inversion symmetry.
The reversal sequence AF → FM for the ellipsoids (Figure 11b) resembles that for the stripes except for the magnetization inhomogeneities. The latter make the hysteresis curve more rounded and eventually narrower. The switching fields for the AF → FM and FM → -FM transition are very close in the case of ellipsoids.
The comparison of the S-W model with micromagnetic simulations for the stripes and ellipsoids (Figure 12) reveals analogous properties as for 7 particles with a particularly wide region of the AF configuration, and the several-stage switching when started from FM with decreasing field for the stripe system.
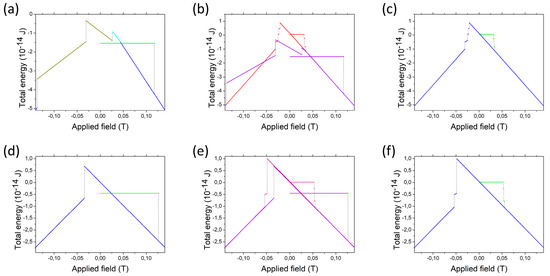
Figure 12.
Energies of the subsequent configurations of the models of 8 stripes and ellipsoids discussed in this section, upper panel: stripes, lower panel: ellipsoids. The leftmost (a,d) S-W model, the rightmost (c,f) micromagnetic calculations, the central parts (b,e) comparison of both.
4. Discussion and Conclusions
The study reveals the impact of the particle shapes, chain lengths and the approximations employed on the switching mechanisms in selected 1D equidistant systems of macrospins. The elongation of the particles in the direction perpendicular to the chain axis favors AF configuration as a ground state. Once a FM configuration is reached with a strong enough applied field the ground state can only be recovered in the S-W discrete spin model with strong enough ratio of dipolar to anisotropic interactions and short-enough interparticle separation. The behavior has been obtained here with the parameters corresponding to the stripes with the infinite chain length as a result of an artificial concentration of the charge in one point. The recovery of the AF configuration when starting from an FM one in a real system may be a challenging task in the design of spintronic devices. The question of an appropriate shape ensuring this behavior is still open.
A particularity of the reversal of the FM configuration in the infinite chain of stripes is the occurrence of a tilted intermediate configuration with a nonvanishing longitudinal component of magnetization. The component arises as a result of an inclination of the discrete spins in the S-W model towards the chain axis which is a qualitative manifestation of an S-shaped inhomogeneity of magnetization determined in the micromagnetic simulations. The inclination occurs with a decreasing applied field as a spontaneous symmetry breaking analogous to a continuous phase transition. The tilted configuration does not appear in the chains of ellipsoids where no visible inhomogeneities of magnetization are discernable. Whereas the discrete S-W model reproduces qualitatively the reversal of infinite chains, it fails to describe the FM → FM reversals of finite chains. In particular the S-W model infers a reversal initiated by the innermost macrospins, whereas the micromagnetic simulations predict a reversal starting from the outermost particles. Moreover, the precursor inhomogeneities in the stripe-shaped macrospins do not produce a longitudinal magnetization component but rather exhibit C-shaped patterns growing at the chain extremities, with, however, no net deviation from the axial magnetization. An extension of the discrete S-W model is, therefore needed. We have shown that a distensibility introduced to the S-W model is not sufficient to account for the phenomenon at least in the linear approximation. Works are now in progress to develop the minimal model adequate for the switching of finite systems.
Author Contributions
Conceptualization D.K. and P.Z., methodology D.K. and P.Z., micromagnetic computations D.K., discrete spin modelling, P.Z., visualization D.K., editing D.K., writing D.K. and P.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The numerical calculations were performed at Poznan Supercomputing and Networking Center (Grant No. 424).
Acknowledgments
The authors thank Magdalena Laskowska for suggesting them the present research. We thank Jarosław Kłos of UAM Poznań for valuable discussions on the shape anisotropy parameters.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aiempanakit, M.; Jearnkulprasert, N.; Panyajirawut, P. Patterning of Nanoparticle Arrays by Self-assembly Lithography. Mater. Today Proc. 2017, 4, 6009–6014. [Google Scholar] [CrossRef]
- Hua, F.; Shi, J.; Lvov, Y.; Cui, T. Patterning of Layer-by-Layer Self-Assembled Multiple Types of Nanoparticle Thin Films by Lithographic Technique. Nano Lett. 2002, 2, 1219–1222. [Google Scholar] [CrossRef]
- Ormonde, A.D.; Hicks, E.C.M.; Castillo, J.; van Duyne, R.P. Nanosphere Lithography: Fabrication of Large-Area Ag Nanoparticle Arrays by Convective Self-Assembly and Their Characterization by Scanning UV−Visible Extinction Spectroscopy. Langmuir 2004, 20, 6927–6931. [Google Scholar] [CrossRef] [PubMed]
- Pease, R.F.; Chou, S.Y. Lithography and Other Patterning Techniques for Future Electronics. Proc. IEEE 2008, 96, 248–270. [Google Scholar] [CrossRef]
- Martín, J.I.; Nogués, J.; Liu, K.; Vicent, J.L.; Schuller, I.K. Ordered magnetic nanostructures: Fabrication and properties. J. Magn. Magn. Mater. 2003, 256, 449–501. [Google Scholar] [CrossRef]
- Chappert, C. Planar Patterned Magnetic Media Obtained by Ion Irradiation. Science 1998, 280, 1919–1922. [Google Scholar] [CrossRef]
- Menéndez, E.; Liedke, M.O.; Fassbender, J.; Gemming, T.; Weber, A.; Heyderman, L.J.; Rao, K.V.; Deevi, S.C.; Suriñach, S.; Baró, M.D.; et al. Direct Magnetic Patterning due to the Generation of Ferromagnetism by Selective Ion Irradiation of Paramagnetic FeAl Alloys. Small 2008, 5, 229–234. [Google Scholar] [CrossRef]
- Fassbender, J.; Grenzer, J.; Roshchupkina, O.; Choi, Y.; Jiang, J.S.; Bader, S.D. The effect of ion irradiation and annealing on exchange spring magnets. J. Appl. Phys. 2009, 105, 023902. [Google Scholar] [CrossRef]
- Devolder, T.; Chappert, C.; Chen, Y.; Cambril, E.; Bernas, H.; Jamet, J.P.; Ferré, J. Sub-50 nm planar magnetic nanostructures fabricated by ion irradiation. Appl. Phys. Lett. 1999, 74, 3383–3385. [Google Scholar] [CrossRef]
- Heyderman, L.J.; Stamps, R.L. Artificial ferroic systems: Novel functionality from structure, interactions and dynamics. J. Phys. Condens. Matter. 2013, 25, 363201. [Google Scholar] [CrossRef] [PubMed]
- Mitterer, C. Borides in Thin Film Technology. J. Solid State Chem. 1997, 133, 279–291. [Google Scholar] [CrossRef]
- Mu, C.; Jing, J.; Dong, J.; Wang, W.; Xu, J.; Nie, A.; Xiang, J.; Wen, F.; Liu, Z. Static and dynamic characteristics of magnetism in permalloy oval nanoring by micromagnetic simulation. J. Magn. Magn. Mater. 2019, 474, 301–304. [Google Scholar] [CrossRef]
- Huang, B.; Clark, G.; Navarro-Moratalla, E.; Klein, D.R.; Cheng, R.; Seyler, K.L.; Zhong, D.; Schmidgall, E.; McGuire, M.A.; Cobden, D.H.; et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017, 546, 270–273. [Google Scholar] [CrossRef]
- Lin, G.T.; Zhuang, H.L.; Luo, X.; Liu, B.J.; Chen, F.C.; Yan, J.; Sun, Y.; Zhou, J.; Lu, W.J.; Tong, P.; et al. Tricritical behavior of the two-dimensional intrinsically ferromagnetic semiconductor CrGeTe3. Phys. Rev. B 2017, 95. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, H.Y.; Wang, X.S.; Wang, X.R. Breaking the current density threshold in spin-orbit-torque magnetic random access memory. Phys. Rev. B 2018, 97. [Google Scholar] [CrossRef]
- Laskowska, M.; Bałanda, M.; Fitta, M.; Dulski, M.; Zubko, M.; Pawlik, P.; Laskowski, Ł. Magnetic behaviour of Mn12-stearate single-molecule magnets immobilized inside SBA-15 mesoporous silica matrix. J. Magn. Magn. Mater. 2019, 478, 20–27. [Google Scholar] [CrossRef]
- Mu, C.; Hu, S.; Wang, J.; Kimura, T. Thermo-electric effect in a nano-sized crossed Permalloy/Cu junction under high bias current. Appl. Phys. Lett. 2013, 103, 132408. [Google Scholar] [CrossRef]
- Oh, S.; Jang, B.J.; Chae, H. Sensitivity Enhancement of a Vertical-Type CMOS Hall Device for a Magnetic Sensor. J. Electromagn. Eng. Sci. 2018, 18, 35–40. [Google Scholar] [CrossRef]
- Nordquist, K. Process development of sub-0.5 μm nonvolatile magnetoresistive random access memory arrays. J. Vac. Sci. Technol. B 1997, 15, 2274. [Google Scholar] [CrossRef]
- White, R.L.; Newt, R.M.H.; Pease, R.F.W. Patterned media: A viable route to 50 Gbit/in/sup 2/ and up for magnetic recording? IEEE Trans. Magn. 1997, 33, 990–995. [Google Scholar] [CrossRef]
- Cowburn, R.P. Room Temperature Magnetic Quantum Cellular Automata. Science 2000, 287, 1466–1468. [Google Scholar] [CrossRef] [PubMed]
- Brown, W.F., Jr. Micromagnetics; Interscience Publishers: New York, NY, USA, 1963. [Google Scholar]
- Laskowska, M.; Pastukh, O.; Konieczny, P.; Dulski, M.; Zalsiński, M.; Laskowski, L. Magnetic Behaviour of Mn12-Stearate Single-Molecule Magnets Immobilized on the Surface of 300 nm Spherical Silica Nanoparticles. Materials 2020, 13, 2624. [Google Scholar] [CrossRef] [PubMed]
- Laskowska, M.; Pastukh, O.; Kuźma, D.; Laskowski, Ł. How to Control the Distribution of Anchored, Mn12–Stearate, Single-Molecule Magnets. Nanomaterials 2019, 9, 1730. [Google Scholar] [CrossRef] [PubMed]
- Laskowski, L.; Kityk, I.; Konieczny, P.; Pastukh, O.; Schabikowski, M.; Laskowska, M. The Separation of the Mn12 Single-Molecule Magnets onto Spherical Silica Nanoparticles. Nanomaterials 2019, 9, 764. [Google Scholar] [CrossRef]
- Kuźma, D.; Montoncello, F.; Sobieszczyk, P.; Wal, A.; Giovannini, L.; Zieliński, P. Spin wave propagation properties across configurational antiferro/ferro-magnetic transitions. J. Appl. Phys. 2018, 124, 223902. [Google Scholar] [CrossRef]
- Kuźma, D.; Rychły, J.; Sobieszczyk, P.; Kłos, J.W.; Montoncello, F.; Zieliński, P. Edge Modes in the Switching Mechanism of Finite Chains of Macrospins. Proceedings 2019, 26, 11. [Google Scholar] [CrossRef]
- Akjouj, A.; Dobrzyński, L.; Al-Wahsh, H.; El Boudouti, E.H.; Leveque, G.; Pennec, Y.; Djafari-Rouhani, B. Magnonics; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 978-0-12-813366-8. [Google Scholar]
- Levy, J.C.S. (Ed.) Magnetic Structures of 2D and 3D Nanoparticles: Properties and Applications; Jenny Stanford Publishing: Singapore, 2016; ISBN 978-981-4613-67-5. [Google Scholar]
- Laskowska, M.; Kityk, I.; Pastukh, O.; Dulski, M.; Zubko, M.; Jedryka, J.; Cpałka, K.; Zieliński, P.M.; Laskowski, Ł. Nanocomposite for photonics—Nickel pyrophosphate nanocrystals synthesised in silica nanoreactors. Microporous Mesoporous Mater. 2020, 306, 110435. [Google Scholar] [CrossRef]
- Nisoli, C.; Moessner, R.; Schiffer, P. Colloquium: Artificial spin ice: Designing and imaging magnetic frustration. Rev. Mod. Phys. 2013, 85, 1473–1490. [Google Scholar] [CrossRef]
- Zhou, X.; Chua, G.L.; Singh, N.; Adeyeye, A.O. Large Area Artificial Spin Ice and Anti-Spin Ice Ni80Fe20 Structures: Static and Dynamic Behavior. Adv. Funct. Mater. 2016, 26, 1437–1444. [Google Scholar] [CrossRef]
- Wang, R.F.; Nisoli, C.; Freitas, R.S.; Li, J.; McConville, W.; Cooley, B.J.; Lund, M.S.; Samarth, N.; Leighton, C.; Crespi, V.H.; et al. Artificial ‘spin ice’ in a geometrically frustrated lattice of nanoscale ferromagnetic islands. Nature 2006, 439, 303–306. [Google Scholar] [CrossRef]
- Grimsditch, M.; Jaccard, Y.; Schuller, I.K. Magnetic anisotropies in dot arrays: Shape anisotropy versus coupling. Phys. Rev. B 1998, 58, 11539–11543. [Google Scholar] [CrossRef]
- Rivkin, K.; Heifetz, A.; Sievert, P.; Ketterson, J. Resonant modes of dipole-coupled lattices. Phys. Rev. B 2004, 70. [Google Scholar] [CrossRef]
- Stoner, E.C.; Wohlfarth, E.P. A mechanism of magnetic hysteresis in heterogeneous alloys. Philos. Trans. R. Soc. Lond. Ser. A 1948, 240, 599–642. [Google Scholar] [CrossRef]
- Wohlfarth, E.P. Relations between Different Modes of Acquisition of the Remanent Magnetization of Ferromagnetic Particles. J. Appl. Phys. 1958, 29, 595–596. [Google Scholar] [CrossRef]
- Jamet, S.; Rougemaille, N.; Toussaint, J.C.; Fruchart, O. Head-to-head domain walls in one-dimensional nanostructures. In Magnetic Nano- and Microwires; Elsevier: Amsterdam, The Netherlands, 2015; pp. 783–811. [Google Scholar]
- Shinjo, T. Magnetic Vortex Core Observation in Circular Dots of Permalloy. Science 2000, 289, 930–932. [Google Scholar] [CrossRef]
- Schneider, M.; Hoffmann, H.; Zweck, J. Magnetic switching of single vortex permalloy elements. Appl. Phys. Lett. 2001, 79, 3113–3115. [Google Scholar] [CrossRef]
- Yin, L.F.; Wei, D.H.; Lei, N.; Zhou, L.H.; Tian, C.S.; Dong, G.S.; Jin, X.F.; Guo, L.P.; Jia, Q.J.; Wu, R.Q. Magnetocrystalline Anisotropy in Permalloy Revisited. Phys. Rev. Lett. 2006, 97, 067203. [Google Scholar] [CrossRef]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; Waeyenberge, B.V. The design and verification of MuMax3. AIP Adv. 2014, 4, 107133. [Google Scholar] [CrossRef]
- Exl, L.; Bance, S.; Reichel, F.; Schrefl, T.; Stimming, H.P.; Mauser, N.J. LaBonte’s method revisited: An effective steepest descent method for micromagnetic energy minimization. J. Appl. Phys. 2014, 115, 17D118. [Google Scholar] [CrossRef]
- Kuźma, D. Spin Dynamics in Inhomogeneous and Defected Low Dimensional Systems. Ph.D. Thesis, Institute of Nuclear Physics PAN, Krakow, Poland, 2018. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).