Abstract
In order to optimize the use of compact porous media as flow and heat transfer devices, it is imperative to understand those coherent structures of the associated flow that generate and sustain turbulence. Given the deficiency of data regarding this area in the literature, this study has been carried out to fill this need. To this end, a series of particle image velocimetry measurements were conducted to capture a turbulent flow field bounded by a model permeable medium of 85% porosity. The bulk Reynolds numbers based on the bulk velocity through the entire flow domain and the depth of flow over the permeable boundary are approximately 5.0 × 103 and 2.0 × 104. By applying velocity gradient eigenanalysis, quadrant decomposition, multi-point correlations, and proper orthogonal decomposition, requisite information about the coherent structures of the flow field is extracted. The results indicate the existence of spatial structures whose order, size, and orientation are dependent on the Reynolds number and location along the permeable boundary. While the largest scales are marked by sweeps, ejections, and high vortex activity, there is evidence of inward and outward interactive events at the upstream portions of the permeable boundary layer flow. This work helps to clarify some observations made on turbulent flow over the compact permeable boundary.
1. Introduction
Turbulent flows over permeable wall boundaries are of considerable importance in natural and engineering applications such as groundwater hydrology, mass transfer in packed beds, gas turbine blade cooling systems, and wood drying processes [1]. Similar to canonical turbulent boundary layers [2], understanding the structure of a turbulent boundary layer over a permeable wall is imperative to developing requisite turbulent flow control and heat transfer techniques. Consequently, there is a rising need to understand those coherent structures of the flow that are integral to the generation and self-sustenance of turbulence in the flow. It is on this subject matter, then, that this study focuses.
Prior investigations of the coherent structures over permeable boundaries have, however, been limited. Perhaps, one of the most notable initial observations was from the numerical simulations of Breugem et al. [3]. In that work, the authors solved the volume-averaged Navier–Stokes equations of the flow field around porous media of packed beds of a wide range of porosities (0%, 60%, 80%, and 95%) and of small mean particle diameters. The inlet conditions were modeled with a prescribed mean velocity profile or an instantaneous velocity field from a previous simulation. Using autocorrelations of the velocity, they detected relatively large vortical structures in the region close to the highly permeable boundaries. In contrast with solid boundaries, these structures were found to be more irregular and neither elongated nor streaky.
Zhu et al. [4] subsequently utilized particle image velocimetry (PIV) to study the turbulent flow above a large mature corn canopy. Using quadrant-hole analysis, they concluded that large-scale structures that dominate the Reynolds stresses and turbulent production rates apparently bear very little correlation with each other. However, sweep events were found to be the largest contributors to Reynolds stresses and production rates.
In another study, Suga et al. [2] undertook PIV measurements of a turbulent flow over a 3 m long porous medium. Foamed ceramics of porosity ~80% were used as the porous medium. The tests were conducted to investigate the mechanism of the development of the turbulent vortex structure over porous walls of varying permeability and over a wide range of Reynolds numbers. They were able to show whole-flow field realizations with indicators of hairpin vortices close to the permeable wall boundary. Using conditional statistics, Suga et al. identified sweeps to be the most dominant very near the permeable wall, whilst ejections are prevalent in the buffer region. They also pointed out that stronger sweeps tend to move toward the wall whilst ejections tend to lose their strength as the wall permeability increases. From those direct observations, Suga et al. [2] were able to contrive a conceptual scenario of the development of the vortex structure at a distinctive range of moderate permeability Reynolds number.
Mannes et al. [5] also conducted a separate experimental program to study the effects of permeability on wall turbulence. The velocities were obtained from laser Doppler anemometry measurements of the turbulent open-channel flow over highly porous (i.e., over 96%) polyurethane foam. Wide ranges of permeability and Reynolds numbers were considered. Through quadrant analysis, these researchers were able to demonstrate that, similar to rough wall turbulent boundary layer flows, flows at permeable walls have a near-wall region where sweeps dominate and an outer region where ejections dominate. However, as the wall permeability increased, the near-wall flow was found to be more coherent and marked mainly by successions of sweeps and ejections. Additionally, Mannes et al. used spectral analysis to identify the development of shear-instability eddies over the wall with the highest permeability. The sizes of these eddies were noted to be proportional to the shear penetration depth. Subsequently, they argued that the near-wall structure of turbulent flows over permeable walls is determined by rival mechanisms between attached and shear instability eddies. They also proposed that for a given wall permeability flow condition, the ratio between the shear penetration depth and the boundary layer thickness may be used to evaluate which eddy structure dominates the near-wall region.
Using the lattice Boltzmann method (LBM), Kuwata and Suga [6] performed a direct numerical analysis (DNS) of the flow over a porous boundary. The porous medium was modeled using arrays of interconnected staggered cubes of porosity 71%, and the Reynolds number was kept constant. Periodic boundary conditions were applied to the streamwise and spanwise directions with a constant streamwise pressure difference. The data were examined using two-point autocorrelations, one-dimensional energy spectra, and snapshot proper orthogonal decomposition (POD) analyses. They observed that compared with the case of an impermeable wall, the streaks of vortex structures over the porous layer are much vaguer in their presence and are about twice as wide. In particular, the first and second modes of their POD analysis of the pressure field showed clear spanwise-transverse rolls emanating from Kelvin–Helmholtz (K-H) instability. The cores of those structures were also found to be regularly aligned over the porous layer. Motlagh and Taghizadeh [7] also performed a snapshot POD analysis to educe the dominant structures of large-eddy simulations of plane turbulent flow over a permeable boundary. Three porosities were studied, namely 0, 80% and 95%, and the Reynolds number was kept constant. Their work showed the potency of wall permeability to influence the size and shape of the large-scale, energetic dominant structures of the flow.
In a succession of works [8,9], the research group Suga later investigated the effects of permeability anisotropy by means of LBM DNS and PIV experiments. Specifically, the porous media used in the experiments were 3 m long and of 70% porosity. They observed through two-point correlation analysis of the simulations that the streamwise component of the permeability tensor allows the development of streamwise large-scale perturbations induced by K-H instability. Quadrant analysis of the PIV data also showed that the streamwise component of the permeability tensor also influences the contribution from sweeps and ejections to the Reynolds shear stress.
More recently, Alfonsi et al. [10] studied the turbulent flow in natural rough beds using large-eddy simulations validated by three-component acoustic Doppler velocimeter measurements. The flow field was a fully-developed turbulent open-channel flow bounded by a permeable bed composed of pebbles of a median size of 70 mm. A novel flow visualization method based on the turbulent kinetic energy rate definition was proposed. When using this, a much higher population of vortices within the inertial subrange was found close to the permeable boundary compared to the location further away from the boundary. Additionally, with the aid of a Q-criterion method based on the velocity-gradient tensor second invariant, worm-like coherent structures were observed. These structures were particularly noted to have intense vortical motion.
In summary, there are a number of numerical and experimental studies documenting the multi-dimensional regions of the flow where a field variable exhibits substantial correlation with itself or with another variable at spatial or temporal scales larger than the smallest scales of the flow [11]. As the foregoing review represents the main substance of the study of those coherent structures associated with turbulence over porous boundaries, they are substantially few in comparison with the body of literature pertaining to single-point assessments (see review in ref. [12]). Indeed, in all of the studies surveyed, the permeable boundaries are modeled, to register a fully-developed flow at the region of study, or assigned a model entry flow. Thus, to the author’s knowledge, there is no such information on the coherent motions and structures pertaining to compact porous media. This is a significant deficiency in the literature, given that in many situations, a compact permeable boundary is preferred in order to control the flow turbulence or to augment the heat transfer [13,14,15]. Some of this deficiency is corrected using in this study by conducting two-dimensional PIV measurements at the edge of the turbulent flow over a model permeable boundary. The permeable boundary is modeled as a square array of pin-fin rods such that the porosity is 85% and the filling fraction is 21%. The purpose of the tests is to study the coherent motions of the turbulent flow over a compact porous medium for a wide range of Reynolds numbers. This work complements a previous study on single-point turbulence statistics of the flow field of a compact permeable boundary [12] by supplying a more spatially resolved measurement to study the inherent spatial structures. More importantly, this study uniquely presents a wide-ranging evaluation of the coherent structures using eigenanalysis of the velocity gradient tensor, two-point autocorrelations, quadrant decomposition, and POD analysis.
The paper is organized as follows. The experimental technique and methods of analyses are described in Section 2 and Section 3. In Section 4, the results of the analyses are presented along with some pertinent discussion. Finally, a summary of the most important conclusions is provided in Section 5.
2. Experimental Technique
2.1. Test Channel and Model Porous Medium
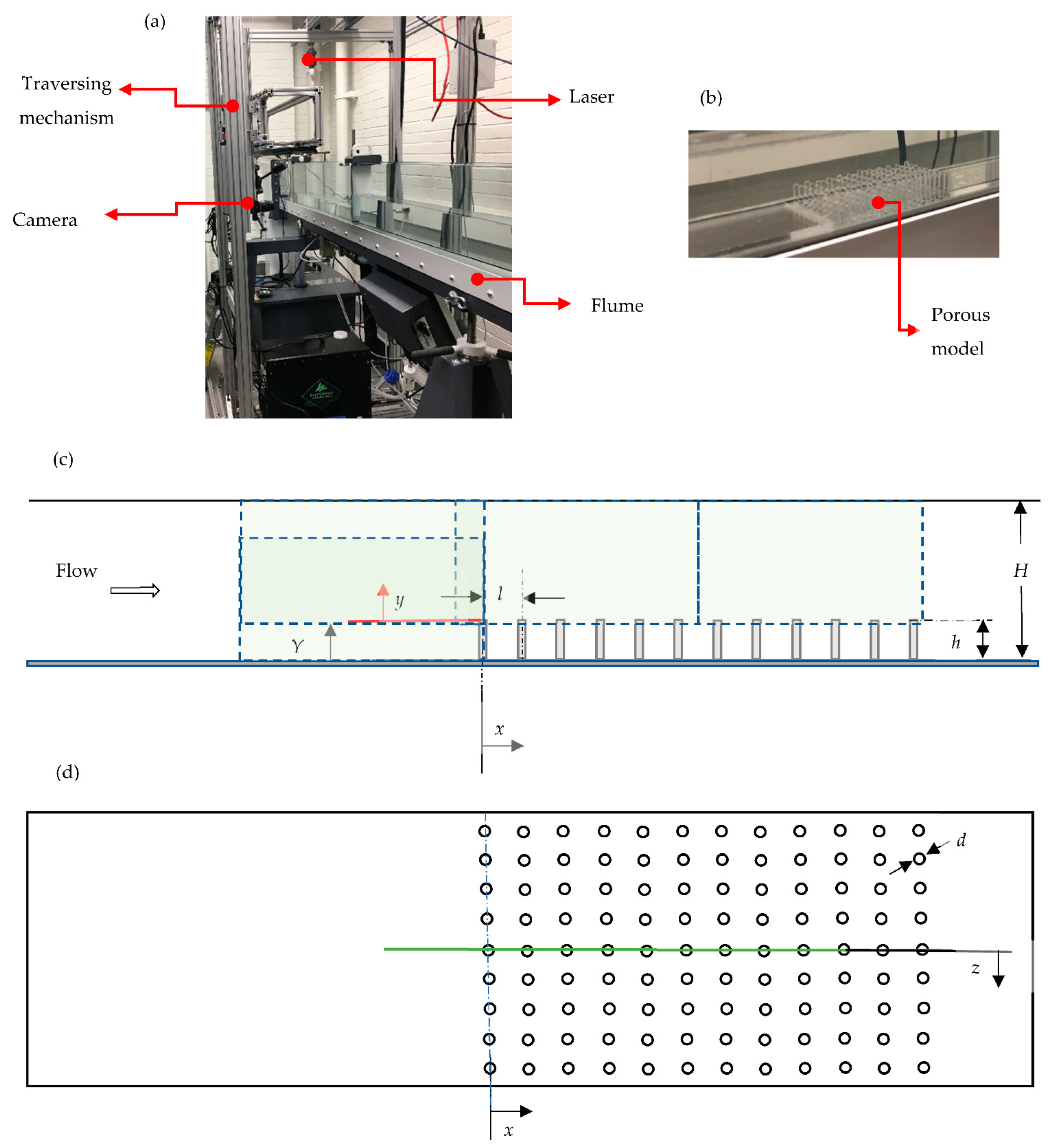
The experimental set-up is made up of a model test channel, a porous medium model, a closed-circuit flow transport channel, and a planar particle image velocimetry (PIV) system. The entire set-up is depicted in Figure 1, along with a definition of the relevant Cartesian coordinate system employed.
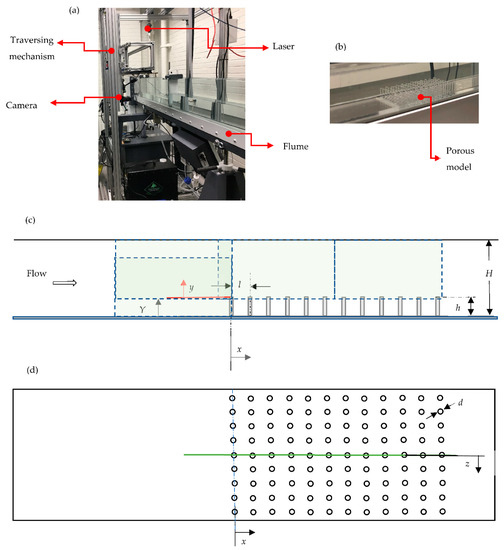
Figure 1.
(a) Experimental set-up; (b) porous model in the test channel; (c) side view of the porous medium model, with blue dashed boxes indicating 4 planes of measurement; (d) top view of the porous model with green line indicating midspan location of the laser sheet. Note that the difference between the current arrangement and ref [12] is that in the present work, (1) a different lens is coupled to the camera for higher resolution measurement; (2) different planar positions are measured; and (3) different flow rates are tested.
The model channel was fabricated from 6 mm thick transparent acrylic plates. After cutting them into the required sizes, the plates were glued into internal dimensions of length 2500 mm, width 69 mm, and depth H = 43 mm. In order to create a section for tripping the flow, fourteen square rods were used. They were aligned in length along the span of the channel and equidistantly spaced in the streamwise direction. They were glued on the first 90 mm portion of both upper and lower walls of the channel entrance. The model channel also had a section created for the installation of the porous medium model.
As shown in Figure 1b,c, the porous medium model consists of a plate with holes drilled into it in a square array. In all, twelve holes were drilled in the streamwise (x) direction, while nine holes were drilled in the spanwise (z) direction so that the model is essentially compact in size. The holes were drilled with a center-to-center distance l of 7.19 mm between immediate holes. Transparent acrylic rods of nominal diameter d = 3.18 mm were inserted into the holes, culminating in a porous medium height h of 9.06 mm. Consequently, the porosity and filling fraction of the porous medium model are 85% and 21%, respectively.
The assembly of the test section was accomplished by fixing the model test channel and porous medium model in the recirculating flume. This assembly was designed such that the location such that the center of the most upstream column of the rods was 1200 mm from the flow entry. With respect to Figure 1, it must be noted that the Cartesian coordinate directions used are such that the origin of the streamwise (x = 0) is located 1200 mm from the flow entry. The origins of the wall-normal directions (y = 0 and Y = 0) are fixed on top of the porous medium and the lower wall of the channel, respectively. The origin of the spanwise direction (z = 0) is also located in the midspan of the channel.
2.2. Measurement Technique
Velocity measurements were made using a two-dimensional two-component PIV system. The system consists of an Nd:YAG Dual Cavity 200 mJ/pulse laser of wavelength 532 nm, a 12-bit charged couple device camera of 1608 × 1208-pixel array and 7.4 μm pixel pitch, a programmable timing unit, and a dual-processor computer with a 32-gigabyte random access memory on which a PIV software (DaVis-10) was installed. In executing the technique, the working fluid (water) was seeded with silver-coated hollow glass spheres with mean diameter 10 μm and specific gravity 1.4. The flow field was illuminated by a thin sheet of light generated by the pulsed laser head connected to a set of cylindrical lenses. The light scattered by the seeding particles in the flow was then captured and recorded as digital images using the camera with a 55 mm focal length Nikon lens coupled to it. The programmable timing unit was used to match the trigger rate of the laser as well as the image capturing rate of the camera. Data were acquired and monitored on the computer, with further post-processing and plots performed using DaVis-10, MATLAB, OriginLab, and TecPlot 360 software.
In order to optimize measurements, several steps were taken in the selection and operation of the PIV hardware and related test space. With respect to the neutral buoyancy of the seeding particles, the assessment of their suitability was performed by considering the settling velocity and the response time parameters [12,16]. These were estimated to be 21.8 × 10−6 m s−1 and 2.22 × 10−6 s, respectively. With such values being insignificant relative to the mean velocities and sampling time used in the tests, it was predicted that the seeding particles would faithfully follow the fluid flow. Additionally, the laser was also focused into a thin sheet of light of ~ 1.5 mm, and kept within the area of interest. Reflections were reduced by maintaining dark and dull surfaces wherever possible. The intensity of the laser was also carefully regulated to allow sufficient illumination within all parts of the test section. Furthermore, the camera was equipped with an orange filter of band-pass wavelength of 532 nm ± 10 nm so that all the camera light exposure would be entirely due to the laser. In order to facilitate movement of the camera and laser in an orthogonal plane, both hardware was moved on a traversing mechanism within a least count of ±0.5 mm. Such movements were achieved while keeping the distance between the camera and the laser unchanged.
During the measurement, the laser pulse separation time was estimated through an iterative process such that the particle displacement was no more than a quarter of the interrogation area [17]. By applying particle image diameters of no less than 5 pixels, the effects of peak-locking were curtailed. Overall, a field of view of 45.6 mm × 34.2 mm in the x and y directions respectively was used. This resulted in a scale factor of 35.3 pixels per mm. Using an image sampling rate of 5 Hz, 6000 instantaneous image pairs were acquired for each round of measurement. In processing the data, the initial interrogation area was set to a size of 128 pixels × 128 pixels, followed by a validation step taken to eliminate outliers. Eventually, each interrogation window was also segmented into 32 pixels × 32 pixels. This ensured that for a sub-pixel accuracy of 0.1, the dynamic range is would be approximately 80.
By setting a 75% overlap between neighboring interrogation areas, supplementary vectors were provided so that the distances between neighboring vectors in physical units were 0.26 mm in both streamwise and wall-normal directions. Thus, the spatial resolution presented herein is much better than that of our previous work [12], allowing for a better evaluation of the spatial structures of flow. Assuming local equilibrium, the Kolmogorov length scale (η) and the Taylor microscale (λ) were assessed as outlined in ref [12]. For the entry flow, η was approximately 41% to 136% of the vector spacing, and λ was estimated to be 93 to 274 times the vector spacing. This means that the current tests are expected to adequately resolve the wide range of spatial scales expected within the flow.
2.3. Test Conditions and Uncertainty Limits
The test conditions are summarized in Table 1. Systematic measurements of the velocity data in the test section were conducted for two rounds of tests. These tests are hereafter denominated A and B, respectively. For each test, four x–y midspan planes were captured, as schematized in Figure 1b. This was performed by moving both camera and laser to view the top entry, bottom entry, and two planes of flow bounded by the porous medium.

Table 1.
Boundary layer test conditions of the entry flow.
In this work, the components of the time-averaged velocities in the streamwise and wall-normal directions are respectively indicated by mean velocities U and V. The turbulent intensities in either direction are also denoted as u and v, respectively. The bulk velocity Ub was determined as a line average of the time-averaged streamwise velocity across the entire depth of the test channel. The Reynolds numbers based on this velocity and the depth of the free flow (H−h) are approximately 5.0 × 103 and 2.0 × 104, respectively, for Tests A and B. Other boundary layer parameters were computed following definitions detailed in ref. [12]. The maximum velocity Ue, boundary layer thickness δ, displacement thickness δ*, momentum thickness θ, shape factor H (=δ*/θ) have been summarized in Table 1 for Tests A and B.
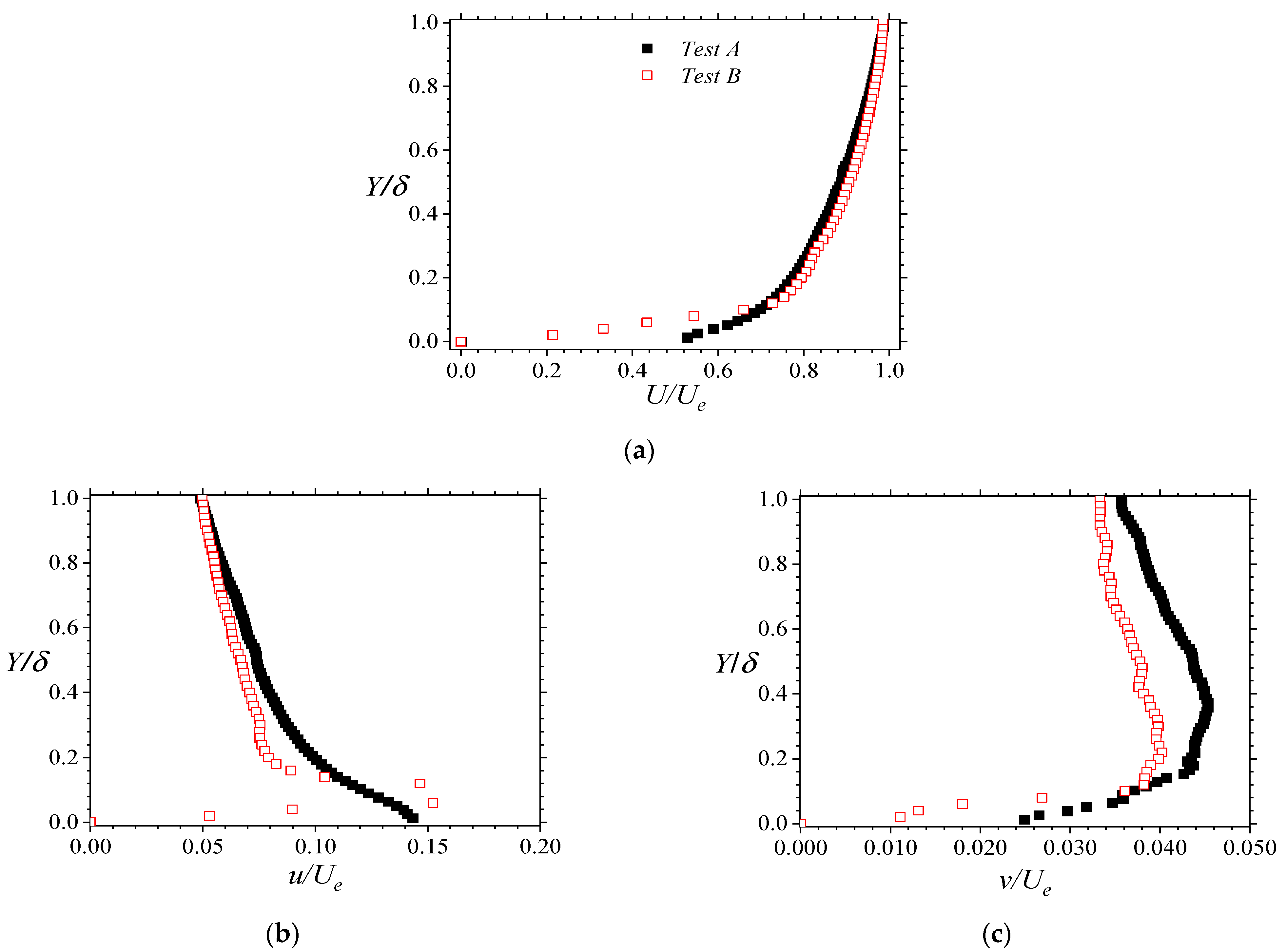
Each of the streamwise components of the entry mean flow data for the respective test conditions is plotted in Figure 2. In Figure 2a, this is performed in outer coordinates (with Ue and δ as the scaling parameters). Furthermore, as shown in Figure 2b,c, the relative background levels at the edge of the entry boundary layer is ~5%. This compares reasonably with values reported in zero-pressure gradient turbulent boundary layer studies [18]. The statistical relative uncertainties of the mean velocities, velocity intensities, Reynolds normal stresses, and Reynolds shear stresses were found to be no more than ±1.5%, ±2.0%, ±2.3%, and ±3.3% of their respective peak values.
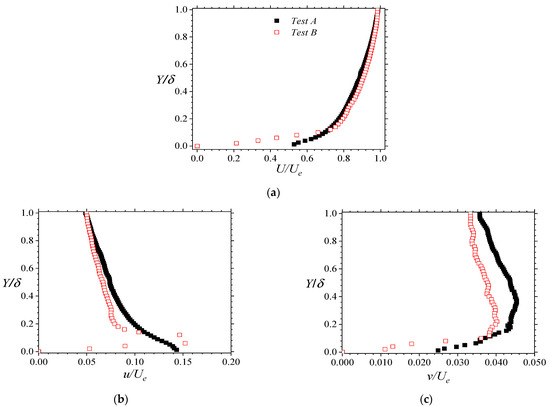
Figure 2.
Streamwise component of the mean entry velocity U in (a) outer coordinates (U normalized by the maximum entry velocity Ue). Streamwise (b) and wall-normal (c) components of the turbulence intensities (u and v, respectively).
3. Methods of Educing Coherent Structures
In this work, four methods of extracting coherent structures are used, namely, engen-analysis of the velocity gradient tensor, quadrant decomposition, two-point correlations, and proper orthogonal decomposition.
3.1. Eigenanalysis of the Velocity Gradient Tensor
In order to distinguish vortices in the flow, an eigen-analysis of the velocity gradient tensor was conducted. In doing this, unambiguous vortex identification criteria for identifying the swirling and shear strengths of the flow were applied. This is based on the fact that the local velocity gradient tensor will have one real eigenvalue and a pair being of the form b ± √c. If c is positive, then it is shear. On the other hand, if c is negative (thus resulting in a pair of complex eigenvalues), then it is an indication of a swirl [19,20].
For the present work, a two-dimensional two-component PIV was used. As the complete local velocity gradient tensor is unavailable through that technique, a two-dimensional assessment of the swirling and shear strength was performed by determining the eigenvalues of the in-plane velocity gradient matrix [21,22]. For the x–y plane, this is obtained as follows
The solution to Equation (1) is given by
The shear strength λcr is defined at a location where the solution is real, while the swirling strength λci is at a location where the solution is complex. The magnitudes of the shear and swirling strengths are thus respectively determined by
where
and
where
3.2. Two-Point Correlations of Velocity Fluctuations
Two-point correlations were computed to determine the distances over which the turbulence field was correlated across the flow. As reviewed in Section 1, such correlations have been used extensively to quantify the extent of coherent structures. In other boundary layer studies, these have also been used to provide indications of the shape and inclinations of the associated coherent structures [23,24].
In general, the two-point correlation function RAB between any two arbitrary quantities A and B at a given reference location (xref, yref) is determined as follows:
In Equation (5), and are the spatial separations between A and B in the streamwise and wall-normal directions, respectively. The symbols and respectively represent the root-mean-square values of A and B at (xref, yref) and . In this work, only two-point auto-correlations of the streamwise and wall-normal fluctuating velocities are reported.
Approximations of the average angle (i.e., β in degrees) of streamwise inclination of the autocorrelation of the streamwise component of the velocity fluctuation (i.e., Ruu) were determined. These were performed by fitting a least-square line through points consisting of the extreme points on the five contour levels (i.e., 0.5, 0.6, 0.7, 0.8, and 0.9) and the self-correlation peak of Ruu.
3.3. Quadrant Decomposition
Introduced by Willmarth and Lu [25], quadrant decomposition has long been used as a tool for evaluating the intensity of Reynolds shear stress produced by coherent structures of the flow. This method involves dividing the local flow behavior into four quadrants, depending on the sign of the streamwise and wall-normal velocity fluctuations (i.e., u′ and v′, respectively). By doing this, the turbulent events of the boundary layer are unambiguously defined. Thus, for the first quadrant (Q1: u′ > 0 and v′ > 0), outward motions of high-speed fluid towards the center of the flow field are denoted. For the second quadrant (Q2: u′ < 0, v′ > 0), the movement of low-speed fluid away from the wall and towards the wall (i.e., ejection) is signified. For the third quadrant (Q3: u′ < 0 and v′ < 0) and fourth quadrant (Q4: u′ > 0 and v′ < 0), the inward motion of low-speed fluid toward the wall and the in-rush of high-speed fluid (i.e., sweep) are respectively designated.
Following Lu and Willmarth [26], the mean Reynolds shear stress at each point was decomposed into the respective quadrant contributions with the exclusion of a hyperbolic hole of size D by the following equation:
In Equation (6), N is the total number of fluctuating velocity vectors. This parameter is equivalent to the total number of PIV realizations per round of plane testing (i.e., N = 6000). On the other hand, IQ is a detector function given by
The parameter D is a specified hole size, representing a threshold on the strength of the Reynolds shear stress-producing events. In this work, D = 0, thus allowing all Reynolds shear stress events to be included in the decomposition.
3.4. Proper Orthogonal Decomposition
Proper orthogonal decomposition (POD) was used to decompose the test data into an optimal set of basis functions (i.e., spatial eigenfunctions or modes). This was performed so as to extract the energetically dominant modes in the flow. As coherent structures are deemed to possess a substantial portion of the total turbulence kinetic energy, POD is a useful tool for examining them [7]. In this work, the method of snapshots [27] was used to conduct the POD analysis in a manner as laid out by Agelin-Chaab [28]. This method is known to considerably simplify the calculation of the autocovariance matrix POD analysis, reducing the order of the eigenvalue problem to the number of snapshots [7].
The method was implemented for N snapshots with M grid points. Each snapshot corresponds to the instantaneous PIV images or realizations. The grid points are the total number of vectors in each instantaneous image. For the two-dimensional PIV data used, the focus was on the fluctuating parts of two velocity components. Thus, the ensemble-average velocity for a sequence of N snapshots was first computed. The fluctuating portions of the streamwise and wall-normal velocities were then accumulated for all N snapshots and arranged in a matrix U of the form (, ), where n = 1,…, N and j = 1,…, M. Subsequently, the symmetric positive definite cross-covariance matrix C (=UTU) was then computed. For i = 1, … N, a set of N eigenvalues (=λi) was then obtained and arrayed in decreasing order of magnitude (i.e., λ1 > λ1 > λ1 > 0). A corresponding set of orthonormal eigenvectors Ai that satisfies the corresponding eigenvalue problem C Ai = λi Ai was also obtained. From these eigenvectors, the normalized empirical eigenfunctions (or POD modes) were determined as follows
In Equation (8), is the nth component of the eigenvector Ai that corresponds to λi, and the in the denominator stands for the L2-norm of the vector enclosed. It should be noted that the expansion of the so-called POD coefficient was computed as an = ΨTu′n where Ψ = [ϕ1, ϕ2 … ϕN]. A reconstruction of the fluctuating velocities could thus be accomplished using
As the POD analysis is performed on the fluctuating velocity components, each eigenvalue represents a depiction of the turbulent kinetic energy associated with the corresponding POD mode. Thus, the total of all the eigenvalues and the energy fraction associated with the ith mode are respectively:
and
4. Results and Discussion
In this section, results are presented with a specific focus on the flow above and close to the permeable wall. Some of the relevant turbulent structures are analyzed by first identifying and distinguishing the zones of vortex motion in the permeable boundary layer flow and their dynamical generation. Their order, shape, extent, and orientation are then considered. Subsequently, specific events associated with the motions of these structures are determined. The analysis is then completed with an overview of the dominant energy modes associated with the structures.
4.1. Identification and Distinction of Vortex Regions
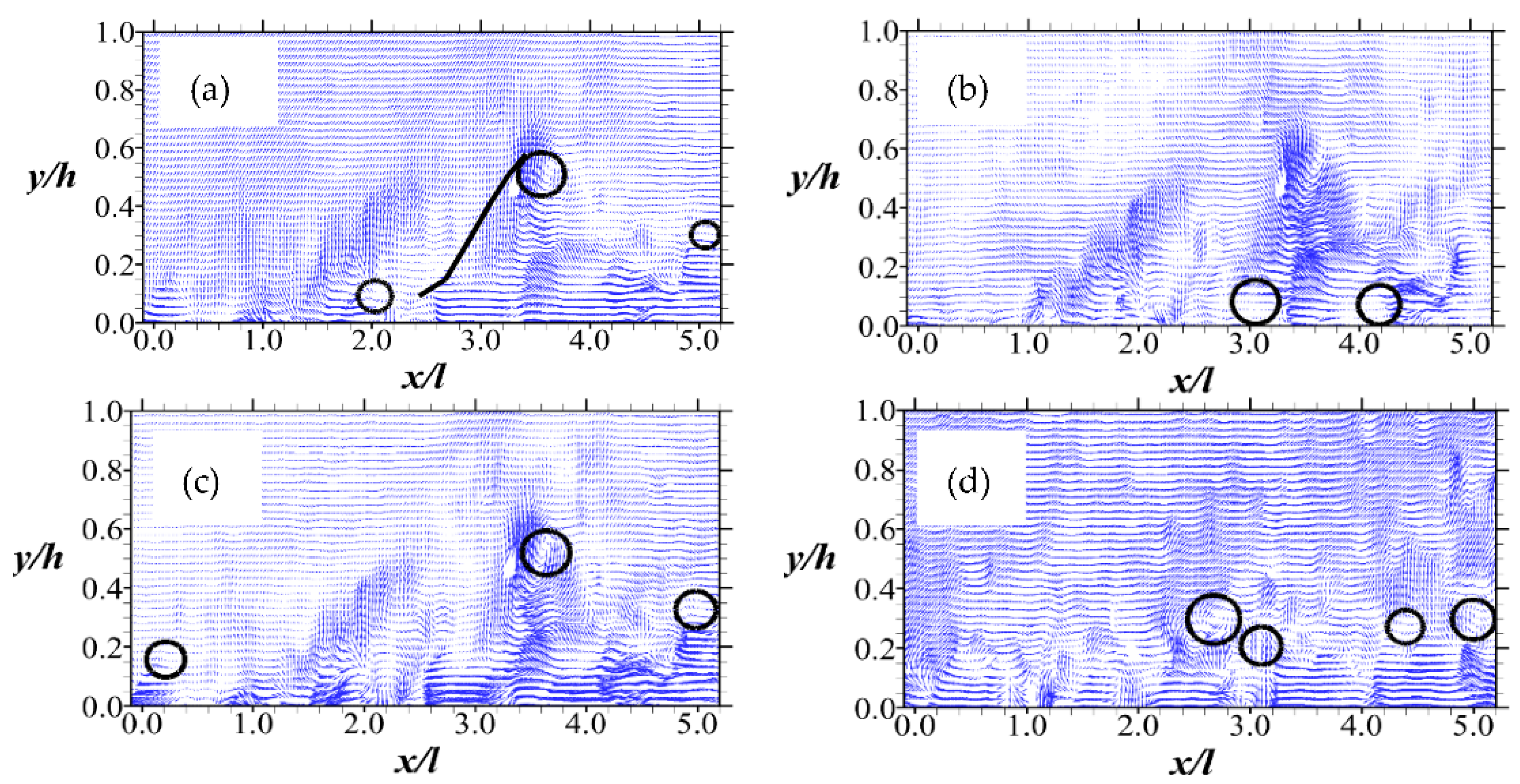
The identification of vortex regions has been one of the highlights of previous studies of turbulent flow over permeable boundaries (e.g., ref. [2]). This is because it provides important information about the size, reach, and motions of organized structures in a turbulent flow. With planar PIV data, one is able to visualize vortices on whole flow field vector maps through decompositional methods such as Galilean, Reynolds, and large-eddy simulation (LES) methods [22]. Examples of these are shown in Figure 3. With the Galilean decomposition, large-scale vortex cores are identified. Indeed, there are few indicators of hairpin vortices close to the permeable wall. This is shown in Figure 3a, where features such as the vortex head, inclined areas of ejection vectors, stagnation points, and inclined shear layer [29] are apparent. The small-scale vortices are more evident using the Reynolds decomposition and LES method. In Figure 3a–c, these features are compared for the same measurement taken at the same instant during Test A. Another sample Galilean decomposition is presented for Test B data in Figure 3d. Overall, these maps display a wide range of vortex cores, apparently within a wall-normal height of 60% of the porous medium depth h.
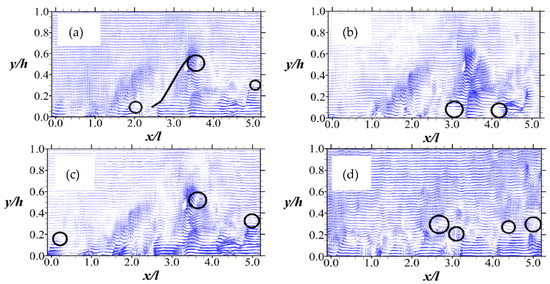
Figure 3.
Vector maps identifying vortices using instantaneous fluctuating vector fields for Test A through (a) Galilean decomposition of using a convection velocity of 0.8 Ub (b) Reynolds decomposition; and (c) LES decomposition. In (d), vortices are identified for Test B using a convection velocity of 0.8 Ub in a Galilean decomposition. For all the maps, the vortices are shown using circles. A shear layer is indicated by a line extending from the circle (vortex head).
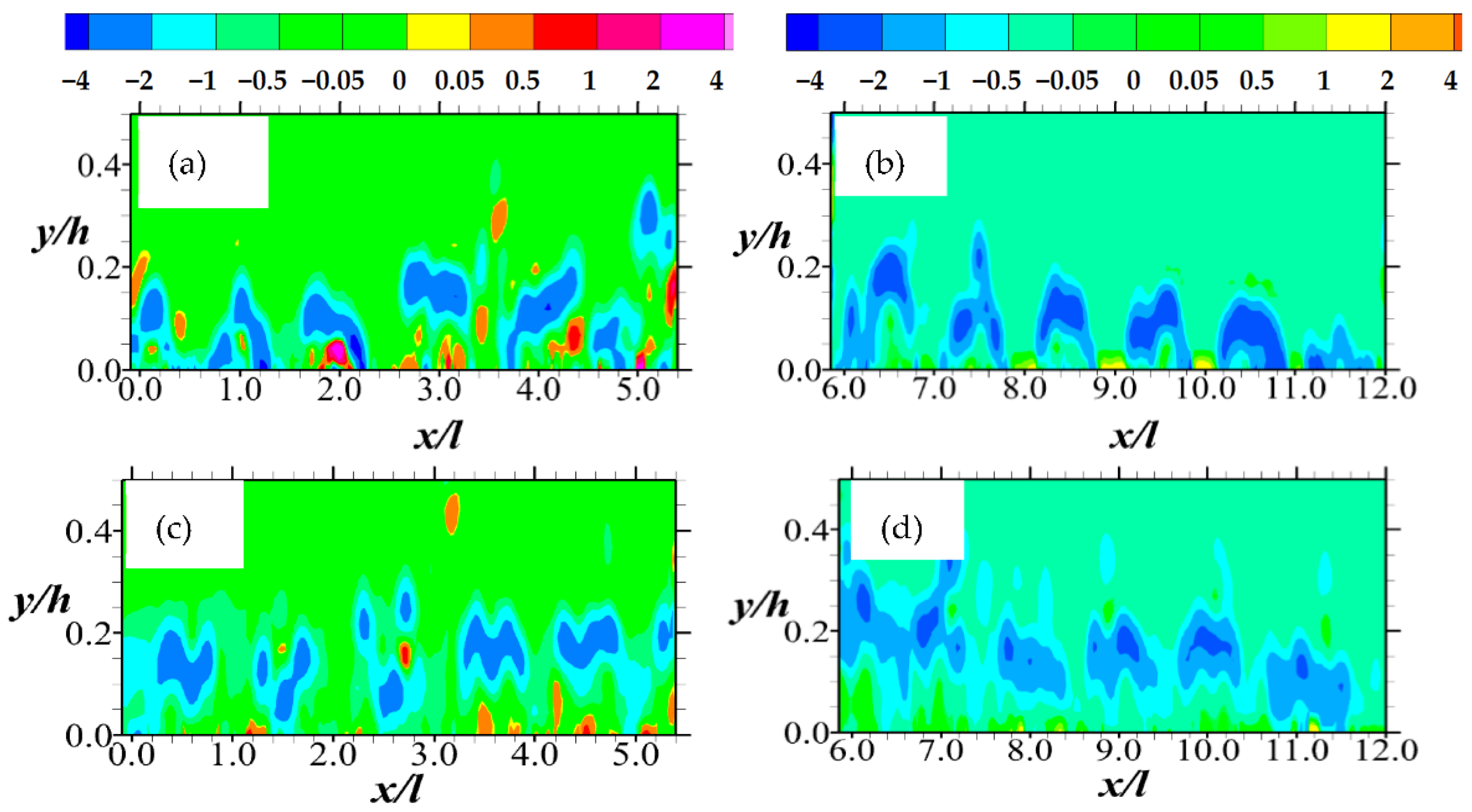
A more common criterion for vortex identification, however, is the vorticity parameter. By using that criterion in Figure 4, a complex but organized system of vortex cores of mean spanwise vorticities (Ωz = ∂V/∂x − ∂U/∂y) is shown. These cores are positioned close to the permeable boundary. While there are isolated small regions of intense positive vorticities, the negative vorticities are more widespread and bigger. The reason why these regions have negative vorticities is that those regions have a relatively small mean wall-normal velocity gradient in the streamwise coordinate (∂V/∂x) compared with the mean streamwise velocity gradient in the wall-normal direction (∂U/∂y). It is also noted that the intensities of the vorticities appear to decline downstream. This is consistent with observations in a previous study regarding the dissipation of vorticity downstream of the compact porous medium [12].
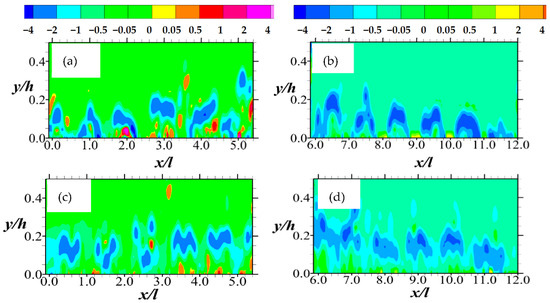
Figure 4.
Mean vorticity normalized by the maximum streamwise entry velocity and the diameter of the rods are shown in (a,b) for Test A, and (c,d) for Test B. Note that the legends for (a,c) and (b,d) are not the same. Those for these plots (a,c) and (b,d) are above (a), and (b) respectively. Furthermore, note that (a,c) are closer to the inlet and (b,d), downstream.
The locations and sizes of these vortex cores are dependent on the Reynolds number and streamwise locations with respect to the porous boundary. In terms of the locations, for example, the vortex cores of Test A are generally found just above the porous medium rods. Consequently, they also tend to rise above the boundary, up to a height of 0.40 h. The vorticities of Test B, on the other hand, perhaps being freer to communicate with the porous medium through the pore spacing, are found in between the rods. Thus they barely rise beyond a magnitude of 0.30 h, except for the rare case of a peak vortex. It is also clear that while the streamwise extent of the vortex cores is 60% or less of the distance between the rods for the first six columns of rods, they are more extensive downstream. It appears that due to the compactness of the porous medium, the vortex cores have a downward inclination downstream of the porous medium.
While an important criterion for detecting vortex regions, vorticity maps are not able to distinguish between regions arising from pure rotation and those from shear. Thus, as outlined in Section 3.1, to show such distinctions of vorticity generation, eigenanalysis of the mean velocity gradient are used to retrieve the shear and swirling strengths. The results of these analyses are shown in Figure 5 and Figure 6, respectively, normalized by the maximum entry velocity and the rod diameter. Unsurprisingly, the contour plots in Figure 5 show that the dynamical generation of the vortex cores of the flow is mostly due to shear. The shear regions appear to extend from within the porous medium itself. For the case of Test A, the shear strength is highest at the very edge of the permeable boundary. This is indicative of the kind of high shear zones that tend to activate Kelvin–Helmholtz instabilities that lead to the formation of spanwise rollers [2,12]. It is also noteworthy that these shear regions are elongated and intermitted with thin regions of no shear. While these are certainly not the streaky structures associated with boundary layer flows of impermeable walls [29], they are reminiscent of them, and more so at higher Reynolds number flows. However, instead of being aligned in the streamwise direction, these ‘streaky’ structures associated with the shear strength are aligned in the wall-normal directions. In Figure 6, the regions of vorticity emanating from swirls are shown to be sparse and generally detached from the permeable boundary. However, at a higher Reynolds number, rotation becomes a more effective method of generating vorticity. These are the vorticities that peak off at a relatively higher wall-normal location compared to the others.
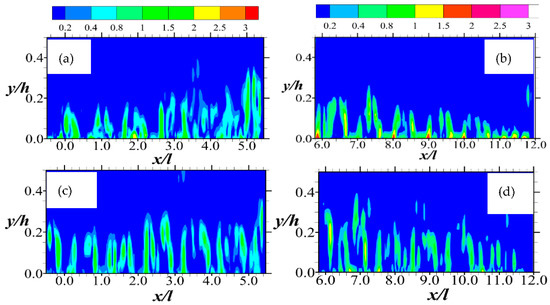
Figure 5.
Shear strength are shown in (a,b) for Test A, and (c,d) for Test B. Normalization was performed using the maximum streamwise entry velocity and the diameter of porous media rods. Note that the legends for (a,c) and (b,d) are not the same. Those for these plots (a,c) and (b,d) are above (a), and (b) respectively. Furthermore, note that (a,c) and are closer to the inlet and (b,d) downstream.
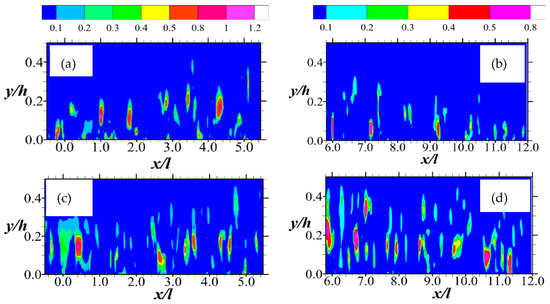
Figure 6.
Swirling strength are shown in (a,b) for Test A, and (c,d) for Test B. Normalization was performed using the maximum streamwise entry velocity and the diameter of porous media rods. Note that the legends for (a,c) and (b,d) are not the same. Those for these plots (a,c) and (b,d) are above (a), and (b) respectively. Furthermore, note that (a,c) are closer to the inlet and (b,d) downstream.
4.2. Special Features of Spatial Structures
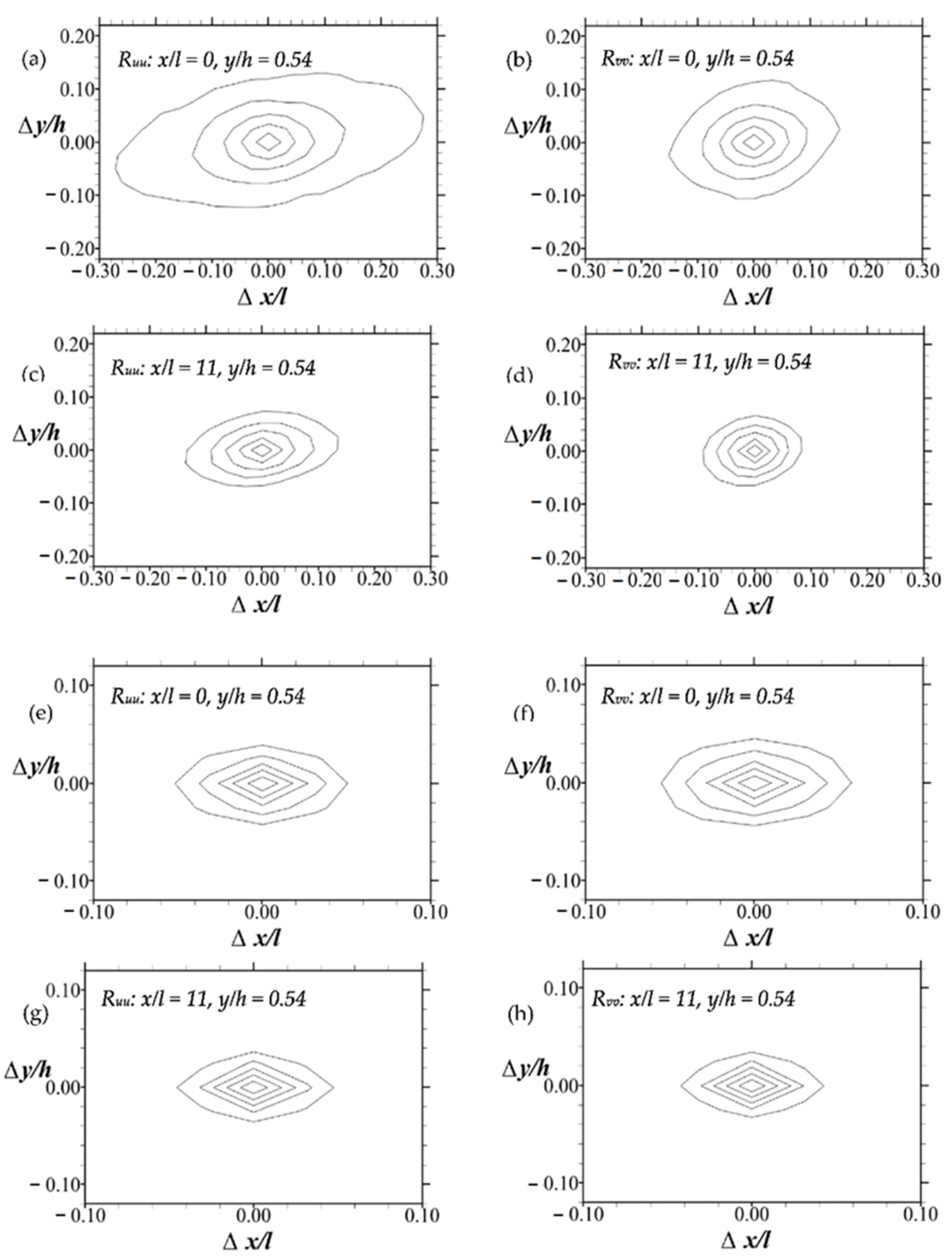
In order to investigate the order, shape, extent, and orientation of the coherent structures in further detail, two-point spatial autocorrelation functions of the streamwise fluctuating velocities (Ruu) and the wall-normal fluctuating velocities (Rvv) are used. The spatial coherence of organized structures of the flow is illustrated using sample iso-contours of the correlation profiles in Figure 7. For those plots, the contours are centered at (x/l = 0, y/h = 0.54), and (x/l = 11, y/h = 0.54) for both Tests A and B. The contour levels for each of the plots are 0.5, 0.6, 0.7, 0.8, and 0.9, respectively, in an inward direction towards the core of the contour. These results pertain to extreme streamwise locations immediately above the rods of the permeable boundary and within the midspan plane. Thus, they provide a satisfactory preliminary insight into the evolution of organized structures across the permeable boundary layer turbulent flow.
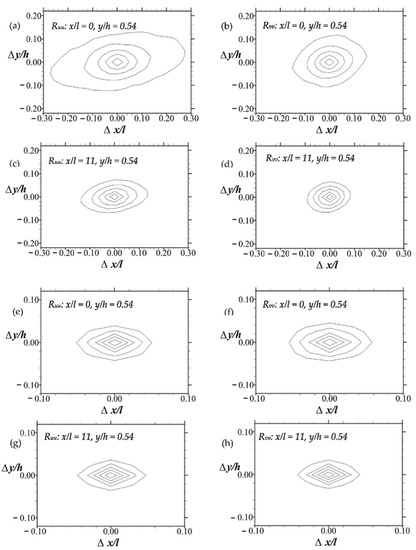
Figure 7.
Sample iso-contours of Ruu and Rvv. Plots in (a–d) are for Test A, and (e–h) are for Test B. The contour levels for each of the plots are 0.5, 0.6, 0.7, 0.8, and 0.9, respectively, in an inward direction towards the core of the contour.
It is evident that the Ruu contours are larger and more elongated in shape along the stream than in the wall-normal direction. There is also a quasi-streamwise alignment of the contours. These features are particularly so around the most upstream column of rods of the permeable boundary and less so at the most downstream rod locations. The extent and elongation of Ruu contours point to the existence of spatial structures of the flow that are more organized in the streamwise direction relative to the wall-normal direction. Compared with Ruu, the Rvv contours are more condensed and rounded. Overall, some of these observations are similar to those reported elsewhere for channel flows over smooth and rough impermeable walls [30].
Following the methodology outlined in previous works [30,31], a more comprehensive assessment of the evolution of the average size and inclination of the correlation function contours is conducted. This is performed on the basis that such an assessment will provide an indication of the extent, shape, and orientation of structures such as hairpin vortices associated with turbulent boundary layers [24]. In order to study the wall-normal changes in size and inclinations associated with the autocorrelation functions, contours of Ruu and Rvv were obtained for different wall-normal positions (ranging from y/h = 0.04 to 1.54) per two fixed streamwise locations (at x/l = 0 and 11 respectively). The streamwise variations were studied by examining the contours of Ruu and Rvv retrieved from various streamwise locations (x/l = 0.10 to 11.80), for which the wall-normal location is fixed at y/h = 0.243 (i.e., close to the permeable boundary).
In order to estimate the relative contour sizes, the streamwise and wall-normal spatial extents of Rvv (signified by Lxvv and by Lyvv, respectively) were correspondingly evaluated as the streamwise and wall-normal distances between the extreme points on the Rvv = 0.5 contour level. For the Ruu contours, the streamwise extent of Ruu (signified by Lxuu) was evaluated as twice the distance between the most downstream point on the Ruu = 0.5 contour level and the self-correlation peak. The wall-normal extent of Ruu (signified by Lyuu) was also evaluated as the wall-normal distance between the furthest and closest locations from the permeable boundary on the Ruu = 0.5 contour level. It is noted that these central locations of the contours were selected in a way that assessments are unaffected by the edges of the respective image frames. The results of the wall-normal and streamwise variations of the spatial extents of the contours are respectively presented in Figure 8 and Figure 9. In order to magnify wall-normal differences, Figure 8 is shown as log-linear plots. Approximations of the average angles of streamwise inclination of Ruu (i.e., β in degrees) were also made as described in Section 3.2. The results are shown in Figure 10.
In general, the data in Figure 8 confirm the observations qualitatively deduced from Figure 7. However, additional details are apparent. Firstly, the trend in wall-normal variations of the streamwise and wall-normal spatial extents of the correlation functions are similar at the downstream and upstream locations of the permeable boundary. Just above the boundary, the spatial extents are usually less than 10% of the diameter d of the porous medium rods. However, the sizes tend to increase initially with the wall-normal location. The sizes then dip slightly after peaking off (for Test A), or they plateau at 1.5 h (for Test B). The initial increment in extent is Reynolds number dependent. While that of Test B (the higher Reynolds number test) is marginal, Test A (the lower Reynolds number test) is up to three times the corresponding value of Test A. Notwithstanding this difference, the general increase implies that further away from the permeable boundary, the flow’s spatial structures tend to be more correlated. Indeed, it appears that this wall-normal correlation is much better at the leading edge of the porous boundary than at the trailing edge.
Additionally, as presented in Figure 8, the ratios of the streamwise to wall-normal extents for Ruu, are, on average, 1.8 and 1.4 at x/l = 0 and 11. For Rvv, the ratios of the extents are closer to 1. While the ratios for Ruu are less than what has been reported for turbulent flows over smooth walls or rough walls, that of Rvv are comparable with those reported for both kinds of near-wall boundary layer flows [32].
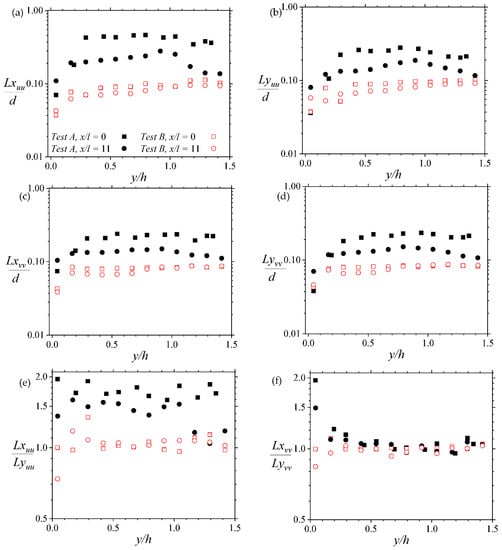
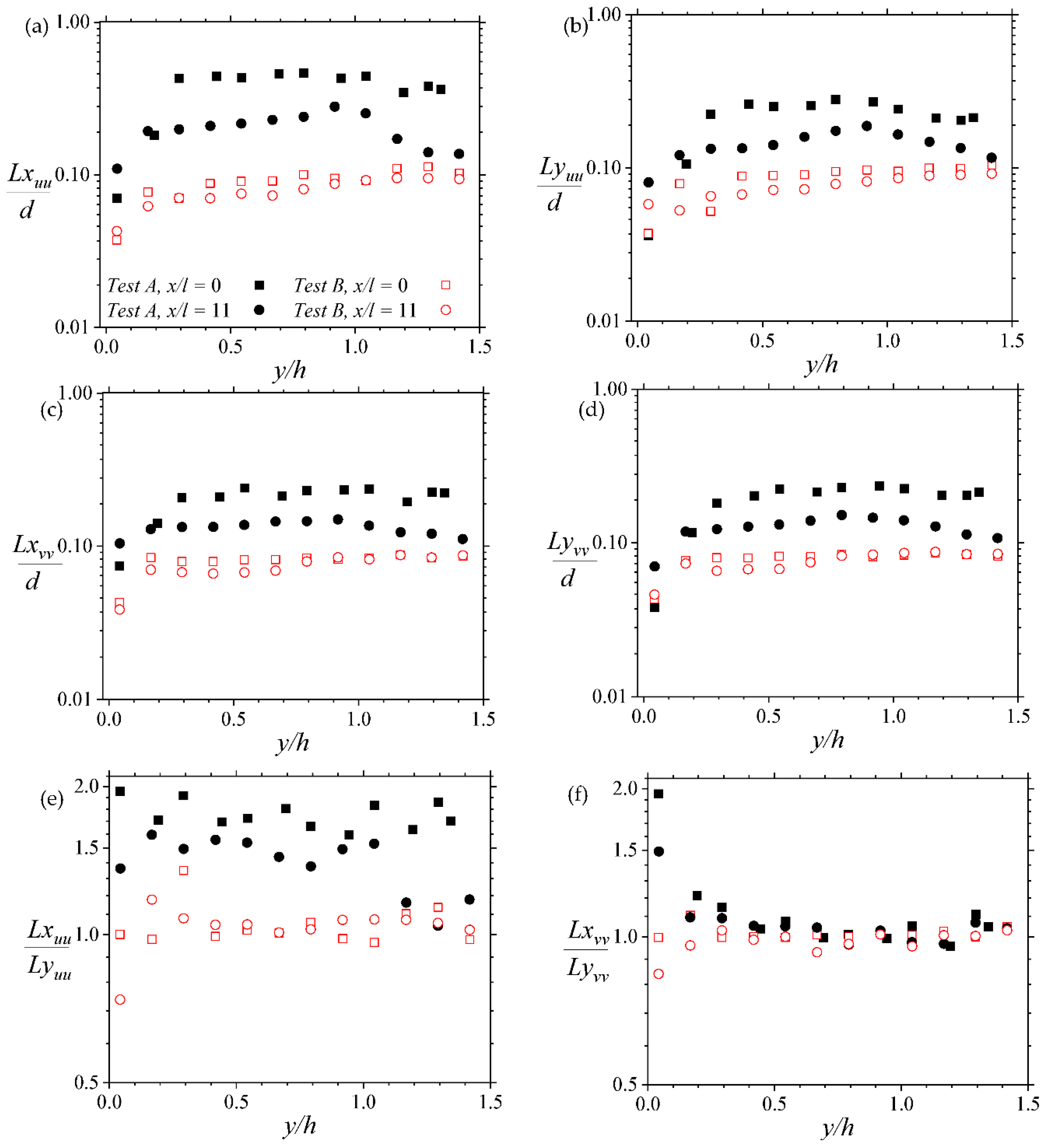

Figure 8.
Log-linear plots showing wall-normal variations of the streamwise and wall-normal extents of the two-point correlations (2PC) at two streamwise locations above the porous boundary. Note that Lxuu, Lyuu, Lxvv, Lyvv are respectively the streamwise extent of the 2PC of the streamwise velocity, wall-normal extent of the 2PC of the streamwise velocity, streamwise extent of the 2PC of the wall-normal velocity, wall-normal extent of the 2PC of the wall-normal velocity. Legend in (a) applies to all plots in (b–f).
Figure 8.
Log-linear plots showing wall-normal variations of the streamwise and wall-normal extents of the two-point correlations (2PC) at two streamwise locations above the porous boundary. Note that Lxuu, Lyuu, Lxvv, Lyvv are respectively the streamwise extent of the 2PC of the streamwise velocity, wall-normal extent of the 2PC of the streamwise velocity, streamwise extent of the 2PC of the wall-normal velocity, wall-normal extent of the 2PC of the wall-normal velocity. Legend in (a) applies to all plots in (b–f).

From Figure 9, it may also be inferred that for Test B, the spatial extents of the correlation function contours and their streamwise/wall-normal ratios are independent of the streamwise location. Thus, the spatial structures are not expected to grow along the stream over a compact porous medium at such high Reynolds numbers. However, at much lower Reynolds numbers, such as in Test A, the spatial extents reduce dramatically along the stream to a minimum at approximately x/l = 5. Subsequently, their values become constant further downstream. The reason for this initial sharp decline is unclear. Nevertheless, these observations are consistent with vortex zone markers apparent in the vector maps that were previously reviewed.
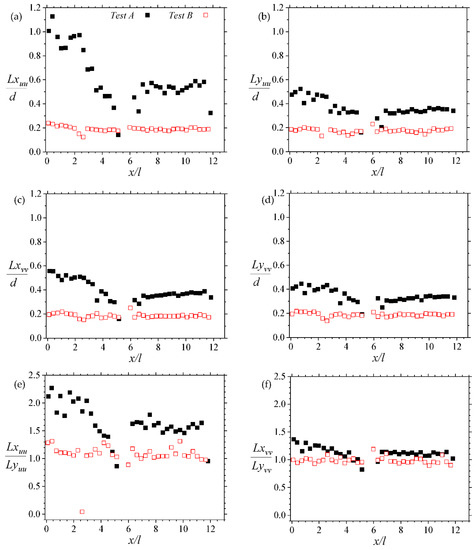

Figure 9.
Linear plots showing streamwise variations of the streamwise and wall-normal extents of the two-point correlations (2PC) for Tests A and B. Note that Lxuu, Lyuu, Lxvv, Lyvv are respectively the streamwise extent of the 2PC of the streamwise velocity, wall-normal extent of the 2PC of the streamwise velocity, streamwise extent of the 2PC of the wall-normal velocity, wall-normal extent of the 2PC of the wall-normal velocity. Legend in (a) applies to all plots in (b–f).
Figure 9.
Linear plots showing streamwise variations of the streamwise and wall-normal extents of the two-point correlations (2PC) for Tests A and B. Note that Lxuu, Lyuu, Lxvv, Lyvv are respectively the streamwise extent of the 2PC of the streamwise velocity, wall-normal extent of the 2PC of the streamwise velocity, streamwise extent of the 2PC of the wall-normal velocity, wall-normal extent of the 2PC of the wall-normal velocity. Legend in (a) applies to all plots in (b–f).

The results of the assessed angles of inclination are shown in Figure 10. They show that for Test A, the angles decay with the increase in wall-normal distance from the permeable boundary. Along the stream, the angles of streamwise inclination show significant scatter ranging from 0 to ~25 for the first six columns of porous medium rods and then become fairly constant at around 10. For Test B, on the other hand, the flow behavior is quite different. The correlation function contours are essentially aligned perfectly in the streamwise direction.
If the angle of inclination of Ruu is taken as the average inclination of the hairpin packets [31], then those spatial structures are expected to be inclined, as shown in Figure 10. It is important to note, however, that the angles estimated here are much broader than the range (i.e., 15 ± 5) reported for canonical turbulent flows [30,33,34,35].
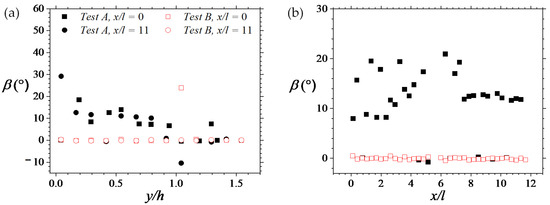
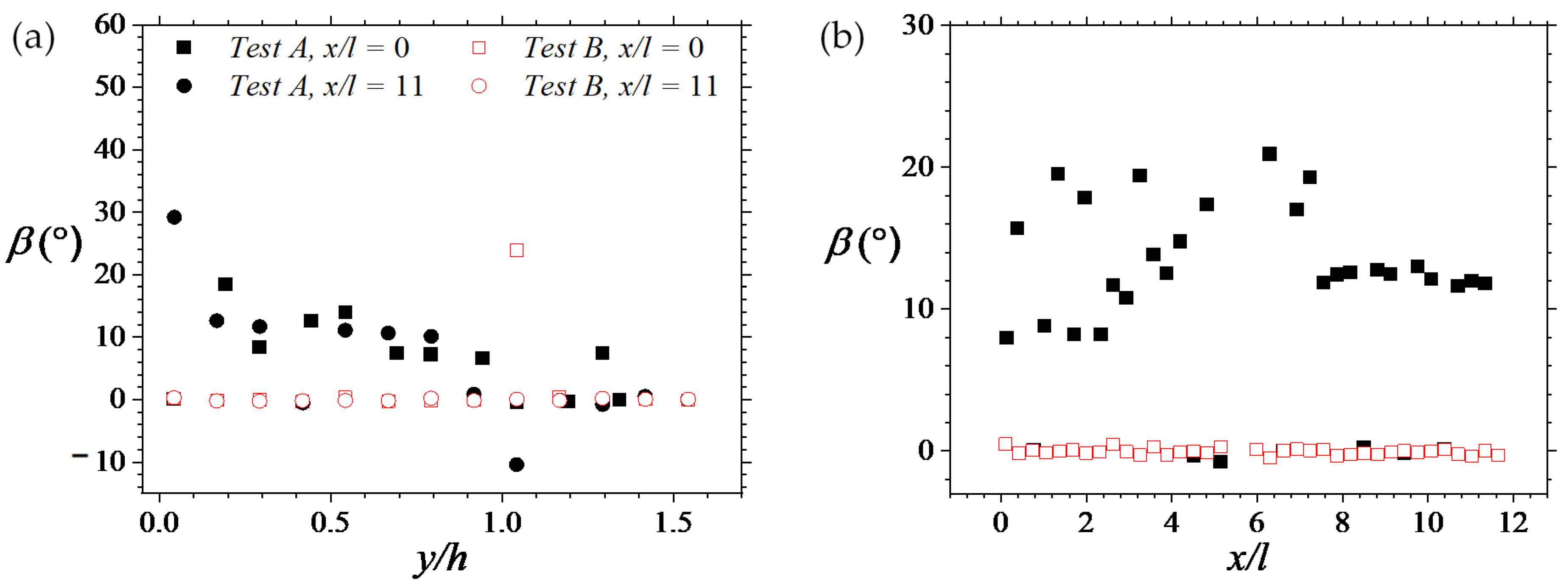

Figure 10.
(a)Wall-normal variation and (b) Streamwise variation of the angle of streamwise inclination of the two-point correlation of the streamwise velocities. Note that for (b), filled boxes represent Test A results whereas red unfilled boxes are for Test B.
Figure 10.
(a)Wall-normal variation and (b) Streamwise variation of the angle of streamwise inclination of the two-point correlation of the streamwise velocities. Note that for (b), filled boxes represent Test A results whereas red unfilled boxes are for Test B.

4.3. Events of Turbulent Motion
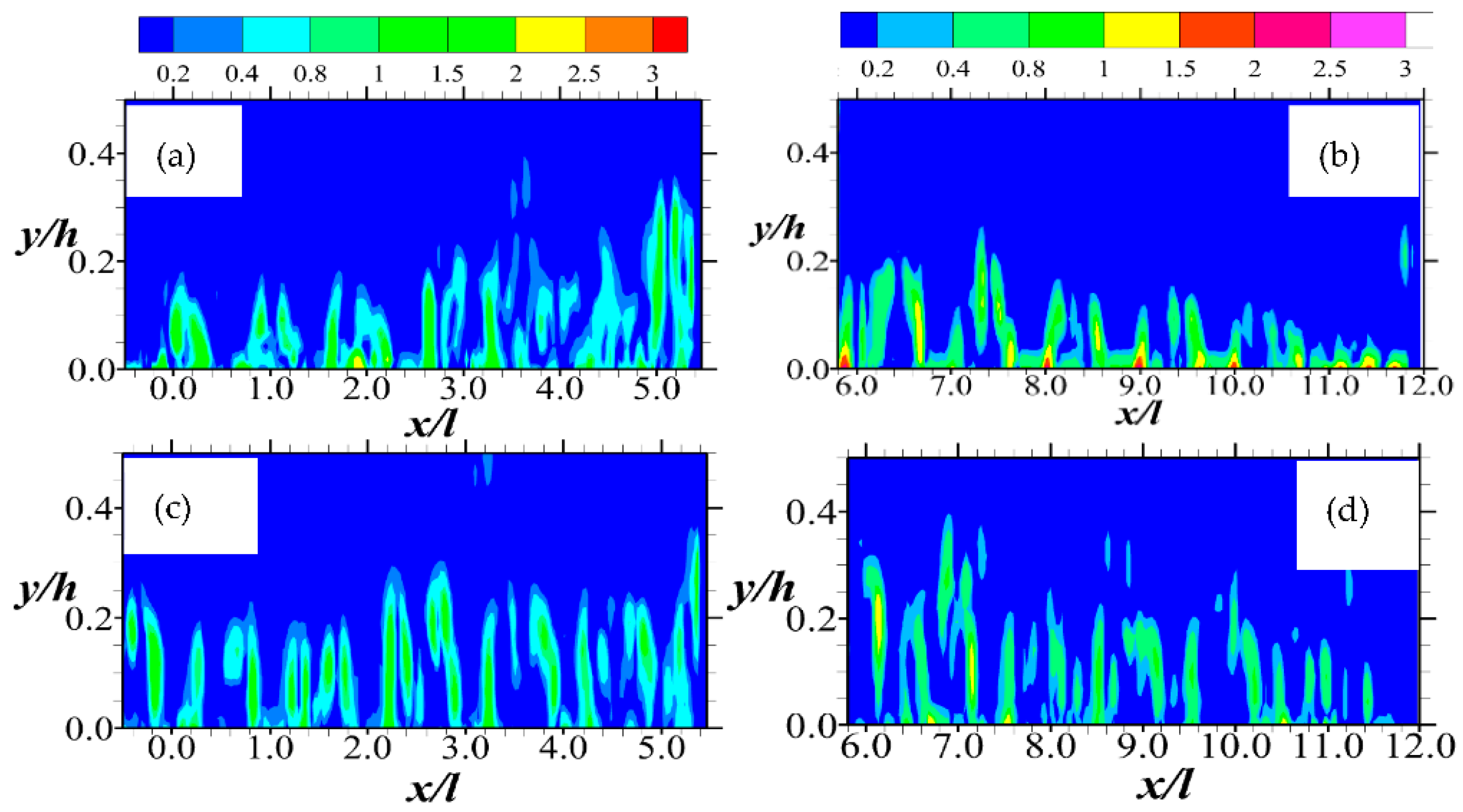
In order to provide some insight into specific events of coherent motions, the information provided through quadrant decomposition is now considered. This analysis serves to specifically characterize the dominant motions associated with the production of Reynolds shear stress. The results are summarily presented through contour plots in Figure 11, Figure 12, Figure 13 and Figure 14. These plots show events of quadrants 1, 3, 2, and 4, respectively, in terms of Reynolds shear stress normalized by the maximum velocity of the entry flow.
As for the spatial features described in Section 4.2, the results that are shown in this section also indicate that the events of turbulence over the permeable boundary are a function of the Reynolds number as well as the streamwise and wall-normal directions. Thus, Figure 11 shows that the outward motions of high-speed fluid towards the center of the flow field are somewhat prevalent at the upstream portion (i.e., the first six columns of rods) of the permeable boundary. Further downstream, however, this outward interaction is sedated, particularly for Test A, where the Reynolds number is relatively low. In addition to these streamwise changes in fluid motion, it is important to note that while the outward interaction of the high-speed fluid appears to grow along the stream, particularly around the upstream rods, they subsequently decline. A comparison of Figure 11 with Figure 12 shows that apart from the most upstream rows of the permeable boundary rods, the outward interactions of Q1 are much more predominant compared to the inward motion of low-speed fluid of Q3.
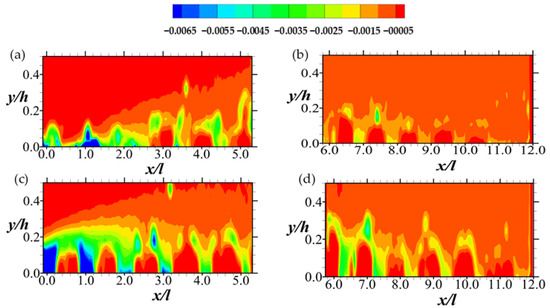
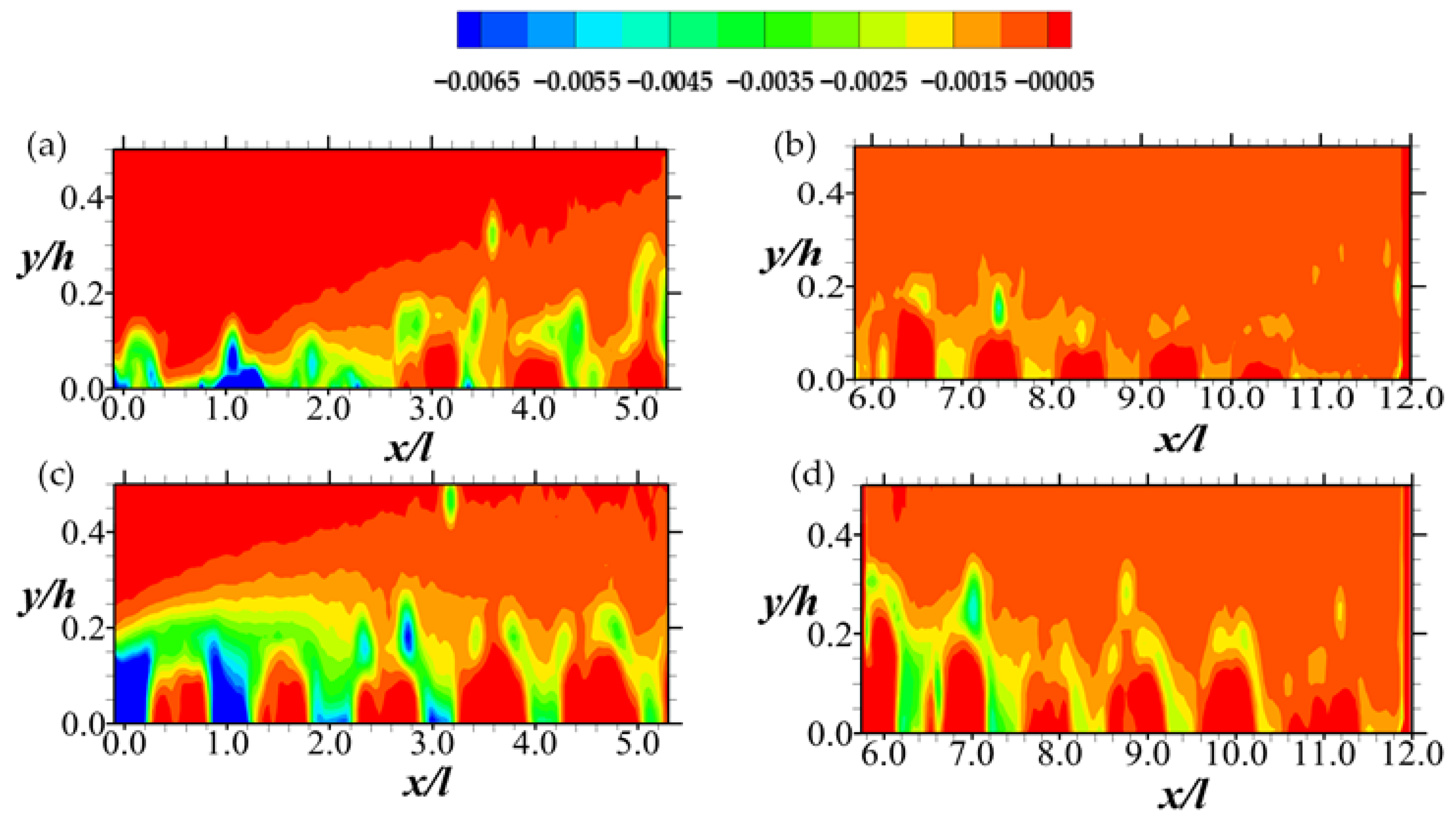
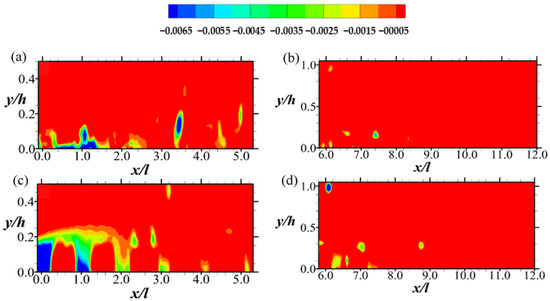
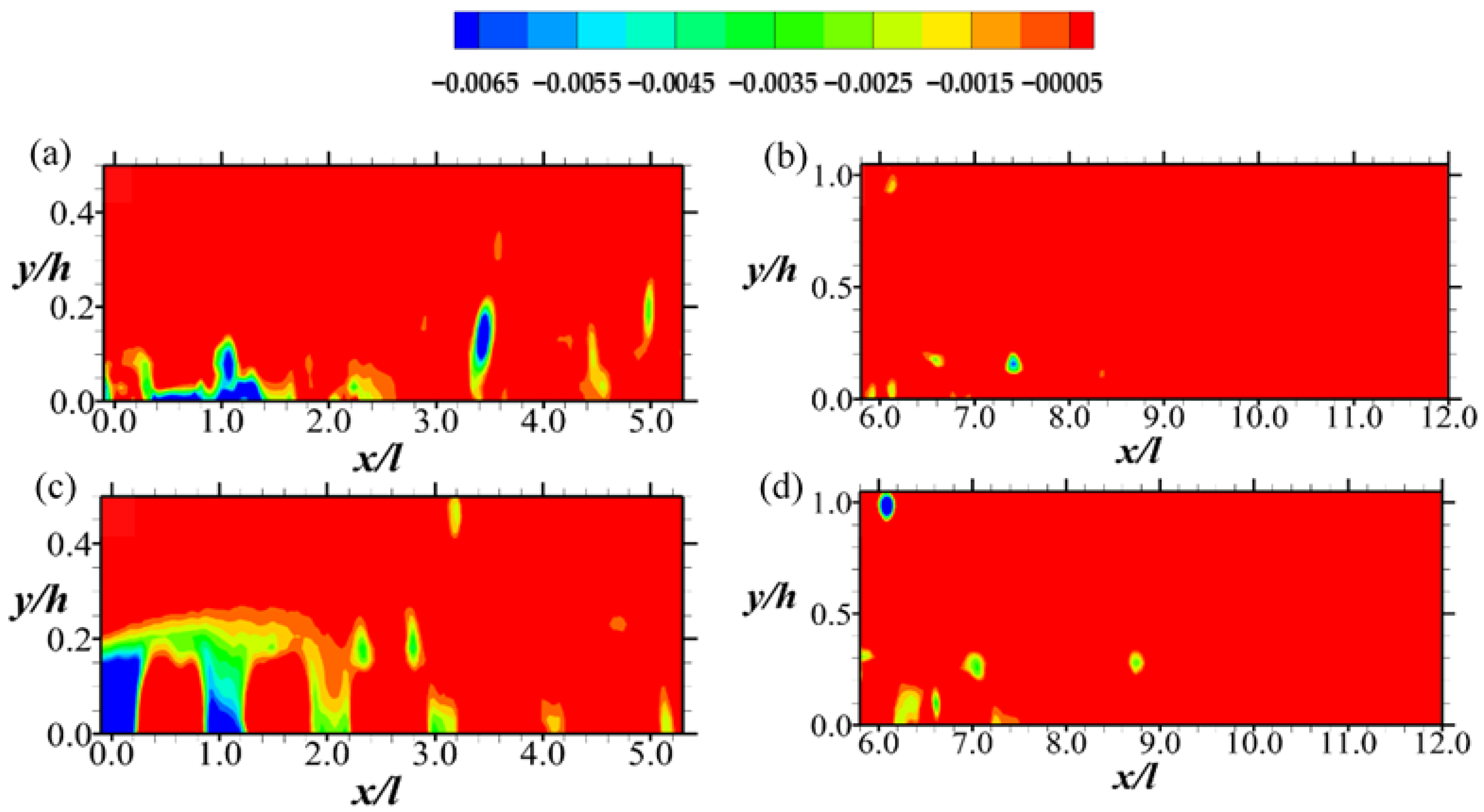

Figure 11.
Contour plots of (from Equation (6)) for Quadrant 1 (Q1) events of the Reynolds shear stress normalized by the respective maximum mean streamwise entry velocity. Note that the hole size (i.e., D in Equation (6)) used is 0. The Q1 events are shown in (a,b) for Test A, and (c,d) for Test B. The legend all the plots are above (a,b).
Figure 11.
Contour plots of (from Equation (6)) for Quadrant 1 (Q1) events of the Reynolds shear stress normalized by the respective maximum mean streamwise entry velocity. Note that the hole size (i.e., D in Equation (6)) used is 0. The Q1 events are shown in (a,b) for Test A, and (c,d) for Test B. The legend all the plots are above (a,b).


Figure 12.
Contour plots of (from Equation (6)) for Quadrant 3 (Q3) events of the Reynolds shear stress normalized by the respective maximum mean streamwise entry velocity. Note that the hole size (i.e., D in Equation (6)) used is 0. The Q3 events are shown in (a,b) for Test A, and (c,d) for Test B. The legend all the plots are above (a,b).
Figure 12.
Contour plots of (from Equation (6)) for Quadrant 3 (Q3) events of the Reynolds shear stress normalized by the respective maximum mean streamwise entry velocity. Note that the hole size (i.e., D in Equation (6)) used is 0. The Q3 events are shown in (a,b) for Test A, and (c,d) for Test B. The legend all the plots are above (a,b).

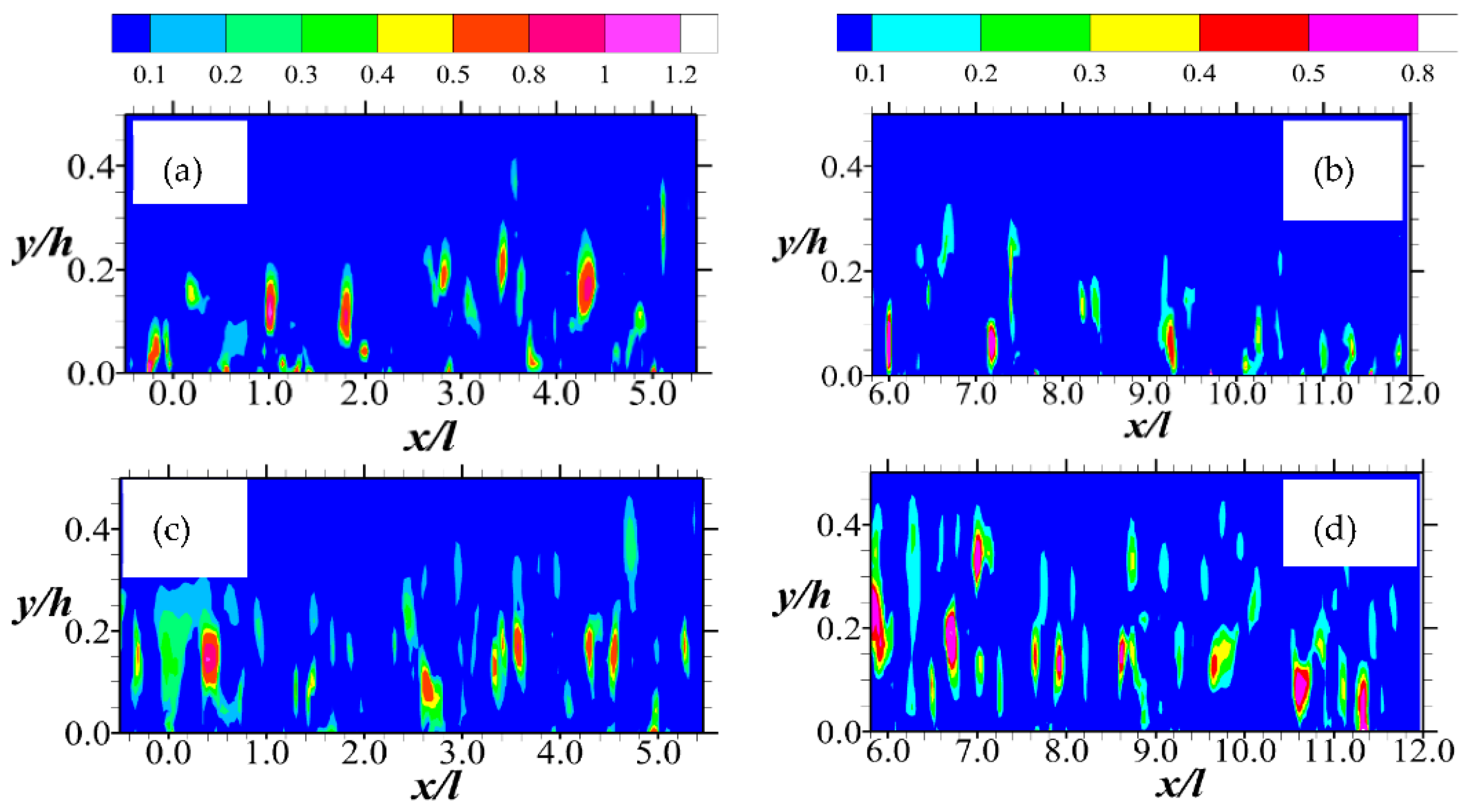
An examination of Figure 13 and Figure 14, on the other hand, indicates that while the intensity of Q1 and Q3 events (i.e., outward and inward interactions) decline downstream, Q2 and Q4 events (i.e., ejections and sweeps, respectively) increase with Q2 dominating slightly. Notably, the results also agree with observations of Suga et al. [2] that both ejections and sweeps tend to be enhanced close to the permeable boundary. However, it appears that as the Reynolds number increases, the contributions of ejection and sweeps to the shear stress decrease significantly in the downstream region of the porous boundary. These sweep and ejection events are symptomatic of dynamic processes of changes that the structures of turbulence undergo in the permeable boundary layer [36].
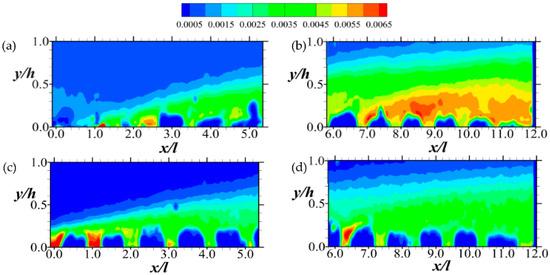
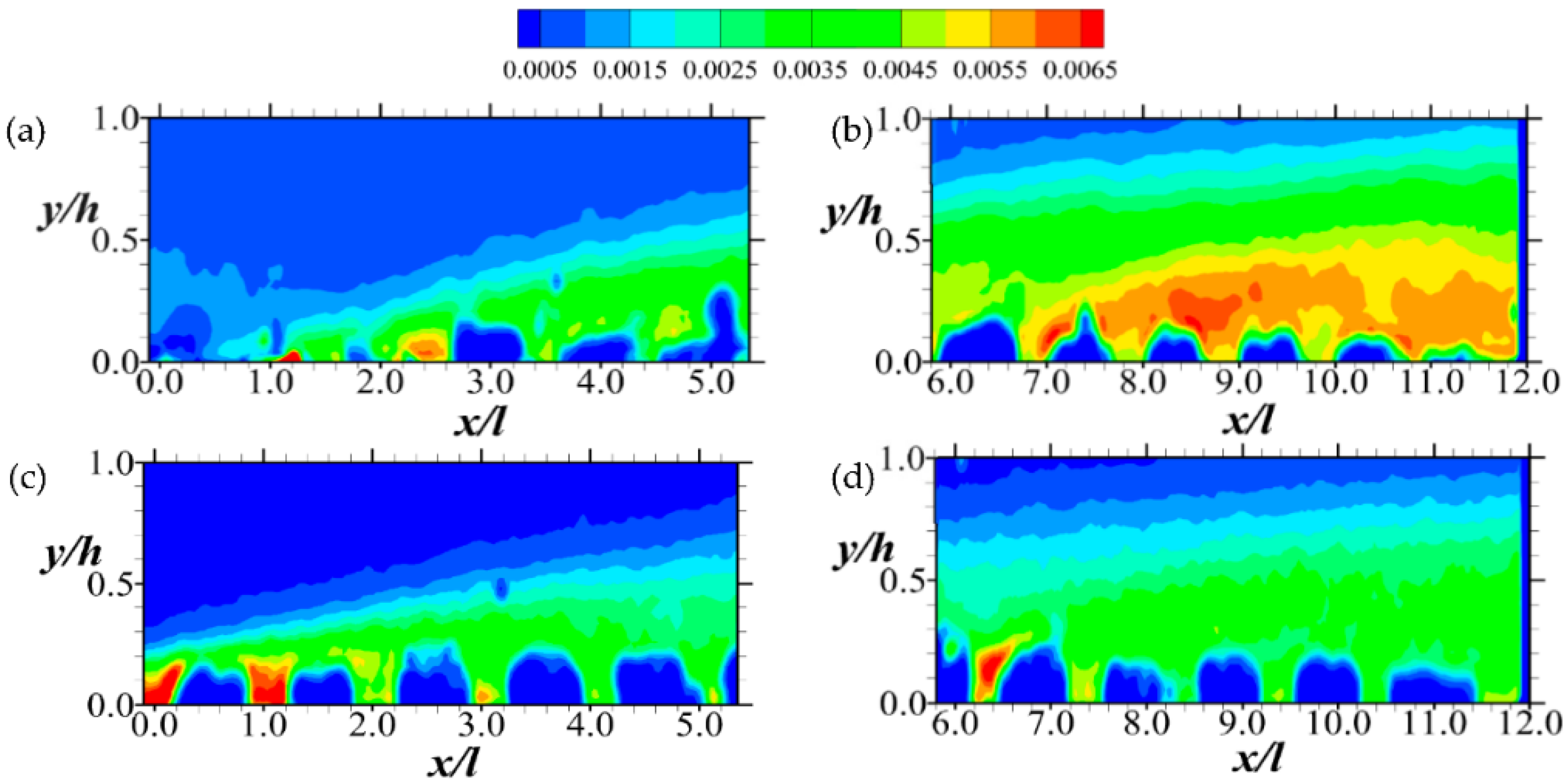
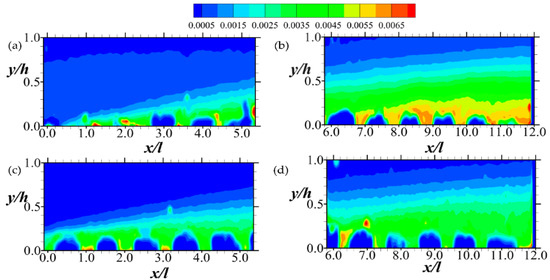
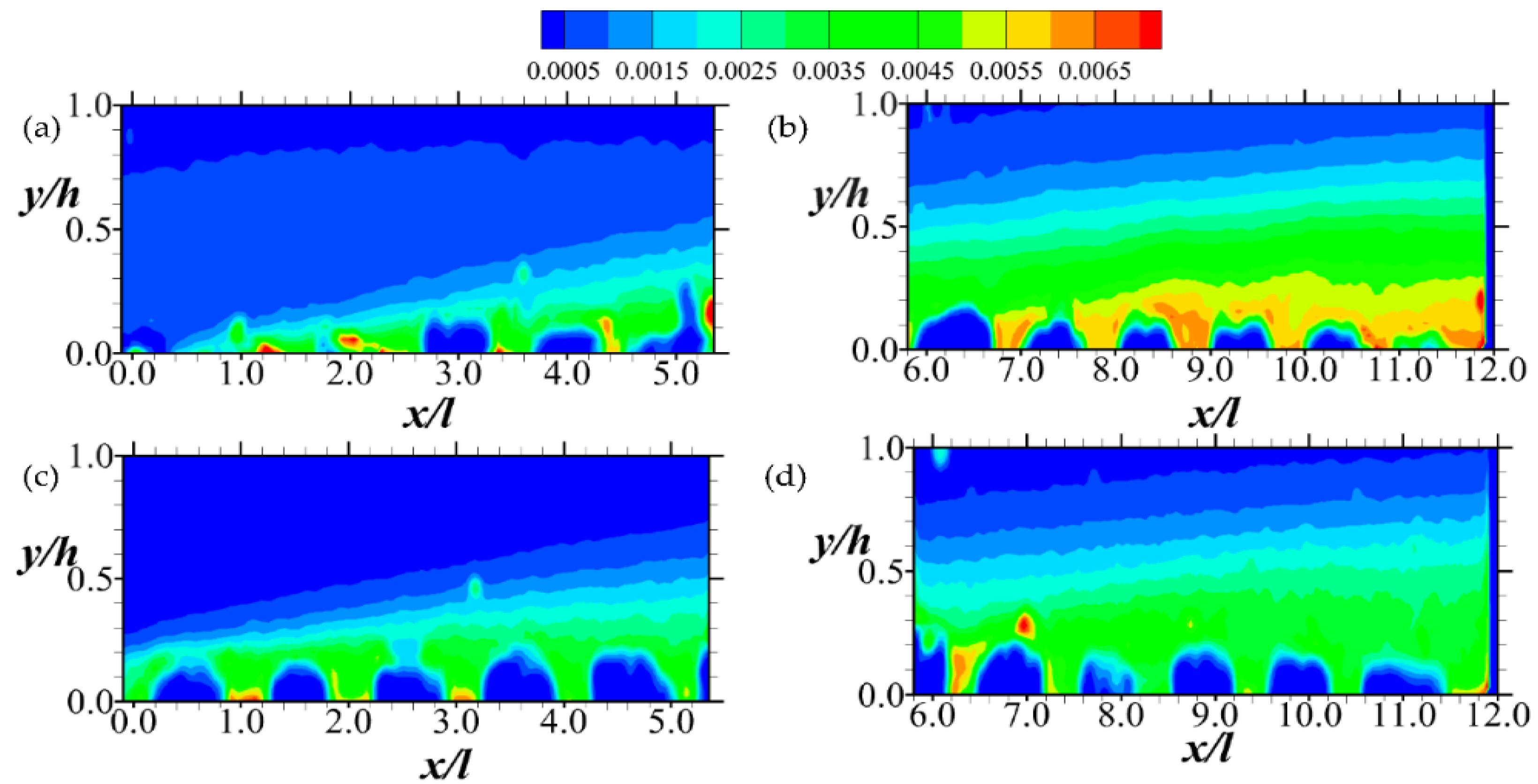

Figure 13.
Contour plots of (from Equation (6)) for Quadrant 2 (Q2) events of the Reynolds shear stress normalized by the respective maximum mean streamwise entry velocity. Note that the hole size (i.e., D in Equation (6)) used is 0. The Q2 events are shown in (a,b) for Test A, and (c,d) for Test B. The legend all the plots are above (a,b).
Figure 13.
Contour plots of (from Equation (6)) for Quadrant 2 (Q2) events of the Reynolds shear stress normalized by the respective maximum mean streamwise entry velocity. Note that the hole size (i.e., D in Equation (6)) used is 0. The Q2 events are shown in (a,b) for Test A, and (c,d) for Test B. The legend all the plots are above (a,b).


Figure 14.
Contour plots of (from Equation (6)) for Quadrant 4 (Q4) events of the Reynolds shear stress normalized by the respective maximum mean streamwise entry velocity. Note that the hole size (i.e., D in Equation (6)) used is 0. The Q4 events are shown in (a,b) for Test A, and (c,d) for Test B. The legend all the plots are above (a,b).
Figure 14.
Contour plots of (from Equation (6)) for Quadrant 4 (Q4) events of the Reynolds shear stress normalized by the respective maximum mean streamwise entry velocity. Note that the hole size (i.e., D in Equation (6)) used is 0. The Q4 events are shown in (a,b) for Test A, and (c,d) for Test B. The legend all the plots are above (a,b).

It is worth emphasizing that the prevalence of Q1 and Q3 events in the upstream region of the porous boundary is a rather uncommon observation. Even in both impermeable and permeable wall turbulence, it is the dominance of Q2 and Q4 events that are often reported [2,4,5]. Nevertheless, in this case, the observation of significant outward and inward interactions—though rare—explains why negative Reynolds shear stress profiles were observed at the upstream region of the porous boundary in earlier work [12]. This occurrence is similar to fluid motions that have been reported for a turbulent flow at the leading edge of forward-facing steps [37] and may perhaps be due to the same physical reasons.
4.4. Characteristics of the Dominant Energy Modes
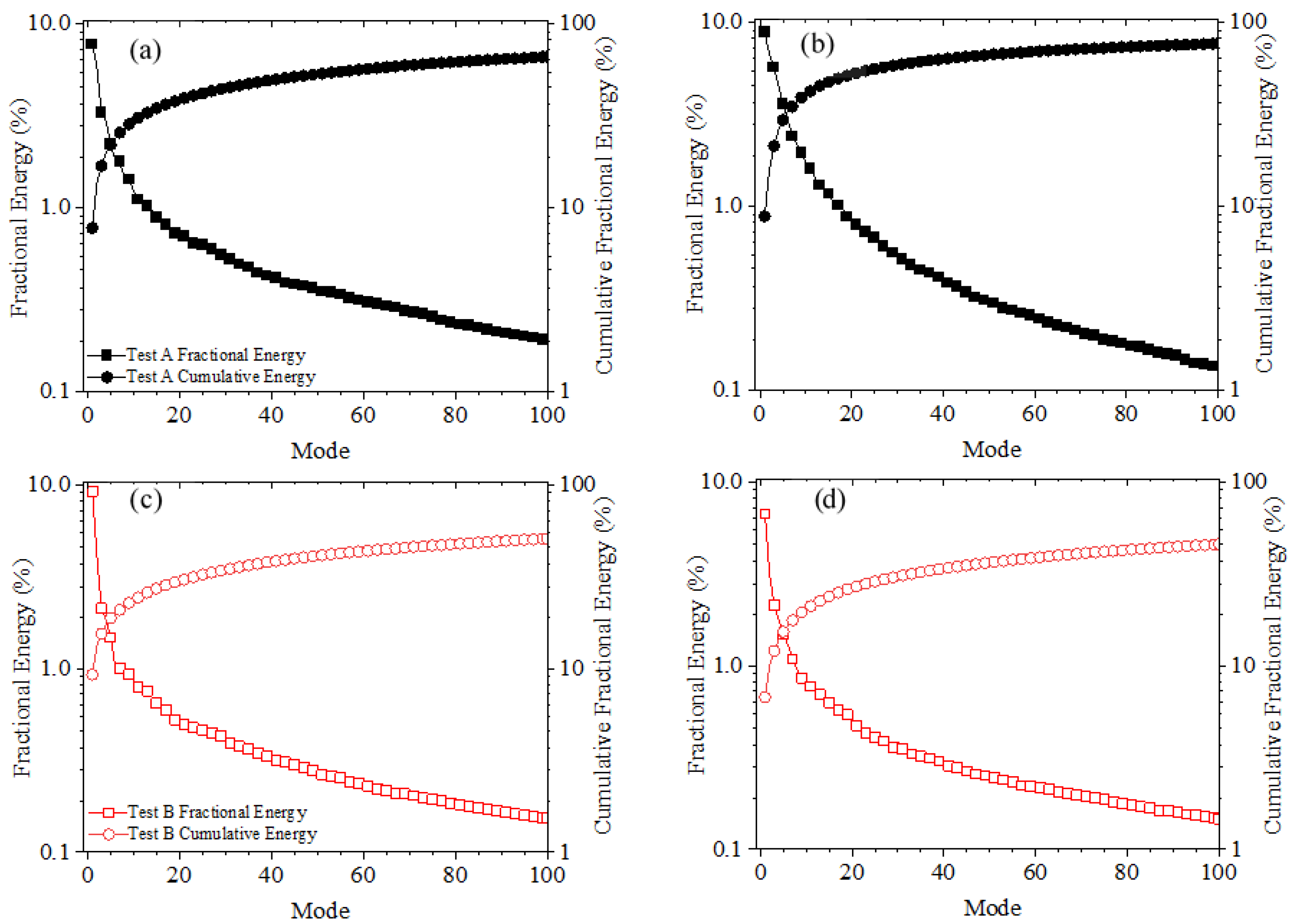
In this section, the large-scale structures are examined through proper orthogonal decomposition (POD) of the PIV measurements. To this end, the number of snapshots (N) required to sufficiently capture the energy content for a given mode was determined. This was performed by considering the convergence of fractional energy associated with the most dominant mode (i.e., mode 1) per N ranging from 10 to 6000. The results are summarized in Table 2 for both planes of measurement in each Test. As shown, as N increases, the fractional energy of mode one decreases until a threshold value is attained where the variation is negligible. This threshold value is N = 4000. In this sample of snapshots, the unchanging values of fractional energy of mode one are 7.8% and (8.65 ± 0.25)% for the data pertaining to planes of measurement in Test A, and 9.3% and 6.8% for those in Test B. Thus, N = 6000 is more than sufficient to conduct the POD analyses. This number is much higher than what has been reported in a number of related studies [6,7].

Table 2.
Convergence of the fractional energy (%) of the most dominant mode per increasing number of snapshots (N).
The energy contents of the low-order modes are shown in Figure 15. This is performed using the spectra of the fractional and cumulative energy contributions of the first 100 modes for the planes of measurement covering the porous boundary condition. The plots indicate an exponential decrease in fractional energy with increasing POD modes. The decay rates are generally greater in the case of Test A relative to Test B. However, the deviation in decay rates between the two tests is greater at 5 < x/l < 11. To illustrate this, for Test A, 50% of the total energy over the permeable boundary is captured by the first 41 modes and 18 modes at 0 < x/l < 5 and 5 < x/l < 11 respectively. For test B, 50% fractional energy is captured by the first 92 and 130 modes at 0 < x/l < 5 and 5 < x/l < 11 respectively. Overall, a substantial number of modes (~1550) are required to represent 90% of the fractional energy.
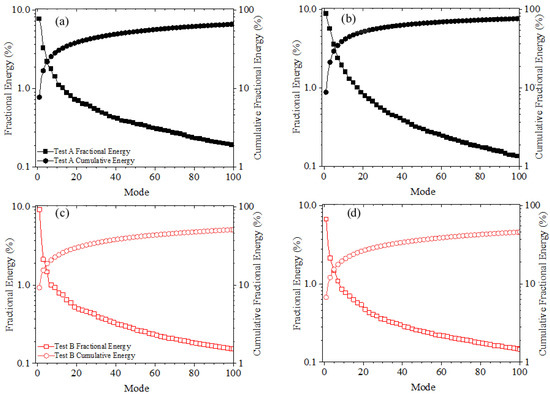
Figure 15.
Fractional and cumulative energy spectra in (a,c) plane covering 0 < x/l < 5; and (b,d) plane covering 5 < x/l < 11. Legends in (a,c) apply to (b,d) respectively.
As the first five POD modes have the largest individual values of fractional energy, special attention is focused on them to study the dynamics of the large-scale structures of the flow. Streamwise contours superimposed on vector maps for the eigenmodes are presented in Figure 16 and Figure 17 for Tests A and B, respectively. It is important to note that as these are velocity fluctuations of the dominant energy modes, they may be used to reveal regions that correspond to high energy activities of vortices and turbulence events [38,39]. Consequently, the results are interpreted using vortex indicators and quadrant definitions (as noted in the figures) to deduce requisite large-scale structures, motions, and events.
Figure 16 indicates that at the highest energy mode, the flow over the permeable boundary at a relatively low Reynolds number is marked by ejections (Q2 events) that are mostly uniform. However, lower energy modes include other motions. At progressively lower-energy modes (e.g., two to four, for instance), the flow is segregated into regions of Q2 and Q4 (sweep) events. Close to alternating regions of Q2 and Q4 events, circulating flow structures are apparent, indicating vortex activity. These Q2 and Q4 events are weaker at lower energy modes. However, they tend to be more in number, along with indicators of vortex activities.
For Test B, the results (shown in Figure 17) are strikingly different from that of Test A in a number of ways. The most important difference is that Q3 (inward motion of high-speed fluid) and Q1 (outward motion of low-speed fluid) events appear at the upstream section of the permeable boundary at modes one and two. Furthermore, vortex activities are detected as early as mode two. However, it is not until the fourth mode that alternating regions of Q2 and Q4 appear, following the phenomenon in Test A. These POD results essentially confirm observations made in Section 4.3 about Q1, Q2, Q3, Q4 event markers in the large-scale structural dynamics.
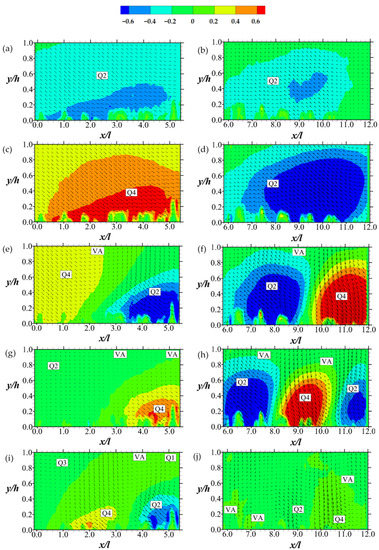
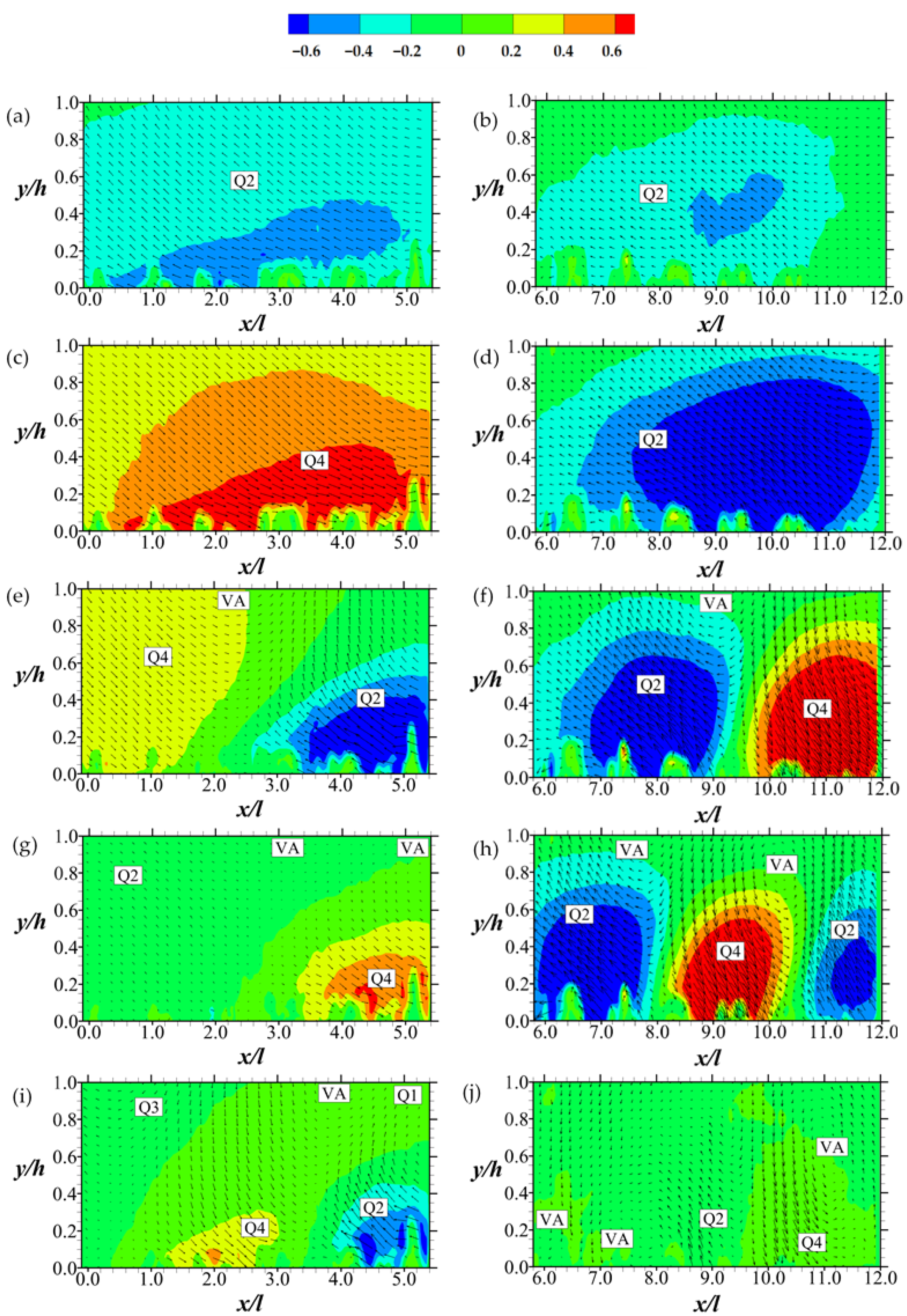
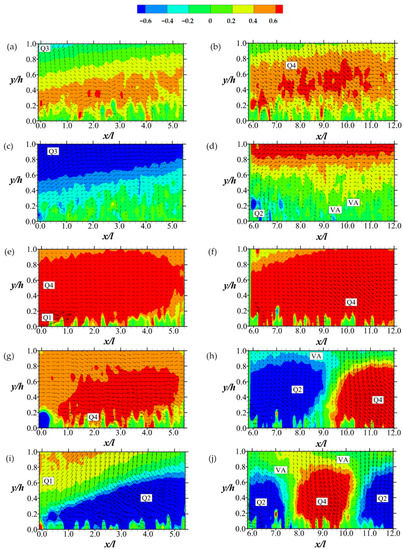
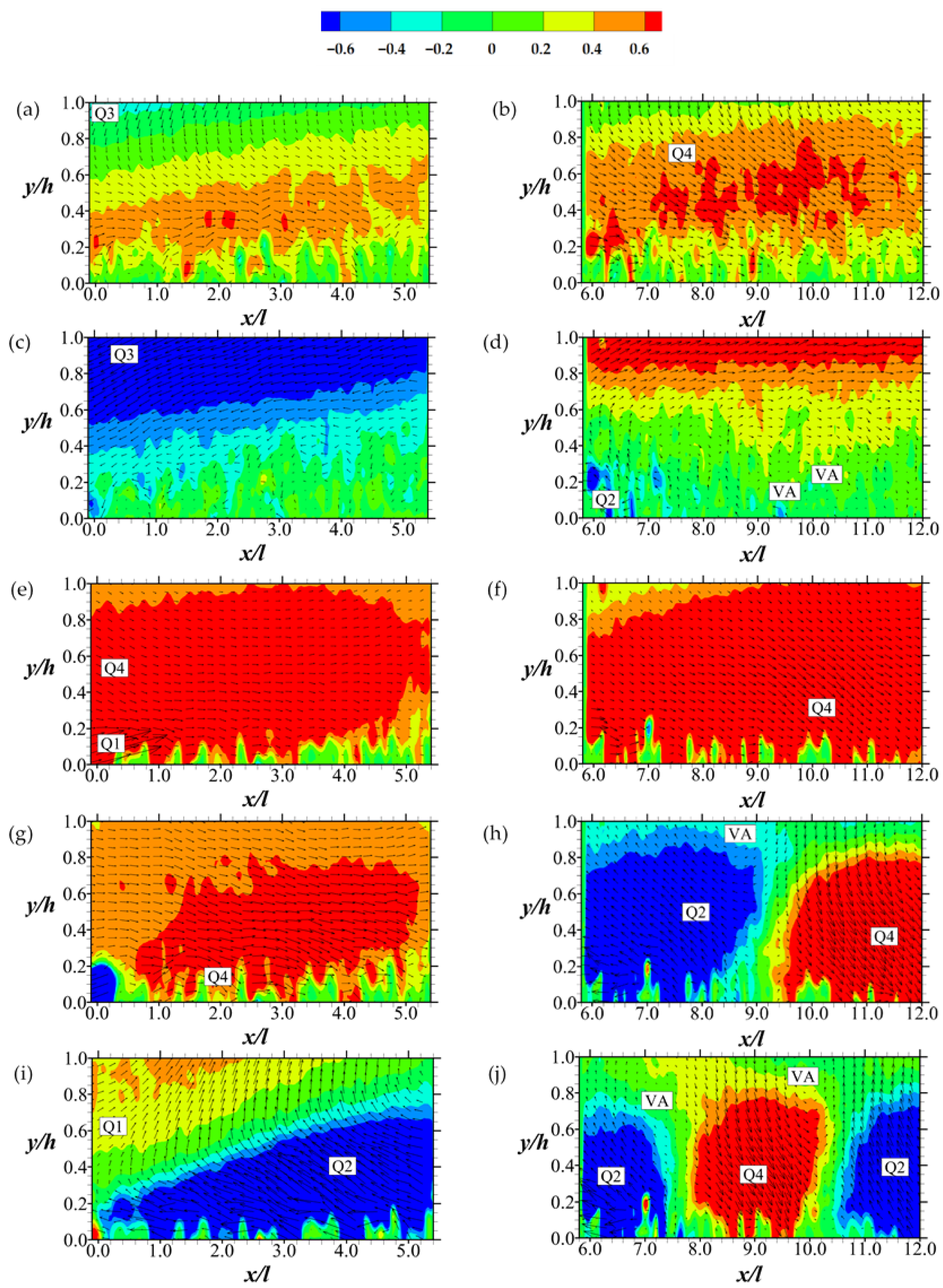

Figure 16.
Streamwise contours and vectors of eigenmodes for Test A. (a,b) are mode 1 with 7.8% and 8.9% fractional energies respectively; (c,d) are mode 2 with 5.8% and 6.8% fractional energies respectively, (e,f) are mode 3 with 3.3% and 5.7% fractional energies respectively; (g,h) are mode 4 with 3.0% and 4.6% fractional energies respectively; (i,j) are mode 5 with 2.2% and 3.6% fractional energies respectively. Legend of the plots are above the plots. Q markers are for quadrant events; VA stands for vortex activity. Scaling of vector magnitudes are not the same for all the plots.
Figure 16.
Streamwise contours and vectors of eigenmodes for Test A. (a,b) are mode 1 with 7.8% and 8.9% fractional energies respectively; (c,d) are mode 2 with 5.8% and 6.8% fractional energies respectively, (e,f) are mode 3 with 3.3% and 5.7% fractional energies respectively; (g,h) are mode 4 with 3.0% and 4.6% fractional energies respectively; (i,j) are mode 5 with 2.2% and 3.6% fractional energies respectively. Legend of the plots are above the plots. Q markers are for quadrant events; VA stands for vortex activity. Scaling of vector magnitudes are not the same for all the plots.


Figure 17.
Contours of eigenmodes for Test B. (a,b) are of mode 1 with 9.3% and 6.8% fractional energies respectively; (c,d) are of mode 2 with 4.1% and 3.2% fractional energies respectively, (e,f) are of mode 3 with 2.1% and 2.1% fractional energies respectively; (g,h) are of mode 4 with 1.9% and 1.8% fractional energies respectively; (i,j) are of mode 5 with 1.5% and 1.5% fractional energies respectively. Legend of the plots are above the plots.
Figure 17.
Contours of eigenmodes for Test B. (a,b) are of mode 1 with 9.3% and 6.8% fractional energies respectively; (c,d) are of mode 2 with 4.1% and 3.2% fractional energies respectively, (e,f) are of mode 3 with 2.1% and 2.1% fractional energies respectively; (g,h) are of mode 4 with 1.9% and 1.8% fractional energies respectively; (i,j) are of mode 5 with 1.5% and 1.5% fractional energies respectively. Legend of the plots are above the plots.

5. Conclusions
In this work, essential features of the coherent structure of a turbulent flow over a compact permeable boundary have been investigated. The data used in the study are from planar PIV measurements of a flow over a porous medium. The porous medium was modeled by a square array of rods of porosity 85%, and the characteristic bulk Reynolds numbers tested were 5.0 × 103 and 2.0 × 104. Using eigenanalysis of the velocity gradient tensor, two-point correlations and quadrant decomposition of the fluctuating velocities, and proper orthogonal decomposition of the instantaneous velocity, the flow data have been assessed. The major conclusions of the study are summarized in the following paragraphs.
For the permeable boundary layer flow, there exists a range of vortex cores within the flow, most of which are generated through shear. These regions of the vorticity generated by shear are elongated and streaky. Those regions of vorticity generated from local rotation are, on the other hand, sparse.
The order, extent, and inclination of the spatial structures of the flow are dependent on the Reynolds number and the location in the flow. They tend to be more organized in the streamwise direction than the wall-normal direction. However, they also tend to be more correlated with an increase in wall-normal distance from the permeable boundary. While their sizes remain the same along the stream at high Reynolds numbers, at lower Reynolds numbers, they shrink initially at the upstream section of the permeable boundary. Furthermore, at a lower Reynolds number, the angle of inclination of the spatial structures may range from 0 to 24° at the initial upstream locations but become constant at 10° further downstream. For high turbulent flows, however, these structures are essentially aligned perfectly in the streamwise direction.
There are substantial inward and outward interactions due to fluid motion at the upstream portion of the permeable boundary. This explains why negative values of Reynolds stress have been reportedly measured at such locations in previous studies. Ejections and sweeps of fluid, however, dominate the turbulence activities downstream of the permeable boundary, albeit declining as the Reynolds number of the flow increases. Consistent with these observations, a study of the low-order POD modes of the flow shows that while the large-scale coherent motions at low Reynolds numbers are marked by ejections, sweeps, and vortex activity, those of higher Reynolds numbers also include inward and outward interactive movements.
In closing, it is worth pointing out that this work focuses on one kind of porous medium model of a single porosity. Hence the results are obviously not general. However, the insight gleaned from this study is an initial but important step in understanding distinctive characteristics of the coherent structures of the turbulent flow field bounded by a compact permeable boundary.
Funding
This work was funded by the C Graydon and Mary E Rogers Fellowship.
Data Availability Statement
Not applicable.
Acknowledgments
The author thanks Alexander Karpowicz for his contribution in the initial set-up of the experimental system. The reviewers’ comments are also gratefully acknowledged.
Conflicts of Interest
The author declares no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Choi, C.Y.; Waller, P.M. Momentum transport mechanism for water flow over porous media. J. Environ. Eng. 1997, 123, 792–799. [Google Scholar] [CrossRef]
- Suga, K.; Mori, M.; Kaneda, M. Vortex structure of turbulence over permeable walls. Int. J. Heat Fluid Flow 2011, 32, 586–595. [Google Scholar] [CrossRef]
- Breugem, W.P.; Boersma, B.J.; Uittenbogaard, R.E. The influence of wall permeability on turbulent channel flow. J. Fluid Mech. 2006, 562, 35–72. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Van Hout, R.; Katz, J. PIV measurements in the atmospheric boundary layer within and above a mature corn canopy. Part II: Quadrant-hole analysis. J. Atmos. Sci. 2007, 64, 2825–2838. [Google Scholar] [CrossRef]
- Manes, C.; Poggi, D.; Ridolfi, L. Turbulent boundary layers over permeable walls: Scaling and near-wall structure. J. Fluid Mech. 2011, 687, 141–170. [Google Scholar] [CrossRef] [Green Version]
- Kuwata, Y.; Suga, K. Lattice Boltzmann direct numerical simulation of interface turbulence over porous and rough walls. Int. J. Heat Fluid Flow 2016, 61, 145–157. [Google Scholar] [CrossRef]
- Motlagh, S.Y.; Taghizadeh, S. POD analysis of low Reynolds turbulent porous channel flow. Int. J. Heat Fluid Flow 2016, 61, 665–676. Available online: https://www.sciencedirect.com/science/article/pii/S0142727X16303897 (accessed on 2 April 2022). [CrossRef]
- Kuwata, Y.; Suga, K. Direct numerical simulation of turbulence over anisotropic porous media. J. Fluid Mech. 2017, 831, 41–71. Available online: https://www.cambridge.org/core/article/direct-numerical-simulation-of-turbulence-over-anisotropic-porous-media/C7F40DD72ADB154E700C1A4EE10C3397 (accessed on 2 April 2022). [CrossRef] [Green Version]
- Suga, K.; Okazaki, Y.; Ho, U.; Kuwata, Y. Anisotropic wall permeability effects on turbulent channel flows. J. Fluid Mech. 2018, 855, 983–1016. [Google Scholar] [CrossRef]
- Alfonsi, G.; Ferraro, D.; Lauria, A.; Gaudio, R. Large-eddy simulation of turbulent natural-bed flow. Phys. Fluids 2019, 31, 085105. [Google Scholar] [CrossRef]
- Robinson, S.K. Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 1991, 23, 601–639. [Google Scholar] [CrossRef]
- Arthur, J.K. Turbulent Flow through and over a Compact Three-Dimensional Model Porous Medium: An Experimental Study. Fluids 2021, 6, 337. [Google Scholar] [CrossRef]
- Arthur, J.K.; Schiele, O. Numerical Analysis of Enhanced Heat Transfer Using a Pair of Similar Porous Baffles in a Backward-Facing Step Flow. J. Fluid Flow Heat Mass Transf. 2021, 8, 226–237. [Google Scholar] [CrossRef]
- Assato, M.; Pedras, M.H.; De Lemos, M.J. Numerical solution of turbulent channel flow past a backward-facing step with a porous insert using linear and nonlinear k-ε models. J. Porous Media 2005, 8, 13–29. [Google Scholar] [CrossRef]
- Zhao, Z. Numerical modeling and simulation of heat transfer and fluid flow in a two-dimensional sudden expansion model using porous insert behind that. J. Therm. Anal. Calorim. 2020, 141, 1933–1942. [Google Scholar] [CrossRef]
- Raffel, M.; Willert, C.E.; Kompenhans, J. Particle Image Velocimetry: A Practical Guide; Springer: Berlin, Germany, 1998. [Google Scholar]
- Prasad, A.K. Particle image velocimetry. Curr. Sci. 2000, 79, 51–60. [Google Scholar]
- Durst, F.; Fischer, M.; Jovanović, J.; Kikura, H. Methods to set up and investigate low Reynolds number, fully developed turbulent plane channel flows. J. Fluids Eng. 1998, 120, 496–503. [Google Scholar] [CrossRef]
- Cuissa, J.R.C.; Steiner, O. Vortices evolution in the solar atmosphere-A dynamical equation for the swirling strength. Astron. Astrophys. 2020, 639, A118. [Google Scholar] [CrossRef]
- Zhou, J.; Adrian, R.J.; Balachandar, S.; Kendall, T. Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 1999, 387, 353–396. [Google Scholar] [CrossRef]
- Hutchins, N.; Hambleton, W.T.; Marusic, I. Inclined cross-stream stereo particle image velocimetry measurements in turbulent boundary layers. J. Fluid Mech. 2005, 541, 21–54. [Google Scholar] [CrossRef] [Green Version]
- Adrian, R.J.; Christensen, K.T.; Liu, Z.C. Analysis and interpretation of instantaneous turbulent velocity fields. Exp. Fluids 2000, 29, 275–290. [Google Scholar] [CrossRef]
- Volino, R.J.; Schultz, M.P.; Flack, K.A. Turbulence structure in rough- and smooth-wall boundary layers. J. Fluid Mech. 2007, 592, 263–293. [Google Scholar] [CrossRef]
- Moin, P.; Kim, J. The structure of the vorticity field in turbulent channel flow. Part 1. Analysis of instantaneous fields and statistical correlations. J. Fluid Mech. 1985, 155, 441–464. [Google Scholar] [CrossRef] [Green Version]
- Willmarth, W.W.; Lu, S.S. Structure of the Reynolds stress near the wall. J. Fluid Mech. 1972, 55, 65–92. [Google Scholar] [CrossRef]
- Lu, S.S.; Willmarth, W.W. Measurements of the structure of the Reynolds stress in a turbulent boundary layer. J. Fluid Mech. 1973, 60, 481–511. [Google Scholar] [CrossRef]
- Shirovich, L. Turbulence and the Dynamics of Coherent Structures; Part I: Coherent Structures, Q. Appl. Math. 1987, 45, 561–571. [Google Scholar]
- Agelin-Chaab, M. Experimental Study of Three-Dimensional Offset Jets and Wall Jets. Ph.D. Thesis, University of Manitoba, Winnipeg, MB, Canada, 2010. [Google Scholar]
- Adrian, R.J.; Meinhart, C.D.; Tomkins, C.D. Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 2000, 422, 1–54. [Google Scholar] [CrossRef] [Green Version]
- Tay, G.F.K. Experimental Study of Particle-Induced Turbulence Modification in the Presence of a Rough Wall. Ph.D. Thesis, University of Manitoba, Winnipeg, MB, Canada, 2015. [Google Scholar]
- Volino, R.J.; Schultz, M.P.; Flack, K.A. Turbulence structure in a boundary layer with two-dimensional roughness. J. Fluid Mech. 2009, 635, 75–101. [Google Scholar] [CrossRef] [Green Version]
- Nakagawa, S.; Hanratty, T.J. Particle image velocimetry measurements of flow over a wavy wall. Phys. Fluids 2001, 13, 3504–3507. [Google Scholar] [CrossRef]
- Christensen, K.T.; Adrian, R.J. Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 2001, 431, 433–443. [Google Scholar] [CrossRef]
- Christensen, K.T.; Wu, Y. Visualization and characterization of small-scale spanwise vortices in turbulent channel flow. J. Vis. 2005, 8, 177–185. [Google Scholar] [CrossRef]
- Tomkins, C.D.; Adrian, R.J. Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 2003, 490, 37–74. [Google Scholar] [CrossRef] [Green Version]
- Alfonsi, G. Coherent structures of turbulence: Methods of eduction and results. Appl. Mech. Rev. 2006, 59, 307–323. [Google Scholar] [CrossRef]
- Nematollahi, A. Effects of Upstream Roughness on Turbulent Flow over a Forward-Facing Step. Ph.D. Thesis, University of Manitoba, Winnipeg, MB, Canada, 2019. [Google Scholar]
- Van Oudheusden, B.W.; Scarano, F.; Van Hinsberg, N.P.; Watt, D.W. Phase-resolved characterization of vortex shedding in the near wake of a square-section cylinder at incidence. Exp. Fluids 2005, 39, 86–98. [Google Scholar] [CrossRef]
- Kellnerova, R.; Kukacka, L.; Uruba, V.; Jurcakova, K.; Janour, Z. Detailed Analysis of POD Method Applied on Turbulent Flow; EDP Sciences: Les Ulis, France, 2011. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).