Abstract
Ferrofluid sloshing vibration energy harvesters use ferrofluid sloshing movement as a moving magnet between a fixed coil to induce current and, in turn, harvest energy from external excitations. A symmetric ferrofluid sloshing vibration energy harvester configuration is introduced in this study which utilizes four external, symmetrically placed, permanent magnets to magnetize a ferrofluid inside a tank. An external sinusoidal excitation of amplitude 1 m/s2 is imparted, and the whole system is studied numerically using a level-set method to track the sharp interface between ferrofluid and air. The system is studied for two significant length scales of 0.1 m and 0.05 m while varying the four external magnets’ polarity arrangements. All of the system configuration dimensions are parametrized with the length scale to keep the system configuration invariant with the length scale. Finally, a frequency sweep is performed, encompassing the structure’s first modal frequency and impedance matching to obtain the system’s energy harvesting characteristics.
1. Introduction
Energy harvesting from different ambient sources of energy has become a significant area of research. Energy harvesting entails converting ambient or unused energy into useful electrical energy through a miniature transduction mechanism. It is used mainly in places where large energy conversion devices, such as hydro/steam turbines, IC engines, etc., cannot convert the available ambient energy. Energy harvesting aims to provide a sustainable power source to stand-alone devices, such as sensors, actuators, etc., by utilizing ambient energy and without needing to store energy [1,2,3]. Energy harvesting devices have the potential to replace bulky batteries and deliver lightweight solutions for sensing and actuation and make them essentially wireless [4,5,6]. It is also helpful in increasing general energy conversion devices’ efficiency (for example, thermoelectric devices, which are used for waste heat recovery from heat engines).
Energy harvesting usually requires a transduction mechanism to convert ambient/waste energy into a useful electric energy form [7,8,9]. Figure 1 depicts the working of an energy harvesting device schematically. The energy harvesting device captures ambient or waste energy through an energy capturing mechanism. This captured energy is then used by a transduction mechanism that converts it into useful energy (electric power). The most general examples are thermoelectric devices, piezoelectric devices, ionic polymer metal composites, etc. [1,2,10]. However, recently, energy harvesters have used a liquid state transduction mechanism to obtain electric power through a ferrohydrodynamic vibration energy harvester [11,12]. Fluidic transduction can be applied in energy harvesting by both solid and liquid state transducers. For solid-state transducers, the fluid acts as the energy source for the forcing function required to deform part of the harvester. In liquid state transducers, the fluid acts as both the energy carrier and deformed harvester. This is shown as a schematic in Figure 2 Solid-state transduction mechanisms use any instability created in the flow field to excite the transduction element at a particular frequency (usually the natural frequency of the structure) and harvest energy via inherent electromechanical coupling of the harvester.
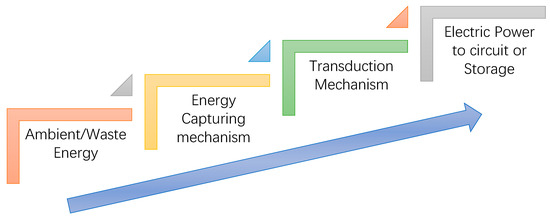
Figure 1.
Schematic representation of an energy harvesting device.
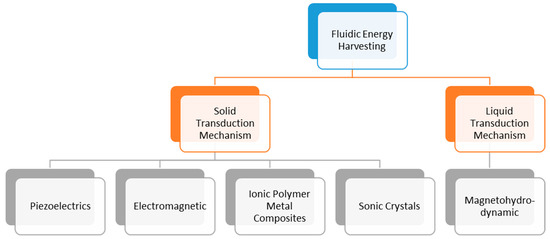
Figure 2.
Classification of fluidic energy harvesting methods.
Sloshing refers to the movement of liquids inside partially filled containers under external excitation [13,14]. It is characterized as an internal free surface flow. Sloshing has typically been an area of interest for the shipping industry, the automobile industry, and intergalactic rocketry [13]. Most of these applications have tried to mitigate the effects of sloshing since, at large scales, a sloshing fluid can cause significant structural damage to the container [15]. Therefore, most research about sloshing has been conducted to mitigate the effects of sloshing using baffles, etc. The solid-state nature of the transduction mechanism in most current vibration energy harvesters usually limits their capabilities, especially in conformability to different shapes and very diverse sensitivity to broadband external excitations. Both of these problems can be addressed if the transduction mechanism is fluidic instead of a solid, and this has been achieved through a Ferrofluid sloshing vibration energy harvesting system [16].
Ferrofluids consist of stable ferrous nanoparticles in colloidal suspension, forming nanoscale magnetic dipoles [17,18] once subjected to an external magnetic field. Each particle is coated with a surfactant such that in the absence of an external magnetic field, the magnetic dipoles are randomly oriented in the carrier fluid and do not coagulate due to the fields generated by the ferromagnetic cores [17]. However, when an external magnetic field is applied, the average direction of the fluid magnetization becomes parallel to the magnetic field lines. This property is known as superparamagnetism and can be used in flow manipulation applications by affecting the ferrofluid through an external magnetic field [17,18,19,20]. One such application, which was briefly discussed above, is to use ferrofluids for energy harvesting. Here the ferrofluid, due to superparamagnetism, becomes a magnet when placed in an external magnetic field. Combining this with an external excitation and a pick-up coil, the ferrofluid sloshing motion can be utilized to harvest energy. This is known as ferrofluid sloshing vibration energy harvesting. Ferrofluid sloshing has been used for generating power from external oscillations. Performance characteristics of one such energy harvesting configuration were conducted, and a plethora of knowledge regarding design rules for such a configuration was proposed [21]. Table 1 shows a list of published Ferrofluid sloshing vibration energy harvesting configurations, which used only a liquid state transduction mechanism consisting of a ferrofluid. The highest power output has been around 80 mW for a 10 m/s2 acceleration.

Table 1.
Ferrofluid sloshing vibration energy harvesting configurations published in literature.
In addition, different configurations have used Ferrofluids to augment a solid-state transduction mechanism. For instance, Ferrofluid is used as a bearing to reduce friction between a moving solid member and a stationary shell, and power is harvested through electromagnetic induction when external excitations are supplied to the system [22,23,24,25]. In these systems, the ferrofluid does not participate as a transduction mechanism but aids in the movement of solid magnetic material in a coil.
In this study, a unique configuration for a ferrofluid sloshing vibration energy harvester (VEH) is proposed, exploiting the harvester’s two symmetry planes by introducing four symmetrically placed powerful magnets to generate sixteen unique combinations of magnetic fields. The idea behind the symmetrical placement of magnets is that it becomes easy to manufacture if the structures are symmetric. Moreover, the sloshing tank proposed in this study has a rectangular elevation, with height being half that of length. The third dimension is assumed to be equal to the length of the tank. This helps in reducing the overall size of the system and increasing the harvested power per unit volume.
The sloshing phenomena is defined numerically by the Navier-Stokes equations, the Maxwell equations, and the Level-set method, and is simulated using COMSOL Multiphysics. The level-set method is utilized to capture the movement of the free surface. The level-set method has been used to perform numerical studies on ferrofluid droplets [28,29,30] and, in this work, similar formulations are adapted to depict a sharp interface between the ferrofluid and air. For convenience and efficiency, the flow simulation is performed as a 2-D flow instead of a 3-D flow using simplifying assumptions published in the literature. Section 2 defines the set-up of the system, and Section 3 comprehends the governing equations used to simulate the multiphysics flow.
2. System Set-Up
Figure 3 represents the configuration with four magnets symmetrically placed at the center planes of the harvesting tank.
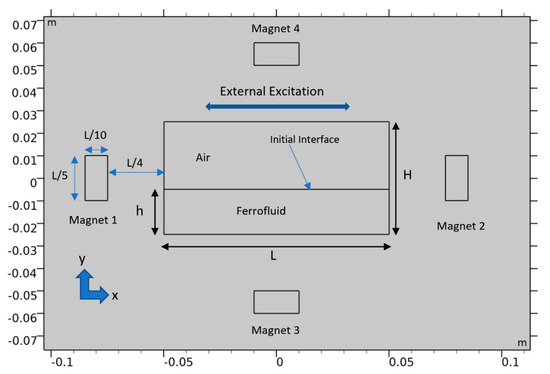
Figure 3.
Schematic representation of the proposed harvester configuration.
The four magnets have length dimensions in terms of the significant length scale (i.e., the tank’s length). The magnets’ thickness is a tenth of the length of the tank, and their width is a fifth of the tank. Such a formulation helps in scaling the system with the actual length of the configuration. The magnets are placed at a distance of from their adjacent tank wall. The height of the tank () is half of its length, and the fill level of the ferrofluid in the tank is . The magnets are labeled from 1 through 4.
For convergence of the magnetic field, a large domain is created around the harvester. This is shown in Figure 4, where the domain is ten times larger than the harvester’s length scale. The harvester receives an external excitation, which is periodic and causes the ferrofluid to slosh inside.
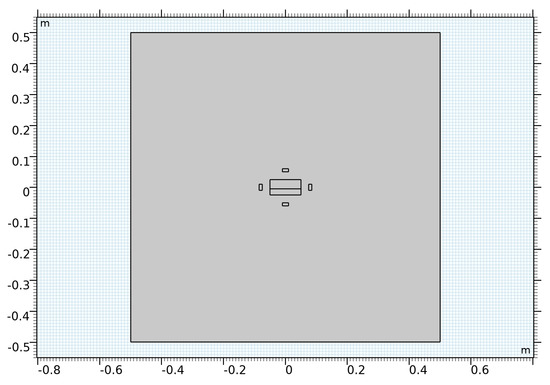
Figure 4.
Harvester and the large domain surrounding it.
3. Governing Equations
The flow inside the domain is governed by Navier-Stokes equations and Maxwell’s equations. The Navier-Stokes equations are as follows
Continuity:
Momentum:
where, is the velocity vector, is the magnetic force, is the external acceleration on the system, which consists of the external excitation and the acceleration due to gravity, and is the force of the surface tension.
Here the external excitation is given as:
where is the amplitude of external excitation and the angular frequency related to the excitation frequency as, . In this study, is varied such that the set of frequencies contain the first modal frequency. This makes the acceleration:
Since the flow is a separated two-phase flow, with an interface separating the two, the properties of the fluids will vary sharply across the interface. This needs to be accounted for using an interface tracking method, which will keep the boundary between the fluids intact and allow the interface to advect with changing flow field. This requires a separate computation step and a separate mathematical treatment/modeling of the moving interface. Several methods are very effective in performing interface tracking computationally such as the volume of fluid method, the Level-set method, the phase-field method, etc. [31]. These methods usually work based on conservation of some physical or attributed numerical quantity, usually the mass or the area under the surface, the gradient of the distance function, etc., to characterize the free surface. This then is used to derive a partial differential equation form of the conserved quantity and is solved with the N-S equations to yield the moving interface profile. One such method mentioned above is the level-set method [32]. The interface is defined as a signed distance function in the level set method and is tracked as a higher dimensional field applied to the flow field, which in turn defines how the flow moves [33,34,35]. However, the level set method proposed initially [34] did not conserve mass or the area correctly, especially in fluid dynamics problems. This prompted further research into conservative level set methods that conserve the mass exactly. One such method is used in this work where the mass is conserved exactly, and the surface is expressed as a constant level set [36,37]. Although level set methods are inherently well suited for representing complex topologies, they become even more effective in tracking sharp interfaces with a conservative level-set formulation [38,39,40]. The mathematical formulation of this sharp interface, the conservative level-set method, is shown below.
Level-set equations for interface tracking:
where is the level set variable, is the re-initialization parameter and is the parameter which controls the thickness of the fluid-air interface. In this work, the value of the re-initialization parameter is set to , which is the characteristic velocity scale for the sloshing setup. The separating surface is given by , i.e., a set of all surfaces where the level set function . This means that the first fluid is from and the second fluid from . This level-set variable creates a higher dimensional field over the flow field and describes all the properties of the two fluids in its terms to represent the separation between the two fluids as a sharp interface. All fluid properties must be represented in terms of the level set variable to fully couple the flow field with the level-set field. Similarly, all interfacial forces must be expressed in terms of the level-set variable.
The surface tension force is expressed in terms of the level-set variable as follows:
where, is the surface tension coefficient, is a Dirac delta function located at the interface, is the curvature of the surface, is the normal vector of the liquid-gas interface, and is the surface gradient operator.
The interface normal is given by:
The Dirac delta function is given by:
The curvature of the surface is given by:
The surface gradient operator is given by:
Additionally, the angle that the fluid makes with the wall while wetting is assumed to be 90°. This is a standard assumption for solving sloshing flows [27,41].
For the fluid domain inside the tank, the properties must be expressed in terms of the level set variable. Density is given as:
Viscosity is given as:
The indices 1 and 2 denote fluid 1 and fluid 2, which is the ferrofluid and air, respectively. Similarly, to calculate the Kelvin body force, the magnetic properties of the fluids must be expressed in terms of the level set variable:
where, is the magnetic field, and the magnetization is given by the constitutive relation:
where, is the magnetic susceptibility and is obtained from the level set function for the whole domain as:
Maxwell’s conservation laws for the system are [17]:
The magnetic field can also be written as:
where, is the magnetic scalar potential.
The boundary conditions for the domain are the no flux boundary condition for the ends of the domain surrounding the harvester. The magnets are such that they have a uniform magnetization of 400 kA/m. The following are the constitutive relations for different regions:
The electromotive force from sloshing is picked up by an external coil with N turns (which are varied to optimize power harvested). The electromotive force is given as:
where is the magnetic flux, obtained by integrating the magnetic flux density over the area. The electromotive force due to the changing magnetic field inside the harvester is picked up by an external coil, which can be wound either along the harvester’s length and gets pitched in the y-direction, or it can be wound along the height of the tank while pitched along the x-direction. Equation (21) represents the expression of inductance of one such rectangle, where is the relative permeability of the material enclosed in the coil.
The current in the wound coil can be found by the series L-R circuit equation:
where is the load resistance and the coil resistance, through which the power output of the harvester is measured, is the inductance of the wound coil, and V is the electromotive force obtained from sloshing. Finally, it is assumed that if a coil is wound along the length (i.e., horizontally wound), the number of turns would be half that of when it is wound along the height (i.e., vertically wound coil). Figure 5 shows the 3-D arrangement of the tank with a horizontally wound coil and Figure 6 shows the arrangement of the tank in 3-D for a vertically wound coil. The four magnets are also shown in the figures, with the depth dimension being equal to that of the height.
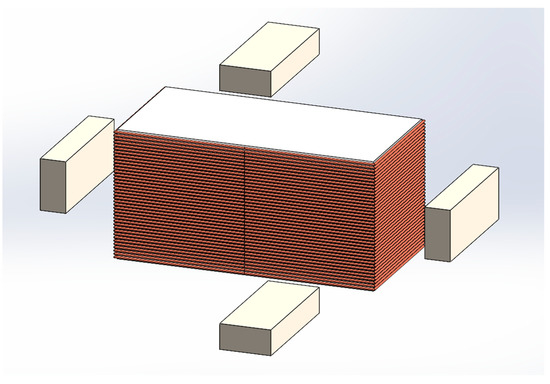
Figure 5.
Arrangement of tank with horizontally wound coil.
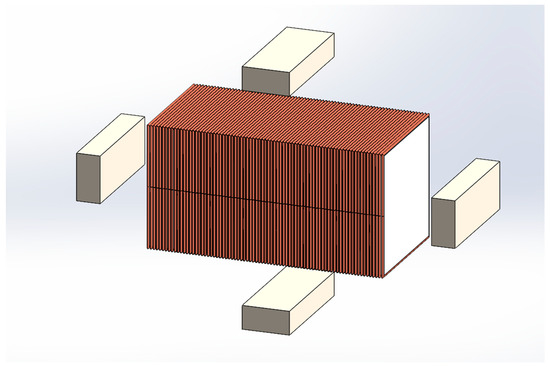
Figure 6.
Arrangement of tank with vertically wound coil.
For vertical winding (along with the height), the magnetic flux’s x component would be used. For horizontal winding (along with the length), the y component of the magnetic flux would be used to calculate the electromotive force. This is formulated in Equation (23).
4. Numerical Modeling and Validation
In this section, the numerical modeling details are discussed. The combined Navier-Stokes, level-set, and Maxwell’s equations are solved in COMSOL Multiphysics using its inbuilt multiphysics capacity. COMSOL is a finite element-based software, which solves partial differential equations using the weak form and shape functions. For computational fluid dynamics applications, especially where Navier-Stokes equations are involved, finite element-based codes need to account for stability errors in the crosswind and streamline direction due to numerical dispersion. This is especially significant when the same order of elements resolves velocity and pressure fields. These stabilizations are inbuilt in COMSOL and are based on Streamline upwinding methods for both pressure and velocity fields [42,43]. Further, as the problem is unsteady, the solution must be marched in time to obtain the system’s state at each time of interest during the simulation. For this, an implicit adaptive time-stepping scheme is used.
The solution is advanced by solving segregated steps at each time step when the tolerance level (which is set to be 1 × 10−4) is reached. This convergence criterion is for both solution and the residual. The following segregated steps of dependent variables are solved in the following order:
- (a)
- Level set variable
- (b)
- Velocity and pressure
- (c)
- Magnetic scalar potential.
To simplify and streamline the computations, the first-order discretization is used for the pressure and velocity fields. Similarly, for the level-set, variable linear elements are used. For the magnetic scalar potential, the element order is maintained at two everywhere in the domain.
Grid convergence studies and adaptive time step control studies were performed on two magnet configurations. It was found that the mesh inside the sloshing domain is both accurate and efficient for a grid size of 0.001 and for a maximum time step value of 2 milliseconds.
To validate COMSOL and the level set method used in the computations, a comparative study was run replicating the published experimental and computational results by Liu et al. [44]. The combination 1H is simulated, and the results are compared in Figure 7. The numerical scheme predictions adopted in the present work match very closely to the reported computational and experimental data in [44] as shown in Figure 7a,b, respectively. The peak voltage near the resonance frequency almost matches perfectly with the experimental data. However, since the spectrum of frequencies in the frequency sweep performed in the present work is not as closely spaced as reported by Liu et al., the internal energy pump, which occurs at around 1.5 Hz, is not as prominent in our simulation of their configuration as shown in Figure 7b.
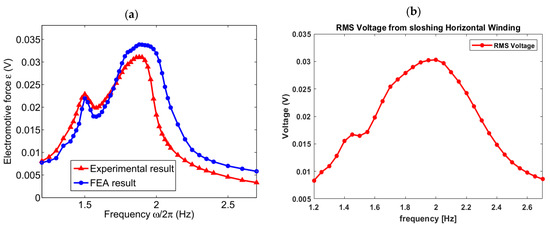
Figure 7.
Comparison between (a) 1H configuration of Liu [44] and (b) present work.
Based on this validation, it is inferred that the level-set formulation and the chosen solvers can simulate the complexities involved in this flow. To advance the work on ferrofluid VEH, a new tank design is proposed in this work, as mentioned in previous sections. This configuration is then subjected to a frequency sweep, with various combinations between the four fixed magnets. The north and south poles of one or more magnets are flipped to generate a new magnetic field distribution. Table 2 lists all of the 16 cases which may arise with different combinations of North and South pole orientations of the magnets. The table lists South/North labels for the magnets, depicting which pole of the magnet faces the tank.

Table 2.
Cases for Magnet orientation.
Two tanks are studied, one where L is 10 cm and the other where L is 5 cm. The fill level is a fraction of the length scale and is set to be L/5. For the two tanks, the frequency sweep is performed to capture the tank’s first resonance frequency within the sweep.
Finally, to maintain energy application parity across tank sizes and frequencies, the external acceleration (a) is kept as constant, at .
i.e.,
Hence when the frequency changes, the amplitude is adjusted to keep the acceleration constant.
To provide additional validation, a video (Video S1) illustrating the surface movement of the ferrofluid from the 2-D simulation for case 10 and frequency 2.05 Hz for the large tank is provided in the supplementary materials. To compare this 2-D simulation with a 3-D full-scale simulation, a 3-D simulation of the whole tank was performed, with the arrangement shown in Figure 5 and Figure 6. To compare this simulation with the 2-D simulation, a mid-plane video (Video S2) is taken from the 3-D simula-tion. The surface evolution of the ferrofluid in these two videos, over 4 time periods, is very similar. Hence, it is safe to assume that the 2-D simulation is a very good ap-proximation of the actual 3-D simulation.
Finally, the properties used for this study are of ferrofluid EFH3 manufactured by Ferrotec corporation [45] and are listed in Table 3.

Table 3.
Ferrofluid property data.
5. Results and Discussion
In this section, simulation results and the performance of the two energy harvesters are discussed. An impedance matching scheme was followed to extract results for the highest extractable power from all these simulation runs for both tanks. Here, the external electrical circuit is considered a series R-L circuit, and the equations for this are formulated in the previous section. To determine the optimal impedance for the system, many pick-up coils were selected, and those pick-up coils were assumed to be connected to a load resistor, the resistance of which is varied from 1 ohm to 105 ohms to generate an impedance matching plot. This was performed for all the frequencies and both the tanks.
For example, Figure 8 and Figure 9 show impedance matching plots for the L = 10 cm tank for the magnet orientation case 7 for frequency of 2.05 Hz using horizontal and vertical pick-up coils of 1000 turns. For the horizontal coil, the optimal load resistor was found to be 103.5 ohms, and for the vertical coil 102.75 ohms. Appendix B shows the time evolution of voltage, current, and external acceleration for this 2.05 Hz case.
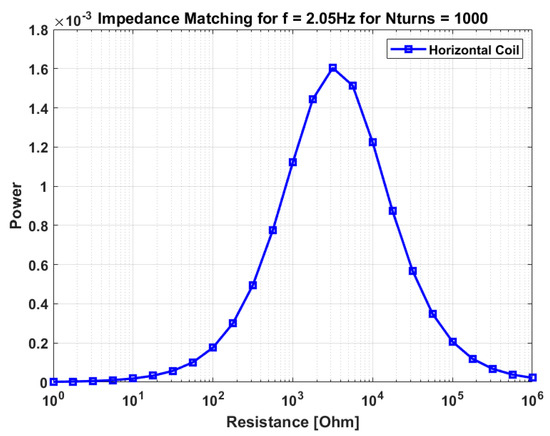
Figure 8.
Impedance matching for horizontal coil of 1000 turns on L = 10 cm tank for frequency = 2.05 Hz.
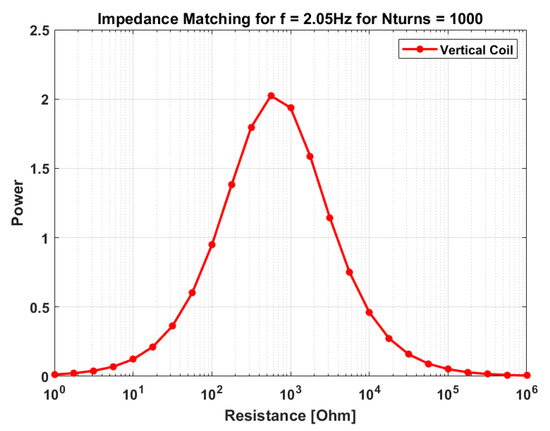
Figure 9.
Impedance matching for Vertical coil of 1000 turns on L = 10 cm tank for frequency = 2.05 Hz.
The following two subsections present simulation runs, and impedance matching results for the two tanks studied in this work.
5.1. Analysis of Output from L = 10 cm Tank
Figure 10 shows how the ferrofluid moves inside the tank near the resonance frequency for the magnet combination case 1. The rest of the 15 cases are displayed in Appendix A.
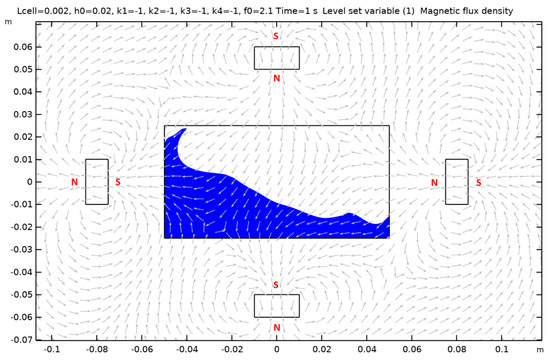
Figure 10.
Surface evolution and magnetic flux density arrow surface for case 1, near resonance frequency for L = 10 cm tank.
The arrows in the above plot depict the magnetic flux lines. The flux lines in a magnet originate from the North Pole and terminate into the South Pole. In the above plot, magnet 1′s South Pole faces the harvester, while magnet 2′s north, magnet 3′s south, and magnet 4′s north, face the harvester. Now, for each of these 16 cases of magnet arrangement, a frequency sweep is performed. Each frequency sweep produces a voltage signal from the harvester. This is then transformed into RMS voltage to quantify the performance characteristics of the harvester. Now to study the maximum performance that the harvester is capable of, nine coils are modeled with different numbers of turns.
Additionally, the power harvested from the harvester cannot be the power that goes directly to the pick-up coil. A load resistor is attached to the circuit, and the power through the load resistance is calculated to measure the harvester’s performance. This forms a series L-R circuit, and Equations (20)–(22) are used to model this circuit. Secondly, to check the maximum power output in the load resistor for the same temporal variation in magnetic flux density, 25 load resistors are modeled. These resistors, combined with the nine coils, are used to estimate peak voltage (RMS) and peak power output (RMS). These two outputs are not necessarily linked to each other, as the peak power may or may not correspond to the peak voltage reported. This is performed to analyze the voltage and power output potential from the two tanks separately. Of course, the ultimate performance can only be analyzed through the power output from the system. However, that is also a function of the circuit one builds to harvest the system’s energy. In our case, it is a series L-R circuit represented by Equation (22). The calculation of the coil resistance is based on the number of turns the pickup coil has. The coil material is chosen to be copper. Table 4 summarizes the properties of the pick-up coils modeled for L = 10 cm tank.

Table 4.
Summary of properties of coils for L = 10 cm tank.
The coil properties are calculated by assuming that the tank depth is 10 cm and both the coils envelop the length along the winding direction completely. This gives the coil diameter for the horizontal coil as and for the vertical coil as , where is the height of the tank and L is the length of the tank. The tank depth is maintained to be equal to the tank’s largest dimension to discount 3-D effects on the 2-D simulation performed in this study. To calculate the coil’s inductance from Equation (21), the relative permeability is calculated by taking a weighted average of the ferrofluid and air’s relative permeabilities. This comes out to be 2, considering air as 1 and ferrofluid as 4.52 (). Finally, to check the power output performance of each coil 25 load resistors () are used, which is usually known as impedance matching. The load resistances are varied from 1 to 105 ohms, with an increment of 100.25 ohms. This covers the total range of coil resistances shown in Table 4.
Figure 11 shows the performance measured by max RMS voltage output when a horizontally wound coil is used for voltage pickup from the tank. These plots are for all the 16 magnet configurations, and almost all the cases have low voltages and have almost the same range. The max voltage noted is around 0.03 V, and it is from magnet case 6 and magnet case 11; both seem identical. It must be noted that the cases seem to be symmetric in their behavior, hence making a pair of eight cases, which must be valid for an oscillatory motion. The RMS voltages are calculated after the first two time periods have elapsed. At this point, it is assumed that the system has equilibrated from the initial jerk, which propels the system in an oscillatory motion. The simulations were run for five time periods, and hence the RMS quantities used are from the last three time periods.
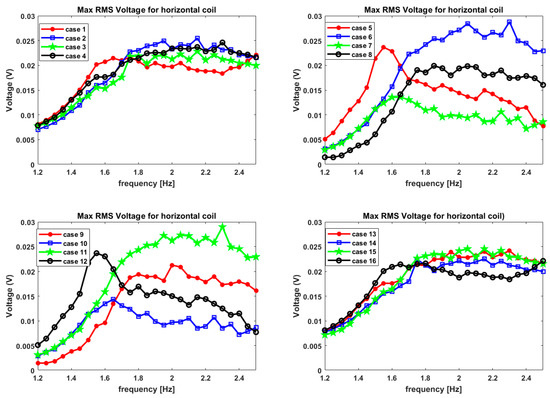
Figure 11.
RMS voltage plots for Cases 1–16 while considering horizontally wound coil for L = 10 cm tank.
For, vertical winding the RMS voltages are shown in Figure 12. They are an order of magnitude higher than the horizontal ones. Cases 7 and 10 achieved the highest RMS voltage output of around 0.15 V. Upon close observation, cases 7 and 10 look very similar to each other solely from the magnets’ placement point of view. This is similar to what was observed for max RMS voltages for the horizontal coil. This can be attributed to symmetric magnet placement in cases 7 & 10 and all the other pairs of cases. The symmetric magnet placement gives rise to magnetic field profiles inside the tank, which are mirror images of each other, which can be deduced from the direction of the magnetic flux lines for these two cases. Secondly, it is observed that there is a secondary peak near 1.5 Hz for both the horizontal and vertical windings. This is due to the internal coupling between modes, generating a non-linear internal energy pump [26,27]. The peak is smeared off since the frequencies in our sweep are equidistant from each other.
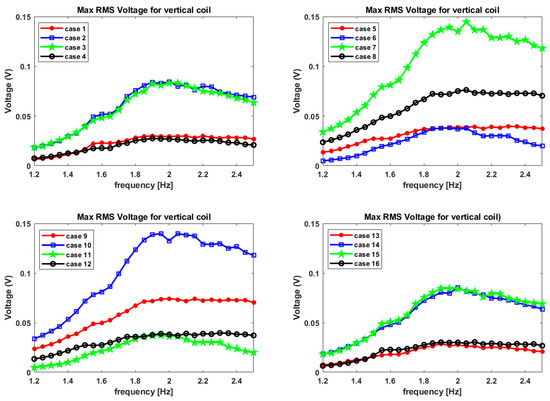
Figure 12.
RMS voltage plots for Cases 1–16 while considering vertically wound coil for L = 10 cm tank.
The RMS current is calculated by solving for instantaneous current from Equation (22) for all of the 9 coils and 25 load resistors to determine the power through the load resistor. Then, the RMS value of this current is taken, and power through the load resistance is calculated using using the value of RMS current pertaining to that particular load resistor and that particular coil. The maxima of the power output for the above 225 cases (i.e., 9 coils and 25 load resistors) is taken for each of the 16 cases of magnet arrangements and all of the 27 frequencies. Figure 13 shows the maximum power through the horizontal winding for all 16 cases, and all of the 27 frequencies are plotted. The maximum power obtained is 0.15 micro-watts () or 0.015 for case 6 and case 11. Here too the symmetry observed for the max voltages is evident. The maximum power value is obtained for a frequency of 2.3 Hz, which points towards shifting the peak from the first modal frequency of 2.0865 Hz. This can be attributed to the magnetic body force exerted on the fluid in the y-direction. Since the magnetic field in the y-direction is considered for electromotive force through the horizontal winding, the shift in the occurrence of the peak power output from the modal frequency is very evident. Hence, the frequency for peak power shifts to the right of the modal frequency for the horizontal winding.
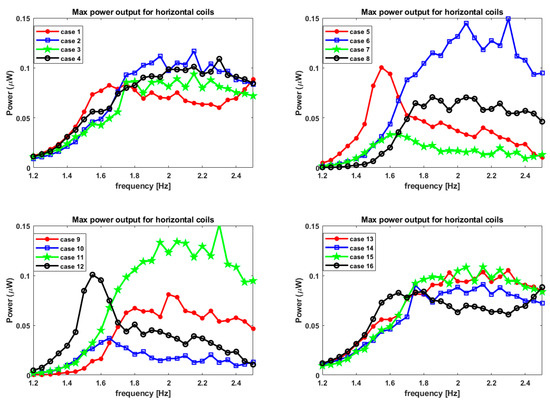
Figure 13.
Maximum power output from the horizontal coil for L = 10 cm tank.
For the vertical coil, the max RMS power for all of the 27 frequencies and 16 magnet cases is plotted in Figure 14. The maximum power is obtained at 2.05 Hz for case 7 and is almost near to 20 micro-watts () or 2 , which is two orders of magnitude higher than that from the horizontal coils. It must be noted that the frequency where the max power output is observed is almost near to the modal frequency of 2.0865 Hz. The shift in the peak occurs towards the left from the modal frequency and is very small compared to that in the horizontal winding case. This can be attributed to the fact that the vertical coil’s output voltage is a function of the magnetic field in the x-direction. The range of the max power extracted using different magnet configurations is very high. The max power out is as low as 0.5 () to the peak of 20 (). This indicates that placing magnets around the tank in a certain way facilitates the power output. It must be restated that the magnets’ position relative to the tank does not change; only the polarity changes. With that change, almost two orders of magnitude of difference are observed in the max power harvested from the device’s vertical winding. This is also true for the horizontal winding case, but the gap between the lowest and highest max powers extracted is not as high as in the case of vertical winding. This provided additional design rules to harness this work into enhancing designs for ferrofluid sloshing vibration energy harvesting systems.
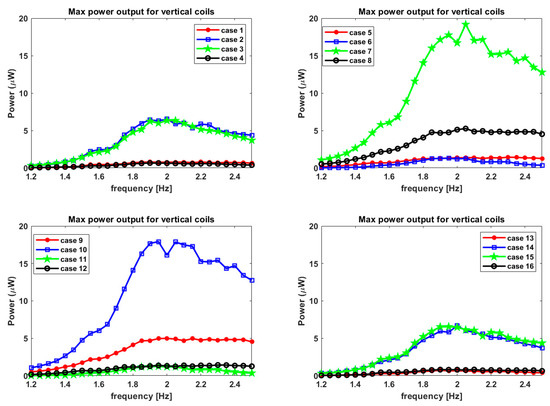
Figure 14.
Maximum power output from the vertical coil for L = 10 cm tank.
5.2. Analysis of Output from L = 5 cm Tank
In this subsection, the tank, which is half the previously discussed tank’s length, is studied. For this tank, the frequencies are varied from 2.2 Hz to 3.5 Hz, which passes through the first modal frequency of 2.96 Hz. The 16 cases of magnet configuration as mentioned in orientation remain the same. Since the length scale L parametrizes all the system dimensions, the whole system’s length becomes half of what it was for the tank studied earlier. This way, the present system becomes identical to the last tank but with a change in the significant length scale. Figure 15 illustrates the surface evolution of the ferrofluid for case 1, for frequency nearest to the resonant frequency. For case 1, the north face of magnet 2 and 4 face the tank while the south face of magnet 1 and 3 face the tank. The plots for the other 15 cases are placed in Appendix A.
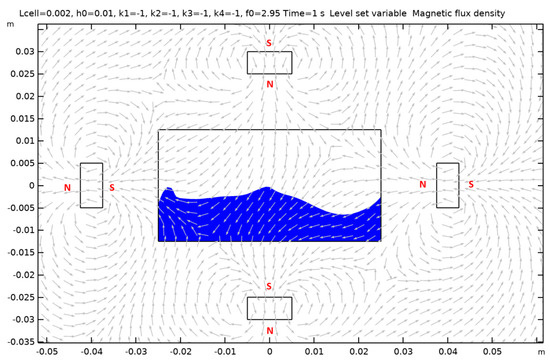
Figure 15.
Surface evolution and magnetic flux density arrow surface for case 1, near resonance frequency for L = 5 cm tank.
Now, for each of these 16 cases of magnet arrangement, a frequency sweep is performed. Each frequency sweep produces a voltage signal from the harvester. This is then transformed into RMS voltage to quantify the performance characteristics of the harvester. Now to study the maximum performance that the harvester is capable of, nine coils are modeled with a different number of turns. Also, the power harvested from the harvester cannot be the power that goes directly to the pick-up coil. A load resistor is attached to the circuit, and the power through the load resistance is calculated to measure the harvester’s performance. This forms a series L-R circuit, and Equations (20)–(22) are used to model this circuit. Secondly, to check the maximum power output in the load resistor for the same temporal variation in magnetic flux density, 25 load resistors are modeled. These resistors combined with nine coils are used to estimate peak voltage (RMS) and peak power output (RMS). These two outputs are not necessarily linked to each other, as in, the peak power may or may not correspond to the peak voltage reported. This is done to analyze the voltage and power output potential from the two tanks separately. Of course, the ultimate performance can only be analyzed through the system’s power output; however, that is also a function of the kind of circuit one builds to harvest the energy from the system. In our case, it is a series L-R circuit represented by Equation (22).
The calculation of the coil resistance is based on the number of turns the pickup coil has. The coil material is chosen to be Copper. Table 5 summarizes the properties of the pick-up coils modeled for L = 5 cm tank. Since the tank’s dimension is halved, the resistance values and the nine coils’ inductance values will also change. The only constants here are the number of turns in the coils and the properties of the magnets used. The coil properties are calculated by assuming that the tank depth is 5 cm, i.e., equal to the length (same as for L = 10 cm tank), and both the coils (Horizontal and Vertical) envelop the length along the winding direction completely. This gives the coil diameter for the horizontal coil as and for the vertical coil as , where is the height of the tank and L is the length of the tank. To calculate the coil’s inductance from Equation (21), the relative permeability is calculated by taking a weighted average of ferrofluid and air’s relative permeabilities. This comes out to be 2, considering air as 1 and ferrofluid as 4.52 (). Finally, to check the power output performance of each coil 25 load resistors () are used, which is usually known as impedance matching. The load resistances are varied from 1 to 105 ohms, with an increment of 100.25 ohms.

Table 5.
Summary of properties of coils for L = 5 cm tank.
Figure 16 the performance measured by max RMS voltage output is displayed when a horizontally wound coil is used for voltage pickup from the tank. These plots are for all the 16 magnet configurations, and almost all the cases have low voltages and have almost the same range. The max voltage noted is around 0.008 V, and it is from magnet case 6 and magnet case 11, like in the case of L = 10 cm tank. However, the harvested voltage is an order of magnitude smaller as compared to the last tank. It must be noted that the cases seem to be symmetric in their behavior, hence making a pair of eight cases, as was observed in the previous tank. The RMS voltages are calculated after the first two time periods have elapsed, at which point it is assumed that the system has equilibrated from the initial jerk, which propels the system in an oscillatory motion. The simulations were run for five time periods, and hence the RMS quantities used are from the last three time periods.
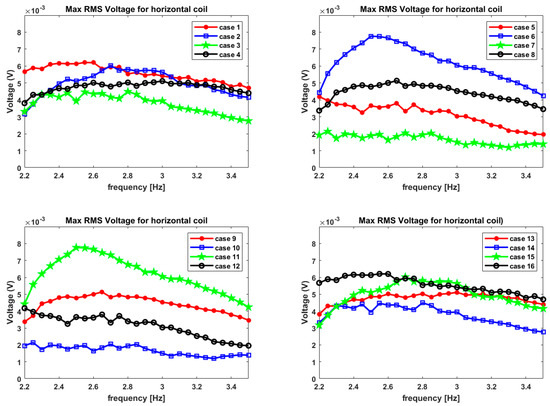
Figure 16.
RMS voltage plots for Cases 1–16 while considering horizontally wound coil for L = 5 cm tank.
For, vertical winding the RMS voltages are shown in Figure 17. They are an order of magnitude higher than the max RMS voltage for horizontal coil, as was observed for L = 10 cm tank. Cases 7 and 10 achieved the highest RMS voltage output of around 0.038 V. The symmetric magnet placement in cases 7 and 10 causes the max RMS voltage observed to be identical. As mentioned in the previous sub-section, the symmetric magnet placement gives rise to magnetic field profiles inside the tank, which are mirror images of each other, which can be deduced from the direction of the magnetic flux lines for these two cases. Similarly, this applies to the other 14 configurations. It can be observed from the voltages and power plots that eight pairs of cases show identical behavior. This would be true for any such system subjected to oscillatory external excitation.
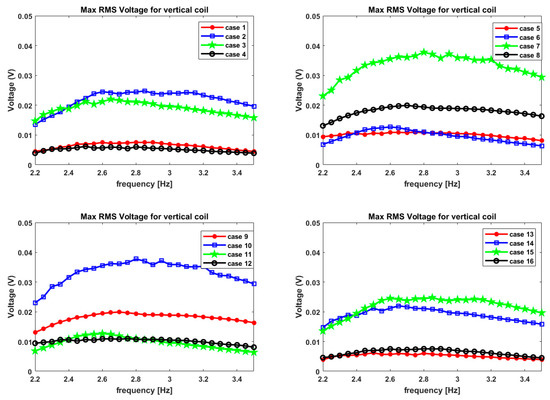
Figure 17.
RMS voltage plots for Cases 1–16 while considering vertically wound coil for L = 5 cm tank.
Secondly, it is observed that there is a secondary peak that was observed for the L = 10 cm tank near 1.5 Hz for both the horizontal and vertical windings, which does not seem to appear for the L = 5 cm tank. This might be due to the inexistence of any non-linear coupling between the sloshing modes of the system, perhaps due to the reduction in size and the increase in the modal frequency from 2 Hz (for L = 10 cm tank) to 3 Hz (for L = 5 cm tank).
The RMS current is calculated by solving for instantaneous current from Equation (22) for all the 9 coils and 25 load resistors to determine the power through the load resistor. Then the RMS value of this current is taken, and power through the load resistance is calculated using , using the value of RMS current pertaining to that particular load resistor and that particular coil. Then the maxima of the power output for the above 225 cases (i.e., 9 coils and 25 load resistors) is taken for each of the 16 magnet arrangements and all the 27 frequencies. Figure 18 shows the maximum power through the horizontal winding for all 16 cases, and all of the 27 frequencies are plotted.
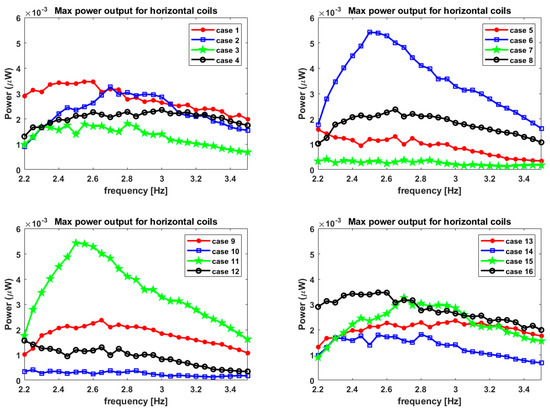
Figure 18.
Maximum power output from horizontal winding for L = 5 cm tank.
The maximum power obtained is 0.005 micro-watts () or 0.5 for case 6 and case 11. Here too, the symmetry observed for the max voltages is evident. The maximum power value is obtained for a frequency of 2.5 Hz, pointing towards shifting the peak from the first modal frequency of 2.96 Hz. This again can be attributed to the magnetic body force exerted on the fluid in the y-direction. Here, the frequency for peak power shifts to the left of the modal frequency for the horizontal winding, unlike the L = 10 cm tank case where the frequency shifted towards the right.
For the vertical coil, the max RMS power for all the 27 frequencies and 16 magnet cases is plotted in Figure 19. The maximum power is obtained at 2.8 Hz for case 7 (and case 10) and is almost near to 0.7 micro-watts () or 70 , which is two orders of magnitude higher than that from the horizontal coils. It must be noted that the frequency where the max power output is observed is nearer to the modal frequency of 2.95 Hz than the horizontal coils. The shift in the peak occurs towards the left from the modal frequency and is very small compared to that in the horizontal winding case. This can be attributed to the fact that the vertical coil’s output voltage is a function of the magnetic field in the x-direction. The range of the max power extracted using different magnet configurations is very high for the vertical winding, as was observed for L = 10 cm case. With that change, almost two orders of magnitude of difference are observed in the max power harvested from the device’s vertical winding. This can also be attributed to the fact that the system’s excitation is in the x-direction. This, coupled with the gravity in the y-direction, makes the harvesting of energy from changes in the magnetic field in the y-direction unattractive. This also makes the power harvested from horizontal windings from all of the 16 cases of magnet arrangements to have a minor variance. This can be useful while designing systems with both x and y excitations or perhaps angular excitation or combining all of the three.
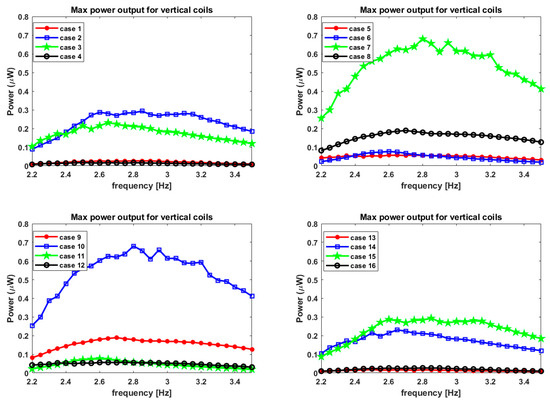
Figure 19.
Maximum power output from Vertical winding for L = 5 cm tank.
6. Conclusions
A completely new design for a ferrofluid sloshing vibration energy harvester is introduced in this work. The design is inherently symmetric since its purpose is to exploit symmetry that can be easy to manufacture. Two tanks, one of length 10 cm and one of length 5 cm, are observed by providing a constant external acceleration of 1 m/s2. The tanks are then subjected to a frequency sweep for 16 different combinations of the four magnets by changing their polarity.
The most important results observed are as follows:
- (a)
- The maximum RMS voltages harvested reached almost 0.15 V
- (b)
- The maximum power after impedance matching was obtained from 10 cm tank, which is around a value of 20 µW or 2.
- (c)
- For a 5cm tank, the highest power output was 0.7 µW, which is higher than what was obtained from the horizontal winding for L = 10 cm tank.
These observations will have a significant impact on the future design of Ferrofluid sloshing VEH’s. Usually, sloshing motion decreases with the decrease in the significant length scale. At low scales, the flow converts into a capillary flow. Hence, miniaturizing these sloshing energy harvesting systems after a particular extent would involve huge trade-offs. However, from the third observation, it can be concluded that miniaturization can still lead to good performance if conducted within limits and if the magnets are oriented optimally, to yield the highest result. Finally, these observations pave the way for future research into miniaturizing the systems. Perhaps a regime like the ‘high-frequency, low amplitude’ might be suitable for harvesting energy from miniaturized Ferrofluid VEH’s. Finally, it is also to be noted that for maintaining the viability of the 2-D simulation as an exact representation of a 3-D tank, the depth of the tank was assumed to be equal to the longest edge of the tank. This increased the wire’s length in winding around the tank as a coil and reduced the harvested power. The power harvested can be increased significantly when the coil is optimized or when a different ‘pick-up’ mechanism is used, which is more efficient than an inductive circuit. Hence, optimizing such systems’ electrical conditioning efficiency would be necessary for future studies to arrive at the most optimal designs for these harvesters.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/fluids6080295/s1.
Author Contributions
Conceptualization, N.A.; methodology, N.A.; software, N.A.; validation, N.A.; formal analysis, N.A.; investigation, N.A.; resources, N.A. and R.G.; data curation, N.A.; writing—original draft preparation, N.A.; writing—review and editing, N.A.; visualization, N.A.; supervision, R.G.; project administration, R.G.; funding acquisition, R.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Most of the relevant data has been presented in this manuscript. Raw data can only be provided at the discretion of the authors due to proprietary constraints. Requests for raw data can be made to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Surface Evolution for L = 10 cm and L = 5 cm Tank
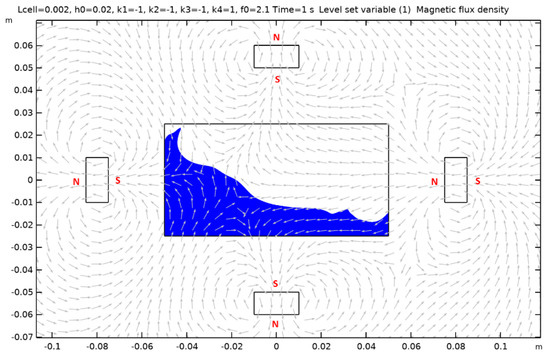
Figure A1.
Case 2.
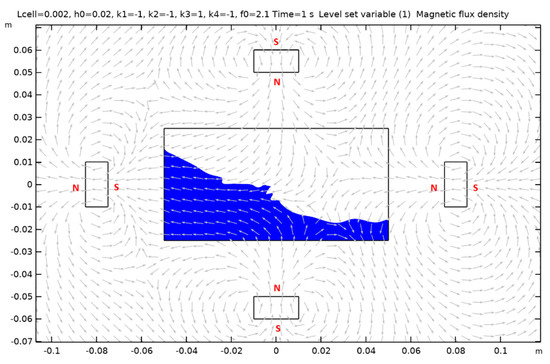
Figure A2.
Case 3.
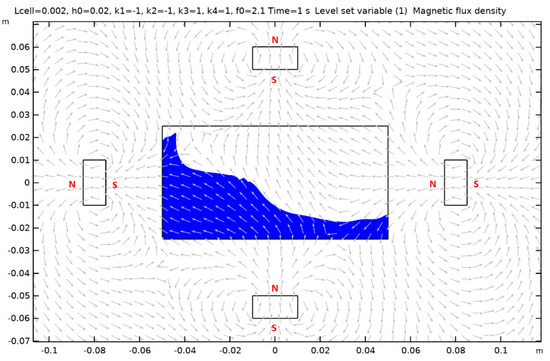
Figure A3.
Case 4.
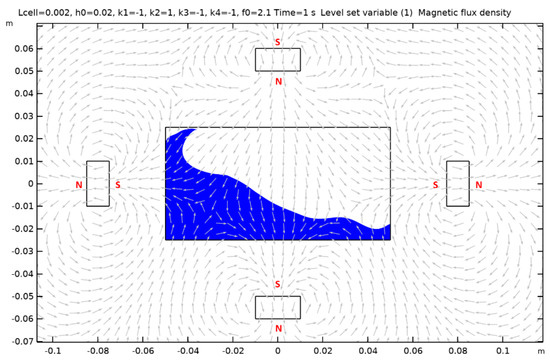
Figure A4.
Case 5.
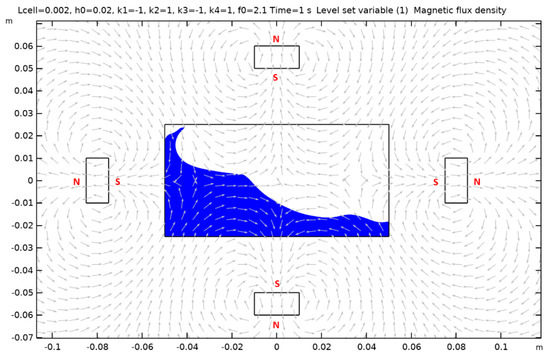
Figure A5.
Case 6.
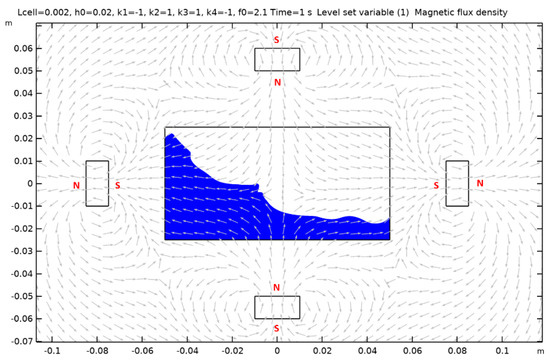
Figure A6.
Case 7.
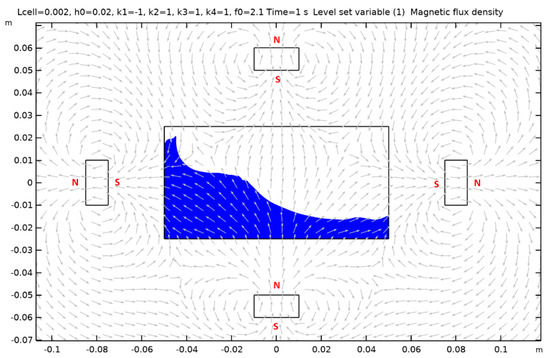
Figure A7.
Case 8.
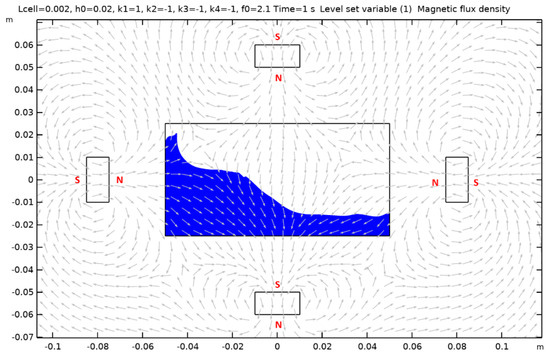
Figure A8.
Case 9.
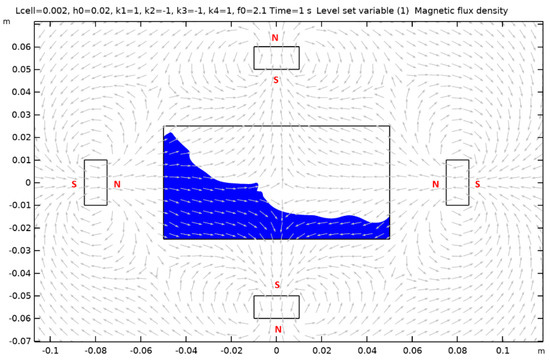
Figure A9.
Case 10.
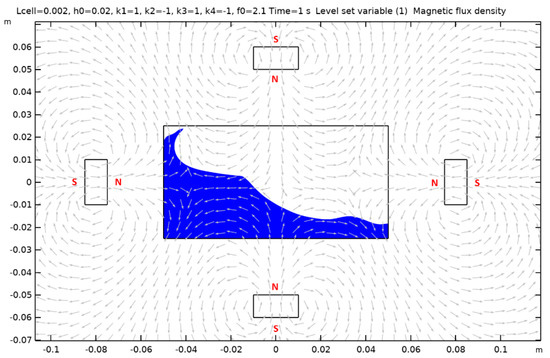
Figure A10.
Case 11.
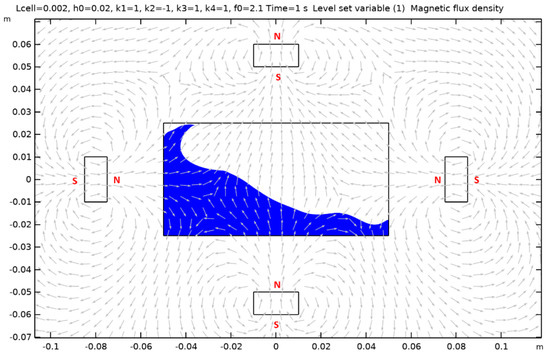
Figure A11.
Case 12.
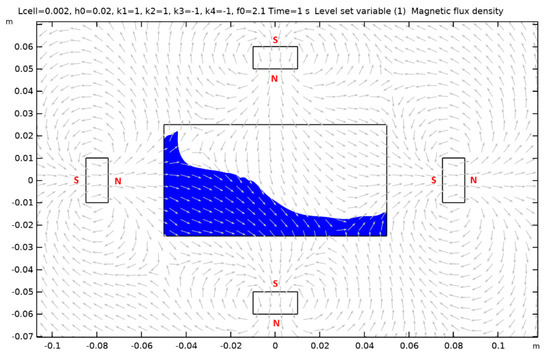
Figure A12.
Case 13.
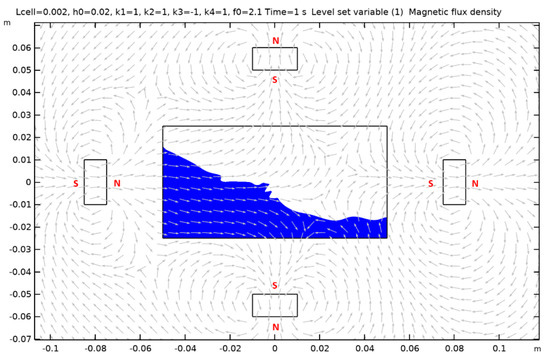
Figure A13.
Case 14.
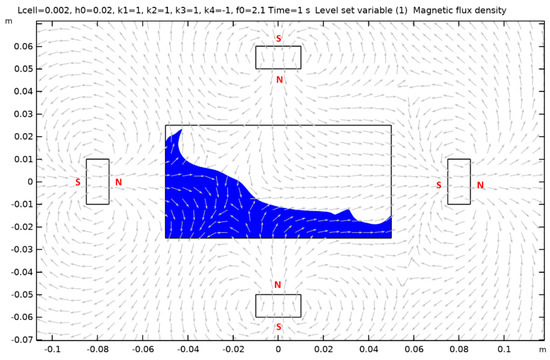
Figure A14.
Case 15.
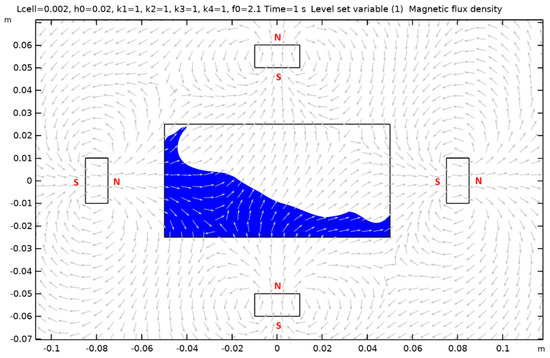
Figure A15.
Case 16.
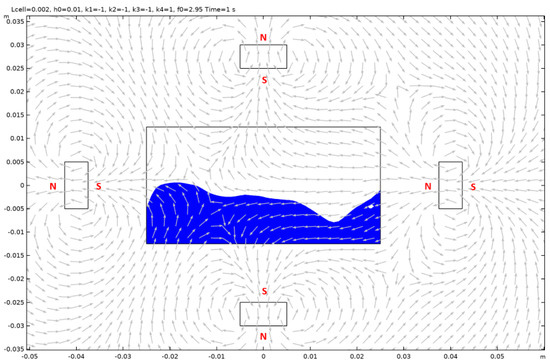
Figure A16.
Case 2.
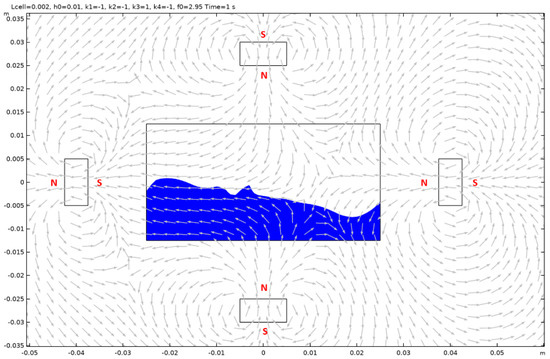
Figure A17.
Case 3.
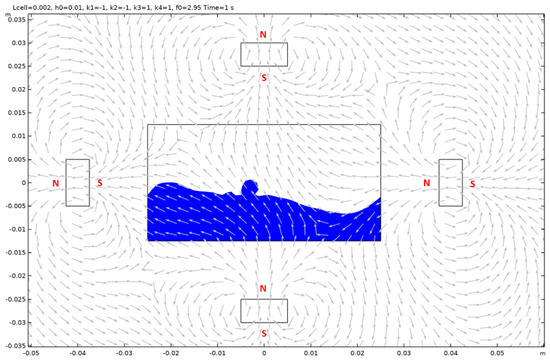
Figure A18.
Case 4.
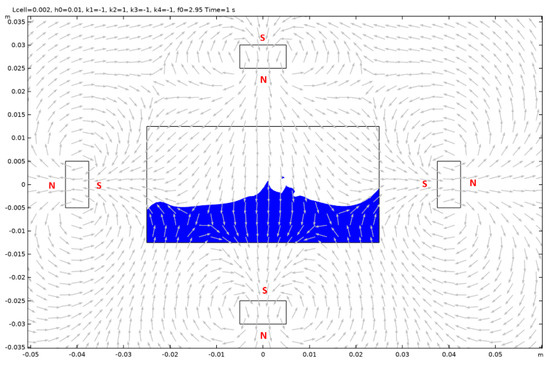
Figure A19.
Case 5.
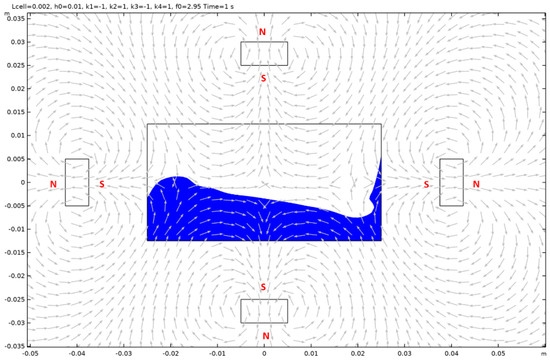
Figure A20.
Case 6.
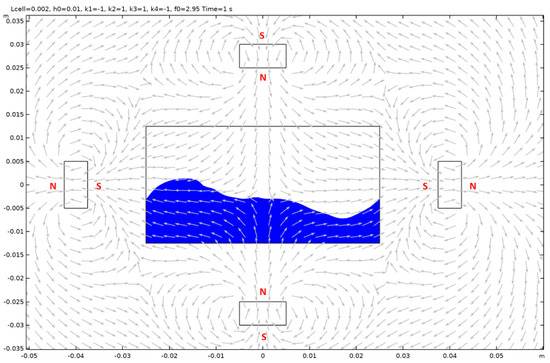
Figure A21.
Case 7.

Figure A22.
Case 8.
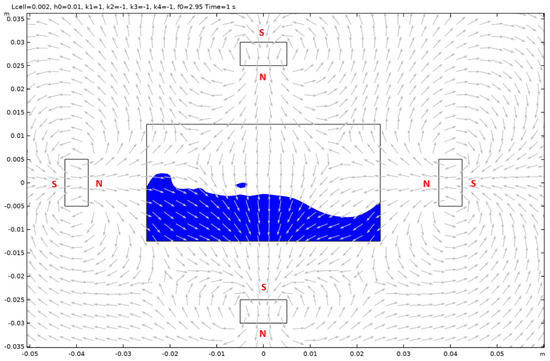
Figure A23.
Case 9.
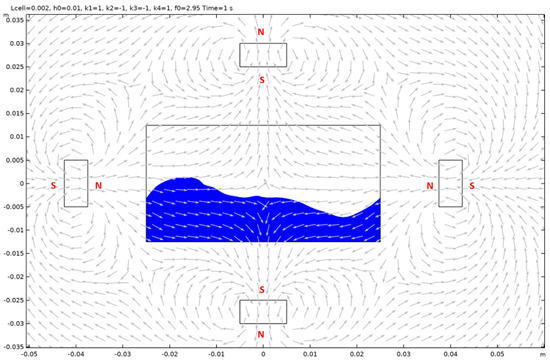
Figure A24.
Case 10.
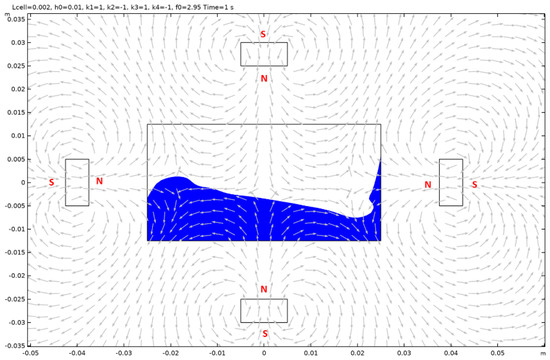
Figure A25.
Case 11.
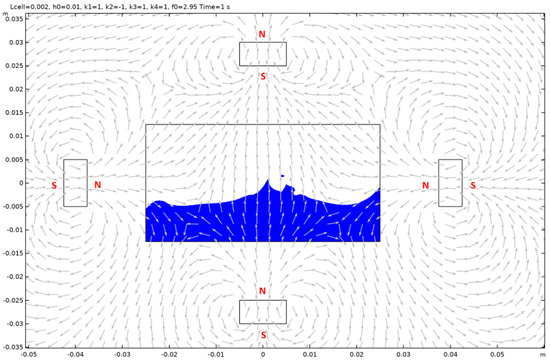
Figure A26.
Case 12.
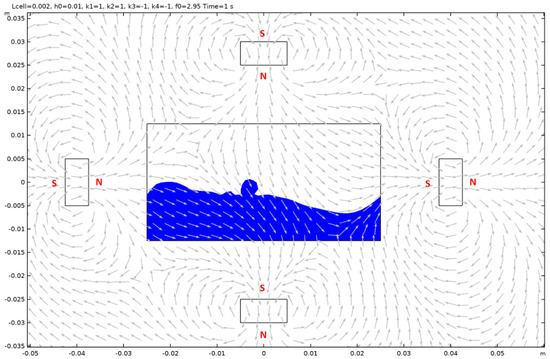
Figure A27.
Case 13.
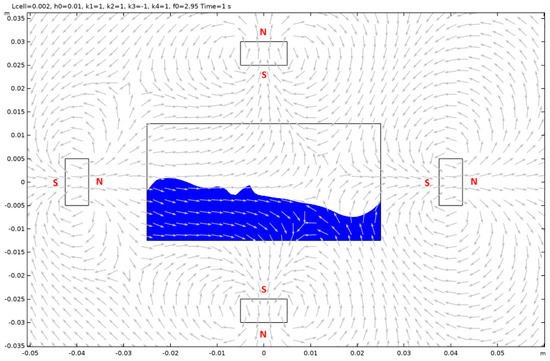
Figure A28.
Case 14.
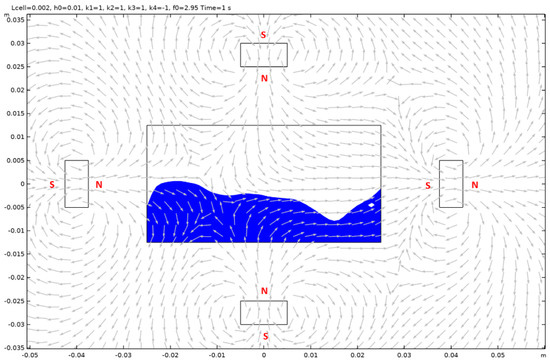
Figure A29.
Case 15.
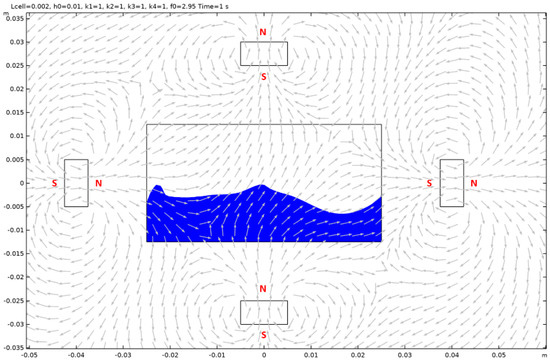
Figure A30.
Case 16.
Appendix B. Waveform Plots for Acceleration, Voltage & Current
Figure A31.
External Excitation.
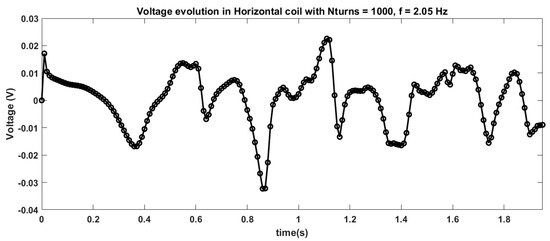
Figure A32.
Voltage evolution for horizontal coil with 1000 turns for case 7 of magnet arrangement and 2.05 Hz frequency of excitation.
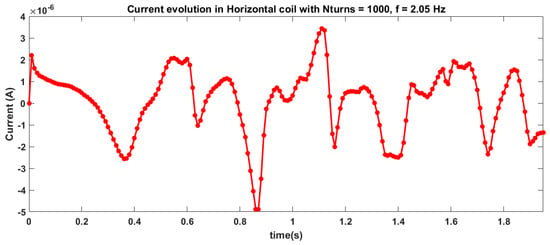
Figure A33.
Current evolution for horizontal coil with 1000 turns for case 7 of magnet arrangement and 2.05 Hz frequency of excita-tion.
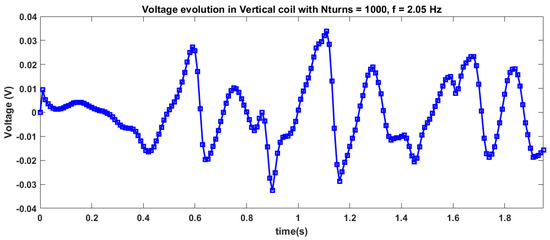
Figure A34.
Voltage evolution for vertical coil with 1000 turns for case 7 of magnet arrangement and 2.05 Hz frequency of excitation.
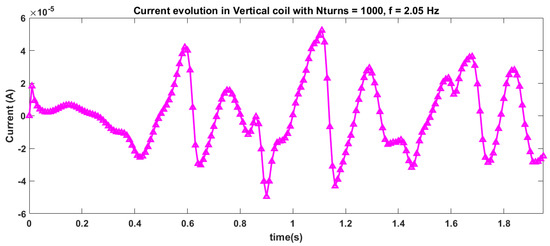
Figure A35.
Current evolution for vertical coil with 1000 turns for case 7 of magnet arrangement and 2.05 Hz frequency of excitation.
References
- Briand, D.; Yeatman, E.; Roundy, S. Micro Energy Harvesting; Wiley-VCH: Hoboken, NJ, USA, 2015. [Google Scholar]
- Niell, A.; Elvin, E. Advances in Energy Harvesting Methods; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Mitcheson, P.D.; Yeatman, E.M.; Rao, G.K.; Holmes, A.S.; Green, T.C. Human and machine motion for wireless electronic devices. Proc. IEEE 2008, 96, 1457–1486. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Lin, L.; Lin, Z. Triboelectric nanogenerators as self-powered active sensors. Nano Energy 2015, 11, 436–462. [Google Scholar] [CrossRef] [Green Version]
- Roundy, S.; Wright, P.K. A piezoelectric vibration based generator for wireless electronics. Smart Mater. Struct. 2004, 13, 1131–1142. [Google Scholar] [CrossRef] [Green Version]
- Challa, V.R.; Prasad, M.G.; Shi, Y.; Fisher, F.T. A vibration energy harvesting device with bidirectional resonance frequency tunability. Smart Mater. Struct. 2008, 17, 15035. [Google Scholar] [CrossRef]
- Thambi, N.; Sastry, A.M. Powering MEMS portable devices—A review of non-regenerative and regenerative power supply systems with special emphasis on piezoelectric energy. Smart Mater. Struct. 2008, 17, 043001. [Google Scholar] [CrossRef] [Green Version]
- Cottone, F.; Vocca, H.; Gammaitoni, L. Nonlinear energy harvesting. Phys. Rev. Lett. 2009, 102, 080601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Erturk, A.; Vieira, W.G.R.; de Marqui, C.; Inman, D.J. On the energy harvesting potential of piezoaeroelastic systems. Appl. Phys. Lett. 2010, 96, 184103. [Google Scholar] [CrossRef]
- Bibo, A.; Masana, R.; King, A.; Li, G.; Daqaq, M.F. Electromagnetic ferrofluid-based energy harvester. Phys. Lett. A 2012, 376, 2163–2166. [Google Scholar] [CrossRef]
- Seol, M.; Jeon, S.; Han, J.; Choi, Y. Ferrofluid-based triboelectric-electromagnetic hybrid generator for sensitive and sustainable vibration energy harvesting. Nano Energy 2017, 31, 233–238. [Google Scholar] [CrossRef]
- Ibrahim, R.A. Liquid Sloshing Dynamics; University Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Price, W.G.; Chen, Y.G. A simulation of free surface waves for incompressible two-phase ows using a curvilinear level set formulation. Int. J. Numer. Methods Fluids 2006, 51, 305–330. [Google Scholar] [CrossRef]
- Bautista-Jacobo, J.L.; Rodríguez-Morales, E.; Montes-Rodríguez, J.J.; Gámez-Cuatzín, H. Effect of baffles on the sloshing in road tankers carrying LPG: A comparative numerical study. Math. Probl. Eng. 2015, 2015, 359470. [Google Scholar] [CrossRef]
- Wang, D.; Chang, K. Electromagnetic energy harvesting from flow induced vibration. Microelectron. J. 2010, 41, 356–364. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Ferrohydrodynamics; Dover Publications: Garden City, NY, USA, 1970. [Google Scholar]
- Hosking, R.J.; Dewar, R.L. Fundamental Fluid Mechanics and Magnetohydrodynamics; Springer: Singapore, 2016. [Google Scholar]
- Anand, N. Application of Ferrohydrodynamic Flows for Heat Transfer Enhancement and Energy Harvesting. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2020. [Google Scholar]
- Anand, N.; Gould, R. Study of Enhanced Self Mixing in Ferrofluid Flow in an Elbow Channel Under the Influence of Non-Uniform Magnetic Field. In Proceedings of the 8th Joint Fluids Engineering Conference, ASME-JSME-KSME 2019, San Francisco, CA, USA, 28 July–1 August 2019. [Google Scholar] [CrossRef]
- Liu, Q.; Daqaq, M.F.; Li, G. Performance analysis of a ferrofluid-based electromagnetic energy harvester. IEEE Trans. Magn. 2018, 54, 1–14. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Q.; Zhao, L.; Tang, Y.; Shkel, A.; Kim, E.S. Vibration energy harvester with low resonant frequency based on flexible coil and liquid spring. Appl. Phys. Lett. 2016, 109, 203901. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Q.; Zhao, L.; Kim, E.S. Non-resonant electromagnetic broad-band vibration-energy harvester based on self-assembled ferrofluid liquid bearing. J. Microelectromechanical Syst. 2017, 26, 809–819. [Google Scholar] [CrossRef]
- Wu, S.; Luk, P.C.K.; Li, C.; Zhao, X.; Jiao, Z. Investigation of an electromagnetic wearable resonance kinetic energy harvester with ferrofluid. IEEE Trans. Magn. 2017, 53, 9. [Google Scholar] [CrossRef]
- Li, C.; Wu, S.; Luk, P.C.K.; Gu, M.; Jiao, Z. Enhanced bandwidth nonlinear resonance electromagnetic human motion energy harvester using magnetic springs and ferrofluid. IEEE/ASME Trans. Mechatron. 2019, 24, 710–717. [Google Scholar] [CrossRef] [Green Version]
- Alazemi, S.F.; Bibo, A.; Daqaq, M.F. A ferrofluid-based energy harvester: An experimental investigation involving internally-resonant sloshing modes. Eur. Phys. J. Spec. Top. 2015, 224, 2993–3004. [Google Scholar] [CrossRef]
- Alazmi, S.; Xu, Y.; Daqaq, M.F. Harvesting energy from the sloshing motion of ferrofluids in an externally excited container: Analytical modeling and experimental validation. Phys. Fluids 2016, 28, 077101. [Google Scholar] [CrossRef] [Green Version]
- Ki, H. Level set method for two-phase incompressible flows under magnetic fields. Comput. Phys. Commun. 2010, 181, 999–1007. [Google Scholar] [CrossRef]
- Capobianchi, P.; Lappa, M.; Oliveira, M.S.N. Deformation of a ferrofluid droplet in a simple shear flow under the effect of a constant magnetic field. Comput. Fluids 2018, 173, 313–323. [Google Scholar] [CrossRef] [Green Version]
- Anand, N.; Gould, R. Modeling Ferrofluid Sloshing Vibration Energy Harvesting Using Level-Set Method. 2020. Available online: https://www.comsol.co.in/paper/download/854041/COMSOLCOnference_2020_NAdishANand.pdf (accessed on 1 June 2021).
- Elgeti, S.; Sauerland, H. Deforming fluid domains within the finite element method. Arch. Comput. Methods Eng. 2014, 23, 323–361. [Google Scholar] [CrossRef] [Green Version]
- Sethian, J.A. Level Set Techniques for Tracking Interfaces: Fast Algorithms, Multiple Regions, Grid Generation and Shape/Character Recognition. 1994. Available online: http://www.ann.jussieu.fr/~frey/papers/levelsets/ (accessed on 5 July 2021).
- Tryggvason, G.; Scardovelli, R.; Zaleski, S. Fluid mechanics with interfaces. In Direct Numerical Simulations of Gas–Liquid Multiphase Flows; Cambridge University Press: Cambridge, UK, 2011; pp. 21–49. [Google Scholar]
- Sethian, J.A. Theory, algorithms, and applications of level set methods for propagating interfaces. Acta Numer. 1996, 5, 309–395. [Google Scholar] [CrossRef] [Green Version]
- Sethian, J.A.; Smereka, P. Level set methods for fluid interfaces. Annu. Rev. Fluid Mech. 2003, 35, 341–372. [Google Scholar] [CrossRef] [Green Version]
- Olsson, E.; Kreiss, G.; Zahedi, S. A conservative level set method for two phase flow II. J. Comput. Phys. 2007, 225, 785–807. [Google Scholar] [CrossRef]
- Walker, C.; Müller, B. A conservative level set method for sharp interface multiphase flow simulation. In Proceedings of the V European Conference on Computational Fluid Dynamics, ECCOMAS CFD 2010, Lisbon, Portugal, 14–17 June 2010; pp. 14–17. [Google Scholar]
- Gibou, F.; Chen, L.; Nguyen, D.; Banerjee, S. A level set based sharp interface method for the multiphase incompressible Navier-Stokes equations with phase change. J. Comput. Phys. 2007, 222, 536–555. [Google Scholar] [CrossRef]
- Fattori, M. A Level Set And Sharp Interface Approach for Simulating Incompressible Two-Phase Flow. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2014. [Google Scholar]
- Sharma, A. Level set method for computational multi-fluid dynamics: A review on developments, applications and analysis. Sadhana Acad. Proc. Eng. Sci. 2015, 40, 627–652. [Google Scholar] [CrossRef] [Green Version]
- Jasper, W.J.; Anand, N. A generalized variational approach for predicting contact angles of sessile nano-droplets on both flat and curved surfaces. J. Mol. Liq. 2019, 281, 196–203. [Google Scholar] [CrossRef]
- Lu, L.; Jiang, S.; Zhao, M.; Tang, G. Two-dimensional viscous numerical simulation of liquid sloshing in rectangular tank with/without baf fl es and comparison with potential fl ow solutions. Ocean Eng. 2015, 108, 662–677. [Google Scholar] [CrossRef]
- Battaglia, L.; Cruchaga, M.; Storti, M.; D’Elía, J.; Aedo, J.N.; Reinoso, R. Numerical modelling of 3D sloshing experiments in rectangular tanks. Appl. Math. Model. 2018, 59, 357–378. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Alazemi, S.F.; Daqaq, M.F.; Li, G. A ferrofluid based energy harvester: Computational modeling, analysis, and experimental validation. J. Magn. Magn. Mater. 2018, 449, 105–118. [Google Scholar] [CrossRef]
- FerroTec. EFH Series Educational Ferrofluid Type: EFH3; Ferrotec (USA) Corporation: Santa Clara, CA, USA, 2019. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).