Abstract
This article discusses the possibility of further reducing the mass of the heat exchanger with stainless steel star-shaped fins while achieving good heat transfer performance. For this purpose, we perforated the fins with holes Ø2, Ø3, and Ø4 mm. Applying computational fluid dynamics (CFD) numerical analysis, we determined the influence of each perforation on the characteristics of the flow field in the liquid–gas type of heat exchanger and the heat transfer for the range of Re numbers from 2300 to 16,000. With a reduction in the mass of the fins to 17.65% (by Ø4 mm), perforated fins had greater heat transfer from 5.5% to 11.3% than fins without perforation. A comparison of perforated star-shaped fins with annular fins was also performed. Perforated fins had 51.8% less mass than annular fins, with an increase in heat transfer up to 26.5% in terms of Nusselt number.
1. Introduction
Finned surfaces are commonly used for efficient heat exchange between liquids and gases. They are placed on the gas side to increase the heat exchange surface. When designing heat exchangers, it is an ordinary requirement to have as little mass as possible, i.e., as little heat transfer surface as possible. Due to the fulfillment of this requirement, various geometric shapes of the fins have been investigated, which are based on analytical models of heat transfer on extended surfaces, but also numerical analysis and experimental research.
Recently, Petrik and Szepesi [1] investigated the heat transfer performance of annular fins experimentally and numerically and then checked them by analytical expressions from the literature.
Chen and Wang [2] analytically defined and experimentally verified the loss of thermal performance to material savings in the case of application of a trapezoidal fin shape instead of a rectangular fin of the constant cross-section.
Martinez et al. [3] analyzed heat transfer and pressure drop on segmented helical fins. Various expressions for heat transfer were experimentally verified on the flue gases.
An increase in the heat transfer can also be realized by adding perforation to fins. For this purpose, the perforations of various shapes and sizes were examined. A review of perforated fins was provided by Zoman and Palande [4].
Liu et al. [5] investigated the application of perforated fins to improve heat transfer on the airside under freezing conditions for tubular heat exchangers. Frost thickness, heat transfer rate, and heat transfer coefficient of perforated heat exchangers were measured. The heat transfer rate and heat transfer coefficient of the perforated fin was enhanced by 38.9% and 31.8%, respectively.
Banerjee et al. [6] numerically analyzed a tubular heat exchanger with circular perforated fins that were 0.5 mm thick—the outer diameter of the fins was 41 mm, and fin pitch was 3.5 mm. One or more holes were placed on the back of the fins in 30° increments. The test was performed with different air velocities in the range of 1 m/s to 5 m/s. Air flowed around tubes, and water vapor condensed inside tubes. Nu number was about 7% greater compared to circular fins without perforation and an increase in pressure drop was 11.87%. The fin area was reduced by 10.79% for the nine-hole case. The authors concluded that the holes at the position of ±120° give the greatest contribution to the enhancement of the heat flux.
Yakar and Karabacak [7] experimentally tested a heat exchanger with annular fins Ø 87 mm and a thickness of 0.5 mm. A 6 mm hole was placed on the fin at different angular positions. The heat exchanger effectiveness was 18% higher for a 60° hole position compared to other hole position angles. At the same time, the pressure drop was 1.16% lower.
Lee et al. [8] experimentally tested perforated circular spiral fins. The fins had two holes in the first case and four holes in the second case. In the first case, enhancement in the heat transfer coefficient was 3.55%, and in the second case, enhancement was 3.31%.
Nadooshan et al. [9] experimentally tested annular fins Ø22 mm and Ø26 mm. The fins were perforated with four holes Ø2.5 mm and Ø3.7 mm, respectively. Air velocities around the fins varied from 3 m/s to 18 m/s, with a step of 3 m/s. Adding perforation led to an enhancement in heat transfer rate up to 8.78% for fins Ø22 mm and up to 2.35% for fins Ø26 mm.
Rai et al. [10] numerically analyzed perforated annular fins for 10,000 ≤ Re ≤ 50,000. The aluminum fins Ø51 were perforated with holes Ø6 mm and attached on tubes Ø29 mm. They varied the number of holes and found the maximum increase in average Nu about 24% at Re = 10,000 in the case with 20 perforations.
Bisen and Sagar [11] analyzed annular fins with various cross-sections and elliptical perforation. They concluded that the triangular profile is more economical compared to rectangular and trapezoidal profiles.
Liu et al. [12] investigated the influence of perforation on fins in the form of thin plain sheets 0.2 mm thick by numerical analysis. They varied the number of perforation holes (5, 9), hole size (Ø4, Ø5, and Ø6 mm), and the fin pitch (7.5, 10, 15, and 20 mm). At the fin pitch of 10 mm, the optimal variant was determined, wherein the j factor improved by 0.3% at Re = 750 and 8.1% at Re = 2350.
Sundar et al. [13] numerically and experimentally tested serrated fins of 1 mm thick with circular perforation under natural convection and radiation. They varied fin width (4 mm to 7 mm), the number of perforations (0 to 3), and the size of perforation (Ø2 mm to Ø4 mm). The results showed that the variant with perforated surfaces had less thermal resistance by approximately 7% to 12% compared to non-perforated surfaces.
Dhanawade et al. [14] experimentally tested the heat transfer on a horizontal flat surface on which rectangular fins were placed. The fins were perforated with rectangular or circular holes. They showed that the circular shape of the perforation gives better results. A very similar study was conducted numerically and experimentally by Ibrahim et al. [15]. They placed circular, rectangular, and triangular perforations on the rectangular fins. The best heat transfer was achieved by the triangular shape of the perforation.
Shaeri and Yaghoubi [16] numerically investigated laterally perforated fins on a horizontal plate with square holes. They concluded that perforated fins have better heat transfer performance than non-perforated fins.
Chingulpitak et al. [17] examined the thermal characteristics of laterally perforated cooling fins with various numbers and diameter of perforations. The optimal variant of perforated fins achieved about 10.6% higher thermal performance compared to the solid fins under equal conditions.
Gupta et al. [18] studied the influence of perforation on the fins of internal combustion engines applying numerical analysis. They varied the number of perforation holes and hole diameter.
Lee et al. [19] recently studied the influence of perforation on stainless steel annular spiral fins by computational fluid dynamics (CFD) analysis. The perforation was located at various angular positions (90°, 120°, and 150°). The fin Ø39.05 mm and thickness 0.4 mm was attached to the tube Ø19.05 mm with a pitch of 5 mm. The heat transfer enhancement of 3% and the enhancement of approximately 11.7% of the j-Colburn factor in the case of six-hole perforations were realized.
Karami and Kamkari [20] experimentally studied the application of perforated fins on the heat transfer characteristics of a vertical tubular heat exchanger with latent heat storage. The phase change process was studied at different water velocities at the inlet to the heat exchanger (0.5 and 1 L/min) and temperatures (55 °C and 65 °C). Experimental results have shown that heat exchangers with perforated fins have an average Nusselt number about 30% higher than heat exchangers with solid fins.
One of the proposals to reduce the heat exchangers mass with enhancement in the heat transfer is to apply star-shaped fins [21,22,23]. The authors constructed tubular heat exchangers with star-shaped fins and analyzed them by CFD simulation. The results were compared with the equivalent case of solid annular fins. With 43.4% less mass of star-shaped fins than standard annular fins, the heat transfer coefficient of star-shaped fins was higher by 10% to 15% in the range of Re numbers from 2300 to 11,500. One of the ideas of further reducing the mass of this type of heat exchangers is fins perforation, which is analyzed in this article.
2. Materials and Methods
This work investigated the possibility of enhancing heat transfer through the application of perforation with geometric patterns. The subject of research was star-shaped perforated fins, placed on tubes through which hot water flowed. There was a cold air stream around tubes and fins. Stainless steel was chosen for the tube and fin material. A numerical method for computational fluid dynamics (CFD) was used to evaluate fluid flow and heat exchange in the modeled heat exchanger.
2.1. The Geometry Description
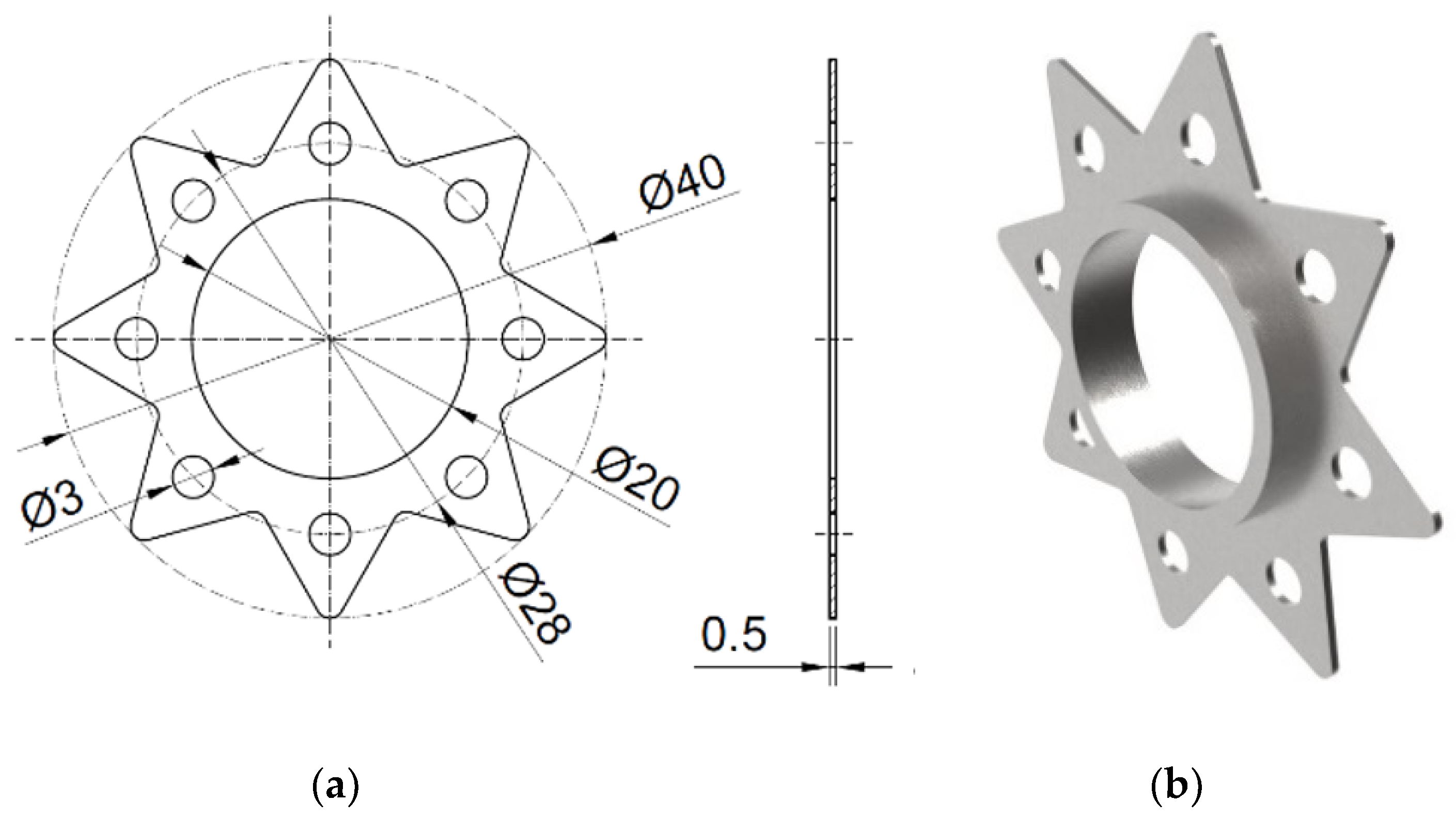
The initial geometry is defined in [21,22]. Star-shaped fins, 0.5 mm thick with an outside diameter of 40 mm, were attached to the tube Ø20 as the reference geometry. The fin had 8 perforated holes of circular shape evenly distributed on a diameter of Ø28 mm. The analysis was performed for 3 sizes of perforations: Ø2 mm, Ø3 mm, and Ø4 mm (Figure 1 shows the holes Ø3 mm).
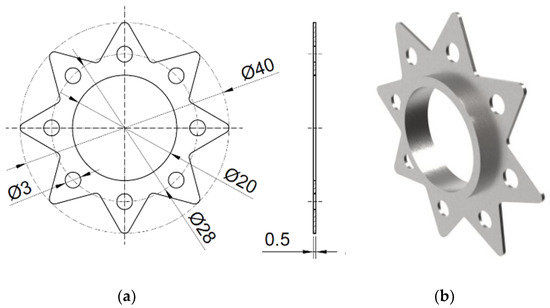
Figure 1.
The geometry of the perforated star-shaped fin (a), and 3D model (b).
2.2. Numerical Analysis
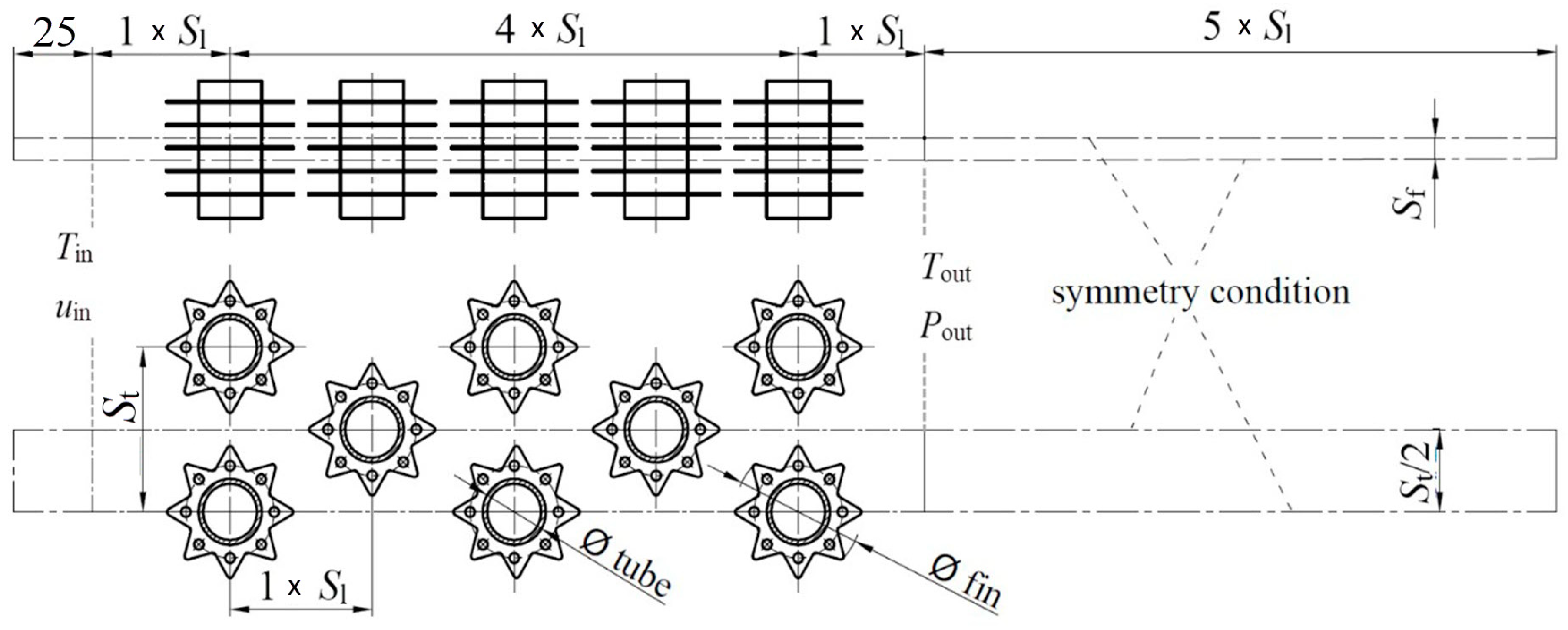
Numerical analysis was performed analogously as described in [21,22]. The same basic settings and boundary conditions were applied. The computational domain is shown in Figure 2.
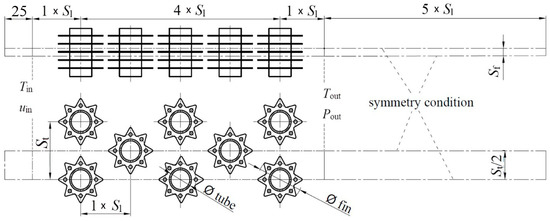
Figure 2.
Computational domain.
The mathematical description of thermal phenomena within a heat exchanger includes certain assumptions and simplifications.
The most common assumption used in defining fluid flow is fluid continuity. The characteristic sizes of the analyzed heat exchanger were large enough that the conditions of the continuum hypothesis were met. Homogeneity and isotropy assumptions were also applied. Homogeneity implies that the physical properties of the substance are the same at all points. In this sense, the air is considered as a homogeneous mixture of gases and is treated as a one-component fluid (dry air). Isotropy implies that the physical properties of matter are the same in all directions. The application of this assumption implied that the fin thermal conductivity was equal in all directions.
The next assumption was that there was no fluid leakage through the walls of the heat exchanger and negligible heat transfer to the environment. The fins were tightly attached to the tube, and thus there was no contact resistance between the tube and the fin surface. A steady-state analysis was performed.
Boundary and initial conditions included the following assumptions:
- The air entering the computational domain had uniform velocity over the cross-section and ranged from 1 m/s to 7 m/s. The turbulence intensity was set to 5%.
- The air temperature at the inlet to the heat exchanger was 288 K.
- Hot water at the inlet to tubes was 353 K. Water has a high thermal capacity, and thus it was assumed that the temperature of the tube inner wall was constant and equal to the water temperature.
- The gauge pressure at the outlet of the channel was zero, which corresponds to atmospheric conditions.
- Hydraulically smooth walls were assumed for outer tube surfaces and fin surfaces.
- The symmetry boundary condition was set at the sides of the computational domain.
- Moreover, the symmetry boundary condition was set for the top, bottom, left, and right sides of the computational domain. Symmetry condition was applied for simplifying the calculation and to reduce the computational domain where possible.
- The normal velocity component on the plane of symmetry was equal to zero, i.e., there was no convective flow through the plane of symmetry. Thus, the temperature gradients and tangential components of the velocity gradients in the normal direction were set to zero.
Table 1 and Table 2 present the geometry and boundary conditions for the heat transfer calculations.

Table 1.
The tube and star-shaped fin data.

Table 2.
Boundary conditions of numerical analysis.
2.3. Governing Equations
The mathematical model used to describe a physical problem is a set of differential equations and constitutive relations, and initial and boundary conditions. The basic equations of fluid dynamics are derived from:
Conservation of mass:
Conservation of momentum:
Conservation of energy:
The established mathematical model is solved by using the finite volume method that is based on dividing the computational domain into small volumes and integration of equations of conservation at these volumes, thus obtaining a system of discrete algebraic equations that are then solved iteratively.
The computational domain was meshed with ANSYS software, Version 17.2 (ANSYS, Inc., Canonsburg, PA, USA), applying a hybrid mesh approach where some parts of the volume meshed with structured mesh, with the remaining volume being meshed with unstructured mesh. Figure 3 shows a 3D view of reference geometry (a) and the mesh detail (b).

Figure 3.
3D view of fins (a) and the mesh detail (b).
The mesh independence study was performed, focusing primarily on Nu and Eu, with mesh 5.8, 8.2, 10.8, and 15 million finite volumes. The test results are shown in Table 3.

Table 3.
The mesh independence test.
A mesh of 15 million finite volumes was selected for this study in order to obtain the most accurate results. k-ω SST turbulence model was used, which was detailed in [21].
3. Results

Table 4.
Output data for the perforation hole Ø2 mm.

Table 5.
Output data for the perforation hole Ø3 mm.

Table 6.
Output data for the perforation hole Ø4 mm.
Data reduction and interpretation are detailed in [21]. Comparison and validation of the results of CFD simulation for annular and star-shaped fins without perforation is presented in [21,22,23].
Flow Characteristics
All figures below show the flow features for the fin with perforation holes Ø4 mm and non-perforated fin. Cases for other hole diameters are not shown because they were similar to the case shown.
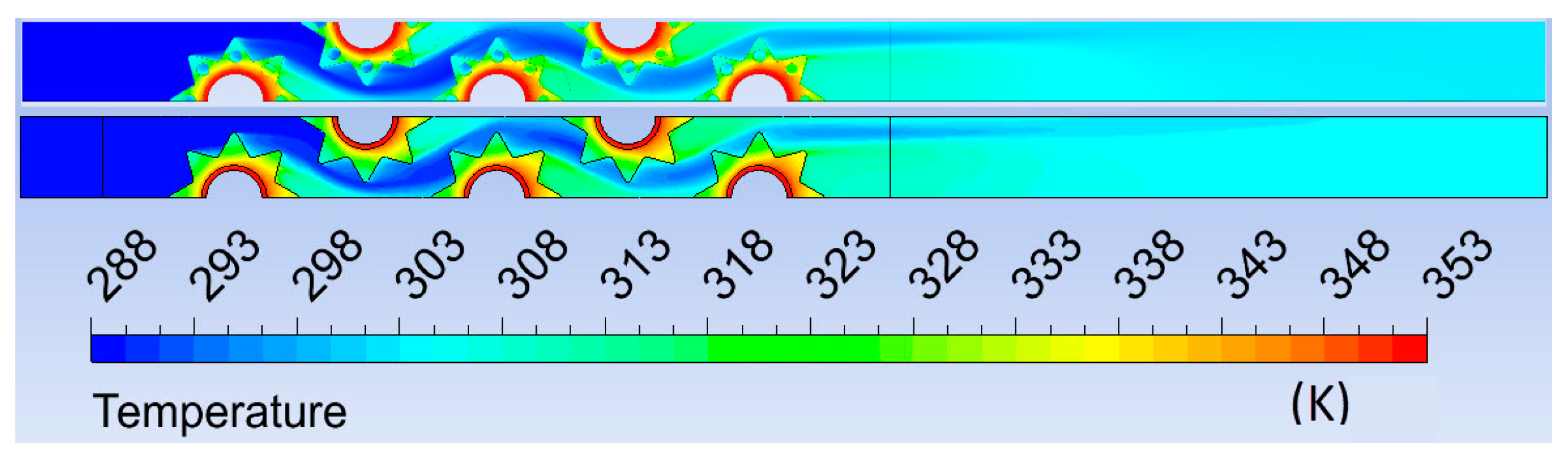
The global temperature, velocity, and pressure distribution in the heat exchanger bundle are important for the comprehension of the local flow and heat transfer processes. Figure 4 presents the local feature of the temperature fields for analyzed fins. The larger temperature drop is visible on perforated fins. Consequently, the efficiency of the perforated fins must have been lower than the efficiency of the non-perforated fins.
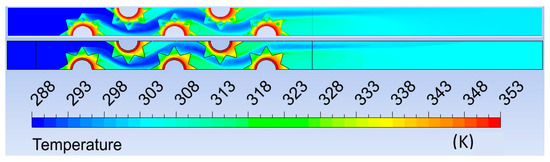
Figure 4.
Temperature fields for perforated and non-perforated fins.
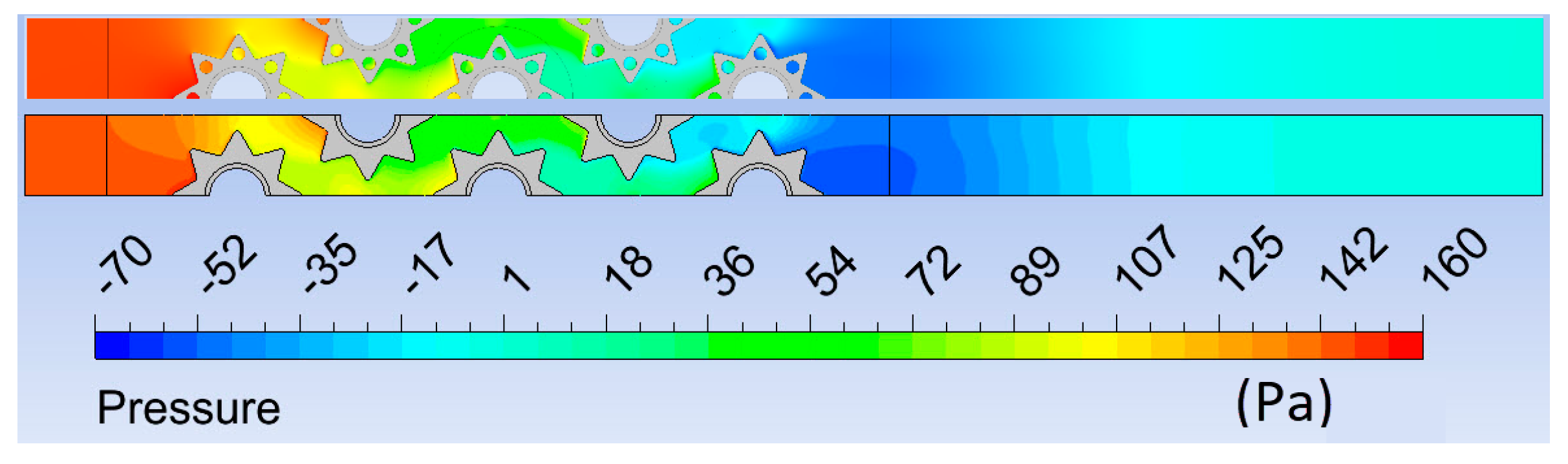
Figure 5 shows the local feature of the pressure. In front of the first row of tubes with perforated fins, slightly higher pressure is visible compared to fins without perforation. Behind the last row of tubes with perforated fins, the created negative pressure was slightly lower compared to the fins without perforation.
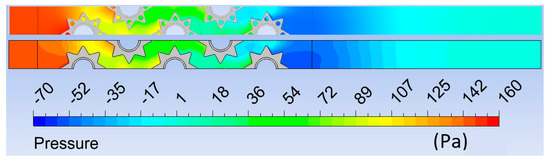
Figure 5.
Pressure fields for perforated and non-perforated fins.
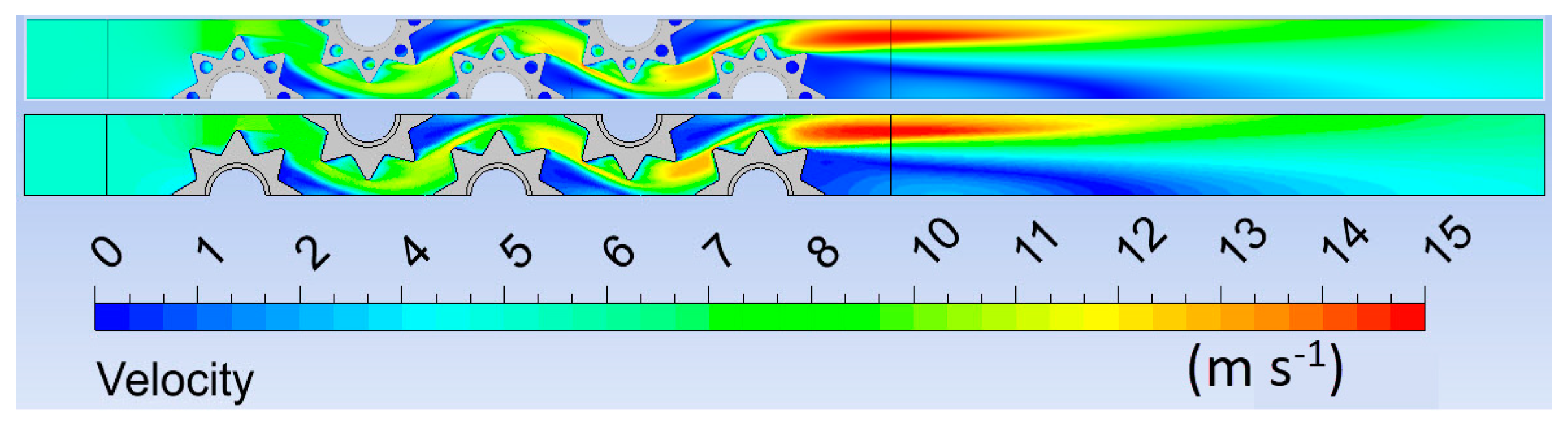
Figure 6 and Figure 7 show the local feature of the air velocity for non-perforated and perforated fins at an inlet air velocity of 5.0 m/s. Figure 6 shows a local feature in cross-section set in the middle of the fin thickness. Larger differences in the flow feature between non-perforated and perforated fins are not noticeable.
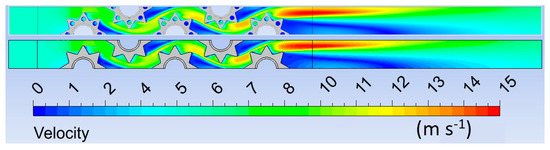
Figure 6.
Velocity fields for perforated and non-perforated fins.
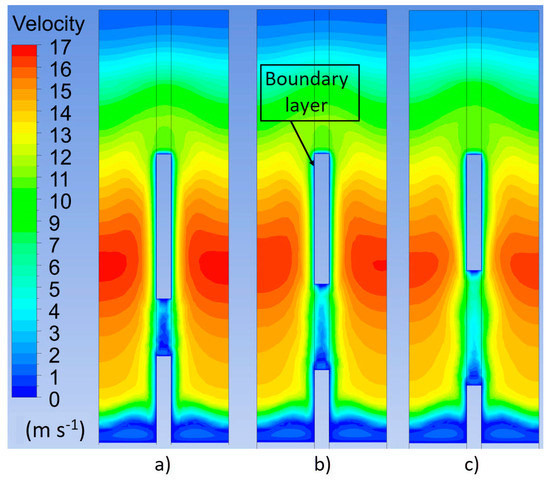
Figure 7.
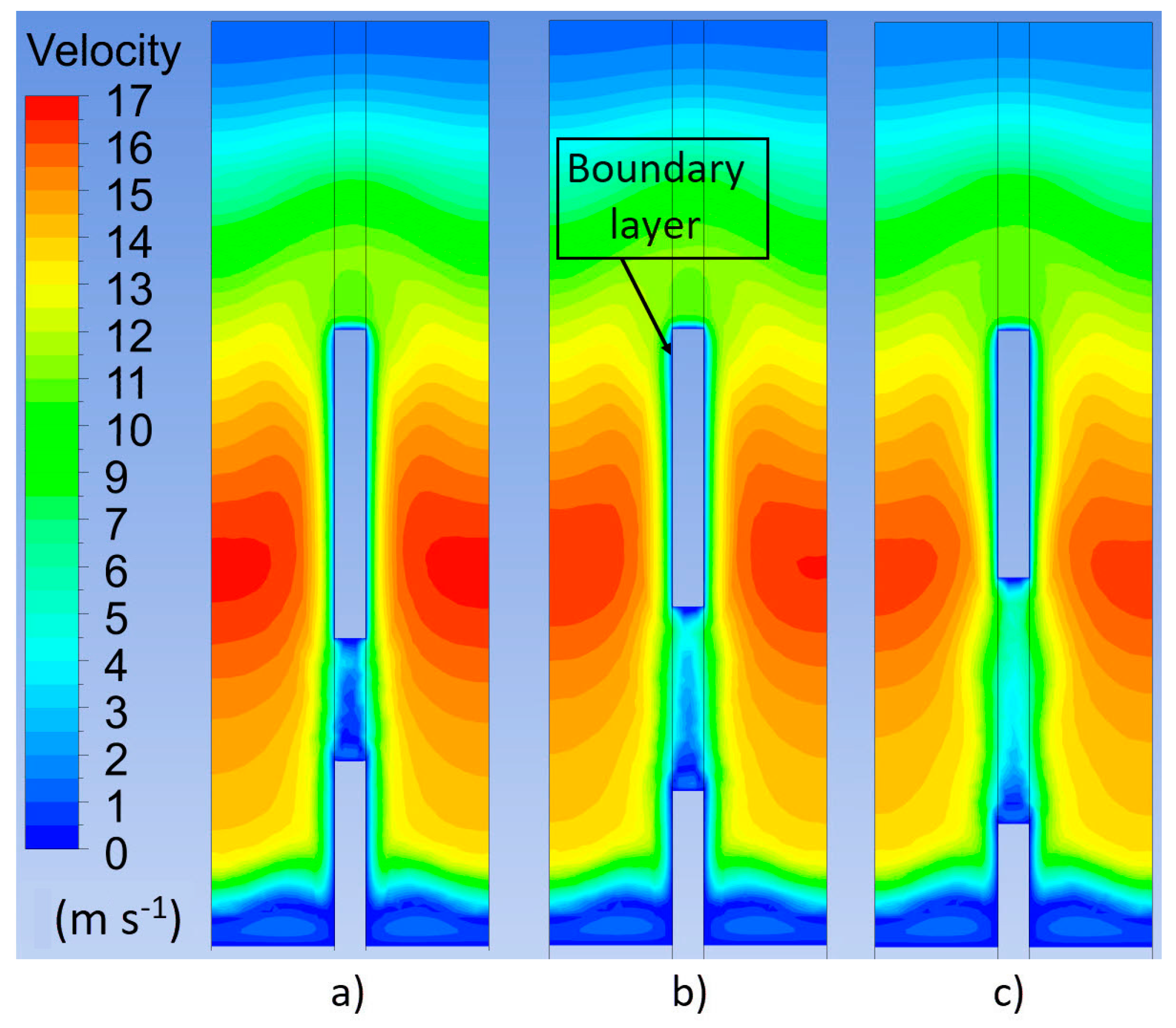
Velocity field in fin cross-section. The fins with hole (a) Ø2 mm, (b) Ø3 mm and (c) Ø4 mm.
In Figure 7, in the cross-section of the fins, a difference in the velocity field in the area of the perforations is visible. At the fins with a perforation of Ø4 mm (Figure 7c), the flow rate through the holes was much higher than in the case of Ø2 mm holes (Figure 7a). This resulted in an enhancement of the heat transfer coefficient in the area of the holes and greater heat dissipation from the fins.
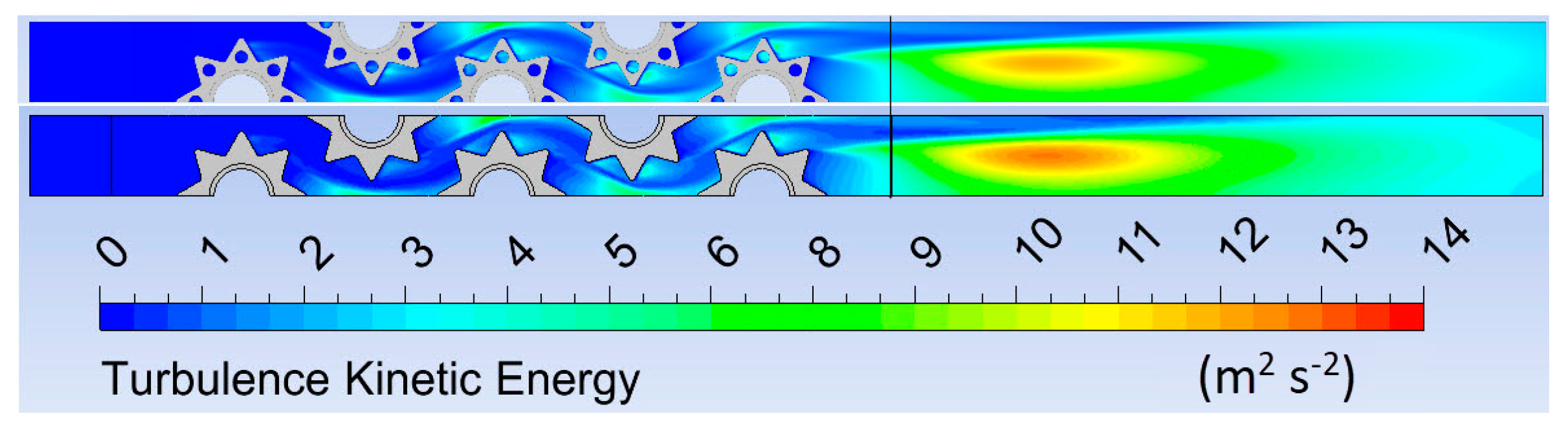
Figure 8 shows higher turbulence kinetic energy in the area of fin perforation, which is in line with the commentary on Figure 7. This was especially pronounced in the third, fourth, and fifth tube rows. This confirms that perforated fins had a better heat transfer than fins without perforation.
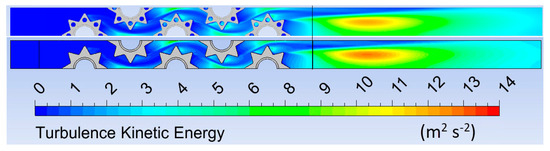
Figure 8.
Turbulence kinetic energy fields for perforated and non-perforated fins.
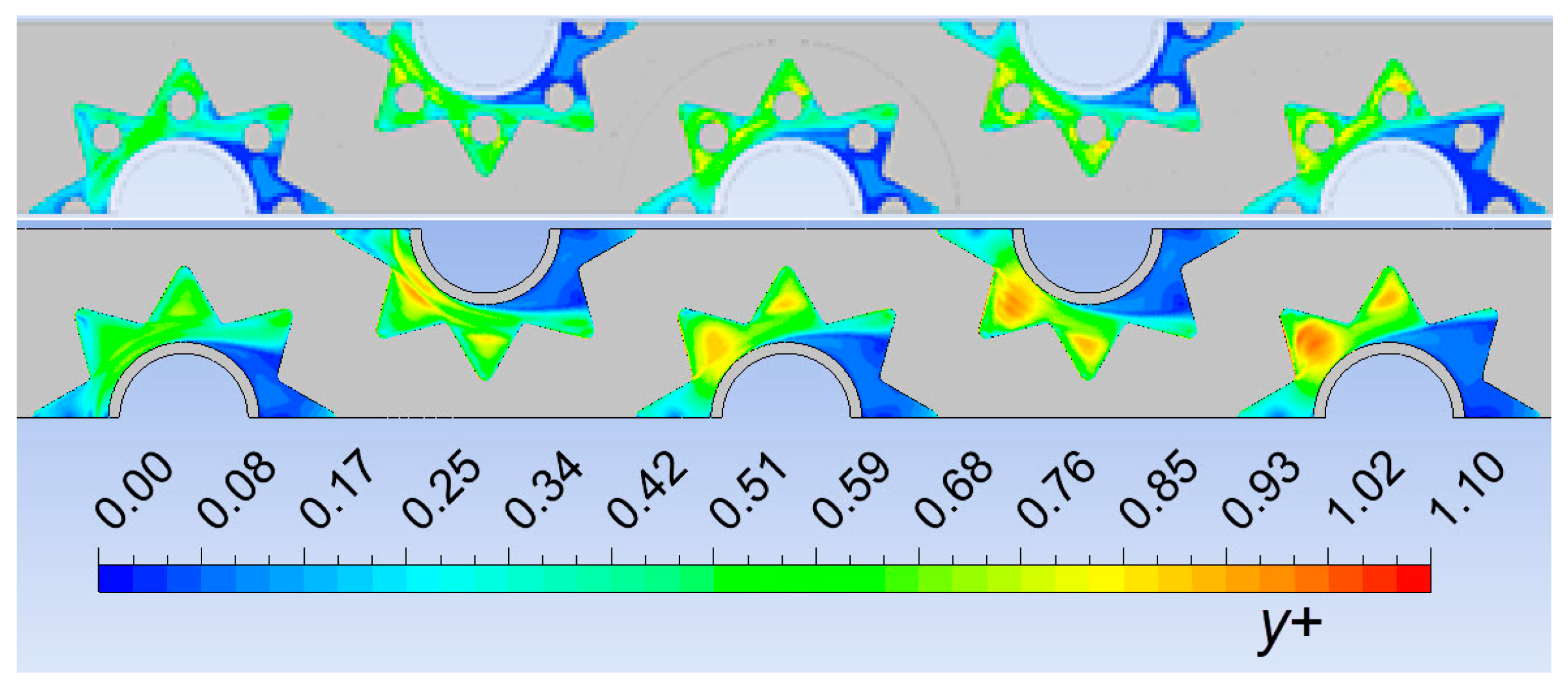
Figure 9 shows dimensionless wall distance y+ for non-perforated and perforated fins at an inlet air velocity of 5.0 m/s. It is visible that in the whole area of perforated fins, y+ was less than 1. This was achieved by fine near-wall mesh that can solve the viscous sublayer (shown in Figure 7). Perforation holes were located in the area where y+ was greatest for non-perforated fins.
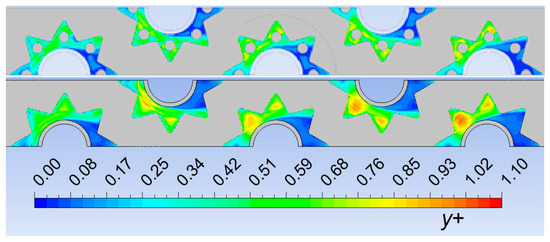
Figure 9.
Dimensionless wall distance y+.
4. Discussion
Heat transfer and pressure drop featured depending on the airflow conditions and the heat exchanger geometry. Thus, the flow and heat transfer characteristics, primarily Reynolds number (Re), Nusselt number (Nu), Colburn factor (j), Euler number (Eu), and friction factor (f) were applied to describe the thermal and hydraulic features of the heat exchanger. These dimensionless features are usually represented by Equations (4)–(8).
The results of the CFD simulation for perforated fins, on the basis of the data given in Table 1, Table 2, Table 3, Table 4 and Table 5, can be represented by the previously mentioned dimensionless features. The presented results for non-perforated star-shaped and solid annular fins were based on the investigation of Bošnjaković et al. [23].
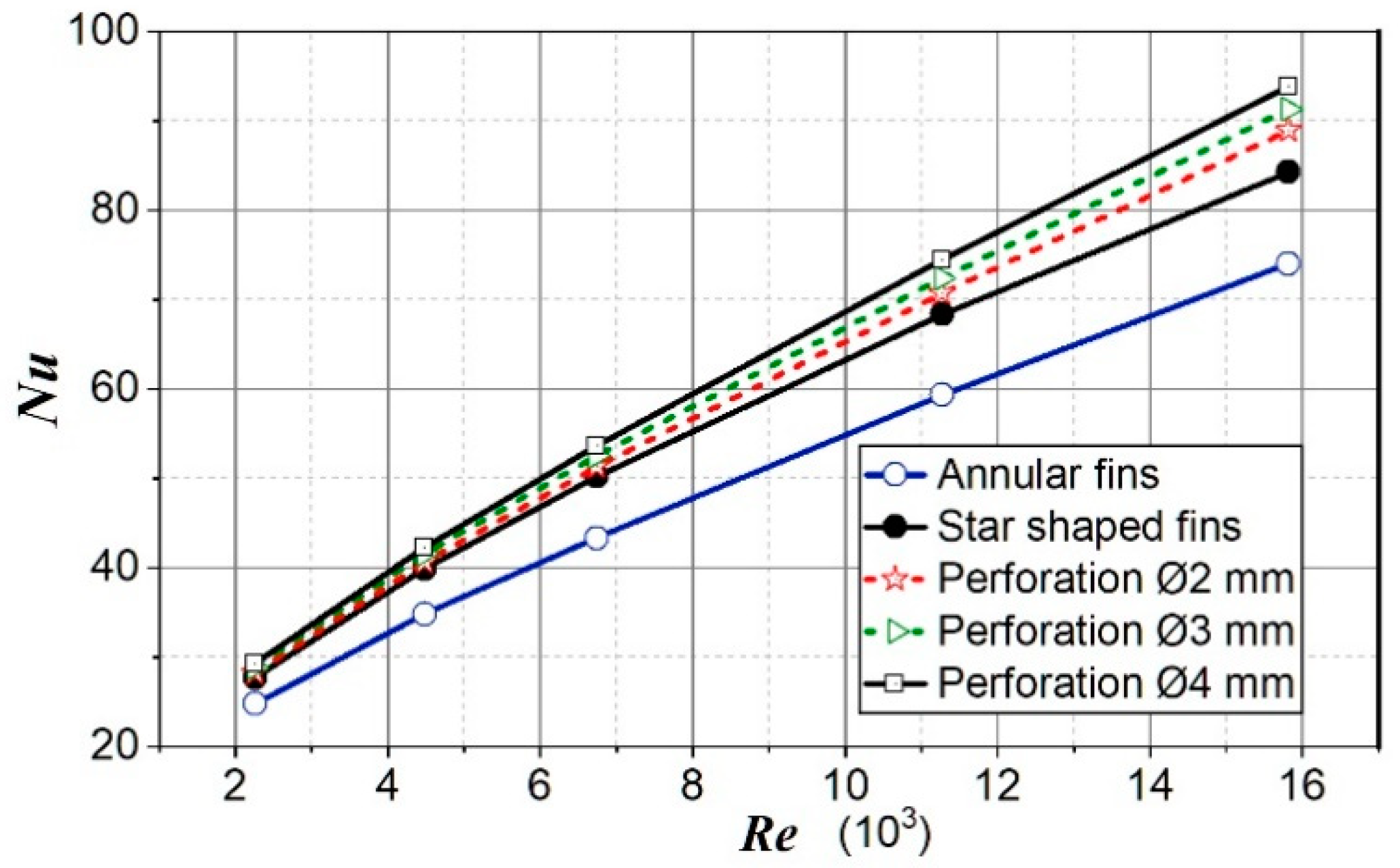
Figure 10 shows that the star-shaped fins with perforation had the greatest Nu number. Moreover, Figure 10 shows that the Nu number increased with increasing perforation hole diameter.
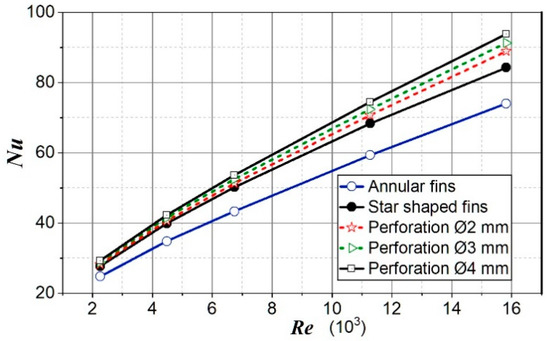
Figure 10.
Nusselt number for analyzed cases.
At the perforation hole Ø2 mm and Re = 16 × 103, Nu number was higher concerning star-shaped fins without perforation by 5.57%, i.e., by 20.1% higher concerning annular fins. At Re = 2.3 × 103, the increase in Nu number concerning annular fins was 14.0% and concerning star-shaped fins without perforation was 1.94%.
At Re = 16 × 103 for perforation Ø4 mm, Nu number was higher with regards to star-shaped fins without perforation by 11.4%, i.e., it was higher by 26.7% concerning annular fins. At Re = 2.3 × 103, Nu number for star-shaped fins was 18.2% greater than for solid annular fins and 5.7% greater than for star-shaped fins without perforation.
Moreover, it can be concluded from Figure 10 that the influence of perforation diameter on the Nu number strengthens with the Re number increase (the curves in the right part of the diagram increasingly separated from each other).
The increase in perforation diameter from Ø2 mm to Ø4 mm had an almost linear effect on the increase in the Nu number.
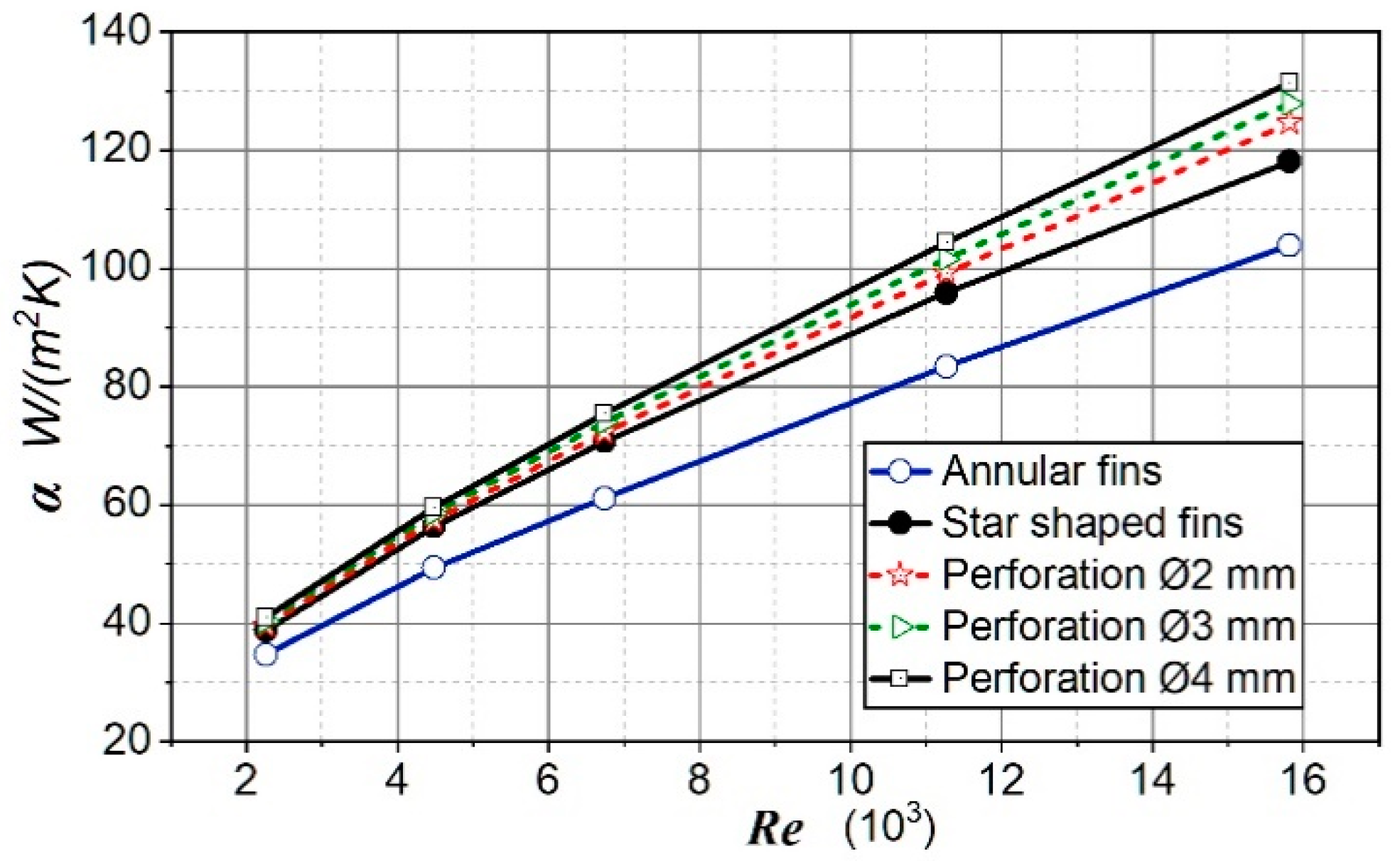
Figure 11 shows the heat transfer coefficient for the analyzed cases. The results are analogous to the results for the Nu number. It is also noticeable that as the Re number increased, the importance of the perforation size on the heat transfer strengthened. This enhancement for perforated fins was up to 12.03% in relation to non-perforated fins, and up to 58.2% in relation to annular fins in the observed range of Re numbers.
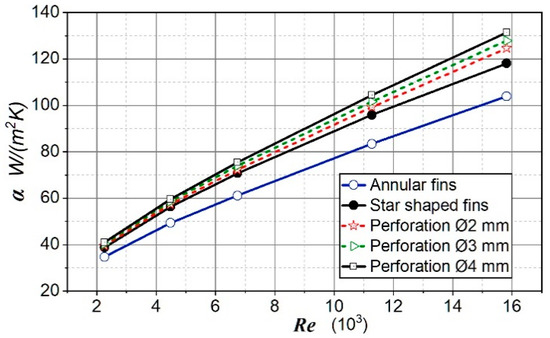
Figure 11.
Heat transfer coefficient for analyzed cases.
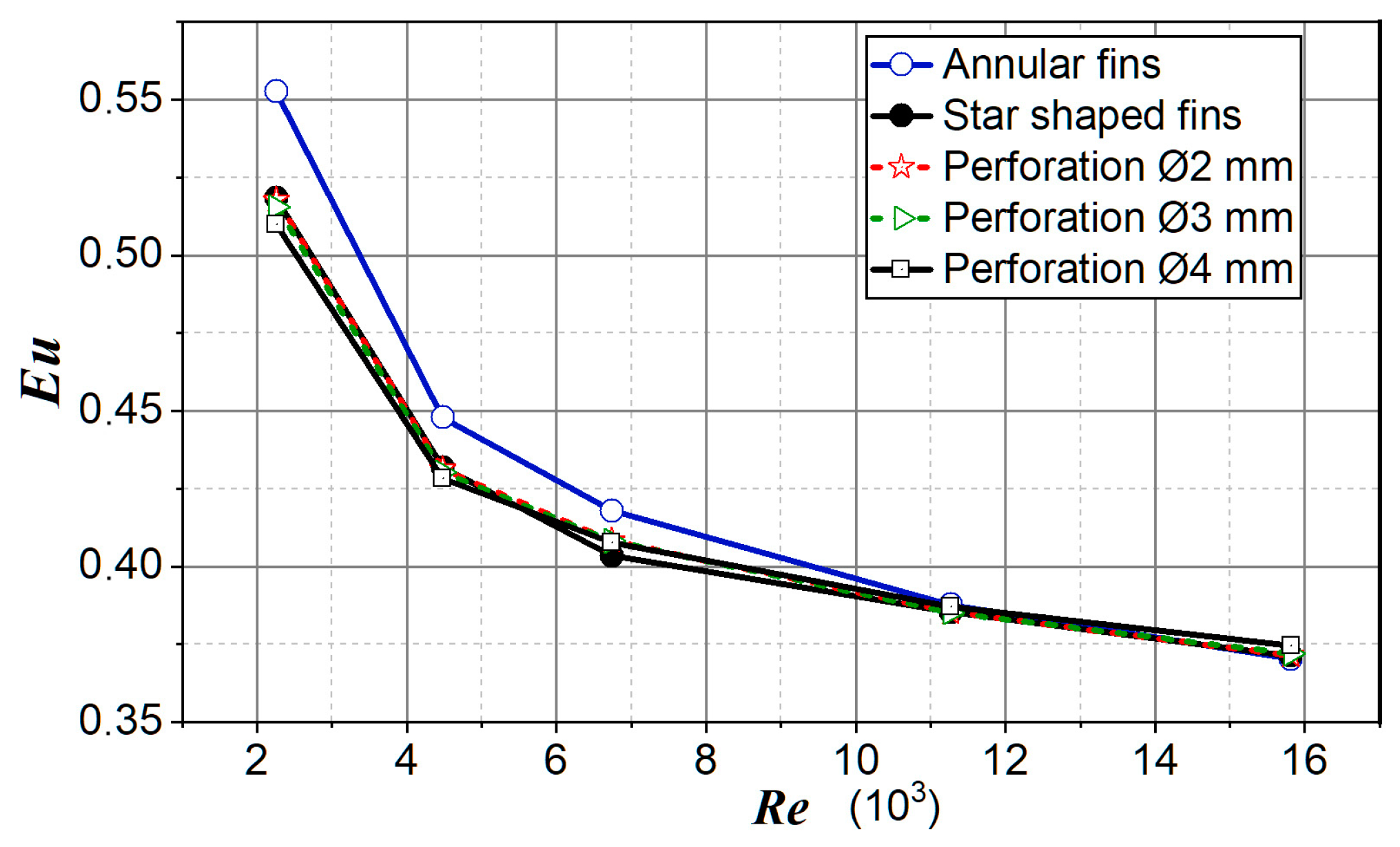
The influence of perforation on the Eu number was small in the whole area of the observed Re numbers (Figure 12). Moreover, at higher airflow speeds, the flow resistances of the tubes and fins strengthened concerning the flow through perforation (at the left end of the diagram, the curves of the perforated fins were more spaced apart).
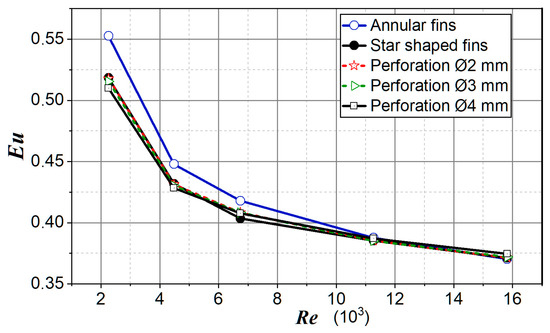
Figure 12.
Euler number for analyzed cases.
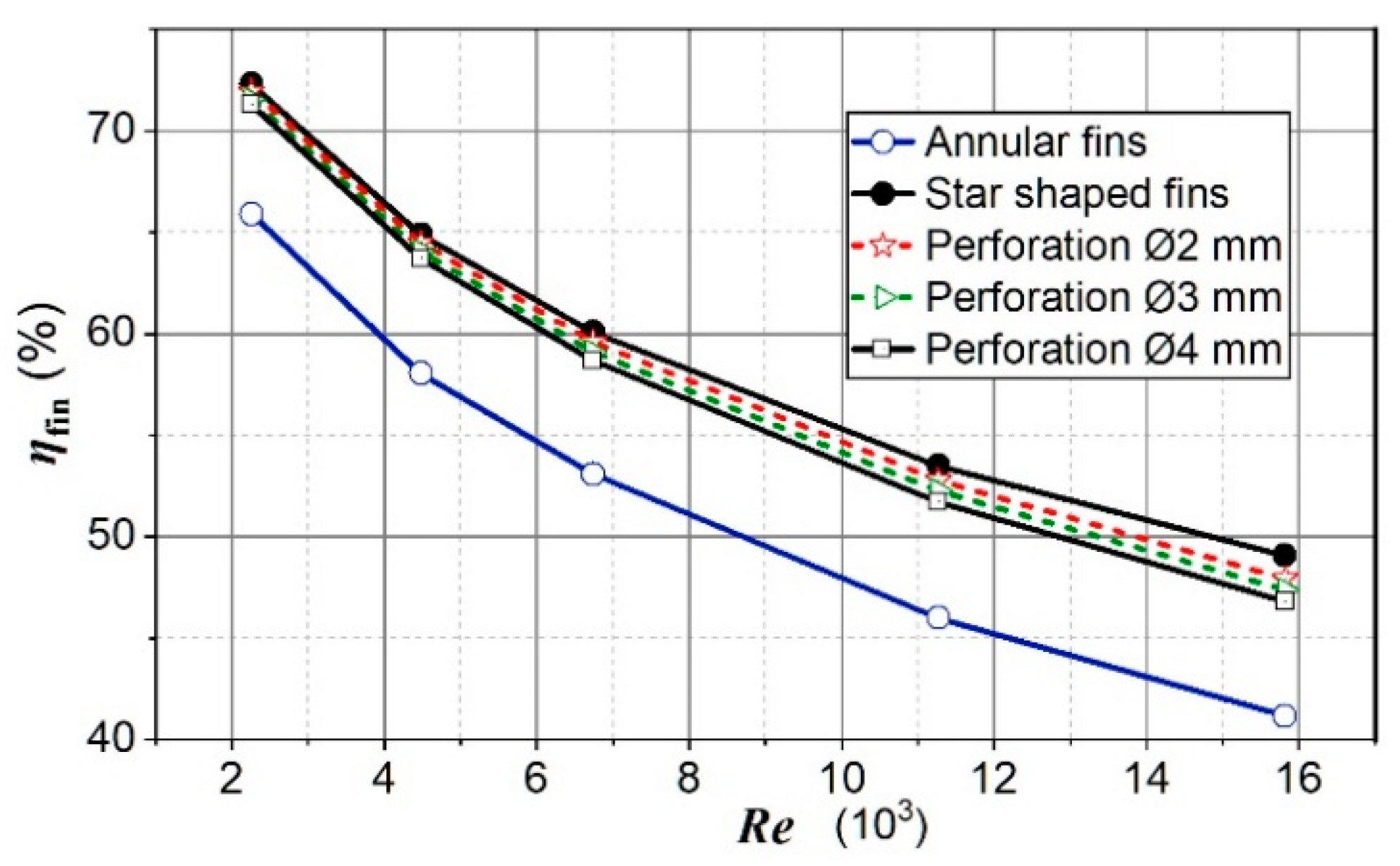
The efficiency of perforated fins was lower than for non-perforated fins. With an increase in air velocity and perforation diameter, the difference in efficiency increased (Figure 13). As the diameter of the perforation increased, the turbulence of the airflow in the area of the opening increased. This led to a reduction of the boundary thermal layer and greater heat dissipation in that surface area. As a result, there was a greater temperature drop in perforation locations. The larger the openings, the greater the temperature drop. The efficiency of the fins showed the uniformity of the temperature field over the fin surface (for the uniform temperature field, the fin efficiency was equal to one). Thus, it is clear that an increase in the temperature drop in the opening area (Figure 4) caused a decrease in fin efficiency.
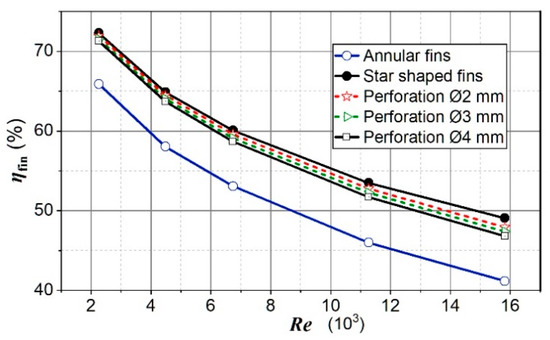
Figure 13.
Fin efficiency for analyzed cases.
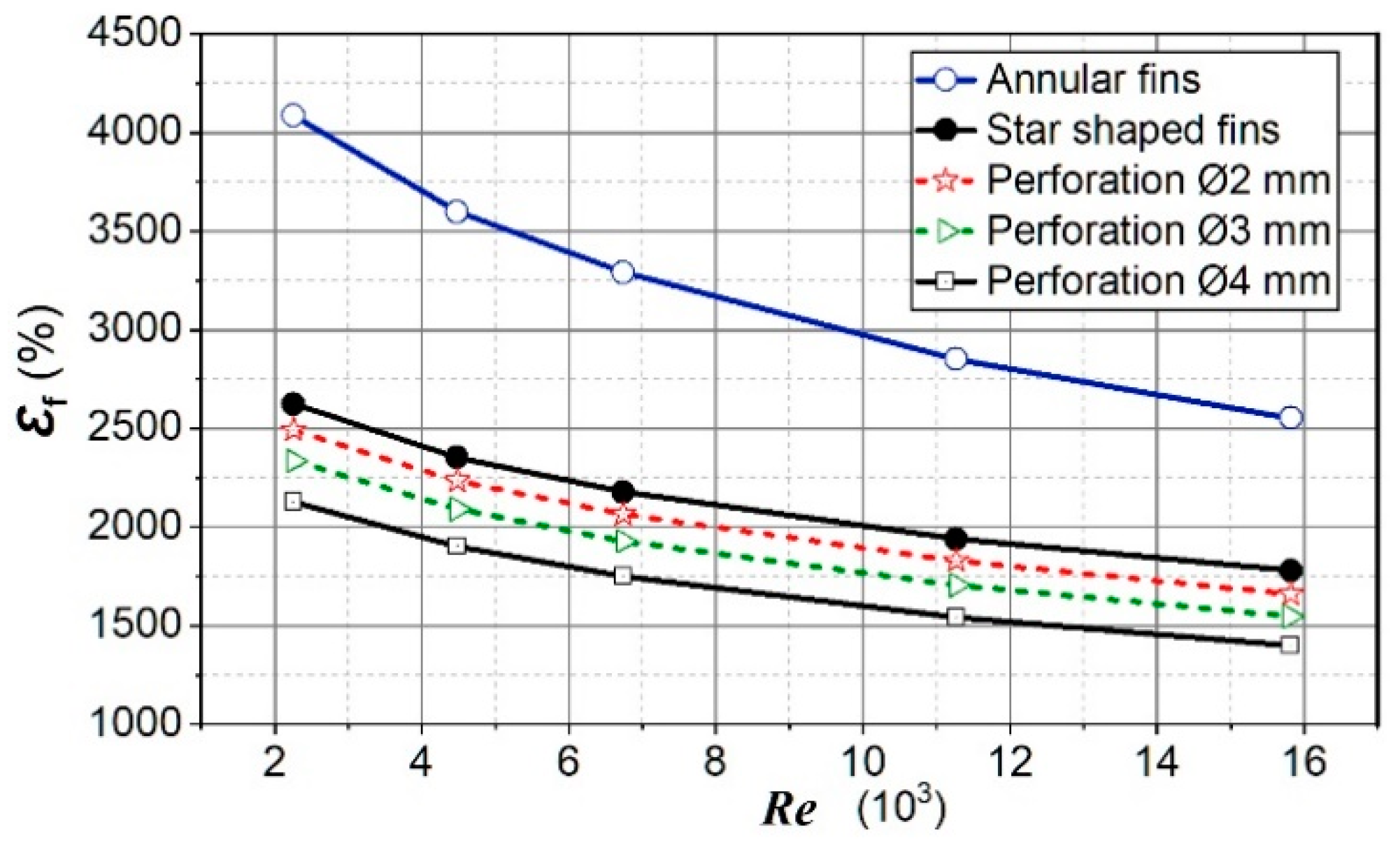
The effectiveness of a fin is proportional to the surface area and efficiency of the fin. Since the fin surface area and the fin efficiency decreases with the increasing size of the perforation hole, it follows that the effectiveness of the perforated fins decreases with the increasing size of the perforation holes. The size of the perforation hole linearly affects the reduction of the fin’s effectiveness (Figure 14).
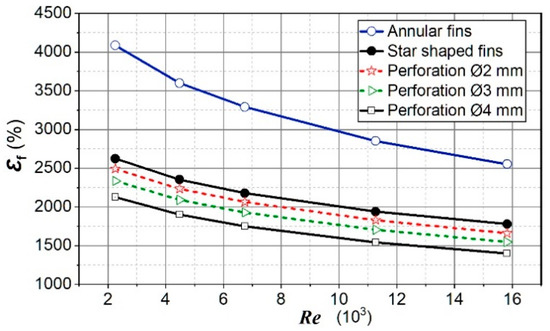
Figure 14.
Fin effectiveness for analyzed cases.
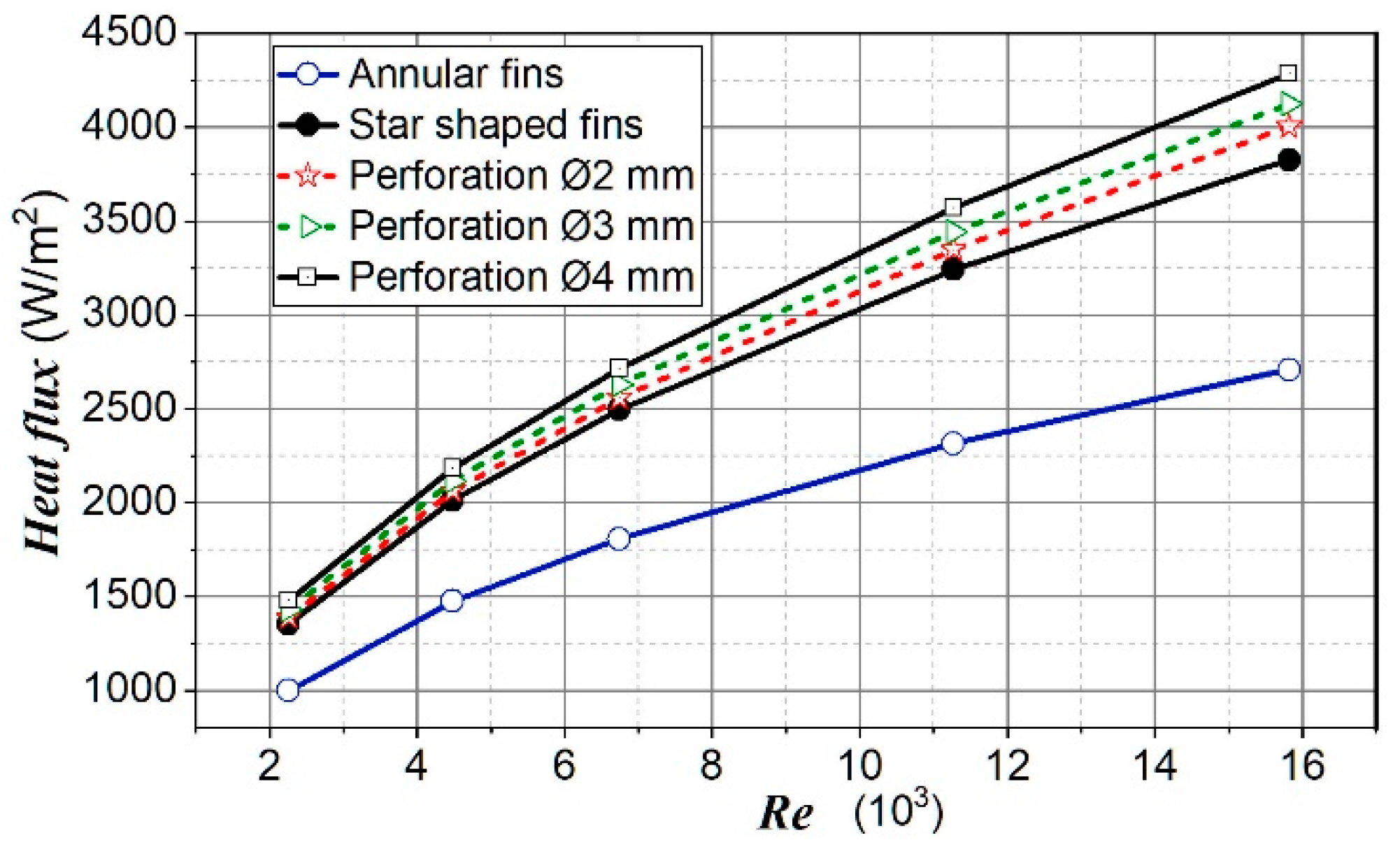
Figure 15 shows the heat flux for analyzed fins. It can be seen as an enhancement in the heat flux for perforated fins. An enhance in heat flux with an increase in perforation size was clearly noticeable. Moreover, it was seen that with increasing Re number, the influence of perforation diameter on heat flux increased. The heat flux for perforated fins was up to 12.03% higher compared to non-perforated fins and up to 58.2% higher compared to annular fins in the observed range of Re numbers.
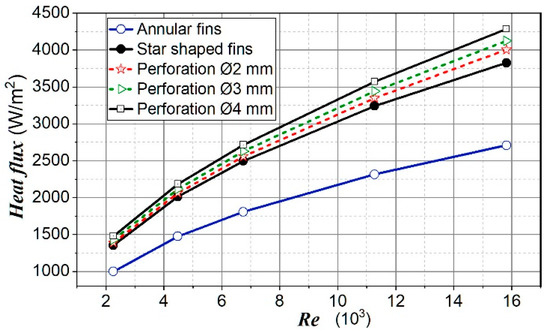
Figure 15.
Heat flux for analyzed cases.
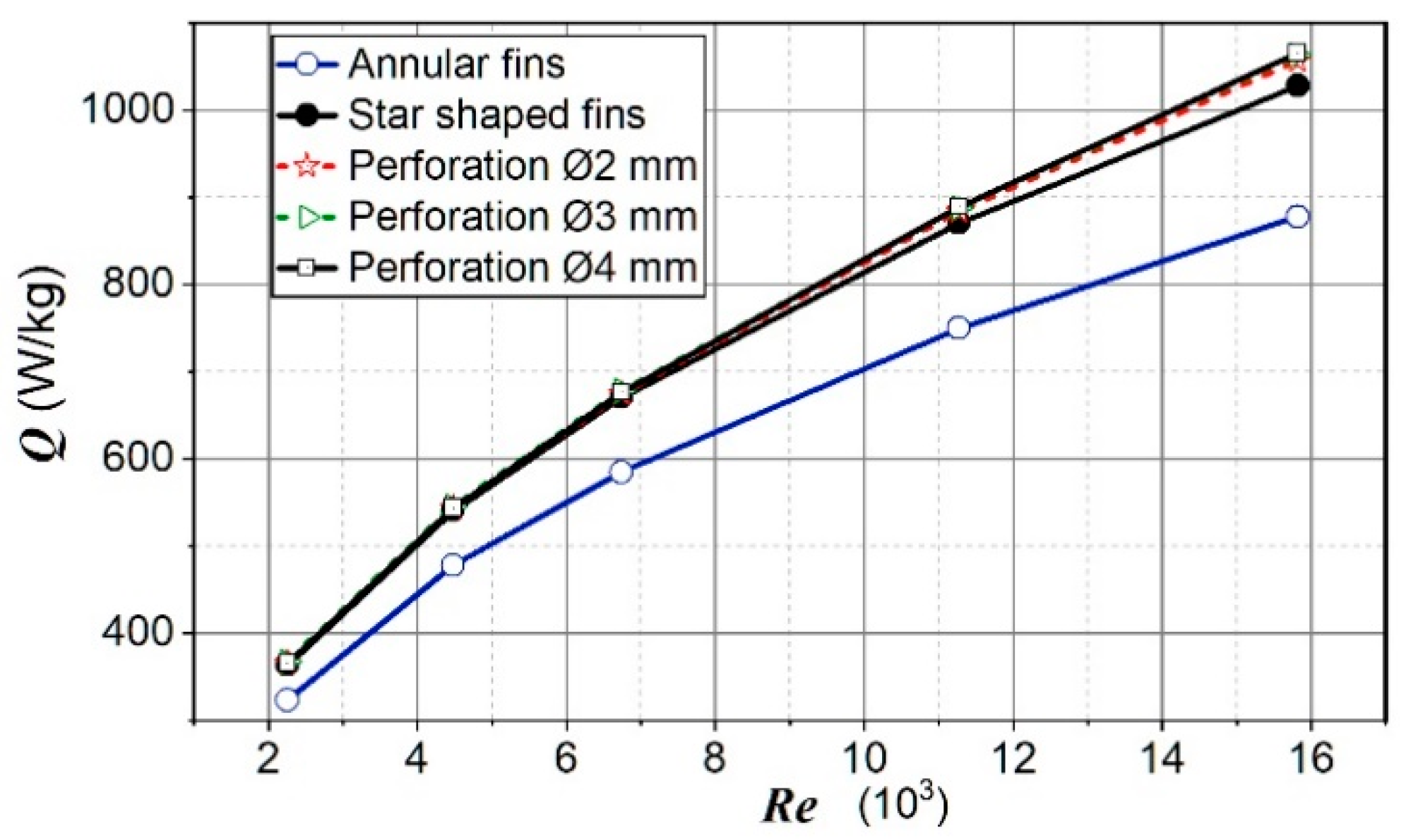
Figure 16 shows the heat transferred per unit of mass for analyzed cases. The difference in the heat transferred per unit of mass for star-shaped fins with perforation and without perforation was not large, especially in the lower Re numbers range.
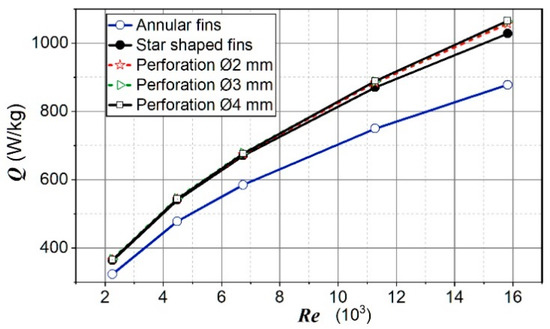
Figure 16.
The heat transferred per unit of mass.
When designing a heat exchanger, it is necessary to choose the geometry of the heat exchange surfaces. The choice is determined by the type of heat exchanger and the type and thermal properties of the fluid. When choosing the geometry of the extended surface, production costs as well as operating costs (pressure drop) should be considered. The characteristics of heat exchange surfaces are usually represented by dimensionless features such as Re, Nu, Eu, j, f (see Equations (1)–(5)), or combinations thereof in the form of “goodness factor“. The literature contains several “goodness factors” by which it is possible to compare surface performance features (LaHaye et al. [24], Kays and London [25], Bergles et al. [26], Fugmann et al. [27]).
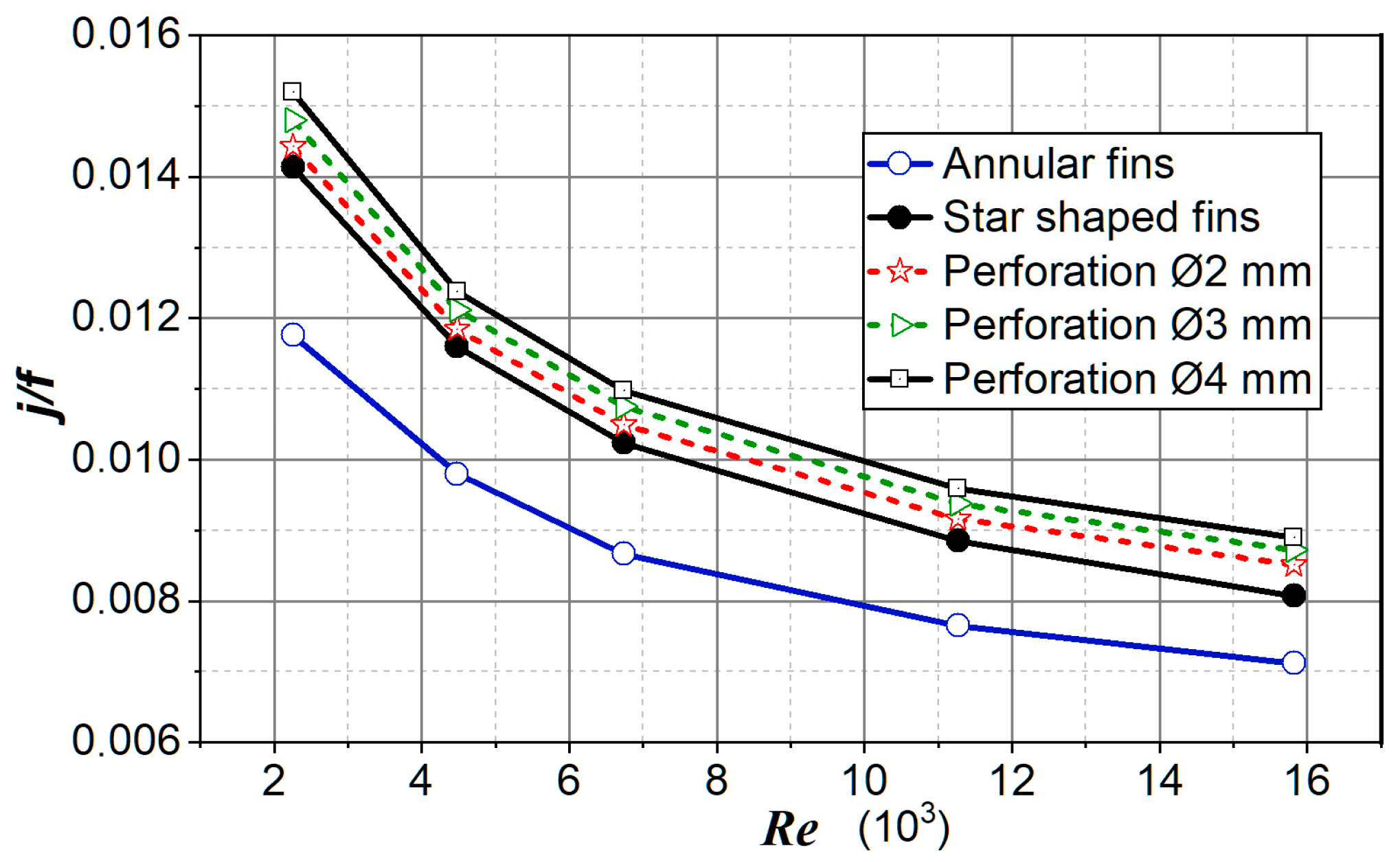
The thermal performance of different surfaces is often compared by drawing j versus f, which compares the convective heat transfer coefficients for the same friction power per unit surface area. The area goodness factor (j/f) is analyzed in order to determine the performance of the heat exchanger. Figure 17 shows the surface goodness factors as a function of the Re number for different fin configurations.
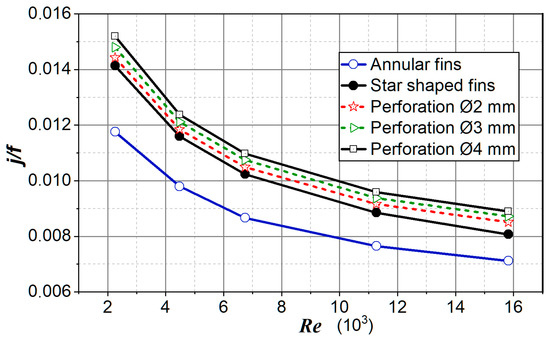
Figure 17.
Area goodness factor.
A high area goodness factor shows that a smaller heat exchange area is necessary. It is evident from Figure 17 that the best area goodness factor of the examined fins was perforated fins with the perforation hole Ø4 mm. Moreover, j/f was higher for lower values of Re numbers, which justified the application of extended surfaces at low Re numbers.
5. Conclusions
This paper numerically investigated the performance of perforated star-shaped fins and compared them to previously numerically analyzed non-perforated star-shaped fins and annular solid fins.
The application of perforation on the fins primarily reduced the mass of the heat exchanger, which is very significant in some applications with steel fins. In the area of perforations, there was greater flow turbulence and an increase in the heat transfer coefficient. There was no significant difference in pressure drop on perforated fins. A higher area goodness factor for perforated fins confirmed these claims. The number and size of perforation holes affected heat exchange, and their importance strengthened with increasing Re number. In the analyzed case of star-shaped fins, a decrease in mass of 17.65% (by hole diameter of 4 mm) and an enhance in heat flux up to 12% in the observed range of Re numbers were found.
Further studies should include analyses of various forms of perforation and additional mass reduction with fin cutting in the wake region of fluid flow. Making a perforation on fins also increases the production costs, which may be analyzed in future research.
Author Contributions
M.B.: conceptualization, methodology, writing—original draft preparation, visualization, data curation, investigation; S.M.: software, data curation, visualization, investigation, validation, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A | surface area | m² |
| d0 | outside tube diameter | mm |
| Eu | Euler number | - |
| f | friction factor | - |
| fi | vector of the mass density of the external forces | N/kg |
| hf | fin height | mm |
| j | Colburn factor | - |
| Nl | number of tubes in the flow direction | - |
| Nu | Nusselt number | - |
| Δp | pressure drop | Pa |
| pout | mass-weighted average pressure outlet of the channel | Pa |
| Q | heat flow rate | W |
| q | heat flux vector | W |
| Re | Reynolds number | - |
| sf | fin pitch | mm |
| sl | longitudinal tube pitch | mm |
| st | transverse tube pitch | mm |
| t | time | s |
| tf | fin thickness | mm |
| Tin | air inlet temperature | K |
| Tout | air outlet temperature | K |
| Tw | tube wall temperature | K |
| U | overall heat transfer coefficient | W/(m2·K) |
| u | air velocity | m/s |
| uff | air velocity at minimum flow area | m/s |
| uin | air velocity at the inlet of the heat exchanger | m/s |
| α0 | actual average gas-side heat transfer coefficient | W/(m2·K) |
| εf | fin effectiveness | - |
| ηf,th | theoretical fin efficiency | - |
| μav | average air kinematic viscosity | m2/s |
| ρav | average air density (at mean air temperature in tube bundle) | kg/m3 |
| λbl | thermal conductivity of boundary layer | W/(m·K) |
| σij | tensor of stress in a fluid | Pa |
References
- Petrik, M.; Szepesi, G. Experimental and Numerical Investigation of the Air Side Heat Transfer of a Finned Tubes Heat Exchanger. Processes 2020, 8, 773. [Google Scholar] [CrossRef]
- Hong-Long, Chen, Wang, Chi-Chuan, Analytical analysis and experimental verification of trapezoidal fin for assessment of heat sink performance and material saving. Appl. Therm. Eng. 2016, 98, 203–212. [CrossRef]
- Martinez, E.; Vicente, W.; Soto, G.; Salinas, M. Comparative analysis of heat transfer and pressure drop in helically segmented finned tube heat exchangers. Appl. Therm. Eng. 2010, 30, 1470–1476. [Google Scholar] [CrossRef]
- Zoman, A.V.; Palande, D.D. Heat transfer enhancement using fins with perforation: A Review. IJESRT 2016, 5, 786–789. [Google Scholar]
- Liu, X.; Yu, J.; Yan, G. An experimental study on the air side heat transfer performance of the perforated fin-tube heat exchangers under the frosting conditions. Appl. Therm. Eng. 2020, 166, 114634. [Google Scholar] [CrossRef]
- Banerjee, R.K.; Karve, M.; Ha, J.H.; Lee, D.H.; Cho, Y.I. Evaluation of Enhanced Heat Transfer within a Four Row Finned Tube Array of an Air Cooled Steam Condenser. Numer. Heat Transf. Part A Appl. 2012, 61, 735–753. [Google Scholar] [CrossRef]
- Yakar, G.; Karabacak, R. Investigation of Thermal Performance of Perforated Finned Heat Exchangers. Exp. Heat Transf. 2015, 28, 354–365. [Google Scholar] [CrossRef]
- Lee, D.H.; Jung, J.M.; Ha, J.H.; Cho, Y. Improvement of heat transfer with perforated circular holes in finned tubes of air-cooled heat exchanger. Int. Commun. Heat Mass Transf. 2012, 39, 161–166. [Google Scholar] [CrossRef]
- Nadooshan, A.A.; Kalbasi, R.; Afrand, M. Perforated fins effect on the heat transfer rate from a circular tube by using wind tunnel: An experimental view. Heat Mass Transfer. 2018, 54, 3047–3057. [Google Scholar] [CrossRef]
- Rai, A.; Bhuvad, S.S.; Sarviya, R.M. Enhancement of Heat Transfer in Perforated Circular Finned-Tube Heat Exchangers: A Numerical Investigation. J. Phys. Conf. Ser. 2020, 1473, 012024. [Google Scholar] [CrossRef]
- Bisen, V.; Sagar, N.K. CFD Analysis of Heat Transfer in Annular Fins of various Profiles having different Shapes of Perforation. Int. J. Res. Appl. Sci. Eng. Technol. 2020, 8, 511–515. [Google Scholar] [CrossRef]
- Liu, X.; Yu, J.; Yan, G. A numerical study on the air-side heat transfer of perforated finned-tube heat exchangers with large fin pitches. Int. J. Heat Mass Transf. 2016, 100, 199–207. [Google Scholar] [CrossRef]
- Sundar, S.; Song, G.; Zahir, M.Z.; Jayakumar, J.S.; Yook, S.-J. Performance investigation of radial heat sink with circular base and perforated staggered fins. Int. J. Heat Mass Transf. 2019, 143, 118526. [Google Scholar] [CrossRef]
- Dhanawade, K.H.; Sunnapwar, V.K.; Dhanawade, H.S. Thermal Analysis of Square and Circular Perforated Fin Arrays by Forced Convection. Int. J. Curr. Eng. Technol. 2013, 2, 109–114. [Google Scholar] [CrossRef]
- Ibrahim, T.K.; Mohammed, M.N.; Mohammed, M.K.; Najafi, G.; Sidik, N.A.; Basrawi, F.; Abdalla, A.N.; Hoseini, S.S. Experimental study on the effect of perforations shapes on vertical heated fins performance under forced convection heat transfer. Int. J. Heat Mass Transf. 2018, 118, 832–846. [Google Scholar] [CrossRef]
- Shaer, M.R.; Yaghoubi, M. Numerical analysis of turbulent convection heat transfer from an array of perforated fins. Int. J. Heat Fluid Flow 2009, 30, 218–228. [Google Scholar] [CrossRef]
- Chingulpitak, S.; Ahn, H.S.; Asirvatham, L.G.; Wongwises, S. Fluid flow and heat transfer characteristics of heat sinks with laterally perforated plate fins. Int. J. Heat Mass Transf. 2019, 138, 293–303. [Google Scholar] [CrossRef]
- Gupta, M.; Yadav, S.; Kumar, R. Assessment of Effect of Perforated Fins on the Performance of Single Cylinder Engine. Int. J. Res. Appl. Sci. Eng. Technol. 2018, 6, 3051–3056. [Google Scholar] [CrossRef]
- Lee, H.J.; Ryu, J.; Lee, S.H. Influence of perforated fin on flow characteristics and thermal performance in spiral finned-tube heat exchanger. Energies 2019, 12, 556. [Google Scholar] [CrossRef]
- Karami, R.; Kamkari, B. Experimental investigation of the effect of perforated fins on thermal performance enhancement of vertical shell and tube latent heat energy storage systems. Energy Convers. Manag. 2020, 210, 112679. [Google Scholar] [CrossRef]
- Bošnjaković, M.; Čikić, A.; Muhič, S.; Stojkov, M. Development of a new type of finned heat exchanger. Tech. Gaz. 2017, 24, 1785–1796. [Google Scholar] [CrossRef]
- Bošnjaković, M.; Muhić, S.; Čikić, A.; Živić, M. How Big Is an Error in the Analytical Calculation of Annular Fin Efficiency? Energies 2019, 12, 1787. [Google Scholar] [CrossRef]
- Bošnjaković, M.; Muhić, S.; Čikić, A. Experimental testing of the heat exchanger with star-shaped fins. Int. J. Heat Mass Transf. 2020, 149, 119190. [Google Scholar] [CrossRef]
- LaHaye, P.G.; Neugebauer, F.J.; Sakhuja, R.K. A generalized prediction of heat transfer surface performance and exchanger optimization. J. Heat Transf. 1974, 96, 511–517. [Google Scholar] [CrossRef]
- Kays, W.M.; London, A.L. Remarks on the behaviour and applications of compact high-performance heat transfer surfaces, General Discussion on Heat Transfer. Aircr. Eng. Aerosp. Technol. 1951, 23, 311–316. [Google Scholar] [CrossRef]
- Bergles, A.E.; Bunn, R.L.; Junkhan, G.H. Extended performance evaluation criteria for enhanced heat transfer surfaces. Lett. Heat Mass Transf. 1974, 1, 113–120. [Google Scholar] [CrossRef]
- Fugmann, H.; Laurenz, E.; Schnabel, L. Multi-Dimensional Performance Evaluation of Heat Exchanger Surface Enhancements. Energies 2019, 12, 1406. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).