Abstract
The Elder problem is one of the well-known examples of an unstable density-driven flow (DDF) and solute transport in porous media. The goal of this research is to investigate the influence of fracture networks on this benchmark problem due to the great importance of the fractured heterogeneity effect on unstable DDF. For this aim, the fractured Elder problem is solved using COMSOL Multiphysics, which is a finite element method simulator. Uniform and orthogonal fracture networks are embedded to analyze free convective flow and development of unstable salt plumes. The results indicate that the mesh sensitivity of the fractured Elder problem is greater than the homogeneous case. Furthermore, it has been shown that in the fractured cases, the onset of instability and free convection occur with lower critical Rayleigh number, which means that fracture networks have a destabilizing effect. Also, we examined the structural properties of fracture networks that control convective flow patterns, and the simulation results show that the strength of convection and instability at the beginning of the intrusion is proportional to the aperture size of the fractures. Moreover, the increase of the fracture’s density leads different modes of transient convective modes, until a specific fracture density after which the transient convective modes become similar to the homogenous case.
Keywords:
Elder problem; convection; instability; fingering; fractured porous media; Sherwood number 1. Introduction
Density-driven flow (DDF) in porous media has been studied extensively over the last few decades because of its practical applications in petroleum engineering, geologic carbon sequestration, geothermal energy systems, groundwater management, oxide fuel cells, solar collectors, thermal insulation systems, nuclear reactors, amongst many others [1,2,3]. The term convection is often used in connection with DDF processes, where groundwater flow is driven by density differences in the fluid, created by differences in temperature and/or concentration, as the primary driving factor that causes a density gradient to occur, and as a result flow and transport in the porous domain can occur due to the buoyancy effect. The term convection has been used in different ways in the literature. Ataie-Ashtiani et al. [4] have discussed and clarified the typical confusion about applications of the convection term. Common classifications of convection include free, forced, mixed, thermohaline [5], double-diffusive [6,7] and thermomagnetic and can take on many different forms and types in more general science and engineering [4]. When the density of the fluid in place increases with depth, the flow system is stable. Conversely, when the density of fluid decreases with depth the system would be potentially unstable and fingering patterns may develop at the interface under certain hydrogeologic conditions [3]. Unstable configurations can be found in several industrial and environmental applications such as in carbon dioxide (CO2) injection in geological reservoirs [8,9,10], geothermal systems [11] and saltwater infiltration from inland sabkha or salt lakes [12,13].
The Elder problem has been widely used to investigate unstable DDF in porous media [14]. Details about the historical account of the genesis, evolution, and resolution of the Elder problem can be found in Simmons and Elder [15] and Elder et al. [16]. The classic Elder problem originated from a thermal experiment, which was initially set up to investigate transient thermal natural convection patterns [14]. Voss and Souza [17] reformulated this problem into a solute analogue to thermal convection. The solute Elder problem has become a popular benchmark for variable-density flow and transport simulators [18,19]. The key issue for benchmarking is the mesh sensitivity of the Elder problem solutions. For instance, Johannsen [20] provided a bifurcation diagram with respect to the Rayleigh number (Ra) and showed that several steady solutions could exist. The existence of multiple steady solutions has also been explained by Van Reeuwijk et al. [21]. With a bifurcation analysis, the authors confirmed the fact that the multiple steady states are an intrinsic characteristic of the Elder problem and not related to numerical artifacts. Ataie-Ashtiani et al. [22] explored the influence of mass transport boundary condition on the convective mode and showed that multiple solutions exist, no matter what the type of boundary conditions that are employed. Besides benchmarking purposes, the Elder problem has been also used to provide physical insight into unstable DDF processes. For instance, Post and Prommer [23] investigated the effect of multicomponent geochemical reactions. Xie et al. [24] studied the effect of transient solute boundary conditions on DDF in an unstable setting. Graf and Boufadel [25] extended the Elder problem for application to partially saturated systems. Lu et al. [26] developed dual-domain mass transfer in the Elder problem to explore the kinetic mass transfer effects on unstable DDF.
The impact of heterogeneities of the porous medium on DDF processes is well documented in the literature i.e., [1,12,27,28,29,30]. The effect of heterogeneity on the Elder problem has been studied in Prasad and Simmons [31], using a stochastic framework. Fractured configurations are a particular style of heterogeneity, as fractures may be the preferential pathways of convective flow. The effect of fractures on unstable DDF processes has been investigated in several papers using a variety of configurations. In this context, Graf and Therrien [32] studied dense plume migration in orthogonal and irregular fracture networks, using a 2D porous enclosure as the conceptual model. For non-orthogonal fracture networks, they indicated that convection cells form and overlap both the porous matrix and fractures. For fractures with irregular orientation, they indicated that the migration of a dense plume is sensitive to the geometry of the network and the connectivity to the source. Based on the Horton-Rogers-Lapwood (HRL) problem, Vujevic et al. [33] investigated the impact of a fracture network on instability and fingering. They found that irregular fracture networks would destabilize the flow system. They also demonstrated that the factors, which determine the strength of free convection, are continuous fracture circuits, fracture length in discontinuous fracture networks and fracture to matrix permeability ratio. Hirthe and Graf [34] developed an efficient model to simulate DDF in fractured domains by optimizing fracture networks. All these studies are based on 2D numerical simulations that neglect the convection patterns within the fractures. Based on a Rayleigh stability analysis, Simmons et al. [35] investigated unstable DDF in low-permeable domains with vertical fractures. They analyzed the possible modes of intrafracture (within the fracture) and interfracture (between fractures through the porous layers) free convection. They defined the conditions for occurrence of each mode. For intrafracture convection, they analyzed two modes either parallel to the fracture plane or perpendicular to the fracture plane. They found that, in low-permeable porous layer, the most likely mode is the intrafracture convection parallel to the plane of fracture. Graf and Therrien [36] extended their previous study to 3D domains with 2D fractures. They showed fingering phenomena within the fractured planes. Graf and Therrien [36] also compared density-driven geothermal flow to density-driven haline flow. They found that for typical matrix and fracture hydraulic conductivities, heat conduction diminishes the growth of thermal instability while low mass diffusion enables unstable haline ‘fingering’ within fractures. Vujevic and Graf [37] investigated the effect of combined inter-and intra-fracture convection modes in fracture networks on unstable DDF in low-permeable layer. They realized that for regular networks, the most important mode is the interfracture convection.
Despite the significant effect of fractured heterogeneity on unstable DDF and the importance of the Elder problem for understanding unstable DDF processes, to the best of our knowledge, this problem has never been investigated in the case of a fractured domain. Thus, the main objective of the present paper is to address this gap by examining the effect of orthogonal fracture networks on the Elder problem. In this context, we address three particular research questions: (1) The effect of fracture networks on the mesh sensitivity and bifurcation states of the Elder problem, (2) the impact of fracture networks on the critical Rayleigh number for the onset of instability and (3) how do the structural properties of fracture networks (aperture and density of the fractures) control convective flow patterns? For this purpose, we considered a new configuration of the Elder problem (fractured Elder problem) by embedding orthogonal fracture networks and we performed numerical simulations using COMSOL Multiphysics (COMSOL, Inc., Palo Alto, CA, USA), which is a commercial finite element simulation package widely used in various physical and engineering applications.
This paper is structured as follows: First, in the Methods section, the conceptual model of the fractured Elder problem is presented, the governing equations and the different fractured scenarios are summarized, some measurable characteristics are defined to be used in our analysis and the COMSOL model is briefly presented. In the Results and Discussion section, first, the validity of the COMSOL model results is investigated, then we address the three research questions formulated in this paper using this new model.
2. Methods
2.1. Conceptual Model
The domain and boundary conditions of the fractured Elder problem considered in this study are similar to the adapted Elder problem as used by Voss and Souza [17], Lu et al. [26] and Post and Prommer [23]. The domain was 600 m wide and 150 m high, as in Figure 1. All boundaries were impermeable to flow, and the top left and right corner nodes were two nodes with an imposed head. The middle part of the top surface had a constant concentration, which was sufficiently high to cause the onset of fingering instability. For all other boundaries, a no-flow boundary condition was assigned. The density contrast between the saltwater and the freshwater was equal to 200 kg/m3 as in Lu et al. [26] and Post and Prommer [23].
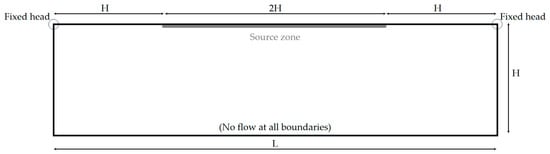
Figure 1.
The fractured Elder problem domain and boundary conditions. All boundaries were impermeable to flow.
2.2. Fractured Domain Scenarios
In this study, we investigated scenarios including networks of orthogonal fractures. Several scenarios dealing with different fracture density were considered (as shown in Figure 2). Scenario A corresponds to the homogeneous case. Increasing fracture density was considered in scenarios B to F.
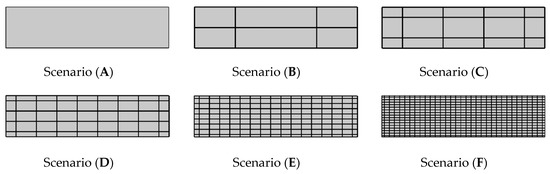
Figure 2.
Different scenarios of the fractured Elder problem: (A) homogenous domain, (B–F) orthogonal fracture networks with increasing fracture density.
2.3. Governing Equations
DDF in the pours matrix was governed by variable-density flow and mass transport equations [38]. The mass conservation was ensured by the continuity equation and the velocity based on Darcy’s law using the freshwater head formulation are as follows:
where S is the storage coefficient, h is the equivalent freshwater head [L], t is the time [T], u is the velocity [LT−1], is freshwater density [ML−3], g is the gravity [LT−2], μ is the fluid dynamic viscosity [ML−1T−1], is the intrinsic permeability of the porous matrix [L2], ρ is the mixed fluid density [ML−3] and is the unit vector in the z-direction.
For solute transport, the following equation represents the mass balance in a non-deformable porous medium:
where is the porosity of the medium [-], c is the relative solute concentration [-], and D is the molecular diffusion coefficient [L2T−1] (as is common for the Elder problem, the dispersion coefficients are neglected).
Equations (1), (2) and (3) are coupled by a linear function which relates the density () and the salt concentration (c) as follows:
where is the saltwater density at the source boundary.
The discrete fracture network approach was used to take into account the fractures which are embedded as 1D lines in the 2D porous domain. The same mathematical model was used to simulate DDF in fractures but by considering specific permeability (kfr) and porosity (). We should mention that Simmons et al. [35] investigated unstable DDF in fractured low-permeability porous media (vertical fractures). They studied interfracture and intrafracture convection modes. Based on a Rayleigh stability analysis, they defined conditions required for the onset of convection in each mode. Simmons et al. [36] showed that, in the low-permeable porous layer, the most likely mode is the intrafracture convection parallel to the plane of fracture. The assumptions considered in this work (2D porous domain and 1D fractures) do not allow for considering the intrafracture convection modes which require 3D simulations (3D porous domain and 3D fractures). As the aim of this work is to investigate the fractured Elder problem with dense orthogonal fracture networks that require dense grids associated to prohibitive computational costs, we adopted the discrete fracture network approach and we limited the study to the interfracture convection mode. A similar approach has been used in Graf and Therrien [32], Vujevic et al. [33], Hirthe and Graf [34] and Koohbor et al. [39]. For regular networks, Vujevic and Graf [37] have shown that the most important mode is the interfracture convection.
The fracture permeability (kfr [L2]) can be calculated as a function of the fracture aperture using the cubic law [35], as follows:
where 2b is the fracture aperture.
The bulk permeability in the case of orthogonal fracture network is calculated as in Vujevic et al. [33]:
where 2B is the fracture spacing.
The physical parameters used in this work are summarized in Table 1.

Table 1.
Physical parameters used in COMSOL for the fractured Elder problem (Rayleigh number (Ra) = 400).
2.4. The Rayleigh Number
The non-dimensional analysis of these equations leads to one parameter governing the natural convection processes which is the Rayleigh number (Ra). This number is defined as the ratio of the buoyancy forces that drive flow to diffusive forces that dissipate it. Ra is defined by [31]:
We should mention that in this work Ra is defined using the permeability of the porous matrix (). Ra is used to indicate the extent of instability and characterize the onset of free convection. For the standard Elder problem (homogeneous domain) we have . The situation is unstable as the Raleigh number is larger than the critical value for the onset of instability (). For an infinitely long porous domain with impermeable top and bottom surfaces subject to constant concentrations, the critical Rayleigh number is estimated to be [15,21].
2.5. The Average Sherwood Number
To characterize free convection, we used the dimensionless Sherwood number (Sh). Sh is commonly used as an indicator for the strength of convection, and equal to the ratio of the actual mass transfer due to free convection to the rate of the mass transfer due to diffusion [3,26]. The average Sherwood number over the source zone boundary can be calculated using the concentration gradient, as follows:
2.6. The Simulation Tool: COMSOL Multiphysics®
COMSOL Multiphysics was used in this work to perform the simulations of the fractured Elder problem. This software package has an interactive environment for modeling scientific problems based on the finite element method. To simulate DDF, we coupled the “Darcy’s flow” interface from the “Subsurface flow” module and the “transport of diluted species in porous media” interface from the “chemical species transport” model, as in Mozafari et al. [40] and Koohbor et al. [39]. The fluid density is expressed analytically in terms of salt concentration as in Equation (4). The developed COMSOL model was based on the full mathematical model without the Boussinesq approximation. Johannsen [20] demonstrated that such an approximation could be invalid for the Elder problem. The interface “Fracture flow” was used to include fractures via the discrete fracture approach. Triangular meshes generated by the COMSOL meshing tool were used to perform the simulations which were run for the time-dependent mode (transient conditions). 2D triangular cells were used to represent the matrix and 1D cells to represent the fractures. The fracture cells were positioned along the sides of the matrix triangular cells [39]. The average Sherwood number was automatically calculated using the “Derived value” tool of the COMSOL post-processing interface.
3. Results and Discussion
3.1. Verification of the COMSOL Model
The developed COMSOL model is verified based on the standard Elder problem (homogeneous domain, scenario A), by comparison with the results of Lu et al. [26] which are obtained using SEAWAT-2000. The parameters used for this simulation are given in Table 1. As in Lu et al. [26], a square mesh was used for these simulations. The computational mesh consists of 2756 square elements, which is almost equivalent to the mesh used in Lu et al. [26]. The concentration distributions after 1, 5, 10, 20 and 50 years are plotted in Figure 3. The results compare well with Lu et al. [26] (see Figure 2 in that paper). The results are also in agreement with the classification suggested by van Reeuwijk et al. [21] and Simmons and Elder [15]. The concentration distribution is similar to the solution S1 defined in those papers. The Sherwood number is also in good agreement with Lu et al. [26]. But we should mention that in Lu et al. [26], the porosity is not considered in the evaluation of the Sherwood number. Here, the Sherwood number is calculated to be 0.16. In Lu et al. [26], it is less than 0.1.

Figure 3.
Concentration distribution of the homogeneous Elder problem.
3.2. Mesh Sensitivity Analysis
One of the notable issues of the Elder problem is its mesh sensitivity. In this section, we investigate the effect of fractures on the uniqueness of the results of the fractured Elder problem and compare that with the mesh sensitivity of the standard homogeneous case. We run the COMSOL model for scenarios (A) and (C), for three different mesh sizes. For scenario (C), we set the aperture of . Three mesh levels with 1253 (A1), 5116 (A2) and 4,5485 (A3) nodes are used for scenario (A). Equivalent mesh levels consisting of 1264 (C1), 5143 (C2) and 45527 (C3) nodes are used for scenario (C). To reduce the computational time, numerical simulations are performed in half of the domain by exploiting the symmetry of the domain. The corresponding concentration distributions are given in Figure 4. As one can see in Figure 4, the free convection patterns in the standard Elder problem (scenario A) vary with mesh resolution. For instance, as shown for case A1 after 3 years and 5 years, we have four fingers (two fingers illustrated for the half the domain), and after 10 years we have 2 separate fingers below the top boundary in the whole domain, whereas for the finer mesh sizes of cases A2 and A3, after 3 years and 5 years we would have five fingers and, after 10 years, an extra finger would appear below the center of the top boundary. Meanwhile, we can see that the variation of the results for different mesh sizes of the fractured Elder problem (scenario C) is more than the standard one (scenario A). In Figure 4 we can observe not only a variation in the number of fingers, but also the shape of the fingers of cases C1, C2, and C3 is more significant than the variation of cases A1, A2 and A3. In this regard, Figure 5 illustrates the mesh sensitivity of maximum local Sherwood number beneath the source zone at the top boundary for these two scenarios (which occurs after three years). It is obvious that for scenario (C), we have a more change in the Sherwood number than for scenario (A). Moreover, Figure 6 gives the variation of the time average concentration at the center of the bottom surface (x = 300 m and y = 0 m) versus the mesh size (number of nodes in the computational mesh), for scenarios (A) and (C). This figure shows that there is more significant variation of concentration for scenario (C) than scenario (A). Taking all the information obtained into account leads to the conclusion that the sensitivity of the fractured Elder problem would be greater than in the homogeneous case, and fractures increase the sensitivity of the Elder problem to the underlying mesh used in the numerical solution.
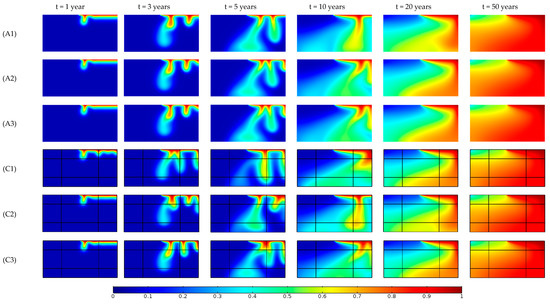
Figure 4.
Relative concentration distribution for scenarios (A) and (C) for different levels of mesh refinement: (A1), (A2) and (A3) correspond to grids with 2509, 10,235 and 90,973 triangular elements respectively. (C1), (C2) and (C3) correspond to grids with 2671, 1,0565 and 9,1875 triangular elements respectively.
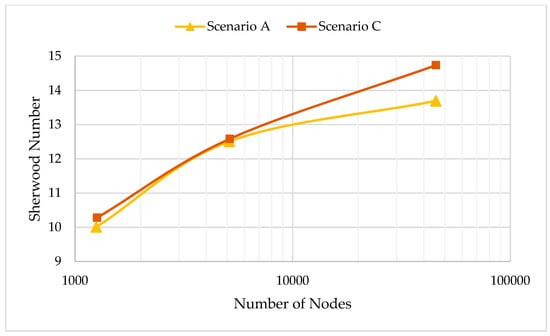
Figure 5.
Variation of the average Sherwood number after three years (t = 3 years) versus the number of nodes used in the simulations (scenarios A and C).
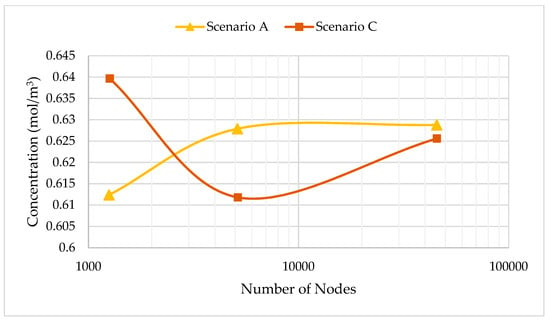
Figure 6.
Variation of the time average concentration at a local point (x = 300 m; y = 0 m) versus the number of nodes used in the simulations (scenarios A and C).
3.3. Effect of Fractures on the Onset of Instability
For the standard Elder problem, the critical value of the Rayleigh number for the onset of instability is [15]. The main goal of this section is to understand the effect of fractures on the onset of instability. Our objective is to understand if the fracture network will destabilize (means instability will appear with ) or stabilize (means instability will appear with ) the system. We developed simulations for the homogeneous case (scenario A) and for a selected fractured case (scenario D), for different values of Rayleigh number. For scenario (D), we set the aperture of . In each case of different Ra, the intrinsic permeability of the medium is constant ( (m2)); therefore, Ra would be changed by only modifying the diffusion coefficient. The values of the Rayleigh number for our simulations are 20, 40 and 60 which correspond to the diffusion coefficients equal to , and (m2 s−1) for both scenarios. The corresponding concentration distributions at times of 1, 3, 5 and 10 years are plotted in Figure 7. As one can observe, for = 40 and 60 at scenario (A), the initial appearance of fingers are obvious, which means we have an unstable system, and it confirms the fact that if Ra exceeds a value of 40, we would have the onset of instability the in homogeneous Elder problem. The results of scenario (D) show that the convective flow patterns of scenario (D) have higher strength of free convection than scenario (A). Figure 7 indicates that the onset of free convection in the fractured Elder problem is expected to occur with lower , and fracture porous media would destabilize this problem. This is consistent with the results of Simmons et al. [1] and Sharp et al. [41]. To confirm these results, Figure 8 shows the plot of the variation of the Sherwood number versus time, for all simulations. We can observe that the curve corresponding to scenario (A) at Ra = 20 is quite smooth, which indicates that there is no convection in this case and the solute flux is mainly diffusive. At Ra = 40, the curve for scenario (A) is perturbed with a prompt change between 2 and 3 years. The same behavior can be observed at Ra = 60, but the curve is perturbed between 1 and 6 years. This means that the perturbations represent the onset of instability. If we follow the same analysis for scenario (D), we can conclude that, in this case, the onset on instability occurs at a lower Rayleigh number as the curves are more perturbed than scenario (A). It is relevant to note that heterogeneity can become unstable, starting at a certain time but then stabilize the system at a later time. Figure 7, which gives the concentration distributions at local times, cannot be used to indicate if this phenomenon occurs in this case. However, it is clear from Figure 8 that this phenomenon does not exist as the perturbations of the Sherwood number appears once for all cases.
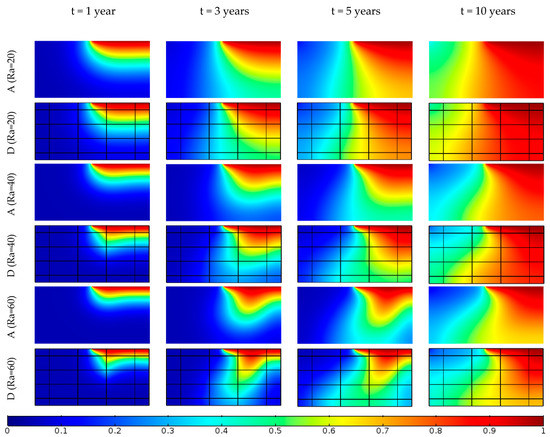
Figure 7.
Solute distribution of half of the domain of scenarios (A) and (D) for different Rayleigh numbers at simulation times of 1, 3, 5 and 10 years.
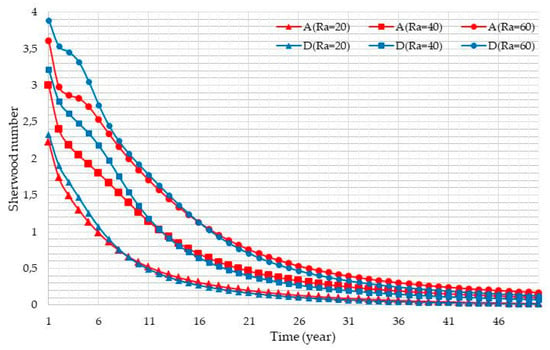
Figure 8.
The local Sherwood number beneath the source zone in the top layer versus time for different Rayleigh numbers for scenarios A and D.
3.4. Effect of Fracture Aperture
For characterizing geologic controls in networks of fractures, the aperture plays an important role. In this section, we explore the impact of fracture aperture on the concentration profiles and the fingering process associated with instability. To do so, we have studied this effect on scenario (D). Four different cases are simulated in COMSOL for different apertures. These cases are (D1), (D2), (D3) and (D4), which correspond to aperture sizes (2b) equal to , , , and . The parameters of intrinsic permeability of the porous medium and the diffusion coefficient are the same as homogeneous Elder problem, which results in Ra = 400 (Rayleigh number is based on the permeability of the porous domain). The corresponding fracture and bulk values of permeability are given in Table 2. Figure 9 shows the results of the solute distribution of this simulation at times of 1, 3, 5 and 10 years. It is clear from this figure that the fracture aperture influences the fingering processes. At t = 1 year, the increase of fracture aperture leads to more fingers that are related to the fracture presence, and the convective flow in the fracture moves up (see Figure 10). The increase of fracture aperture increases the velocity of the upward flow in the fractures and pushes the saltwater toward the source within the fractures. At t = 3 years, the fracture aperture does not affect the number of fingers. More horizontal expansion of the fingers can be observed around the fractures. At t = 5 and 10 years, the fracture aperture influences the number of fingers as well as the concentration distribution.

Table 2.
Fractured network parameters.
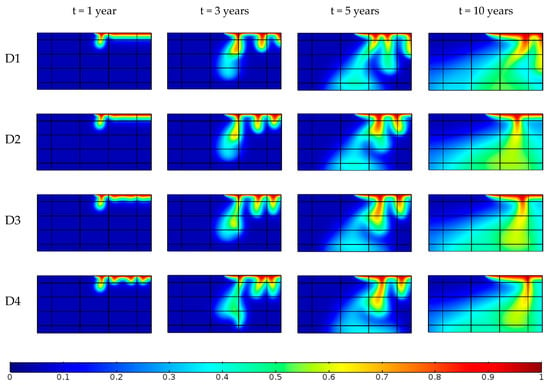
Figure 9.
Solute distribution of half of domain of scenario (D) for different fracture aperture at simulation times of 1, 3, 5 and 10 years. The fracture aperture from D1 to D4 increases.
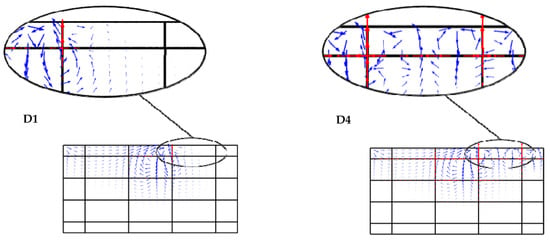
Figure 10.
Velocity fields of cases D1 and D4 at simulation time of 1 year. Blue arrows and red arrows represent velocity vectors in porous matrix and fractures, respectively.
For illustration, Figure 11 shows the average of local Sherwood number beneath the source zone in the top layer at different times versus the aperture size of fracture (Including aperture 2b = 0 which represents homogeneous case or scenario A). As one can see in this figure, at t = 2 years, the Sherwood number increases by enlarging the aperture size. Besides, for the later times (t = 10, 20, 30, 40 and 50 years), the value of Sherwood numbers for the cases of different aperture sizes are almost equal and with increasing the simulation time, the Sherwood number decreases. Therefore, Figure 2 confirms the issue discussed above, and shows that for the early times of the intrusion of fractured Elder problem, the strength of convection and instability is proportional to the aperture size of fracture; however, at the other times, the stability of the system for different aperture size of fractures would be the same.
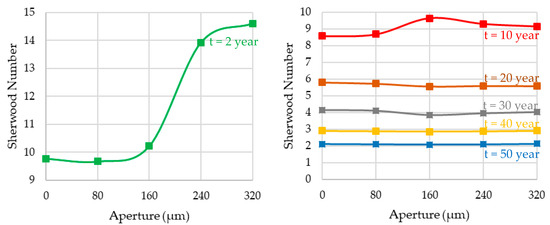
Figure 11.
Variation of the average Sherwood number versus the fracture aperture (scenario D).
3.5. Effect of Fracture Density
In this section, we investigated the effect of fracture density on the convective flow patterns. Thus, we performed simulations for all the fractured scenarios that involve variable fracture spacing. All the parameters for the porous media and fluid are considered the same as for the standard Elder problem (Table 1), which result in Ra = 400. The fracture aperture (2b) was calculated based on the fracture spacing (2B) in order to have the same bulk permeability for all scenarios. The fracture network parameters for all the scenarios are given in Table 2 The solute distributions of all scenarios at times of 1, 3, 5, 10, 20 and 50 years are depicted in Figure 12. The first observation is that, except slight deviations where the fingers meet the vertical fracture, the convective modes in scenarios (A) and (B) are quite similar and this is for all shown times. This seems to be logical as the fracture density of scenario (B) is very low and because the vertical fracture is not in contact with the source zone. This is also confirmed in Figure 13 which shows the variation of the Sherwood number for all scenarios at 2, 10, 20 and 50 years. The Sherwood numbers for scenarios (A) and (B) are almost the same. For scenario (C) as shown in Figure 12, the transient convective modes are different from the homogenous case (scenario A). The increase of the fracture network density affects the fingering processes. A vertical fracture crosses the source zone and leads to two more fingers at t = 1 year. These two fingers can be attributed to the upward convective flow in this vertical fracture that pushes the saltwater towards the upper surface. With more saltwater diffusion from the source, the fingers gather together and lead to one finger at 5 years, but concentration distribution and the number of fingers remain different from those observed in scenario (A). The concentration distribution becomes similar to scenario (A) after 50 years. Similar behavior can be observed for scenario (D), but concentration distribution and number of fingers become similar to scenario (A) earlier at t = 20 years. For scenarios (E) and (F), the transient convective modes tend to behave like scenario (A). This makes sense as the fracture aperture becomes very small, the domain behaves as homogenous when the density of fractures is relatively high and the bulk permeability is the same for all scenarios. Another point in Figure 12 which should be taken into consideration is that at t = 50 years the system, despite its scenario, approaches a stationary state with uniform solute concentration and no fluid motion. As depicted in Figure 13, the difference between the Sherwood numbers of fractured scenarios and that of the homogenous case increases with the fracture density until an optimal value after which this difference decreases. Moreover, as said before, the overall value of Sherwood number decreases during time for all the scenarios due to the convergence to a stationary state, as Figure 13.
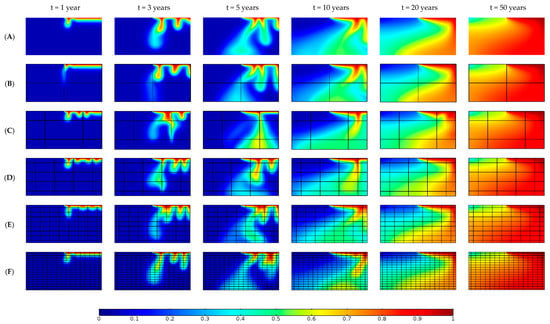
Figure 12.
Solute distribution of half of domain of all the scenarios at simulation times of 1, 3, 5, 10, 20 and 50 years.
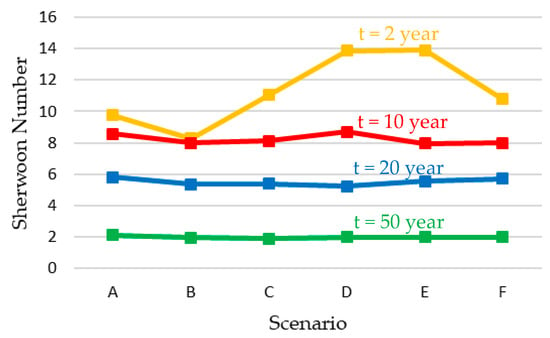
Figure 13.
The local Sherwood number beneath the source zone for all the scenarios at 2, 10, 20 and 50 years.
4. Conclusions
The existence of various numerical solutions made the Elder problem one of the most popular unstable DDF problems. In the current study, we investigated the influence of uniform and orthogonal fracture networks on this problem. The simulation results, developed by COMSOL Multiphysics, have been explored to see the change of free convective flow patterns and the fingering phenomenon. The main findings can be summarized in the three following items:
- (1)
- Embedding fracture networks in the Elder problem increases the mesh sensitivity and bifurcation states of this problem. In other words, by changing the mesh size, the fractured Elder problem has more variation in both the number and shape of the plumes than the non-fractured case.
- (2)
- Fracture networks have a destabilizing impact on the Elder problem. It means that the onset of instability of fractured Elder problem occurs with the value of Rayleigh number lower than 40 which is the critical Rayleigh number of onset of instability.
- (3)
- Concerning how the structural properties of fracture networks control convective flow patterns, we explored the effect of aperture fractures and density of the fracture networks. By enlarging the aperture size in a fractured case of Elder problem, the instability increases at an early time, and since the convective flow in the fractures moves up there would be a higher number of fingers at the beginning. However, the system will be stable at the other times, and the simulation results will be the same for different aperture sizes. In addition, as the fracture density increases, various transient convective modes obtained which are different from the non-fractured case at the beginning; nonetheless, this difference exists until an optimal fracture density, and after that, the high dense fractured scenarios behave similarly to the homogeneous case in fingering processes and plume patterns.
The presented work can be a foundation for further unstable DDF numerical modeling of fractured Elder problem. It would be useful to extend this model for fracture networks, without being limited to only vertical and horizontal fractures, and also simulate them in 3D with more complexity to approach real-world fractured media.
Author Contributions
P.S. model development and writing original draft preparation; M.F. writing—review, editing and analysis; B.A.-A. formulation of the research questions, reviewing the paper and research supervision; C.T.S. reviewing the paper and research supervision.
Funding
This research received no external funding.
Acknowledgments
The authors Behzad Ataie-Ashtiani and Craig T. Simmons acknowledge support from the National Centre for Groundwater Research and Training, Australia. Behzad Ataie-Ashtiani appreciates the support of the Research Office of the Sharif University of Technology, Iran.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Simmons, C.T.; Fenstemaker, T.R.; Sharp, J.M. Variable-density groundwater flow and solute transport in heterogeneous porous media: Approaches, resolutions and future challenges. J. Contam. Hydrol. 2001, 52, 245–275. [Google Scholar] [CrossRef]
- Diersch, H.-J.G.; Kolditz, O. Variable-density flow and transport in porous media: Approaches and challenges. Adv. Water Resour. 2002, 25, 899–944. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 4th ed.; Springer Science + Business Media: New York, NY, USA, 2013. [Google Scholar]
- Ataie-Ashtiani, B.; Simmons, C.T.; Irvine, D.J. Confusion about “Convection”! Groundwater 2018, 56, 683–687. [Google Scholar] [CrossRef] [PubMed]
- Yadav, D.; Lee, D.; Cho, H.-H.; Lee, J. The onset of double diffusive nanofluid convection in a rotating porous medium layer with thermal conductivity and viscosity variation: A revised model. J. Por. Media 2016, 19, 31–46. [Google Scholar] [CrossRef]
- Murray, B.T.; Chen, C.F. Double-diffusive convection in a porous medium. J. Fluid Mech. 1989, 201, 147. [Google Scholar] [CrossRef]
- Umavathi, J.C.; Yadav, D.; Mohit, M.B. Linear and nonlinear stability analyses of double-diffusive convection in a porous medium layer saturated in a Maxwell nanofluid with variable viscosity and conductivity. Elixir Mech. Eng. 2015, 79, 30407–30426. [Google Scholar]
- Hoteit, H.; Fahs, M.; Soltanian, M.R. Assessment of CO2 Injectivity during Sequestration in Depleted Gas Reservoirs. Geosciences 2019, 9, 199. [Google Scholar] [CrossRef]
- Islam, A.W.; Lashgari, H.R.; Sephernoori, K. Double diffusive natural convection of CO2 in a brine saturated geothermal reservoir: Study of non-modal growth of perturbations and heterogeneity effects. Geothermics 2014, 51, 325–336. [Google Scholar] [CrossRef]
- Yadav, D.; Kim, M.C. Theoretical and numerical analyses on the onset and growth of convective instabilities in a horizontal anisotropic porous medium. J. Por. Media 2014, 17, 1061–1074. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Graf, T.; Guevara Morel, C.R. Free thermal convection in heterogeneous porous media. Geothermics 2016, 64, 152–162. [Google Scholar] [CrossRef]
- Wooding, R.A.; Tyler, S.W.; White, I. Convection in groundwater below an evaporating Salt Lake: 1. Onset of instability. Water Resour. Res. 1997, 33, 1199–1217. [Google Scholar] [CrossRef]
- Nield, D.A.; Simmons, C.T.; Kuznetsov, A.V.; Ward, J.D. On the evolution of salt lakes: Episodic convection beneath an evaporating salt lake. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Elder, J.W. Transient convection in a porous medium. J. Fluid Mech. 1967, 27, 609–623. [Google Scholar] [CrossRef]
- Simmons, C.T.; Elder, J.W. The Elder Problem. Groundwater 2017, 55, 926–930. [Google Scholar] [CrossRef] [PubMed]
- Elder, J.; Simmons, C.; Diersch, H.-J.; Frolkovič, P.; Holzbecher, E.; Johannsen, K. The Elder Problem. Fluids 2017, 2, 11. [Google Scholar] [CrossRef]
- Voss, C.I.; Souza, W.R. Variable density flow and solute transport simulation of regional aquifers containing a narrow freshwater-saltwater transition zone. Water Resour. Res. 1987, 23, 1851–1866. [Google Scholar] [CrossRef]
- Fahs, M.; Younes, A.; Mara, T.A. A new benchmark semi-analytical solution for density-driven flow in porous media. Adv. Water Resour. 2014, 70, 24–35. [Google Scholar] [CrossRef]
- Voss, C.I.; Simmons, C.T.; Robinson, N.I. Three-dimensional benchmark for variable-density flow and transport simulation: Matching semi-analytic stability modes for steady unstable convection in an inclined porous box. Hydrogeol. J. 2010, 18, 5–23. [Google Scholar] [CrossRef]
- Johannsen, K. On the Validity of the Boussinesq Approximation for the Elder Problem. Comput. Geosci. 2003, 7, 169–182. [Google Scholar] [CrossRef]
- Van Reeuwijk, M.; Mathias, S.A.; Simmons, C.T.; Ward, J.D. Insights from a pseudospectral approach to the Elder problem. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Ataie-Ashtiani, B.; Simmons, C.T.; Werner, A.D. Influence of Boundary Condition Types on Unstable Density-Dependent Flow. Groundwater 2014, 52, 378–387. [Google Scholar] [CrossRef] [PubMed]
- Post, V.E.A.; Prommer, H. Multicomponent reactive transport simulation of the Elder problem: Effects of chemical reactions on salt plume development. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Xie, Y.; Simmons, C.T.; Werner, A.D.; Ward, J.D. Effect of transient solute loading on free convection in porous media. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Graf, T.; Boufadel, M.C. Effect of viscosity, capillarity and grid spacing on thermal variable-density flow. J. Hydrol. 2011, 400, 41–57. [Google Scholar] [CrossRef]
- Lu, C.; Shi, L.; Chen, Y.; Xie, Y.; Simmons, C.T. Impact of kinetic mass transfer on free convection in a porous medium. Water Resour. Res. 2016, 52, 3637–3653. [Google Scholar] [CrossRef]
- Fahs, M.; Younes, A.; Makradi, A. A Reference Benchmark Solution for Free Convection in A Square Cavity Filled with A Heterogeneous Porous Medium. Numer. Heat Transf. Part B Fundam. 2015, 67, 437–462. [Google Scholar] [CrossRef]
- Irvine, D.J.; Sheldon, H.A.; Simmons, C.T.; Werner, A.D.; Griffiths, C.M. Investigating the influence of aquifer heterogeneity on the potential for thermal free convection in the Yarragadee Aquifer, Western Australia. Hydrogeol. J. 2015, 23, 161–173. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V.; Simmons, C.T. The Effect of Strong Heterogeneity on the Onset of Convection in a Porous Medium: Non-periodic Global Variation. Transp. Porous Media 2009, 77, 169–186. [Google Scholar] [CrossRef]
- Nield, D.A.; Simmons, C.T. A discussion on the effect of heterogeneity on the onset of convection in a porous medium. Transp. Porous Media 2007, 68, 413–421. [Google Scholar] [CrossRef]
- Prasad, A.; Simmons, C.T. Unstable density-driven flow in heterogeneous porous media: A stochastic study of the Elder [1967b] “short heater” problem. Water Resour. Res. 2003, 39, SBH 4-1–SBH 4-21. [Google Scholar] [CrossRef]
- Graf, T.; Therrien, R. Variable-density groundwater flow and solute transport in irregular 2D fracture networks. Adv. Water Resour. 2007, 30, 455–468. [Google Scholar] [CrossRef]
- Vujević, K.; Graf, T.; Simmons, C.T.; Werner, A.D. Impact of fracture network geometry on free convective flow patterns. Adv. Water Resour. 2014, 71, 65–80. [Google Scholar] [CrossRef]
- Hirthe, E.M.; Graf, T. Fracture network optimization for simulating 2D variable-density flow and transport. Adv. Water Resour. 2015, 83, 364–375. [Google Scholar] [CrossRef]
- Simmons, C.T.; Sharp, J.M.; Nield, D.A. Modes of free convection in fractured low-permeability media. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Graf, T.; Therrien, R. Stable-unstable flow of geothermal fluids in fractured rock. Geofluids 2009, 9, 138–152. [Google Scholar] [CrossRef]
- Vujević, K.; Graf, T. Combined inter- and intra-fracture free convection in fracture networks embedded in a low-permeability matrix. Adv. Water Resour. 2015, 84, 52–63. [Google Scholar] [CrossRef]
- Shao, Q.; Fahs, M.; Hoteit, H.; Carrera, J.; Ackerer, P.; Younes, A. A 3-D Semianalytical Solution for Density-Driven Flow in Porous Media. Water Resour. Res. 2018, 54, 10094–10116. [Google Scholar] [CrossRef]
- Koohbor, B.; Fahs, M.; Ataie-Ashtiani, B.; Belfort, B.; Simmons, C.T.; Younes, A. Uncertainty analysis for seawater intrusion in fractured coastal aquifers: Effects of fracture location, aperture, density and hydrodynamic parameters. J. Hydrol. 2019, 571, 159–177. [Google Scholar] [CrossRef]
- Mozafari, B.; Fahs, M.; Ataie-Ashtiani, B.; Simmons, C.T.; Younes, R. On the use of COMSOL Multiphysics for seawater intrusion in fractured coastal aquifers. E3S Web Conf. 2018, 54, 00020. [Google Scholar] [CrossRef]
- Sharp, J.M., Jr.; Fenstemaker, T.R.; Simmons, C.T.; McKenna, T.E.; Dickinson, J.K. Potential salinity-driven free convection in a shale-rich sedimentary basin: Example from the Gulf of Mexico basin in south Texas. Bulletin 2001, 85, 2089–2110. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).