Solar Thermal Collector Roughened with S-Shaped Ribs: Parametric Optimization Using AHP-MABAC Technique

Abstract

The current examination used a multi-criteria decision-making (MCDM) approach to optimize the roughness parameters of S-shaped ribs (SSRs) in a solar thermal collector (STC) duct using air as the working fluid. Different SSRs were tested to identify the combination of parameters resulting in the best performance. Geometrical parameters such as relative roughness pitch ($P_R/e_{RH}$) varied from 4 to 12, relative roughness height ($e_{RH}/D_{hd}$) from 0.022 to 0.054, arc angle (${\alpha }_{Arc}$) from 30° to 75°, and relative roughness width ($W_{Duct}/w_{RS}$) from 1 to 4. The Nusselt number (${Nu}_{RP}$) and friction factor ($f_{RP}$), findings which impact the STC performance, rely on SSRs. The performance measurements show that no combination of SSR parameters lead to the best enhancement heat transfer rate at low enhancement in the friction. So, a hybrid multi-criteria decision-making strategy using the Analytical Hierarchy Process (AHP) for criterion significance and Multi Attributive Border Approximation Area Comparison (MABAC) for alternative ranking was used to determine which combination of geometrical parameters will result in the optimum performance of a roughened STC. This work employs a hybrid MCDM technique to optimise the effectiveness of an STC roughened with SSRs. To optimize the SSR design parameters, this study used the hybrid AHP-MABAC technique for analytical assessment of a roughened STC. The optimization results showed that the STC roughened with SSRs achieved the optimum performance at $P_R/e_{RH}$ = 8, $e_{RH}/D_{hd}$ = 0.043, ${\alpha }_{Arc}$ = 60° and $W_{Duct}/w_{RS}$ = 3.

1. Introduction

Energy has been the driving force for industrialization and worldwide economic growth. The rapid exhaustion of fossil fuel reserves, which predominate the existing energy structure, necessitates the immediate development of alternative renewable energy sources. Solar energy is an abundant, renewable, and non-polluting resource [1,2]. An STC is an efficient method for capturing and transforming solar energy into thermal energy for heating purposes [3,4]. The optimal design of an STC guarantees maximum solar energy utilization; it captures solar radiation and conveys the heat to the flowing air. Nevertheless, the limited effectiveness of an STC is attributed to the low heat absorption of the collector and the inadequate thermal conductivity of air. Improving the heat transfer rate via active and passive techniques is a principal solution investigated by researchers to tackle these difficulties [5,6]. Among these two methods, passive methods have gained prominence because of their simplicity and lack of external power requirements compared with active ones. The passive techniques include the use of treated surfaces [7], artificial rough surfaces [8], extended surfaces [9], turbulators [10], nanofluids [11], and swirl flow devices [12,13].

Artificially rough surfaces on the absorber plates are an efficient passive method for improving the heat transfer in STCs. By disturbing the laminar sub-layer and generating turbulence, they markedly enhance the convective heat transfer relative to other passive techniques, such as extended surfaces or swirl flow devices. Their design is straightforward, economical, and facilitates manufacturing, rendering them suitable for extensive, budget-friendly applications. In contrast to more intricate methods, artificially roughened surfaces result in low-pressure losses, attaining an improved equilibrium between heat transmission and pumping power. Common designs on the absorber plates include ribs [14], grooved surfaces [15], dimples [16], and protrusions [17].

Ribs have certain benefits compared to other artificial roughness methods. Their geometry is highly customizable, allowing for optimization under specific operating conditions while balancing the growth of heat transfer and pressure drop. Ribs enhance the effective efficiency compared to more disruptive approaches such as protrusions, ensuring a practical balance between performance and energy losses [18]. The increase in the heat transfer is calculated in terms of the Nusselt number ($Nu$) which is a ratio of the convective to conductive heat transfer from the absorber plate to a fluid. The artificial roughness results in the enhancement of friction which is measured in terms of the friction factor ($f$). The Reynold number ($Re$) provides information about the type of flow.

Thakur and Thakur [19] have examined the effect of W-shaped ribs. W-shaped ribs offer distinct benefits over V-shaped ribs by generating four secondary flow vortices rather than two. These vortices augment turbulence and more effectively disrupt the thermal barrier layer, resulting in enhanced heat transfer. Wang et al. [20] have used S-shaped ribs with gaps to enhance the performance of STCs; the S-shape creates flow reattachment zones and secondary vortices, more effectively breaking laminar layers. The S-shaped ribs enhance the thermal efficiency by as much as 48%, achieving a maximum Nu increase of 5.42. Shayan et al. [21] also found that by using an S-shaped rib, the S-shape induces flow reattachment zones, hence enhancing the heat transmission dramatically. It attains a Nu of 4.875 times greater than that of a smooth duct. The characteristics of S-shaped roughness provide it with an efficient design for STCs, optimizing the heat transfer enhancement while minimizing friction losses.

Experimental investigations necessitate the extensive testing of all the parameters of the SAH with roughness ribs, making the process both expensive and time intensive. Moreover, conducting an exhaustive analysis of the influence of every variable on the heat transmission, friction factor, and performance of the heat exchanger is thorough and rigorous. Consequently, an optimization methodology should be utilized to quantitatively forecast the diverse elements influencing the system performance and ascertain the principal criteria for an ideal design. Plenty of researchers have focused on improving and optimizing the performance of various STCs through diverse methodologies. MCDM methodologies, like VIKOR, MOORA, MABAC, and TOPSIS, provide the concurrent optimization of opposing objectives, such as heat transfer, pressure drop, and effective efficiency, providing equitable solutions. These methods effectively investigate the design space by examining many factors, including roughness geometry and the $Re$, with fewer experimental trials, thus conserving time and money. The amalgamation of analytical and experimental methodologies, exemplified by hybrid techniques, guarantees elevated precision and efficient decision making, facilitating optimal SAH designs with negligible validation discrepancies. Benhamza et al. [22] investigated the optimization of a finned STC for food drying through a mix of experimental analysis and response surface methodology (RSM). The optimization method aims to attain three primary objectives: thermal efficiency, output air temperature, and exergetic improvement potential (IP). The research determines the ideal design parameters as a length-to-width ratio of 1.28, an air duct height of 0.067 m, and 49 fins. Under these conditions, the SAH attains a thermal efficiency of 51.78% and an IP of 1397.34 W, indicating a 15.76% increase in thermal efficiency and a 19.33% improvement in IP relative to baseline designs. These findings indicate considerable potential for enhancing the SAH efficacy in food drying applications. Mohanty et al. [23] examined the optimization of a three-sided roughened STC via a combination of RSM and Multi-Objective Particle Swarm Optimization (MOPSO). Critical parameters, such as the $Re,$ mass flow rate, and relative roughness pitch, have been changed to optimize thermal efficiency and the $Nu.$ The optimization determined the optimal performance at the $Re$ ranging from 12,000 to 13,000 and a relative roughness pitch of 10 mm, resulting in a thermal efficiency between 63% and 75% and a $Nu$ between 65 and 80. A confirmatory test corroborated the results with a 3.39% margin of error. This hybrid optimization method provides significant insights for upgrading SAH designs and improving energy efficiency while reducing the pressure drop. Kumar et al. [24] used hybrid CRITIC-COPRAS MCDM techniques to examine the effectiveness of an impingement jet solar air heater. Mishra et al. [25] examined the optimization of geometric parameters for multi-arc protrusion obstacles in an impingement jet solar air path utilizing the AHP-TOPSIS MCDM methodology. Chauhan and Kim [26] optimized the effectiveness of an STC through the application of the VIKOR approach, an MCDM tool. The entropy approach is initially employed to allocate weights to various characteristics, indicating their significance. VIKOR subsequently rates potential absorber designs utilizing utility and regret metrics, locating the best options that reconcile heat transfer enhancement with pressure loss minimization. The research found that dimpled and protruded arc-shaped absorbers markedly enhance thermal and exergetic efficiency compared to traditional designs. Singh et al. [27] performed an extensive evaluation of the multi-objective optimization via the ratio analysis (MOORA) method and its fuzzy extensions, emphasizing applications in many domains, such as SAH optimization. MOORA evaluates alternatives by optimizing advantageous criteria and minimizing detrimental ones, providing an effective method for balancing trade-offs in decision making. In solar air heaters, MOORA is employed to optimize parameters such as the absorber plate design, airflow rate, and thermal efficiency, hence enhancing the performance through the assessment of numerous conflicting criteria. Its incorporation of entropy or fuzzy methodologies improves the decision making in uncertain conditions. Goel et al. [28] enhanced the efficiency of an SAH by incorporating hybrid artificial roughness beneath the absorber plate, which integrates transverse ribs and discrete inclined ribs. This study used RSM to analyze the impacts of four critical parameters: relative roughness height, pitch, attack angle, and the$Re.$Empirical models for the $Nu$, $f,$ and thermo-hydraulic performance ($\eta$) were constructed via regression analysis. The AHP-WASPAS approach determines an ideal configuration, corroborated by experimental validation. The sensitivity analysis and rank reversal tests validate the resilience of the proposed decision framework, notwithstanding a slight susceptibility to alterations in weights. The AHP-WASPAS method is a hybrid MCDM strategy that integrates the Analytical Hierarchy Process and the Weighted Aggregated Sum Product Assessment. This combination harnesses the advantages of both methodologies to enhance the decision-making precision and dependability, especially for intricate issues with several competing criteria. Salman et al. [29] examined analytically the performance enhancement of a jet-impinged solar air collector, including dimple-roughened absorber plates. The study used a hybrid MCDM approach to determine the ideal geometric and flow characteristics that enhance heat transfer and reduce frictional losses. The ideal design was established with a dimple height ratio of 0.027, a pitch ratio of 0.27, and an arc angle of 60° at the $Re$ of 15,000.

The published literature recommends the availability of AHP and MABAC methods as decision-making techniques in various domains. MCDM techniques have been utilized extensively to explore the optimum design parameters of artificial roughness. However, their implication in the design optimization of STC roughened with SSRs has yet to be examined. In the current analytic study, the findings of previous experimental work [30] were used to optimize the SSR parameters leading to the best performance of roughened STC. This earlier study [30] established the fundamental impact of S-shaped ribs on heat transfer and flow dynamics, demonstrating significant improvements in ${\mathit{N}\mathit{u}}_{\mathit{R}\mathit{p}}$ and thermal efficiency. However, this came at the cost of enhanced friction. The enhancement in heat transfer and friction factors has been comprehensively studied at various mass flow rates(m) with air as working fluid. However, none of the design considerations satisfy the desirable outcome of achieving the best heat transfer with minimal friction increase. So, in the present analytical examination more analysis is carried out to select the most appropriate combination of design parameters resulting in the best performance of roughened STC utilizing hydrid MCDM techniques. The novelty of the present work lies in the fact that the present analytic examination is able to recognize/verify the suitable combination of design parameters leading to best performance of STC roughened with SSRs. The main objective of present analytical examination is to support designers and researchers in the domain of solar heating systems in the identification and selection of appropriate design parameters. The ${\mathit{P}}_{\mathit{R}}/{\mathit{e}}_{\mathit{R}\mathit{H}}$ spacing between ribs influences reattachment points of flow and directly affects the heat transfer rates. Relative roughness height (${\mathit{e}}_{\mathit{R}\mathit{H}}/{\mathit{D}}_{\mathit{h}\mathit{d}}$) affects turbulence intensity and friction. Arc angle modifies the secondary flows. The ${\mathit{W}}_{\mathit{D}\mathit{u}\mathit{c}\mathit{t}}/{\mathit{w}}_{\mathit{R}\mathit{S}}$ ratio is used to quantify the extent of artificial roughness applied to surfaces. This roughness enhances heat transfer by creating turbulence and disrupting the laminar sub-layer. The research highlights the use of a hybrid MCDM technique, AHP-MABAC, to select the best combination of roughness parameters—${\mathit{P}}_{\mathit{R}}/{\mathit{e}}_{\mathit{R}\mathit{H}}$, ${\mathit{W}}_{\mathit{D}\mathit{u}\mathit{c}\mathit{t}}/{\mathit{w}}_{\mathit{R}\mathit{S}},$ ${\mathit{e}}_{\mathit{R}\mathit{H}}/{\mathit{D}}_{\mathit{h}\mathit{d}}$, and ${\mathit{\alpha }}_{\mathit{A}\mathit{r}\mathit{c}}$. This combination resulted in the optimal performance of the roughened STC. This study emphasizes the possibility of integrating STC with SSRs to markedly improve performance of SAHs, applicable in energy-efficient heating systems.

2. Experimental Investigation

2.1. Experimental Setup

A rectangular STC was used for experiments consisting of three main sections: an entrance section, a test section, and an exit section. The three sections were placed one next to the other. Air was passed through the duct of the STC by using a centrifugal blower. An opening in the rectangular duct permitted the intake of ambient air. A rectangular mixing chamber at the end of the duct exit portion connected it to a galvanized iron (GI) pipe, allowing air to exit the outlet. A calibrated orifice plate and a U-tube manometer were used to measure the airflow rate. The experimental setup employed in this work is schematically shown in Figure 1.

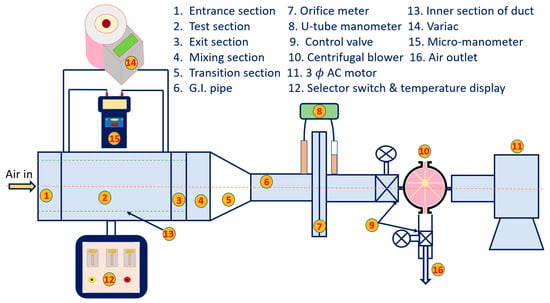
Figure 1. Schematic representations of an experimental setup.

Figure 2 demonstrates the schematic representations of a roughened absorber plate, highlighting its geometric features. The absorber plate is textured by affixing circular wires (ribs) in an ‘S’ shape. Roughness characteristics were articulated in a non-dimensional format, including $P_R/e_{RH}$, $e_{RH}/D_{hd}$, ${\alpha }_{Arc}$, and $W_{Duct}/w_{RS}$. The spectrum of roughness and operational parameters utilized in the current study was based on a previous experimental examination presented in Table 1 [30].

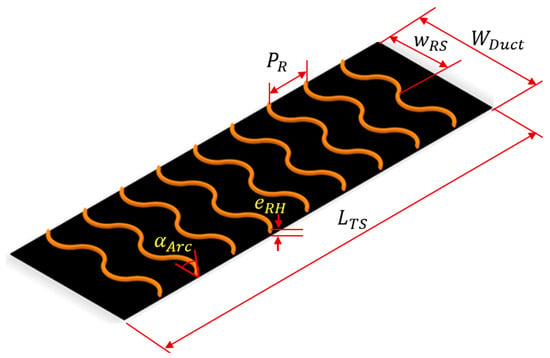
Figure 2. Schematic representations of the roughened absorber plate.

Table 1. Range of operational conditions and roughness parameters [30].

Sr. No.	Parameter	Range
1	$Re$	2400–20,000
2	$e_{RH}/D_{hd}$	0.022–0.054
3	${\alpha }_{Arc}$	30–75°
4	$P_R/e_{RH}$	4–16
5	$W_{Duct}/w_{RS}$	1–4

2.2. Methodology for Data Reduction

During experimentation, orifice meter, manometer and thermocouples were utilized to measure temperature and pressure drop at various mass flow rates throughout the day. Control valves are adjusted to get the desired m of fluid in the duct. To ensure the arrival of quasi-steady state conditions; observations of temperature were taken at regular interval of 10–15 min. The observations were noted for pressure drops across the test section of duct, pressure across the orifice plate to measure the air flow rates, temperature of absorber plates, temperature of air at inlet and outlet of the duct and ambient temperature. Twelve, four and four calibrated copper-constantan thermocouples were used to measure absorber plate, inlet and outlet temperature respectively. So experimental data is huge as observations were taken across the day at various flow rates and to carry out the analysis, data must be reduced.

2.2.1. The Mean Plate Temperature ($T_{MPT}$) and Mean Fluid Temperature ($T_{MF}$)

The mean plate temperature ($T_{MPT}$) was taken as the arithmetic mean of temperatures recorded by twelve thermocouples at different locations on the absorber plate. The inlet temperature of the fluid ($T_{INT}$) and outlet temperature of the fluid ($T_{OUT}$) were calculated by taking the average of the temperatures noted from four respective thermocouples. Then, the mean fluid temperature ($T_{MF}$) was taken as the arithmetic mean of the calculated values of $T_{INT}$ and $T_{OUT}$.

The equations which were used for the calculation of the mass flow rate, the Reynolds number, Nusselt number, friction factor, and thermal and effective efficiency are given below, and a flow chart for the same is shown in Figure 3 [31,32].

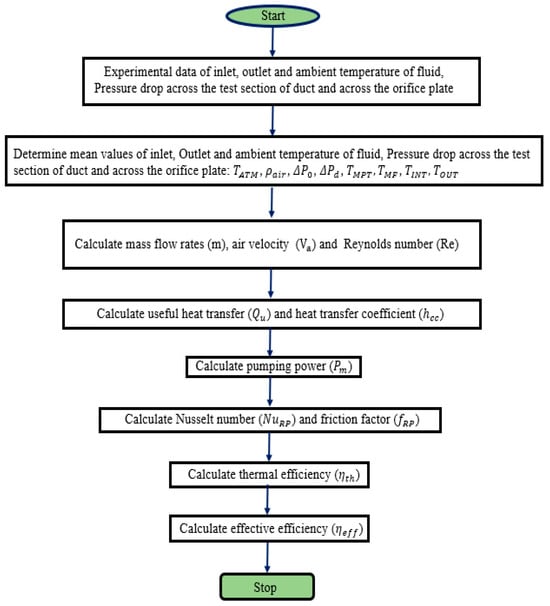
Figure 3. Flow chart for calculation.

2.2.2. Mass Flow Rate of Fluid ($m$)

The m was calculated from the values of ${\Delta P}_0$ using the following equation:

$$m=C_d{A}_{OR}{\left[{\displaystyle \frac{2{\rho }_{air}\left(\Delta P_o\right)}{1-{\beta }^4}}\right]}^{{\displaystyle \frac{1}{2}}}$$

(1)

where the symbols have their meanings as given in the nomenclature. The pressure drop was calculated using the equation:

$${\Delta P}_0={\rho }_{air}\times g\times {\Delta h}_0.$$

(2)

where $g=9.81 \mathrm{m}/{\mathrm{s}}^2,$ and ${\Delta h}_0$ is the difference of head in the manometer.

2.2.3. Velocity of Fluid ($V_a$) and Reynolds Number ($Re$)

The velocity of the fluid was calculated using the equation:

$$V_a={\displaystyle \frac{m}{{\rho }_{air}\times W_{duct}\times H_{duct}}}$$

(3)

The $Re$ at the experimentation section of the STC was calculated using the following equation.

$$Re={\displaystyle \frac{{{\rho }_{air}\times V}_a\times D_{hd}}{{\mu }_{air}}}$$

(4)

where $D_{hd}$ is the hydraulic diameter of the channel and calculated using the equation given below:

$$D_{hd}={\displaystyle \frac{4\times W_{duct}\times H_{duct}}{2\times \left(W_{duct}+H_{duct}\right)}}$$

(5)

Other symbols have their meanings as given in the nomenclature.

2.2.4. Convective Heat Transfer Coefficient ($h_{cc}$)

The heat transfer rate, $Q_u,$ of air was computed by following the formula:

$$Q_u=m{C}_p (T_{OUT}-T_{INT}).$$

(6)

The $h_{cc}$ was determined using the equation given below:

$$h_{CC}={\displaystyle \frac{Q_u}{A_{Abs}\left(T_{MPT}-T_{MF}\right)}} .$$

(7)

2.2.5. Pumping Power ($P_m)$

The pumping power required to run the setup was calculated as below:

$$P_m={\displaystyle \frac{m\times {\Delta P}_d}{{\rho }_{air}}} .$$

(8)

where the symbols have their meanings as given in the nomenclature.

2.2.6. Nusselt Number (${Nu}_{RP}$)

The ${ h}_{cc}$ was employed to compute the Nusselt number (${Nu}_{RP}$) and is given by the following equation;

$${Nu}_{RP}={\displaystyle \frac{h_{CC}{D}_{hd}}{k_{air}}}.$$

(9)

where $k_{air}$ is the thermal conductivity of air. The thermal conductivity of air ($k_{air}$) is given by $k_{air}=0.0257{\left({\displaystyle \frac{T_{MF}}{293}}\right)}^{0.8}$.

2.2.7. Friction Factor ($f_{RP}$)

The $f_{RP}$ was computed from the computed values of ${\Delta P}_d$ over the experimental portion of the distance ($L_{TS}$) using the Darcy–Wiesbach equation which is given below:

$$f_{RP}={\displaystyle \frac{2\times {\Delta P}_d\times D_{hd}}{4\times {\rho }_{air}\times L_{TS}\times {V_{a }}^2}} .$$

(10)

2.2.8. Thermal Efficiency (${\eta }_{th}$) and Effective Efficiency (${\eta }_{eff}$)

The thermal efficiency (${\eta }_{th}$) is the ratio of the useful heat energy gain to the rate of total incident solar energy and is computed as:

$${\eta }_{th}={\displaystyle \frac{Q_u }{{I_{RAD}\times A}_{Abs}}}.$$

(11)

where $I_{RAD}$ is the incident solar insolation.

The artificial roughness on the absorber plate leads to the enhancement in the heat transfer rate, but it also increases the friction factor; thus, the required pumping power also increases. Hence, the effective efficiency of the roughened STC is calculated as:

$${\eta }_{eff}={\displaystyle \frac{Q_u-P_m/C_{con} }{{I_{RAD}\times A}_{Abs}}}.$$

(12)

where $P_m$ is the pumping power, and $C_{con}$ is the efficiency of conversion from mechanical to thermal power and given by:

$$C_{con}={\eta }_{fan}\ast {\eta }_{mot}\ast {\eta }_{trs}\ast {\eta }_{tpp}.$$

where ${\eta }_{fan}, {\eta }_{mot}, {\eta }_{trs}, \mathrm{and} {\eta }_{tpp}$ are the efficiencies of the fan, electric motor, electrical transmission, and of the thermal power plant, respectively. The recommended value of $C_{con}$ is 0.18 as suggested by Cortés and Piacentini [33].

3. Methodology

In order to arrive at the optimal design values, the integrated AHP-MABAC [29,34] methodology is considered to be one of the most advanced designs and optimization techniques. It is used to evaluate control parameters on an individual basis.

3.1. Selection of Alternatives and Criteria

According to the aims, the criteria and the alternatives for a particular MCDM issue are outlined in the first stage. In the present work, the alternatives are the parameters of the roughness elements. The details of the alternatives (ALTs) and criteria are provided in the next section. A performance matrix was computed on the basis of the selected alternatives and criteria. Generally, a performance matrix ($P_{AC}$) for any MCDM problem with “p” alternatives; $A_i, i=1,2,3,\dots ..p$ and “q” criteria; $C_j, j=1,2\dots q$ is expressed as:

$$P_{AC}=\begin{array}{cc}& \begin{array}{ccc}\begin{array}{ccc}\begin{array}{cc}{C}_1& C_2\end{array}& \dots & \dots \dots \dots .\end{array}& \dots \dots .& C_q\end{array}\\ \begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{A}_1\\ A_2\end{array}\\ :\end{array}\\ :\end{array}\\ :\\ A_p\end{array}& \left|\begin{array}{c}\begin{array}{ccc}\begin{array}{ccc}\begin{array}{cc}{p}_{11}& p_{12}\end{array}& ..& \dots \end{array}& \dots \dots \dots \dots & p_{1q}\end{array}\\ \begin{array}{ccc}\begin{array}{ccc}\begin{array}{cc}{p}_{21}& p_{22}\end{array}& ..& \dots \end{array}& \dots \dots \dots \dots .& p_{2q}\end{array}\\ \begin{array}{c}\begin{array}{ccc}\begin{array}{ccc}\begin{array}{cc}:& :\end{array}& :& \dots \dots \dots \end{array}& \dots \dots \dots \dots \dots .& :\end{array}\\ .\\ \begin{array}{c}\begin{array}{ccc}\begin{array}{ccc}\begin{array}{cc}:& :\end{array}& :& \dots \end{array}& \dots .& \dots \dots \dots ..\dots \dots :\end{array}\\ \begin{array}{ccc}\begin{array}{ccc}\begin{array}{cc}{p}_{p1}& p_{p2}\end{array}& ..& \dots \end{array}& \dots \dots \dots \dots & p_{pq}\end{array}\end{array}\end{array}\end{array}\right|\end{array}$$

(13)

An element $p_{ij}$of the performance matrix signifies the performance score of the “ith” alternative ($A_i$) concerning the “j^th” criterion ($C_j$).

3.2. Weight Computation of the Criteria Using the AHP Method

It is common practice to use AHP when attempting to determine the relative significance of activities inside an MCDM challenge. A pairwise comparison matrix was constructed using a standardized comparison scale of 9 points. For “q” criteria, Cj, j = 1, 2, …, q, the pairwise comparison matrix ${PC}_{q\times q}$ is constructed as:

$${PC}_{q\times q}=\begin{array}{cc}& \begin{array}{ccc}\begin{array}{ccc}\begin{array}{cc}{C}_1& C_2\end{array}& \dots & \dots \dots \dots .\end{array}& \dots \dots .& C_q\end{array}\\ \begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{C}_1\\ C_2\end{array}\\ :\end{array}\\ :\end{array}\\ :\\ C_q\end{array}& \left|\begin{array}{c}\begin{array}{ccc}\begin{array}{ccc}\begin{array}{cc}{pc}_{11}& {pc}_{12}\end{array}& ..& \dots \end{array}& \dots \dots \dots \dots & {pc}_{1q}\end{array}\\ \begin{array}{ccc}\begin{array}{ccc}\begin{array}{cc}{pc}_{21}& {pc}_{22}\end{array}& ..& \dots \end{array}& \dots \dots \dots \dots .& {pc}_{2q}\end{array}\\ \begin{array}{c}\begin{array}{ccc}\begin{array}{ccc}\begin{array}{cc}:& :\end{array}& :& \dots \dots \dots \end{array}& \dots \dots \dots \dots \dots .& :\end{array}\\ .\\ \begin{array}{c}\begin{array}{ccc}\begin{array}{ccc}\begin{array}{cc}:& :\end{array}& :& \dots \end{array}& \dots .& \dots \dots \dots ..\dots \dots :\end{array}\\ \begin{array}{ccc}\begin{array}{ccc}\begin{array}{cc}{pc}_{q1}& {pc}_{q2}\end{array}& ..& \dots \end{array}& \dots \dots \dots \dots & {pc}_{qq}\end{array}\end{array}\end{array}\end{array}\right|\end{array}\hspace{1em}{pc}_{ij}=1 if i=j, {pc}_{ij}={\displaystyle \frac{1}{{pc}_{ij}}}, i\ne j{ \& pc}_{ij}\ne 0.$$

(14)

Every element of the constructed comparison matrix ${PC}_{q\times q}$ is a measure of the criterion weight. Criterion weights were computed using the right eigenvector “$u$” which corresponds to the leading eigenvalue.

$${PC}_{q\times q} u={\lambda }_{max}u.$$

(15)

where ${\lambda }_{max}$ is the leading eigenvalue of the matrix ${PC}_{q\times q},$ and $u$ is the corresponding eigenvector.

According to the reports in the literature, the reliability of pairwise comparison results is closely linked to the AHP superiority. In the case of an entirely consistent pairwise comparison matrix, the matrix should have ${\lambda }_{max}=q$ and a rank of 1. The consistency is confirmed to ensure the reliability of the assessments. The consistency ratio (${Cn}_R$) is obtained as:

$${Cn}_R={\displaystyle \frac{{\lambda }_{max}-q}{q-1}}\times {\displaystyle \frac{1}{{Rm}_I}}.$$

(16)

where ${Rm}_I$ represents the matrix’s random index, and the order of the pairwise comparison matrix determines its value. If the evaluation of ${Cn}_R$ is less than the authorized maximum limit of 0.1, the AHP findings are considered acceptable. If the ${Cn}_R$ value is more than 0.1, the pairwise comparison matrix is reconstructed in order to enhance the consistency.

3.3. Final Ranking of the Alternatives: The MABAC Approach

The normalization of the constructed performance matrix was performed using the equations given below to make them comparable.

$$\left\{\begin{array}{c}{P}_{ij}^{*}={\displaystyle \frac{p_{ij}-p_i^{-}}{p_i^{+}-p_i^{-}}}, Higher is better\\ P_{ij}^{*}={\displaystyle \frac{p_{ij}-p_i^{+}}{p_i^{-}-p_i^{+}}}, Lower is better\end{array}\right.$$

(17)

where $P_{ij}^{*}$ denotes the normalized value of the $P_{ij}$ element of the performance matrix. Further, $p_i^{+}=\mathit{max}\left(p_{ij}\right), i=1 \mathrm{to} p$ and $p_i^{-}=\mathit{min}\left(p_{ij}\right), i=1 \mathrm{to} p$.

Thereafter, a weighted normalized performance matrix was obtained by using the equation given below:

$${\overline{\omega }}_{ij}=w_j+\left(P_{ij}^{*}\times w_j\right); i=\left(1,2\dots \dots .p\right), j=\left(1,2\dots \dots .q\right).$$

(18)

The following equation was used to generate the structure of the border approximation area matrix:

$${BA}_j={\left({\prod }_{i=1}^p{\overline{\omega }}_{ij}\right)}^{1/p}; j=\left(1,2\dots \dots .q\right).$$

(19)

The weighted normalized decision matrix’s element distance was calculated using the border approximation area matrix as:

$${ds}_{ij}={\overline{\omega }}_{ij}-{BA}_j ; i=\left(1,2\dots \dots .p\right), j=\left(1,2\dots \dots q\right).$$

(20)

Finally, the following formula was used to determine each alternative’s total distance from the estimated border area.

$${\mathsf{\Psi }}_i={\sum }_{j=1}^q{ds}_{ij}; i=\left(1,2\dots \dots ..p\right).$$

(21)

Alternatives were ranked based on the calculated value of ${\mathsf{\Psi }}_i,$ and the ALTs with the highest ${\mathsf{\Psi }}_i$ value were ranked 1st while the ALTs with the lowest ${\mathsf{\Psi }}_i$ value was listed last.

4. Results and Discussion

The current research attempted to identify the optimal design parameters of SSRs within the STC using the MCDM technique. As discussed in the methodology section, the alternatives (ALTs) were defined. The ALTs were different combinations of roughness parameters: $P_R/e_{RH}$, $e_{RH}/D_{hd}$, ${\alpha }_{Arc}$ and $W_{Duct}/w_{RS}$. A total of 31 alternatives were defined as listed in Table 2. Three decision-making criteria (Cr), namely ${Nu}_{RP}$, $f_{RP}$, and ${\eta }_{eff}$ were considered to find the best alternatives as listed in Table 3. The criteria were obtained from the experimentation with a roughened STC and demonstrated in Figure 4, Figure 5 and Figure 6. Under a number of different sets of parameters, the enhancement of the ${Nu}_{RP}$ is depicted in Figure 4. The ${Nu}_{RP}$ attained its highest value of 311.53 for A-7 and the lowest value of 216.82 for A-1. The variation in the $f_{RP}$ with geometrical parameters or different ALTs is shown in Figure 5. The $f_{RP}$ attained its highest value of 0.0214 at A-8 and the lowest value of 0.0127 for A-17. The ${\eta }_{eff}$ of the roughened STC which was used as third criteria is depicted in Figure 6. For the best performance of the STC, the enhancement in the heat transfer should be high, and enhancement in the friction factor should be low. None of the alternatives/combinations of geometrical parameters fulfilled these requirements, leading to the need for MCDM methods.

Table 2. List of alternatives.

ALTs	$\frac{{\mathit{P}}_{\mathit{R}}}{{\mathit{e}}_{\mathit{R}\mathit{H}}}$	$\frac{{\mathit{W}}_{\mathit{D}\mathit{u}\mathit{c}\mathit{t}}}{{\mathit{w}}_{\mathit{R}\mathit{S}}}$	${\mathit{\alpha }}_{\mathit{A}\mathit{r}\mathit{c}}$	$\frac{{\mathit{e}}_{\mathit{R}\mathit{H}}}{{\mathit{D}}_{\mathit{h}\mathit{d}}}$
A-1	4	1	60°	0.043
A-2	4	2	60°	0.043
A-3	4	3	60°	0.043
A-4	4	4	60°	0.043
A-5	8	1	60°	0.043
A-6	8	2	60°	0.043
A-7	8	3	60°	0.043
A-8	8	4	60°	0.043
A-9	12	1	60°	0.043
A-10	12	2	60°	0.043
A-11	12	3	60°	0.043
A-12	12	4	60°	0.043
A-13	16	1	60°	0.043
A-14	16	2	60°	0.043
A-15	16	3	60°	0.043
A-16	16	4	60°	0.043
A-17	8	1	30°	0.043
A-18	8	2	30°	0.043
A-19	8	3	30°	0.043
A-20	8	4	30°	0.043
A-21	8	1	45°	0.043
A-22	8	2	45°	0.043
A-23	8	3	45°	0.043
A-24	8	4	45°	0.043
A-25	8	1	75°	0.043
A-26	8	2	75°	0.043
A-27	8	3	75°	0.043
A-28	8	4	75°	0.043
A-29	8	3	60°	0.022
A-30	8	3	60°	0.032
A-31	8	3	60°	0.054

Table 3. Performance matrix comprising ALTs and criteria.

ALTs	${\mathit{N}\mathit{u}}_{\mathit{R}\mathit{P}}$ (Cr-I)	${\mathit{f}}_{\mathit{R}\mathit{P}}$ (Cr-II)	${\mathit{\eta }}_{\mathit{e}\mathit{f}\mathit{f}}$ (Cr-III)
A-1	216.82	0.0156	0.63794
A-2	240.06	0.0164	0.68131
A-3	257.29	0.0168	0.71298
A-4	248.83	0.0174	0.69609
A-5	252.3	0.0173	0.70095
A-6	280.18	0.0189	0.74009
A-7	311.53	0.0201	0.80187
A-8	305.35	0.0214	0.77918
A-9	242.22	0.0163	0.68832
A-10	266.18	0.0177	0.72578
A-11	303.39	0.0193	0.78014
A-12	286.46	0.0194	0.75436
A-13	234.13	0.0145	0.68421
A-14	253.26	0.0157	0.70724
A-15	285.46	0.0156	0.76649
A-16	275.02	0.0163	0.73836
A-17	219.08	0.0127	0.65665
A-18	232.03	0.0135	0.67421
A-19	263.2	0.0172	0.72305
A-20	256.21	0.0162	0.71024
A-21	234.2	0.0154	0.68197
A-22	261.16	0.0157	0.72469
A-23	294.23	0.0183	0.77210
A-24	286.44	0.0194	0.75176
A-25	240.87	0.0156	0.68783
A-26	256.95	0.0163	0.71210
A-27	305.06	0.0191	0.79174
A-28	290.26	0.0202	0.76464
A-29	249.02	0.0154	0.70164
A-30	265.06	0.0172	0.72582
A-31	283.73	0.0189	0.74804

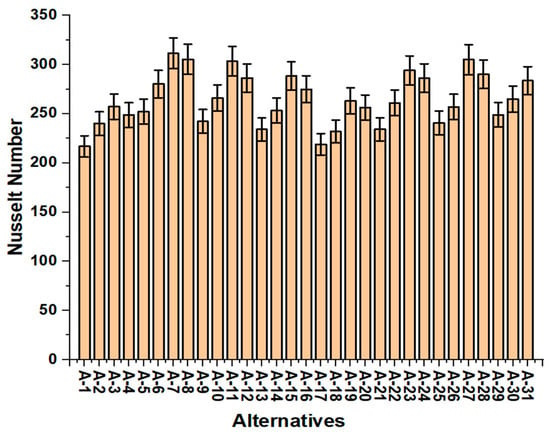
Figure 4. Variation in ${Nu}_{RP }$with alternatives.

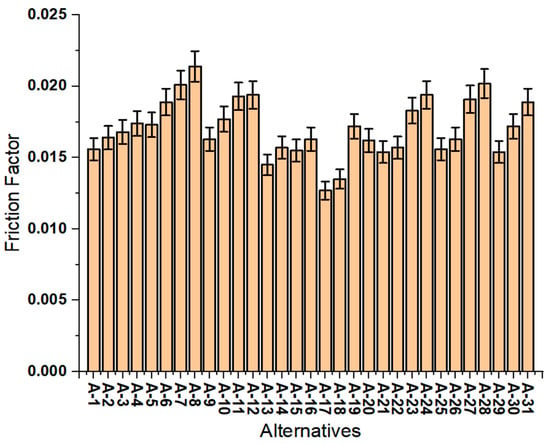
Figure 5. Variation in $f_{RP}$ with alternatives.

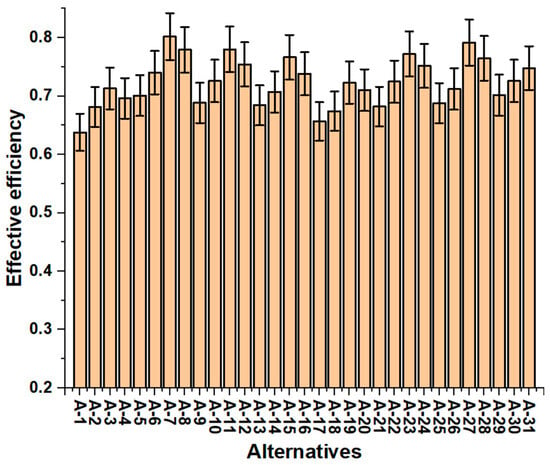
Figure 6. Variation in ${\eta }_{eff}$ with alternatives.

A performance matrix ($P_{AC}$) was computed based on the selected alternatives and criteria using Equation (12). The performance matrix for the MCDM problem with 31 alternatives ($A_i, i=1,2,3,\dots ..31$ and 3 criteria; $C_j, j=1,2,3)$ is shown in Table 3.

An element, $p_{ij},$of the performance matrix signifies the performance score of the “ith” alternative $A_i$concerning the “jth” criterion $C_j$.

4.1. Weightage to Each Criterion

The AHP methodology was employed to find the weights of the criteria used. A nine-point scale was used in the construction of a pairwise comparison matrix system. For three criteria, the pairwise comparison matrix $P_{3\times 3}$ was created as presented in Table 4. The architecture for the suggested AHP-MABAC approach was carried out to ensure that the evaluations were sufficiently trustworthy. In accordance with the order of the pairwise comparison matrix that was generated, the ${Cn}_R$ was decided. The obtained value of ${Cn}_R$ was 0.0079, which is below the maximum consistency limit of 10%, implying that the weights of the criteria that were determined were suitable for the analysis ranking. The AHP outcomes are shown in Table 5. The final obtained weights for ${Nu}_{RP}$, $f_{RP},$ and ${\eta }_{eff}$ were 0.540, 0.163, and 0.297, respectively.

Table 4. Pairwise comparison matrix.

ALTs	${\mathit{N}\mathit{u}}_{\mathit{R}\mathit{P}}$ (Cr-I)	${\mathit{f}}_{\mathit{R}\mathit{P}}$ (Cr-II)	${\mathit{\eta }}_{\mathit{e}\mathit{f}\mathit{f}}$ (Cr-III)
Cr-1	1	3	2
Cr-II	1/3	1	1/2
Cr-III	½	2	1

Table 5. Results of AHP.

Consistency Parameters	Weight
${\mathit{\lambda }}_{\mathit{m}\mathit{a}\mathit{x}}=3.009$	0.540
RI = 0.58	0.163
CR = 0.0079	0.297

4.2. Final Ranking of the Alternatives: The MABAC Approach

After obtaining the criteria’s weights using AHP, the MABAC technique was used to rank the ALTs according to how well they performed overall. The normalization of the constructed performance matrix was performed using Equation (13). Table 6 shows the normalized performance matrix. The weighted normalized matrix was obtained using Equation (14) and is shown in Table 7. Equation (15) was used to obtain the border approximation area matrix, which can be seen in Table 8. The distance of alternatives in the weighted normalized performance matrix was calculated using Equation (16). Finally, Equation (17) was used to obtain the total distance of each ALT from the estimated border area. This was used to find the ranking of alternatives; maximum ${\mathsf{\Psi }}_i$ value was ranked first while the alternative with the lowest ${\mathsf{\Psi }}_i$ value was ranked last as mentioned in Table 9.

Table 6. Normalized performance matrix.

	Cr-I	Cr-II	Cr-III
A-1	0.00000	0.66667	0.00000
A-2	0.24538	0.57471	0.26456
A-3	0.42730	0.52874	0.45775
A-4	0.33798	0.45977	0.35475
A-5	0.37462	0.47126	0.38434
A-6	0.66899	0.28736	0.62316
A-7	1.00000	0.14943	1.00000
A-8	0.93475	0.00000	0.86161
A-9	0.26819	0.58621	0.30735
A-10	0.52117	0.42529	0.53585
A-11	0.91405	0.24138	0.86748
A-12	0.73530	0.22989	0.71018
A-13	0.18277	0.79310	0.28226
A-14	0.38475	0.65517	0.42277
A-15	0.72474	0.66667	0.78420
A-16	0.61451	0.58621	0.61256
A-17	0.02386	1.00000	0.11413
A-18	0.16060	0.90805	0.22127
A-19	0.48971	0.48276	0.51918
A-20	0.41590	0.59770	0.44102
A-21	0.18351	0.68966	0.26857
A-22	0.46817	0.65517	0.52920
A-23	0.81734	0.35632	0.81843
A-24	0.73509	0.22989	0.69433
A-25	0.25393	0.66667	0.30432
A-26	0.42371	0.58621	0.45240
A-27	0.93169	0.26437	0.93825
A-28	0.77542	0.13793	0.77292
A-29	0.33999	0.68966	0.38860
A-30	0.50934	0.48276	0.53606
A-31	0.70647	0.28736	0.67165

Table 7. Weighted normalized performance matrix.

	Cr-I	Cr-II	Cr-III
A-1	0.54000	0.27167	0.29700
A-2	0.67251	0.25668	0.37558
A-3	0.77074	0.24918	0.43295
A-4	0.72251	0.23794	0.40236
A-5	0.74229	0.23982	0.41115
A-6	0.90125	0.20984	0.48208
A-7	1.08000	0.18736	0.59400
A-8	1.04476	0.16300	0.55290
A-9	0.68482	0.25855	0.38828
A-10	0.82143	0.23232	0.45615
A-11	1.03359	0.20234	0.55464
A-12	0.93706	0.20047	0.50792
A-13	0.63869	0.29228	0.38083
A-14	0.74777	0.26979	0.42256
A-15	0.93136	0.27167	0.52991
A-16	0.87183	0.25855	0.47893
A-17	0.55289	0.32600	0.33090
A-18	0.62672	0.31101	0.36272
A-19	0.80444	0.24169	0.45120
A-20	0.76459	0.26043	0.42798
A-21	0.63909	0.27541	0.37676
A-22	0.79281	0.26979	0.45417
A-23	0.98136	0.22108	0.54007
A-24	0.93695	0.20047	0.50322
A-25	0.67712	0.27167	0.38738
A-26	0.76881	0.25855	0.43136
A-27	1.04311	0.20609	0.57566
A-28	0.95873	0.18548	0.52656
A-29	0.72359	0.27541	0.41241
A-30	0.81505	0.24169	0.45621
A-31	0.92150	0.20984	0.49648

Table 8. Border approximation area matrix.

${\mathit{N}\mathit{u}}_{\mathit{R}\mathit{P}}$ (Cr-I)	${\mathit{f}}_{\mathit{R}\mathit{P}}$ (Cr-II)	${\mathit{\eta }}_{\mathit{e}\mathit{f}\mathit{f}}$ (Cr-III)
0.79172	0.22961	0.43380

Table 9. Distance of alternatives from border approximate area and ranking.

ALTs	Distance of Alternatives from Border Approximate Area			${\mathit{\psi }}_{\mathit{i}}$	Ranking
A-1	−0.25172	0.04206	−0.13680	−0.34646	31
A-2	−0.11921	0.02707	−0.05822	−0.15037	27
A-3	−0.02098	0.01957	−0.00085	−0.00225	19
A-4	−0.06921	0.00833	−0.03144	−0.09232	23
A-5	−0.04943	0.01021	−0.02265	−0.06187	22
A-6	0.10953	−0.01977	0.04828	0.13804	12
A-7	0.28828	−0.04225	0.16020	0.40623	1
A-8	0.25304	−0.06661	0.11910	0.30553	4
A-9	−0.10690	0.02894	−0.04552	−0.12348	25
A-10	0.02971	0.00271	0.02235	0.05477	15
A-11	0.24187	−0.02727	0.12084	0.33544	3
A-12	0.14534	−0.02914	0.07412	0.19033	8
A-13	−0.15303	0.06267	−0.05297	−0.14333	26
A-14	−0.04395	0.04018	−0.01124	−0.01501	20
A-15	0.13964	0.04206	0.09611	0.27780	6
A-16	0.08011	0.02894	0.04513	0.15419	11
A-17	−0.23883	0.09639	−0.10290	−0.24535	30
A-18	−0.16500	0.08140	−0.07108	−0.15468	28
A-19	0.01272	0.01208	0.01740	0.04220	16
A-20	−0.02713	0.03082	−0.00582	−0.00214	18
A-21	−0.15263	0.04580	−0.05704	−0.16386	29
A-22	0.00109	0.04018	0.02037	0.06165	13
A-23	0.18964	−0.00853	0.10627	0.28739	5
A-24	0.14523	−0.02914	0.06942	0.18550	9
A-25	−0.11460	0.04206	−0.04642	−0.11896	24
A-26	−0.02291	0.02894	−0.00244	0.00359	17
A-27	0.25139	−0.02352	0.14186	0.36973	2
A-28	0.16701	−0.04413	0.09276	0.21564	7
A-29	−0.06813	0.04580	−0.02139	−0.04371	21
A-30	0.02333	0.01208	0.02241	0.05782	14
A-31	0.12978	−0.01977	0.06268	0.17268	10

It is observed that the alternative A-7 has the highest value (0.40623), followed by A-27 (0.36973), and the alternative A-1 has the lowest value (−0.34646).

5. Conclusions

This research proposes an MCDM model to select the parameters of roughness in the form of SSRs. Thirty-one alternatives and three performance-deciding criteria were considered. No single alternative satisfied all the performance requirements simultaneously, so the MCDM model becomes very important in deciding the alternative leading to the best performance. According to the AHP-MABAC evaluation’s findings, having $P_R/e_{RH}$ of 8, $e_{RH}/D_{hd}$ of 0.043, ${\alpha }_{Arc}$ of 60°, and $W_{Duct}/w_{RS}$ of 3 is found to be the best. According to the results of the hybrid technique and previous experimental findings [30], the following conclusions are significant:

• The ${Nu}_{Rp}$ and $f_{Rp}$ of the STC are strongly affected by the characteristics of roughness.
• The presence of ribs creates turbulence, improving convective heat transmission by disturbing the thermal boundary layer and producing secondary vortices. Flow reattachment zones enhance the heat exchange efficiency. Nevertheless, heightened turbulence also elevates the friction factor, resulting in increased pressure losses. The optimization of the rib parameters ensures a balance between the enhancement of heat transmission and the resistance to flow. Comprehending these fluid flow principles is essential for the design of efficient STCs, minimizing energy losses, and enhancing the overall thermal performance.
• The STC with SSRs having parameters of $P_R/e_{RH}$ of 8, $e_{RH}/D_{hd}$ of 0.043, ${\alpha }_{Arc}$ of 60°, and $W_{Duct}/w_{RS}$ of 3 is considered the ideal design.
• For the best design/rank-1 alternative, the maximum value of ${\eta }_{eff}$ was obtained.
• It was discovered that the hybrid AHP-MABAC technique has the highest level of agreement between its analytical and experimental results.