FADEL: Ensemble Learning Enhanced by Feature Augmentation and Discretization
Abstract
1. Introduction
2. Related Works
2.1. Techniques for Handling Class Imbalance in Machine Learning
2.2. Feature Discretization and Optimal Interval Selection Methods
2.3. Ensemble Learning and Multi-Model Integration Strategies
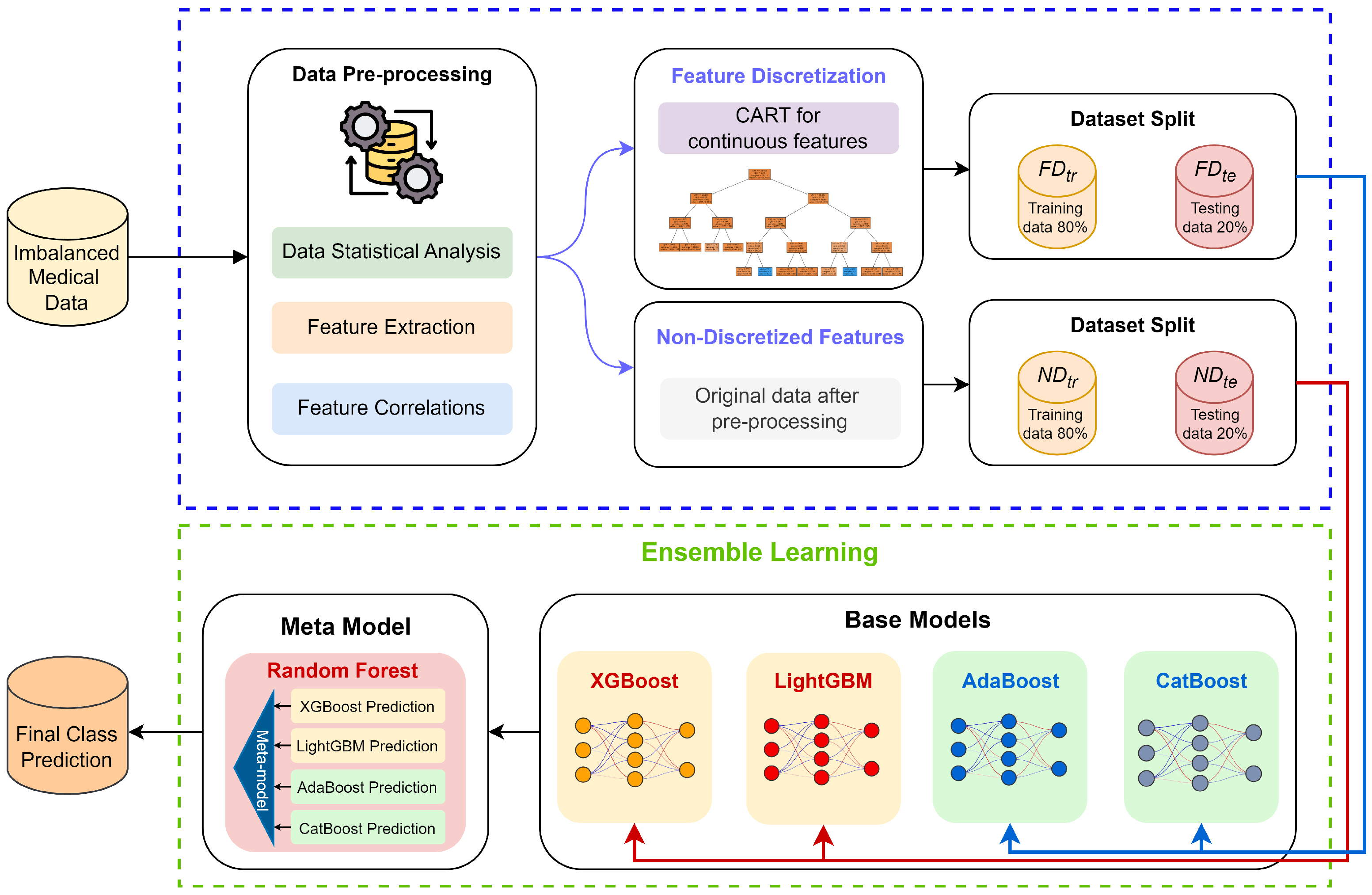
3. Methods
3.1. Framework Overview
3.2. Feature Discretization Based on CART Decision Tree
| Algorithm 1 CART-based Feature Discretization |
| Input: Continuous feature column , labels , max tree depth , max leaf nodes .
Output: Discretized feature indices .
|
3.3. Base Models Construction
| Algorithm 2 FADEL Base Models Construction |
| Input: Feature space , labels , dataset Output: Trained models
|
3.4. Ensemble Learning-Based Prediction
| Algorithm 3 FADEL Ensemble Learning-based Prediction |
| Input: Test sample ; trained base models ; Random Forest meta-model RF with T trees Output: Final prediction
|
4. Experimental Study
- Statistical Analysis
- Assessment Measures
- Base Models
4.1. Experiment on the Analysis of Non-Discretized Versus Feature Discretization Across the CGMH Test Set and KMUH Validation Set
4.2. Comparison of Predictive Performance of Ensemble Models Trained with Data-Level Augmentation Techniques
5. Discussion
6. Limitations and Future Work
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, H.; Garcia, E.A. Learning from Imbalanced Data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar] [CrossRef]
- Galar, M.; Fernandez, A.; Barrenechea, E.; Bustince, H.; Herrera, F. A Review on Ensembles for the Class Imbalance Problem: Bagging-, Boosting-, and Hybrid-Based Approaches. IEEE Trans. Syst. Man Cybern. C Appl. Rev. 2012, 42, 463–484. [Google Scholar] [CrossRef]
- Mathew, R.M.; Gunasundari, R. A Review on Handling Multiclass Imbalanced Data Classification in Education Domain. In Proceedings of the 2021 International Conference on Advance Computing and Innovative Technologies in Engineering (ICACITE), Greater Noida, India, 4–5 March 2021; pp. 752–755. [Google Scholar] [CrossRef]
- Su, Q.; Hamed, H.N.A.; Isa, M.A.; Hao, X.; Dai, X. A GAN-Based Data Augmentation Method for Imbalanced Multi-Class Skin Lesion Classification. IEEE Access 2024, 12, 16498–16513. [Google Scholar] [CrossRef]
- Edward, J.; Rosli, M.M.; Seman, A. A New Multi-Class Rebalancing Framework for Imbalance Medical Data. IEEE Access 2023, 11, 92857–92874. [Google Scholar] [CrossRef]
- Aftabi, S.Z.; Ahmadi, A.; Farzi, S. Fraud Detection in Financial Statements Using Data Mining and GAN Models. Expert Syst. Appl. 2023, 227, 120144. [Google Scholar] [CrossRef]
- Li, X.; Wu, X.; Wang, T.; Xie, Y.; Chu, F. Fault Diagnosis Method for Imbalanced Data Based on Adaptive Diffusion Models and Generative Adversarial Networks. Eng. Appl. Artif. Intell. 2025, 147, 110410. [Google Scholar] [CrossRef]
- Basha, S.J.; Madala, S.R.; Vivek, K.; Kumar, E.S.; Ammannamma, T. A Review on Imbalanced Data Classification Techniques. In Proceedings of the 2022 International Conference on Advanced Computing Technologies and Applications (ICACTA), Coimbatore, India, 4–5 March 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Salmi, M.; Atif, D.; Oliva, D.; Abraham, A.; Ventura, S. Handling Imbalanced Medical Datasets: Review of a Decade of Research. Artif. Intell. Rev. 2024, 57, 273. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-Sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive Synthetic Sampling Approach for Imbalanced Learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2014; Volume 27. [Google Scholar]
- Xu, L.; Skoularidou, M.; Cuesta-Infante, A.; Veeramachaneni, K. Modeling Tabular Data Using Conditional GAN. In Advances in Neural Information Processing Systems; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Chen, W.; Yang, K.; Yu, Z.; Shi, Y.; Chen, C.L.P. A Survey on Imbalanced Learning: Latest Research, Applications and Future Directions. Artif. Intell. Rev. 2024, 57, 137. [Google Scholar] [CrossRef]
- Johnson, J.M.; Khoshgoftaar, T.M. Survey on Deep Learning with Class Imbalance. J. Big Data 2019, 6, 27. [Google Scholar] [CrossRef]
- Pavlyshenko, B. Using Stacking Approaches for Machine Learning Models. In Proceedings of the 2018 IEEE Second International Conference on Data Stream Mining & Processing (DSMP), Lviv, Ukraine, 21–25 August 2018; pp. 255–258. [Google Scholar] [CrossRef]
- Lu, M.; Hou, Q.; Qin, S.; Zhou, L.; Hua, D.; Wang, X.; Cheng, L. A Stacking Ensemble Model of Various Machine Learning Models for Daily Runoff Forecasting. Water 2023, 15, 1265. [Google Scholar] [CrossRef]
- Ghasemieh, A.; Lloyed, A.; Bahrami, P.; Vajar, P.; Kashef, R. A Novel Machine Learning Model with Stacking Ensemble Learner for Predicting Emergency Readmission of Heart-Disease Patients. Decis. Anal. J. 2023, 7, 100242. [Google Scholar] [CrossRef]
- Loch-Olszewska, H.; Szwabiński, J. Impact of Feature Choice on Machine Learning Classification of Fractional Anomalous Diffusion. Entropy 2020, 22, 1436. [Google Scholar] [CrossRef]
- van der Walt, C.M.; Barnard, E. Data Characteristics That Determine Classifier Performance. SAIEE Afr. Res. J. 2007, 98, 87–93. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’16), San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st Conference on Neural Information Processing Systems (NeurIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 3149–3157. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased Boosting with Categorical Features. In Proceedings of the 32nd International Conference on Neural Information Processing Systems (NeurIPS 2018), Montréal, QC, Canada, 3–8 December 2018; Curran Associates Inc.: Red Hook, NY, USA; pp. 6639–6649. [Google Scholar]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Mujahid, M.; Kına, E.; Rustam, F.; Villar, M.G.; Alvarado, E.S.; Diez, I.D.L.T.; Ashraf, I. Data Oversampling and Imbalanced Datasets: An Investigation of Performance for Machine Learning and Feature Engineering. J. Big Data 2024, 11, 87. [Google Scholar] [CrossRef]
- Wang, S.; Dai, Y.; Shen, J.; Xuan, J. Research on Expansion and Classification of Imbalanced Data Based on SMOTE Algorithm. Sci. Rep. 2021, 11, 24039. [Google Scholar] [CrossRef]
- Alkhawaldeh, I.M.; Albalkhi, I.; Naswhan, A.J. Challenges and Limitations of Synthetic Minority Oversampling Techniques in Machine Learning. World J. Methodol. 2023, 13, 373–378. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, M.; Khushi, M. SMOTE-ENC: A Novel SMOTE-Based Method to Generate Synthetic Data for Nominal and Continuous Features. Appl. Syst. Innov. 2021, 4, 18. [Google Scholar] [CrossRef]
- Zhu, T.; Liu, X.; Zhu, E. Oversampling with Reliably Expanding Minority Class Regions for Imbalanced Data Learning. IEEE Trans. Knowl. Data Eng. 2023, 35, 6167–6181. [Google Scholar] [CrossRef]
- Majeed, A.; Hwang, S.O. CTGAN-MOS: Conditional Generative Adversarial Network Based Minority-Class-Augmented Oversampling Scheme for Imbalanced Problems. IEEE Access 2023, 11, 85878–85899. [Google Scholar] [CrossRef]
- Yan, Y.; Zhu, Y.; Liu, R.; Zhang, Y.; Zhang, Y.; Zhang, L. Spatial Distribution-Based Imbalanced Undersampling. IEEE Trans. Knowl. Data Eng. 2023, 35, 6376–6391. [Google Scholar] [CrossRef]
- Wang, Z.; Cao, C.; Zhu, Y. Entropy and Confidence-Based Undersampling Boosting Random Forests for Imbalanced Problems. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 5178–5191. [Google Scholar] [CrossRef] [PubMed]
- Arefeen, M.A.; Nimi, S.T.; Rahman, M.S. Neural Network-Based Undersampling Techniques. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1111–1120. [Google Scholar] [CrossRef]
- Liu, H.; Hussain, F.; Tan, C.L.; Dash, M. Discretization: An Enabling Technique. Data Min. Knowl. Discov. 2002, 6, 393–423. [Google Scholar] [CrossRef]
- Rajbahadur, G.K.; Wang, S.; Kamei, Y.; Hassan, A.E. Impact of Discretization Noise of the Dependent Variable on Machine Learning Classifiers in Software Engineering. IEEE Trans. Softw. Eng. 2021, 47, 1414–1430. [Google Scholar] [CrossRef]
- García, S.; Luengo, J.; Sáez, J.A.; López, V.; Herrera, F. A Survey of Discretization Techniques: Taxonomy and Empirical Analysis in Supervised Learning. IEEE Trans. Knowl. Data Eng. 2013, 25, 734–750. [Google Scholar] [CrossRef]
- Thaiphan, R.; Phetkaew, T. Comparative Analysis of Discretization Algorithms on Decision Tree. In Proceedings of the 2018 IEEE/ACIS 17th International Conference on Computer and Information Science (ICIS), Singapore, 12–14 June 2018; pp. 63–67. [Google Scholar] [CrossRef]
- Xie, Z.-H.; Wu, W.-Z.; Wang, L.-X. Optimal Scale Selection in Multi-Scale Interval-Set Decision Tables. In Proceedings of the 2023 International Conference on Machine Learning and Cybernetics (ICMLC), Adelaide, Australia, 9–12 December 2023; pp. 310–314. [Google Scholar] [CrossRef]
- Liu, X.; Wang, H. A Discretization Algorithm Based on a Heterogeneity Criterion. IEEE Trans. Knowl. Data Eng. 2005, 17, 1166–1173. [Google Scholar] [CrossRef]
- Alazaidah, R. A Comparative Analysis of Discretization Techniques in Machine Learning. In Proceedings of the 2023 24th International Arab Conference on Information Technology (ACIT), Ajman, United Arab Emirates, 18–20 December 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Blessie, E.C.; Karthikeyan, E. RELIEF-DISC: An Extended RELIEF Algorithm Using Discretization Approach for Continuous Features. In Proceedings of the 2011 Second International Conference on Emerging Applications of Information Technology (EAIT), Kolkata, India, 19–20 February 2011; pp. 161–164. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, L.; Wei, B. Imbalanced Data Classification Based on Improved Random-SMOTE and Feature Standard Deviation. Mathematics 2024, 12, 1709. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble Learning: A Survey. WIREs Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Mienye, I.D.; Sun, Y. A Survey of Ensemble Learning: Concepts, Algorithms, Applications, and Prospects. IEEE Access 2022, 10, 99129–99149. [Google Scholar] [CrossRef]
- Altalhan, M.; Algarni, A.; Turki-Hadj Alouane, M. Imbalanced Data Problem in Machine Learning: A Review. IEEE Access 2025, 13, 13686–13699. [Google Scholar] [CrossRef]
- Zhu, T.; Hu, X.; Liu, X.; Zhu, E.; Zhu, X.; Xu, H. Dynamic Ensemble Framework for Imbalanced Data Classification. IEEE Trans. Knowl. Data Eng. 2025, 37, 2456–2471. [Google Scholar] [CrossRef]
- Iosifidis, V.; Papadopoulos, S.; Rosenhahn, B.; Ntoutsi, E. AdaCC: Cumulative Cost-Sensitive Boosting for Imbalanced Classification. Knowl. Inf. Syst. 2023, 65, 789–826. [Google Scholar] [CrossRef]
- Maki, H.; Maki, Y.; Shimamura, Y.; Fukaya, N.; Ozawa, Y.; Shibamoto, Y. Differentiation of Kawasaki disease from other causes of fever and cervical lymphadenopathy: A diagnostic scoring system using contrast-enhanced CT. Am. J. Roentgenol. 2019, 212, 665–671. [Google Scholar] [CrossRef]
- Lam, J.Y.; Chen, Z.; Wang, X.; Liu, Y.; Sun, L.; Gong, F. A machine-learning algorithm for diagnosis of multisystem inflammatory syndrome in children and Kawasaki disease in the USA: A retrospective model development and validation study. Lancet Digit. Health 2022, 4, e717–e726. [Google Scholar] [CrossRef]
- Xu, E.; Nemati, S.; Tremoulet, A.H. A deep convolutional neural network for Kawasaki disease diagnosis. Sci. Rep. 2022, 12, 11438. [Google Scholar] [CrossRef]
- Li, C.; Liu, Y.; Liu, D.; Wang, W.; Wang, J.; Hu, Y. A machine learning model for distinguishing Kawasaki disease from sepsis. Sci. Rep. 2023, 13, 12553. [Google Scholar] [CrossRef]
- Portman, M.A.; Magaret, C.A.; Barnes, G.; Peters, C.; Rao, A.; Rhyne, R. An artificial intelligence derived blood test to diagnose Kawasaki disease. Hosp. Pediatr. 2023, 13, 201–210. [Google Scholar] [CrossRef]
- Fabi, M.; Dondi, A.; Andreozzi, L.; Frazzoni, L.; Biserni, G.B.; Ghiazza, F.; Dajti, E.; Zagari, R.M.; Lanari, M. Kawasaki disease, multisystem inflammatory syndrome in children, and adenoviral infection: A scoring system to guide differential diagnosis. Eur. J. Pediatr. 2023, 182, 4889–4895. [Google Scholar] [CrossRef]



| Notations | Mathematical Meanings | Notations | Mathematical Meanings |
|---|---|---|---|
| Feature-discretized training dataset | Feature-discretized testing dataset | ||
| Non-discretized (original) training dataset | Non-discretized (original) testing dataset | ||
| Input feature space | Label space | ||
| Complete dataset | T | Number of trees in the Random Forest meta-model | |
| Non-discretized feature projection function | Discretized feature projection function | ||
| Non-discretized feature vector | Discretized feature vector | ||
| Mapping function of the m-th base learner | Raw output score of the m-th base learner | ||
| Predicted probability of the m-th base learner | p | Vector of base learners’ predicted probabilities | |
| Final predicted label | Output value function of tree t | ||
| Region of the l-th leaf node in tree t | k-th threshold of the j-th feature | ||
| Number of intervals for discretizing the j-th feature | Discretization mapping function | ||
| k-th interval of the j-th feature | Max number of leaf nodes in CART for feature j | ||
| Max depth of the CART tree for feature j | Second-order Hessian of the loss function | ||
| First-order gradient of the loss function | Split penalty term in XGBoost and LightGBM | ||
| L2 regularization in XGBoost and LightGBM | Empirical risk of the m-th base learner | ||
| Loss function (e.g., logistic loss) | AdaBoost weight of sample i at iteration t | ||
| AdaBoost weight of the t-th weak learner | Sigmoid function |
| Kaohsiung Chang Gung Memorial Hospital (N = 79,400) | Kaohsiung Medical University Chung-Ho Memorial Hospital (N = 1582) | |||||||
|---|---|---|---|---|---|---|---|---|
| Characteristics |
Children with KD (N = 1230) |
Febrile Controls (N = 78,170) |
Odds Ratio (95% CI) | p -Value |
Children with KD (N = 62) |
Febrile Controls (N = 1520) |
Odds Ratio (95% CI) | p -Value |
| Birth, mean (SD) | ||||||||
| Age, y | 1.2 (1.2) | 1.8 (1.6) | 0.603 (0.563–0.646) | <0.001 | 2.4 (2.5) | 3.1 (1.9) | 0.832 (0.696–0.995) | 0.002 |
| Gender, No. (%) | ||||||||
| Male | 746 (60.7%) | 44,037 (56.3%) | 0.555 (0.482–0.639) | 0.002 | 40 (64.5%) | 1020 (67.1%) | 0.951 (0.504–1.797) | 0.431 |
| Blood, mean (SD) | ||||||||
| RBC, µL | 4.3 (0.4) | 4.5 (0.6) | 0.197 (0.091–0.423) | <0.001 | 4.4 (0.5) | 4.6 (0.5) | 69.5 (1.66–2909.689) | 0.042 |
| WBC, µL | 14.1 (5.2) | 10.8 (5.9) | 1.001 (0.988–1.014) | <0.001 | 13.6 (5.6) | 10.1 (5.3) | 0.947 (0.888–1.01) | <0.001 |
| Hemoglobin, g/dL | 11.1 (1.1) | 12 (1.8) | 1.44 (0.863–2.403) | <0.001 | 11.3 (1.2) | 12.0 (1.1) | 1.55 (0.898–2.805) | <0.001 |
| Hematocrit, % | 33.4 (3.1) | 35.6 (4.9) | 1.069 (0.883–1.295) | <0.001 | 34.2 (2.9) | 35.8 (2.9) | 0.057 (0.005–0.648) | <0.001 |
| MCH, pg/cell | 25.7 (2.3) | 27.1 (3.5) | 0.623 (0.541–0.719) | <0.001 | 25.7 (3.2) | 26.5 (2.5) | 2.258 (1.082–4.711) | 0.007 |
| MCHC, g/dL | 33.3 (1.1) | 33.6 (1.2) | 0.954 (0.776–1.173) | <0.001 | 33.1 (1.3) | 33.5 (1.1) | 0.044 (0.003–0.58) | <0.001 |
| RDW | 13.4 (1.4) | 14.1 (2.1) | 0.665 (0.633–0.7) | <0.001 | 13.6 (1.4) | 13.3 (1.7) | 0.843 (0.655–1.084) | 0.072 |
| Platelets, µL | 350.1 (125.8) | 294.2 (125) | 1.002 (1.001–1.003) | <0.001 | 324.6 (119.1) | 263.7 (90.7) | 1.004 (1.001–1.008) | <0.001 |
| Neutrophils-segments, % | 56.3 (15.4) | 49.3 (19.9) | 1.186 (1.147–1.227) | <0.001 | 58.2 (18.0) | 57.9 (19.3) | 0.981 (0.924–1.04) | 0.9 |
| Neutrophils-bands, % | 1.6 (3.2) | 0.7 (2.1) | 1.232 (1.182–1.283) | <0.001 | 4.8 (7.2) | 2.8 (6.2) | 0.957 (0.887–1.034) | 0.007 |
| Lymphocyte, % | 32.1 (13.9) | 38.3 (18.3) | 1.156 (1.116–1.196) | <0.001 | 26.3 (13.8) | 29.5 (16.6) | 0.972 (0.913–1.035) | 0.114 |
| Monocyte, % | 6.8 (3.4) | 8.4 (4.3) | 1.039 (0.998–1.081) | <0.001 | 6.8 (3.3) | 8.1 (3.6) | 0.934 (0.844–1.034) | 0.004 |
| Eosinophils, % | 2.5 (2.7) | 1.8 (2.9) | 1.325 (1.275–1.376) | <0.001 | 2.5 (2.7) | 0.8 (1.6) | 1.2 (1.071–1.345) | <0.001 |
| Basophils, % | 0.2 (0.4) | 0.3 (0.4) | 1.175 (1.026–1.347) | 0.006 | 0.2 (0.4) | 0.3 (0.4) | 0.851 (0.394–1.836) | 0.345 |
| AST, U/L | 77.9 (117.1) | 51 (130.6) | 0.997 (0.997–0.998) | <0.001 | 84.0 (102.0) | 42.5 (31.9) | 0.991 (0.986–0.997) | <0.001 |
| ALT, U/L | 76.0 (108.3) | 34.6 (78.9) | 1.005 (1.004–1.006) | <0.001 | 91.0 (127.8) | 21.0 (24.6) | 1.021 (1.013–1.029) | <0.001 |
| CRP, mg/dL | 74.9 (61.5) | 20.1 (32.8) | 1.015 (1.014–1.017) | <0.001 | 79.9 (49.5) | 23.4 (34.8) | 1.022 (1.016–1.028) | <0.001 |
| Urine, mean (SD) | ||||||||
| WBC count in urine, count/hpf | 54.3 (101.6) | 49.9 (66.8) | 0.992 (0.991–0.993) | 0.023 | 11.3 (21.9) | 4.5 (13.9) | 0.986 (0.968–1.004) | <0.001 |
| Urine, No. (%) | ||||||||
| Pyuria | 526 (42.8%) | 5416 (6.9%) | 0.093 (0.079–0.108) | <0.001 | 22 (31.9%) | 195 (10.2%) | 2.604 (1.09–6.219) | <0.001 |
| Notation | Parameter Description | Value |
|---|---|---|
| Feature-Discretization Parameters | ||
| Maximum depth of the CART tree for discretizing feature j | 3 | |
| Maximum number of leaf nodes in the CART tree for feature j | 8 | |
| Split Criterion | Criterion used to measure the quality of a split | Gini impurity |
| Minimum Samples per Leaf | Minimum number of samples required to be at a leaf node | 5 |
| Minimum Samples per Split | Minimum number of samples required to split an internal node | 2 |
| Ensemble Learning Model Parameters | ||
| Random Forest Meta-model | ||
| T | Number of trees in Random Forest meta-model | 100 |
| XGBoost and LightGBM Base models | ||
| Split penalty term in XGBoost and LightGBM | 0 | |
| L2 regularization parameter in XGBoost and LightGBM | 1 | |
| CatBoost Base model | ||
| Number of boosting iterations in CatBoost | 100 | |
| Learning rate in CatBoost | 0.1 | |
| Maximum depth of trees in CatBoost | 6 | |
| AdaBoost Base model | ||
| Number of estimators in AdaBoost | 50 | |
| Learning rate in AdaBoost | 1 | |
| Metric | Kaohsiung Chang Gung Memorial Hospital KD Test Set | Kaohsiung Medical University Chung-Ho Memorial Hospital KD Validation Set | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Non-Discretized
(Original Data) |
Feature-Discretized
(Feature Augmentation) |
Non-Discretized
(Original Data) |
Feature-Discretized
(Feature Augmentation) | |||||||||
| XGBoost | LightGBM |
Stacking
Model | CatBoost |
Stacking
Model |
FADEL
Model | XGBoost | LightGBM |
Stacking
Model | CatBoost |
Stacking
Model |
FADEL
Model | |
| Recall/Sensitivity (%) | 84.7 | 80.8 | 80.8 | 90.4 | 91.3 | 90.8 | 82.3 | 80.6 | 80.6 | 85.5 | 96.8 | 91.9 |
| F1 Score (%) | 67.1 | 63.6 | 70.0 | 57.6 | 58.5 | 61.7 | 31.6 | 31.3 | 42.4 | 29.7 | 17.8 | 28.9 |
| G-mean (%) | 91.6 | 89.4 | 89.5 | 94.1 | 94.6 | 94.5 | 84.2 | 83.5 | 86.0 | 84.8 | 78.5 | 86.7 |
| Specificity (%) | 99.0 | 98.9 | 99.2 | 98.1 | 98.1 | 98.4 | 86.2 | 86.4 | 91.8 | 84.1 | 63.7 | 81.9 |
| Feature | Kaohsiung Chang Gung Memorial Hospital KD Training Set | Kaohsiung Medical University Chung-Ho Memorial Hospital KD Validation Set | ||
|---|---|---|---|---|
|
Non-
Discretized (Original Data) |
Feature-
Discretized (Feature Augmentation) |
Non-
Discretized (Original Data) |
Feature-
Discretized (Feature Augmentation) | |
| WBC | 11.10 | 0.30 | 1.36 | 0.51 |
| RBC | −0.31 | 0.50 | 0.81 | 1.29 |
| Hemoglobin | 0.96 | 0.06 | −0.64 | 0.04 |
| Hematocrit | 0.88 | 0.39 | −0.51 | 0.34 |
| MCH | 0.30 | 0.74 | −1.81 | 0.68 |
| MCHC | −0.68 | −0.25 | −0.54 | −0.16 |
| RDW | 2.11 | 1.16 | 3.84 | 2.23 |
| Platelets | 1.09 | −0.23 | 1.07 | 0.11 |
| Segment | −0.07 | −0.66 | −0.39 | −1.09 |
| Band | 6.25 | 1.32 | 3.06 | 1.03 |
| Lymphocyte | 0.28 | 0.87 | 0.67 | 1.68 |
| Monocyte | 1.74 | −0.07 | 1.08 | −0.17 |
| Eosinophil | 4.15 | 0.25 | 10.19 | 1.06 |
| Basophil | 6.53 | 1.38 | 4.44 | 1.47 |
| AST | 114.53 | 0.84 | 18.85 | 1.77 |
| ALT | 78.73 | 3.67 | 10.20 | 4.10 |
| CRP | 3.76 | 1.62 | 2.92 | 1.32 |
| UWBC | 5.35 | −1.26 | 5.29 | 3.30 |
| Metric | Kaohsiung Chang Gung Memorial Hospital KD Test Set | Kaohsiung Medical University Chung-Ho Memorial Hospital KD Validation Set | ||||||
|---|---|---|---|---|---|---|---|---|
|
Non-Discretized (Original Data) |
Feature-Discretized
(Feature Augmentation) |
Non-Discretized (Original Data) |
Feature-Discretized (Feature Augmentation) | |||||
| XGBoost |
Stacking Model |
Stacking Model |
FADEL Model | XGBoost |
Stacking Model |
Stacking Model |
FADEL Model | |
| Recall/Sensitivity (%) | 80.8 | 96.1 | 97.4 | 95.6 | 80.6 | 85.5 | 91.9 | 90.3 |
| F1 Score (%) | 69.7 | 47.1 | 40.2 | 47.8 | 40.2 | 32.8 | 19.5 | 27.5 |
| G-mean (%) | 89.5 | 96.4 | 96.4 | 96.2 | 85.7 | 85.9 | 79.8 | 85.6 |
| Specificity (%) | 99.2 | 96.7 | 95.5 | 96.8 | 91.0 | 86.3 | 69.3 | 80.9 |
| Authors | Method | Study Population | KD Datasets N (Positive, Negative) | Sensitivity | Specificity | G-Mean |
|---|---|---|---|---|---|---|
| Maki et al., 2018 [48] | Logistic Regression | Japan | 129 (37, 92) | 86% | 86% | 86% |
| Lam et al., 2022 [49] | Feedforward Neural Networks | USA | 1517 (775, 742) | 92% | 95% | 93% |
| Xu et al., 2022 [50] | Convolutional Neural Network | - | 2035 (1023, 1012) | 80% | 85% | 82% |
| Li et al., 2023 [51] | Logistic Regression | China | 608 (299, 309) | 86% | 84% | 84% |
| Portman et al., 2023 [52] | Least-Angle Regression | USA | 150 (50, 100) | 92% | 86% | 88% |
| Fabi et al., 2023 [53] | Clinical Score and Clinic-Lab Score | Italy | 90 (34, 56) | 98% | 83% | 90% |
| FADEL | Ensemble Learning with Feature Augmentation | Taiwan | 79,400 (1230, 78,170) | 91% | 98% | 95% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hung, C.-S.; Lin, C.-H.R.; Chen, S.-H.; Zheng, Y.-C.; Yu, C.-H.; Hung, C.-W.; Huang, T.-H.; Tsai, J.-H. FADEL: Ensemble Learning Enhanced by Feature Augmentation and Discretization. Bioengineering 2025, 12, 827. https://doi.org/10.3390/bioengineering12080827
Hung C-S, Lin C-HR, Chen S-H, Zheng Y-C, Yu C-H, Hung C-W, Huang T-H, Tsai J-H. FADEL: Ensemble Learning Enhanced by Feature Augmentation and Discretization. Bioengineering. 2025; 12(8):827. https://doi.org/10.3390/bioengineering12080827
Chicago/Turabian StyleHung, Chuan-Sheng, Chun-Hung Richard Lin, Shi-Huang Chen, You-Cheng Zheng, Cheng-Han Yu, Cheng-Wei Hung, Ting-Hsin Huang, and Jui-Hsiu Tsai. 2025. "FADEL: Ensemble Learning Enhanced by Feature Augmentation and Discretization" Bioengineering 12, no. 8: 827. https://doi.org/10.3390/bioengineering12080827
APA StyleHung, C.-S., Lin, C.-H. R., Chen, S.-H., Zheng, Y.-C., Yu, C.-H., Hung, C.-W., Huang, T.-H., & Tsai, J.-H. (2025). FADEL: Ensemble Learning Enhanced by Feature Augmentation and Discretization. Bioengineering, 12(8), 827. https://doi.org/10.3390/bioengineering12080827









