Unveiling Asymptotic Behavior in Precipitation Time Series: A GARCH-Based Second Order Semi-Parametric Autocorrelation Framework for Drought Monitoring in the Semi-Arid Region of India
Abstract
1. Introduction
- (1)
- examine zero autocorrelation coefficients using the second-order semi-parametric eigenfunction eigendecomposition algorithm;
- (2)
- implement the GARCH model to analyze the temporal volatility, persistence, and extreme events of drought conditions;
- (3)
- compare ten drought indices to assess the severity and duration of historical drought events across multiple timescales;
- (4)
- analyze the temporal lagged association between meteorological and agricultural droughts.
2. Study Area
3. Materials and Methods
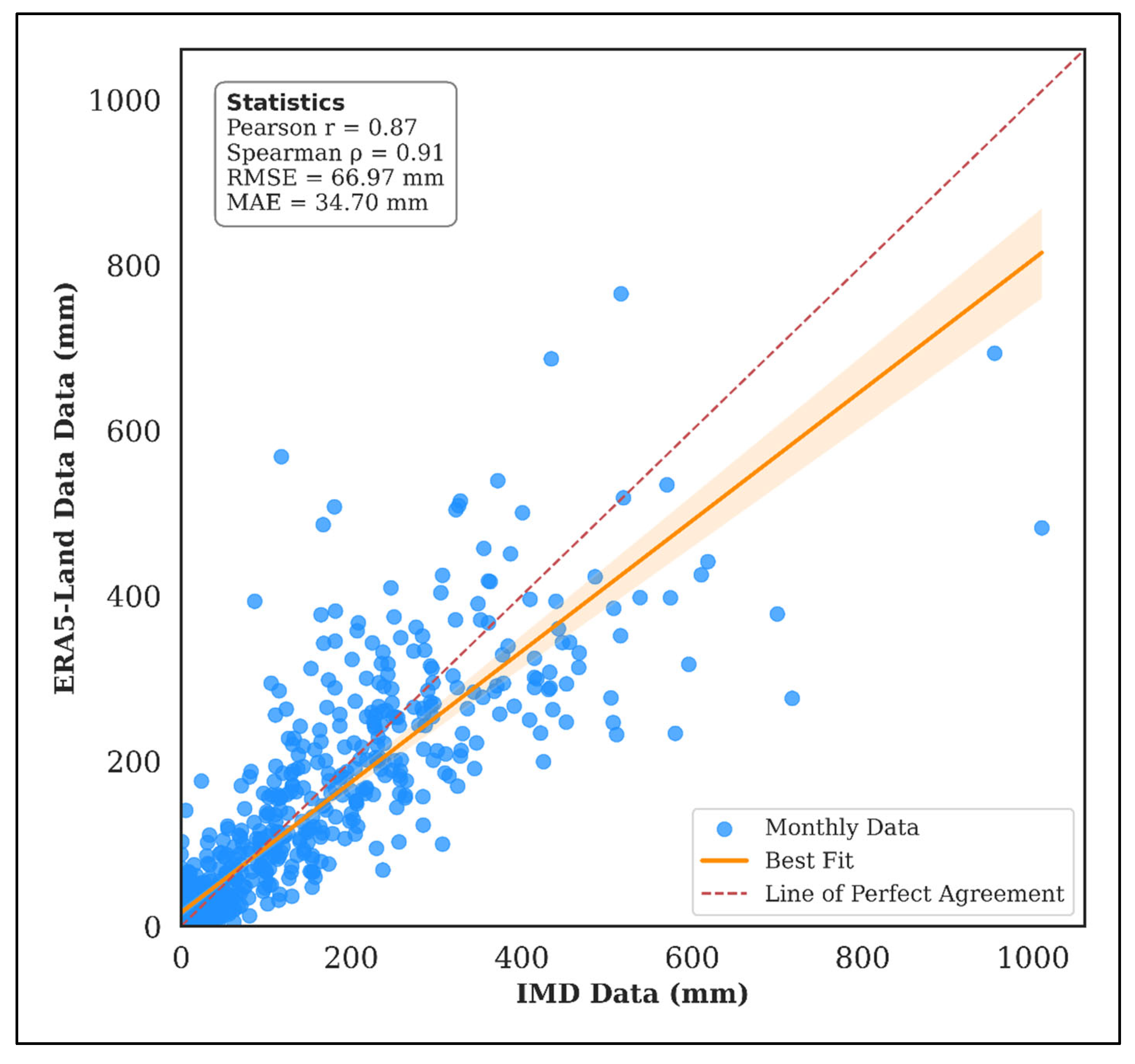
3.1. Data Collection
3.2. Second Order Eigenfunction Eigendecompostion Geospatial Autocorrelation
3.3. Generalized Autoregressive Conditional Heteroscedastic (GARCH) Model
3.4. Drought Indices
3.5. Comparison of Drought Indices Based on Non-Parametric Spearman’s Rank Correlation Coefficient
3.6. Drought Indices Performance Based on Severity, Time Period, and Statistical Criteria
3.7. Non-Parametric Spearman’s Cross-Correlation Function (SCCF)
4. Results and Discussion
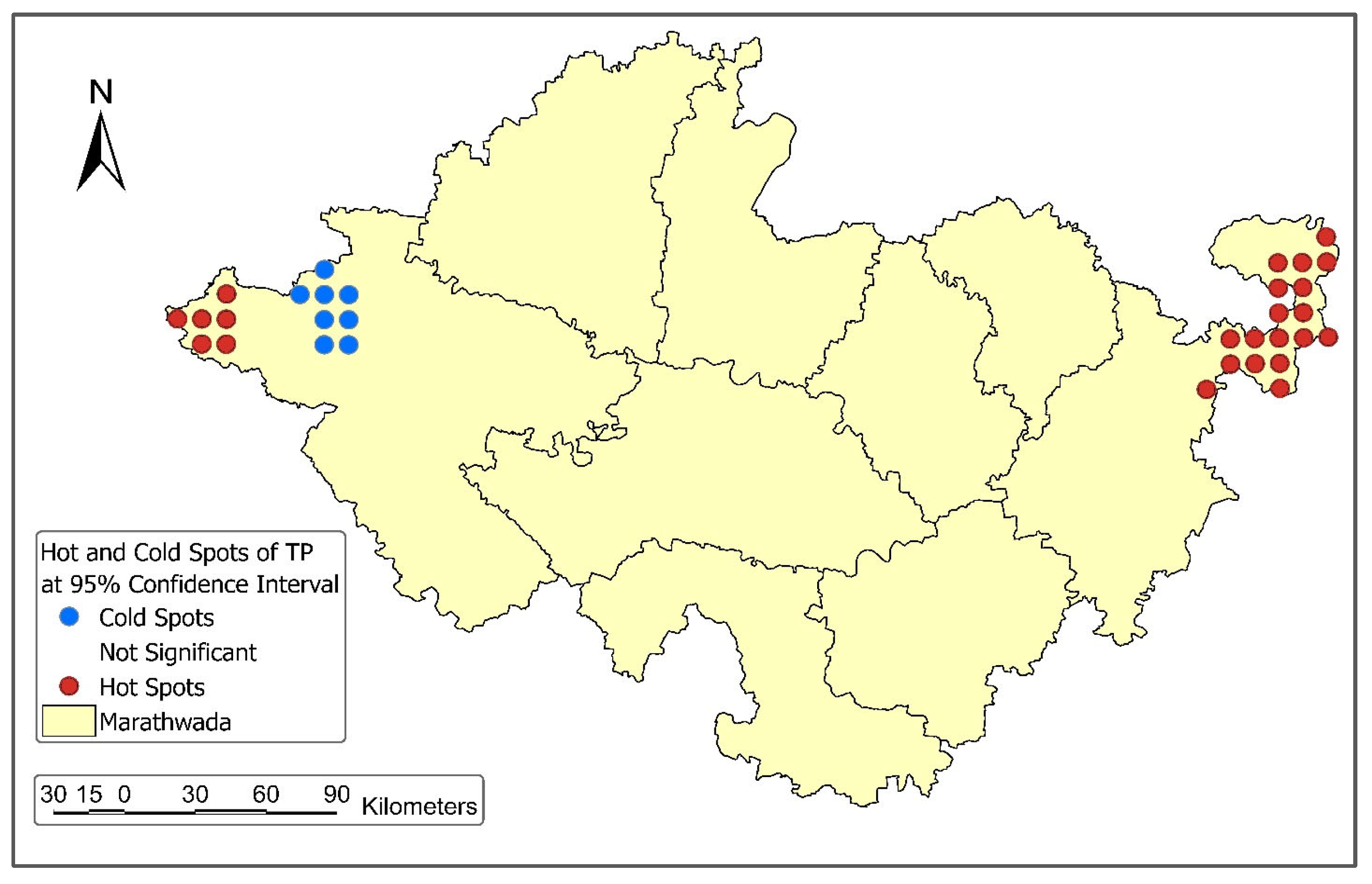
4.1. Spatial Clustering of Total Precipitation Patterns
4.2. Temporal Volatility Dynamics of Total Precipitation
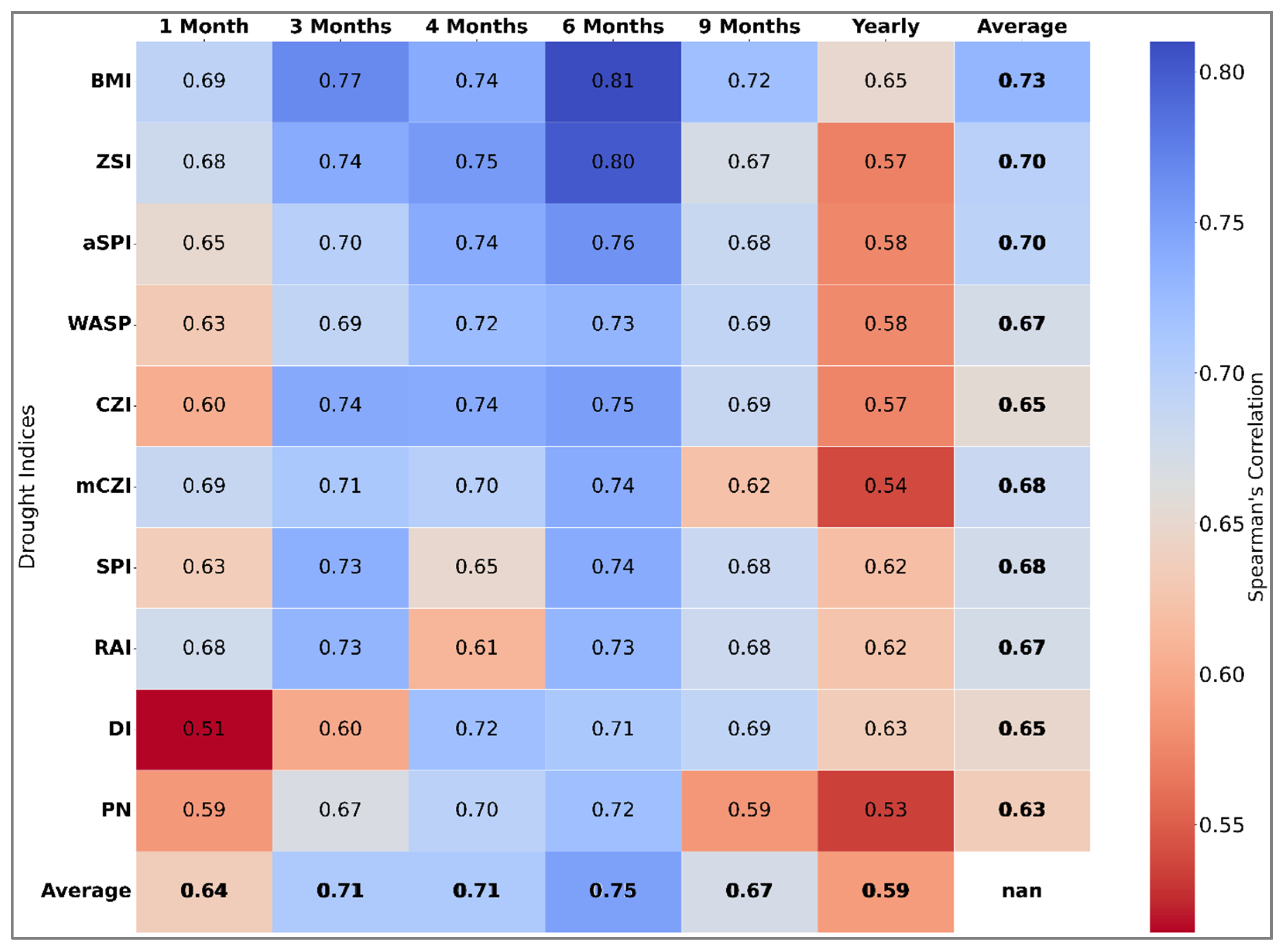
4.3. Comparison of Drought Indices Using Spearman Correlation
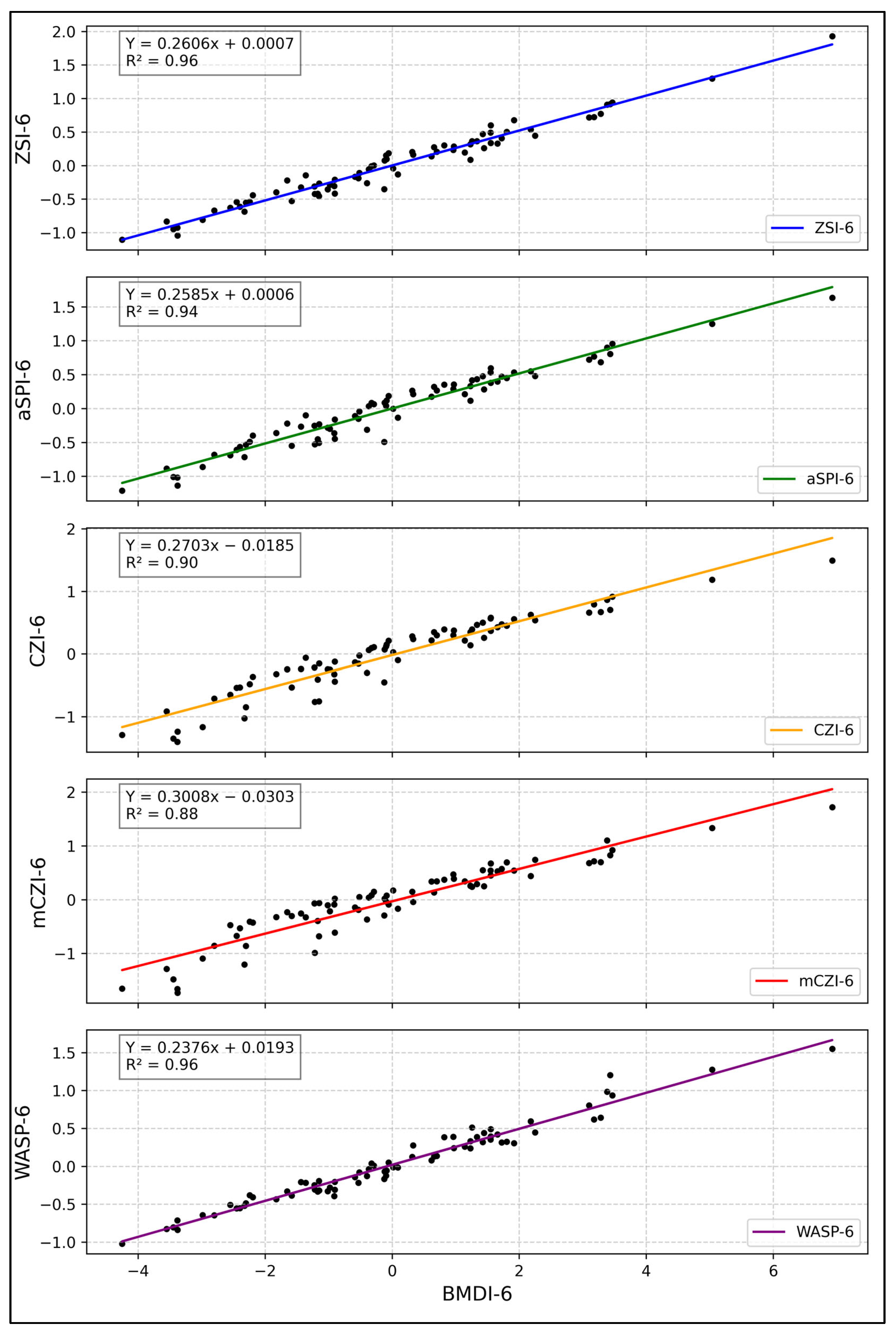
4.4. Evaluation of Drought Indices Using Statistical Performance
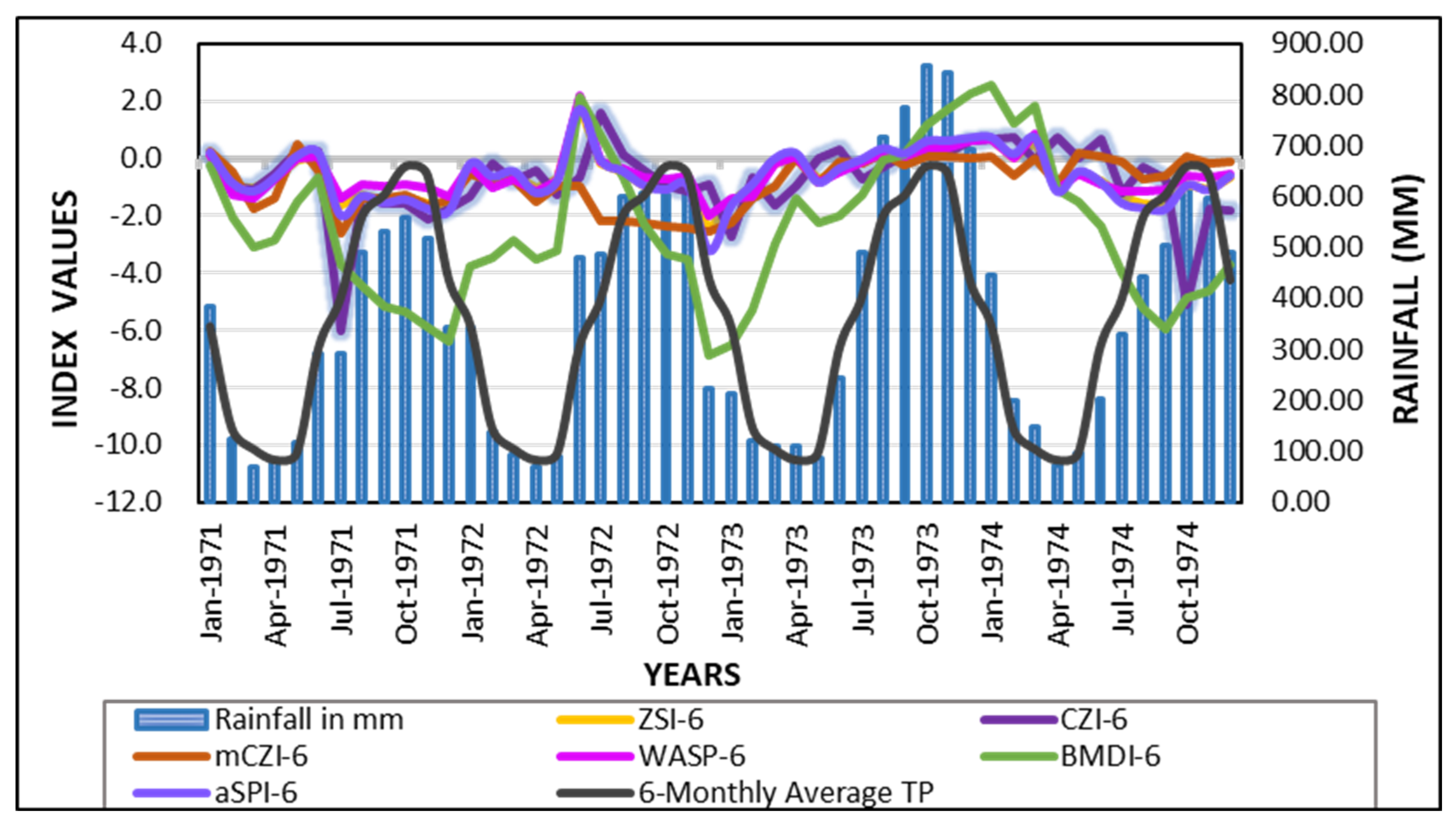
4.5. Evaluation of Drought Indices Using Historical Events
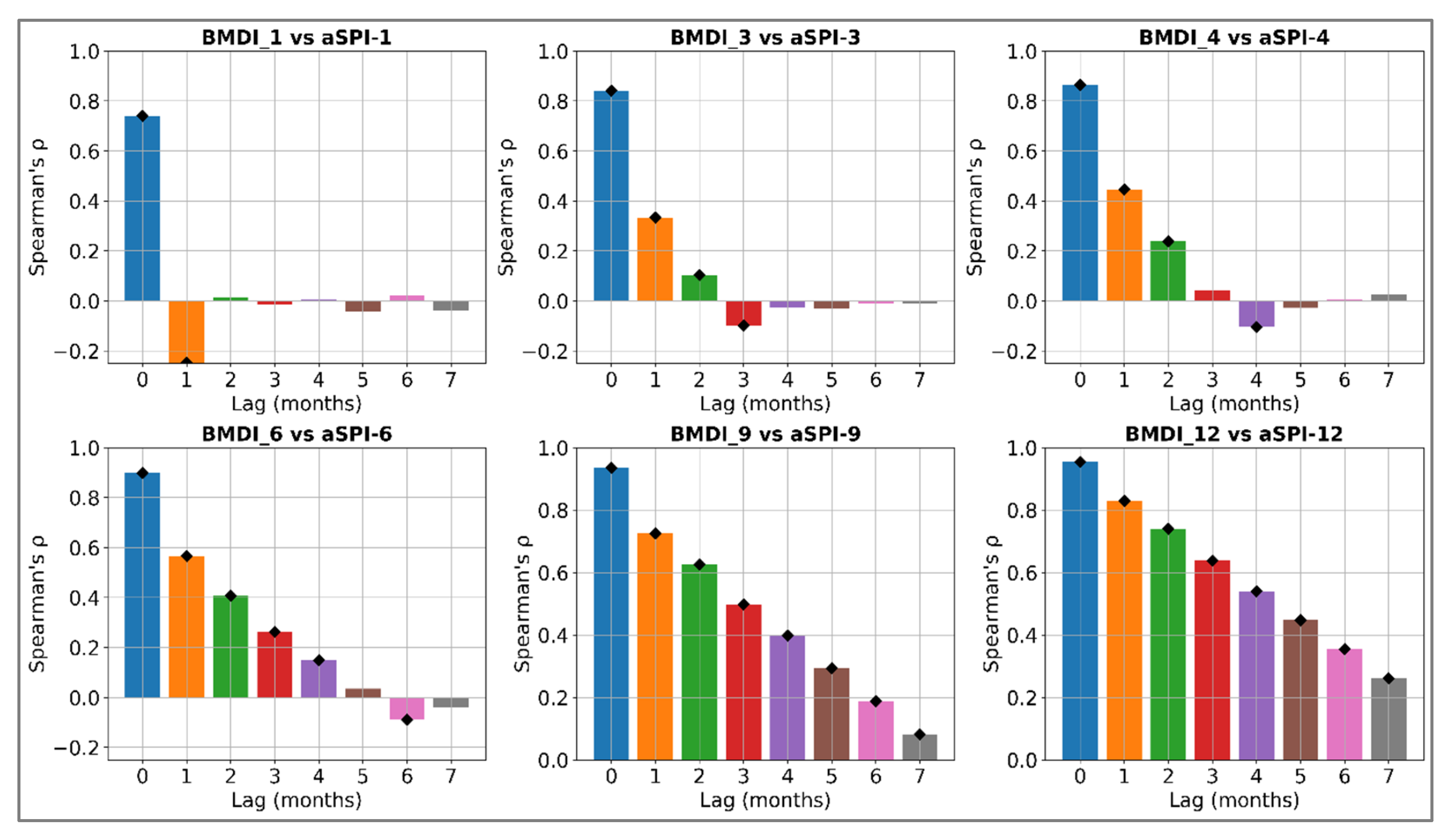
4.6. Time Lag Association Between Meteorological and Agricultural Droughts
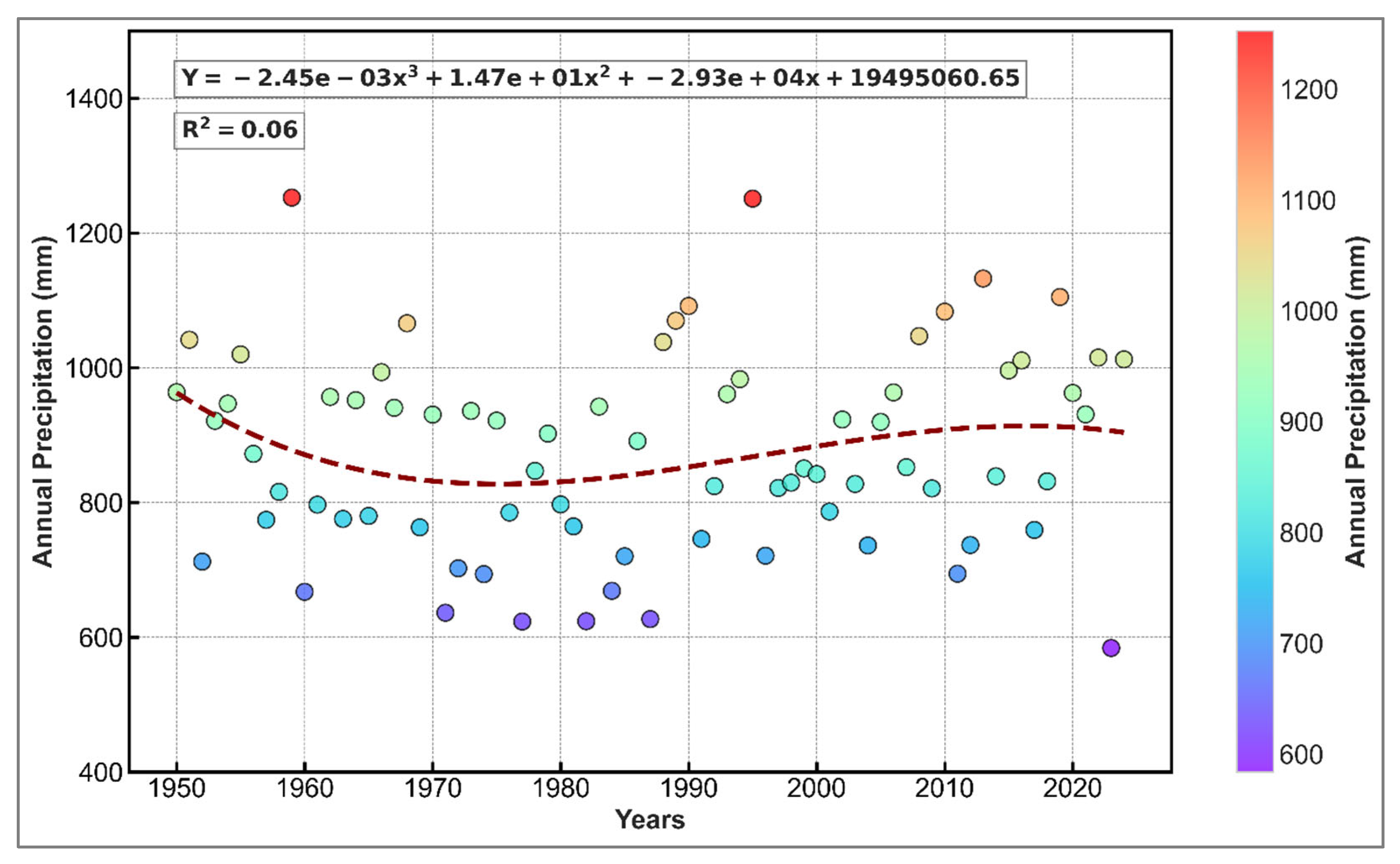
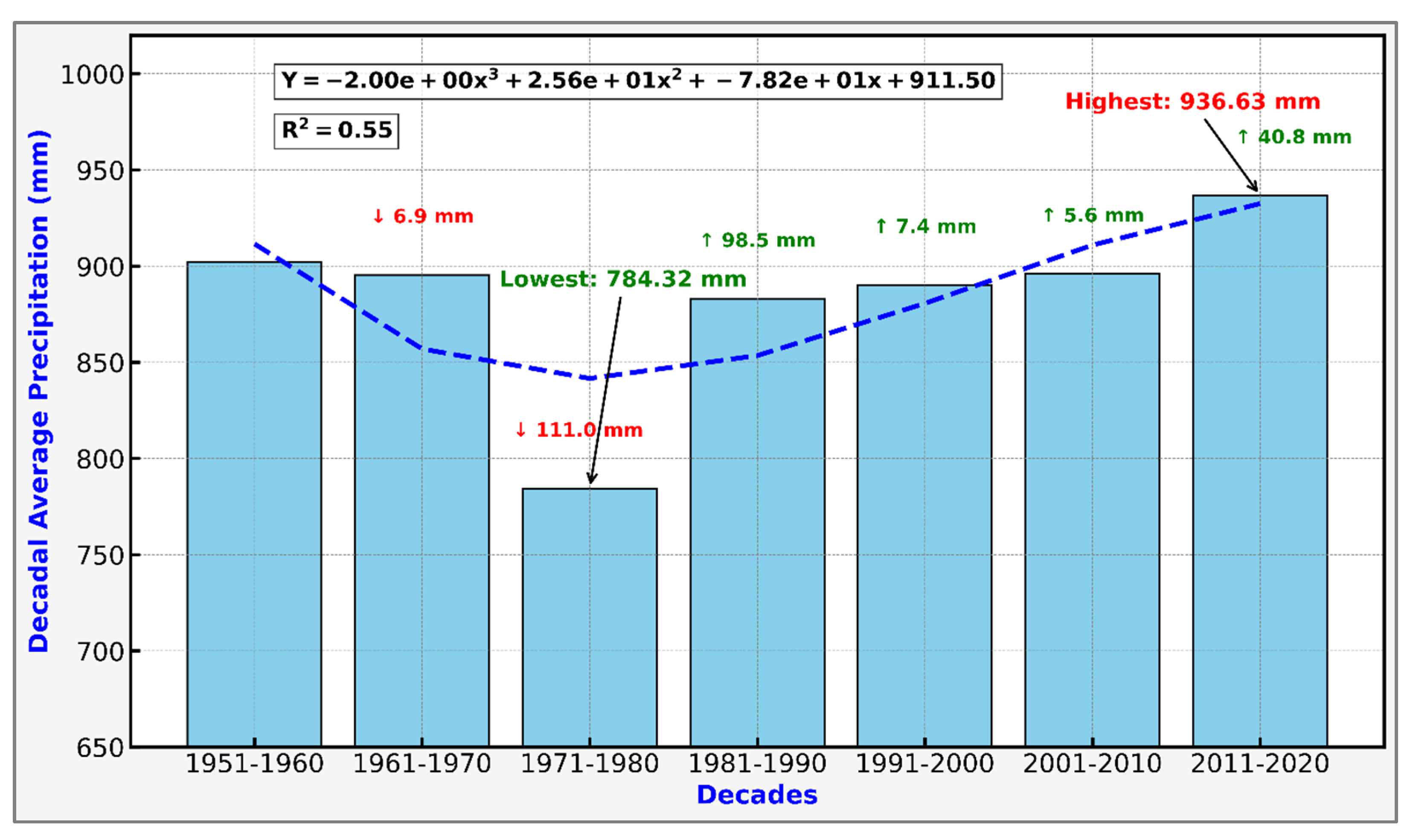
4.7. Annual and Decadal Trends in Total Precipitation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Dracup, J.A.; Lee, K.S.; Paulson, E.G., Jr. On the definition of droughts. Water Resour. Res. 1980, 16, 297–302. [Google Scholar] [CrossRef]
- Ding, Y.; Xu, J.; Wang, X.; Peng, X.; Cai, H. Spatial and temporal effects of drought on Chinese vegetation under different coverage levels. Sci. Total Environ. 2020, 716, 137166. [Google Scholar] [CrossRef]
- Wang, T.; Tu, X.; Singh, V.P.; Chen, X.; Lin, K.; Zhou, Z.; Tan, Y. Assessment of future socioeconomic drought based on CMIP6: Evolution, driving factors and propagation. J. Hydrol. 2023, 617, 129009. [Google Scholar] [CrossRef]
- Wilhite, D.A. Drought as a natural hazard: Concepts and definitions. In Droughts; Routledge: Oxfordshire, UK, 2016; pp. 3–18. [Google Scholar]
- Ma, S.; Zhang, S.; Wang, N.; Huang, C.; Wang, X. Prolonged duration and increased severity of agricultural droughts during 1978 to 2016 detected by ESA CCI SM in the humid Yunnan Province, Southwest China. Catena 2021, 198, 105036. [Google Scholar] [CrossRef]
- Zhang, L.; Jiao, W.; Zhang, H.; Huang, C.; Tong, Q. Studying drought phenomena in the Continental United States in 2011 and 2012 using various drought indices. Remote Sens. Environ. 2017, 190, 96–106. [Google Scholar] [CrossRef]
- Adnan, S.; Ullah, K.; Shuanglin, L.; Gao, S.; Khan, A.H.; Mahmood, R. Comparison of various drought indices to monitor drought status in Pakistan. Clim. Dyn. 2018, 51, 1885–1899. [Google Scholar] [CrossRef]
- Mishra, V.; Aadhar, S.; Mahto, S.S. Anthropogenic warming and intraseasonal summer monsoon variability amplify the risk of future flash droughts in India. npj Clim. Atmos. Sci. 2021, 4, 1. [Google Scholar] [CrossRef]
- Mahto, S.S.; Mishra, V. Dominance of summer monsoon flash droughts in India. Environ. Res. Lett. 2020, 15, 104061. [Google Scholar] [CrossRef]
- Svoboda, M.D.; Fuchs, B.A. Handbook of Drought Indicators and Indices; World Meteorological Organization: Geneva, Switzerland, 2016; Volume 2. [Google Scholar]
- Huang, K.; Wu, J.; Fu, Z.; Du, J. Comparative analysis of drought indices in the tropical zones of China. Sci. Total Environ. 2024, 947, 174530. [Google Scholar] [CrossRef]
- Alahacoon, N.; Edirisinghe, M. A comprehensive assessment of remote sensing and traditional based drought monitoring indices at global and regional scale. Geomat. Nat. Hazards Risk 2022, 13, 762–799. [Google Scholar] [CrossRef]
- Pan, Y.; Zhu, Y.; Lue, H.; Yagci, A.L.; Fu, X.; Liu, E.; Xu, H.; Ding, Z.; Liu, R. Accuracy of agricultural drought indices and analysis of agricultural drought characteristics in China between 2000 and 2019. Agric. Water Manag. 2023, 283, 108305. [Google Scholar] [CrossRef]
- Pathak, A.A.; Dodamani, B. Comparison of meteorological drought indices for different climatic regions of an Indian river basin. Asia-Pac. J. Atmos. Sci. 2020, 56, 563–576. [Google Scholar] [CrossRef]
- Uddin, M.A.; Kamal, A.M.; Shahid, S.; Chung, E.-S. Volatility in rainfall and predictability of droughts in northwest Bangladesh. Sustainability 2020, 12, 9810. [Google Scholar] [CrossRef]
- Bouznad, I.-E.; Guastaldi, E.; Zirulia, A.; Brancale, M.; Barbagli, A.; Bengusmia, D. Trend analysis and spatiotemporal prediction of precipitation, temperature, and evapotranspiration values using the ARIMA models: Case of the Algerian Highlands. Arab. J. Geosci. 2020, 13, 1281. [Google Scholar] [CrossRef]
- Ghosh, S.; Mukhoti, S.; Sharma, P. Quantifying rainfall-induced climate risk in rainfed agriculture: A volatility-based time series study from semi-arid India. Agric. Water Manag. 2025, 319, 109775. [Google Scholar] [CrossRef]
- Tijdeman, E.; Stahl, K.; Tallaksen, L.M. Drought characteristics derived based on the standardized streamflow index: A large sample comparison for parametric and nonparametric methods. Water Resour. Res. 2020, 56, e2019WR026315. [Google Scholar] [CrossRef]
- Pandya, P.A.; Gontia, N.K. Correlation vs. Kappa statistic: A new perspective on comparing meteorological drought indices. Theor. Appl. Climatol. 2025, 156, 19. [Google Scholar] [CrossRef]
- Vergni, L.; Todisco, F.; Di Lena, B. Evaluation of the similarity between drought indices by correlation analysis and Cohen’s Kappa test in a Mediterranean area. Nat. Hazards 2021, 108, 2187–2209. [Google Scholar] [CrossRef]
- Bilal, S.B.; Gupta, V. Deciphering the spatial fingerprint of drought propagation through precipitation, vegetation and groundwater. Int. J. Climatol. 2024, 44, 4443–4461. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, Z.; Shao, Q.; He, H.; Guo, X. From meteorological to agricultural drought: Propagation time and probabilistic linkages. J. Hydrol. Reg. Stud. 2023, 46, 101329. [Google Scholar] [CrossRef]
- Ogunrinde, A.T.; Adigun, P.; Xue, X.; Koji, D.; Jing, Q. Spatiotemporal analysis of drought patterns and trends across Africa: A multi-scale SPEI approach (1960–2018). Int. J. Digit. Earth 2025, 18, 2447342. [Google Scholar] [CrossRef]
- Raziei, T.; Pereira, L.S. Relating the drought precipitation percentiles index to the standardized precipitation index (SPI) under influence of aridity and timescale. Water Resour. Manag. 2024, 38, 5739–5758. [Google Scholar] [CrossRef]
- Terzi, T.B.; Önöz, B. Drought analysis in the Seyhan River Basin based on standardized drought indices using a new approach considering seasonality. Environ. Earth Sci. 2025, 84, 30. [Google Scholar] [CrossRef]
- Öz, F.Y.; Özelkan, E.; Tatlı, H. Comparative analysis of SPI, SPEI, and RDI indices for assessing spatio-temporal variation of drought in Türkiye. Earth Sci. Inform. 2024, 17, 4473–4505. [Google Scholar] [CrossRef]
- Rogelj, J.; Luderer, G.; Pietzcker, R.C.; Kriegler, E.; Schaeffer, M.; Krey, V.; Riahi, K. Energy system transformations for limiting end-of-century warming to below 1.5 C. Nat. Clim. Change 2015, 5, 519–527. [Google Scholar] [CrossRef]
- Srivastava, A.; Maity, R. Unveiling an Environmental Drought Index and its applicability in the perspective of drought recognition amidst climate change. J. Hydrol. 2023, 627, 130462. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–183. [Google Scholar]
- Dogan, S.; Berktay, A.; Singh, V.P. Comparison of multi-monthly rainfall-based drought severity indices, with application to semi-arid Konya closed basin, Turkey. J. Hydrol. 2012, 470, 255–268. [Google Scholar] [CrossRef]
- Li, L.; Cai, H. A comparative study of various drought indices at different timescales and over different record lengths in the arid area of northwest China. Environ. Sci. Pollut. Res. 2024, 31, 25096–25113. [Google Scholar] [CrossRef] [PubMed]
- Bhalme, H.N.; Mooley, D.A. Large-scale droughts/floods and monsoon circulation. Mon. Weather Rev. 1980, 108, 1197–1211. [Google Scholar] [CrossRef]
- Kumar, V.; Chu, H.-J. Spatiotemporal consistency and inconsistency of meteorological and agricultural drought identification: A case study of India. Remote Sens. Appl. Soc. Environ. 2024, 33, 101134. [Google Scholar] [CrossRef]
- Pividori, M.; Ritchie, M.D.; Milone, D.H.; Greene, C.S. An efficient, not-only-linear correlation coefficient based on clustering. Cell Syst. 2024, 15, 854–868.e3. [Google Scholar] [CrossRef]
- Abu Arra, A.; Şişman, E. New Insights into Meteorological and Hydrological Drought Modeling: A Comparative Analysis of Parametric and Non-Parametric Distributions. Atmosphere 2025, 16, 846. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, X.; Yu, H.; Chen, Z.; Du, W.; Chen, N. Incorporating spatial autocorrelation into deformable ConvLSTM for hourly precipitation forecasting. Comput. Geosci. 2024, 184, 105536. [Google Scholar] [CrossRef]
- Khoorani, A.; Balaghi, S.; Mohammadi, F. Projecting drought trends and hot spots across Iran. Nat. Hazards 2024, 120, 9489–9502. [Google Scholar] [CrossRef]
- Griffith, D.A. Spatial filtering. In Spatial Autocorrelation and Spatial Filtering: Gaining Understanding Through Theory and Scientific Visualization; Springer: Berlin/Heidelberg, Germany, 2003; pp. 91–130. [Google Scholar]
- Kwon, M.; Sung, J.H. Changes in future drought with HadGEM2-AO projections. Water 2019, 11, 312. [Google Scholar] [CrossRef]
- Pieper, P.; Düsterhus, A.; Baehr, J. A universal Standardized Precipitation Index candidate distribution function for observations and simulations. Hydrol. Earth Syst. Sci. 2020, 24, 4541–4565. [Google Scholar] [CrossRef]
- Romero, D.; Alfaro, E.J. Systematic Biases in Tropical Drought Monitoring: Rethinking SPI Application in Mesoamerica’s Humid Regions. Meteorology 2025, 4, 18. [Google Scholar] [CrossRef]
- Cammalleri, C.; Spinoni, J.; Barbosa, P.; Toreti, A.; Vogt, J.V. The effects of non-stationarity on SPI for operational drought monitoring in Europe. Int. J. Climatol. 2022, 42, 3418–3430. [Google Scholar] [CrossRef]
- Lisonbee, J.; Nielsen-Gammon, J.; Trewin, B.; Follingstad, G.; Parker, B. Drought assessment in a changing climate: A review of climate normals for drought indices. J. Appl. Serv. Clim. 2024, 2024, 1–17. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Karami, M.; Shabanlou, S.; Mazaheri, H.; Mokhtari, S.; Najarchi, M. Integration of the Non-linear Time Series GARCH Model with Fuzzy Model Optimized with Water Cycle Algorithm for River Streamflow Forecasting. Int. J. Comput. Intell. Syst. 2024, 17, 156. [Google Scholar] [CrossRef]
- Wang, W.; Wang, J.; Romanowicz, R. Uncertainty in SPI calculation and its impact on drought assessment in different climate regions over China. J. Hydrometeorol. 2021, 22, 1369–1383. [Google Scholar] [CrossRef]
- Madadgar, S.; Moradkhani, H. Spatio-temporal drought forecasting within Bayesian networks. J. Hydrol. 2014, 512, 134–146. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Jones, P.W. First-and second-order conservative remapping schemes for grids in spherical coordinates. Mon. Weather Rev. 1999, 127, 2204–2210. [Google Scholar] [CrossRef]
- Pai, D.; Rajeevan, M.; Sreejith, O.; Mukhopadhyay, B.; Satbha, N. Development of a new high spatial resolution (0.25 × 0.25) long period (1901–2010) daily gridded rainfall data set over India and its comparison with existing data sets over the region. Mausam 2014, 65, 1–18. [Google Scholar] [CrossRef]
- Getis, A.; Griffith, D.A. Comparative spatial filtering in regression analysis. Geogr. Anal. 2002, 34, 130–140. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The analysis of spatial association by use of distance statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Spearman, C. The Proof and Measurement of Association between Two Things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Engle, R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econom. J. Econom. Soc. 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar]
- Sjölander, P. A stationary unbiased finite sample ARCH-LM test procedure. Appl. Econ. 2011, 43, 1019–1033. [Google Scholar] [CrossRef]
- Ljung, G.M.; Box, G.E. On a measure of lack of fit in time series models. Biometrika 1978, 65, 297–303. [Google Scholar] [CrossRef]
- Jarque, C.M.; Bera, A.K. Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Econ. Lett. 1980, 6, 255–259. [Google Scholar] [CrossRef]
- Ampadu, S.; Mensah, E.T.; Aidoo, E.N.; Boateng, A.; Maposa, D. A comparative study of error distributions in the GARCH model through a Monte Carlo simulation approach. Sci. Afr. 2024, 23, e01988. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Liu, X.; Yu, S.; Yang, Z.; Dong, J.; Peng, J. The first global multi-timescale daily SPEI dataset from 1982 to 2021. Sci. Data 2024, 11, 223. [Google Scholar] [CrossRef]
- Zhan, C.; Liang, C.; Zhao, L.; Jiang, S.; Zhang, Y. Differential responses of crop yields to multi-timescale drought in mainland China: Spatiotemporal patterns and climate drivers. Sci. Total Environ. 2024, 906, 167559. [Google Scholar] [CrossRef] [PubMed]
- Choi, M.; Jacobs, J.M.; Anderson, M.C.; Bosch, D.D. Evaluation of drought indices via remotely sensed data with hydrological variables. J. Hydrol. 2013, 476, 265–273. [Google Scholar] [CrossRef]
- Oyounalsoud, M.S.; Abdallah, M.; Yilmaz, A.G.; Siddique, M.; Atabay, S. A new meteorological drought index based on fuzzy logic: Development and comparative assessment with conventional drought indices. J. Hydrol. 2023, 619, 129306. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, Y.-P.; Wang, G. Agricultural drought prediction using climate indices based on Support Vector Regression in Xiangjiang River basin. Sci. Total Environ. 2018, 622, 710–720. [Google Scholar] [CrossRef]
- Jain, V.K.; Pandey, R.P.; Jain, M.K.; Byun, H.-R. Comparison of drought indices for appraisal of drought characteristics in the Ken River Basin. Weather Clim. Extrem. 2015, 8, 1–11. [Google Scholar] [CrossRef]
- Wable, P.S.; Jha, M.K.; Shekhar, A. Comparison of drought indices in a semi-arid river basin of India. Water Resour. Manag. 2019, 33, 75–102. [Google Scholar] [CrossRef]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Willmott, C.J.; Wicks, D.E. An empirical method for the spatial interpolation of monthly precipitation within California. Phys. Geogr. 1980, 1, 59–73. [Google Scholar] [CrossRef]
- Khooriphan, W.; Niwitpong, S.-A.; Niwitpong, S. Bayesian estimation of rainfall dispersion in Thailand using gamma distribution with excess zeros. PeerJ 2022, 10, e14023. [Google Scholar] [CrossRef] [PubMed]
- Sienz, F.; Bothe, O.; Fraedrich, K. Monitoring and quantifying future climate projections of dryness and wetness extremes: SPI bias. Hydrol. Earth Syst. Sci. 2012, 16, 2143–2157. [Google Scholar] [CrossRef]
- Cerpa Reyes, L.J.; Ávila Rangel, H.; Herazo, L.C.S. Adjustment of the standardized precipitation index (SPI) for the evaluation of drought in the arroyo pechelín basin, Colombia, under zero monthly precipitation conditions. Atmosphere 2022, 13, 236. [Google Scholar] [CrossRef]
- De Burgh-Day, C.; Dillon, F. A Hybrid Parametrisation for Precipitation Probability of Exceedance Data; Australian Bureau of Meteorology: Melbourne, Australia, 2021.
- Haight, F.A. Handbook of the Poisson Distribution; Wiley: Hoboken, NJ, USA, 1967. [Google Scholar]
- Goodman, L.A. The multivariate analysis of qualitative data: Interactions among multiple classifications. J. Am. Stat. Assoc. 1970, 65, 226–256. [Google Scholar] [CrossRef]
- Gelman, A. Analysis of variance—Why it is more important than ever. Ann. Stat. 2005, 33, 1–53. [Google Scholar] [CrossRef]
- Pearson, K. VII. Note on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar] [CrossRef]
- Hauke, J.; Kossowski, T. Comparison of values of Pearson’s and Spearman’s correlation coefficients on the same sets of data. Quaest. Geogr. 2011, 30, 87–93. [Google Scholar] [CrossRef]
- Tigkas, D.; Vangelis, H.; Tsakiris, G. Drought characterisation based on an agriculture-oriented standardised precipitation index. Theor. Appl. Climatol. 2019, 135, 1435–1447. [Google Scholar] [CrossRef]
- Chang, D.; Li, S.; Lai, Z. Effects of extreme precipitation intensity and duration on the runoff and nutrient yields. J. Hydrol. 2023, 626, 130281. [Google Scholar] [CrossRef]
- Ghasempour, R.; Roushangar, K.; Alizadeh, F. Hybrid models for drought forecasting: Integration of multi pre-processing-data driven approaches and non-linear GARCH time series model. Arab. J. Geosci. 2023, 16, 361. [Google Scholar] [CrossRef]
- Modarres, R.; Ouarda, T.B. Modelling heteroscedasticty of streamflow times series. Hydrol. Sci. J. 2013, 58, 54–64. [Google Scholar] [CrossRef]
- Salehnia, N.; Alizadeh, A.; Sanaeinejad, H.; Bannayan, M.; Zarrin, A.; Hoogenboom, G. Estimation of meteorological drought indices based on AgMERRA precipitation data and station-observed precipitation data. J. Arid Land 2017, 9, 797–809. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Carrao, H.; Barbosa, P.; Vogt, J. World drought frequency, duration, and severity for 1951–2010. Int. J. Clim. 2014, 34, 2792–2804. [Google Scholar] [CrossRef]
- Gibbs, W.J.; Maher, J.V. Rainfall deciles drought inddicators. In Bureau of Meteorology Bulletin No. 48; Bureau of Meteorology: Melbourne, Australia, 1967. [Google Scholar]
- Mwinjuma, M.; Wang, R.; Mtupili, M.; Twaha, M. Comparisons of SPI and SPEI in capturing drought dynamics: A Global assessment across arid and humid regions. Atmos. Res. 2025, 329, 108475. [Google Scholar] [CrossRef]
- Nadi, M.; Shiukhy Soqanloo, S. Modification of standardized precipitation index in different climates of Iran. Meteorol. Appl. 2023, 30, e2155. [Google Scholar] [CrossRef]
- Mo, K.C.; Lyon, B. Global meteorological drought prediction using the North American multi-model ensemble. J. Hydrometeorol. 2015, 16, 1409–1424. [Google Scholar] [CrossRef]
- Ribeiro, A.; Pires, C. Seasonal drought predictability in Portugal using statistical–dynamical techniques. Phys. Chem. Earth Parts A/B/C 2016, 94, 155–166. [Google Scholar] [CrossRef]
- Wu, H.; Svoboda, M.D.; Hayes, M.J.; Wilhite, D.A.; Wen, F. Appropriate application of the standardized precipitation index in arid locations and dry seasons. Int. J. Clim. 2006, 27, 65–79. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z. Uncertainty analysis of standardized precipitation index due to the effects of probability distributions and parameter errors. Front. Earth Sci. 2020, 8, 76. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Candidate distributions for climatological drought indices (SPI and SPEI). Int. J. Climatol. 2015, 35, 4027–4040. [Google Scholar] [CrossRef]
- Guttman, N.B. Accepting the standardized precipitation index: A calculation algorithm 1. JAWRA J. Am. Water Resour. Assoc. 1999, 35, 311–322. [Google Scholar] [CrossRef]
- Guenang, G.; Komkoua, M.; Pokam, M.; Tanessong, R.; Tchakoutio, S.; Vondou, A.; Tamoffo, A.; Djiotang, L.; Yepdo, Z.; Mkankam, K. Sensitivity of SPI to distribution functions and correlation between its values at different time scales in Central Africa. Earth Syst. Environ. 2019, 3, 203–214. [Google Scholar] [CrossRef]
- Blain, G.C.; Meschiatti, M.C. Inadequacy of the gamma distribution to calculate the Standardized Precipitation Index. Rev. Bras. Eng. Agric. Ambient. 2015, 19, 1129–1135. [Google Scholar] [CrossRef]
- Leasor, Z.T.; Quiring, S.M.; Svoboda, M.D. Utilizing objective drought severity thresholds to improve drought monitoring. J. Appl. Meteorol. Climatol. 2020, 59, 455–475. [Google Scholar] [CrossRef]
- Ntale, H.K.; Gan, T.Y. Drought indices and their application to East Africa. Int. J. Climatol. J. R. Meteorol. Soc. 2003, 23, 1335–1357. [Google Scholar] [CrossRef]
- Oughton, E. The Maharashtra droughts of 1970-73: An analysis of scarcity. Oxf. Bull. Econ. Stat. 1982, 44, 169. [Google Scholar] [CrossRef]
- Wu, R.; Kinte, J.L., III. Analysis of the relationship of US droughts with SST and soil moisture: Distinguishing the time scale of droughts. J. Clim. 2009, 22, 4520–4538. [Google Scholar] [CrossRef]
- Salimi, H.; Asadi, E.; Darbandi, S. Meteorological and hydrological drought monitoring using several drought indices. Appl. Water Sci. 2021, 11, 11. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. FAO Rome 1998, 300, D05109. [Google Scholar]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Pachore, A.B.; Remesan, R.; Kumar, R. Multifractal characterization of meteorological to agricultural drought propagation over India. Sci. Rep. 2024, 14, 18889. [Google Scholar] [CrossRef]
- Torelló-Sentelles, H.; Franzke, C.L. Drought impact links to meteorological drought indicators and predictability in Spain. Hydrol. Earth Syst. Sci. 2022, 26, 1821–1844. [Google Scholar] [CrossRef]
- Zhang, H.; Ding, J.; Wang, Y.; Zhou, D.; Zhu, Q. Investigation about the correlation and propagation among meteorological, agricultural and groundwater droughts over humid and arid/semi-arid basins in China. J. Hydrol. 2021, 603, 127007. [Google Scholar] [CrossRef]
- Houmma, I.H.; Hadri, A.; Boudhar, A.; Karaoui, I.; Oussaoui, S.; El Khalki, E.M.; Chehbouni, A.; Kinnard, C. Analysis of the propagation characteristics of meteorological drought to hydrological drought and their joint effects on low-flow drought variability in the Oum Er Rbia Watershed, Morocco. Remote Sens. 2025, 17, 281. [Google Scholar] [CrossRef]
- Odongo, R.A.; De Moel, H.; Van Loon, A.F. Propagation from meteorological to hydrological drought in the Horn of Africa using both standardized and threshold-based indices. Nat. Hazards Earth Syst. Sci. 2023, 23, 2365–2386. [Google Scholar] [CrossRef]
- Yang, X.; Wu, F.; Yuan, S.; Ren, L.; Sheffield, J.; Fang, X.; Jiang, S.; Liu, Y. Quantifying the impact of human activities on hydrological drought and drought propagation in China using the PCR-GLOBWB v2.0 model. Water Resour. Res. 2024, 60, e2023WR035443. [Google Scholar] [CrossRef]
| Parameters | Values |
|---|---|
| Mean | 73.23 mm |
| Median | 22.08 mm |
| Sum | 65,914.82 mm |
| Range | 623.10 mm |
| Standard Error | 3.40 |
| Standard Deviation | 101.76 |
| Variance | 10,356.21 |
| Kurtosis | 3.77 |
| Skewness | 1.95 |
| Confidence Interval | 6.65 |
| Parameters | Values |
|---|---|
| Global Moran’s Index (I) | 0.91 |
| Z-Score | 32.93 |
| p-value | <0.001 |
| Parameters | sGARCH (1,1) | eGARCH (1,1) |
|---|---|---|
| ADF Statistics | −17.24 | |
| p-Value of ADF Test | 0.01 | |
| Chi-Square of ARCH LM (Pre-GARCH) | 276.02 | |
| Distribution Type | Skewed Student’s t | |
| p-value of ARCH LM Test (Pre-GARCH) | <0.001 | <0.001 |
| Omega | 37.01 | 6.31 |
| Alpha | 0 | 2.27 |
| Beta | 0.99 | 0.35 |
| Gamma | −0.16 | Not Available for sGARCH |
| Akaike Information Criterion (AIC) | 11.07 | 10.55 |
| Bayesian Information Criterion (BIC) | 11.13 | 10.62 |
| p-value of the Jarque–Bera test for residuals | <0.001 | <0.001 |
| p-value of the Ljung–Box test for residuals | <0.001 | 0.98 |
| p-value of the Ljung–Box test for variance | <0.001 | 0.27 |
| Chi-Square of ARCH LM (Post-GARCH) | 70.35 | 17.07 |
| p-value of ARCH LM Test (Post-GARCH) | <0.001 | 0.072 |
| Timescales in Months | Drought Indices |
|---|---|
| One | BMDI, ZSI, and RAI |
| Three to Four | BMDI, ZSI, aSPI, and CZI |
| Six | BMDI, ZSI, and aSPI |
| Nine to Twelve | BMDI, ZSI, aSPI, WASP, and DI |
| DIs | r | R | RMSE | SEE | SEM | MAE | STDEV |
|---|---|---|---|---|---|---|---|
| ZSI-6 | 0.98 | 0.96 | 0.11 | 0.11 | 0.06 | 0.09 | 1.00 |
| aSPI-6 | 0.97 | 0.94 | 0.10 | 0.13 | 0.06 | 0.11 | 1.00 |
| WASP-6 | 0.98 | 0.96 | 0.13 | 0.10 | 0.06 | 0.07 | 1.00 |
| CZI-6 | 0.95 | 0.90 | 0.19 | 0.19 | 0.07 | 0.15 | 1.14 |
| mCZI-6 | 0.94 | 0.88 | 0.23 | 0.24 | 0.08 | 0.19 | 1.09 |
| SPI-6 | 0.77 | 0.60 | 0.36 | 0.36 | 0.08 | 0.28 | 1.00 |
| RAI-6 | 0.77 | 0.59 | 0.69 | 0.70 | 0.12 | 0.53 | 1.90 |
| DI-6 | 0.75 | 0.57 | 1.03 | 1.04 | 0.18 | 0.79 | 2.85 |
| PN-6 | 0.98 | 0.96 | 2.95 | 2.99 | 1.78 | 2.29 | 30.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choudhari, N.; Jacob, B.G.; Elshorbany, Y.; Collins, J. Unveiling Asymptotic Behavior in Precipitation Time Series: A GARCH-Based Second Order Semi-Parametric Autocorrelation Framework for Drought Monitoring in the Semi-Arid Region of India. Hydrology 2025, 12, 254. https://doi.org/10.3390/hydrology12100254
Choudhari N, Jacob BG, Elshorbany Y, Collins J. Unveiling Asymptotic Behavior in Precipitation Time Series: A GARCH-Based Second Order Semi-Parametric Autocorrelation Framework for Drought Monitoring in the Semi-Arid Region of India. Hydrology. 2025; 12(10):254. https://doi.org/10.3390/hydrology12100254
Chicago/Turabian StyleChoudhari, Namit, Benjamin G. Jacob, Yasin Elshorbany, and Jennifer Collins. 2025. "Unveiling Asymptotic Behavior in Precipitation Time Series: A GARCH-Based Second Order Semi-Parametric Autocorrelation Framework for Drought Monitoring in the Semi-Arid Region of India" Hydrology 12, no. 10: 254. https://doi.org/10.3390/hydrology12100254
APA StyleChoudhari, N., Jacob, B. G., Elshorbany, Y., & Collins, J. (2025). Unveiling Asymptotic Behavior in Precipitation Time Series: A GARCH-Based Second Order Semi-Parametric Autocorrelation Framework for Drought Monitoring in the Semi-Arid Region of India. Hydrology, 12(10), 254. https://doi.org/10.3390/hydrology12100254






