Abstract
The Athabasca River flows through the Lower Athabasca Region (LAR) in Alberta, Canada, which is characterized by variable inter-annual weather, long winters and short summers. LAR is important for the extraction of energy resources and industrial activities that lead to environmental concerns, including river pollution and exploitation. This study attempts to forecast the Athabasca River at Fort McMurray and understand the suitability of HEC-HMS (Hydrologic Engineering Center-Hydrologic Modeling System) in cold weather regions, characterized by poorly gauged streams. Daily temperature and precipitation records (1971–2014) were employed in two calibration–validation schemes: (1) a temporally dependent partition (1971–2000 for calibration; 2001–2014 for validation) and (2) a temporally independent partition (alternating years assigned to calibration and validation). The temporally independent approach achieved superior performance, with a Nash–Sutcliffe efficiency of 0.88, outperforming previously developed regional models. HEC-HMS successfully reproduced hydrologic dynamics and peak discharge events under conditions of sparse hydroclimatic data and limited computational inputs, underscoring its robustness for operational forecasting in data-scarce, cold-climate catchments. However, long-term projections may be subject to uncertainty due to the exclusion of anticipated changes in land use and climate forcing. These results substantiate the applicability of HEC-HMS as a cost-effective and reliable tool for hydrological modeling and flow forecasting in support of water resource management, particularly in regions subject to industrial pressures and associated environmental impacts.
1. Introduction
River systems are essential to various economic sectors that are reliant on water such as agriculture, energy production, fisheries, and others. To sustain healthy and functional river systems, effective management tools such as river flow forecasting models are necessary. These tools support water resource management by providing real-time and future projections of river conditions, including monitoring data, climate change impacts, flood risk mapping, and other strategies that promote sustainable planning for current and future human uses [1,2].
In Canada, particularly in Alberta, the provincial government is responsible for overseeing proper water resource management. Alberta’s major river systems—Peace River, Athabasca River, and the North and South Saskatchewan Rivers—are routinely monitored for water quantity and quality. Annual reports summarize these conditions, identify key issues, and propose design improvements and future development projects [1].
The Athabasca River basin is a major tributary of the Mackenzie River system—one of the most extensive and ecologically significant freshwater networks in North America—ultimately discharging into the Arctic Ocean. The Lower Athabasca Region (LAR) in Alberta represents a strategic hub in Canada’s energy sector, encompassing large-scale oil sands operations that make substantial contributions to the national economy. The Athabasca River, Alberta’s longest river system, originates in the Canadian Rockies near Jasper and flows over 1500 km northward into Lake Athabasca. Its lower stretch lies within the LAR, home to the world’s third-largest oil reserve (about 168.1 thousand million barrels), trailing only Venezuela (about 303.8 thousand million barrels) and Saudi Arabia (about 297.5 thousand million barrels) [3]. Over the past four decades, the LAR has experienced significant population increase and land use changes, particularly near Fort McMurray, the region’s largest urban service center. The Athabasca River is the primary source of water for tar sands mining operations. Extracting one barrel of extra-heavy crude oil requires three to four barrels of fresh water [4].
These industrial activities have raised concerns among scientists, environmentalists, and other stakeholders regarding the region’s environmental sustainability. Issues include water quality and quantity, climate change impacts on water resources, and pollution caused by oil and gas extraction [5,6]. Extensive industrial development has also transformed land uses, contributing to increased spring runoff and a heightened risk of flooding [7,8,9]. Wavelet analyses of historical climate and flow data demonstrated that the Athabasca River flow is expected to gradually increase during the mid-century [10].
The flow of the Athabasca River is significantly influenced by the region’s extreme intra-annual climatic variations, driven by its cold weather conditions. The LAR experiences long, harsh winters with temperatures dropping as low as −53.3 °C (−63.9 °F) in February and short, warm summers with highs reaching 40.3 °C (104.5 °F) in June [11]. This results in an extreme temperature difference of nearly 90 °C (194 °F) between seasons. Consequently, climatic factors such as temperature and precipitations significantly affect river flow throughout the year. In winter, precipitation and snowmelt contribute to the river flow to a lesser extent, whereas spring and summer see substantial contributions from rainfall-runoff and snowmelt [8]. To track these climatic impacts, weather and hydrometric stations collect data on precipitation, temperature, humidity, and other variables in hourly, daily, and monthly intervals. Along the Athabasca River, there are ten active weather stations and six hydrometric stations [12,13]. However, historical records for some locations such as Windfall station (07AE001) are incomplete. This station recorded data only during spring and summer between 1979 and 2018, leading to significant data gaps.
River flow forecasting in the existing literature employs three primary approaches: process-based, data-driven, and hybrid models.
- Process-based models rely on local climate, land use, and topographic data to mathematically simulate hydrological processes of a watershed. These models are commonly used to generate future flow projections in both gauged and ungauged areas under various climate change and land use scenarios [14,15].
- Data-driven models use historical hydrometric records, such as data from upstream stations to predict river flow downstream. These models rely on mathematical expressions to represent input-output relationships without incorporating the physical characteristics of the watershed. They are often used for real-time or short-term forecasting [16,17].
- Hybrid methods combine the strengths of process-based and data-driven models, enabling forecasts for both in the long- and short-term scenarios.
Each of these approaches serves distinct purposes in managing river systems and adapting to changing environmental conditions. In fact, process-based and data-driven methods have been applied in the LAR to forecast the Athabasca River flow at Fort McMurray. Toth et al. [18] used the WATFLOOD model, a process-based approach, using discharge, topography, temperature, and precipitation from 1965 to 1989 to calibrate and validate the model, achieving a Nash-Sutcliffe Efficiency (NSE) coefficient of 0.72. Similarly, Eum et al. [19] used Variable Infiltration Capacity (VIC) model with various Global Circulation Model (GCM) derived climate change projections, incorporating data on discharge, climate, vegetation and soil from 1979 to 2010, and obtained an NSE of 0.84 Rood et al. [20] adopted a simpler interpolation approach, forecasting flows using discharge data from various locations along the Athabasca River between 1957 and 2011. At Fort McMurray, their model achieved an NSE of 0.79. Eum et al. [21] revisited the VIC model, incorporating additional variables such as temperature, precipitation, snow accumulation/melt, infiltration into frozen soil, land use, and soil drainage from 1985 to 2010, resulting in an NSE of 0.74. Shresta et al. [22] used the Soil and Water Assessment Tool (SWAT), another process-based model, requiring snowpack, elevation bands, groundwater, soil drainage, soil–vegetation slope, and pond/reservoir hydraulic conductivity data. Using data from 1980 to 2013, the model produced an NSE of 0.91. Droppo et al. [23] also applied the VIC model with similar inputs to Eum et al. [21] and for the period 1985–2010, and found an NSE of 0.74, comparable to Eum et al. [21].
The MIKE-SHE hydrological model has been successfully applied in cold weather regions [24]. The authors indicated that the LAR is a complex hydrological system where climate change (CC) and land-use/land-cover change (LULCC) inputs significantly affect water resource availability. The findings revealed that CC has a more pronounced impact than LULCC, with CC causing reduction in annual streamflow (7.9%), evapotranspiration (4.8%), and recharge (6.9%). LULCC reduces streamflow and recharge, but increased evapotranspiration. The authors stressed the importance of considering these factors when assessing the hydrological system’s behavior. Holmes et al. [25] investigated CHARM/WATFLOOD hydrological model in the LAR focusing on processes such as snowmelt, glacier melt, evaporation, groundwater recharge. Their study indicated that the model was particularly sensitive to evapotranspiration and infiltration, particularly in reach routing systems. This suggested that ‘black box’ models, which are calibrated without considering these processes, could yield biased results, affecting future streamflow projections. Similarly, Shresta and Wang [26] evaluated the sensitivity of the SWAT model in the LAR, noting that it was particularly responsive to precipitation and temperature, as these variables directly influence snowmelt processes. They also found that canopy storage—water per unit leaf area—directly affects evapotranspiration rates. These results aligned closely with those of Holmes et al. [25], who observed similar sensitivities using WATFLOOD. Kerkhoven and Gan [27] employed the Modified Interaction Soil–Biosphere–Atmosphere (MISBA) model, a complex environmental modeling scheme, to assess the hydrological impacts of vegetation shifts in the LAR under various climate change scenarios. Their findings suggested that climate change could result in drier conditions in the ARB due to rising temperatures, potentially causing forest retreat and grassland expansion, which would lead to increased runoff. Hwang et al. [28] used the HydroGeoSphere (HGS) simulator, integrating surface water and variably saturated subsurface flow and evapotranspiration processes, to quantify the influence of peatlands and forestlands on the ARB’s surface water and groundwater systems. Their results indicated that groundwater recharge and surface runoff are the primary contributors to stream water in the ARB.
Based on the current research progress, in this paper we focused on:
- I.
- Applying the HEC-HMS (Hydrologic Engineering Center-Hydrologic Modeling System) to forecast the Athabasca River flow at Fort McMurray, particularly under cold-weather conditions;
- II.
- Evaluating the HEC-HMS model’s sensitivity to calibration and validation using temporally independent datasets;
- III.
- Comparing HEC-HMS results with those previously developed models.
HEC-HMS, developed by the U.S. Army Corps of Engineers, simulates the complete hydrological processes of dendritic watershed systems [29]. This software is free for non-military users, though live training and troubleshooting are not provided. However, the platform offers extensive documentation to guide users through model development [30]. HEC-HMS has been successfully applied in regions with significant land use changes and industrial development [31], cold regions [32], natural disaster-prone areas [33], small catchments [34], and larger watersheds [35]. The application of HEC-HMS in cold regions by Bhuiyan et al. [32] was characterized by extensive data requirements, in contrast to the present study, which evaluates the model’s performance under data-scarce conditions. Despite the growing need for accurate hydrologic forecasting in cold-climate regions, particularly those with limited hydrometric coverage, there remains a significant gap in assessing the performance of widely accessible, process-based models such as HEC-HMS under such constraints. Existing research in the LAR has largely relied on data-intensive or region-specific models, which often lack transferability to poorly gauged catchments and may be impractical for long-term operational use. Moreover, few studies have rigorously tested model robustness under alternative calibration–validation strategies, leaving uncertainties about optimal approaches for maximizing predictive accuracy with limited records. This study addresses these gaps by systematically evaluating HEC-HMS in a data-scarce, industrially impacted watershed, employing both temporally dependent and temporally independent calibration–validation schemes to assess model resilience across varying temporal data structures.
In selecting an appropriate modeling framework for the LAR, several factors favored HEC-HMS over alternatives such as WATFLOOD, VIC, and SWAT. First, its modular structure and flexible process representation allow adaptation to data-scarce, cold-region basins, where snowmelt, frozen soil infiltration, and limited gauging data pose major challenges. Second, its relatively low computational demand makes it practical for operational forecasting without requiring high-performance computing resources. Third, its open-access availability removes licensing barriers, enabling broader adoption by water managers, Indigenous communities, and researchers in remote areas. These features collectively position HEC-HMS as a cost-effective, scalable, and transferable solution for cold-region runoff prediction. This research evaluates whether HEC-HMS can overcome current forecasting challenges, particularly in accurately reproducing peak flows. Demonstrating robust performance would establish HEC-HMS as a dependable tool for water resource managers, policy makers, and community stakeholders in similar regions worldwide, with the potential for broader application through regionalization. Finally, HEC-HMS addresses the challenge of data scarcity in hydrologic modeling by incorporating flexible model structures and simplified process representations that can operate effectively with limited hydroclimatic inputs. Unlike physically based models that require extensive spatially distributed datasets, HEC-HMS offers conceptual and empirical approaches—such as the temperature index method for snowmelt and lumped or semi-distributed runoff generation methods—that rely primarily on readily available meteorological and streamflow records. This adaptability allows for the simulation of key hydrologic processes, including precipitation–runoff transformation, snow accumulation and melt, and channel routing, even in poorly gauged catchments.
This study directly contributes to several United Nations Sustainable Development Goals (SDGs) by enhancing the capacity for informed water resource management in data-scarce, cold-climate regions. Through the successful application of HEC-HMS to forecast river discharge in the Athabasca River at Fort McMurray, the research supports SDG 6 (Clean Water and Sanitation) by providing a reliable, cost-effective modeling framework for safeguarding water availability and quality in a watershed heavily influenced by industrial activity. By accurately simulating hydrologic dynamics and peak flows with limited input data, the study also advances SDG 13 (Climate Action), offering a tool adaptable to future climate variability and extremes. Regionally, the work addresses SDG 15 (Life on Land) by enabling better protection of aquatic and riparian ecosystems under pressure from oil sands development and associated pollution risks. The ability to generate robust forecasts under sparse data conditions further aligns with SDG 9 (Industry, Innovation, and Infrastructure) by demonstrating technological resilience and operational practicality in challenging environments. Overall, the findings underscore the importance of accessible hydrologic modeling approaches for balancing economic development with environmental stewardship, ensuring that resource extraction in the LAR is managed in a manner consistent with long-term sustainability objectives.
2. Materials and Methods
2.1. Study Area and Data Requirements
The Athabasca River, the largest undammed river in Alberta, spans 1231 km from its source in the Canadian Rockies to its terminus at Lake Athabasca. Fort McMurray, situated along the river’s lower reaches, is the largest settlement in this region, with a population of 66,573 as of 2016. At Fort McMurray, the Athabasca River’s mean annual discharge is 20,860 km3 [36]. The river’s water is primarily withdrawn for agricultural and industrial purposes, with increasing withdrawals over time raising environmental and social concerns regarding the sustainability of the LAR [37]. Figure 1 shows the study area, including the municipality of Fort McMurray.
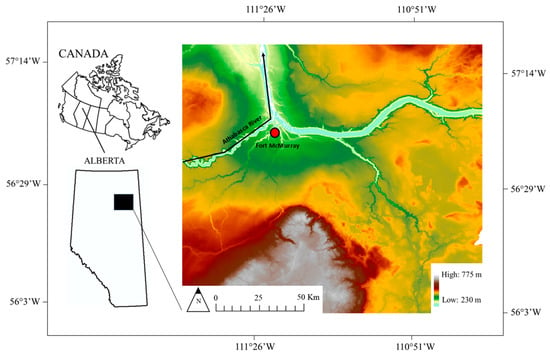
Figure 1.
Area of study showing the Athabasca River and the area around Fort McMurray, used for the HEC-HMS model development.
The river’s flow at Fort McMurray fluctuates significantly throughout the year. Average flow rates range from about 850 m3/s during the warmer months (May to October) to slightly below 200 m3/s during the colder months (November to April). Peak flow rates can exceed 3000 m3/s during an above-average spring freshet. Climatic variables also vary considerably: the lowest average daily temperature is −18 °C in January while the highest is 17.5 °C in July. Average daily precipitation ranges from a low of 0.4 mm in January to a high of 80.7 mm in July [11].
The study primarily examined the applicability of the HEC-HMS model for simulating river flow in cold-weather regions. Climatic data, including daily temperature and precipitation from 1971 to 2014, were available from Environment and Natural Resources Canada [11]. Two stations within this timeframe were identified:
- Station ID: 3062697, FORT MCMURRAY A, located at 56°39′12″ N 111°13′24″ W.
- Station ID: 3062693, FORT MCMURRAY A, located at 56°39′00″ N 111°13′00″ W.
Flow data for the Athabasca River at Fort McMurray during the same time period were obtained from the Water Survey of Canada website [38]. The specific station used for model calibration and validation was 07DA001, “Below Fort McMurray”, located at 56°46′49″ N 111°24′07″ W.
In addition to climate variables, the model required a Digital Elevation Model (DEM), land use maps, and soil drainage information. The DEM, with a 10-meter resolution, was obtained from the University of Calgary DEM Index Map [39]. Land use maps, referencing the year 2015 and featuring a 30-meter resolution, was sourced from the Canada Centre for Remote Sensing (CCRS) [40]. Soil drainage data, provided by the Alberta Soil Information Survey [41], indicated that the predominant soil type in the study area was gray luvisols with medium drainage level.
2.2. Hydrologic Design Formulation Using HEC-HMS
The HEC-HMS software (version 4.13 for Windows) supports a variety of hydrologic analysis procedures, including event infiltration, unit hydrographs, and hydrologic routing. It also offers algorithms for continuous simulations, such as evapotranspiration, snowmelt, and soil moisture accounting. HEC-HMS is widely used for estimating water availability, urban drainage, flow forecasting, future urbanization impact, reservoir spillway design, flood damage reduction, floodplain regulation, and systems operation [29].
During the calibration phase, HEC-HMS requires users to specify the following: (i) subbasin loss method to estimate excess precipitation contributing to runoff, typically influenced by soil infiltration characteristics; (ii) subbasin transform method to calculate runoff resulting from subbasin net precipitation; and (iii) reach routing method to compute runoff routing within the basin. This study employed the Soil Conservation Service (SCS) Curve Number (CN) as the subbasin loss method, the SCS Unit Hydrograph (UH) as the subbasin transform method, and the Muskingum method for reach routing.
The SCS CN method estimates precipitation excess using precipitation and CNs assigned to each subbasin. CNs are derived from the area’s hydrologic soil group and land use. The mathematical expression for calculating precipitation excess is as follows:
where Pe represents the precipitation excess, P is the accumulated precipitation depth, and S is the potential maximum retention, which quantifies a basin’s capacity to retain storm precipitation. The value of S was calculated using the following formula:
The SCS UH method requires the user to input lag times for each subbasin. Lag time, also referred to as basin lag, is the time interval between the center of mass of precipitation excess and the peak of the UH. It is mathematically expressed as:
where Tc represents the time of concentration, which depends on the basin’s geology, topography, and land use. It is defined as the time required for a water droplet to travel from the most distant point within a basin to its outlet. Tc can be calculated using the following formula:
where L is the flow length, and Y is the basin slope (%).
The Muskingum method for reach routing requires two parameters: (i) the Muskingum K, represents the travel time through the reach. This can range from 0.0 to 0.5, where 0 represents maximum attenuation and 0.5 no attenuation. Through model calibration, K was set to 0.5 in this study; and (ii) the Muskingum X, a dimensionless coefficient ranging from 0 to 0.5. When X is set to 0, the storage within the reach depends solely on the outflow, simulating level pool routing (e.g., detention basin) and resulting in maximum attenuation of the inflow hydrograph. Conversely, when X is set to 0.5, storage is equally influenced by both inflow and outflow, resulting in no attenuation to the inflow hydrograph as it moves through the reach. In this study, the X parameter was set to 0.25, balancing attenuation and the progression of the inflow hydrograph through the reach [30].
When air temperature is below the freezing point, precipitation generally falls as snow and accumulates on the land surface. In many watersheds, seasonal snowpack formation is an integral component of the annual hydrologic cycle, with accumulation occurring through winter. The snow water equivalent (SWE)—the depth of water obtained from melting a unit column of snow—is the standard metric for quantifying snowpack water content. The current implementation of this phenomenon in the model employs a temperature index approach, which includes a conceptual representation of snowpack energy to estimate liquid water available at the soil surface for infiltration and runoff. A physically based energy balance method is under development for future releases [29]. The temperature index method extends the degree-day approach for snowpack modeling by incorporating a conceptual representation of cold energy storage, limited memory of antecedent conditions, and additional meteorological factors. Unlike the fixed melt rate per degree above freezing in the standard degree-day method—used in SWAT and WATFLOOD, for example—the melt coefficient in the temperature index method varies with snowpack and atmospheric conditions.
Temperature is used to distinguish rain from snow. Snowmelt is calculated as the melt rate multiplied by the temperature difference above the base temperature (typically 0 °C); melt is zero when air temperature is below this threshold. The snowmelt method in HEC-HMS differs from those in other hydrologic models such as WATFLOOD and SWAT primarily in its reliance on a temperature index (degree-day) approach, rather than a fully physically based energy balance. HEC-HMS represents snowpack dynamics conceptually, accounting for cold energy storage and adjusting melt rates based on atmospheric and snowpack conditions. This approach requires relatively few inputs—primarily air temperature and precipitation—making it computationally efficient and practical in data-sparse basins, including many cold-region watersheds. In contrast, WATFLOOD incorporates a more physically oriented degree-day approach that integrates additional cold-region processes, such as snow redistribution and frozen soil infiltration, which can enhance realism but require more extensive datasets. SWAT employs a similar temperature index method for snowmelt but integrates it within a broader physically based watershed framework, coupling snowmelt to soil water balance, evapotranspiration, and land management operations. While WATFLOOD and SWAT can more explicitly account for spatial heterogeneity and complex snow–land interactions, they are often more data-intensive and computationally demanding. HEC-HMS’s simpler parameterization allows for rapid calibration and operational forecasting, though it may be less accurate in representing microclimatic variations or energy fluxes affecting snowmelt, especially under climate change scenarios or highly heterogeneous terrain conditions.
2.3. Model Development
Time series data for daily flow, total daily precipitations, and daily temperature spanning from 1971 to 2014 was used in this study. Two techniques were applied to partition for model calibration and validation. The first technique, referred to as “Method 1”, divided the 1971–2014 dataset based on temporal dependency. Specifically, data from 1 January 1971 to 31 December 2000, was used for model calibration, while data from 1 January 2001, to 31 December 2014, was reserved for model validation. The second technique, “Method 2”, followed a temporally independent approach, where alternate years were allocated for model calibration (i.e., 1971, 1973, 1975, …, 2013) and validation (i.e., 1972, 1974, 1976, …, 2014). These two approaches were selected in alignment with Belvederesi et al. [8,9] to assess the impact of temporally dependent versus independent data on model accuracy. A schematic diagram of the developed model is presented in Figure 2. This methodology was consistently applied to both the temporally dependent (Method 1) and independent (Method 2) approaches.
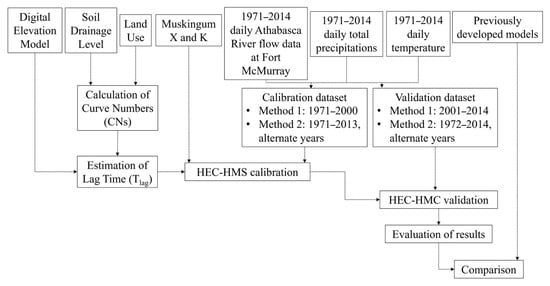
Figure 2.
Schematic diagram illustrating the steps involved in the development of the HECHMS model, including the explanatory variables.
The hydrologic parameters required for calibrating the HEC-HMS model such as lag time and Muskingum parameters were calculated using Formulas (1)–(4) and other methods previously outlined.
2.4. Estimation of Model Performance
This study employed the Root Mean Square Error (RMSE) and the NSE coefficient to assess the accuracy of the results produced by HEC-HMS. These metrics were chosen because they are commonly used in most hydrologic modeling literature, facilitating comparison with previously developed models. The mathematical formulations for RMSE and NSE are as follows:
where Y is the forecasted flow, is the mean of the forecasted flow, X is the observed flow; is the mean of the observed flow, n is the sample size. The RMSE is measured in m3/s, with a lower value (closer 0) indicating higher accuracy. The NSE values range from −∞ to 1, with 1 representing the highest possible model accuracy.
3. Results
3.1. Model Calibration
The climatic variables and flow data used as calibration inputs for the HEC-HMS model (i.e., daily total precipitations, temperature, and Athabasca River flow at Fort McMurray) varied between Method 1 and Method 2. Specifically, daily total precipitation between 1 January 1971, and 31 December 2000, ranged from 0 to 94.5 mm, with the highest amounts typically recorded in August. During the colder months (November to April), average temperatures often fell below freezing, resulting in precipitation in the form of snow. The minimum temperature recorded in Fort McMurray during this period was −39.9 °C in December, while the maximum is 26.7 °C in August. The Athabasca River flow at Fort McMurray was lowest in the winter months and highest in the summer. The highest flow recorded in the 1971–2000 period was 4700 m3/s in July, while the lowest was 88.6 m3/s in January. During winter, the average flow was 192 m3/s, which then increased significantly due to the spring freshet in late April and May. The largest flow was typically observed in June and July, with an average of around 1200 m3/s, followed by a decrease from August through November.
The data inputs used for Method 2 followed a similar pattern to those in Method 1. By using alternate annual from 1 January 1971 to 31 December 2013, the HEC-HMS was calibrated with daily total precipitation ranging from a minimum of 0 and maximum of 57.5 mm in July. Temperatures vary between −38 °C in January and 25.6 °C in July, while the Athabasca River flow ranged from 75 m3/s in December to 4410 m3/s in July. While comparing the time series for daily total precipitations, temperature, and Athabasca River flow at Fort McMurray used in Method 1 and Method 2, it was evident that there were discrepancies in calibration inputs depending on whether temporally dependent or independent variables are used. Notably, the temperature values in Method 2 were generally about 1 °C higher than those in Method 1. Additionally, river flow records in Method 2 tent to be lower overall than those in Method 1 during both winter and summer months. Precipitation values used for calibration in Method 2 were, on average, also lower than those used in Method 1.
Figure 3 presents the results produced by HEC-HMS, including the number of subbasins, the reach routing system, and key model parameters such as the CNs and lag time (Tlag), and subbasins’ characteristics such as basin slope and drainage density. Drainage density, which represents the sum of channel lengths per unit area, provided insight into the subbasin’s shape and hydrological behavior. A higher drainage density suggested a more dendritic (branched) subbasin. These results applied to both Method 1 and Method 2.
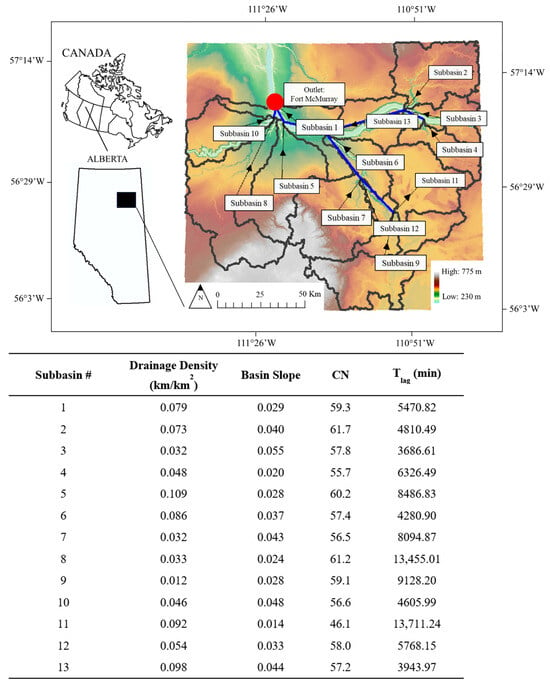
Figure 3.
Map of the area of interest showing the HEC-HMS results, including the number of subbasins, reach routing systems, and key information for each subbasin such as drainage density, basin slope, Curve Numbers (CNs), and lag time (Tlag). The red dot shows the outlet location in Fort McMurray.
The drainage density ranged from 0.012 km/km2 in Subbasin 9 to 0.109 km/km2 in Subbasin 5, indicating that Subbasin 5 is nearly 10 times more dendritic than Subbasin 9. The average basin slope was 3.4%, with values ranging from 1.4% in Subbasin 11 to 5.5% in Subbasin 3. As expected, lower slopes were associated with longer lag times, as the distance for precipitated water to travel to the subbasin outlet increased. For example, Subbasin 3, with the steepest slope, also had the shortest lag time (i.e., 3686 min), as water traveled faster due to increased slope. Conversely, Subbasin 11, with the lowest slope, had the longest lag time (i.e., 13,711.24 min). Subbasin 11 also showed the lowest CN, equal to 46.1. Notably, about 25% of the land Subbasin 11 was categorized as “water” or “wetland”. In contrast, Subbasin 2 had the highest CN, equal to 61.7, and was primarily forested, with approximately 70% of the area covered by “temperate or sub-polar needleleaf forest” and about 23% by “temperate or sub-polar shrubland”. The “temperate or sub-polar shrubland” cover type in Subbasin 2 was the largest among all subbasins, which might have contributed to its high CN. This could be explained by the fact that small or short vegetation typical of shrublands had lower canopy interception and retention compared to needleleaf forests [42]. Subbasin 2 was particularly critical due to its short lag time, high CN, and steep slope, which together resulted in a larger runoff contribution during significant rainfall events, and snowmelt, especially with increasing temperatures.
3.2. Model Validation
The HEC-HMS model was validated using both Method 1 and Method 2. Method 1 used a validation dataset spanning from 1 January 2001 to 31 December 2014, while Method 2 used a validation dataset from 1 January 1972, and 31 December 2014, consisting of alternate years (i.e., 1972, 1974, 1976, …, 2014). Table 1 summarizes the results, providing details on the method used, the sample size for the validation dataset, the NSE and the RMSE values. The “Cold weather” method referred to results captured between 1 December and 16 April of each year in the validation set, while “Warm weather” method referred to the results obtained between 17 April and 30 November.

Table 1.
Summary of the results: Nash-Sutcliffe coefficient (NSE) and Root Mean Square Error (RMSE) for Method 1 and Method 2, with cold (1 December to 16 April) and warm (17 April to 31 November) weather splits.
For the entire dataset, the results showed that Method 1 and Method 2 both yielded an RMSE of 181 m3/s, indicating the two methods performed similarly. The NSE was 0.87 for Method 1 and 0.88 for Method 2, with the small difference (0.01) insufficient to suggest a clear advantage for either method in the overall application. However, when analyzing the “Cold weather” results, a 16 m3/s difference in RMSE was observed between the two methods. Specifically, Method 1 outperformed Method 2, with NSE of 0.79 and 0.78, respectively. This difference might have been due to the larger sample size in the “Cold weather” dataset for Method 2, which likely included more outliers.
For the “Warm weather” dataset, the RMSE for Method 1 was approximately 2 m3/s higher, indicating slightly lower accuracy compared to Method 2. However, the NSE for Method 2 was 0.88, also suggesting marginally lower accuracy. These contrasting results led to the conclusion that neither Method 1 nor Method 2 provided a distinct advantage in terms of accuracy for the “Warm weather” application.
To further analyze the model outcomes and better understand the frequency of error deviations, additional analyses were conducted. Figure 4 and Figure 5 provide graphical summary of the results for Method 1 and Method 2, including: (a) time series of the observed and forecasted daily Athabasca River flow at Fort McMurray, (b) scatter plots comparing the observed against the forecasted Athabasca River flow at Fort McMurray, with 20% and 40% margin of error lines, and (c) bar charts displaying the distribution of data within each error deviation group (0–5%, 5–10%, 10–15%, …, above 50%) for the cold weather, warm weather, and entire-year applications.
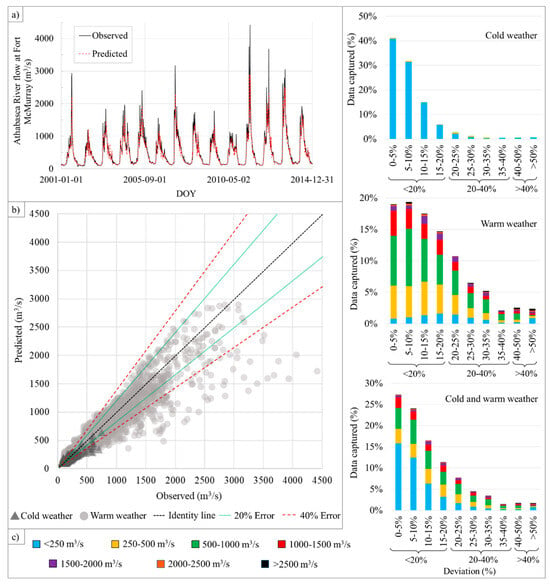
Figure 4.
Results for Method 1: (a) validation results (time series of daily observed and forecasted river flow between 2001 and 2014); (b) scatter plots comparing observed versus the forecasted values, with the “cold weather” period defined as 1 December to 16 April, and “warm weather” period from 17 April to 30 November; and (c) bar charts showing the percentage of data points falling within each error deviation category (i.e., 0–5%, 5–10%, etc.).
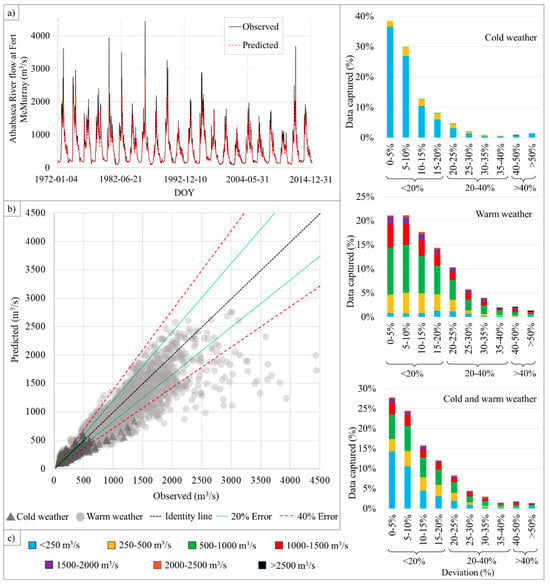
Figure 5.
Results for Method 2: (a) validation results (time series of daily observed and forecasted river flow between 1972 and 2014, with alternate years); (b) scatter plots comparing observed versus the forecasted values, with the “cold weather” period defined as 1 December to 16 April, and “warm weather” period from 17 April to 30 November; and (c) bar charts showing the percentage of data points falling within each error deviation category (i.e., 0–5%, 5–10%, etc.).
In Figure 4 and Figure 5, panels (a) showed that the timing of flow peaks was accurately detected, with high precision, for both Method 1 and 2. However, the magnitude of the flow was consistently underestimated throughout the entire validation period. This trend was observed in both methods. As demonstrated in panels (b) of Figure 4 and Figure 5, the flow was generally under-forecasted in both the cold and warm weather periods. The number of data points falling outside the 40% error margin was notably larger for under-forecasted values compared to over-forecasts. Although Method 2 appeared to produce more values with errors greater than 40%, it is important to note that the dataset used for Method 2 was larger than that of Method 1.
The error deviation results were detailed in panel (c) of Figure 4 and Figure 5, where bar charts for the cold weather, warm weather, and full-year applications represented the percentage of data points falling within each error deviation category. For the cold-weather period, approximately 40% of the data fell within a 5% error, about 70% within a 10% error, and around 93% within a 20% error. Overall, about 70% of the data fell under less than 20% error range. It was worth noting that the “Cold weather” dataset primarily consisted of flow values under 500 m3/s. In contrast, the “Warm weather” dataset included a wide range of flow magnitudes, ranging from below 250 m3/s to above 2500 m3/s. The results for this period indicated that 68% of data fell within a 20% error range for Method 1, while Method 2 captured 75% of the data within the same range. Finally, for the full-year application, approximately 80% for both Method 1 and 2 was captured within a 20% error margin, indicating relatively high accuracy in the overall performance for both methods.
4. Discussion
4.1. Significance of the Results and Model Limitations
This study demonstrated that using HEC-HMS as hydrological model offers a practical approach for forecasting river flow, considering the region’s current hydrology in terms of temperature and precipitation rates, while minimizing complex descriptors that could increase model computation times, resource demands, and requirements. The model also showed limited sensitivity to time dependent variables in the calibration phase, using historical records of precipitations and temperature from point locations. Additionally, as HEC-HMS is provided by the US Army Corps of Engineers, it extends its suitability beyond purely scientific applications to include various engineering uses [29]. The HEC-HMS models adopted in the scope of this study successfully simulated the Athabasca River flow at Fort McMurray with high accuracy during both colder and warmer months (i.e., NSE equal to 0.79 and 0.81, respectively). Data from nearby stations for total precipitations, temperature, and river flow at Fort McMurray, along with land use, soil, and DEM maps were used to calculate flow at a specific downstream location. This means that the calibration and validation process relied on data from specific gauges as explanatory variables to replicate the hydrology within the watershed. Incorporating gridded precipitation and temperature maps could improve model accuracy, particularly when forecasting river flow in poorly gauged and ungauged locations, in cold weather regions. These maps could address issues of underestimation and flow peak forecasting by informing the model about runoff distribution. Notably, larger model errors (i.e., >50%) were observed during flow peaks, suggesting that the magnitude of the flow peaks was often underestimated, likely due to simplifications in the simulation of snowmelt processes and the use of point location for temperature and precipitation inputs over gridded maps. This limitation, together with the use of 2015 land use maps might mislead future predictions given the rapid industrial developments and corresponding land use changes in the area. We recommend using gridded precipitation and temperature data and multiple land use maps, such as those collected every five years, to more accurately capture the impact of both past and current developments on river flows to increase flood forecasting capabilities.
The use of Method 1 and Method 2 with time series data, which incorporated different calibration and validation datasets, did not yield significantly different results. This suggests that temporally dependent variables did not have a substantial impact on the performance of the HEC-HMS model and did not pose a major limitation to its development. However, to further investigate this, additional analyses were conducted to ensure that the HEC-HMS model results could be compared with those of previously developed models from the local literature that employed a similar approach to model calibration and validation.
Hydrological models are often associated with uncertainties when simulating hydrological processes. Key sources of these uncertainties include the input data, parameter estimation, simplifications made in representing the natural system, calibration, and the model’s structure [43]. In ungauged and poorly gauged areas, these uncertainties can significantly reduce model accuracy and reliability. Additionally, cumulative effects assessment (CEA), which systematically evaluates the impacts of incremental, accumulating, and interacting stressors, could support model development. However, due to the rapid industrial development in the LAR, measuring the cumulative effects of climate change and anthropogenic interventions is challenging. This makes it difficult to accurately inform the model of the short- and long-term changes that influence river flow [44]. Incorporating CEA into the HEC-HMS model could enhance its potential and applicability.
4.2. Comparison Against Previously Developed Models
Comparing the results of this study with previously developed process-based models for the same area, such as MIKE-SHE [43], CHARM/WATFLOOD [25], SWAT [22,45], MISBA [27], HGS [28], and VIC [19,21] we concluded that HEC-HMS demonstrated similar or superior performance potential while requiring fewer explanatory variables (e.g., precipitation and temperature) for model calibration. In particular, Aryal et al. [43] obtained NSE equal to 0.76 and emphasized the importance of considering factors like evapotranspiration and infiltration when assessing changes in system hydrology, a point also supported by Holmes et al. [25] in their use of CHARM/WATFLOOD, who obtained a NSE equal to 0.72 using meteorological and routing inputs. While HEC-HMS performed well in the short term, it was not capable of accurately forecasting river flows over the long term (30–50 years) or capturing significant changes in watershed hydrology, particularly in relation to climate change impacts. Dastour et al. [46], Aryal et al. [24], and Zaghloul et al. [47] stressed the importance of incorporating climate change scenarios alongside land use changes when modeling the ARB, as runoff was a major contributor to river flow. MISBA [27] could overcome this limitation, excelling in long-term projections that incorporate various climate change scenarios. However, the results were not reported using NSE, preventing a direct comparison of model performance with HEC-HMS. Overall, the SWAT application by Shresta and Wang [45] achieved an NSE of 0.91, higher than the 0.82 obtained in this study using HEC-HMS, averaged across all cases (total annual, cold, and warm periods). HEC-HMS outperformed SWAT when compared to Betrie et al. [22], who reported an NSE of 0.79. Additionally, Hwang et al. [28] identified groundwater recharge and surface runoff as the main contributors to streamflow in the ARB. The HEC-HMS results, which used precipitation inputs, supported this conclusion, as the flow estimates were primarily influenced by surface runoff. HEC-HMS showed lower sensitivity to temperature and precipitation compared to SWAT [45], though it occasionally produced biased results, particularly in spring when it failed to accurately capture snowmelt timing due to the high inter-annual variability. This limitation can be overcome by incorporating key modifiers—such as lapse rates for elevation effects, precipitation phase discrimination, and variable melt coefficients to reflect changing snowpack conditions. The ability to discretize watersheds into elevation bands further refines the timing by accounting for differences in snow accumulation and melt rates across altitudinal gradients. Although these approaches do not resolve all physical processes in detail, they exploit the strongest and most accessible predictors of melt timing, enabling robust simulations in data-scarce environments. River flow simulations under climate change scenarios can be improved by integrating downscaled climate projections capable of representing altered precipitation patterns, temperature regimes, and snowmelt dynamics. Using bias-corrected outputs from global or regional climate models ensures that input variables such as temperature, precipitation, and land use changes reflect realistic local conditions. Scenario-based simulations allow for the assessment of multiple plausible futures, capturing a range of hydrologic responses to warming trends, shifts in snow-to-rain ratios, and changes in extreme event frequency. It is recommended to incorporate elements such as flexible parameterization—dynamic melt coefficients, soil moisture thresholds, and infiltration rates—to enable models to adapt to projected seasonal and inter-annual variability. In snow-dominated watersheds, explicitly representing changes in snow accumulation, timing of melt, and rain-on-snow events improves spring runoff projections. Coupling hydrologic models with uncertainty analysis and ensemble modeling further refines projections by quantifying the range of possible river flow outcomes, thus improving the robustness of results, especially in areas where a lack of long continuous streamflow data, important for identifying regime shift changes, could represent a study limitation [48].
Compared with traditional models, HEC-HMS employs simplified temperature-index snowmelt and runoff processes that require fewer input variables (e.g., basic meteorological data and limited watershed characteristics), making it suitable where detailed datasets—such as soil profiles, vegetation parameters, or high-resolution climate data—are unavailable. In terms of computational efficiency, HEC-HMS is less computationally intensive, enabling quicker simulations and easier integration into operational forecasting workflows in remote or resource-limited settings. HEC-HMS’s modular design allows users to select and customize hydrologic components (e.g., snowmelt, infiltration, routing) appropriate to local conditions without the complexity of fully distributed models like VIC or SWAT. User accessibility and open access are also advantages as HEC-HMS is freely available with extensive documentation and community support, reducing barriers to adoption in research and management compared to proprietary or highly complex models. Its capability to perform reasonable simulations with limited calibration data suits data-scarce cold regions where gauging networks are sparse or incomplete, unlike data-demanding models that depend on comprehensive observations. While simplified, HEC-HMS incorporates conceptual snowpack energy balance elements and potential elevation band discretization, enabling representation of snowmelt dynamics critical in cold climates. These advantages position HEC-HMS as a practical, robust tool for hydrologic modeling and water resource management in cold, data-limited environments.
5. Conclusions
This study used the HEC-HMS model to simulate the Athabasca River flow at Fort McMurray, utilizing station climate data for daily total precipitation, temperature, and river flow, along with land use, soil, and DEM maps as model inputs. The results demonstrated that HEC-HMS could accurately forecast river flow across both colder and warmer periods throughout the year. Two calibration and validation methods were explored: Method 1 applied a temporally dependent approach to the 1971–2014 time range, using data from 1 January 1971 to 31 December 2000, for model calibration and from 1 January 2001 to 31 December 2014, for validation. Method 2, on the other hand, divided the same time range using a temporally independent approach, allocating alternate annual data for calibration (e.g., 1971, 1973, 1975, …, 2013) and validation (e.g., 1972, 1974, 1976, …, 2014). The results from both methods did not differ significantly, suggesting that HEC-HMS was relatively insensitive to whether temporally dependent or independent datasets were used during model development. Method 2 showed slightly higher Nash-Sutcliffe efficiency (NSE) at 0.88 and lower root mean square error (RMSE) at 181.81 m3/s compared to Method 1 (NSE = 0.87, RMSE = 181.88 m3/s).
In conclusion, the HEC-HMS model is recommended for simulating river flow in poorly gauged cold regions. Using time series data instead of average daily data is strongly recommended, as the latter can introduce larger errors due to increased sensitivity to temporally dependent variables during calibration. While HEC-HMS effectively simulates hydrologic processes in data-scarce cold regions, its simplified temperature-index snowmelt approach occasionally produces biases, particularly in spring, due to challenges in accurately capturing snowmelt timing under high inter-annual variability. Future developments could include the use of gridded climate data (e.g., precipitation and temperature) to further enhance model performance. Enhanced accuracy under climate change scenarios could be achieved by incorporating bias-corrected downscaled climate projections, scenario-based simulations, and flexible parameterization to capture seasonal and inter-annual variability. Additionally, coupling HEC-HMS with uncertainty analysis and ensemble modeling would strengthen its predictive robustness. These advancements would allow the model to retain its computational efficiency and minimal data requirements while improving its capability to forecast flow dynamics in cold, remote, and poorly gauged watersheds. The findings of this study contribute to the understanding of process-based models in cold regions experiencing intensive anthropogenic development, with potential applications in river flow forecasting, flood management, and other hydrological studies that support local communities in the LAR and similar regions worldwide.
Author Contributions
Conceptualization, Q.K.H.; Methodology, Q.K.H.; Formal analysis, C.B.; Supervision, G.A.; Funding acquisition, G.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All the data were collected by the government agencies and are freely accessible to the public. The data presented in this study are available in the references [11,12,13].
Acknowledgments
The authors would like to thank the Water Survey of Canada for providing us the historical average daily water flow data during the 1971 to 2014 period.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
References
- Government of Alberta. Lower Athabasca Region—Surface Water Quantity Management Framework for the Lower Athabasca River. Available online: https://open.alberta.ca/publications/9781460121733 (accessed on 23 July 2025).
- Shrubsole, D.; Walters, D.; Veale, B.; Mitchell, B. Integrated Water Resources Management in Canada: The experience of watershed agencies. Int. J. Water Resour. Dev. 2017, 33, 349–359. [Google Scholar]
- BP Statistical Review of World Energy. Available online: https://www.bp.com/en/global/corporate/energy-economics/statistical-review-of-world-energy/oil.html (accessed on 23 July 2025).
- Government of Canada. Oil Sands: A Strategic Resource for Canada, North America and the Global Market. Available online: https://publications.gc.ca/site/eng/9.805592/publication.html (accessed on 23 July 2025).
- Klemt, W.H.; Kay, M.L.; Wiklund, J.A.; Wolfe, B.B.; Hall, R.I. Assessment of vanadium and nickel enrichment in Lower Athabasca River floodplain lake sediment within the Athabasca Oil Sands Region (Canada). Environ. Pollut. 2020, 265, 114920. [Google Scholar] [CrossRef]
- Peters, D.L.; Watt, D.; Devito, K.; Monk, W.A.; Shrestha, R.R.; Baird, D.J. Changes in geographical runoff generation in regions affected by climate and resource development: A case study of the Athabasca River. J. Hydrol. Reg. Stud. 2022, 29, 100981. [Google Scholar] [CrossRef]
- McFadyen, S.A. Disturbance Related Patterns in Fish Community Structure and Function in River Systems of the Lower Athabasca Oil Sands Region, Alberta. Ph.D. Thesis, University of Victoria, Victoria, BC, Canada, 2015. Available online: https://dspace.library.uvic.ca/handle/1828/7038 (accessed on 23 July 2025).
- Belvederesi, C.; Dominic, J.A.; Hassan, Q.K.; Gupta, A.; Achari, G. Predicting River Flow Using an AI-Based Sequential Adaptive Neuro-Fuzzy Inference System. Water 2020, 12, 1622. [Google Scholar] [CrossRef]
- Belvederesi, C.; Dominic, J.A.; Hassan, Q.K.; Gupta, A.; Achari, G. Short-Term River Flow Forecasting Framework and Its Application in Cold Climatic Regions. Water 2020, 12, 3049. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Vujadinovic, T.; Hassan, Q.K. Application of the Least-Squares Wavelet software in hydrology: Athabasca River Basin. J. Hydrol. Reg. Stud. 2021, 36, 100847. [Google Scholar] [CrossRef]
- Government of Canada. Historical Climate Data. Available online: https://climate.weather.gc.ca/ (accessed on 23 July 2025).
- Government of Canada. Real-Time Hydrometric Data Map Search. Available online: https://wateroffice.ec.gc.ca/map/index_e.html (accessed on 23 July 2025).
- Alberta Climate Information Service. Current and Historical Alberta Weather Station Data Viewer. Available online: https://acis.alberta.ca/weather-data-viewer.jsp (accessed on 23 July 2025).
- Wagena, M.B.; Goering, D.; Collick, A.S.; Bock, E.; Fuka, D.R.; Buda, A.; Easton, Z.M. Comparison of short-term streamflow forecasting using stochastic time series, neural networks, process-based, and Bayesian models. Environ. Model. Softw. 2020, 126, 104669. [Google Scholar] [CrossRef]
- Bhusal, A.; Parajuli, U.; Regmi, S.; Kalra, A. Application of Machine Learning and Process-Based Models for Rainfall-Runoff Simulation in DuPage River Basin, Illinois. Hydrology 2022, 9, 117. [Google Scholar] [CrossRef]
- Veiga, V.B.; Hassan, Q.K.; He, J. Development of Flow Forecasting Models in the Bow River at Calgary, Alberta, Canada. Water 2014, 7, 99–115. [Google Scholar] [CrossRef]
- Ahani, A.; Shourian, M.; Rahimi Rad, P. Performance Assessment of the Linear, Nonlinear and Nonparametric Data Driven Models in River Flow Forecasting. Water Resour. Manag. 2018, 32, 383–399. [Google Scholar] [CrossRef]
- Toth, B.; Pietroniro, A.; Conly, F.M.; Kouwen, N. Modelling Climate Change Impacts in the Peace and Athabasca Catchment and Delta: Hydrological Model Application. Hydrol. Process. 2006, 20, 4197–4214. [Google Scholar] [CrossRef]
- Eum, H.-I.; Yonas, D.; Prowse, T. Uncertainty in Modelling the Hydrologic Responses of a Large Watershed: A Case Study of the Athabasca River Basin, Canada. Hydrol. Process. 2014, 28, 4272–4293. [Google Scholar] [CrossRef]
- Rood, S.B.; Stupple, G.W.; Gill, K.M. Century-Long Records Reveal Slight, Ecoregion-Localized Changes in Athabasca River Flows. Hydrol. Process. 2014, 29, 805–816. [Google Scholar] [CrossRef]
- Eum, H.-I.; Dibike, Y.; Prowse, T. Climate-Induced Alteration of Hydrologic Indicators in the Athabasca River Basin, Alberta, Canada. J. Hydrol. 2017, 544, 327–342. [Google Scholar] [CrossRef]
- Shresta, N.; Wang, J. Hydrological Modeling of Athabasca River Basin, Canada using Soil and Water Assessment Tool (SWAT). In Proceedings of the Calgary GeoConvention 2017, Calgary, AB, Canada, 18–19 May 2017. [Google Scholar]
- Droppo, I.; Prowse, T.; Bonsal, B.; Dibike, Y.; Beltaos, S.; Krishnappan, B.; Eum, H.; Kashyap, S.; Shakibaeinia, A.; Gupta, A. Regional Hydroclimatic and Sediment Modeling: Oil Sands Monitoring Program; Technical Report Series; Government of Alberta: Edmonton, AB, Canada, 2018.
- Aryal, S.; Babel, M.S.; Gupta, A.; Farjad, B.; Khadka, D.; Hassan, Q.K. Assessment of hydrological baseline condition and its alteration in Athabasca River Basin, Canada. J. Hydrol. Reg. Stud. 2024, 53, 101805. [Google Scholar] [CrossRef]
- Holmes, T.L.; Stadnyk, T.A.; Asadzadeh, M.; Gibson, J.J. Variability in flow and tracer-based performance metric sensitivities reveal regional differences in dominant hydrological processes across the Athabasca River basin. J. Hydrol. Reg. Stud. 2022, 41, 101088. [Google Scholar] [CrossRef]
- Shrestha, N.; Du, X.; Wang, J. Assessing Climate Change Impacts on Freshwater Resources of the Athabasca River Basin, Canada. Sci. Total Environ. 2017, 601, 425–440. [Google Scholar] [CrossRef]
- Kerkhoven, E.; Gan, T.Y. Differences in the Potential Hydrologic Impact of Climate Change to the Athabasca and Fraser River Basins of Canada with and without Considering Shifts in Vegetation Patterns Induced by Climate Change. J. Hydrometeorol. 2013, 14, 963–976. [Google Scholar] [CrossRef]
- Hwang, H.-T.; Park, Y.-J.; Sudicky, E.A.; Berg, S.J.; McLaughlin, R.; Jones, J.P. Understanding the Water Balance Paradox in the Athabasca River Basin, Canada. Hydrol. Process. 2018, 32, 729–746. [Google Scholar] [CrossRef]
- US Army Corps of Engineers. HEC-HMS. Available online: https://www.hec.usace.army.mil/software/hec-hms/ (accessed on 23 July 2025).
- US Army Corps of Engineers. Tutorials and Guides. Available online: https://www.hec.usace.army.mil/software/hec-hms/training.aspx (accessed on 23 July 2025).
- Ouédraogo, W.A.A.; Raude, J.M.; Gathenya, J.M. Continuous Modeling of the Mkurumudzi River Catchment in Kenya Using the HEC-HMS Conceptual Model: Calibration, Validation, Model Performance Evaluation and Sensitivity Analysis. Hydrology 2018, 5, 44. [Google Scholar] [CrossRef]
- Bhuiyan, H.A.K.M.; McNairn, H.; Powers, J.; Merzouki, A. Application of HEC-HMS in a Cold Region Watershed and Use of RADARSAT-2 Soil Moisture in Initializing the Model. Hydrology 2017, 4, 9. [Google Scholar] [CrossRef]
- Mandal, S.P.; Chakrabarty, A. Flash flood risk assessment for upper Teesta River basin: Using the hydrological modeling system (HEC-HMS) software. Model. Earth Syst. Environ. 2016, 2, 59. [Google Scholar] [CrossRef]
- Tassew, B.G.; Belete, M.A.; Miegel, K. Application of HEC-HMS Model for Flow Simulation in the Lake Tana Basin: The Case of Gilgel Abay Catchment, Upper Blue Nile Basin, Ethiopia. Hydrology 2019, 6, 21. [Google Scholar] [CrossRef]
- Gumindoga, W.; Rwasoka, D.T.; Nhapi, I.; Dube, T. Ungauged runoff simulation in Upper Manyame Catchment, Zimbabwe: Application of the HEC-HMS model. Phys. Chem. Earth 2017, 100, 371–382. [Google Scholar] [CrossRef]
- Athabasca River Basin Research Institute. About the Athabasca River Basin. Available online: http://arbri.athabascau.ca/About-the-Athabasca-River-basin/Index.php (accessed on 23 July 2025).
- Sauchyn, D.J.; St-Jacques, J.M.; Luckman, B.H. Long-term reliability of the Athabasca River (Alberta, Canada) as the water source for oil sands mining. Proc. Natl. Acad. Sci. USA 2015, 112, 12621–12626. [Google Scholar] [CrossRef]
- Government of Canada. Water Survey of Canada. Available online: https://www.canada.ca/en/environment-climate-change/services/water-overview/quantity/monitoring/survey.html (accessed on 23 July 2025).
- University of Calgary. Digital Elevation Model Maps. Available online: https://sands.ucalgary.ca/App/DEMIndexMaps/index.html (accessed on 23 July 2025).
- Natural Resources Canada. Land Cover. Available online: https://natural-resources.canada.ca/maps-tools-publications/satellite-elevation-air-photos/satelite-imagery/land-cover (accessed on 23 July 2025).
- Government of Alberta. Alberta Soil Information Survey. Available online: https://www.alberta.ca/alberta-soil-information-viewer.aspx (accessed on 23 July 2025).
- Zheng, C.; Jia, L. Global canopy rainfall interception loss derived from satellite earth observations. Ecohydrology 2020, 13, e2186. [Google Scholar] [CrossRef]
- Aryal, S.; Babel, S.M.; Gupta, A.; Farjad, B.; Khadka, D.; Hassan, Q. Attribution of the Climate and Land Use Change Impact on the Hydrological Processes of Athabasca River Basin, Canada. Hydrology 2025, 12, 7. [Google Scholar] [CrossRef]
- Squires, A.J.; Westbrook, C.J.; Dubé, M.J. An approach for assessing cumulative effects in a model river, the Athabasca River basin. Integr. Environ. Assess. Manag. 2010, 6, 119–134. [Google Scholar] [CrossRef]
- Betrie, G.D.; Deng, B.; Wang, J. Integrated Modelling of the Athabasca River Basin Using SWAT. In 2015 Proceedings of Science and Technology Innovations; Athabasca University Press: Alberta, Canada, 2015; pp. 27–38. [Google Scholar]
- Dastour, H.; Ghaderpour, E.; Zaghloul, M.S.; Farjad, B.; Gupta, A.; Eum, H.; Achari, G.; Hassan, Q.K. Wavelet-based spatiotemporal analyses of climate and vegetation for the Athabasca river basin in Canada. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103044. [Google Scholar] [CrossRef]
- Zaghloul, M.S.; Ghaderpour, E.; Dastour, H.; Farjad, B.; Gupta, A.; Eum, H.; Achari, G.; Hassan, Q.K. Long Term Trend Analysis of River Flow and Climate in Northern Canada. Hydrology 2022, 9, 197. [Google Scholar] [CrossRef]
- Dastour, H.; Gupta, A.; Achari, G.; Hassan, Q.K. A Robust Regime Shift Change Detection Algorithm for Water-Flow Dynamics. Water 2023, 15, 1571. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).