Optimizing Resilient Sustainable Citrus Supply Chain Design
Abstract
1. Introduction
2. Literature Review
2.1. Resilience in Agri-Food Supply Chains
2.2. Citrus Supply Chains
3. Proposed Mathematical Model
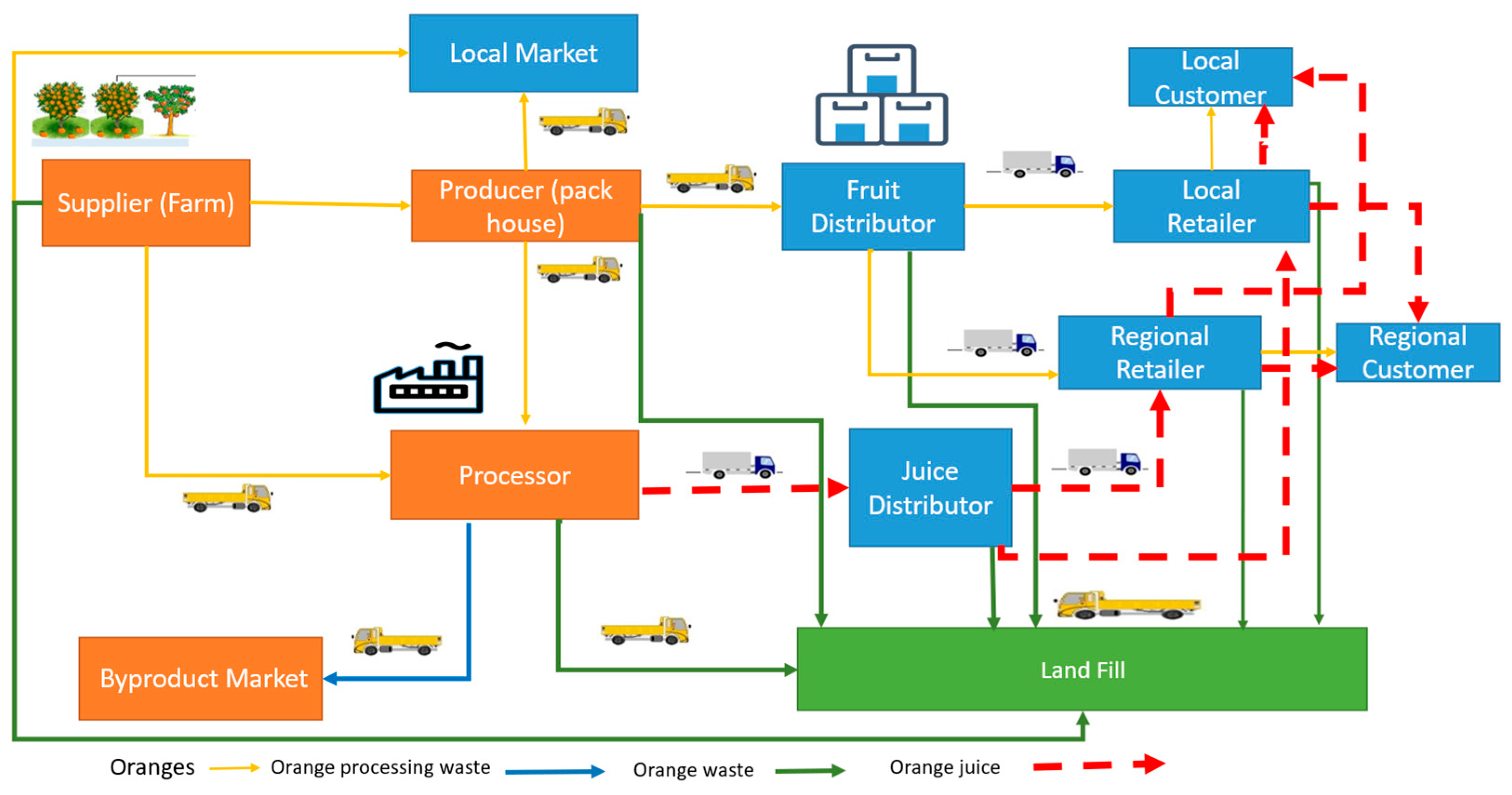
3.1. Citrus Supply Chain and Model Description
3.2. Model Assumptions
- The return flows of products are not considered.
- The CPW is assumed to be sent to one byproduct market, although different byproducts are generated. This is because the CPW can be sold as animal feed, for example.
- The demand is deterministic, according to the forecasted quantities.
- No backorders are allowed, and all demand should be met.
- Wages are considered the same for all stakeholders in the same echelon and depend on the number of units produced.
- Inventory costs at retailers are the same for both fruit and juice, since they are stored in a refrigerated space, and they take up almost the same area.
- Transportation vehicles among stakeholders have unlimited capacity since they are outsourced.
3.3. Model Indices
3.4. Model Decision Variables
3.5. Model Objective Function
3.6. Model Constraints
4. Model Application
4.1. Complete Citrus Supply Chain
4.2. Case Study in Egypt
5. Results and Discussions
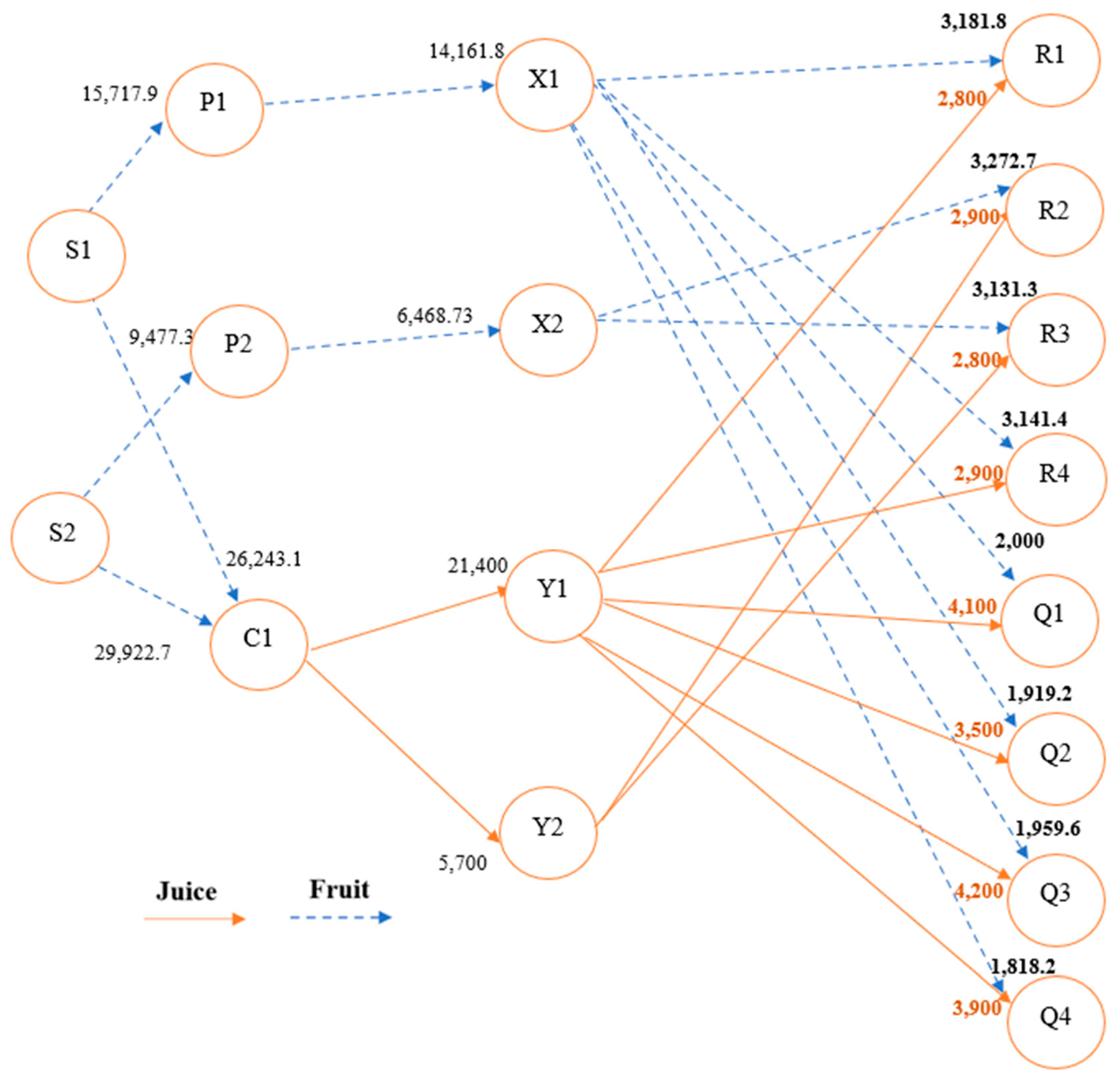
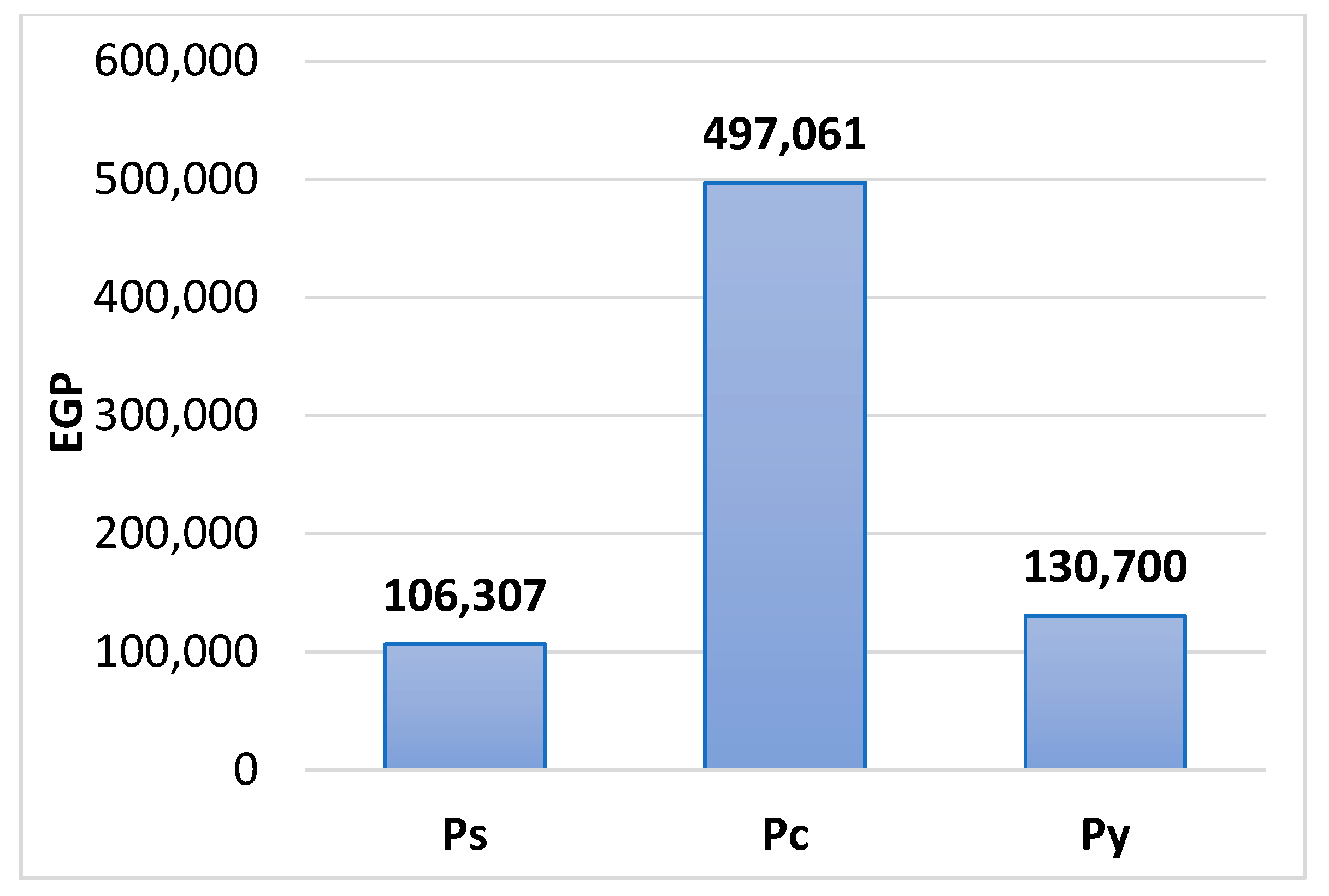
5.1. Complete Supply Chain Model Results
5.2. Disruption Scenarios in Complete Supply Chain Model Results
5.2.1. Disruptions at Supplier
5.2.2. Disruptions at Packhouse
5.2.3. Disruptions at Processor
5.2.4. Disruptions at Outbound Logistics
5.3. Case Study Model Results
6. Conclusions and Implications
6.1. Conclusions
6.2. Managerial Implications
- A multi-supplier strategy aids in achieving supply chain resilience in the event of complete disruptions in one of the suppliers.
- Having more than one packhouse could be sufficient for being resilient without increasing the capacities of existing packhouses in the case of complete disruption in one of the packhouses.
- In case one of the processors completely fails, it might be essential to increase the capacity of the operational processors or have a backup facility with enough capacity.
- It might be necessary to consider an alternative port in case of disruptions in present ports.
6.3. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Supplier parameters | ||
| αsps | Selling price of one kg of fruit from supplier s to packhouse (LE/kg) | |
| αscs | Selling price of one kg of fruit from supplier s to processer (LE/kg) | |
| αsos | Selling price of one kg of fruit from supplier s to local market (LE/kg) | |
| VCsst | Variable cost at supplier s in time t (LE/period) | |
| ECsst | Energy cost at supplier s in time t (LE/period) | |
| TRCsoso | Transportation cost from supplier s to local market o (LE/km/kg) | |
| TRCslsl | Transportation cost from supplier s to landfill l (LE/km/kg) | |
| Ysoso | Distance between supplier s and local market o (km) | |
| Yslsl | Distance between supplier s and landfill l (km) | |
| λsst | Production quantity at supplier s in time t (kgs/period) | |
| θss | Percentage of fruit waste at supplier s (percent) | |
| MQss | Percentage of non-conforming fruit going to local market from supplier s (percent) | |
| Packhouse parameters | ||
| αpxp | Selling price of one kg of fruit from packhouse p to fruit distributor (LE/kg) | |
| αpcp | Selling price of one kg of fruit from packhouse p to processor (LE/kg) | |
| αpop | Selling price of one kg of fruit from packhouse p to local market (LE/kg) | |
| VCppt | Variable cost at packhouse p in time t (LE/period) | |
| MCppt | Maintenance cost at packhouse p in time t (LE/period) | |
| ECppt | Energy cost at packhouse p in time t (LE/period) | |
| TRCspsp | Transportation cost from supplier s to packhouse p (LE/km/kg) | |
| TRCpopo | Transportation cost from packhouse p to local market o (LE/km/kg) | |
| TRCplpl | Transportation cost from packhouse p to landfill l (LE/km/kg) | |
| Yspsp | Distance between supplier s and packhouse p (km) | |
| Ypopo | Distance between packhouse p and local market o (km) | |
| Yplpl | Distance between packhouse p and landfill l (km) | |
| hpp | Inventory holding cost of one kg of fruit at packhouse p (LE/kg) | |
| θpp | Percentage of fruit waste at packhouse p (percent) | |
| MQpp | Percentage of non-conforming fruit going to local market from packhouse p (percent) | |
| λhpp | Holding inventory capacity at packhouse p (kgs) | |
| λppt | Production capacity at packhouse p in time t (kgs/period) | |
| Processor parameters | ||
| αcyc | Selling price of juice from processor c to fruit distributor (LE/kg) | |
| αcbc | Selling price of juice processing waste from processor c to byproduct market (LE/kg) | |
| VCcct | Variable cost at processor c in time t (LE/period) | |
| MCcct | Maintenance cost at processor c in time t (LE/period) | |
| ECcct | Energy cost at processor c in time t (LE/period) | |
| TRCscsc | Transportation cost from supplier s to processor c (LE/km/kg) | |
| TRCpcpc | Transportation cost from packhouse p to processor c (LE/km/kg) | |
| TRCclcl | Transportation cost from processor c to landfill l (LE/km/kg) | |
| Yscsc | Distance between supplier s and processor c (km) | |
| Ypcpc | Distance between packhouse p and processor c (km) | |
| Yclcl | Distance between processor c and landfill l (km) | |
| hcc | Inventory holding cost per unit of juice at processor c (LE/kg) | |
| θcc | Percentage of fruit waste at processor c (percent) | |
| λhcc | Holding inventory capacity at processor c (kgs) | |
| λcct | Production capacity at processor c in time t (kgs/period) | |
| Fruit distributor parameters | ||
| αxrx | Selling price of one kg of fruit from fruit distributor x to local retailer (LE/kg) | |
| αxqx | Selling price of one kg of fruit from fruit distributor x to regional retailer (LE/kg) | |
| Wx | Wages at fruit distributor (LE/kg) | |
| MCxxt | Maintenance cost at fruit distributor x in time t (LE/period) | |
| ECxxt | Energy cost at fruit distributor x in time t (LE/period) | |
| hxx | Inventory holding cost of one kg of fruit at fruit distributor x (LE/kg) | |
| TRCpxpx | Transportation cost from packhouse p to fruit distributor x (LE/km/kg) | |
| TRCxlxl | Transportation cost from fruit distributor x to landfill l (LE/km/kg) | |
| Ypxpx | Distance between packhouse p and fruit distributor x (km) | |
| Yxlxl | Distance between fruit distributor x and landfill l (km) | |
| θxx | Percentage of the fruit waste at fruit distributor x (percent) | |
| λhxx | Holding inventory capacity at fruit distributor x (kgs) | |
| Juice distributor parameters | ||
| αyry | Selling price of juice from juice distributor y to local retailer (LE/kg) | |
| αyqy | Selling price of juice from juice distributor y to regional retailer (LE/kg) | |
| Wy | Wages at juice distributor (LE/kg) | |
| MCyyt | Maintenance cost at juice distributor y in time t (LE/period) | |
| ECyyt | Energy cost at juice distributor y in time t (LE/period) | |
| TRCcycy | Transportation cost from processor c to juice distributor y (LE/km/kg) | |
| Ycycy | Distance between processor c and juice distributor y (km) | |
| hyy | Inventory holding cost per unit of juice at juice distributor y (LE/kg) | |
| λhyy | Holding inventory capacity at juice distributor y (kgs) | |
| Local retailer parameters | ||
| αfrr | Selling price of one kg of fruit at local retailer r (LE/kg) | |
| αjrr | Selling price of one kg of juice at local retailer r (LE/kg) | |
| Dfrrt | Demand for fruit at local retailer r in time t (kg/period) | |
| Djrrt | Demand for juice at local retailer r in time t (kg/period) | |
| Wr | Wages at local retailer (LE/kg) | |
| MCrrt | Maintenance cost at local retailer r in time t (LE/period) | |
| ECrrt | Energy cost at local retailer r in time t (LE/period) | |
| TRCxrxr | Transportation cost from fruit distributor x to local retailer r (LE/km/kg) | |
| TRCyryr | Transportation cost from juice distributor y to local retailer r (LE/km/kg) | |
| TRCrlrl | Transportation cost from local retailer r to landfill l (LE/km/kg) | |
| Yxrxr | Distance between fruit distributor x and local retailer r (km) | |
| Yyryr | Distance between from juice distributor y and local retailer r (km) | |
| Yrlrl | Distance between local retailer r and landfill l (km) | |
| hrr | Inventory holding cost per unit at local retailer r (LE/kg) | |
| θrr | Percentage of the fruit waste at local retailer r (percent) | |
| λhfrr | Holding inventory capacity of fruit at local retailer r (kgs) | |
| λhjrr | Holding inventory capacity of juice at local retailer r (kgs) | |
| Regional retailer parameters | ||
| αfqq | Selling price of one kg of fruit at regional retailer q (LE/kgs) | |
| αjqq | Selling price of one kg of juice at regional retailer q (LE/kgs) | |
| Dfqqt | Demand for fruit at regional retailer q in time t (kg/period) | |
| Djqqt | Demand for juice at regional retailer q in time t (kg/period) | |
| Wq | Wages at regional retailer (LE/kg) | |
| MCqqt | Maintenance cost at regional retailer q in time t (LE/period) | |
| ECqqt | Energy cost at regional retailer q in time t (LE/period) | |
| TRCxqxq | Transportation cost from fruit distributor x to regional retailer q (LE/km/kg) | |
| TRCyqyq | Transportation cost from juice distributor y to regional retailer q (LE/km/kg) | |
| TRCqlql | Transportation cost from regional retailer q to landfill l (LE/km/kg) | |
| Yxqxq | Distance between fruit distributor x and regional retailer q (km) | |
| Yyqyq | Distance between from juice distributor y and regional retailer q (km) | |
| Yqlql | Distance between regional retailer q and landfill l (km) | |
| hqq | Inventory holding cost per unit at regional retailer q (LE/kg) | |
| θqq | Percentage of the fruit waste at regional retailer q (percent) | |
| λhfqq | Holding inventory capacity of fruit at regional retailer q (kgs) | |
| λhjqq | Holding inventory capacity of juice at regional retailer q (kgs) | |
| Abbreviations | ||
| DC | Cost of waste disposal for one kg of fruit (LE/kg) | |
| M | Big value | |
| Auxiliary variables | ||
| PS | Profits of suppliers (LE) | |
| REVSst | Revenue at supplier s in time t (LE/period) | |
| TCSst | Total cost at supplier s in time t (LE/period) | |
| COTSst | Transportation cost related to supplier s in time t (LE/period) | |
| PP | Profits of packhouses (LE) | |
| REVPpt | Revenue at packhouse p in time t (LE/period) | |
| TCPpt | Total cost at packhouse p in time t (LE/period) | |
| PCPpt | Purchasing cost at packhouse p in time t (LE/period) | |
| COTPpt | Transportation cost related to packhouse p in time t (LE/period) | |
| HCPpt | Holding cost at packhouse p in time t (LE/period) | |
| PC | Profits of processors (LE) | |
| REVCct | Revenue at processor c in time t (LE/period) | |
| TCCct | Total cost at processor c in time t (LE/period) | |
| PCCct | Purchasing cost at processor c in time t (LE/period) | |
| COTCct | Transportation cost related to processor c in time t (LE/period) | |
| HCCct | Holding cost at processor c in time t (LE/period) | |
| PX | Profits of fruit distributors (LE) | |
| REVXxt | Revenue at fruit distributor x in time t (LE/period) | |
| TCXxt | Total cost at fruit distributor x in time t (LE/period) | |
| PCXxt | Purchasing cost at fruit distributor x in time t (LE/period) | |
| COTXxt | Transportation cost related to fruit distributor x in time t (LE/period) | |
| HCXxt | Holding cost at fruit distributor x in time t (LE/period) | |
| PY | Profits of juice distributors (LE) | |
| REVYyt | Revenue at juice distributor y in time t (LE/period) | |
| TCYyt | Total cost at juice distributor y in time t (LE/period) | |
| PCYyt | Purchasing cost at juice distributor y in time t (LE/period) | |
| COTYyt | Transportation cost related to juice distributor y in time t (LE/period) | |
| HCYyt | Holding cost at juice distributor y in time t (LE/period) | |
| PR | Profits of local retailers (LE) | |
| REVRrt | Revenue at local retailer r in time t (LE/period) | |
| TCRrt | Total cost at local retailer r in time t (LE/period) | |
| PCRrt | Purchasing cost at local retailer r in time t (LE/period) | |
| COTRrt | Transportation cost related to local retailer r in time t (LE/period) | |
| HCRrt | Holding cost at local retailer r in time t (LE/period) | |
| PQ | Profits of regional retailers (LE) | |
| REVQqt | Revenue at regional retailer q in time t (LE/period) | |
| TCQqt | Total cost at regional retailer q in time t (LE/period) | |
| PCQqt | Purchasing cost at regional retailer q in time t (LE/period) | |
| COTQqt | Transportation cost related to regional retailer q in time t (LE/period) | |
| HCQqt | Holding cost at regional retailer q in time t (LE/period) | |
References
- Sherman, E. 94% of the Fortune 1000 are Seeing Coronavirus Supply Chain Disruptions: Report. 2020. Available online: https://fortune.com/2020/02/21/fortune-1000-coronavirus-china-supply-chain-impact/ (accessed on 10 April 2025).
- Emenike, S.N.; Falcone, G. A review on energy supply chain resilience through optimization. Renew. Sustain. Energy Rev. 2020, 134, 110088. [Google Scholar] [CrossRef]
- Mariana, O.S.; Alzate, C.; Ariel, C. Comparative environmental life cycle assessment of orange peel waste in present productive chains. J. Clean. Prod. 2021, 322, 128814. [Google Scholar] [CrossRef]
- Knoema. Agriculture Crops Production Citrus Fruit Production. 2023. Available online: https://knoema.com/atlas/World/topics/Agriculture/Crops-Production-Quantity-tonnes/Citrus-fruit-production#:~:text=Citrus%20fruit%20production%20of%20World,by%20our%20digital%20data%20assistant (accessed on 10 April 2025).
- FAO. FAO Stat: Food and Agriculture Data. 2025. Available online: https://www.fao.org/faostat/en/#data/TCL (accessed on 10 April 2025).
- Beshara, S.; Kassem, A.; Fors, H.; Harraz, N. A Comprehensive Review and Mapping Citrus Supply Chains from a Sustainability Perspective across the European Union, Middle East, and Africa. Sustainability 2024, 16, 8582. [Google Scholar] [CrossRef]
- Valverde, C. Report Name: Citrus Annual; EU Citrus Annual Report; USDA: Washington, DC, USA, 2021; pp. 1–20. [Google Scholar]
- USDA/FAS. Citrus: World Markets and Trade. In U.S. Production and Exports Forecast Down Despite Global Gains; United States Department of Agriculture, Foreign Agricultural Service: Washington, DC, USA, 2021; pp. 1–13. [Google Scholar]
- Beshara, S.; Fors, H.; Harraz, N. Designing Supply Chain to Hedge Against Disruptions: A Review of Literature in General and Agro Food Supply Chains; IEOM Society International: Southfield, MI, USA, 2022; pp. 135–146. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, P.; Han, X. Agri-food supply chain network disruption propagation and recovery based on cascading failure. Phys. A Stat. Mech. Its Appl. 2022, 589, 126611. [Google Scholar] [CrossRef]
- Zhao, G.; Liu, S.; Lopez, C.; Chen, H.; Lu, H.; Mangla, S.K.; Elgueta, S. Risk analysis of the agri-food supply chain: A multi-method approach. Int. J. Prod. Res. 2020, 58, 4851–4876. [Google Scholar] [CrossRef]
- Behzadi, G.; O’Sullivan, M.J.; Olsen, T.L.; Zhang, A. Allocation flexibility for agribusiness supply chains under market demand disruption. Int. J. Prod. Res. 2018, 56, 3524–3546. [Google Scholar] [CrossRef]
- Gholami-Zanjani, S.M.; Jabalameli, M.S.; Klibi, W.; Pishvaee, M.S. A robust location-inventory model for food supply chains operating under disruptions with ripple effects. Int. J. Prod. Res. 2021, 59, 301–324. [Google Scholar] [CrossRef]
- Esteso, A.; Alemany, M.M.E.; Ortiz, A. Conceptual framework for designing agri-food supply chains under uncertainty by mathematical programming models. Int. J. Prod. Res. 2018, 56, 4418–4446. [Google Scholar] [CrossRef]
- Stone, J.; Rahimifard, S. Resilience in agri-food supply chains: A critical analysis of the literature and synthesis of a novel framework. Supply Chain Manag. 2018, 23, 207–238. [Google Scholar] [CrossRef]
- Ravulakollu, A.K.; Urciuoli, L.; Rukanova, B.; Tan, Y.H.; Hakvoort, R.A. Risk based framework for assessing resilience in a complex multi-actor supply chain domain. Supply Chain Forum 2018, 19, 266–281. [Google Scholar] [CrossRef]
- Bottani, E.; Murino, T.; Schiavo, M.; Akkerman, R. Resilient food supply chain design: Modelling framework and metaheuristic solution approach. Comput. Ind. Eng. 2019, 135, 177–198. [Google Scholar] [CrossRef]
- Liao, Y.; Kaviyani-Charati, M.; Hajiaghaei-Keshteli, M.; Diabat, A. Designing a closed-loop supply chain network for citrus fruits crates considering environmental and economic issues. J. Manuf. Syst. 2020, 55, 199–220. [Google Scholar] [CrossRef]
- Behzadi, G.; O’Sullivan, M.J.; Olsen, T.L. On metrics for supply chain resilience. Eur. J. Oper. Res. 2020, 287, 145–158. [Google Scholar] [CrossRef]
- Mohib, A.M.N.; Deif, A.M. Supply chain multi-state risk assessment using universal generating function. Prod. Plan. Control 2020, 31, 699–708. [Google Scholar] [CrossRef]
- Sharma, P.; Vishvakarma, R.; Gautam, K.; Vimal, A.; Kumar Gaur, V.; Farooqui, A.; Varjani, S.; Younis, K. Valorization of citrus peel waste for the sustainable production of value-added products. Bioresour. Technol. 2022, 351, 127064. [Google Scholar] [CrossRef]
- Gholami-Zanjani, S.M.; Klibi, W.; Jabalameli, M.S.; Pishvaee, M.S. The design of resilient food supply chain networks prone to epidemic disruptions. Int. J. Prod. Econ. 2021, 233, 108001. [Google Scholar] [CrossRef]
- Abu Hatab, A.; Lagerkvist, C.J.; Esmat, A. Risk perception and determinants in small- and medium-sized agri-food enterprises amidst the COVID-19 pandemic: Evidence from Egypt. Agribusiness 2021, 37, 187–212. [Google Scholar] [CrossRef]
- Ali, A.; Xia, C.; Ismaiel, M.; Ouattara, N.B.; Mahmood, I.; Anshiso, D. Analysis of determinants to mitigate food losses and waste in the developing countries: Empirical evidence from Egypt. Mitig. Adapt. Strateg. Glob. Change 2021, 26, 23. [Google Scholar] [CrossRef]
- Zhao, G.; Vazquez-Noguerol, M.; Liu, S.; Prado-Prado, J.C. Agri-food supply chain resilience strategies for preparing, responding, recovering, and adapting in relation to unexpected crisis: A cross-country comparative analysis from the COVID-19 pandemic. J. Bus. Logist. 2023, 45, e12361. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, C. Designing a two-stage model for the resilient agri-food supply chain network under dynamic competition. Br. Food J. 2024, 126, 662–681. [Google Scholar] [CrossRef]
- Miranda-Ackerman, M.A.; Azzaro-Pantel, C.; Aguilar-Lasserre, A.A. A green supply chain network design framework for the processed food industry: Application to the orange juice agrofood cluster. Comput. Ind. Eng. 2017, 109, 369–389. [Google Scholar] [CrossRef]
- Peña-Orozco, D.L.; Gonzalez-Feliu, J.; Salazar-Aguirre, L.T.; Arenas-Ruiz, M.A. Sustainability Fruit Supply Chain Design in the Context of Decentralized Smallholders: Modelling Framework and Sensitivity Analysis. LOGI—Sci. J. Transp. Logist. 2023, 14, 43–54. [Google Scholar] [CrossRef]
- Darley-Waddilove, J.I. Allocating Commodity Volumes in the Citrus Export Cold Chain. Master’s Thesis, Stellenbosch University, Stellenbosch, South Africa, 2021. [Google Scholar]
- Cheraghalipour, A.; Paydar, M.M.; Hajiaghaei-Keshteli, M. A bi-objective optimization for citrus closed-loop supply chain using Pareto-based algorithms. Appl. Soft Comput. J. 2018, 69, 33–59. [Google Scholar] [CrossRef]
- Imbachi, C.G.A.; Larrahondo, A.F.C.; Orozco, D.L.P.; Cadavid, L.R.; Bastidas, J.J.B. Design of an inventory management system in an agricultural supply chain considering the deterioration of the product: The case of small citrus producers in a developing country. J. Appl. Eng. Sci. 2018, 16, 523–537. [Google Scholar] [CrossRef]
- Roghanian, E.; Cheraghalipour, A. Addressing a set of meta-heuristics to solve a multi-objective model for closed-loop citrus supply chain considering CO2 emissions. J. Clean. Prod. 2019, 239, 118081. [Google Scholar] [CrossRef]
- Aslan, H.; Zereyak, E.; Rad, S.T. Modelling of Citrus Production and Export Process: Eastern Mediterrenean Region of Turkey. Karadeniz Uluslararası Bilimsel Dergi 2020, 48, 169–187. [Google Scholar] [CrossRef]
- Sahebjamnia, N.; Goodarzian, F.; Hajiaghaei-Keshteli, M. Optimization of multi-period three-echelon citrus supply chain problem. J. Optim. Ind. Eng. 2020, 13, 39–53. [Google Scholar] [CrossRef]
- Goodarzian, F.; Fakhrzad, M.B. A New Multi-Objective Mathematical Model for A Citrus Supply Chain Network Design: Metaheuristic Algorithms. J. Optim. Ind. Eng. 2021, 14, 127–144. [Google Scholar] [CrossRef]
- Peña Orozco, D.L.; Gonzalez-Feliu, J.; Rivera, L.; Mejía Ramirez, C.A. Integration maturity analysis for a small citrus producers’ supply chain in a developing country. Bus. Process Manag. J. 2021, 27, 836–867. [Google Scholar] [CrossRef]
- Güner, G.G.; Utku, D.H. An Optimization Approach for a Fresh Food Supply Chain: An Application for the Orange Supply Chain Design in Turkey. Düzce Üniversitesi Bilim Ve Teknol. Derg. 2021, 9, 1563. [Google Scholar] [CrossRef]
- Alzubi, E.; Noche, B. A multi-objective model to find the sustainable location for citrus hub. Sustainability 2022, 14, 4463. [Google Scholar] [CrossRef]
- Alzubi, E.; Shbikat, N.; Noche, B. A system dynamics model to improving sustainable performance of the citrus farmers in Jordan Valley. Clean. Prod. Lett. 2023, 4, 100034. [Google Scholar] [CrossRef]
- Goodarzian, F.; Ghasemi, P.; Santibanez Gonzalez, E.D.; Tirkolaee, E.B. A sustainable-circular citrus closed-loop supply chain configuration: Pareto-based algorithms. J. Environ. Manag. 2023, 328, 116892. [Google Scholar] [CrossRef] [PubMed]
- Paredes-Rodríguez, A.M.; Osorio-Gómez, J.C.; Orejuela-Cabrera, J.P. Dynamic evaluation of distribution channels in a fresh food supply chain from a sustainability and resilience approach. Alex. Eng. J. 2024, 106, 42–51. [Google Scholar] [CrossRef]
- Goodarzian, F.; Kumar, V.; Ghasemi, P. Investigating a citrus fruit supply chain network considering CO2 emissions using meta-heuristic algorithms. Ann. Oper. Res. 2024, 332, 1301. [Google Scholar] [CrossRef]
- Zhao, S.; You, F. Resilient supply chain design and operations with decision-dependent uncertainty using a data-driven robust optimization approach. AIChE J. 2019, 65, 1006–1021. [Google Scholar] [CrossRef]









| Reference | Type of Disruption | Strategy | ||
|---|---|---|---|---|
| Complete | Partial | Proactive | Reactive | |
| Behzadi et al. [12] | D | BT and BM | ||
| Esteso et al. [14] | DC–P | Tech and MS | BS and Cp | |
| Stone & Rahimifard [15] | X | Tech, I, and MS | BS, BT, Cp, Cd, and A | |
| Ravulakollu et al. [16] | X | Tech | ||
| Bottani et al. [17] | S–D | MS | ||
| Liao et al. [18] | D | I | ||
| G. Zhao et al. [11] | X | -- | -- | |
| Behzadi et al. [19] | T | BT | ||
| Mohib & Deif [20] | S | MS | ||
| Sharma et al. [21] | X | Tech | ||
| Gholami-Zanjani, Jabalameli et al. [13] | D–P | Tech and MS | BS and Cp | |
| Gholami-Zanjani, Klibi et al. [22] | X | BS, Cp, Cd, and A | ||
| Abu Hatab et al. [23] | X | -- | -- | |
| Li et al. [10] | S–R | Tech and F | A | |
| Ali et al. [24] | X | -- | -- | |
| G. Zhao et al. [25] | X | MS and I | BS, BT, Cp, and Cd | |
| Li & Zhang [26] | X | MS and I | A | |
| Reference | Export | Traceability | Facility Location | Quality | Waste | CO2 Emissions | Economic | Social | Contracts | CircularityConsideration | Standardization | Logistics | Technology | Pricing |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Miranda-Ackerman et al. [27] | X | X | X | X | X | X | ||||||||
| Cheraghalipour et al. [30] | X | X | X | X | X | |||||||||
| Imbachi et al. [31] | X | X | X | X | ||||||||||
| Roghanian & Cheraghalipour [32] | X | X | X | X | X | X | ||||||||
| Aslan et al. [33] | X | X | X | X | X | X | ||||||||
| Liao et al. [18] | X | X | X | X | ||||||||||
| Sahebjamnia et al. [34] | X | X | X | |||||||||||
| Darley-waddilove [29] | X | X | X | X | X | |||||||||
| Goodarzian & Fakhrzad [35] | X | X | X | X | ||||||||||
| Peña Orozco et al. [36] | X | X | ||||||||||||
| Güner & Utku [37] | X | X | X | |||||||||||
| Alzubi & Noche [38] | X | X | X | X | ||||||||||
| Alzubi et al. [39] | X | X | X | X | X | |||||||||
| Goodarzian et al. [40] | X | X | X | X | X | X | ||||||||
| Peña-Orozco et al. [28] | X | X | X | X | ||||||||||
| Paredes-Rodríguez et al. [41] | X | X | X | X | X | |||||||||
| Goodarzian et al. [42] | X | X |
| Reference | Decision Variable | Objective | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strategic | Tactical | Operational | Financial | Customer | Sustainability | ||||||||||||
| Location | Number of Facilities | Capacity | Allocation | Inventory | Supplier Selection | Produced Quantity | Product Flow | Transportation Mode | Profit | Cost | Responsiveness | Lead Time | Waste | CO2 | Byproduct | Social | |
| Miranda-Ackerman et al. [27] | X | X | X | X | X | X | X | ||||||||||
| Cheraghalipour et al. [30] | X | X | X | X | X | X | X | ||||||||||
| Imbachi et al. [31] | X | X | X | ||||||||||||||
| Roghanian & Cheraghalipour [32] | X | X | X | X | X | X | X | X | |||||||||
| Aslan et al. [33] | X | X | X | ||||||||||||||
| Liao et al. [18] | X | X | X | X | X | ||||||||||||
| Sahebjamnia et al. [34] | X | X | X | X | X | ||||||||||||
| Darley-waddilove [29] | X | X | X | ||||||||||||||
| Goodarzian & Fakhrzad [35] | X | X | X | X | X | X | |||||||||||
| Peña Orozco et al. [36] | X | X | X | ||||||||||||||
| Güner & Utku [37] | X | X | X | ||||||||||||||
| Alzubi & Noche [38] | X | X | X | ||||||||||||||
| Alzubi et al. [39] | X | X | X | X | |||||||||||||
| Goodarzian et al. [40] | X | X | X | X | X | X | X | X | |||||||||
| Peña-Orozco et al. [28] | X | X | X | X | X | ||||||||||||
| Goodarzian et al. [42] | X | X | X | X | X | ||||||||||||
| Reference | Farm | Packhouse | Processor | Byproduct Processor | Distributor | Retailer | Consumer |
|---|---|---|---|---|---|---|---|
| Miranda-Ackerman et al. [27] | X | X | X | ||||
| Cheraghalipour et al. [30] | X | X | X | ||||
| Imbachi et al. [31] | X | X | X | ||||
| Roghanian & Cheraghalipour [32] | X | X | X | X | X | X | |
| Aslan et al. [33] | X | X | X | ||||
| Liao et al. [18] | X | X | X | X | X | ||
| Sahebjamnia et al. [34] | X | X | X | X | |||
| Darley-waddilove [29] | X | X | |||||
| Goodarzian & Fakhrzad [35] | X | X | X | ||||
| Peña Orozco et al. [36] | X | X | X | ||||
| Güner & Utku [37] | X | X | X | X | |||
| Alzubi & Noche [38] | X | X | X | ||||
| Alzubi et al. [39] | X | X | |||||
| Goodarzian et al. [40] | X | X | X | ||||
| Peña-Orozco et al. [28] | X | X | X | ||||
| Paredes-Rodríguez et al. [41] | X | X | X | X | |||
| Goodarzian et al. [42] | X | X | X |
| s = 1, 2, …, S | Set of Farms | q = 1, 2, …, Q | Set of Regional Retailers |
| p = 1, 2, …, P | Set of Packhouses | o = 1, 2, …, O | Set of Local Markets |
| c = 1, 2, …, C | Set of Processors | b = 1, 2, …, B | Set of Byproduct Markets |
| x = 1, 2, …, X | Set of Orange Distributors | l = 1, 2, …, L | Set of Landfills |
| y = 1, 2, …, Y | Set of Juice Distributors | t = 1, 2, …, T | Set of Time Periods |
| r = 1, 2, …, R | Set of Local Retailers |
| NSPspt | Transported amounts of fruits from supplier s to packhouse p at time t (kgs/period) |
| NSCsct | Transported amounts of fruits from supplier s to processor c at time t (kgs/period) |
| NSOsot | Transported amounts of fruits from supplier s to local market o at time t (kgs/period) |
| NSLslt | Transported amounts of fruit waste from supplier s to landfill l at time t (kgs/period) |
| NPCpct | Transported amounts of fruits from packhouse p to processor c at time t (kgs/period) |
| NPXpxt | Transported amounts of fruits from packhouse p to fruit distributor x at time t (kgs/period) |
| NPOpot | Transported amounts of fruits from packhouse p to local market o at time t (kgs/period) |
| NPLplt | Transported amounts of fruit waste from packhouse p to landfill l at time t (kgs/period) |
| NCYcyt | Transported amounts of juice from processor c to juice distributor y at time t (kgs/period) |
| NCBcbt | Transported amounts of juice processing waste from processor c to byproduct market b at time t (kgs/period) |
| NCLclt | Transported amounts of fruit waste from processor c to landfill l at time t (kgs/period) |
| NXRxrt | Transported amounts of fruits from fruit distributor x to local retailer r at time t (kgs/period) |
| NXQxqt | Transported amounts of fruits from fruit distributor x to regional retailer q at time t (kgs/period) |
| NXLxlt | Transported amounts of fruit waste from fruit distributor x to landfill l at time t (kgs/period) |
| NYRyrt | Transported amounts of juice from juice distributor y to local retailer r at time t (kgs/period) |
| NYQyqt | Transported amounts of juice from juice distributor y to regional retailer q at time t (kgs/period) |
| NRLrlt | Transported amounts of fruit waste from local retailer r to landfill l at time t (kgs/period) |
| NQLqlt | Transported amounts of fruit waste from regional retailer r to landfill l at time t (kgs/period) |
| IPpt | Inventory level at packhouse p in time t (kgs/period) |
| ICct | Inventory level at processor c in time t (kgs/period) |
| IXxt | Inventory level at fruit distributor x in time t (kgs/period) |
| IYyt | Inventory level at juice distributor y in time t (kgs/period) |
| IFRrt | Inventory level of fruit at local retailer r in time t (kgs/period) |
| IJRrt | Inventory level of juice at local retailer r in time t (kgs/period) |
| IFQqt | Inventory level of fruit at regional retailer r in time t (kgs/period) |
| IJQqt | Inventory level of juice at regional retailer r in time t (kgs/period) |
| Ppt | Packed amounts of fruits at packhouse p at time t (kgs/period) |
| Cct | Processed amounts of fruits at processor c at time t (kgs/period) |
| EJct | Extracted amount of juice from processing of 1 kg of oranges at processor c in time t (kgs/period) |
| EBct | Extracted amount of CPW from processing of 1 kg of oranges at processor c in time t (kgs/period) |
| BSst | 1 if supplier s in time t is functioning, otherwise 0 |
| BPpt | 1 if packhouse p in time t is functioning, otherwise 0 |
| BCct | 1 if processor c in time t is functioning, otherwise 0 |
| BXxt | 1 if fruit distributor x in time t is functioning, otherwise 0 |
| BYyt | 1 if juice distributor y in time t is functioning, otherwise 0 |
| BRrt | 1 if local retailer r in time t is functioning otherwise 0 |
| BQqt | 1 if regional retailer q in time t is functioning, otherwise 0 |
| Source | Landfill (L) | Production | Inventory | Local Market (O) | Byproduct Market (B) |
|---|---|---|---|---|---|
| S1 | L1: 213 | - | - | O1: 426 | - |
| S2 | L1: 200 | - | - | O2: 400 | - |
| P1 | L1: 471.54 | 14,161.8 | - | O1: 1084.5 | - |
| P2 | L2: 284.3 | 8539.1 | Fruit: 2070.3 | O1: 1.14, O2: 653.9 | - |
| C1 | L1: 1965.8 | 54,200 | - | - | B1: 27,100 |
| X1 | L1: 141.6 | - | - | - | - |
| X2 | L2: 64.68 | - | - | - | - |
| R1 | L1: 31.8 | - | - | - | - |
| R2 | L2: 32.7 | - | Fruit: 120 | - | - |
| R3 | L2: 31.3 | - | - | - | - |
| R4 | L1: 31.4 | - | - | - | - |
| Q1 | L1: 20 | - | - | - | - |
| Q2 | L1: 19.2 | - | - | - | - |
| Q3 | L1: 19.6 | - | - | - | - |
| Q4 | L1: 18.18 | - | - | - | - |
| Source | Landfill (L) | Production | Inventory | Local Market (O) | Byproduct Market (B) |
|---|---|---|---|---|---|
| S1 | L1: 213 | - | - | O1: 426 | - |
| S2 | L1: 200 | - | - | O2: 400 | - |
| P1 | L1: 606.8 | 18,223.5 | - | O1: 1395.6 | - |
| C1 | L1: 2038.3 | 56,200 | - | - | B1: 28,100 |
| X1 | L1: 173.6 | - | - | - | - |
| X2 | L2: 29.4 | - | - | - | - |
| R1 | L1: 31.3 | - | - | - | - |
| R2 | L2: 29.1 | - | - | - | - |
| R3 | L2: 31.7 | - | - | - | - |
| R4 | L1: 31.3 | - | - | - | - |
| Q1 | L1: 19.7 | - | - | - | - |
| Q2 | L1: 19.7 | - | - | - | - |
| Q3 | L1: 19.2 | - | - | - | - |
| Q4 | L1: 18.18 | - | - | - | - |
| Source | Landfill (L) | Production | Inventory | Local Market (O) | Byproduct Market (B) |
|---|---|---|---|---|---|
| S1 | L1: 213 | - | - | O2: 426 | - |
| C1 | L2: 1468.6 | 40,492.4 | 4246.2 | - | B1: 20,246.2 |
| Source | Landfill (L) | Production | Inventory | Local Market (O) | Byproduct Market (B) |
|---|---|---|---|---|---|
| S2 | L1: 200 | - | - | O2: 400 | - |
| C1 | L1: 1468.6 | 20,507.6 | - | - | B1: 10,253.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bishara, S.; Harraz, N.; Elwany, H.; Fors, H. Optimizing Resilient Sustainable Citrus Supply Chain Design. Logistics 2025, 9, 66. https://doi.org/10.3390/logistics9020066
Bishara S, Harraz N, Elwany H, Fors H. Optimizing Resilient Sustainable Citrus Supply Chain Design. Logistics. 2025; 9(2):66. https://doi.org/10.3390/logistics9020066
Chicago/Turabian StyleBishara, Sherin, Nermine Harraz, Hamdy Elwany, and Hadi Fors. 2025. "Optimizing Resilient Sustainable Citrus Supply Chain Design" Logistics 9, no. 2: 66. https://doi.org/10.3390/logistics9020066
APA StyleBishara, S., Harraz, N., Elwany, H., & Fors, H. (2025). Optimizing Resilient Sustainable Citrus Supply Chain Design. Logistics, 9(2), 66. https://doi.org/10.3390/logistics9020066





