Abstract
Background: A hospital’s operating theater service system is a large-scale, complicated system that must be carefully managed to offer the best possible results for its patients. Unlike other industries such as manufacturing and logistics, system dynamics (SD) methodologies are not extensively applied in hospital operating theaters. This study deals with the future development and possible future scenarios for hospital operating rooms in Bangladesh. Methods: Due to demographic dynamics and demographic processes, increased pressures on hospital care are expected in Bangladesh. The SD model anticipates possible future scenarios, reconciles service capacities and the variability of patient demand, and reduces patient congestion and waiting times in the hospital area. This study introduces a causal loop diagram to show a causal link between the hospital operating theater system variables. It also introduces a stock flow diagram to understand the dynamic behavior of the system. Results: The model validation testing reports that in extreme conditions, such as a 50% reduction in the patient arrival rate, the model is valid and runs as usual. Conclusions: This first work of SD modeling for hospital operating theater systems can help healthcare managers, decision makers, or researchers of any responsibility level make better predictions in order to reduce patient waiting times and backlogs and make appropriate decisions.
1. Introduction
The sterile chamber in which surgical operations are performed is called an operating room. The operating theater consists of operating rooms and post-operative care units. The operating room system in a hospital is increasingly interconnected and interdependent. With the increase in competition and public health challenges along with dwindling resources, it is increasingly important to deliver hospital services more efficiently. In Bangladesh, hospital operating theater systems are complex, and long waiting times are common phenomena. Offering proper treatment to the right patient at the right time is not only the definition of high-quality care, but it is also essential for the long-term sustainability of our healthcare system. However, the Bangladeshi hospital delivery system frequently falls short of balancing the supply of hospital services with the demand for such care. Because of the extreme and natural volatility in demand, maintaining this synchronization for any length of time is impossible. The most crucial problem at hand right now is changing demand. To ensure that healthcare is coordinated to fulfill the highest levels of patient demands, new governance structures and decision-makers must be established. Hospitals must find, assess, and implement modern operating room management strategies if they are to deliver efficient and high-quality healthcare services.
Bangladesh is a densely populated country. Human diseases, as well as hospitals, increase with the increase in population. However, due to the lack of an appropriate management system, patients in hospitals suffer very much. Sometimes, they are required to wait for operating theater services for four, five, or even more days. Although waiting times should depend on the urgency class of a patient, the absence of analyses and modelling for capacity services and demand, along with the insufficient number of infrastructural and professional facilities, makes it difficult for emergency patients to be treated within 24 h. However, there is a general policy that emergency patients usually must be treated within 24 h; acute patients should be treated within a week, and elective patients within 4–6 weeks. The availability of resources and appropriate professionals makes everything very unpredictable. Also, post-operative care, such as intensive care units (ICUs) or post-anesthesia care units (PACUs), plays a crucial role in determining patient backlog and patient waiting times. Hence, there is a waiting time for most patients to be treated in an operating theater. Patients’ lives become at risk, and hospital management fails to appropriately predict patients’ demand for variety. As a result, management is unable to synchronize service capacity and patient demand variability, resulting in an increase in patient backlog and waiting times. We should contribute to the elimination or minimization of these difficulties because both health and time are valuable resources.
Hospital care systems are complex, consisting of several dependent systems and processes that adapt to the changing environment and operate non-linearly. Traditional methods for evaluating and modeling often underestimate the wider impact of the hospital system, which can be important in achieving the desired system goals and is often observed in complex operating room systems in hospitals. Researchers and decision makers in hospital operating rooms may underestimate or overlook the interactions between people, processes, technology, and the facility design. Interventions in the hospital operating room system must consider the dynamics and complexity of the context of the hospital operating room system in which the intervention takes place. This article describes a way for dynamically modeling the intervention system of a hospital operating room system, which could be useful in certain situations.
Researchers and decision makers employ various approaches to reduce hospital complexity, patient waiting times, and the patient backlog for service, including system dynamics (SD) modeling, lean philosophy implementation, scheduling, etc. SD modeling is one of the most suitable and efficient methods for addressing the issue by considering the dynamic nature of the healthcare system. It is a computer-based simulation modeling methodology that was developed at the Massachusetts Institute of Technology in the 1950s by J. Forrester as a tool for managers to analyze complex problems [1]. SD can be briefly defined as a methodology based on feedback systems borrowed from the control theory developed by Forrester and is the most appropriate technique to easily handle non-linearity and time delays, as well as the multi-loop structures of complex and dynamic systems to enhance system thinking and system learning. Causal loop diagrams are used to represent feedback loop systems diagrammatically, and they are a communication tool of feedback structures, representing the principal feedback loops of systems, which generate the reference dynamic behavior of such systems. Given that SD modeling can be applied qualitatively and has strong connections to issue structuring methods, such as causal or influence correlation diagrams, it can be used to gain a better understanding of the relationships between the various components of a hospital operating service (HOTS) system. Furthermore, system dynamics offers a rigorous approach for bringing the interconnectedness of different processes into focus.
This article introduces dynamic system modeling methods for evaluating system interventions for operating room service delivery in hospitals. Unlike traditional assessments, a dynamic system approach understands system complexity and anticipates bottom-up and top-down consequences of changes in complex operating room service delivery systems. This article is intended to help researchers and decision makers to decide whether these simulation methods are suitable for addressing specific problems in the operating room system. It is a primer for researchers and decision makers in operating theater delivery and implementation sciences who are confronted with complicated issues in providing effective and efficient care that can be solved with system interventions. Only a few studies have been conducted on modeling hospital operating theater systems that manage patient-related issues. No study has been reported on the SD modeling of the hospital operating theater system of Bangladesh. Also, system dynamics was chosen specifically for its ability to (1) relate patterns of behavior to system structures, (2) quantify the causal links between demand and patient waiting times, and (3) assess potential changes to system structure and management decision heuristics that will improve system performance in the long term. Thus, the goal of this study is to develop an SD model of a HOTS system of Bangladesh with the following specific objectives: (i) to create an operating service system that reacts to immediate service requirements; (ii) to examine the effects of improving resource flexibility in a genuine medical service system with unpredictable demand fluctuations; and (iii) to predict future events based on the hospital’s operating system factors.
The significance and objectives of this study are briefly discussed, along with the relationship between industrial engineering and hospitals. Section 2 attempts to summarize the literature review study and outline the key pieces of this study’s literature that provide significant and essential information. Section 3 contains the causal loop diagram, stock-flow diagram, parameter estimates, input data, and study model validation for the hospital operating theater service system. Section 4 presents this study’s findings and discussions. The conclusion section makes the final remarks and includes this study’s limitations and recommendations.
2. Literature Review
Several studies on the topic of hospital services have been conducted to date. The findings of these investigations are vastly different from one another. According to studies, prices are not the most key factor in determining hospital demand [2,3,4,5]. Other research, on the other hand, suggests that prices are a significant factor of hospital demand [6,7]. According to Ali and Noman [8], income levels have had a favorable impact on hospital demand in Bangladesh. They did not mention the limitations of their work. Using time-series data, Akbari et al. [9] assessed the demand for public hospitals in Pakistan and discovered that the availability of services was undoubtedly the most important factor of hospital demand. In a separate study by Turyamureba, M. et al. (2022) showed that geographical location significantly influenced healthcare utilization [10].
In Ghana, Appiah-Kubi and Politics [11] discovered that education, location, and socioeconomic all have an impact on hospital use. The challenge of predicting the need for hospital with panel data was highlighted by Jochmann and León-González [12]. They calculated the effect of individual treatment using the Markov chain Monte Carlo (MCMC) technique to predict the demand model. According to Mwabu et al. [13], demand for the medical treatment is inelastic in terms of the cost of use. According to Eme Ichoku and Leibbrandt [14], waiting hours are not a significant barrier to hospitalization. Based on panel data, Riphahn et al. [15] estimate the incentive effect on hospital demand in Germany. The elasticity of demand for hospital treatment is low, and it is resistant to changes in financial and non-financial opportunity costs, according to the researchers. In their model, they also included an unpleasant decision and moral haze. In these investigations, several demand determinants were employed, which were crucial in identifying appropriate variables for this study.
Price, income, and education are the key factors for hospital treatment demand in Bolivia, according to Li [16]. In Ghana, Lavy and Quigley [17] discovered that family income is a key factor of demand for hospital care quality and intensity, while the price of hospital care was found to be a less relevant determinant of demand for hospital care quality and intensity. Low-income households in rural Kenya were more likely than higher-income families to seek care, according to Mwabu et al. [18]. Price and travel time had a significant role in the rationing of rural hospitals in Cote d’Ivoire, according to Lo [19]. On the Malay Peninsula, Heller and medicine [3] observed that income is a decisive factor for hospital treatment demand. The factors that influence the demand for the hospital treatment are crucial for optimizing hospital utilization and developing appropriate policy framework of this industry. Furthermore, the extent to which these factors influence demand is also important in determining the performance of the hospital supply chain. Most studies have focused on applying various econometric methodologies to pick recipients of healthcare from various providers. In this study, a new hospital application definition was created to address these concerns. The demand for hospital operating room services was directly anticipated, thanks to the system dynamics model, which better explains the elements driving the demand. Hence, developing a proper management strategy is the key for sustainable performance of the operations theater.
Health maintenance and recovery receives special attention from people because it is undeniably the most significant issue in life, both personally and socially. Delivering services correctly at the right time improves patient satisfaction, but it depends on a lot more than just the latest technology. When planning and scheduling operation theater services, surgical clinics, or operating theaters must consider a variety of human resources and facilities [20,21]. As the performance of the healthcare system is impacted by numerous stakeholders, operation theater planning and scheduling processes are particularly a very complex task [22]. For instance, proper delivery of the healthcare services result in patient satisfaction, which cannot be obtained only through technology; the conduct and the performance of the personnel also have a significant impact [23]. Heydari, M. et al. (2022) demonstrated that attempts to reduce healthcare costs by reducing the number of hospital beds, healthcare worker salaries, reimbursement to healthcare providers, number of workforce, or by using any other strategy that affects supply and demand for healthcare services may result in unforeseen consequences or even be counterproductive [24]. However, implementing an effective operations management strategy involves developing models that assist hospital managers in improving operations theater scheduling policies, demand forecasts, and medium- and short-term staffing plans while taking into account how demand evolves in a networked manner [24]. In this study, a system dynamics model was developed to enhance the operations management strategy.
According to Sterman, “System dynamics is a method to enhance learning in complex systems” [25]. A hospital operating room is a complex system due to its various dimensions, procedures, and underlying dynamics. The demand for the healthcare services is determined by the complex demographic dynamics. Additionally, the availability of medical workers is influenced by numerous factors making an extensive list of complexities. As a result, SD is a viable technique for improving the comprehension as well as the quality of planning contained within the operating room system.
In his book “The Logic of Failure”, Dorner [26] wrote, “ Failure does not strike like a bolt from the blue; it develops gradually according to its own logic“ [26]. Policy makers dealing with complex systems must understand the dynamic logic of the systems in which they participate. Due to misconceptions about how the operating room system would evolve, a potential failure of the hospital operating room system is likely to develop over time. The major goal of hospital administrators is to make sure that medical resources are used as efficiently as possible. Surgeries are performed when necessary, and the patient flow is maximized without adding unnecessary expenses or having too long patient waiting times. These goals can be achieved through appropriate planning and operations management as most of the surgery delays or cancellations are due to the ineffective and erroneous planning and scheduling of operation theater time [21]. It is vital to gain a deeper understanding of the operating room system. As the literature analysis reveals, health authorities have lost their interest in the future demands of the hospital sector. A strategy based on SD has the potential to improve learning and prevent future errors.
Homer and Hirsch [27] argue that “The System modeling methodology is well suited to address the dynamic complexity that characterizes many public health issues” [27]. It is further suggested that “System dynamics shows promise as a means of modeling multiple interacting diseases and risks, the interaction of delivery systems and diseased populations, and matters of national and state policy” [27]. Homer and Hirsch [27] underline the fact that “many public health interventions fall short of their goals because they are made in piecemeal fashion, rather than comprehensively and from a whole system perspective”. An SD model of a hospital’s operating room system in Bangladesh provides a complete and comprehensive picture of the system that could be a useful tool in preventing future shortages in Bangladesh’s elderly care.
Taylor and Dangerfield [28] stress that SD is well fitted for analyzing feedback effects. “The system dynamics method is specifically designed for the analysis of feedback mechanisms” [28]. In the context of hospital care in Bangladesh, several key feedback effects play a role, and these are accounted for in the modeling exercise provided in this work. González-Busto and García [29] address the subject of reducing patient waiting times in the hospital service system in their paper Waiting Lists in Spanish Public Hospitals: An Approach to the Dynamics of Systems. While their research focuses on Spanish hospitals, the dynamics at play are also applicable to Bangladeshi hospitals. Waiting lists, according to the article, are a sign of inefficient hospital service. Several guidelines for lowering waiting lists are described in this article. However, it emphasizes that political counsel is crucial. When public institutions are extremely behind, González-Busto and García [29] recommend outsourcing private services. This strategy could be essentially for the future surgical service of hospitals in Bangladesh.
Two groups exist in the systemic literature on hospital services: one focuses on specific diseases while the other addresses more general political and managerial issues. Disease-oriented literature includes oral health [30]; cardiovascular diseases [31,32]; diabetes [33,34]; obesity [35]; smoking [36]; and chronic diseases in general [37,38]. Management-focused literature includes the adoption of EHIR [39]; telecare [40]; patient flow [41]; safe design capacity [42]; and waiting lists [43]. We position our work as an expansion on existing work and managerial modeling, i.e., management-focused modeling. The strategies required to develop system dynamics capabilities in hospital environments are covered in this paper.
The aforementioned literature highlighted the dynamic characteristics of the hospital service systems in Bangladesh and other countries, along with the applicability of SD as a tool for modeling the hospital system. It is observed that no research has focused on SD approach to model the operating room service systems of Bangladeshi hospitals. SD captures significant feedback effects and enables a comprehensive understanding of complex systems. Yet systems analysts played only a nominal role in the planning and strategy for the hospital’s operating room. A model and analysis of the system’s dynamics can provide valuable information. Additionally, there are currently no simulations or empirical evidence that can shed light on the extent to which Bangladeshi healthcare professionals and patients can benefit from the dynamic system modeling in terms of reduced patient backlogs, shorter patient waiting times, and improved care capacity in the healthcare operating room.
3. Materials and Method
3.1. Description of the Case Study
Patients in Bangladesh must wait for extended periods of time in the hospital, the backlog of patients is growing, and service providers are frustrated by the mismatch between patient demand and service availability. A well-known hospital, which is in Jashore, Bangladesh, is the case study of this paper. The findings of this study are based on a combination of direct observation, semi-structured interviews, SD simulations, and empirical analysis. We received immediate access to the participants and data from the hospital’s operating room service system in a well-known hospital system. It is preferred to have a healthcare system providing the right care to the right patient at the right time along with the long-run viability of the system. However, Bangladeshi hospitals have delivery systems that frequently fail to balance the demand for healthcare with the provision of hospital services. This can be attributed to the demand variability that makes it impossible to maintain the synchronization for any length of time. The most critical issue currently facing operating theater delivery may be demand unpredictability. To ensure that the supply of care can be synchronized to match the peaks and troughs of patient demand, new management structures and decision heuristics must be developed. Defining, assessing, and implementing innovative hospital operating theater service delivery management techniques is essential for developing efficient and effective healthcare systems.
3.2. System Dynamic Model
There are seven key steps involved in developing a system dynamic model that are shown in Figure 1. System dynamic modeling is an approach to understanding the behavior of complex systems over time. It deals with internal feedback loops and time delays that affect the behavior of the entire system. It is described as an analytical modeling approach whose roots could be said to lie in the theoretical approach of general systems. Using SD simulations allows us to see not just events but also patterns of behavior over time. Sometimes the simulation looks backward to historical results. On the other hand, it looks forward to the future to predict possible future results. Understanding patterns of behavior, in lieu of focusing on day-to-day events, can provide a radical change in perspective. It shows how a system’s structure is the cause of its successes and failures. This structure is represented by a series of causal linked relationships. Here, Vensim PLE for windows version 8.2.1 software and STELLA® software, version 8.0 for Windows, were used to construct a system dynamic simulation. STELLA®, version 8.0 software was used to develop a stock flow diagram of the hospital operating theater service (HOTS) system whereas Vensim PLE, version 8.2.1 software provided us with the causal loop diagram of the HOTS system. In this model following STELLA, version 8.0 software specifications were used:

Figure 1.
System dynamic modeling process.
One day is considered as the least-time unit for this model. The duration of the dynamic behavior in this study was assumed to be 90 days. This was assumed to be sufficient although the system parameters are subject to uncertainty.
3.3. Causal Loop Diagram of HOTS System
A causal loop diagram is a causal diagram that depicts the relationships between the various variables in a system. Figure 2 shows a causal loop diagram of the hospital operating theater service system created with VENSIM PLE, version 8.2.1 software. This figure displays three closed or feedback loops B1, B2, and B3 refer where B1, B2 are counterclockwise and B3 is clockwise. All of them are negative feedback loops, also referred to as balancing loops [25]. It is obvious, from Figure 2, that the HOTS system causal loop diagram does not include a reinforcing loop.
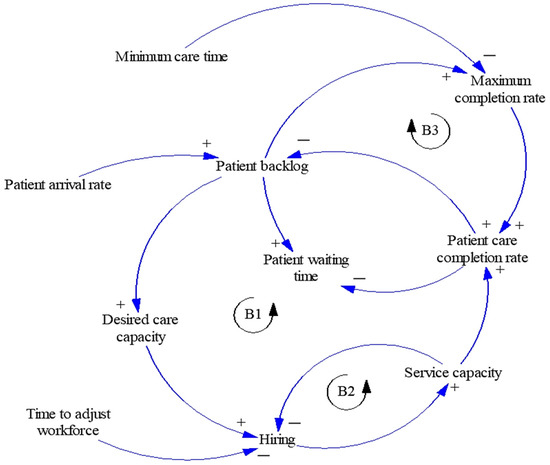
Figure 2.
Causal loop diagram of the HOTS system.
A causal loop diagram is used to represent the feedback loops of a system diagrammatically and evaluates system components and variables. It defines the elements of the system, causal relationships, and direction in system elements. Table 1 summarizes the HOTS system’s balancing loops (B1, B2, and B3), elements in loop and the causal relationships and direction in the elements of the HOTS system.

Table 1.
Summary of the causal loop diagram of the HOTS system.
3.4. Stock Flow Diagram of the HOTS System
The HOTS system’s stock-flow diagram is developed from the hospital operating theater service system’s causal loop diagram (Figure 2). Patient backlog and service capacity are state variables in the causal loop diagram, and they are represented by the stock. The patient arrival rate represents an influx (patient/day) into the stock-patient backlog, whereas the patient completion rate represents an outflow. The intake (patient/day) into the stock-service capacity is measured by the workforce recruiting or firing rate. Figure 3 depicts the stock-flow diagram for the HOTS system obtained from the causal loop diagram.
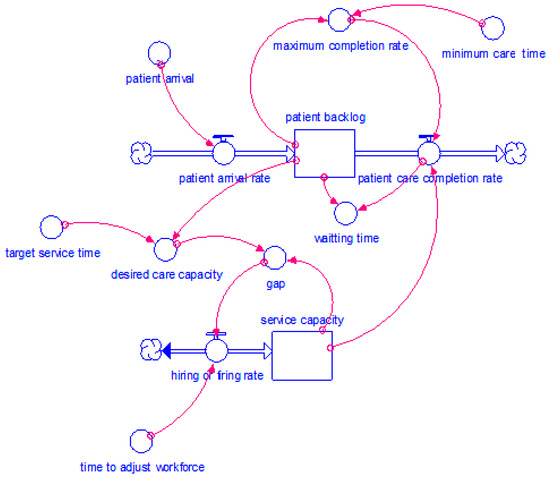
Figure 3.
Stock flow diagram of the hospital operating theater service system.
The stock flow diagram represents integral finite difference equations involving the variables of the feedback loop structure of the system and simulates dynamic behavior of the system. The stock-flow diagram of the HOTS system has 13 elements. They are two stocks, three flows and eight converters. The elements or parts of the stock flow diagram of the HOTS system (Figure 3) are introduced and categorized in Table 2.

Table 2.
The parameters of the Stock flow diagram of the HOTS system.
The STELLA Equations of the Stock Flow Diagram
The STELLA equations of the stock flow diagram are given below:
| patient_backlog(t) = patient_backlog (t − dt) + (patient_arrival_rate − patient_completion_rate) × dt | (1) |
| INIT patient_backlog = 12 A mismatch between the number of patients requiring care and the number of professionals and infrastructures providing care affects the care capacity. If there is a higher number patients who require health care service compared to the care capacity, then there will always be some patient waiting to receive health service. This incomplete number of patients is called patient backlog and for the case hospital of this study found the patient backlog to be 12 patients. | |
| INFLOWS: | |
| patient_arrival_rate = patient_arrival | (2) |
| OUTFLOWS: | |
| patient_completion_rate = MIN(service_capacity,maximum_completion_rate) | (3) |
| service_capacity(t) = service_capacity(t − dt) + (hiring_or_firing_rate) × dt | (4) |
| INIT service_capacity = 2 Service capacity is the maximum number patients who can receive health service in a day. Considering the amount of professionals and infrastructure the case hospital can provide service to two patients per day only. | |
| INFLOWS: | |
| hiring_or_firing_rate = gap/time_to_adjust_workforce | (5) |
| desired_care_capacity = patient_backlog/target_service_time | (6) |
| gap = desired_care_capacity-service_capacity | (7) |
| maximum_completion_rate = patient_backlog/minimum_care_time | (8) |
| minimum_care_time = 1/3 | |
| target_service_time = 1.5 | |
| time_to_adjust_workforce = 20 Planning for the workforce and patients is performed every day. It requires future demand forecasting, understanding the dynamic behavior of the organization for the variety of variables. Adjusting the workforce is about hiring new professionals that requires a lot of time and meticulous effort. Minimum time to adjust the workforce was found to be 20 days. | |
| waiting_time = (patient_backlog/patient_completion_rate) × 24 | (9) |
3.5. Model Parameter Choice
This study of SD includes Forrester’s investigations of parameter determination based on descriptive information acquired from system modeling participants. This type of data is known as disaggregated data. Estimating parameters with disaggregated data can be accomplished through a variety of methods, including a time-consuming technique, an examination approach, interviewing relevant experienced persons, researching literature and historical data, and so on. Disaggregated data from this study can be used to evaluate the workforce adjustment period, minimal care time, target service time, patient backlog, and service capacity. The equations for STELLA’s patient backlog and service capacity are shown in Equations (1) and (4), respectively. Since the average value can be estimated using data that can be generated from disaggregated data, the equation is not used to calculate it. Only the model’s operation needs to be described by the equation.
Input Data
A reputable hospital provided the input data. For this investigation, we obtained 90 calendar days of patient arrival rate data from a HOTS system. The gathered results are shown graphically in Figure 4. The hospital manager supplied us with rough average statistics on the patient backlog, service capacity, minimum care time, target service time, and time to adjust the workforce because other relevant data are not available.
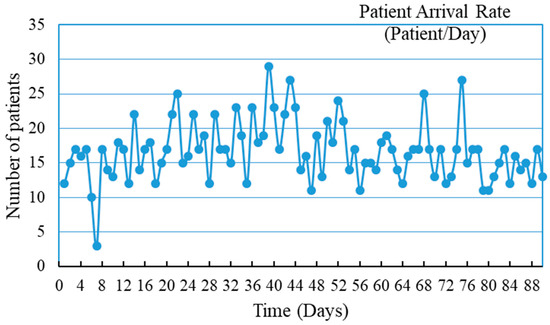
Figure 4.
Patient’s arrival rate graph shows the number of patients arriving every day during the study period.
Table 3 lists the essential parameter values. The model’s structural consistency is checked, and it yields plausible behaviors.

Table 3.
Parameter values of the model.
3.6. Sensitivity Analysis
The parameters of the model were given numerical values and stated in terms of equations along with the parameter values to simulate the model once the dynamic hypothesis was developed, which involved mapping the model’s stock and flow diagrams. One of the key stages in model design is parameter estimation. A reliable estimate of parameters is crucial for providing consistent system behavior throughout time. A sensitivity analysis of the parameters is also necessary to comprehend how parameter values affect the system behavior as well as appropriate calculation of model the parameters. Additionally, using sensitivity analysis, one may determine the level of accuracy needed for the parameter estimate so that the model is dependable and practical.
3.6.1. Sensitivity to Parameter Target Service Time
The parameters of an SD model contain uncertainty. As a result, sensitivity analysis is a critical step in ensuring the correctness of simulated results and the model’s resilience to changes in parameter values. Calculating the sensitivity of the important parameters is a smart idea as it shows the fluctuations in output due to the fluctuation in input. The sensitivity analysis was performed using STELLA.
Model target service time is one of the critical parameters affecting the model behavior in this investigation. Figure 5, Figure 6 and Figure 7 show the variations in waiting times, patient backlogs, and the service capacity, respectively, for the target service times of 0.5 (line-1), 1.5 (line-2), and 2.5 days (line-3). Although the patient backlog and service capacity were assessed in terms of the number of patients per day, the waiting time in this case was calculated in hours.
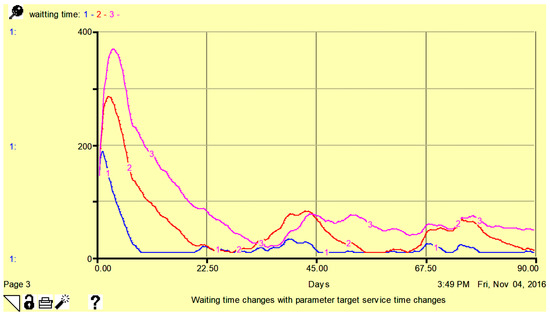
Figure 5.
Sensitivity of waiting time to parameter target service time: 0.5 days (line-1), 1.5 days (line-2), and 2.5 days (line-3). Here, vertical axis shows waiting time in hours.
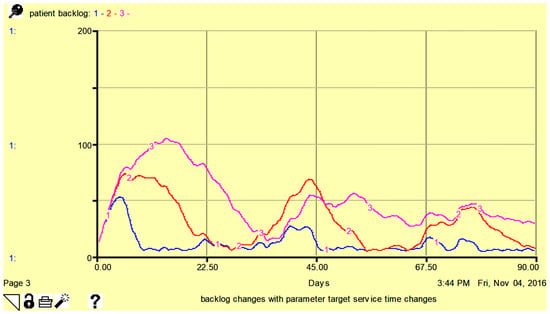
Figure 6.
Sensitivity of patient backlog to parameter target service time 0.5 days (line-1), 1.5 days (line-2), and 2.5 days (line-3). Here, vertical axis shows the number of patients per day.
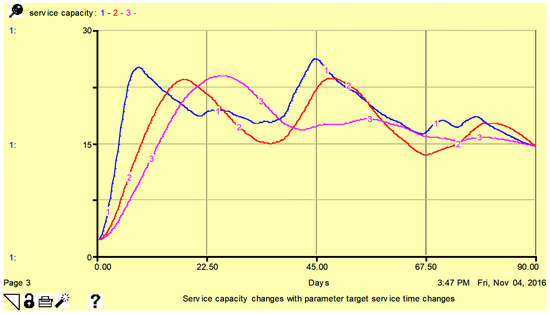
Figure 7.
Sensitivity of service capacity to parameter target service time 0.5 days (line-1), 1.5 days (line-2), and 2.5 days (line-3). Here, vertical axis shows the number of patients per day.
From Figure 5, Figure 6 and Figure 7, it is obvious that with minor changes in service capacity, there are corresponding adjustments in patient waiting times, patient backlog, and service capacity with a higher sensitivity observed for patient wait time. In Figure 7, the service capacity is higher for a smaller number of target service times.
3.6.2. Sensitivity to Parameter Time to Adjust Workforce
The time it takes to adjust the workforce is one of the crucial components of this research model. Figure 8, Figure 9 and Figure 10 show the period to adapt the workforce of 15 days (line-1), 20 days (line-2) and 25 days (line-3), the change in waiting time, patient backlog, and service capacity, respectively.
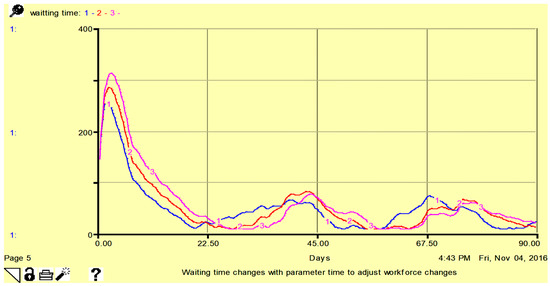
Figure 8.
Sensitivity of patient waiting time to parameter time to adjust workforce: 15 days (line-1), 20 days (line-2), and 25 days (line-3). Here, vertical axis shows waiting time in hours.
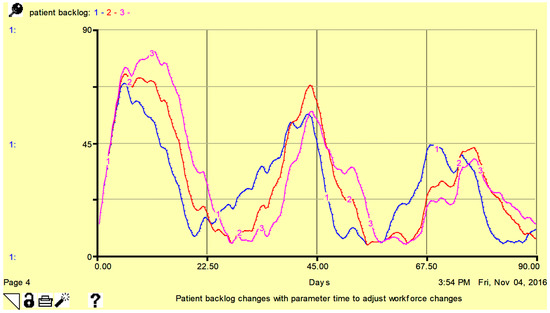
Figure 9.
Sensitivity of patient backlog to parameter time to adjust workforce: 15 days (line-1), 20 days (line-2), and 25 days (line-3). Here, vertical axis shows the number of patients per day.
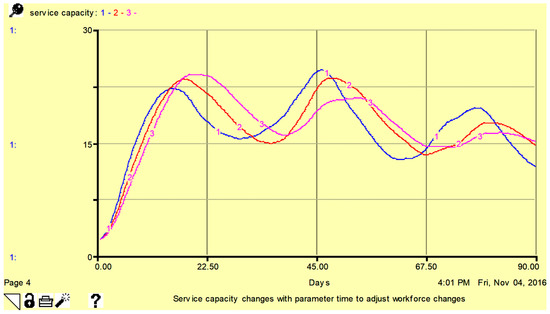
Figure 10.
Sensitivity of service capacity (waiting time, backlog and service) to parameter time to adjust workforce: 15 days (line-1), 20 days (line-2), and 25 days (line-3). Here, vertical axis shows the number of patients per day.
From Figure 8, Figure 9 and Figure 10, it is obvious that with minor changes in time to adjust the workforce, patient wait time, patient backlog, and service capacity change. Higher sensitivity is observed for patient wait time. In Figure 10, service capacity is higher for a smaller amount of time to adjust the workforce.
3.7. Model Validation
The validity and utility of dynamic models should be compared to the descriptive and dynamic models instead of comparing models against a hypothetical ideal [44]. Validation along with the sensitivity analysis is one of the major tests for building trust in the SD model. Thus, it is the process of developing confidence in the model’s soundness. The following tests can be used to build confidence in SD models:
- i.
- Structural tests;
- ii.
- Behavior tests;
- iii.
- Policy implications tests.
It is vital to remember that not all tests should be run while validating a model, instead, only the tests required to determine the model’s credibility should be performed. In this study, three types of structural tests and one type of behavior test were performed for model validation.
- Structural Tests of the model
The structure validity tests are the initial step in validating a SD model. The validity of the model structure is determined by comparing the model structure to real-world data in direct validation structure tests. It is performed by comparing mathematical equations and logical relationships to real-world knowledge. There is no need to simulate the model. Structure confirmation tests are the most difficult to do because we must directly compare the model’s equations with the information of the real system. It is the model’s qualitative validation. Three tests were run in this instance, including the structure validation test, parameter validation test, and the extreme condition test.
3.7.1. Structure Validation Test
The model’s equations are empirically compared to relationships found in the real world using the structural validation test. The relationships between the equations in the model should match the system’s descriptive knowledge. The aims, pressures, and constraints of the real system should be reflected in the structure of the model. Compared to certain other tests, verifying a model’s structure is easier and requires less expertise. Table 4 contrasts the correlations in the real world with the model equations.

Table 4.
Comparing the equations of the model with relationships in the real system.
The linkages in the equations of our study model structure are consistent with the descriptive information of the system, as shown in Table 4. All the equations are supported by evidence and based on available data. The model’s structure corresponds to the real system’s observable goals, pressures, and restrictions.
3.7.2. Parameter Validation Test
The second structure test, called the parameter confirmation test, compares constant parameters to actual data conceptually and numerically. In the actual world, each constant (and variable) should have a separate meaning. The objectives of the two tests, structural and parameter verification, are related and shared. Sensitivity analysis has already finished the model’s parameter validation tests. The desired service time (according to Figure 5, Figure 6 and Figure 7) and the time to adapt to the workforce (according to Figure 8, Figure 9 and Figure 10) are two parameters that were validated. Based on the findings of the sensitivity analysis, the graphs show the expected results.
3.7.3. Extreme Condition Test
This is an important direct structural test for the model’s robustness under direct extreme situations, which analyzes the validity of the equations by comparing the plausibility of the generated values to what would happen in real life under similar conditions. It is simple to predict which variables and what values they will take in a real-world system under extreme conditions. To detect a problem in the model structure and to improve the model’s usefulness for policy research, the model of the HOTS system is evaluated under extreme situations. One extreme condition for the HOTS system may certainly be a 50% reduction in patient arrival rate. Figure 11 shows the simulated waiting time, patient backlog, and service capacity under a 50% reduction in patient arrival rate. Since the patient arrival rate is reduced by 50%, the waiting time, patient backlog, and service capacity are reduced in this diagram. The reductions are compared to the results shown in Figure 12, which are obtained under normal conditions. The outcomes followed the expected patterns of outcomes and reality. As a result, the model was proven to be dependable and valid in extreme conditions.
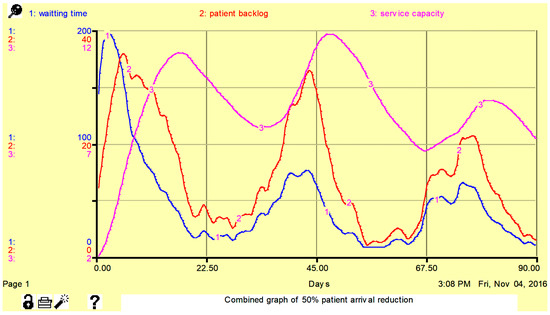
Figure 11.
Simulated waiting time, patient backlog, and service capacity under extreme conditions. Here, the unit for the patient backlog and service capacity are the number of patients per day, and for the waiting time, it is number of hours.
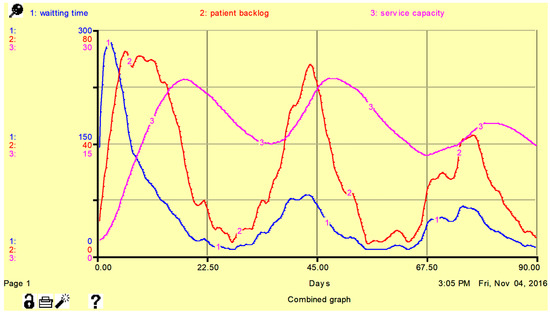
Figure 12.
Simulated waiting time, patient backlog, and service capacity under normal conditions. Here, the unit for the patient backlog and service capacity are the number of patients per day, and for the waiting time, it is number of hours.
- Behavior Tests of the model
The behavior validity tests are the second critical phase in the validation of an SD model, and they should be performed after the structural validation tests. A behavior sensitivity test is run to show how responsive the model behavior is to variations in parameter values. This is like the sensitivity analysis where variations in output are measured with respect to input. The parameter sensitivity test assesses whether or not a model would fail previously passed behavior tests when realistic changes in parameter values occur. To address the effects of the two parameters, target service time and time to adjust the workforce, a sensitivity analysis of the HOTS system was simulated. Figure 5, Figure 6 and Figure 7 depicted the effect of target service time, whereas Figure 8, Figure 9 and Figure 10 depicted the effect of workforce adjustment time. The system dynamic model of the HOTS system parameters was found to be sensitive to the changes in input parameter values of the target service time and the time to adjust the work force. This can be attributed to the model of a real system.
4. Results and Discussion
A system dynamic model of HOTS was developed to identify and accurately foresee patient demand for diversity promptly and match the service capacity with the fluctuating patient demand. It was realized that the model can predict future situations and it is valid. So, it will help maintain service capacity and make better decisions. If the service capacity of the HOTS system can satisfy the patient demand variation, the patient backlog and patient waiting time will be reduced.
According to the causal loop shown in Figure 2, patient backlog rises with higher patient arrival rates and falls with higher patient care completion rates, while desired care capacity rises with higher patient backlogs. Similarly, hiring rises with higher desired care capacity and falls with higher time to adjust the workforce, and service capacity rises with higher hiring. The patient care completion rate also rises. The HOTS’s causal loop diagram makes it easier to see how different variables in the system are connected. The managers of the healthcare operating theater system will be able to better grasp the links and dependencies among operating theater variables.
From the sensitivity analysis, it is obvious that with minor changes in input parameters, such as target service time and time to adjust workforce, the patient waiting time, patient backlog, and service capacity change. This can be observed in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 and all the graphs indicated predicted results.
Patients are currently complaining in substantial numbers about the HOTS system, which is solely the result of poor management and poor planning. Patients may have to wait four, five, or even more days to begin receiving their healthcare service, which increases the risk of patient death. The inability of the HOTS system’s management to match service capacity with fluctuating patient demand leads to a backlog of patients and lengthy wait times. Our model is accurate and can forecast future events. As a result, it will help with decision making and maintaining the service capacity. If the service capacity can accommodate the variation in patient demand, the patient backlog and waiting time will be reduced.
5. Conclusions
Because of the aging population and increasing demand for hospital services, operating theater managers in Bangladeshi hospitals are having serious capacity planning issues. Traditional approaches to dealing with hospital mismanagement can lead to severe consequences because of the increased patient backlog and longer waiting time. Hence, there is a need to route the patient’s treatment path toward a properly managed and well-organized healthcare system.
This study used conceptual modeling to depict patients’ treatment paths. Our qualitative model helps researchers better understand the resources needed during their journeys. The SD model was developed to help in understanding the dynamic complexity induced by various aspects of HOTS system. The causal loop diagram displays the problem’s feedback structure and highlights the connections between the pertinent variables. The flow of patients from the HOTS system’s input point to exit point is then depicted in a stock-flow diagram. The model can be helpful to policymakers in their efforts to understand and solve issues with hospital operating room patients, service capacity, and projecting the outcomes of prospective related initiatives, despite its small size and complexity.
The SD model is extremely useful for anticipating the impact of future events on service performance. Its key advantage is its capacity to qualitatively evaluate numerous hypothetical scenarios because of the ease with which acute and post-acute care capacities, as well as the model’s parameters, can be adjusted. Combining a stock and flow system appears to be more efficient than utilizing either method independently. Stock measures, such as expanding post-acute capacity, may only briefly alleviate the situation and may even drive increased demand, which may seem counterintuitive. A combination of stock and flow interventions, on the other hand, was proven to be potentially extremely beneficial in lowering constraints on acute service supply.
The SD model is helpful for predicting how future events may affect the performance of a HOTS. Due to the ease with which acute and post-acute care capacities, as well as the model’s parameters can be changed, it can qualitatively evaluate a wide range of speculative scenarios. Combining a stock and flow system is more effective than using each strategy separately. Expanding post-acute capacity is one example of a stock measure that may only temporarily improve the situation and may even boost demand, which may seem paradoxical. On the other hand, it was demonstrated that a combination of stock and flow interventions has the potential to be incredibly helpful in reducing supply bottlenecks for acute services. Academics and planners can gain valuable insights from these findings. This outcome also illustrates the value of advanced planning approaches like SD and how they can be applied to assess suggested strategies prior to implementation. Continuous data gathering must be required in each local community for the model to help decision makers identify the essential local level efforts.
Only the relevant hospital patients and operating theater service systems are included in the model. Another significant obstacle is the difficulty of data collection, as most of the hospitals did not have all the previously significant data on file. Based on their experiences, the hospital management provided us with approximate average numbers for multiple parameters. Our model was assessed using only three distinct structural tests and one behavior test. Further research can be conducted on the SD modeling of hospital operating theater service systems, building on existing studies.
Future research could broaden this study’s scope to encompass all patients and the entire hospital system. All significant information that may be needed for management, development, or future research should be retained by the hospital. More research on a hospital operating theater model should be performed using precise data for each parameter to ensure more trustworthy results. All tests that increase confidence should be taken into consideration in further studies.
Author Contributions
Conceptualization, M.M.R., R.K. and H.Y.; methodology, M.M.R., R.K., M.M. and M.A.H.; writing—original draft preparation, M.M.R., R.K. and M.M.,; writing—review and editing, M.M.R., R.K., M.M, M.A.H. and H.Y.; visualization, R.K. and H.Y.; supervision, M.M.R.; project administration, M.M.R. and R.K.; funding acquisition, M.M.R. and H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Forrester, J.W. System dynamics, systems thinking, and soft OR. Syst. Dyn. Rev. 1994, 10, 245–256. [Google Scholar] [CrossRef]
- Akin, J.S.; Guilkey, D.K.; Popkin, B.M. The demand for child health services in the Philippines. Soc. Sci. Med. Med. Econ. 1981, 15, 249–257. [Google Scholar] [CrossRef]
- Heller, P.S. A model of the demand for medical and health services in Peninsular Malaysia. Soc. Sci. Med. 1982, 16, 267–284. [Google Scholar] [CrossRef]
- Schwartz, J.B.; Akin, J.S.; Popkin, B.M. Price and income elasticities of demand for modern health care: The case of infant delivery in the Philippines. World Bank Econ. Rev. 1988, 2, 49–76. [Google Scholar] [CrossRef]
- Ching, P. User fees, demand for children’s health care and access across income groups: The Philippine case. Soc. Sci. Med. 1995, 41, 37–46. [Google Scholar] [CrossRef] [PubMed]
- Mwabu, G.M. Health care decisions at the household level: Results of a rural health survey in Kenya. Soc. Sci. Med. 1986, 22, 315–319. [Google Scholar] [CrossRef]
- Gertler, P.; Locay, L.; Sanderson, W. Are user fees regressive?: The welfare implications of health care financing proposals in Peru. J. Econom. 1987, 36, 67–88. [Google Scholar] [CrossRef]
- Ali, K.J.; Noman, A.N.K. An analysis of demand for health care in Bangladesh: The case of Rajshahi. Bangladesh Econ. Stud. 2010, 12, 34–50. [Google Scholar]
- Akbari, A.H.; Rankaduwa, W.; Kiani, A.K. Demand for public health care in Pakistan. Pak. Dev. Rev. 2009, 48, 141–153. [Google Scholar] [CrossRef]
- Turyamureba, M.; Yawe, B.L.; Oryema, J.B. Factors Influencing the Choice of Private Health Care Providers in Uganda. Afr. J. Econ. Rev. 2022, 10, 148–164. [Google Scholar]
- Appiah-Kubi, K. Access and utilisation of safe motherhood services of expecting mothers in Ghana. Policy Politics 2004, 32, 387–407. [Google Scholar] [CrossRef]
- Jochmann, M.; León-González, R. Estimating the demand for health care with panel data: A semiparametric Bayesian approach. Health Econ. 2004, 13, 1003–1014. [Google Scholar] [CrossRef] [PubMed]
- Mwabu, G.; Wang’ombe, J.; Nganda, B. The demand for medical care in Kenya. Afr. Dev. Rev. 2003, 15, 439–453. [Google Scholar] [CrossRef]
- Eme Ichoku, H.; Leibbrandt, M. Demand for healthcare services in Nigeria: A multivariate nested logit model. Afr. Dev. Rev. 2003, 15, 396–424. [Google Scholar] [CrossRef]
- Riphahn, R.T.; Wambach, A.; Million, A. Incentive effects in the demand for health care: A bivariate panel count data estimation. J. Appl. Econom. 2003, 18, 387–405. [Google Scholar] [CrossRef]
- Li, M. The Demand for Medical Care, Evidence form Urban Areas in Bolivia. World Bank—Living Stand. Meas. 1996, 1, 123. [Google Scholar]
- Lavy, V.; Quigley, J.M. Willingness to Pay for the Quality and Intensity of Medical Care: Evidence from Low Income Households in Ghana; UC Berkeley, Department of Economics: Berkeley, CA, USA, 1991; Available online: https://escholarship.org/uc/item/4p02g6nq (accessed on 29 October 2023).
- Mwabu, G.; Ainsworth, M.; Nyamete, A. Quality of medical care and choice of medical treatment in Kenya: An empirical analysis. J. Hum. Resour. 1993, 28, 838–862. [Google Scholar] [CrossRef]
- Dor, A.; Gaag, J.V.D. The Demand for Medical Care in Developing Countries. World Bank—Living Stand. Meas. 1988, 1, 35. [Google Scholar]
- Ahmadi-Javid, A.; Jalali, Z.; Klassen, K.J. Outpatient appointment systems in healthcare: A review of optimization studies. Eur. J. Oper. Res. 2017, 258, 3–34. [Google Scholar] [CrossRef]
- Guerriero, F.; Guido, R. Operational research in the management of the operating theatre: A survey. Health Care Manag. Sci. 2011, 14, 89–114. [Google Scholar] [CrossRef]
- Zhu, S.; Fan, W.; Yang, S.; Pei, J.; Pardalos, P.M. Operating room planning and surgical case scheduling: A review of literature. J. Comb. Optim. 2019, 37, 757–805. [Google Scholar] [CrossRef]
- Carthon, J.M.B.; Hatfield, L.; Brom, H.; Houton, M.; Kelly-Hellyer, E.; Schlak, A.; Aiken, L. System-level improvements in work environments lead to lower nurse burnout and higher patient satisfaction. J. Nurs. Care Qual. 2021, 36, 7–13. [Google Scholar] [CrossRef] [PubMed]
- Heydari, M.; Lai, K.K.; Fan, Y.; Li, X. A Review of Emergency and Disaster Management in the Process of Healthcare Operation Management for Improving Hospital Surgical Intake Capacity. Mathematics 2022, 10, 2784. [Google Scholar] [CrossRef]
- Sterman, J. System Dynamics: Systems Thinking and Modeling for a Complex World. Mass. Inst. Technol. Eng. Syst. Div. 2002. Available online: http://hdl.handle.net/1721.1/102741 (accessed on 29 October 2023).
- Dorner, D. The Logic of Failure: Recognizing and Avoiding Error. In Complex Situations; Metropolitan Books: New York, NY, USA, 1996. [Google Scholar]
- Homer, J.B.; Hirsch, G.B. System dynamics modeling for public health: Background and opportunities. Am. J. Public Health 2006, 96, 452–458. [Google Scholar] [CrossRef]
- Taylor, K.; Dangerfield, B. Modelling the feedback effects of reconfiguring health services. J. Oper. Res. Soc. 2005, 56, 659–675. [Google Scholar] [CrossRef][Green Version]
- González-Busto, B.; García, R. Waiting lists in Spanish public hospitals: A system dynamics approach. Syst. Dyn. Rev. J. Syst. Dyn. Soc. 1999, 15, 201–224. [Google Scholar] [CrossRef]
- Hirsch, G.; Bergan, T.; Goodman, M. Examining Alternatives for Improving the Nation’s Oral Health: A System Dynamics Model of the Dental Care Delivery System. In A Report to the Division of Dentistry, Bureau of Health Manpower; DHEW: Washington, DC, USA, 1975. [Google Scholar]
- Hirsch, G.; Myers, R. Designing Strategies for Particular Health Problems: The Indiana Cardiovascular Disease Model; Indiana Health Planning and Development Agency: Indianapolis, IN, USA, 1975. [Google Scholar]
- Luginbuhl, W.H.; Forsyth, B.R.; Hirsch, G.B.; Goodman, M.R. Prevention and rehabilitation as a means of cost containment: The example of myocardial infarction. J. Public Health Policy 1981, 2, 103–115. [Google Scholar] [CrossRef]
- Homer, J.; Hirsch, G.; Minniti, M.; Pierson, M. Models for collaboration: How system dynamics helped a community organize cost-effective care for chronic illness. Syst. Dyn. Rev. J. Syst. Dyn. Soc. 2004, 20, 199–222. [Google Scholar] [CrossRef]
- Jones, A.P.; Homer, J.B.; Murphy, D.L.; Essien, J.D.; Milstein, B.; Seville, D.A. Understanding diabetes population dynamics through simulation modeling and experimentation. Am. J. Public Health 2006, 96, 488–494. [Google Scholar] [CrossRef]
- Homer, J.; Milstein, B.; Dietz, W.; Buchner, D.; Majestic, E. Obesity population dynamics: Exploring historical growth and plausible futures in the US. In Proceedings of the 24th International System Dynamics Conference, Nijmegen, The Netherlands, 13–27 July 2006. [Google Scholar]
- Tengs, T.O.; Osgood, N.D.; Chen, L.L. The cost-effectiveness of intensive national school-based anti-tobacco education: Results from the tobacco policy model. Prev. Med. 2001, 33, 558–570. [Google Scholar] [CrossRef] [PubMed]
- Hirsch, G.; Immediato, C.S. Microworlds and generic structures as resources for integrating care and improving health. Syst. Dyn. Rev. J. Syst. Dyn. Soc. 1999, 15, 315–330. [Google Scholar] [CrossRef]
- Homer, J.; Hirsch, G.; Milstein, B. Chronic illness in a complex health economy: The perils and promises of downstream and upstream reforms. Syst. Dyn. Rev. J. Syst. Dyn. Soc. 2007, 23, 313–343. [Google Scholar] [CrossRef]
- Erdil, N.; Emerson, R. Modeling the dynamics of electronic health records adoption in the US healthcare system. In Proceedings of the 2008 International Conference of the System Dynamics Society, Athens, Greece, 20–24 July 2008. [Google Scholar]
- Bayer, S.; Barlow, J.; Curry, R. Assessing the impact of a care innovation: Telecare. Syst. Dyn. Rev. J. Syst. Dyn. Soc. 2007, 23, 61–80. [Google Scholar] [CrossRef]
- Wolstenholme, E. A patient flow perspective of UK Health Services: Exploring the case for new “intermediate care” initiatives. Syst. Dyn. Rev. J. Syst. Dyn. Soc. 1999, 15, 253–271. [Google Scholar] [CrossRef]
- Wolstenholme, E.; Monk, D.; McKelvie, D.; Arnold, S. Coping but not coping in health and social care: Masking the reality of running organisations beyond safe design capacity. Syst. Dyn. Rev. 2007, 23, 371–389. [Google Scholar] [CrossRef]
- Van Ackere, A.; Smith, P.C. Towards a macro model of National Health Service waiting lists. Syst. Dyn. Rev. J. Syst. Dyn. Soc. 1999, 15, 225–252. [Google Scholar] [CrossRef]
- Forrester, J.W. Principles of Systems; MIT Press: Cambridge, MA, USA, 1968. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).