Holographic Tailoring of Structured Light Field with Digital Device

Abstract

Structured light fields have attracted much attention due to rich spatial degrees of freedom. The tailoring of an arbitrary structured light field on demand is the precondition for the application of structured light. Therefore, the computer holography method used to reconstruct a coherent light field wavefront has been naturally applied for generating structured light. In this work, we comprehensively demonstrate the principles and procedures of pure-phase computer-generated holography (PP-CGH) and binary-amplitude computer-generated holography (BA-CGH) methods for tailoring structured light, realized by two digitally programmable devices: liquid-crystal spatial light modulators ($\mathrm{Lc}\text{-}\mathrm{SLM}$) and digital micromirror devices (DMD), respectively. Moreover, we first compare the two approaches in detail and clarify the recipe to obtain a high tailoring accuracy and efficiency, which will help researchers to better understand and utilize the holographic tailoring of structured optical fields.

1. Introduction

The spatial structure of light is a very important manipulation dimension of an optical field, along with other physical degrees of freedom, such as time, amplitude, wavelength (frequency), polarization and phase [1,2,3]. Thirty years ago, L. Allen pointed out that vortex light beams carrying optical orbital angular momentum (OAM) led to a connection between the OAM in quantum optics and the helical phase of the beam in physical optics [4]. The feature of optical OAM has attracted intense research on vortex beams [5,6], and has triggered a flourish of development in the field of structured light [1,7,8,9,10]. In recent years, structured beams have found important applications in optical communication, optical trapping, imaging, optical sensing, etc. [11,12,13,14]. Those application scenarios, in return, impose increasing highly demands on high-quality, flexible, robust and fast tailoring techniques of structured light.

As a general tool to reconstruct a coherent light field wavefront, the computer holography is naturally applied to tailor structured light fields [15,16,17,18]. Thanks to the recent development of high-resolution, pixelated, programmable commercial spatial light modulators, the combination of computer holography and spatial light modulators has opened up a new and highly efficient route of structured light customization [19,20]. Specifically, the pure-phase computer-generated holography (PP-CGH) and binary-amplitude computer-generated holography (BA-CGH) were implemented in two programmable devices: liquid-crystal spatial light modulators ($\mathrm{Lc}\text{-}\mathrm{SLM}$) and digital micro-mirror devices (DMD), respectively [21,22,23,24]. Various laser modes were created by the CGH method, including the Laguerre–Gaussian beams, Ince–Gaussian beams and non-diffracting beams, as well as cylindrically symmetric vector-vortex beams [24,25,26,27,28]. The CGH methods based on these two digital devices are widely used to tailor structured light due to their high flexibility and excellent tailoring quality.

In this article, we describe the modulation principle and procedure of PP-CGH and BA-CGH methods in detail. In addition, we theoretically analyze the relationship between the tailoring accuracy and number of available pixels by taking vortex light as an example, and point out the optimization route and modulation limit for the use of pixelated modulation devices. Furthermore, to the best of our knowledge, we compare, for the first time, the modulation efficiencies of two methods and clarify the reasons in detail. This work provides a recipe for the tailoring of structured light using the CGH approach.

2. Materials and Methods

The Laguerre–Gaussian (LG) mode family that contains OAM is the most common type of structured beams. We employed LG modes hereinafter to compare the digital CGH methods based on $\mathrm{Lc}\text{-}\mathrm{SLM}$ and DMD. The wave function of LG modes with zero radial index can be indicated as [4,29]:

$$\begin{array}{cc}\hfill \mathrm{L}{\mathrm{G}}_0^{\ell }\left(r,z\right)=& \sqrt{\frac{2}{\pi \left|\ell \right|!}}\frac{1}{\omega }{\left(\frac{\sqrt{2}r}{\omega }\right)}^{\left|\ell \right|}exp\left(-\frac{r^2}{{\omega }^2}\right)exp\left(i\ell \varphi \right)\hfill \\ \hfill & exp\left\{ik\left[z+\frac{r^{2}z}{2\left(z^2+z_R^2\right)}\right]-i\left(\left|\ell \right|+1\right){\theta }_{Gouy}\right\}\hfill \end{array}$$

(1)

where $\omega ={\omega }_0\sqrt{1+{\left(z/z_R\right)}^2}$ is radius of Gaussian beam, ${\omega }_0$ is waist radius, $z_R=\pi {\omega }^2/\lambda$ is the Rayleigh length, $\lambda$ is wavelength, r and $\varphi$ are radial and angular coordinates in the polar coordinate system, respectively, and $k=2\pi /\lambda$ and ${\theta }_{Gouy}={tan}^{-1}\left(z/z_R\right)$ are wavenumber and Gouy phase, respectively. Notably, ℓ is the topological charge (TC) of OAM beam, which contributes to the twisted phase. The LG modes have the most concise phase structure at the beam waist ($z=0$), which is favorable for the mode tailoring, and can be reduced to:

$$\begin{array}{cc}\hfill \mathrm{L}{\mathrm{G}}_0^{\ell }\left(r,0\right)=& \sqrt{\frac{2}{\pi \left|\ell \right|!}}\frac{1}{{\omega }_0}{\left(\frac{\sqrt{2}r}{{\omega }_0}\right)}^{\left|\ell \right|}exp\left(-\frac{r^2}{{\omega }_0^2}\right)exp\left(i\ell \varphi \right)\hfill \end{array}$$

(2)

The intensity and phase pattern of OAM beams at beam waist plane are shown in Figure 1. The sign ‘+’ and ‘−’ of TC (ℓ) correspond to the phase growth along clockwise and counterclockwise directions, respectively. Moreover, OAM beams with the same $\left|\ell \right|$ have same intensity distribution, and the beam radius is proportional to the square of the beam quality factor.

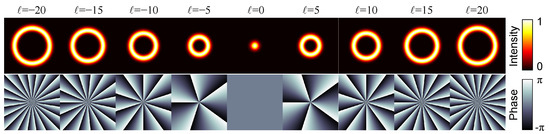
Figure 1. Intensity (top) and phase (bottom) pattern of LG mode with different TC $(\ell )$.

As a universal tailoring method for scalar structured lights, CGH approach relies on pixelated spatial light modulation device in experiment. The transfer function of PP-CGH hologram for $\mathrm{Lc}\text{-}\mathrm{SLM}$ is given by [22,24]:

$$\begin{array}{cc}\hfill T_{SLM}\left(x,y\right)& =exp\left\{i\Psi \left[A,\Phi +2\pi \left(u_{0}x+v_{0}y\right)\right]\right\}\hfill \\ \hfill & =\sum _{q=-\infty }^{\infty }{c}_q^{A}exp\left[iq\Phi \right]exp\left[iq\left(u_{0}x+v_{0}y\right)\right]\hfill \\ \hfill & =exp⟨i\left\{sin\left[\Phi +2\pi \left(u_{0}x+v_{0}y\right)\right]J_1^{-1}\left(CA\right)\right\}⟩\hfill \end{array}$$

(3)

where $A\in \left[0,1\right]$ and $\Phi \in \left[0,2\pi \right]$ are normalized amplitude and phase of target structured light field, $J_1^{-1}$ is inverse of $1st$ Bessel function $C\approx 0.681$ and $u_0$ and $v_0$ are the reciprocals of the linear grating period in x and y directions, respectively.

Similarly, the transfer function of BA-CGH hologram for DMD is given by [23,25]:

$$\begin{array}{c}\hfill T_{DMD}\left(x,y\right)=\frac{1}{2}+\frac{1}{2}\mathrm{sign}⟨cos\left[\Phi +2\pi \left(u_{0}x+v_{0}y\right)\right]+cos\left\{arcsin\left[A\right]\right\}⟩\end{array}$$

(4)

Detailed derivations of Equations (3) and (4) can be found in Appendix A and Appendix B. By calculating Equation (3) over a discrete complex amplitude of light field, a phase matrix was obtained whose element corresponds to pixel position on the $\mathrm{Lc}\text{-}\mathrm{SLM}$ screen. Then, a PP-CGH hologram that creates LG beams could be generated. The same applies for binary amplitude matrix of the DMD. The generation procedures of PP-CGH (top row) and BA-CGH (bottom row) of ${\mathrm{LG}}_0^{10}$ are shown in Figure 2, which visually demonstrates the calculation process of Equations (3) and (4).

Figure 2. An example of constructing CGH hologram, (a–d) are construction method for PP-CGH (where $J_1^{-1}$ is inverse of $1st$ Bessel function), (e–h) are construction method for BA-CGH and (d,h) are phase gray hologram and binary amplitude hologram of ${\mathrm{LG}}_0^{10}$, respectively.

Note that the linear grating $2\pi \left(u_{0}x+v_{0}y\right)$ in Equations (3) and (4) is used to separate the input light into different orders, as shown in Figure 3a,b. When a planar wave illuminates the PP-CGH or BA-CGH of the target optical field ${\mathrm{LG}}_0^{10}$ as inserted in Figure 3c, the far-field of modulated light has multiple spatially separated orders with different patterns, as shown in Figure 3c. By extracting the $+1$ order, we obtained the desired ${\mathrm{LG}}_0^{10}$ beam, with the simulated results shown in Figure 3d,e for PP-CGH and BA-CGH method, respectively. To avoid the overlapping of target beam and other beams, one can increase the frequency of diffraction grating and thus enlarge the spacing between diffraction orders.

Figure 3. Schematic diagram of PP-CGH and BA-CGH for generating structured light. (a,b) show that the input beam is modulated and diffracted into multiple orders for the binary amplitude hologram and phase gray hologram, respectively. (c) shows the partially separated orders on the far-field pattern of binary amplitude or phase gray diffracted hologram of ${\mathrm{LG}}_0^{10}$ mode by illuminating a plane wavefront, while the intensity and phase of target beam are inserted in the upper left corner. (d,e) shows the reconstructed intensity and phase by extracting the +1st diffraction order for PP-CGH and BA-CGH, respectively.

3. Results and Discussion

In order to estimate the generation method of a structured light field, there are two crucial issues to keep in mind. First, one should examine whether the target structured light field can be generated perfectly, and, if not, how to obtain the highest possible tailoring precision. Second, one should check the generation efficiency of a target structured light field and the room for improvement. Hereinafter, we use ${\mathrm{LG}}_0^{\ell }$ modes as an example to analyze and compare the results of PP-CGH and BA-CGH methods in details.

3.1. Precision of Holographic Tailoring

The methods based on BA-CGH and PP-CGH can perfectly tailor arbitrary scalar structured light fields in theory. However, since the DMD and $\mathrm{Lc}\text{-}\mathrm{SLM}$ are pixelated devices, the finite limit of resolution degrades the quality of the reconstructed beam both in the simulation and experiment. The complex amplitude correlation degree between the reconstructed field and theoretical field can be used as an efficient indicator to evaluate the reconstruction quality [30,31], as given by:

$$\begin{array}{c}\hfill \gamma =\frac{\int \int E_{\mathrm{s}}^{*}\left(x,y\right)E_{\mathrm{t}}\left(x,y\right)dxdy}{\sqrt{\int \int {\left|E_{\mathrm{s}}\left(x,y\right)\right|}^{2}dxdy\int \int {\left|E_{\mathrm{t}}\left(x,y\right)\right|}^{2}dxdy}}\end{array}$$

(5)

where $E_{\mathrm{t}}\left(x,y\right)$ and $E_{\mathrm{s}}\left(x,y\right)$ are theoretical and simulated light fields from reconstruction, respectively, and sign ‘*’ means the conjugate. $\gamma =0$ indicates that both fields are orthogonal, whereas $\gamma =1$ indicates that they are identical. $\gamma$ with a larger value implies a better reconstruction quality.

Importantly, to alleviate the deterioration in reconstruction quality due to a limited resolution, one can increase the number of effectively utilized pixels of the spatial light modulator. Figure 4 illustrates the azimuthal phase discretization of ${\mathrm{LG}}_0^1$, and the reconstructed results under different available pixel numbers. The blue circles in Figure 4a mark the sampling regions of a $40\times 40$ phase diagram at different radius proportions ($25\%$, $50\%$ and $80\%$). Figure 4b displays the corresponding discretized azimuthal phase of ${\mathrm{LG}}_0^1$, whereas Figure 4c shows the intensity distribution with corresponding radii. Figure 4d shows the reconstructed intensity and phase, with the value of $\gamma$ shown in the upper left corner of each subfigure. It can be seen that employing a more discretized azimuthal phase—that is, more pixels are utilized in the light field—results in a more accurate reconstruction. The complex amplitude correlation degree of the reconstructed field at 31, 62 and 100 pixels are 0.86, 0.95 and 0.97, respectively. In addition, the OAM spectrum shown in Figure 4e demonstrates that the $80\%$ aperture has the best performance in suppressing the other TC ($\ell \ne 1$) components, leading to the least OAM inter-mode crosstalk. For a target light field that is located closer to the coordinate origin, fewer pixels can be utilized, thereby suffering from more severe deterioration in the reconstruction. As such, it is necessary to make full use of available pixels when using the pixelated spatial light modulator.

Figure 4. Schematic of reconstructed vortex beam under discretized azimuthal phase. (a) The phase sampling in a finite resolution $(40\times 40)$ phase diagram, (b) the discretized azimuthal phase with different pixels, (c) intensity of the vortex light field with different radii, where (d,e) are the intensity, phase and OAM spectrum of the reconstructed field. (b1–e1, b2–e2 and b3–e3 correspond to the optical field radius proportion of $25\%$, $50\%$ and $80\%$, respectively, relative to the computational aperture).

In addition to resolution, the phase structure of the beam itself also affects the modulation quality. For a phase distribution with a more drastic phase change, a higher resolution is required to reconstruct the light field. We calculated the complex amplitude correlation degree of reconstructed field for nine ${\mathrm{LG}}_0^{\ell }$ modes [${\mathrm{LG}}_0^9$, ${\mathrm{LG}}_0^{17}$, ${\mathrm{LG}}_0^{25}$, ${\mathrm{LG}}_0^{33}$, ${\mathrm{LG}}_0^{41}$, ${\mathrm{LG}}_0^{49}$, ${\mathrm{LG}}_0^{57}$, ${\mathrm{LG}}_0^{65}$, ${\mathrm{LG}}_0^{63}$] in 10 types of resolution settings [40 × 40, 80 × 80, 120 × 120, 160 × 160, 200 × 200, 240 × 240, 280 × 280, 320 × 320, 360 × 360, 400 × 400]. The diameter of the vortex light of different TCs is equal to 50% of the calculated surface size. Therefore, the numbers of available pixels corresponding to different resolutions are $1\times 62,2\times 62,\cdots ,9\times 62$ and $10\times 62$, respectively. The complex amplitude correlation degree $\gamma$ in Figure 5 indicates that, as the TC increases, the tailoring accuracy reduces at the same number of pixels, whereas, for the same TC, enlarging the number of available pixels enhances the tailoring accuracy. Note that $\gamma$ has a nonlinear variation trend versus the number of available pixels utilized. For the case of $\ell =41$, $\gamma$ is always less than $10\%$ with the available pixel number below 310, then grows to $62\%$ at 440 pixels, reaches $83\%$ at 502 pixels and increases further to $93\%$ at 565 pixels. Thus, one may need 11, 13 and 14 available pixels in a $2\pi$ phase range to reconstruct the field with the value of $\gamma$ over $70\%$, $80\%$ and $90\%$, respectively. As a result, it is estimated that a vortex beam with TC as high as 300 can be generated with $\gamma >70\%$ by fully utilizing a SLM resolution of 1920 × 1080 pixels. In addition, the complex amplitude correlation degrees of PP-CGH and BA-CGH methods are almost the same for all simulated cases, with the average difference less than $1\%$. In this regard, two devices are interchangeable when only considering the tailoring quality of the beam field.

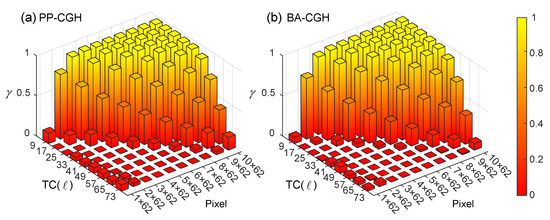
Figure 5. The complex amplitude correlation degree of vortex beam versus different TCs and different available pixel numbers for PP-CGH (a) and BA-CGH (b).

3.2. Efficiency of Holographic Tailoring

In this subsection, we focus on the modulation efficiency of two methods. As stated above, the digital holographic tailoring methods require the illumination of a planar light wave on the CGH hologram. The efficiency of holographic tailoring can be expressed as the energy of +1st order (target beam, in Figure 3c) $P_{+1}$ divided by the energy of the input planar wave within the computational aperture $P_{\mathrm{in}}$:

$$\begin{array}{c}\hfill {\eta }_{mod}=\frac{P_{+1}}{P_{\mathrm{in}}}\end{array}$$

(6)

where $mod$ denotes $PP$ and $BA$ for PP-CGH and BA-CGH methods, respectively.

We calculated the holographic tailoring efficiency for vortex light ($TC=0$ to 10) at a spatial resolution of $400\times 400$, where the beam spot radius covers 628 azimuthal pixels on the spatial light modulator. In this condition, the complex amplitude correlation degrees for all tailored vortex optical fields exceed $95\%$. The tailoring efficiencies of PP-CGH and BA-CGH in Figure 6a,b demonstrate that the efficiency increases with TC for both PP-CGH and BA-CGH methods; and PP-CGH has a tailoring efficiency that is three times as large as that of BA-CGH for all cases with different TCs.

Figure 6. Tailored efficiency of holographic generation for vortex beams. (a) Bar chart of tailoring efficiency for PP-CGH and BA-CGH methods, (b) ratio of tailoring efficiencies of two methods, (c) the ratio of target light field energy to energy within the computational aperture and (d) extraction efficiency of target light field for PP-CGH and BA-CGH methods.

Furthermore, we show that the energy of target field $P_{A(x,y)}$, where $A(x,y)$ are amplitude-normalized $L{G}_0^{\ell }$ modes, reduces rapidly as the TC reduces, as illustrated in Figure 6c, where the ratio is the energy of the target field divided by the energy of the input planar wave (consistent) within the computational aperture. In addition, it is interesting that the extraction efficiency ($P_{+1}/P_{A(x,y)}$) is consistent against varying TC, as shown in Figure 6d, which suggests that the tailoring efficiency depends mainly on the intensity distribution of the target light field itself when using the holographic modulated tailoring of PP-CGH and BA-CGH. It is shown that approximately $30\%$ and $10\%$ of energy within the covering area of the target beam on the modulator can be converted to the target light field at the far field, using PP-CGH and BA-CGH methods, respectively.

The discrepancy between the two methods in term of the tailoring efficiency can be well explained by reviewing the structured light tailoring principles. Figure 7a,e illustrate the intensity and phase distribution of the target beam ($\ell =10$). Figure 7b–d are the modulated normalized light field distribution of input light, zero order and +1st order in the PP-CGH method, respectively. Figure 7c shows that 68% of the energy of the input light is directly tailored in the covering region of the target beam on the modulator. Then, $45\%$ of the tailored energy is distributed to +1st order (the target beam), whereas the other $45\%$ is located at the −1st order and the other $10\%$ is located at the higher order. In total, the reconstructed beam obtains $100\%\times 68\%\times 45\%\approx 30\%$ of the energy of the target area (as shown in Figure 7d). In contrast, Figure 7f–g are the normalized distribution of modulated light, zero order and +1st order in the BA-CGH method, respectively. Only half the energy of the input light within the target area is modulated due to 0/1 grating, as shown in Figure 7f. Then, approximately 50% of the modulated energy remains at zero order, whereas the other 45% is equally divided into the +1st order (target beam) and −1st order, and the other $10\%$ is located at the higher order, as indicated in Figure 7g. In total, the reconstructed beam obtains $100\%\times 50\%\times 50\%\times 45\%\approx 11\%$ of the energy of the target area, as shown in Figure 7d. In this regard, to achieve a higher tailoring efficiency, we need to cover the modulation area with the target light field as much as possible, or make the input light match the size of the target light field to distribute more energy into the target beam.

Figure 7. Schematic of tailoring of vortex beams ($\ell =10$) with PP-CGH and BA-CGH methods, (a) energy of target is $100\%$, (b–d) and (e–g) are the modulated normalized light field distribution of input light, 0th order, and +1st order in the PP-CGH and BA-CGH method, respectively, while extraction efficiencies (inserted in upper right coner) of PP-CGH method and BA-CGH method are 30% and $11\%$, respectively.

3.3. Discussion

The above analysis indicates that the two methods have a similar tailoring quality. However, in terms of the modulation efficiency, the efficiency of BA-CGH is only approximately one third that of PP-CGH. In addition, the devices for realizing PP-CGH and BA-CGH tailoring have their own characteristics in terms of cost, modulation speed, wavelength and polarization, as compared in Table 1. It is shown that structured light tailoring with an amplitude binary mask in DMD has a much faster modulation speed and moderately lower cost, which is beneficial to wider application scenarios. In addition, there are other parameters characterizing the digital devices, e.g., in the case of Lc-SLM: diffraction efficiency, number of gray levels/phase levels that can be addressed and fill factor; and, in the case of DMD: diffraction efficiency and fill factor, which can mildly influence the tailoring performance.

Table 1. Comparison of $\mathrm{Lc}\text{-}\mathrm{SLM}$ and DMD for structured light tailor.

Modulator	$\mathbf{Lc}\text{-}\mathbf{SLM}$	DMD
Traits	Low refresh rate (50–500 Hz); polarization-sensitive; wavelength-sensitive; temperature-sensitive; relatively high efficiency(≤20%); expensive	High refresh rate (10 kHz–30 kHz); polarization-insensitive; wavelength-insensitive; temperature-insensitive; low efficiency(≤5%); relatively cheap

4. Conclusions

In summary, we have comprehensively demonstrated the structured light tailoring methods for PP-CGH and BA-CGH and the corresponding tailoring accuracy and efficiency. In theory, both methods can theoretically tailor arbitrary structured light perfectly. However, in practical applications, pixelated modulation devices introduce tailoring error and loss. We theoretically summarize the relationship between the tailoring accuracy and modulated pixel for the example of a vortex beam, and point out the optimization route and tailoring limit for the use of pixelated modulation devices. In addition, we demonstrate that PP-CGH has a tailoring efficiency three times that of BA-CGH. We conclude that one should always make the target beam cover as many pixels as possible on the modulator plane to obtain a higher tailoring accuracy and efficiency. This analysis will help researchers better use the digital holography method to achieve customized structured optical fields.