Abstract
We discuss the sensitivity to optical feedback of a semiconductor ring laser that is made to emit in a single-longitudinal mode by applying on-chip filtered optical feedback in one of the directional modes. The device is fabricated on a generic photonics integration platform using standard components. By varying the filtered feedback strength, we can tune the wavelength and directionality of the laser. Beside this, filtered optical feedback results in a limited reduction of the sensitivity for optical feedback from an off-chip optical reflection when the laser is operating in the unidirectional regime.
1. Introduction
Many studies have shown that semiconductor lasers are very sensitive to optical feedback, i.e., to part of the laser light being reflected back into the laser cavity with a delay [1,2,3,4,5,6]. Such coherent optical feedback (COF) is often difficult to avoid in practical systems, as it can be caused, for example, by reflections from a fiber tip or from other boundaries between materials with different refractive indices in the optical system to which the laser beam is coupled. COF can lead to linewidth narrowing for very weak feedback [2], but for larger feedback strengths it will typically introduce unwanted instabilities in the laser output [3]. For example, it has been shown that COF can lead to linewidth broadening [4], chaotic intensity fluctuations [5] and coherence collapse [6].
In order to avoid or suppress the COF-induced instabilities, several approaches have been investigated [7,8,9]. The most straightforward way to avoid them is to place an optical isolator with a large isolation ratio at the output of the laser. This works well to avoid COF-induced dynamics, but is an expensive approach as the isolator needs magneto-optic materials that—for technological reasons—cannot easily be integrated on the laser chip. Moreover, the optical isolator needs to be accurately aligned with the laser chip to avoid propagation losses of the emitted beam. Because of the high cost of such external isolators, there is considerable interest in other approaches to achieve the goal of suppressing the COF-induced dynamics in a semiconductor laser.
A laser with a ring-shaped cavity is inherently interesting for the purpose of suppressing feedback dynamics, as any externally reflected light will be re-injected in the cavity in the direction opposite to that of the initially emitted beam: imagine such a ring laser to emit in the clockwise (CW) directional mode, optical feedback will then result in part of this beam being coupled into the counterclockwise (CCW) directional mode. In [7], a weak optical isolator is integrated in the laser cavity in order to make one of the directional modes dominant, such that the COF is injected in the directional mode that is switched-off, hence reducing its destabilizing effect. But this approach requires complex components in the laser cavity to achieve the required weak optical isolation, making the laser system difficult to control. Another ring-laser based device was studied in [9], where the fabrication process of the semiconductor ring laser (SRL) is optimized to such a degree that coupling between the directional modes through backscattering is very low. This results in unidirectional operation (i.e., the laser emits in one of the directional modes) of the fabricated SRLs, which leads to a strong suppression of feedback-induced dynamics [8] as compared to a Fabry–Perot laser fabricated on the same chip. However, when using generic integration platforms—which are not optimized for one specific purpose—the backscattering will typically be much higher, resulting in bidirectional operation (i.e., the power in the two directional modes being roughly equal) of fabricated SRLs [10,11].
In this paper, we investigate the feedback sensitivity of an SRL that we designed and fabricated using the generic JeppiX fabrication platform [12]. Because of a substantial amount of backscattering between the directional modes, the SRL itself will typically emit bidirectionally. In this design, we included on-chip filtered optical feedback (FOF) paths that have been shown [11] to make the SRL emit in a single-longitudinal mode. Controlling the FOF also allows us to tune the emitted wavelength of the SRL. Moreover, as we will discuss in the next sections, the FOF in this SRL has as a side effect that it makes the emission (somewhat) unidirectional. Based on the above mentioned work in [8] on unidirectional SRLs, we thus expect our SRL design to be less sensitive to optical feedback from off-chip reflections. In order to check the effectiveness of this approach, we experimentally and numerically study in this paper the sensitivity of our SRL design to undesired external optical feedback.
The remainder of the paper is structured as follows. In Section 2 we describe the layout of the SRL and we detail the experimental setup. The results of the experiments and numerical simulations are shown in Section 3, whereas Section 4 is devoted to the discussions of the results. Finally, we end the paper with conclusions in Section 5.
2. Materials and Methods
2.1. Layout of the SRL
The layout of the device is illustrated by the picture shown in Figure 1. It has been fabricated using the standard building blocks from the Oclaro foundry, and a detailed description of the layout is given in [11]. As can be seen in Figure 1, the SRL has a racetrack-shaped geometry and optical gain is provided by two semiconductor optical amplifier (SOA) sections that are electrically interconnected. The laser cavity also contains two 2 × 2 multi-mode interference (MMI) couplers, which each couple 50% of the light out of the cavity. The outputs of the top MMI are coupled to the edges of the laser chip such that the CW and CCW modes can be measured. The bottom MMI in Figure 1 couples to two FOF branches. Each of these branches consists of a phase shifter (PS), an SOA and a distributed Bragg reflector (DBR). These components can be electrically tuned by adapting the current injected in the attached contact pad, such that we have control over the center wavelength (by changing the DBR current), the strength (by changing the SOA current) and the phase (by changing the PS current) of the FOF. Feedback arms 1 and 2 are used to control the FOF into the CW and CCW directions, respectively.
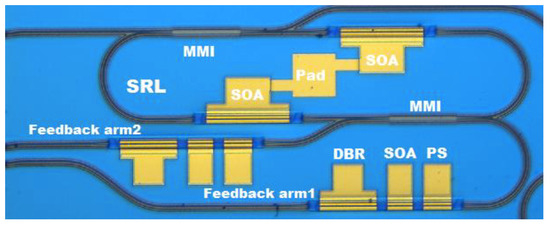
Figure 1.
Image of the semiconductor ring laser with filtered feedback, in which the different laser and feedback components are indicated.
2.2. Experimental Setup
To measure the static and dynamic characteristics of the SRL, we used the setup that is schematically depicted in Figure 2. The SRL was mounted on a temperature-controlled heat sink, with which we stabilized the temperature of the laser chip at 21 °C. In principle, each of the contact pads visible in Figure 1 can be connected to a current source using electrical contact probes, but for the work presented in this paper only the laser pad and the SOA pad in feedback arm 2 were contacted. This allowed us to change the laser’s injection current Ilaser and the current ISOA1 that controls the strength of the FOF of arm 2. It should be noted that we have obtained similar results when using FOF from feedback arm 1, with the difference being that the roles of the CW and the CCW modes are then reversed. Light emitted in the CW and in the CCW direction was collected outside the laser chip using lensed fibers. Light emitted in the CCW direction was sent through a feedback loop, and was coupled back with a time delay of about 50 ns into the CW directional mode. The COF feedback loop consisted of a circulator, an external SOA, an optical bandpass filter, a 2 × 2 single-mode splitter and a polarization controller. The circulator directed the CCW light from the laser towards the external SOA. The current ISOA2 injected in this external SOA was used to control the COF strength. Next, the amplified light was sent through a tunable bandpass filter with a bandwidth of 0.3 nm of which the center wavelength was tuned to the SRL’s wavelength. This tunable filter was needed to remove the amplified spontaneous emission noise—introduced by the external SOA—from the feedback signal. The polarization controller was used to adjust the polarization of the re-injected light such that it matched the emitted polarization direction. Light was re-injected into the SRL chip using the third port of the circulator. The splitter coupled 50% of the light out of the feedback loop such that we could measure its temporal and spectral properties. The optical spectrum was measured with a scanning spectrum analyzer set at a resolution of 0.02 nm. Time traces of the intensity fluctuations were measured using a 12 GHz photo-detector coupled to a fast oscilloscope of which the input bandwidth was set at 13 GHz in the experiments discussed in Section 3.
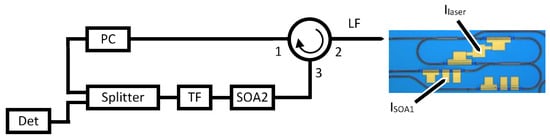
Figure 2.
Schematic of the experimental setup. LF, lensed fiber; SOA2, semiconductor optical amplifier used to tune the coherent optical feedback (COF) strength; TF, tunable optical bandpass filter; Det, fast opto-electronic detector; PC, polarization controller.
2.3. Rate-Equation Model
The behavior of the SRL under the effect of FOF and/or COF can be simulated using different models [13,14]. In this work, we used a two-directional mode rate equation model of the SRL [15], extended with Lang–Kobayashi terms, to take into account the optical feedbacks [16]. The equations of this models are:
Equations (1) and (2) describe the evolution of the slowly varying complex electric fields Ecw and Eccw of the CW and CCW directions, respectively. The number of carriers, N, is described by Equation (3). We have limited ourselves to one longitudinal mode (LM). The values of the different parameters are as follows: κ = 200 ns−1 is the field decay rate, α = 3.5 is the linewidth enhancement factor, μ = 1.2 is the normalized injection current, γ = 0.4 ns−1 is the carrier inversion decay rate. The effect of the backscattering is taken into account using the dissipative backscattering parameter kd = 0.2 ns−1 and the conservative backscattering parameter kc = 0.88 ns−1 which have been used for both of the two directional modes. The differential gain functions are given by:
where s = 0.005 is the self-saturation and c = 0.01 is the cross-saturation between the two directions of the same LM. represents the strength of the COF. is the delay time of the COF which is measured in our setup to be 50 ns. represents the strength of the FOF. As the FOF couples the CW mode back into the CCW mode, we only include an FOF term in Equation (2). The bandwidth of the filter in the feedback loop is adiabatically eliminated from Equation (2) as this filter bandwidth is much larger than the bandwidth of the fluctuations in Ecw and Eccw. is the propagation time in the FOF section which is integrated on the chip and is very small. Therefore, we take τ2 equal to zero in the simulations. Here it is important to mention that the feedback scheme in this study is different from the feedback scheme which has been discussed in [17,18], where self-feedback has been investigated. The last terms in Equations (1) and (2) represent the effect of spontaneous emission noise coupled to the CW/CCW modes [18,19]. D represents the noise strength expressed as D = D0(N + G0N0/κ), where D0 is the spontaneous emission factor, G0 = 10−12 m3s−1 is the gain parameter, N0 = 1.4 × 1024 m−3 is the transparency carrier density. ξi (t)(i = cw, ccw) are two independent complex Gaussian white noises with zero mean and correlation Time is rescaled to photon lifetime τph = 5 ps.
3. Results
3.1. Experimental Results
Using the setup of Figure 2, we first measured the static characteristics of the studied SRL. The output power of the two directional modes is shown in Figure 3 as a function of the laser injection current (without pumping the SOAs in the FOF arms). The threshold current of this device was 34 mA. For all currents not too far above threshold, the power in the two directional modes was roughly equal, showing that this SRL always operates in the bidirectional regime [13], which indicates that there was a substantial amount of backscattering in SRLs fabricated on the used platform. For some laser bias currents, the SRL emitted in a single longitudinal mode, but for most values of the laser injection current, the laser emitted multiple longitudinal modes. The longitudinal mode spacing was measured to be 0.2 nm. The DBRs in the FOF arms have a peak intensity reflection of 0.58 and a reflection bandwidth of 2 nm. In [11] we have shown that a sufficiently large amount of feedback in either of the FOF channels resulted in single longitudinal mode operation, that the wavelength of the emitted mode could be changed by changing the DBR center reflection wavelength, and that this wavelength could be fine-tuned using the phase shifters in the FOF arms.
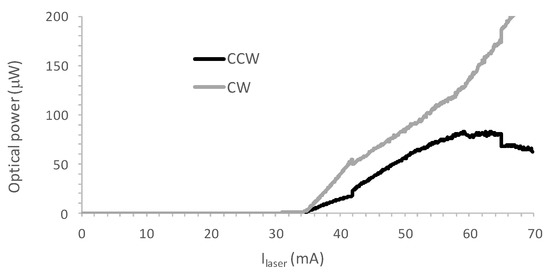
Figure 3.
Output power of the two directional modes versus laser injection current while the current in the filtered optical feedback (FOF) section is equal to 0 mA.
If we only applied FOF in one of the arms, the FOF had an additional effect that made the SRL somewhat unidirectional. This is illustrated by the measurement shown in Figure 4, where we plot the power in the two directional modes as a function of the current ISOA1 injected in the SOA of FOF arm 2 in Figure 1. The laser current Ilaser was kept constant, as shown in Figure 4, at a value of 60 mA. For low values of ISOA1, most power was emitted in the CW direction. But as ISOA1 was ramped up, the power in the CCW direction gradually increased at the expense of the power in the CW direction. This is to be expected from the feedback configuration used in this experiment as the FOF in feedback arm 2 coupled light from the CW direction into the CCW direction. The power distribution over the two directional modes is further detailed at the right-hand side of Figure 4, where we plot the ratio between the power in the CCW direction and the power in the CW direction. This so-called directional mode suppression ratio (DMSR) increased most strongly when ISOA1 increased from 0 to 11 mA, and then continued to increase at a slower pace for still higher values of ISOA1.
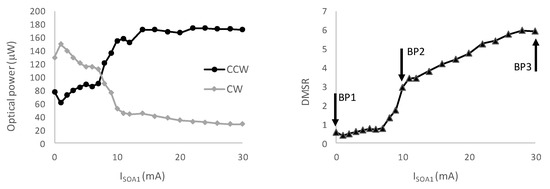
Figure 4.
Output power of the two directional modes versus current injected in the semiconductor optical amplifier (SOA) in the FOF arm 2 (left) and directional mode suppression ratio as a function of the SOA current in the FOF arm (right) at a laser injection current of 60 mA.
Based on Figure 4, we identified three interesting bias points (indicated by the black arrows) at which we wanted to investigate the sensitivity to COF. The first bias point, BP1, corresponds to ISOA1 = 0 mA, as in that case there was no FOF and we measured the feedback sensitivity of the SRL itself. The second bias point, BP2, that we would further investigate corresponds to ISOA1 = 11 mA, as in this case the FOF clearly favored the CCW directional mode. Finally, the third selected bias condition, BP3, corresponds to ISOA1 = 30 mA and in this case the directional mode suppression ratio was greatest. For BP2 and BP3, the SRL emitted a single longitudinal mode whose wavelength of 1551.555 nm was determined by the reflection spectrum of the DBR in feedback arm 2. For BP1, the output of the SRL was also single-mode but the emission wavelength of 1538.405 nm was determined by the gain maximum.
Next, we measured time traces of the intensity in the CCW direction for different values of the current ISOA2 injected in the external SOA. We first calibrated the amplification of the external amplifier by measuring the power transmitted through the external SOA as a function of its bias current (while keeping the laser current Ilaser and the FOF current ISOA1 constant). For small values of ISOA2, the CW intensity was rather constant with some noise-induced fluctuations around the steady state. This is illustrated in Figure 5 (left) at a setting (Ilaser, ISOA1, ISOA2) = (60 mA, 11 mA, 500 mA). Increasing ISOA2 eventually led to undamping of the relaxation oscillations as illustrated in Figure 5 (middle) for (Ilaser, ISOA1, ISOA2) = (60 mA, 11 mA, 600 mA). This marks the onset of the COF-induced dynamics. For larger values of the COF strength, the feedback-induced dynamical fluctuations became stronger and more complex as illustrated in Figure 5 (right) for (Ilaser, ISOA1, ISOA2) = (60 mA, 11 mA, 700 mA).
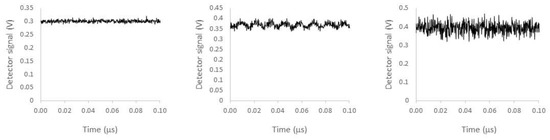
Figure 5.
Time traces of the laser’s output as measured by the detector in the setup of Figure 2 at a laser injection current of 60 mA and an SOA current in the FOF path of 11 mA for different strengths of the COF by changing the current injected in SOA2 in the COF path: ISOA2 = 500 mA (left), ISOA2 = 600 mA (middle) and ISOA2 = 700 mA (right).
In order to quantify the strength of the feedback-induced dynamics in a simple way, we used the following metric: we extracted the rescaled STD as the ratio between the standard deviation of the laser intensity fluctuations σlaser and the mean value of the detector signal. Calculating this ratio is equivalent to rescaling the time traces such that the average value of the detector signal is equal to one. We performed this rescaling of the STD to make the extracted values independent of the average power coupled to the read-out fiber. The noise of the oscilloscope and the photo-detector are compensated for when extracting the value of σlaser from the time traces by assuming that the noise of these sources is Gaussian and is independent from the fluctuations in the laser’s intensity. To perform this compensation, we measured a time trace of the detector signal (using the same oscilloscope settings as when measuring the laser’s intensity) without optical input to the detector. From this time-trace, we determined the standard deviation σdet of the detector and oscilloscope noise (the mean value of the detector and oscilloscope noise was measured to be close to zero). Using the standard deviation σtimetrace extracted from the intensity time trace, we estimate the standard deviation of the intensity fluctuations σlaser to be .
In Figure 6 we plot the value of the rescaled STD for the three bias conditions BP1, BP2 and BP3 mentioned above. The COF signal strength, plotted on the horizontal axis of Figure 6, was changed by changing ISOA2 and was obtained by measuring the optical power after the splitter in Figure 2 when the feedback loop was open. For each of the bias conditions, the STD was small for small values of the COF strength, as there were not yet any feedback-induced dynamics in the time traces. When increasing the COF strength, we can see in Figure 6 that the onset of the feedback-induced dynamics was lowest for bias condition BP1, i.e., without FOF to stabilize the laser. When FOF was applied (see measurements for BP2 and BP3 in Figure 6), the onset of the COF dynamics was shifted to larger values of the feedback strength, but this shift was not large for BP2 and BP3: the shift in the onset when comparing BP1 to BP2 was roughly a factor of 2 and was thus rather modest as compared to the suppression of feedback dynamics in strongly unidirectional SRLs [7,8]. Moreover, when increasing the FOF strength from BP2 to BP3, we actually observed a slight drop in the onset of the COF dynamics. The experiments thus show only a limited effectiveness of the proposed FOF scheme to suppress these dynamical fluctuations, and this effectiveness is furthermore dependent on the exact value of the applied FOF strength. The reason behind these observations will be clarified based on numerical simulations of the system in Section 3.2.
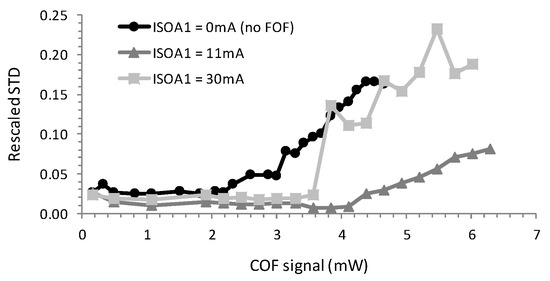
Figure 6.
Rescaled STD from time traces of the laser’s output as a function of the COF signal strength as measured after the splitter in Figure 2 for different values of the ISOA1 (which controls the FOF strength).
3.2. Results from Numerical Simulations
Using the rate-equations that have been introduced in Section 2.3, we performed a series of numerical simulations that mimic the experiments described above. In these simulations we set the normalized injection current to 1.2 and we selected particular values for the FOF and COF strengths in order to simulate time-traces of the directional powers. We remark here that we have obtained similar behavior for other values of the pump strength. From these time traces, we then extracted the STD of the intensity fluctuations in a similar manner to that used in the experiments represented in Figure 6. We show in Figure 7 (left) the simulated time traces when the strength of the COF was = 0.4 ns–1 (as this is a good setting to show the effect of the FOF on the onset of the laser dynamics). In the red time trace of Figure 7 (left), FOF was not used whereas the FOF strength was set to 2 ns–1 in the blue time trace of Figure 7 (left). Using FOF, the intensity fluctuations in the time trace became smaller as compared to the case without FOF. We also notice that the average intensity in the CCW direction increased due to the FOF, as it enhances the CCW mode (see also Figure 4). As a result, the rescaled STD was smaller for the trace in Figure 7 (left) corresponding to = 2 ns–1.
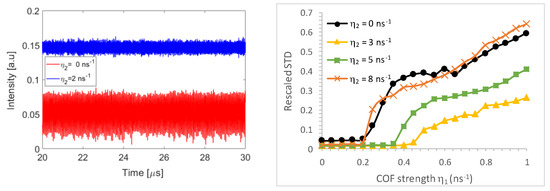
Figure 7.
Simulated time traces in the CCW direction when the COF strength is η1 = 0.4 ns–1 without FOF in red and with FOF using η2 = 2 ns–1 in blue (left). Standard deviation of the simulated time traces of the laser’s output as a function of the COF strength η1 for different values of the FOF strength η2 (right).
The rescaled STD of the time traces was measured in the experiments to be 0.02. We used this value to estimate D0 to be 2 × 10−6 ns−1 in order to find the same rescaled STD in the simulations without COF. Similarly to the experiments, we started by calculating the mean value and the STD of the time traces without FOF ( = 0 ns−1). We increased the strength of the COF by increasing from 0 to 1.0 ns−1 in steps of 0.05 ns−1 while the rest of the parameters were fixed ( = 0 ns−1). Next, we repeated the calculations of the mean value and the STD of the time traces, but this time with FOF by setting to 3 ns−1, 5 ns−1 and 8 ns−1, while the rest of parameters were kept unchanged. We plot the rescaled STD from the simulations in Figure 7 (right) as a function of the COF strength . At low values of the COF strength, the STD is relatively small and remains approximately constant when changing the COF strength. The onset of COF-induced dynamics is visible in these curves as the point at which the STD starts to rapidly increase with increasing COF strength. Similarly to the experiments, the onset happened first for the laser without FOF around = 0.2 ns−1. When FOF was applied, the onset first shifted to larger COF strengths, but this shift is albeit rather limited. When further increasing the FOF strength, the onset of the dynamics shifted erratically and we did not observe a continuous increase in the onset. These numerical results thus agree qualitatively with our experimental trends and observations discussed in Section 3.1, and show that the FOF scheme presented in Figure 1 does not really help to reduce the COF-induced dynamics.
To further elucidate the stabilizing effect of the FOF on the SRL’s dynamical behavior, we computed and analyzed the so-called Lyapunov exponents, λi, from the model described in Equations (1)–(3) without noise (setting D = 0). By studying the Lyapunov spectrum, we tried to understand how FOF influences both the stability and complexity of the chaotic dynamics that might have arisen. For the computation of the Lyapunov exponents, we applied the ideas of Farmer [20] to our case. Specifically, we integrated the corresponding delay differential equations with an Euler method. This converts the original delay differential equations in a map. We computed the Lyapunov exponents of this map. Only a finite portion of the infinite set of λi can be determined by such a numerical analysis. In Figure 8, we present the five largest Lyapunov exponents vs. the COF strength η1. Due to the field nature of the equations, one exponent will always be zero. If only the maximal exponent is zero, the SRL will be emitting in a continuous wave. If two exponents are zero, while the others are all negative, the laser output will be periodic. If more exponents are zero, the dynamics can correspond to either periodic or quasi-periodic behavior. Once the maximal Lyapunov exponent becomes positive, the SRL will be operating chaotically. From Figure 7 (right) and Figure 8 (left), in the case of no filtered feedback, the increase of the STD around = 0.1 to 0.4 ns–1 can be attributed to a bifurcation from continuous wave emission to periodic oscillations. It is only later, after a regime of quasi-periodic behavior, that the laser became chaotic (around = 0.8 ns–1). With FOF ( = 3.0 ns–1), in Figure 8 (middle), below = 0.7 ns–1, the SRL with filtered feedback was continuously lasing except for some very small windows of periodic behavior. While this seems to indicate that the SRL would be more stably lasing, the negative Lyapunov exponents were now much smaller in amplitude. This indicates that the SRL would be much easier to destabilize due to noise, for example. The bifurcation to chaotic behavior hardly moved and still appeared at feedback strengths around = 0.8 ns–1. However, its accompanying positive Lyapunov exponents were increased significantly, indicating a more complex and less damped dynamical chaotic behavior. For = 8.0 ns–1 (Figure 8 (right)), it is clear that the large region of chaos shifted to lower values of (≈ 0.4 ns–1). Around = 0.2 ns–1, the laser was first destabilized as a small window of mildly chaotic behavior appeared (i.e., only one of the Lyapunov exponents was positive). This onset of chaotic oscillations corresponds to the abrupt change in the rescaled STD observed numerically in Figure 7 (right) and experimentally in Figure 6 for ISOA1 = 30 mA. To conclude, with filtered feedback, the dynamical behavior of the SRL was altered considerably. For some values of the filtered feedback this led to a larger but less stable continuous wave regime and chaos which was more complex. Because of the larger continuous wave regime, the feedback sensitivity was somewhat reduced as compared to the device without FOF.
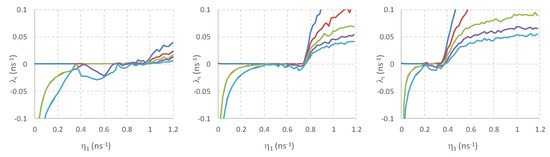
Figure 8.
The five largest Lyapunov exponents: without FOF (i.e., η2 = 0 ns–1) (left), with FOF (i.e., η2 = 3 ns–1) (middle) and with large FOF strength (i.e., η2 = 8 ns–1) (right).
4. Discussion
The above results show that the filtered feedback has only a marginal beneficial effect regarding feedback sensitivity of the SRL. Even more, in several cases the filtered feedback leads to a further destabilization of the laser dynamics. One reason that comes to mind as to why the addition of the filtered feedback does not deliver the desired outcome, is the fact that the SRL is not operating in an ideal unidirectional emission regime, i.e., the CW mode in which the COF signal is reinjected is not fully turned off. To investigate if this might be the issue, we have considered an ideal SRL with no backscattering between the two counter-propagating modes (i.e., kd = kc = 0) in the numerical simulations. In this case, the SRL without any feedback operates in a unidirectional regime with the full output power concentrated either in the CW or CCW mode. In Figure 9, we show the results from a numerical analysis of the Equations (1)–(3) for kd = kc = 0. The left-hand side of Figure 9 shows rescaled STDs obtained from time traces using the procedure described above. For all cases, we find that the STD increases for low COF strengths, which are even lower than in Figure 7. The right-hand side of Figure 9 shows the five largest Lyapunov values describing the noiseless dynamics of the SRL in the case of filtered feedback. Again, at a very low feedback strength ( > 0.05 ns–1), the SRL becomes chaotic. It is clear that even in the case of no backscattering, the filtered feedback actually destabilizes the SRL. This indicates that—for the device layout studied here—a feedback signal in the quiescent directional mode is coupled (through the FOF branch) sufficiently strongly to the dominant directional mode in order to invoke delay-induced dynamical fluctuations.
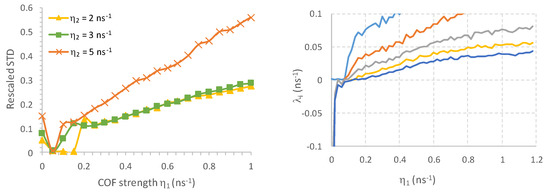
Figure 9.
Standard deviation of the simulated time traces of the laser’s output as a function of the COF strength (left) and the five largest Lyapunov exponents (right) with FOF (η2 = 3 ns–1) when the backscattering is set to zero.
5. Conclusions
In this paper we studied—both experimentally and numerically—an SRL in which on-chip filtered optical feedback is used to tune the wavelength, to enforce single-longitudinal mode operation and to enhance the directionality of the laser. More particularly, we focused on the sensitivity to coherent optical feedback from a longer off-chip delay path, and we initially speculated that the FOF might result in a higher tolerance to COF. However, our experiments and modeling show that the FOF does not result in a substantial shift of the COF-induced dynamics towards higher COF strengths. We attribute this to the fact that the COF signal after reinjection into the SRL is coupled back into the lasing mode via the filtered feedback. Even when the backscattering would be reduced strongly, our simulations show that this will not result in a beneficial effect for the studied SRL with FOF configuration.
Author Contributions
Conceptualization, G.V., M.K. and G.V.d.S.; methodology, G.V., M.K. and G.V.d.S.; experiments, G.V.; numerical simulations, M.K. and G.V.d.S.; formal analysis, G.V., M.K. and G.V.d.S.; writing—original draft preparation, G.V., M.K. and G.V.d.S.; writing—review and editing, G.V., M.K. and G.V.d.S.; funding acquisition, G.V. and G.V.d.S.
Funding
This research was funded by Research Foundation Flanders (FWO) a.o. under grant numbers G028618N and G029519N, the Hercules Foundation under grant “High-speed real-time characterization of photonic components” and the Research Council of the Vrije Universiteit Brussel. M.K. wishes to acknowledge partial financial support by FWO by ways of EOS Project No. G0F6218N (EOS ID 30467715).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Van Tartwijk, G.H.M.; Lenstra, D. Semiconductorlasers with optical injection and feedback. Quantum Semiclass. Opt. 1995, 7, 87–143. [Google Scholar] [CrossRef]
- Agrawal, G.P. Line narrowing in a single-mode injection laser due to external optical feedback. IEEE J. Quantum Electron. 1984, 20, 468–471. [Google Scholar] [CrossRef]
- Ohtsubo, J. Semiconductor Lasers: Stability, Instability and Chaos, 3rd ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Miles, R.O.; Dandridge, A.; Tveten, A.B.; Taylor, H.F.; Giallorenzi, T.G. Feedback-induced line broadening in cw channel-substrate planar laser diodes. Appl. Phys. Lett. 1980, 37, 990–992. [Google Scholar] [CrossRef]
- Mork, J.; Mark, J.; Tromborg, B. Route to chaos and competition between relaxation oscillations for a semiconductor laser with optical feedback. Phys. Rev. Lett. 1990, 65, 1999–2002. [Google Scholar] [CrossRef] [PubMed]
- Lenstra, D.; Verbeek, B.; den Boef, A. Coherence collapse in singlemode semiconductor lasers due to optical feedback. IEEE J. Quantum Electron. 1985, 21, 674–679. [Google Scholar] [CrossRef]
- Lenstra, D.; van Schaijk, T.T.M.; Williams, K.A. Toward a Feedback-Insensitive Semiconductor Laser. IEEE J. of Sel. Topics in Quantum Electron. 2019, 25, 1–13. [Google Scholar] [CrossRef]
- Li, S.; Pusino, V.; Chan, S.; Sorel, M. Experimental investigation on feedback insensitivity in semiconductor ring lasers. Opt. Lett. 2018, 43, 1974–1977. [Google Scholar] [CrossRef] [PubMed]
- Ermakov, I.; Tronciu, V.; Colet, P.; Mirasso, C. Controlling the unstable emission of a semiconductor laser subject to conventional optical feedback with a filtered feedback branch. Opt. Express 2009, 17, 8749–8755. [Google Scholar] [CrossRef] [PubMed]
- Ermakov, I.V.; Beri, S.; Ashour, M.M.; Danckaert, J.; Docter, B.B.; Bolk, J.; Leijtens, X.J.; Verschaffelt, G. Semiconductor Ring Laser With On-Chip Filtered Optical Feedback for Discrete Wavelength Tuning. IEEE J. Quantum Electron. 2012, 48, 129–136. [Google Scholar] [CrossRef]
- Verschaffelt, G.; Khoder, M. Directional power distribution and mode selection in micro ring lasers by controlling the phase and strength of filtered optical feedback. Opt. Express 2018, 26, 14315–14328. [Google Scholar] [CrossRef] [PubMed]
- Leijtens, X.J.M. JePPIX: The platform for Indium Phosphide-based photonics. IET Optoelectron. 2011, 5, 202–206. [Google Scholar] [CrossRef]
- Sorel, M.; Giuliani, G.; Scire, A.; Miglierina, R.; Donati, S.; Laybourn, P.J.R. Operating Regimes of GaAsAlGaAs Semiconductor Ring lasers: Experiment and model. IEEE J. Sel. Top. Quantum Electron. 2003, 39, 1187–1195. [Google Scholar] [CrossRef]
- Radziunas, M.; Khoder, M.; Tronciu, V.; Danckaert, J.; Verschaffelt, G. Tunable semiconductor ring laser with filtered optical feedback: Traveling wave description and experimental validation. J. Opt. Soc. Am. B 2018, 35, 380–390. [Google Scholar] [CrossRef]
- Sorel, M.; Laybourn, P.J.R.; Scire, A.; Balle, S.; Giuliani, G.; Miglierina, R.; Donati, S. Alternate oscillations in semiconductor ring lasers. Opt. Lett. 1992, 27, 1994–2002. [Google Scholar] [CrossRef] [PubMed]
- Lang, R.; Kobayashi, K. External optical feedback effects on semiconductor injection laser properties. IEEE J. Quantum Electron. 1980, 16, 347–355. [Google Scholar] [CrossRef]
- Khoder, M.; Van der Sande, G.; Verschaffelt, G. Effect of External Optical Feedback on Tunable Micro-Ring Lasers Using On-Chip Filtered Feedback. IEEE Photonics Technol. Lett. 2016, 28, 959–962. [Google Scholar] [CrossRef]
- Khoder, M.; Nguimdo, R.M.; Bolk, J.; Leijtens, X.J.M.; Danckaert, J.; Verschaffelt, G. Wavelength switching speed in semiconductor ring lasers with on-chip filtered optical feedback. IEEE Photonics Technol. Lett. 2014, 26, 520–523. [Google Scholar] [CrossRef]
- Sunada, S.; Harayama, T.; Arai, K.; Yoshimura, K.; Tsuzuki, K.; Uchida, A.; Davis, P. Random optical pulse generation with bistable semiconductor ring lasers. Opt. Express 2011, 19, 7439–7450. [Google Scholar] [CrossRef] [PubMed]
- Farmer, J.D. Chaotic attractors of an infinite-dimensional dynamical system. Phys. D: Nonlinear Phenom. 1982, 4, 366–393. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).