Abstract
High-accuracy and high-precision inter-satellite ranging enhances the orbital accuracy of the Global Navigation Satellite System and facilitates Autonomous Navigation without requiring ground stations. This study proposes a novel phase discrimination method based on pseudo-random code phase modulation coherent laser ranging, which solves the problem of mutual restriction between ranging accuracy and ranging precision in the traditional method. The early–late correlation peaks are obtained via data shifting, while the early and late codes remain unchanged. The characteristic parameters of the early–late discriminator model are calibrated by the actual ranging system, which achieves enhanced ranging accuracy and precision simultaneously. Ground test results indicate that for the static target, the accuracy of the distance measurement is 0.56 mm, while the precision is 0.34 mm. The ranging accuracy of the proposed method has improved by a factor of 91 compared to the traditional method. For dynamic targets, the accuracies of the distance and speed measurements are 0.38 mm and 0.44 mm/s, respectively.
1. Introduction
The Global Navigation Satellite System (GNSS) has been widely applied in many fields and has become an essential infrastructure for societal development. The four major GNSSs all employ constellations primarily composed of Medium-Earth Orbit (MEO) satellites. The MEO satellites of the global positioning system (GPS) are unevenly distributed across six orbital planes, whereas the MEO satellites of Russia’s Global Navigation Satellite System (GLONASS), the European Union’s Galileo, and China’s BeiDou Navigation Satellite System (BDS) form Walker constellations, which are distributed across three orbital planes [1]. The GNSS orbits are primarily tracked by ground stations, which usually need to be evenly distributed throughout the globe to ensure a suitable observation geometry. However, because of limitations in the number and distribution of ground stations, not all GNSS satellites can be tracked at a sufficiently high accuracy. Currently, the 1D accuracy of GPS and GLONASS orbits, based on ground station observations provided by the International GNSS Service (IGS), is better than 3 cm [2]. In contrast, the orbital accuracy of the BDS is lower because of its relatively small number of unevenly distributed ground stations [3].
Inter-satellite ranging can enhance the orbital accuracy of navigation satellites by combining the orbital data obtained from ground stations. This capability also enables GNSSs to navigate autonomously without requiring the support of ground stations, thereby improving their survivability in extreme conditions. In 2011, Fernández [4] described a GNSS exploratory project conducted by the European Space Agency (ESA), which analyzed the effects of introducing inter-satellite microwave ranging and communication links to improve GNSS and signal propagation performance. The results indicated that inter-satellite links (ISLs) are able to more effectively maintain the accuracy of satellite orbits and clocks. In practical applications, from the early 1990s, GPS satellites of the IIR series were already equipped with cross-link capabilities as part of the so-called Autonomous Navigation (AUTONAV) mode [5]. The GPS IIR satellites determined inter-satellite distances using a time-division, dual-frequency two-way mode of the ultra-high frequency (UHF) band [6]. However, the UHF band was prone to significant multipath errors and noise [7]. Therefore, subsequent GPS ISLs used the Ka-band [8]. The second generation of GLONASS satellites, GLONASS-M, employed inter-satellite microwave links to measure distances and to improve ephemeris and clock accuracy [1]. The BDS also primarily used Ka-band ISLs to autonomously determine satellite orbits and synchronize inter-satellite times, achieving inter-satellite ranging errors of less than 0.25 ns [9].
Compared to microwaves, optical waves have shorter wavelengths, superior directionality, higher signal-to-noise ratio gain, and greater modulation bandwidth. Therefore, laser ranging has a very high potential for ISLs as a high-precision ranging method, and it has been used to achieve favorable results in fiber-based time–frequency synchronization and satellite orbit determination [10,11,12,13]. Inter-satellite ranging carriers are also beginning to shift from microwaves to optical waves to enhance clock synchronization and ranging capabilities between satellites. In 2013, Pasynkov et al. reported on a verification experiment for laser communication ranging technology conducted between the GLONASS-728 and GLONASS-747 satellites, which achieved an inter-satellite ranging precision of 3 cm [14]. Furthermore, the next-generation satellite GLONASS-K2 incorporated laser ISLs to further enhance the accuracy of its orbit determination and clock synchronization [1,15]. Michalak et al. introduced the Kepler navigation system proposed by the German Aerospace Center (DLR) [16]. The space segment of this system was comprised of 24 Galileo-like MEO satellites and six Low-Earth Orbit (LEO) satellites equipped with ultra-stable optical clocks. These satellites were equipped with both microwave and laser payloads for inter-satellite ranging. In 2020, Yu et al. proposed a pseudo-code incoherent laser ranging scheme based on a regenerative synchronization mechanism for inter-satellite ranging scenarios involving relatively stationary satellites [17]. This scheme was validated in laboratory tests. The slave station utilized a delay-locked loop to track and regenerate the pseudo-random code from the master station. The master station determined the distance information by calculating the phase difference between the received pseudo-random code and the transmitted pseudo-random code. The compensated ranging error was mm, which was affected by the receiver clock error generated by the code tracking loop and the clock error produced by the clock source. In 2021, Zhu et al. designed an integrated solution for inter-satellite communication and ranging, successfully conducting on-orbit verification experiments with two satellites (BEIDOU-3 M21 and BEIDOU-3 M22) in the same circular orbit [18]. The ranging scheme consisted of both coarse and fine distance measurements. Coarse ranging was achieved using the header of integer frames within, per second. The synchronization of symbols and data clock recovery was then implemented in hardware using code tracking loops. Finally, the fine phase (fine range) between the transmission clock and data reception clock was determined by constructing a reference clock, ultimately achieving a ranging precision of 2.6 mm. Yu et al. proposed an inter-satellite ranging scheme based on pseudo-random code amplitude modulation, in which the coarse distance measurement was performed using the cross-correlation method [19]. New early and late codes were constructed by cyclically shifting the punctual code according to the coarse measurement. The fine distance was then determined using the early–late discriminator model with theoretical characteristic parameters. A ranging precision of 0.33 mm was achieved using fiber optics. However, within a distance of 150 mm (corresponding to a time delay of 500 ps), the ranging deviation was 6 mm (corresponding to a time delay deviation of 20 ps). As the measurement range increased, particularly when the time delay exceeded the width of one chip, the ranging deviation also increased. Ranging deviation can significantly affect the application of inter-satellite laser ranging to satellite orbit determination. Although orbit determination requires multiple measurements, the deviation of each measurement cannot be directly eliminated in the orbit determination software, preventing the high-precision characteristics of laser ranging from being effectively utilized.
To achieve high-accuracy ranging and reduce inter-satellite laser ranging deviations, this study proposes a pseudo-random code phase-shift coherent laser ranging phase discrimination method that employs data shifting and a discriminator with calibrated characteristic parameters, which solves the problem of mutual restriction between ranging accuracy and ranging precision in the traditional method. In contrast to the traditional method, the proposed method shifts the data according to the position determined by the punctual code correlation peak. The shifted data are then cross-correlated and normalized with fixed early and late codes to accurately determine the fine distances. Additionally, a suite of varying distances is utilized in conjunction with a real-ranging system to calibrate the characteristic parameters of the phase discrimination model. A comparison between this method and the traditional method revealed that after calibration, the characteristic parameters of the phase discrimination model for the actual system differed from the theoretical values. For static target ranging, the ranging precisions of the proposed and traditional methods were 0.34 mm and 0.38 mm, respectively, and their ranging accuracies were 0.56 mm and 51.05 mm, respectively. The proposed method improved the ranging accuracy by a factor of 91. For dynamic targets, the ranging accuracies of the proposed and traditional methods were 0.13 mm and 0.20 mm, respectively, and their maximum ranging deviations were −0.38 mm and −1.26 mm, respectively. Furthermore, as the target distance increased, the distance deviation of the traditional method reached a maximum value before gradually decreasing, exhibiting periodicity, with a period equal to one code width. For speed measurements, the proposed method achieved an accuracy of 0.58 mm/s and a precision of 0.44 mm/s.
2. Principle
A schematic of the coherent ranging system, which is phase-modulated by a pseudo-random binary code, is illustrated in Figure 1a. Fiber optic coupler 1 (FOC1) divides the laser into two parts: the signal and the local oscillator . The signal is phase-modulated with the pseudo-random code using an electro-optic phase modulator (EOPM). An acousto-optic modulator (AOM) is used to shift the frequency of the signal by a specified amount . Finally, the frequency-shifted signal is transmitted through a variable optical attenuator (VOA) and a collimator. The backscattered signal from the target and local oscillator are optically mixed using a 2 × 2 fiber optic coupler 2 (FOC2), leading the coherent light to a balanced detector, where it is converted into an electrical signal of intermediate frequency (IF). The pseudo-random code is generated by an arbitrary waveform generator (AWG), which produces a pseudo-random code synchronization pulse (PCSP) at the beginning of each pseudo-random code sequence to be fed into the acquisition module. The acquisition module is a digital storage oscilloscope (DSO), which samples the IF electrical signal triggered by the PCSP. Subsequently, the sampled data are processed on a computer to determine the distance and velocity of the target. The reference output clock (REF-Clock) of the DSO serves as the reference clock for the AWG to ensure that the transmission and reception of the system are synchronized.
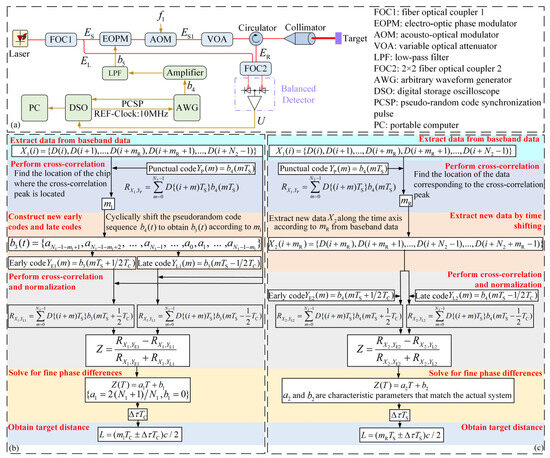
Figure 1.
Schematic of distance measurement and flowchart of traditional and proposed distance measurement methods. (a) Schematic of distance measurement. (b) Traditional ranging flowchart. (c) Proposed ranging flowchart.
The two output signals of FOC1 with a splitting ratio of are expressed as [20]
where , , and denote the frequency, amplitude, and initial phase of the laser, respectively.
Here, is a pseudo-random code composed of −1 and +1, is the gate function, denotes the chip duration, denotes the length of the pseudo-random code, , and represents the impulse response of the low-pass filter (LPF).
The signal is expressed as
where is the phase modulation depth factor, and is the frequency shift caused by the AOM. The expression for the backscattered light
from the target is
where is the Doppler shift generated by the target velocity, is the time delay of light to and from the target, and is the amplitude attenuation coefficient. The backscattered light is mixed with the local oscillation light by FOC2 with a splitting ratio of . The output voltage of the balanced detector is expressed as
where , is the transimpedance of the balanced detector, is the dielectric constant, is the speed of light, is the refractive index of the medium, represents the responsivity of the photodiode, represents the effective optical receiving area of the photodiode [20], , the sampling frequency of the analog-to-digital converter (ADC) is (, where is the sampling period), and is the noise. The variable is discretely sampled via
and is digitally demodulated, resulting in baseband data expressed as
where represents the impulse response of the low-pass filter.
For ease of reading, the symbols involved in Equations (1)–(8) are summarized in Table A1 in Appendix A. Additionally, the symbols involved in the traditional and proposed methods are summarized in Table A2 in Appendix A.
The traditional ranging flow [19,21,22] is illustrated in Figure 1b. A segment of data, denoted as , with a length of , is extracted from the baseband data and subsequently cross-correlated with the punctual code . The length of is . The coarse distance is determined according to the position of the chip where the correlation peak is located, where represents the speed of light. A new pseudo-random code is generated by cyclically shifting the original pseudo-random code according to . New early and late codes are derived from . Next, and are cross-correlated with to obtain and , which are then used to compute . The fractional part of the chip, representing the fine time delay, is derived inversely as according to the early–late discrimination model (, ) [21]. The ultimate distance of the target is . The early–late discrimination model used in the traditional method is a theoretical model in which the parameter is a theoretical value that is relevant to the length of the pseudo-random code, and the parameter is equal to 0. The correlation function of the pseudo-random code determines the early–late discriminant model [21,23]. The theoretical pseudo-random code has a rectangular waveform with an infinitely wide bandwidth. Its correlation function is [23]
where denotes the real part of the complex number , is the phase difference of the pseudo-random code, is the spectral density of the pseudo-random code, and is the signal power. When the bandwidth of the pseudo-random code is finite, its correlation function is [23]
where is the transfer function of the LPF. Figure 2 shows the correlation functions of the theoretical pseudo-random code and the pseudo-random code with a bandwidth of 250 MHz. As shown in Figure 2, the correlation function of the theoretical pseudo-random code is a triangle. The LPF changes the correlation function of the pseudo-random code, and the correlation function of the band-limited pseudorandom code is no longer a triangle. Therefore, the early–late discriminant models of pseudo-random codes with different bandwidths are also different. The actual ranging system is band-limited, and the devices used in the system are not ideal. When the theoretical phase discrimination model is applied to the actual ranging system, it can result in ranging deviations that decrease the accuracy of the ranging. Therefore, the characteristic parameters of the early–late discriminator model need to be calibrated to improve the ranging accuracy.
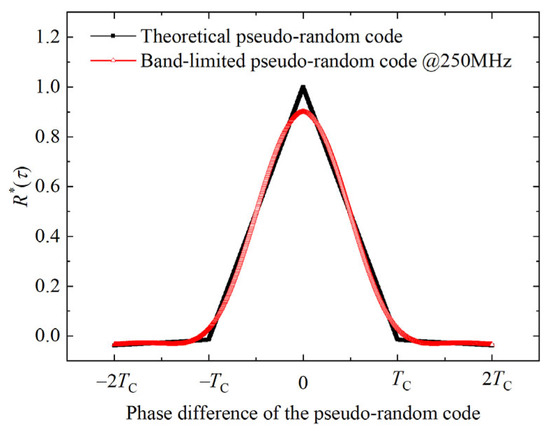
Figure 2.
Correlation functions of pseudo-random codes with different bandwidths.
To solve this problem, this study calibrates the characteristic parameters of the phase detection model utilized in the real-world system. After this calibration, the fine time delay is calculated according to the calibrated parameters, thereby improving the accuracy of the distance measurements. The flow of the ranging process is illustrated in Figure 1c. The data position corresponding to the correlation peak is obtained via cross-correlation. The coarse distance is . A segment of data , with a length of , is extracted along the time axis according to . Then, is correlated with and to obtain . Finally, the fine distance () is obtained via an inverse calculation using the phase discrimination model that matches the actual system. The distance of the target is . Because the characteristic parameters and in the phase discrimination model are calibrated based on the actual system, the model matches the actual system. The proposed method can significantly improve the ranging accuracy.
The proposed methodology initially employs this ranging system to establish a characteristic parameter calibration system with variable time delays. It calculates the value for different time delays, where the actual time delay interval is less than the ADC sampling period . This principle is depicted at the top of Figure 3. The position of the sampling point of the DSO in the chip is changed by adjusting the retroreflector position, which effectively changes the phase of the sampled data. Within the distance corresponding to the sampling period, the retroreflector steps forward each time for a total of steps. The pseudo-random code synchronization pulse and the target echo are sampled simultaneously at each position, and cycles of pseudo-random code are sampled. A pseudo-random sequence of length is extracted at each position from the target echo data , where is aligned with . The mean value of at each position is computed. By performing a least squares fitting on sets of data , one can derive the characteristic parameters and of the phase discrimination model that matches the actual ranging system, as shown in the upper right area of Figure 3. During the ranging process, the peak position is obtained using the cross-correlation method, and the data of length are obtained according to . is obtained by performing the cross-correlation operation and normalization operation on , , and according to Figure 1c. The phase difference is inversely calculated by taking into the phase discrimination model . The final distance of the target is .
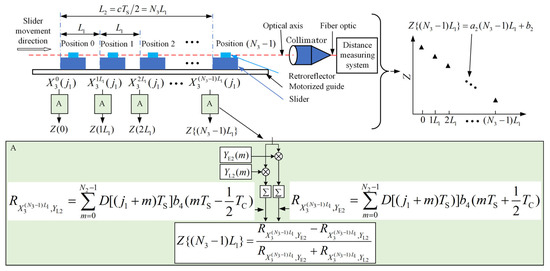
Figure 3.
Calibration of the characteristic parameters.
Figure 4 depicts the procedure for determining the velocity. Initially, a fast Fourier transform (FFT) operation is performed to obtain the frequency . The local orthogonal digital waveforms and are then constructed according to , where is the initial phase. Next, heterodyne demodulation and phase unwrapping are conducted on to derive the phase data , along with the residual frequency difference and the residual phase . Subsequently, curve fitting is performed on the phase data to determine the residual frequency . The speed of the target is expressed as , where represents the wavelength of the light wave.

Figure 4.
Velocity solving flowchart.
In summary, it can be seen from Equations (9) and (10) and Figure 2 that the correlation functions of the theoretical pseudo-random code and bandwidth-limited pseudo-random code are different. The correlation function determines the early–late discriminator model [21,23]. In the traditional method, an early–late discriminator model with theoretical characteristic parameters is used for ranging within the phase range of or by changing the local pseudo-random code. For the actual bandwidth-limited ranging system, this method cannot solve the problem of mutual constraints between ranging accuracy and ranging precision. Therefore, the situation of high ranging precision and poor ranging accuracy occurs [19]. In this paper, the characteristic parameter calibration method and data-shifting method are adopted. An early–late discriminator model with calibrated characteristic parameters is used for ranging within the phase range of . This method solves the problem of mutual restriction between ranging accuracy and ranging precision in the traditional method and achieves good ranging precision and ranging accuracy.
3. Experiments and Results
3.1. Calibration of Characteristic Parameters
Before measuring the distance, calibrating the characteristic parameters and of the ranging system is essential. The principle of the calibration experiment is illustrated in Figure 3. A fiber laser with a wavelength of 1550 nm served as the emitting light source. The balanced detector and collimator were the Thorlabs PDB780CAC and F810APC-1550 models, respectively. The LPF was the Mini-Circuits SLP-250+. The diameter of the retroreflector was 10 mm, and its maximum distance was approximately 3.6 m from the collimator. The motorized guide rail was a Newport IMS series high-performance displacement platform, which offered a travel range of 1 m with an accuracy of ±9 . The AWG was a Keysight M8196A. The DSO was a Teledyne LeCroy LabMaster 10-36Zi-A, which had a sampling period of 0.4 ns, corresponding to a distance resolution of 60 mm. The other main parameters are listed in Table 1.

Table 1.
Parameters.
Each step distance of the retroreflector was 2 mm, corresponding to a time delay interval of ps, which was equivalent to re-interpolating a sampling period into 30 data points. Each distance value and its corresponding value are plotted as the black dots shown in Figure 5. Using least squares fitting, the characteristic values and were obtained, where the R2 (coefficient of determination) value and the sum of the squared residuals indicated a highly accurate fit, confirming that the model was credible. The characteristic parameters of the theoretical phase discrimination model used in the traditional method were and , which differed from the characteristic calibration parameters. The necessity of the calibration process can be fully explained by a comparison to the subsequent distance measurement results.
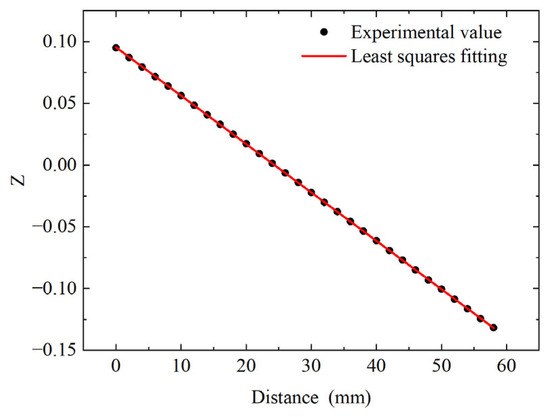
Figure 5.
Z values and linear fitting.
3.2. Static Target Ranging
The retroreflector, which served as the target for measurement, was securely mounted on the slider of the electric guide rail. Initially, the retroreflector was positioned at the furthest point from the collimator, and then it was sequentially shifted 25 mm closer, resulting in a total of 40 steps and 41 distinct positions. In total, 634 distance measurements were recorded at each position.
Figure 6a illustrates the differences between the mean values of the distance measurements at adjacent positions. For the proposed method, the average value over 40 steps was −25.00 mm, with a maximum ranging deviation of −0.56 mm, corresponding to a delay deviation of −1.87 ps. In contrast, the average value over 40 steps for the traditional method was −26.55 mm, with a maximum deviation of −51.05 mm. This discrepancy arose primarily from the mismatch between the theoretical phase discrimination model and the ranging system within the phase discrimination range of . Generally, the mismatch between the phase discrimination model and the actual system can be reduced by increasing the bandwidth of the receiver. However, this increase in bandwidth also raises the noise level, which, in turn, diminishes the signal-to-noise ratio. Figure 6b presents a histogram of the distance measurements. It indicates that the results obtained from the traditional method were dispersed, and those from the proposed method exhibited a higher degree of concentration. The ranging accuracy of the proposed method was higher than that of the traditional method by a factor of approximately 91. This improvement in ranging accuracy was primarily attributed to the fact that the characteristic parameters of the phase discriminative model in the proposed method matched the actual band-limited system. In contrast, the theoretical phase discriminative model of the traditional method was matched to the ideal ranging system, which introduced ranging deviations when used in the actual system.
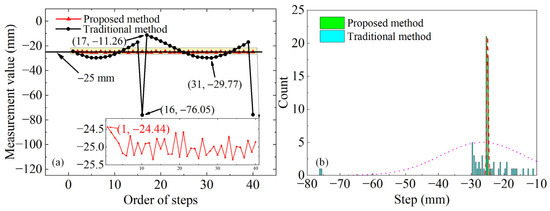
Figure 6.
Measurement results of 40 steps of 25 mm. (a) Ranging accuracy. (b) Histogram of ranging results.
Figure 7 shows the standard deviations of the distance measurements at the 41 positions, indicating that the ranging precisions of the two schemes were comparable. The maximum standard deviation (1σ) of the proposed method was 0.34 mm, which corresponded to a time-delay precision of 1.13 ps. The ranging precision (1σ) of the traditional method was 0.38 mm.
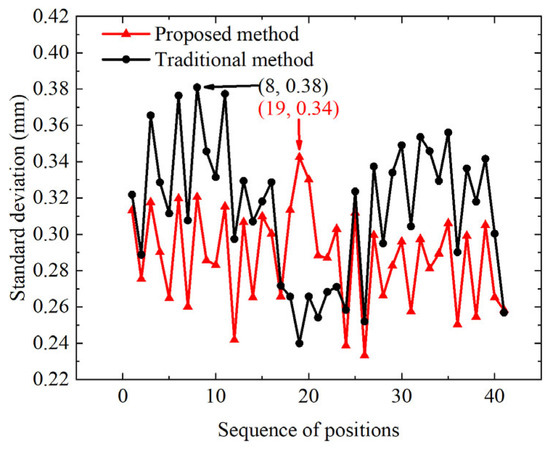
Figure 7.
Standard deviations of the distance measurements at the 41 positions.
Figure 8 shows the cumulative distance measurement results for the 40 steps. Because of the limited length of the guide rail, the range of motion for the retroreflector was restricted to 1000 mm. Figure 8a shows the theoretical distance set by the control terminal of the guide rail, along with the mean values of the distances measured using both the traditional and proposed methods. Figure 8b shows the deviations between the mean measurements of the distances and the theoretical distances. An analysis of Figure 8 revealed that the traditional ranging method exhibited a maximum measurement deviation of 62.95 mm and a minimum deviation of 0.41 mm. Furthermore, the measurement deviation exhibited a periodic pattern with a period of 600 mm, which corresponded to the width of the chip of 4 ns. In contrast, the proposed method exhibited an increasing trend in the measurement deviations within the 0–500 mm range but stabilized in the 500–1000 mm range, with a minimum deviation of 0.00 mm and a maximum deviation of 1.47 mm.
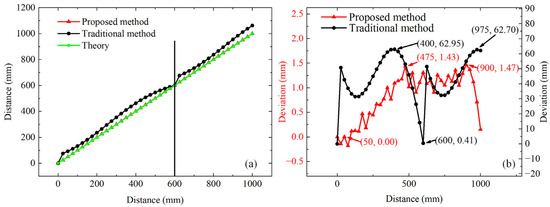
Figure 8.
Measurement results of the accumulated distance of 40 steps. (a) Mean value of the measured distance at 41 positions. (b) Deviation of the measured distance at 41 positions.
Repeated ranging was conducted on static targets to verify the repetitive measurement accuracy of the proposed method. The measurements were repeated three times. Figure 9a shows the differences between the mean values of the measurements and the theoretical distances traveled for each position, with the three sets of results demonstrating a consistent trend. Figure 9b shows the differences between the first set of measurements and the average of the three sets, indicating a maximum deviation of 0.55 mm, which corresponds to a time-delay deviation of 1.83 ps. This ranging deviation was comparable to the 0.56 mm deviation observed in Figure 6a, indicating that the proposed method was highly accurate for both single and repeated ranging. An analysis of Figure 8b and Figure 9 indicated that the 1.47 mm ranging error depicted in Figure 8b was influenced by factors such as the guide rail and the movement of the spot position on the retroreflector.
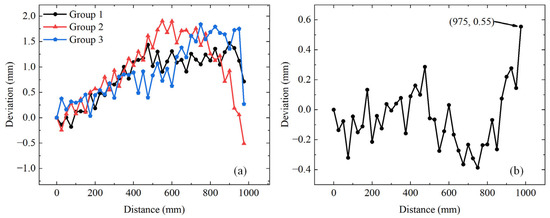
Figure 9.
Three groups of measurements of the distance of the stationary target. (a) The three groups of measurements. (b) Deviations after subtracting the average of the three groups of measurements.
3.3. Dynamic Target Ranging
The retroreflector was set to move at a uniform speed of 500 mm/s. Limited by the storage depth of the DSO, the retroreflector was measured continuously for 5 ms. Figure 10 shows the results of the distance measurements for the moving target. In Figure 10a, the red triangles represent the distance measurements obtained using the proposed method, the black dots represent the distance measurements obtained using the traditional ranging method, and the green line represents the theoretical distance. Figure 10b shows the deviations between the measured and theoretical distances. The maximum ranging deviations for the proposed and traditional methods were −0.38 mm and −1.26 mm, respectively. Additionally, as the target distance increased, the ranging deviation of the traditional method reached a maximum, following the trend of the black dots shown in Figure 8b, with a periodicity of 600 mm. The ranging precisions (standard deviations) of the proposed and traditional methods were 0.13 mm and 0.20 mm, respectively. Compared to the static ranging results presented in the previous section, the ranging accuracy of the proposed method for the moving target was lower than that for the static target because random phase fluctuations occurred between the sampling clocks of the DSO and AWG when the DSO was triggered to sample the data, which disrupted the synchronization between the clocks.
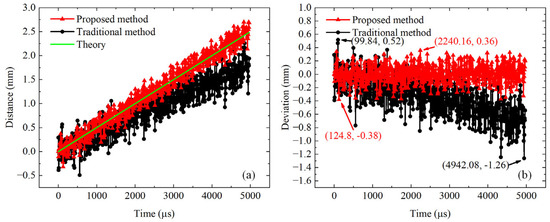
Figure 10.
Measurement results for the relative distances of the moving target. (a) Ranging results. (b) Deviations between the measured and theoretical distances.
3.4. Dynamic Target Speed Measurement
While measuring the distance to the moving target, the proposed method also calculated its velocity. Figure 11 shows the velocity measurements. The average value of the target velocity was 500.44 mm/s, with a deviation of 0.44 mm/s from the set value. The precision (1σ) of the velocity measurement was 0.58 mm/s.
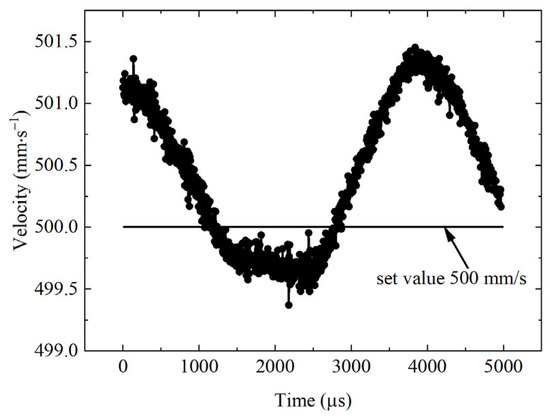
Figure 11.
Velocity measurements for the moving target.
4. Discussion
The separation between neighboring satellites within the same orbital plane of a Walker constellation is approximately on the order of tens of thousands of kilometers, and the optical power received at the terminal is below 1 . We simulated the relationship between the ranging precision and received optical power, as well as the correlation between the received optical power and distance. For inter-satellite laser links, the optical power received at the terminal is [24]
where is the received power; is the transmitted power; is the transmitter gain; ( is the diameter of the transmitting telescope, and is the wavelength); is the optical efficiency of the transmitter (the typical value of which is −1.74 dB); is the path loss of the inter-satellite optical link; ( is the inter-satellite distance); is the link attenuation caused by the channel (which is equal to 1 for ISLs); is the power loss caused by acquisition, pointing, and tracking (APT) misalignment, and its value of −0.56 dB is obtained according to the best matching relationship where the divergence angle of the communication beam is fives times the pointing error; is the receiver gain (the aperture of the receiving telescope is the same as that of the transmitting telescope); and is the optical efficiency of the receiver, which is the same as here [24].
The diameters of both the transmitting and receiving telescopes were fixed at 100 mm, the transmitted power was specified as 25 dB, and the link safety margin was set at 3 dB [24,25,26]. For an inter-satellite distance of 21,343 km in the BDS, the received optical power was .
The coherent receiver uses a local oscillator to improve the signal-to-noise ratio, in which case the noise is predominantly shot noise [27]. Shot noise is modeled as a zero-mean random Gaussian process. In the shot noise limit, the SNR is expressed as [28]
where is the heterodyne efficiency, is the responsivity, is the received optical power, is the electron charge, and is the receiver bandwidth. A Monte Carlo simulation was conducted to analyze the relationship between the received optical power and the ranging precision. The results are depicted as black dots in Figure 12. Additionally, the pink curve in Figure 12 shows the correlation between the received optical power and the range. Figure 12 illustrates that in the shot noise limit, the optical power decreased as the ranging precision increased with distance. The ranging precision deteriorated sharply at an optical power of 27 nW. Here, 27 nW of optical power corresponds to a distance of 8220 km, with a ranging error of 0.15 mm and a time delay error of 0.5 ps. When the received optical power was 3 nW, the corresponding distance was 24,663 km, with a ranging error of approximately 1.51 mm and a time-delay error of approximately 5.03 ps.
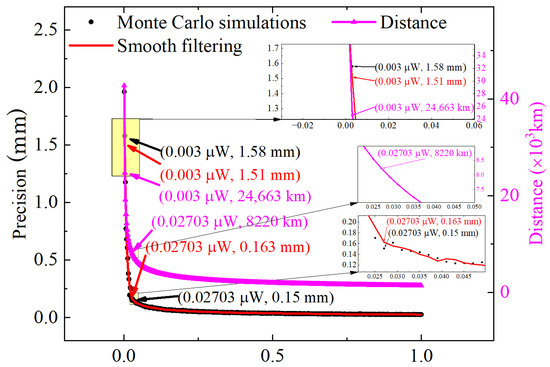
Figure 12.
Relationship between the received optical power and the ranging precision (or distance).
The theoretical waveform of the pseudo-random code is a rectangular wave, its spectrum is infinite wide, its main energy is concentrated in the main lobe, and its theoretical phase discrimination model Z is a linear model, as shown in Figure 13. The bandwidth of the actual ranging system is limited, and the devices used in the system are not ideal. These factors lead to a poor matching between the theoretical phase discrimination model and the actual system. When the theoretical phase discrimination model is used in the actual system, it will bring errors. Figure 14a simulates the relationship between the phase discrimination model and the bandwidth. When the bandwidth becomes small, the phase discrimination model moves away from the theoretical phase discrimination model, and when the bandwidth becomes large, the phase discrimination model approaches the theoretical model. When the system bandwidth is infinitely wide, the phase discrimination model is equal to the theoretical model. As shown in Figure 14a, there is a difference between the phase discrimination model of the band-limited system and the theoretical model. When the theoretical model is applied to a system with limited bandwidth, it results in a decrease in the ranging accuracy. Figure 14a also illustrates the theoretical relationship between the ranging accuracy and ranging range in the traditional method. The phase discrimination range of the pseudo-random code is , corresponding to a chip width, which leads to the ranging accuracy periodically improving and deteriorating as the ranging range increases. When the system bandwidth is equal to one times the chip rate, the ranging accuracy of traditional method becomes very poor within the period, and as the system bandwidth continues to increase, the ranging accuracy of traditional method will gradually improve within the period. Figure 14b simulates the relationship between ranging accuracy, bandwidth, and SNR. In Yu’s article, the SNR for ranging is greater than 21 dB [19]. For comparison, we simulated the variations in ranging accuracy when the SNR is greater than 20 dB. The main energy of the pseudo-random code is concentrated within the main lobe. As the system bandwidth increases, the discrimination model approaches the theoretical discrimination model, improving the ranging accuracy. However, the SNR decreases, leading to a deterioration in the ranging precision, as shown in Figure 14b. This issue is inherent in the traditional method, where the accuracy and precision of the distance measurement are mutually restrictive. This also explains the ranging precision of 0.33 mm and the ranging accuracy of 6 mm mentioned in Yu’s article. The method proposed in this paper reduces the system bandwidth, ensures a high SNR, and improves the ranging accuracy using a discriminator with calibrated characteristic parameters so that the ranging accuracy does not show periodic variations as the ranging range increases. By employing a data-shifting method, the consistency of the discriminator in ranging is maintained. Compared with the traditional method, the proposed method improves the ranging accuracy and ensures a high ranging precision, which solves the situation that the ranging accuracy and ranging precision constrain each other. This is the difference between the proposed method in this paper and the method in Yu’s paper.
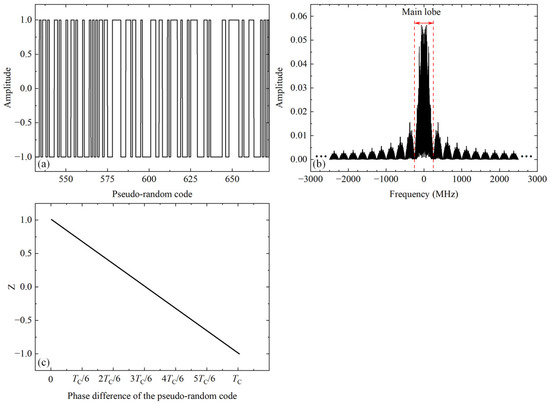
Figure 13.
Time domain and frequency domain plots of pseudo-random code and theoretical early–late discrimination model. (a) Time-domain plot. (b) Frequency-domain plot. (c) Theoretical early–late discrimination model.
Figure 14.
Relationship between the early–late discrimination model and bandwidth and relationship between ranging precision and bandwidth and SNR. (a) Relationship between the early–late discrimination model and bandwidth. (b) Relationship between ranging precision and bandwidth and SNR.
The symbols involved in this section are summarized in Table A3 in Appendix A.
5. Conclusions
In this study, a phase discrimination method using data shifting and a discriminator with calibrated characteristic parameters is proposed, which solves the problem of mutual constraints between ranging accuracy and ranging precision in the traditional method so that the method can achieve highly accurate and precise ranging. Compared to traditional methods, the proposed approach offers two significant improvements. The first improvement is the early–late discrimination method, which shifts data according to the position of the cross-correlation peak of the punctual code. It performs cross-correlation and normalization using fixed early and late codes, ultimately obtaining a fine phase difference via a phase discrimination model that matches the actual system. The second improvement involves the calibration of the characteristic parameters of the phase discrimination model. This process adjusts the target position, refines its spatial distance, and determines the characteristic parameters of the phase discrimination model that match the system via discrete distance values. Ground validation experiments demonstrated that this method can effectively enhance the ranging accuracy while maintaining a high precision. For the same static target with different displacements, the ranging accuracies of the proposed and traditional methods were approximately 0.56 mm and 51.05 mm, respectively, indicating that the ranging accuracy of the proposed method was 91 times higher than that of the traditional method. For dynamic targets, the ranging deviations of the proposed and traditional methods were −0.38 mm and −1.26 mm, respectively. As the target distance increased, the ranging accuracy of the traditional method exhibited periodicity with a period of one chip width, reaching a maximum value before decreasing. Additionally, the accuracy and precision of the velocity measurements performed using the proposed method were 0.44 mm/s and 0.58 mm/s, respectively. Finally, the applicability of the proposed method in real inter-satellite scenarios, spanning tens of thousands of kilometers, was simulated. At a power level of 3 nW, which corresponds to a distance of 24,663 km, the proposed method can achieve a ranging accuracy of 1.51 mm. The results show great potential for the application of the method in inter-stellar ranging, and subsequent work will also validate the method in a practical environment. In addition, the application scenario for the proposed method involves a slow-moving target, while a fast-moving target is not currently involved. The ranging system is coherent, and the velocity of the target can be solved via carrier frequency shift. This velocity is used to perform Doppler compensation for local pseudo-random codes and calibrate the characteristic parameters of the early–late discriminator model to realize the distance measurement of a fast target. This is also the work that needs further improvement and in-depth research in the next steps of the proposed method.
Author Contributions
Conceptualization, C.L., F.Y. and J.S.; methodology, C.L.; software, C.L.; validation, C.L.; formal analysis, C.L., F.Y. and J.S.; investigation, C.L.; resources, Z.L., Y.Z., C.Q. and W.C.; data curation, C.L., F.Y. and J.S.; writing—original draft preparation, C.L.; writing—review and editing, F.Y. and J.S.; visualization, C.L., F.Y. and J.S.; supervision, J.S.; project administration, Z.L.; funding acquisition, F.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported, in part, by the National Key Research and Development Project of China (2022YFB3902503), the Strategic Priority Research Program (XDB 43030400), the National Natural Science Foundation of China (12293033), and the Youth Innovation Promotion Association of Chinese Academy of Sciences (Y2023075).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Dataset is available on request from the authors.
Conflicts of Interest
J.S. is employed by the Shanghai Satellite Network Research Institute Company Limited. Other authors declare no conflicts of interest.
Appendix A

Table A1.
Symbols involved in Equations (1)–(8).
Table A1.
Symbols involved in Equations (1)–(8).
| Symbols | Specification | Symbols | Specification | Symbols | Specification |
|---|---|---|---|---|---|
| Signal before EOPM | Data after low-pass filter | Doppler shift () | |||
| Ranging signal | Length of the pseudo-random code | Time delay of light to and from the target | |||
| Local oscillator | Chip | Constant related to a balanced detector | |||
| , | Splitting ratios of FOC1 and FOC2 | Chip width | Electrical signal after a balanced detector | ||
| Frequency of carrier wave | Gate function | Noise | |||
| Amplitude of carrier wave | , | Impulse response of the LPF | , | Demodulated baseband data | |
| Initial phase of carrier wave | Phase modulation depth factor | Sampling rate () | |||
| Operating frequency of the AOM | Backscattered signal from the target | Speed of light | |||
| Pseudo-random code | Amplitude attenuation coefficient | Refractive index of the medium | |||
| Transimpedance of the balanced detector | Responsivity of the photodiode | \ | \ | ||
| Dielectric constant | Effective optical receiving area of the photodiode | \ | \ |

Table A2.
Symbols involved in the traditional and proposed methods.
Table A2.
Symbols involved in the traditional and proposed methods.
| Symbols Used in Both Methods | Symbols Used in the Traditional Method | Symbols Used in the Proposed Method | |||
|---|---|---|---|---|---|
| Symbols | Specification | Symbols | Specification | Symbols | Specification |
| Baseband data of length after sampling | Position of the chip where the correlation peak is located | Position of the correlation peak | |||
| Punctual code related to | Constructed new pseudo-random code | Early code related to | |||
| Length of the punctual code | New early code related to | Late code related to | |||
| Early–late discrimination model | New late code related to | Baseband data of length | |||
| Distance of the target | Cross-correlation | Cross-correlation | |||
| Fine phase difference of pseudo-random code | Cross-correlation | Cross-correlation | |||
| Correlation function | , | Characteristic parameters | , | Characteristic parameters | |
| Phase difference of the pseudo-random code | \ | \ | Coarse distance | ||
| Real part of the complex number | \ | \ | Fine distance | ||
| Spectral density of the pseudo-random code | \ | \ | Distance corresponding to the sampling period | ||
| Signal power | \ | \ | Distance per movement | ||
| \ | \ | \ | \ | ||
| \ | \ | \ | \ | Cross-correlation | |
| \ | \ | \ | \ | Cross-correlation | |
| \ | \ | \ | \ | Frequency obtained using FFT | |
| \ | \ | \ | \ | Residual frequency difference after FFT | |
| \ | \ | \ | \ | Residual phase | |
| \ | \ | \ | \ | Wavelength | |
| \ | \ | \ | \ | Transfer function of the LPF | |

Table A3.
Symbols involved in Section 4.
Table A3.
Symbols involved in Section 4.
| Symbols | Specification | Symbols | Specification | Symbols | Specification |
|---|---|---|---|---|---|
| Received power | Link attenuation caused by the channel | Responsivity | |||
| Transmitted power | Power loss caused by acquisition | Electron charge | |||
| Transmitter gain | Receiver gain | Receiver bandwidth | |||
| Optical efficiency of the transmitter | Optical efficiency of the receiver | \ | \ | ||
| Path loss of the inter-satellite optical link | Heterodyne efficiency | \ | \ |
References
- Teunissen, P.J.G.; Montenbruck, O. Springer Handbook of Global Navigation Satellite Systems; Springer: Cham, Switzerland, 2017; p. 17. [Google Scholar]
- Li, X.; Zhang, K.; Ma, F.; Zhang, W.; Zhang, Q.; Qin, Y.; Zhang, H.; Meng, Y.; Bian, L. Integrated Precise Orbit Determination of Multi-GNSS and Large LEO Constellations. Remote Sens. 2019, 11, 2541. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)—Achievements, prospects, and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Fernández, F.A. Inter-satellite ranging and inter-satellite communication links for enhancing GNSS satellite broadcast navigation data. Adv. Space Res. 2011, 47, 786–801. [Google Scholar] [CrossRef]
- Michalak, G.; Giorgi, G.; Deprez, C. Enhanced Orbit Determination of GNSSs with Optical Inter-satellite Links. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), St. Louis, MI, USA, 20–24 September 2021. [Google Scholar]
- Rajan, J.A. Highlights of GPS II-R autonomous navigation. In Proceedings of the 58th Annual Meeting of The Institute of Navigation and CIGTF 21st Guidance Test Symposium, Albuquerque, NM, USA, 24–26 June 2002. [Google Scholar]
- Rajan, J.A.; Orr, M.; Wang, P. On-orbit validation of GPS IIR autonomous navigation. In Proceedings of the 59th Annual Meeting of The Institute of Navigation and CIGTF 22nd Guidance Test Symposium, Albuquerque, NM, USA, 23–25 June 2003. [Google Scholar]
- Maine, K.P.; Anderson, P.; Langer, J. Crosslinks for the next-generation GPS. In Proceedings of the IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 8–15 March 2003. [Google Scholar]
- Tang, C.; Hu, X.; Zhou, S.; Liu, L.; Pan, J.; Chen, L.; Guo, R.; Zhu, L.; Hu, G.; Li, X.; et al. Initial results of centralized autonomous orbit determination of the new-generation BDS satellites with inter-satellite link measurements. J. Geod. 2018, 92, 1155–1169. [Google Scholar] [CrossRef]
- Cao, Q.; Tong, Z.; Liu, L.; Wang, J.; Ying, K.; Pang, F.; Gui, Y. Simultaneous transmission of time-frequency and data with co-amplification over urban fiber links. Chin. Opt. Lett. 2024, 22, 011201. [Google Scholar] [CrossRef]
- Yin, Z.; Zheng, M.; Zhang, C.; Guan, S.; Zhou, X.; Liu, Y.; Gang, Z.; Nie, J.; Zhang, Y.; Zhu, X.; et al. Stability-enhanced RF signal transmission over long fiber-optic links. Chin. Opt. Lett. 2024, 22, COL202422. [Google Scholar] [CrossRef]
- Zeng, T.; Shen, Q.; Cao, Y.; Guan, J.-Y.; Lian, M.-Z.; Han, J.-J.; Hou, L.; Lu, J.; Peng, X.-X.; Li, M.; et al. Measurement of atmospheric non-reciprocity effects for satellite-based two-way time-frequency transfer. Photonics Res. 2024, 12, 1274–1282. [Google Scholar] [CrossRef]
- Tang, C.; Hu, X.; Zhou, S.; Guo, R.; He, F.; Liu, L.; Zhu, L.; Li, X.; Wu, S.; Zhao, G.; et al. Improvement of orbit determination accuracy for Beidou Navigation Satellite System with Two-way Satellite Time Freque ncy Transfer. Adv. Space Res. 2016, 58, 1390–1400. [Google Scholar] [CrossRef]
- Pasynkov, V.; Sadovnikov, M.; Sumerin, V.; Shargorodskiy, V. The concept and preliminary results of use of satellite laser ranging for GLONASS accuracy improvement. In Proceedings of the 18th International Workshop on Laser Ranging, Fujiyoshida, Japan, 11–15 November 2013. [Google Scholar]
- Morton, Y.J.; van, Diggelen, F.; Spilker, J.J., Jr.; Parkinson, B.W.; Lo, S.; Gao, G. Position Navigation and Timing Technologies in the 21st Century: Integrated Satellite Navigation, Sensor Systems, and Civil Applications; Wiley: Hoboken, NJ, USA, 2020; Volume 1, p. 91. [Google Scholar]
- Michalak, G.; Glaser, S.; Neumayer, K.; König, R. Precise orbit and Earth parameter determination supported by LEO satellites, inter-satellite links and synchronized clocks of a future GNSS. Adv. Space Res. 2021, 68, 4753–4782. [Google Scholar] [CrossRef]
- Yu, X.; Tong, S.; Zhao, X.; Jiang, J.; Chen, X. Two-way laser regeneration pseudocode rangefinder of intersatellite optical crosslink. Opt. Eng. 2020, 59, 036101. [Google Scholar] [CrossRef]
- Zhu, F.; Lu, S.; Sun, J.; Zhu, R.; Hou, X.; Chen, W. Inter-satellite laser-ranging based on intradyne coherent detection. Appl. Opt. 2021, 60, 8930–8938. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Tong, S.; Zhang, L.; Dong, Y.; Zhao, X.; Qiao, Y. 10.23 Mcps laser pseudo-code ranging system with 0.33 mm (1 σ) pseudo-range measurement precision. Appl. Opt. 2017, 56, 5342–5348. [Google Scholar] [CrossRef] [PubMed]
- Banzhaf, S.; Waldschmidt, C. Phase-Code-Based Modulation for Coherent Lidar. IEEE Trans. Veh. Technol. 2021, 70, 9886–9897. [Google Scholar] [CrossRef]
- Peterson, R.L.; Ziemer, R.E.; Borth, D.E. Introduction to Spread Spectrum Communications; Pearson: Hoboken, NJ, USA, 1995; p. 156. [Google Scholar]
- Spilker, J.J., Jr.; Axelrad, P.; Parkinson, B.W.; Enge, P. Global Positioning System Theory and Applications; American Institute of Aeronautics & Astronautics: Washington, DC, USA, 1996; Volume 1, p. 275. [Google Scholar]
- Holmes, J.K. Coherent Spread Spectrum Systems; John Wiley & Sons, Inc.: New York, NY, USA, 1982; p. 354. [Google Scholar]
- Huilin, J.; Shoufeng, T.; Lizhong, Z. The Technologies and Systems of Space Laser Communication; National Defense Industry Press: Beijing, China, 2010; p. 82. [Google Scholar]
- Patnaik, B.; Sahu, P.K. Inter-satellite optical wireless communication system design and simulation. IET Commun. 2012, 6, 2561–2567. [Google Scholar] [CrossRef]
- Liang, J.; Chaudhry, A.U.; Erdogan, E.; Yanikomeroglu, H. Link Budget Analysis for Free-Space Optical Satellite Networks. In Proceedings of the IEEE 23rd International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMoM), Belfast, UK, 14–17 June 2022. [Google Scholar]
- Sambridge, C.S.; Spollard, J.T.; Sutton, A.J.; McKenzie, K.; Roberts, L.E. Detection statistics for coherent RMCW LiDAR. Opt. Express 2021, 29, 25945–25959. [Google Scholar] [CrossRef] [PubMed]
- Gatt, P.; Henderson, S.W. Laser radar detection statistics: A comparison of coherent and direct detection receivers. In Proceedings of the Conference on Laser Radar Technology and Applications VI, Orlando, FL, USA, 16–20 April 2001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).