Topological Phase Transition by Tuning Central Unit in C₃ Symmetric Lattice of Terahertz Photonic Crystals

Abstract

A terahertz band-switchable photonic topological insulator (PTI) composed of a C₃-symmetric rod-type photonic crystal is designed. By tuning the size of the central cylinder in the lattice, a topological phase transition can occur in the PTI, and the topological nontrivial bandgap can be switched from the first to the second bandgap. In both cases, before and after switching, topological edge-state transport of terahertz waves along zigzag topological domain walls, as well as terahertz corner-state localization in constructed resonant cavities, are numerically demonstrated. In addition, an existence of the topological phase transition is also confirmed when tuning the central unit in the lattice of another C₃-symmetric hole-type photonic crystal. This work provides a new approach for flexible terahertz waveguiding and lasing applications.

1. Introduction

With the principles and concepts of topological physics applied to the field of photonics [1], photonic topological insulators (PTIs) have made great progress over the past several years. Photonic crystal (PhC) has become a commonly used platform for the realization of PTIs [2,3,4]. Due to the difficulty and limitations in adding an extra magnetic field to achieve photonic quantum Hall effects, researchers have strived to develop those approaches without the need for the magnetic field, including spin Hall [5,6,7,8,9,10,11], valley Hall [12,13,14,15,16,17,18,19,20], and high-order PTIs [21,22,23,24,25,26]. A typical spin Hall PTI has a honeycomb lattice consisting of six cylinders with the C6 crystalline symmetry. Valley Hall PTIs achieve a non-trivial topological phase by breaking spatial inversion symmetry. High-order PTIs have been reported based on a 1-D and 2-D SSH model. Specific structures such as Kagome-lattice PTI [27,28,29] can exhibit both valley-Hall and high-order topological phases. This, however, requires precise control of the expanded or shrunken C₃ lattice to attain the phase transition. In recent years, the terahertz (THz) frequency band has shown great potential for ultrahigh bandwidth communication in the Next 6G communication system. Valley Hall PTI becomes a good solution for realizing THz waveguide-type devices [30,31]. For example, an electrically tunable THz topological notch filter is proposed based on valley PhC, with a notch suppression depth exceeding 20 dB and return loss of 13 dB [32]. An air-slot-like valley PhC THz waveguide is presented by combining a bearded interface with a conventional defect [33]. Another metallic THz valley PhC with subtle backscattering of the edge state [34] is also reported. In addition, the use of topological corner states enables the realization of THz cavities [35]. Recently, the quantized cavity modes derived from continuous edge states have attracted attention, as they can also yield ultrahigh Q-factor in the THz regime and hence significantly strengthen THz light-matter interactions [36].

Nevertheless, most publications have realized valley Hall PTIs by symmetrical breaking or structural breathing and have simply focused on the first bandgap, which lacks some convenience and flexibility. In this work, we designed a band-switchable THz PTI with a C₃-symmetric rod-type photonic crystal. We show that the topological phase of the proposed PTI can be easily tuned by adjusting the radius of the central rod, rather than structural breathing in typical Kagome-lattice PTI [27,28,29]. Such phase tuning can result in topological band switching from the first to the second bandgap, providing more flexible operations. In both cases, before and after the switch, we numerically investigated topological edge-state transport of terahertz waves along zigzag topological domain walls and terahertz corner-state localization in constructed resonant cavities. In this study, we explored the topological phase transition of another hole-type photonic crystal by tuning the central unit into a similar C₃-symmetric lattice.

2. Design and Discussion

2.1. PTI with Rod-Type PhC

The proposed rod-type THz PTI with a hexagonal C₃-symmetric PhC lattice, composed of one central cylinder and three outer cylinders in an air background, is illustrated in Figure 1a. The material of the cylinders is high-resistivity silicon with the dielectric constant of ε₁ = 11.7 in the THz range. The lattice constant is a = 300 μm. The radius of the central cylinder is R, which is the main variable of interest. The outer three cylinders have a fixed radius of r = 21 μm, along with a fixed distance of W = 120 μm from the center of the lattice.

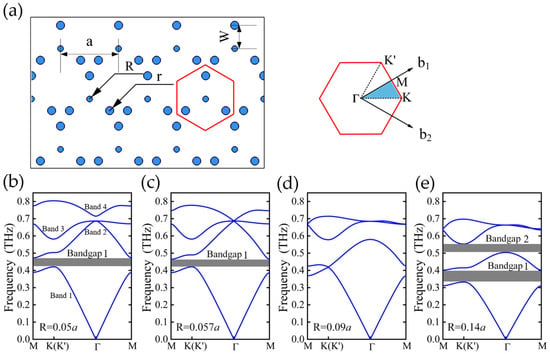
Figure 1. (a) The structure of the rod-type PTI with four cylinders in a C₃-symmetric lattice; (b–e) the photonic band structure of the PTI with different values of the radius R = 0.05a, R = 0.057a, R = 0.09a, and R = 0.14a, respectively.

The photonic band analysis is conducted by using the finite element method with COMSOL Multiphysics 5.6. Figure 1b–e shows the TM band structures (out-of-plane Ez ≠ 0) with the lowest four bands in four different cases of R: R = 0.05a, R = 0.057a, R = 0.09a, and R = 0.14a. It is observed that when R is small (e.g., R = 0.05a), Bandgap 1 opens between Bands 1 and 2. At R = 0.057a, Bands 2, 3, and 4 degenerate to form a Dirac point at Г point. As R rises to 0.09a, Bandgap 1 closes and Band 1, 2 form a Dirac point at the K point. With further increase in R (e.g., R = 0.14a), Bandgap 1 reopens while Bandgap 2 appears between Bands 2 and 3. During the increase of R from 0.05a to 0.14a, both Bandgap 1 and 2 experience topological phase transition at their respective Dirac point, which can be proven by analyzing the topological invariant described by 2-D bulk polarization [37]. The bulk polarization P = (p₁, p₂) related to the Berry connection in 2-D Brillouin Zone is defined as

$$p_i=-{\displaystyle \frac{1}{{\left(2\pi \right)}^2}}{\iint }_{BZ}d{k}_{1}d{k}_2\mathrm{T}r\left[A_i\left(\mathbf{k}\right)\right].$$

(1)

$\left[A_i\left(\mathbf{k}\right)\right]$^mn is the Berry connection matrix with m and n running over occupied bands

$${\left[A_i\left(\mathbf{k}\right)\right]}^{mn}=-i⟨u^m\left(\mathbf{k}\right)\left|{\partial k}_i\right|u^n\left(\mathbf{k}\right)⟩.$$

(2)

$⟨u^n\left(\mathbf{k}\right)⟩$ is the nth band periodic Bloch wavefunction. By using an efficient Wilson loop method [38], we calculated the bulk polarization of the band gaps with different values of R. The Wilson loop along the k₁ direction under N mesh is defined as

$$W_{k_1\to k_1+2\pi ,k_2}=A_{k_1,k_2}{A}_{k_1+d{k}_1,k_2}{A}_{k_1+2d{k}_1,k_2}\dots A_{k_1+Nd{k}_1,k_2}.$$

(3)

The bulk polarization P can be derived from the eigenvalues of Wannier Hamiltonians based on the Wilson loop. When R is small, Bandgap 1 has the polarization P = (1/3, 1/3), indicating a topological nontrivial phase. As R increases, Bandgap 1 experiences a closing at R = 0.09a. After that, it reopens and its polarization becomes P = (0, 0), revealing a topologically trivial phase. In contrast, after Bandgap 2 opens (e.g., R = 0.05a), the polarization of Bandgap 2 is P = (1/3, 1/3), indicating the topological nontrivial bandgap has been switched from Bandgap 1 to Bandgap 2.

The topological edge states are expected to exist at various edges between two PTIs with different 2-D polarization. Edge 1 is composed of the PTI with R = 0.05a and its inverted counterpart, as shown in Figure 2a. The two PTI domains have the nontrivial Bandgap 1 with the same frequency region but opposite polarization of (1/3, 1/3) and (−1/3, −1/3), respectively, leading to the appearance of two edge states colored in red within Bandgap 1. We also find that a conventional hexagonal-lattice rod-type PhC with the rod radius of 0.15a in the unit cell can have an overlap bandgap region with that of the PTI. If we place this conventional PhC with P = (0, 0) adjacent to the PTI with R = 0.05a to form Edge 2 in Figure 2b, the number of edge states will reduce to one. When a topological nontrivial bandgap is switched to Bandgap 2, such as the PTI case with R = 0.14a, Edge 3 or 4 supporting double or single edge states can also be constructed. However, as shown in Figure 2c,d, in Edge 3 and 4, edge states exist only inside Bandgap 2, while there is no edge state in Bandgap 1. This agrees with the previous analysis of the topological invariants and nontrivial band switch.

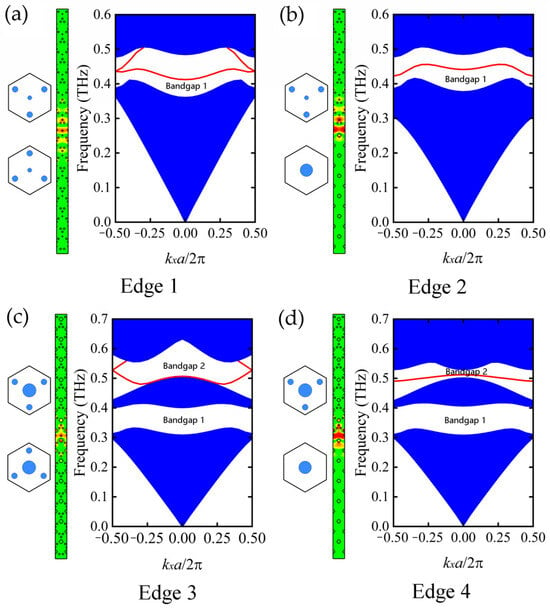
Figure 2. Projected band diagrams and topologically edge states in four types of edges with nontrivial rod-type PTIs. (a) Edge 1 consists of the PTI with R = 0.05a and its inverted counterpart; (b) Edge 2 consists of the PTI with R = 0.05a and a conventional rod-type PhC; (c) Edge 3 consists of the PTI with R = 0.14a and its inverted counterpart; (d) Edge 4 consists of the PTI with R = 0.14a and a conventional rod-type PhC.

In order to explore the stability of these edge states, we conducted full-wave simulations of the edge wave propagation in straight channels as well as non-straight channels with a 120° turn, formed by Edge 1 and 3, respectively. Here, full-field waves are excited by a THz point source located at the input port of the edge channels. As shown in Figure 3a, the straight channel with Edge 1 supports edge waveguiding with a high transmittance within the working band of 0.43–0.47 THz, and the propagation field distribution at 0.46 THz presents clear field confinement to the domain walls. For comparison, in Figure 3c, the non-straight channel has a narrower high-transmission band, and the propagation field distribution exhibits less smoothness and robustness. For two similar channels formed by Edge 3, the high-transmittance bands of the straight and non-straight channels switch to 0.51–0.56 THz, as illustrated in Figure 3b,d. The field distribution of both the straight and non-straight guiding at 0.52 THz demonstrates better performance with suppressed back scattering, even at the turning. The above phenomenon may be attributed to the fact that the edge states in Bandgap 2 of Edge 3 (after topological band switching) occupy a wider single-mode frequency range than those in Bandgap 1 of Edge 1 (before switching). Nevertheless, such band-switchable topological edge-guiding feature provides better flexibility for THz waveguiding applications. It is worth noting that Bandgap 2 is located at a relatively high frequency. Using a high-frequency bandgap for device design allows larger lattice constants due to the frequency normalization characteristics of photonic crystals, which may reduce the difficulty and cost of THz microstructure fabrication.

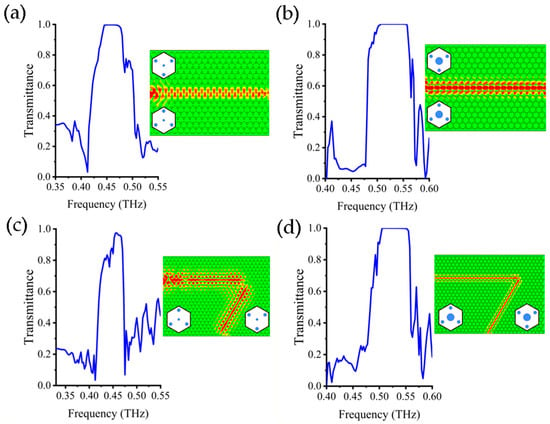
Figure 3. The transmission spectra of four edge channels and the corresponding field distributions of the edge guiding. (a) Straight channel formed by Edge 1; (b) Straight channel formed by Edge 3; (c) Non-straight channel with a 120° turn formed by Edge 1; (d) Non-straight channel with a 120° turn formed by Edge 3.

In addition, we explored terahertz corner-state localization within the aforementioned topological nontrivial band gaps. A corner state is located at the boundary of the boundary and hence is considered the edge state of the edge state [39]. Therefore, the corner states require gapped edge states as a condition for their existence and may appear in the gap between edge states and bulk states. We consider a regular triangle cavity structure with three 60° corners formed by the four edges in Figure 2. Figure 4 illustrates the calculated frequencies of the eigenstates in each cavity, including bulk states (black dots), edge states (blue dots), and corner states (red dots). For the cavity in Figure 4a, using Edge 2 with topological nontrivial PTI inside and conventional PhC outside, the edge states start at 0.406 THz from the lower bulk states. Three corner states near 0.491 THz are sustained within Bandgap 1. The field distributions clearly present highly localized fields at the corners, with the maximal quality factor Q reaching 16957. Here, the Q-factor is calculated by solving the eigenfrequencies ω of the cavity structures following $Q=\frac{\mathrm{R}\mathrm{e}\left(\omega \right)}{2\left|\mathrm{I}\mathrm{m}\left(\omega \right)\right|}$. For the cavity in Figure 4c using Edge 4, which has the nontrivial bandgap switched to Bandgap 2, the edge states start at 0.492 THz from the lower bulk states. Three corner states are also sustained while their frequency is switched to 0.518 THz. Their maximal Q-factor drops slightly but still reaches 13340. However, the cavities using Edge 1 and 3 with topological nontrivial PTI inside and its inverted counterpart outside only sustain edge states in the bandgap, as shown in Figure 4b,d. The absence of the corner states is due to the frequency ranges of those edge states spanning almost the entire bandgap (see Figure 2a,c), which fails to meet the necessary conditions for the existence of corner states. It is worth noting that besides the cavity corner states, the cavity edge states can also yield a high Q-factor. For example, in Figure 4d, the cavity edge state at 0.525 THz has a high Q-factor of 12263. In general, such frequency-switchable cavity states can supply more flexibility in THz resonant cavity applications.

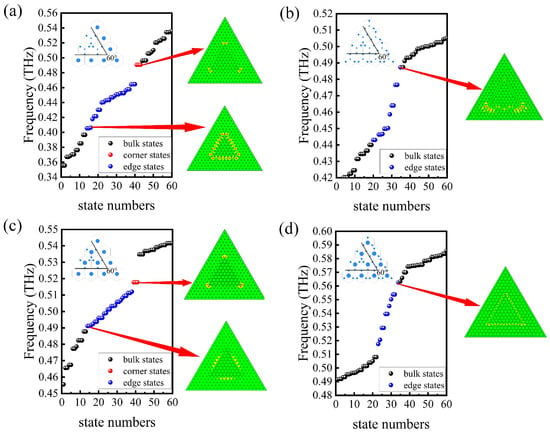
Figure 4. The eigenfrequencies of the triangular cavities with four edge configurations, respectively. (a) The cavity is formed by Edge 2. The insets are the field distributions of one corner state at 0.491 THz and the lowest edge state at 0.406 THz; (b) The cavity is formed by Edge 1. The inset is the field distribution of the highest edge state at 0.487 THz. No corner states are found; (c) The cavity formed by Edge 4. The insets are the field distributions of one corner state at 0.518 THz and the lowest edge state at 0.492 THz; (d) The cavity is formed by Edge 3. The inset is the field distribution of the highest edge state at 0.562 THz. No corner states are found.

2.2. PTI with Hole-Type PhC

To further verify the topological tunability of the proposed C₃-symmetric lattice model, another THz PTI based on an air-hole PhC is designed. As shown in Figure 5a, this air-hole PhC also has a hexagonal C₃-symmetric lattice composed of one central hole and three outer holes in a dielectric background. The background is high-resistivity silicon with ε₁= 11.7 in the THz range. The lattice constant of this THz PTI is a = 400 μm. The central air hole has a radius R = 72 μm, and the outer air hole has a radius r = 56 μm. The distance between the central and the outer holes is W = a/3. We investigate the topological property of the PTI when the central air hole is filled with other materials having different relative permittivity of ε. Figure 5b–d shows the first four TE-mode bands (in-plane Hz ≠ 0) for three different central fillers with ε = 1, ε = 5.5, and ε = 20, respectively. It is found that Bandgap 1 is opened at small ε (e.g., ε = 1) between the first and second bands. At ε = 5.5, Bandgap 1 closes to form a Dirac point. With further increase in ε (e.g., ε = 20), Bandgap 1 reopens to complete a band inversion. Calculations on the 2-D bulk polarization indicate that Bandgap 1 is topologically trivial with P = (0, 0) for ε < 5.5, while it is topologically nontrivial with P = (1/3, 1/3) for ε > 5.5.

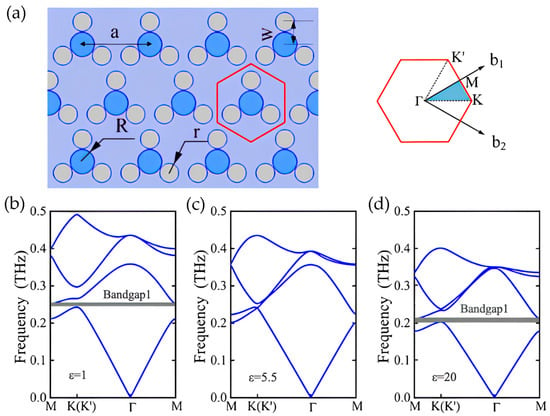
Figure 5. (a) The structure of the hole-type PTI with four holes in a C₃-symmetric lattice; (b–d) The photonic band structure of the PTI when the central air hole is filled with other materials having relative permittivity of ε = 1, ε = 5.5, and ε = 20, respectively.

By placing the nontrivial PTI with ε = 20 adjacent to a conventional hole-type PhC with an overlapping bandgap, we verified the existence of topological edge states. Regardless of whether the PTI is rotated by 60° or not, an edge state always emerges inside Bandgap 1 for Edge 5 and 6, as shown in Figure 6a,b. It is worth noting that the edge states in these two edges exhibit different dispersion and single-mode range. Since the edge state spans the entire frequency range of Bandgap 1, which does not satisfy the aforementioned condition for the existence of corner states, the corner states are not considered here. Finally, we examined the topological waveguiding performance of the edge state of Edge 6. A non-straight edge channel with a 120° turn was constructed, as shown in Figure 7. The non-straight waveguide exhibits nearly lossless transmission within the frequency range of 0.204~0.214 THz, with a maximum transmittance reaching 99.8%. The propagation field distribution at 0.206 THz displays smoothness with minimal backscattering, demonstrating excellent immunity to reflection at the turn. These results prove that we can easily control the topological phase of hole-type PTI with a C₃-symmetric lattice by central fillers, offering greater tunability in realizing THz configurable waveguide-type devices.

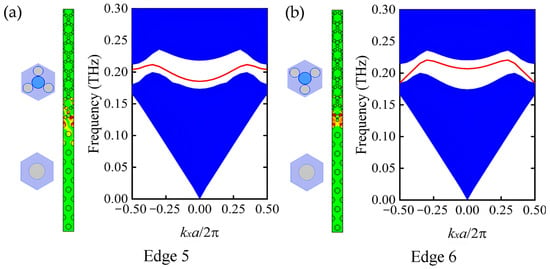
Figure 6. Projected band diagrams and topologically edge states in two types of edges with nontrivial hole-type PTIs. (a) Edge 5 consists of the PTI with ε = 20 and a conventional hole-type PhC; (b) Edge 6 consists of the PTI with ε = 20 rotated by 60° and a conventional hole-type PhC.

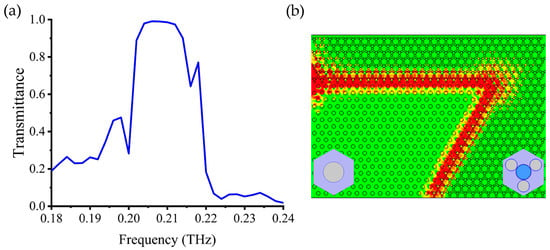
Figure 7. (a) The transmission spectra and (b) the field distribution of the edge guiding at 0.206THz in a non-straight edge channel with a 120° turn formed by Edge 6.

3. Conclusions

In summary, we studied a band-switchable THz PTI formed by a C₃-symmetric rod-type photonic crystal. Bulk polarization calculations confirm that as the size of the central rod increases, the topological nontrivial bandgap transits from the first bandgap to the second bandgap, which provides greater flexibility for device design. Simulations demonstrate that the high transmission band of the PTI-based THz edge waveguide can be switched from a lower frequency band to a higher one. The transmission bandwidth reaches about 50 GHz, and the highest transmittance exceeds 99%. Moreover, highly localized corner states in PTI-based THz cavities can also shift to higher frequencies, with the largest quality factor reaching 16,957. Finally, we confirm the validity of a similar method that tunes the topological phase of another hole-type PTI with a C₃-symmetric lattice by the central fillers. This work may contribute to the realization of THz functional devices and facilitate the development of next-generation communication technologies.