Power Domain Hybrid Modulation-Based Coherent Optical Transmission with Successive Interference Cancelation

Abstract

The 6G era necessitates advanced multiplexing techniques that fully utilize various physical dimensions, including time, frequency, polarization, and space to enhance the achievable bitrate per wavelength and satisfy growing demands for capacity and spectral efficiency. Power domain hybrid modulation (PDHM) emerges as a viable technology to overcome the orthogonal limitations inherent in existing multiplexing schemes. In this paper, we introduce an iterative successive interference cancelation (SIC) algorithm for coherent optical transmission systems employing PDHM. The proposed system multiplexes a 16-ary quadrature amplitude modulation (16-QAM) signal with a quadrature phase shift keying (QPSK) signal at distinct power ratios. With the proposed iterative SIC, the system performance is improved by about one order of magnitude.

1. Introduction

To meet the ever-increasing traffic requirement, a large amount of the research has proposed to push the bit rate per-wavelength in optical transmission from 100 Gb/s quadrature phase shift keying (QPSK) to 400 Gb/s or even 1 Tb/s [1,2]. Generally speaking, there are two approaches that can be used for increasing system capacity. The first approach is to increase the bit rate per wavelength by employing higher-order modulation formats or by raising the symbol rate [3,4,5]. However, this method presents significant challenges: higher-order modulation formats necessitate a higher optical signal-to-noise ratio (OSNR) to maintain desired performance, while achieving higher symbol rates requires components with broader bandwidths. The second approach leverages advanced multiplexing techniques, such as time-division multiplexing (TDM), frequency-division multiplexing (FDM), polarization-division multiplexing (PDM), and space-division multiplexing (SDM) [6,7,8,9,10] in different physical dimensions to minimize interference. Among these, techniques like orthogonal frequency-division multiplexing (OFDM) and Nyquist transmission are particularly notable for their high spectral efficiency [11,12]. To overcome the orthogonal constraint inherent in these conventional multiplexing schemes, power-domain hybrid modulation (PDHM) combined with successive interference cancelation (SIC) has been recently proposed, offering a pathway to superior spectral efficiency [13,14,15]. PDHM introduces power as a new dimension for multiplexing, enabling enhanced transmission capacity without expanding the system’s total bandwidth [16,17]. Furthermore, power-domain multiplexing can imbue networks with novel service-provisioning capabilities. For instance, the high-power layer can be reserved for “mission-critical services” that demand high robustness and low error rates. Conversely, the low-power layer can be allocated for “best-effort services” that are sensitive to spectral efficiency but more tolerant of delay or errors. At the receiver, SIC is employed to separate the superposed signals. The high-power signal is demodulated first by treating the low-power signal as noise. Once decoded, this high-power signal is reconstructed and subtracted from the received signal, allowing for the subsequent demodulation of the low-power signal. A key limitation of this scheme, however, is that the performance of the low-power signal is inherently constrained by the significant noise floor imposed by the high-power signal during the initial demodulation stage. A critical challenge that persistently limited the performance and scalability of these systems was error propagation in the SIC process. As explicitly noted in [14], “the existence of error propagation in SIC” leads to elevated bit error rates (BER), particularly for weaker users. The fundamental issue originates from the traditional, open-loop SIC architecture. Imperfect decoding of the primary user’s signal or inaccuracies in channel estimation introduce residual interference during the cancelation step. This residual error directly biases the recovery of subsequent, lower-power users, creating a vicious cycle that severely degrades overall system performance and constrains the practical number of supportable users. This limitation highlighted the urgent need for a more robust SIC mechanism. To address this bottleneck, researchers have integrated powerful channel coding and iterative feedback mechanisms into the SIC structure. This iterative refinement, conceptually aligned with the principles demonstrated by advanced channel coding in [15], enables a substantially more accurate reconstruction and subtraction of the interfering signal component. By introducing a feedback loop that progressively refines signal estimates, this approach effectively mitigates the error propagation that plagued earlier systems.

In this paper, we propose and investigate an iterative successive interference cancelation (SIC) algorithm for a PDHM system in coherent optical transmission. The system multiplexes a low-power Nyquist-shaped 16-ary quadrature amplitude modulation (QAM16) signal with a high-power QPSK signal. The proposed iterative SIC enhances the conventional process by introducing a dedicated feedback loop to mitigate error propagation. After the initial demodulation of the 16-QAM signal, the decoded symbols are fed back into a second SIC stage to reconstruct and subtract their contribution from the received signal. This generates a refined version of the QPSK signal with reduced interference, which is then re-demodulated to obtain a superior final estimate of the 16-QAM signal. And the results demonstrate that this iterative technique improves the overall system Bit Error Rate (BER) performance by approximately one order of magnitude compared to the conventional single-stage SIC. Furthermore, we benchmark the proposed algorithm against a demultiplexing approach based on a look-up table (LUT). The results confirm that our iterative SIC method achieves a slightly superior performance, validating its efficacy in enhancing recovery fidelity for the lower-power layer in a PDHM scheme.

Overall, the paper presents the PDHM signal transmission for coherent optical transmission with an iterative SIC algorithm. Such a transmission system has the following advantages:

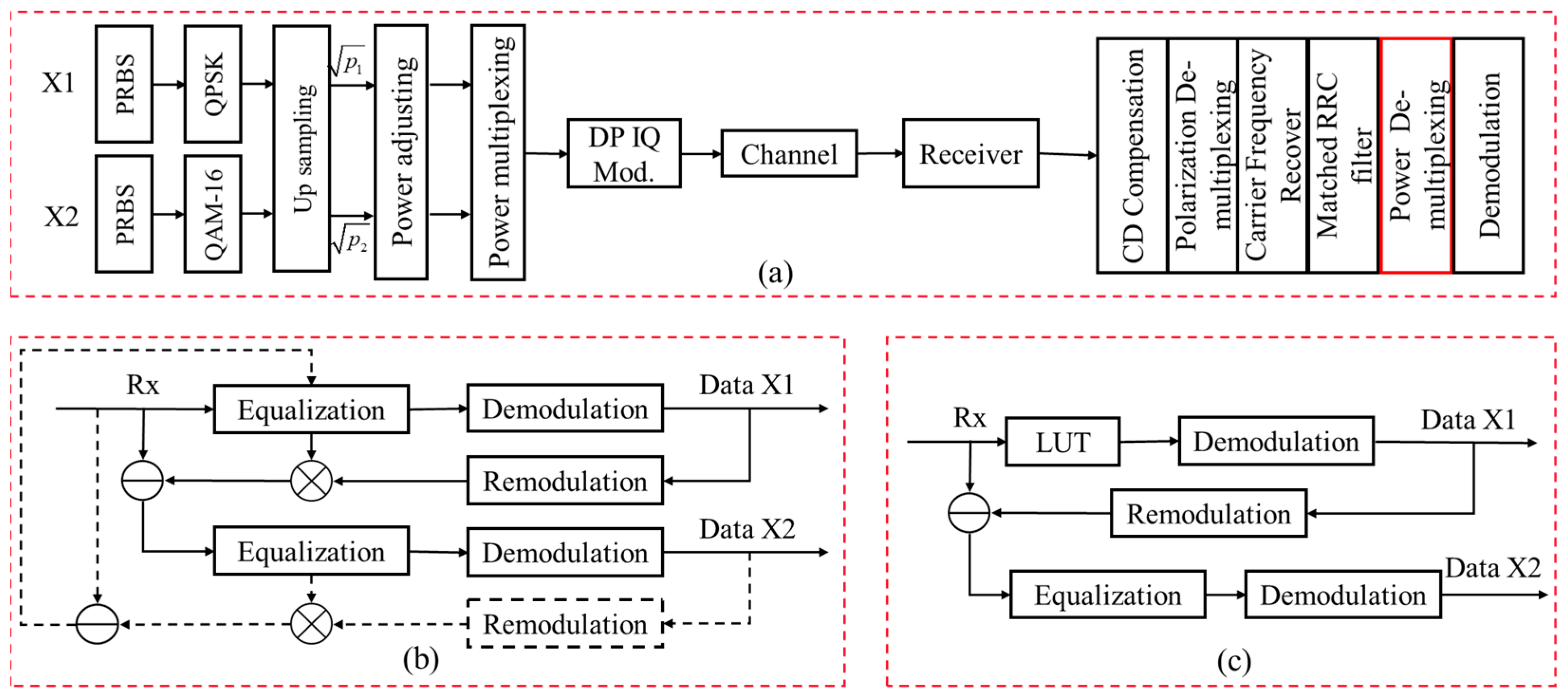
• An integrated, single-channel PDHM architecture. Departing from traditional multi-transmitter PDHM systems that generate and transmit component signals (e.g., QPSK, 16-QAM) via independent TXDSPs and physical channels, our scheme digitally synthesizes the entire PDHM constellation within a single TXDSP. This integrated signal is then transmitted through a unified transceiver and a single channel. This architectural shift eliminates the need for multiple synchronized hardware paths, resulting in a system that is more hardware-efficient, cost-effective, and flexible for practical deployment.
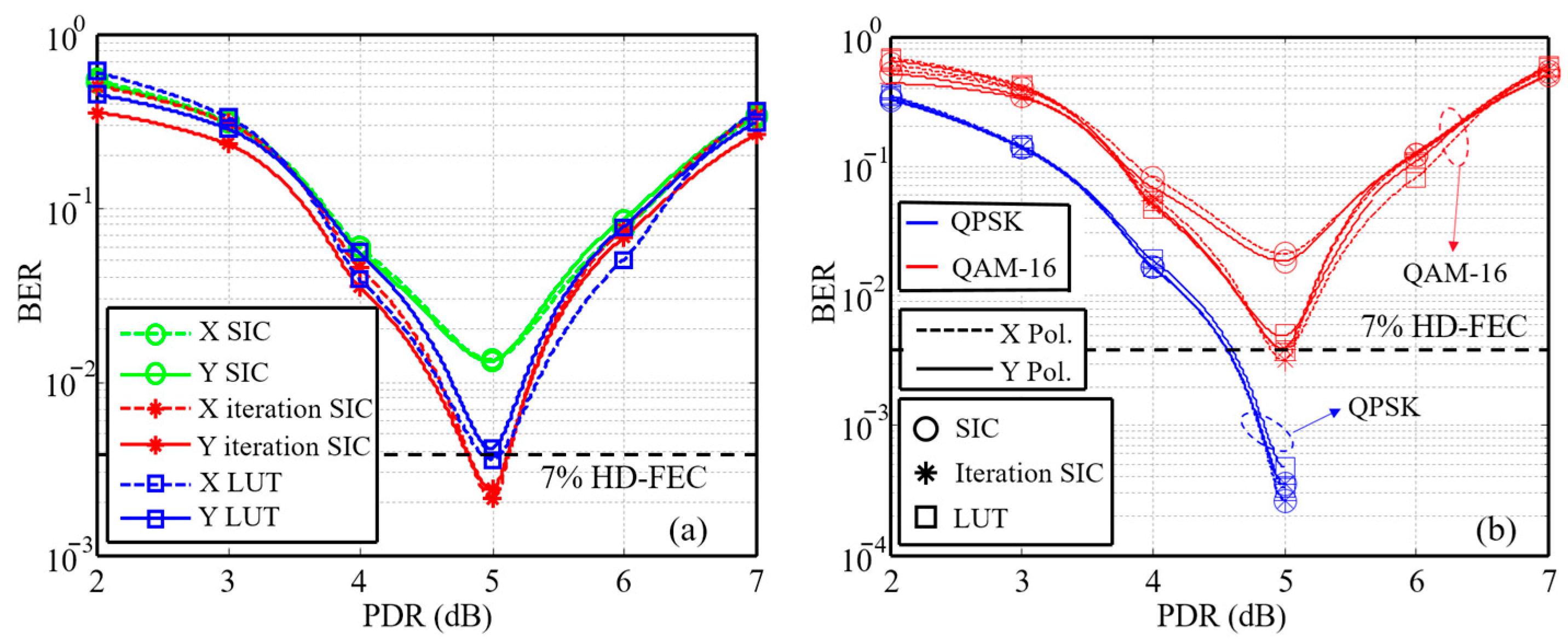
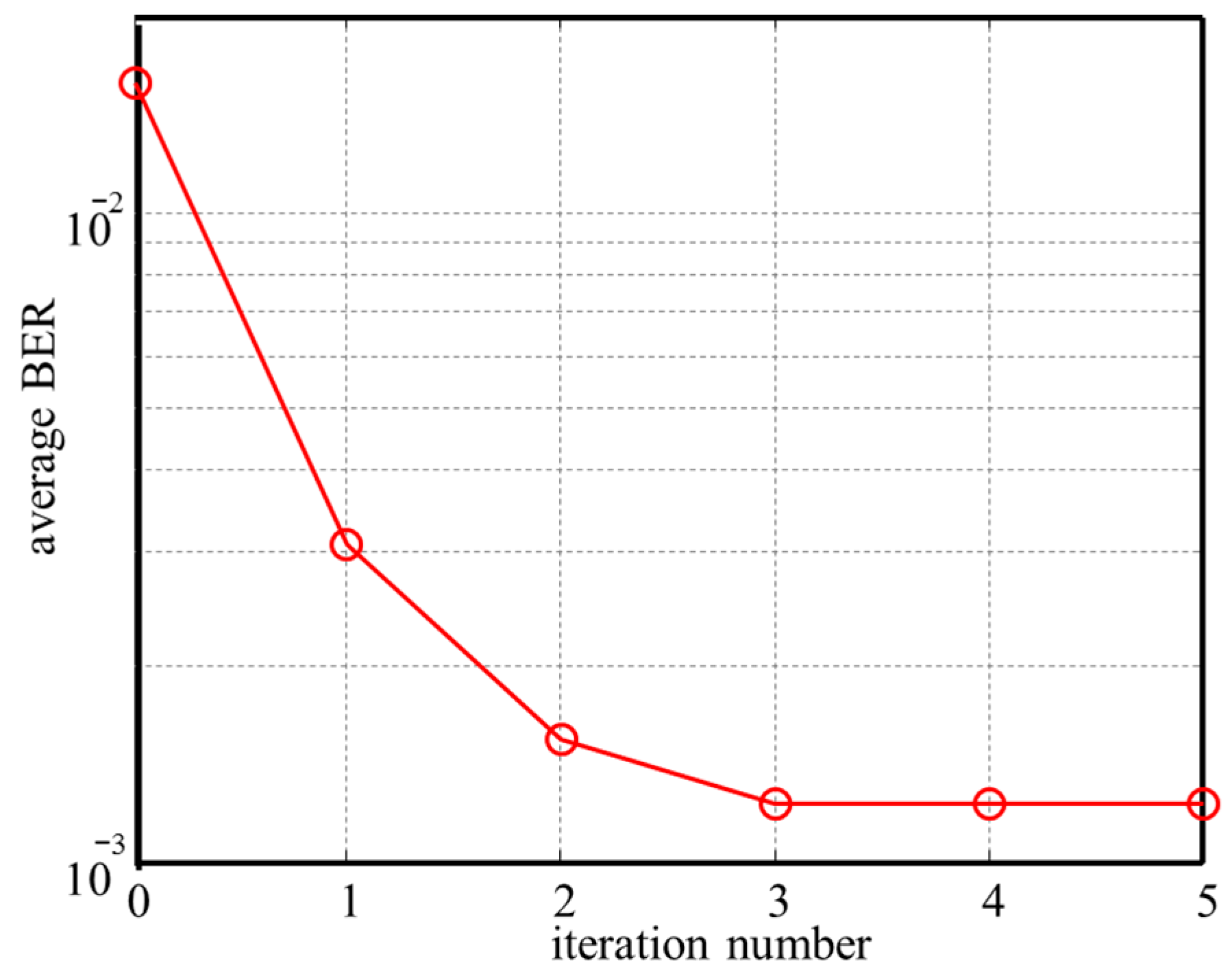
• A novel iterative SIC algorithm is proposed to break the error propagation cycle. A fundamental limitation of traditional SIC is its vulnerability to error propagation, where imperfections in the initial demodulation of the high-power signal lead to failure in recovering the low-power signal. This paper’s key algorithmic breakthrough is an iterative SIC process that introduces a critical feedback loop. This loop uses the initially decoded low-power signal to refine the estimation and cancelation of the high-power interference, thereby breaking the error propagation cycle and achieving a demonstrable performance improvement of approximately one order of magnitude in BER.
• The co-design of PDHM and iterative SIC is the most significant contribution of this paper, these two innovations are mutually enabling. The integrated PDHM architecture produces a deterministic signal perfectly suited for the iterative SIC algorithm. In turn, the iterative SIC provides the robust, low-error de-modulation capability necessary to decode the complex, single-channel PDHM signal. This co-design results in a complete, high-performance, and practical communication system that not only enhances spectral and power efficiency but also introduces inherent flexibility for multi-service provisioning.

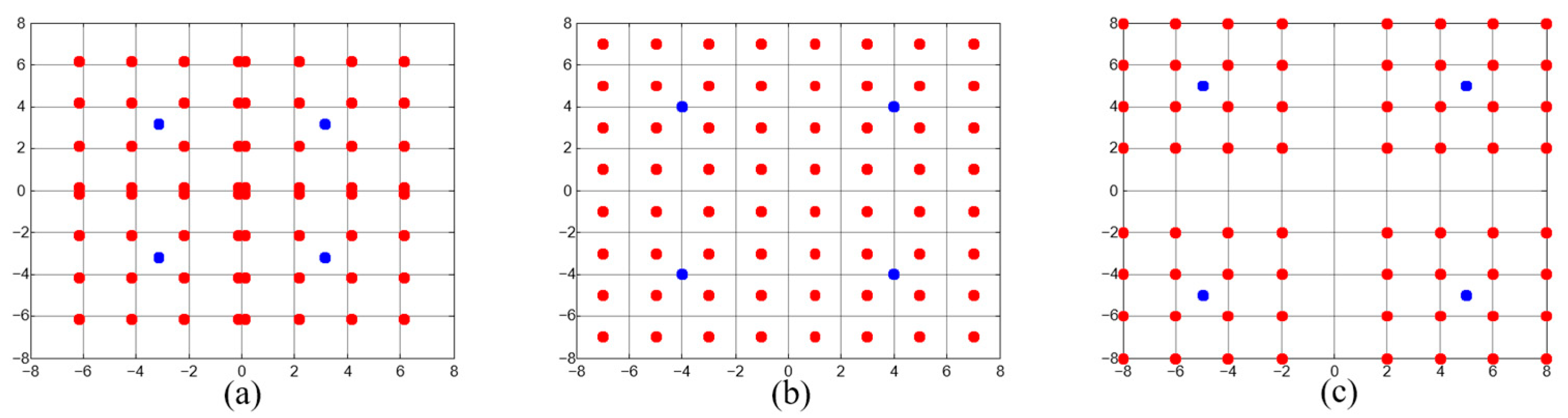
2. The Principle of the Power Domain Signal Multiplexing and De-Multiplexing

Figure 1a gives a global view of the PDHM model. At the transmitter digital signal processing (DSP), two pseudo random bit sequences (PRBS) are mapped into QPSK and QAM-16 signals, receptively. X1 in Figure 1a is coded using QPSK and X2 is coded using QAM-16. Then, the modulated signals are up-sampled and pulse shaping is implemented using root raised cosine (RRC) filters. After that, the brick-wall-shaped QPSK and QAM-16 signals are multiplexed in the power domain with their powers being adjusted to p₁ and p₂. The generated PDHM signal is expressed as,

$$s_{tx}=p_1{\displaystyle \sum _n{a}_{n}g\left(t-n{T}_s\right)+p_2{\displaystyle \sum _n{b}_{n}g\left(t-n{T}_s\right)}}$$

(1)

In Equation (1), $a_n$ and $b_n$ are QPSK and QAM-16 signals, respectively. $g$(t) is the RRC pulse with a roll-off factor of 0.01. $T_s$ is the symbol duration time.

The constellations of the PDHM signals for different power division ratios (PDR) are shown in Figure 2 (red points), We define the power division ratio as PDR(dB) = 10 log₁₀(P _QPSK) − 10 log₁₀(P_16-QAM), where P _QPSK and P_16-QAM are the powers of the QPSK and 16-QAM signals measured in milliwatt, respectively. The blue dots are the constellations of original QPSK signal before power multiplexing in Figure 2. The power of the QPSK signal is higher than that of the QAM-16 signal. The structure of the composite constellation is critically dependent on this ratio. A key finding is that at a specific ratio of 5 dB, the superposition of the QPSK and 16-QAM constellations yields a near-ideal 64-QAM constellation. To further elucidate this relationship, we examine the constellation evolution at 3 dB and 7 dB ratios. For the 3 dB case, the constellation exhibits significant overlap among the lower-amplitude points, resulting in ambiguous decision boundaries. This clustering increases the susceptibility to symbol errors in the presence of noise, particularly for the 16-QAM symbols. For the 7 dB case, the constellation displays more distinct amplitude tiers. This configuration enhances the noise resilience and demodulation fidelity of the dominant QPSK signal. However, this gain is achieved at the expense of the 16-QAM signal’s performance, as its effective signal-to-noise ratio is substantially reduced, pushing it closer to the noise floor. After two branches of PDHM baseband signal through the dual polarization modulation process and fiber transmission, at the receiver side, chromatic dispersion (CD) compensation is conducted first. Then, multiple-input multiple-output (MIMO) processing is performed to separate signals with different polarization states and carrier phase recovery are carried out before the matched filter. Finally, the power de-multiplexing is implemented. In this paper, we compare the performance with different power de-multiplexing methods, including the traditional SIC, the proposed iterative SIC, and the LUT, respectively.

The receiver blocks are shown in Figure 1b,c. In Figure 1b, the solid line is the flow chart of the conventional SIC algorithm. It mainly consists of three steps, the first step is to estimate the channel response with a feed forward equalizer (FFE) and to demodulate the high power signal. For the first step, the lower power signal is treated as the noise. The received signal after chromatic dispersion compensation (CDC) and carrier phase recovery can be expressed as,

$$s_{rx}=s_{tx}+n\left(t\right)=p_1{\displaystyle \sum _n{a}_{n}g\left(t-n{T}_s\right)+p_2{\displaystyle \sum _n{b}_{n}g\left(t-n{T}_s\right)}}+n\left(t\right)$$

(2)

The three terms in Equation (2) are the high power QPSK signal, low power QAM-16 signal and channel noise $n\left(t\right)$. When using FFE to recover the QPSK signal, QAM-16 signal b_n is consider as noise. The next step is to reconstruct the received high power signal by multiplying the channel response to the ideal QPSK signal, and subtract the product from the received signal to obtain the lower power signal. Finally, repeating the FFE progress to recover the QAM-16 signal. Since the SIC treats the lower power signal as noise when estimating the channel response, it may be inaccurate to obtain the lower power signal by using the estimated channel response. Here, we propose an iterative SIC for better channel estimation and signal recovery. As shown in Figure 1b, the dashed line is the flow chart of the iterative SIC algorithm. After SIC, the recovered low power signal is re-modulated and distorted with the estimated channel response, which is then subtracted from the received signal to achieve the higher power signal with a better channel estimation. Finally, using the new channel response to perform the SIC progress. The corresponding signal is expressed as:

$${\widehat{s}}_{rx}=s_{tx}+n\left(t\right)-s_{rm}\left(t\right)$$

(3)

where $s_{rm}\left(t\right)$ is the remodulated QAM-16 signal, after obtaining the QPSK signal, the signal is fed into the FFE to recover the QPSK signal, thus completing one iteration.

The power de-multiplexing technique based on a look-up table (LUT) is illustrated in Figure 1c. This LUT serves as a reference for the receiver, listing the ideal signal constellations, and plays a crucial role in de-multiplexing the superimposed signals according to a pre-defined mapping relation. As shown in Figure 2, the PDHM signal is structured in such a way that it can be split into four distinct regions, each corresponding to a QAM-16 constellation within its respective quadrant. These quadrants are defined by their respective signal power and map the information to higher-order modulation schemes. The center points of each of the four quadrants can be treated as representative of the QPSK signals. In Figure 2, these central points are highlighted as the blue dots, which depict the QPSK components embedded within the PDHM signal. By extracting these central points, the QPSK signal is separated from the composite PDHM signal. After isolating the QPSK components, the next step involves recovering the low-power QAM-16 signal. This recovery process can be achieved using an equalization technique that compensates for signal distortion and interference that may occur during transmission. Following equalization, the QAM-16 signal is demodulated, allowing for the retrieval of the transmitted data. This process effectively separates and recovers the original modulated signals from the multiplexed PDHM format.

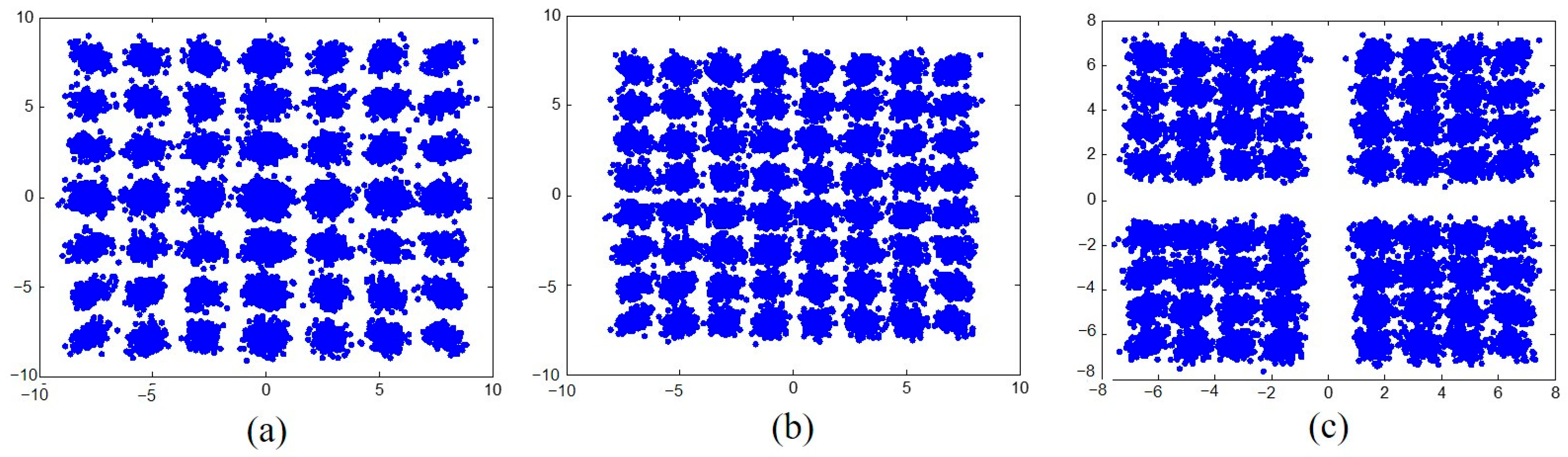
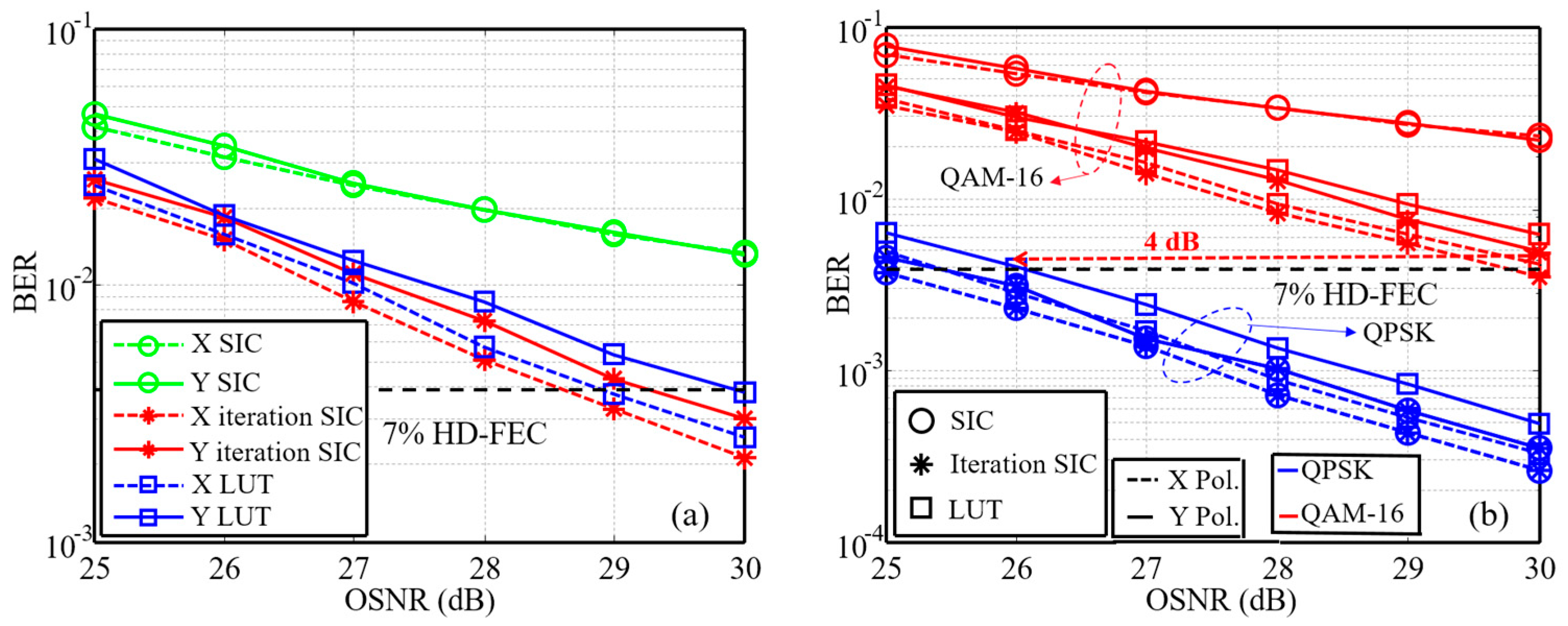
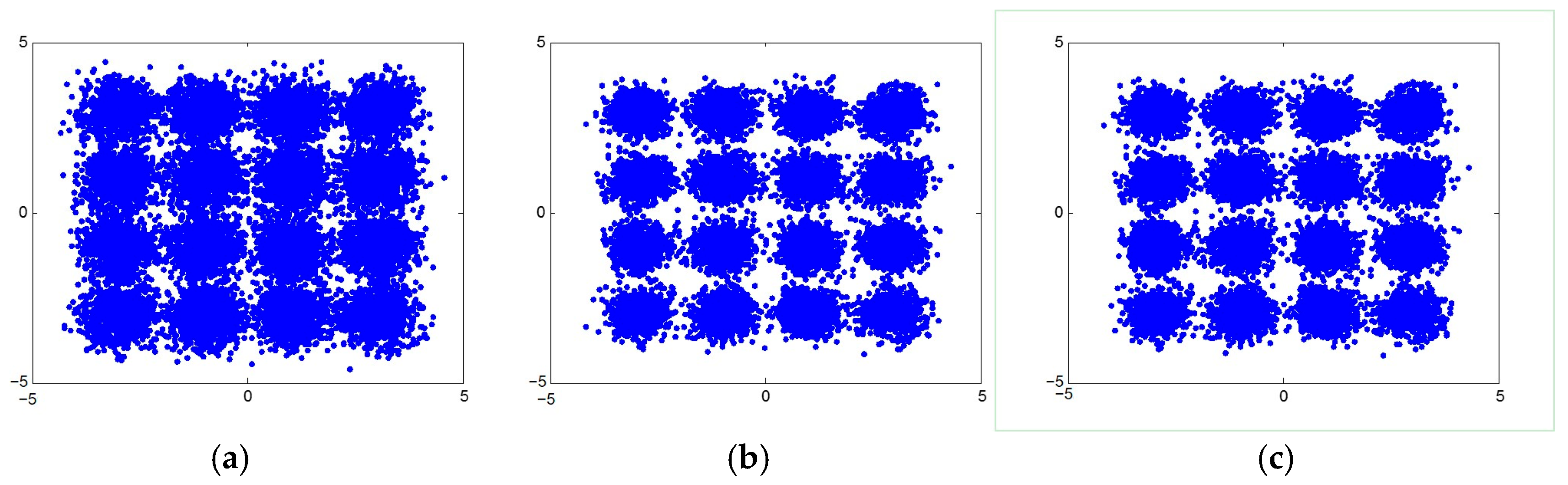
3. Demonstration and Results

To comprehensively evaluate the performance of the proposed PDHM scheme with iterative SIC, we conducted extensive simulations using the commercial software VPItransmissionMaker™ v9.1. The system architecture is illustrated in Figure 3. At the transmitter, the two independent PDHM signals are generated, each comprising a higher-power RRC-shaped QPSK stream and a lower-power 16-QAM stream. These composite PDHM signals are then modulated onto the orthogonal X and Y polarizations of the optical carrier, respectively. The aggregate symbol rate for the entire system is 28 Gbaud. The total achieved data rate is 336 Gb/s (2 × 4 × 28 + 2 × 2 × 28). The optical signals from both polarizations are subsequently combined using a polarization beam combiner (PBC). Prior to transmission, the combined signal is amplified by an Erbium-Doped Fiber Amplifier (EDFA) to adjust the launch optical power into the 80 km span of standard single-mode fiber (SSMF). At the receiver side, another EDFA is applied to compensate for the fiber loss. An optical band-pass filter (OBPF) is then employed to suppress out-of-band amplified spontaneous emission (ASE) noise before the signal is fed into a coherent receiver for detection. The receiver DSP mainly includes CDC, polarization demultiplexing, carrier frequency compensation, matching filtering and power demultiplexing. Note that, in SIC, a 13-tap feed-forward equalizer (FFE), trained using 2% of the total symbols is used for signal recovery. The reconstructed higher-power signal is then subtracted from the composite signal, allowing for the subsequent demodulation of the lower-power signal with minimal interference. To maintain a practical and computationally efficient receiver design, the SIC process is limited to a single iteration. This constraint is intentionally imposed to evaluate the scheme’s performance under low-complexity conditions, which is a critical consideration for real-world implementations. The simulation parameters are shown in

Table 1. The simulation configuration.

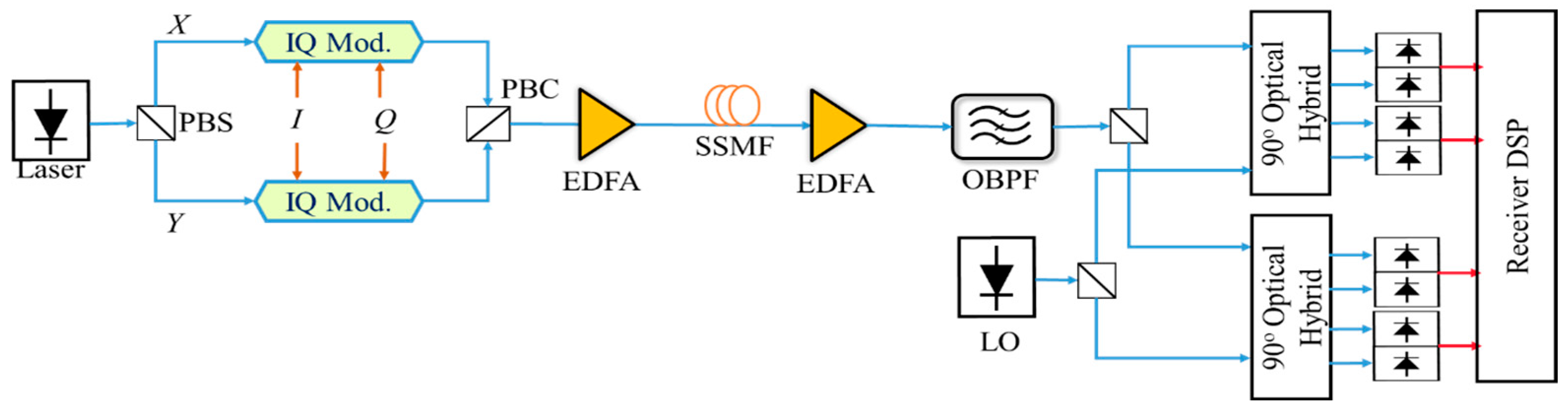
Fiber Length	80 km	Receiver Sensitivity	0.8 A/W
Fiber dispersion	16 ps/nm	Thermal noise	10.0 × 10−12 A/Hz1/2
Fiber nonlinear index	2.6 × 10−20 m2/W	Received optical power	−5 dBm
Polarization mode dispersion coefficient	0.1 × 10−12/31.62 s/sqrt(m)	LO power	0 dBm
Modulation formats	QPSK and 16QAM	CD compensation	Frequency compensation
Rx equalizer	13 taps FFE	RRC roll-off factor	0.01

.

We first evaluated the BER performances versus the PDR for the three considered demodulation techniques: the proposed iterative SIC, traditional SIC, and the LUT method. Figure 4a presents the average BER across both polarizations. The observed BER performances for the X and Y polarizations are nearly identical, validating the symmetry and stability of our PDHM system. The proposed iterative SIC receiver achieves its optimal performance at a PDR of 5 dB, yielding a BER below the 7% hard-decision forward error correction (HD-FEC) threshold of 3.8 × 10⁻³. At this optimal operating point, the iterative SIC scheme demonstrates a performance gain of approximately one order of magnitude in BER over the traditional SIC approach, since traditional SIC take low power signal as noise at, it exists error accumulation problem in low-power signal recovery, while iterative SIC can overcome the error accumulation via feedback to break this cycle. It also marginally outperforms the LUT-based scheme. While the SIC method inherently introduces additional computational complexity and processing latency compared to a direct LUT, it offers a significant advantage in its robustness against dynamic link impairments, a crucial characteristic for practical system deployment. Figure 4b depicts the individual BER performances of the QPSK and 16-QAM sub-signals within each polarization for different PDRs, respectively. As the PDR increases, the QPSK signal has better performance, while the BER of the QAM-16 signal exhibits a valley shape. It can be explained by the constellations of the received signal, as shown in Figure 5. When the PDR is small, such as 3 dB, signifies that the power of the QPSK is twice of the 16-QAM, the QAM16 signal becomes overplayed at the boundary of each quadrant, making it difficult to distinguish. With the increasing PDR, the overlapped part is diminished gradually. While the QAM-16 signal will suffer from high noise when the PDR is increased. For instance, when the PDR is 7 dB, the PDHM signal has a large peak-to-peak level. To avoid the nonlinearity interference of the modulator, the amplitude of the driving signal should be reduced; thus, the PDHM signal with a higher PDR will suffer from low SNRs.

To better understand the performance of the iterative SIC, the average BER performance of the iterative SIC is analyzed as a function of the iteration count at 29 dB OSNR. As shown in Figure 6, after one iteration, the BER performance has significantly improved. When the number of iterations exceeds two, the performance begun to plateaus. To balance the complexity and performance, a single iteration is recommended.

To further evaluate the performance, we measured the BER performance of both the QPSK and 16-QAM signals as a function of the OSNR with the PDR fixed at 5 dB. As shown in Figure 7a, the average BER of both X and Y polarizations can reach 7% HD-FEC limit with ~29 dB OSNRs for iterative SIC, which represents a 0.5 dB improvement in required OSNR compared to the LUT-based scheme, a gain that translates directly into enhanced power budget or extended transmission reach for a practical system. Meanwhile, as shown in Figure 7b, for the proposed iterative SIC technique, the lower power QAM-16 signal requires approximately 4 dB higher OSNR to achieve the same BER compared to the QPSK signal. The LUT-based scheme consistently performs slightly worse than the iterative SIC. This is because its architecture inherently lacks a feedback mechanism for equalization during the 16-QAM demodulation process. Consequently, the noise and distortions from the unresolved QPSK signal are not effectively canceled and transferred to the 16-QAM signal during the demultiplexing process, thereby degrading its BER performance. Figure 8 shows the constellations of the QAM-16 signal for SIC, iterative SIC, and LUT, respectively. For the SIC case the 16-QAM constellation exhibits significant dispersion. This results from an imperfect initial channel estimate, which is corrupted by the strong, un-canceled interference from the QPSK signal; For the iterative SIC case the 16-QAM constellation points are markedly tighter and more clearly defined. The iterative refinement allows for a more accurate recovery and reconstruction of the QPSK signal. This precision in the first stage enables a cleaner cancelation of the QPSK interference, thereby providing a purer signal for the final 16-QAM demodulation. This establishes a direct causal link: the fidelity of the final 16-QAM signal is critically dependent on the accuracy of the preliminary QPSK signal restoration; For the LUT case the constellation quality is intermediate, consistent with its static, non-iterative nature, which lacks the dynamic interference removed capability of the SIC-based approaches.

Based on the above results and analysis, a comprehensive comparison is conducted to evaluate the proposed iterative SIC technique against the LUT benchmark. The key performance and implementation metrics are summarized in

Table 2. Comparative analysis: iterative SIC vs. LUT technique.

Characteristics	Iterative SIC	LUT
Complexity	based on FFE	based on the modulation order
Feasibility	high, applicable to existing DSP-compatible systems	low, especially for high-order modulation signals.
Robustness to signal distortion	high, adaptive update	low, sensitive to dynamic changes
Performance	preferred	inferior

. Meanwhile, the FFE used in SIC or iterative SIC has 13 taps, that means 13 complex multiplications and 12 additions are required in each FFE without considering the coefficients updating process. A quantitative complexity analysis of iterative SIC relative to the standard SIC is shown in

Table 3. Quantitative complexity analysis of iterative SIC.

Description	Iteration SIC	Standard SIC
Taps number of one FFE	13	13
Number of iterations	1	0
Total number of FFE	4	2
Total number of complex multiplications	52	26
Total number of complex additions	48	24

.

4. Conclusions

In this paper, we have proposed and demonstrated an iterative SIC algorithm for a PDHM system. The system integrates a Nyquist-shaped 16-QAM signal with a QPSK signal, multiplexed in the power domain, within a coherent optical transmission system. A comprehensive analysis of different power demultiplexing methodologies is provided, establishing the comparative advantage of our iterative approach. Through validation, we successfully transmitted a 336 Gb/s signal over 80 km of SSMF. The iterative SIC receiver proved highly effective, recovering both signal layers and achieving BER below the 7% HD-FEC threshold. This work not only validates the feasibility of PDHM as a robust technique for significant capacity enhancement but also demonstrates a flexible and selectable strategy for future optical networks, paving the way for efficient resource allocation tailored to diverse service requirements.