Enhanced Optical Wireless Communications via Deep Neural Network Assisted Pre-Equalization for Faster-than-Nyquist Transmission

Abstract

The Faster-than-Nyquist (FTN) technology is widely used in optical wireless communication (OWC) systems to improve data rates and spectrum efficiency. However, it introduces inter-symbol interference (ISI), which can affect communication reliability. To address this issue, we propose a pre-equalization algorithm based on a deep neural network (DNN). The performance analysis primarily focuses on the bit-error-rate (BER) under a Gamma-Gamma atmospheric turbulence channel with varying acceleration factors. Simulation results show that our scheme effectively reduces the degradation in BER caused by ISI. Additionally, we observe an inverse relationship between the BER performance and the atmospheric refractive index constants as well as transmission distance, while a direct proportionality exists with respect to the filter roll-off factor and laser wavelength. Furthermore, comparing with conventional minimum mean square error (MMSE) and zero-forcing (ZF) algorithms highlights the superior performance of our proposal.

1. Introduction

The current communication system is facing significant challenges in meeting the demand for extensive data transmission [1,2]. Therefore, there is an urgent need to enhance both the transmission rate and spectral efficiency [3]. Recently, Faster-than-Nyquist (FTN) technology has regained attention as a promising solution to surpass Shannon’s theory limitations and achieve higher data rates [4,5]. Differing from conventional time-orthogonal systems, FTN compresses symbol intervals at the Nyquist rate while improving spectral efficiency without requiring additional bandwidth [6].

In optical wireless communications (OWC), high baud-rate FTN signals are widely utilized due to their resilience against high-frequency distortions. However, this approach presents challenges such as increased bit-error-rate (BER) and computational complexity at the receiver. While advancements in computing capability have mitigated concerns regarding computational complexity, enhancing reliability remains a fundamental consideration. Considering that employing an equalizer at the receiver end does not completely eliminate inter-symbol interference (ISI) introduced by FTN [7,8,9], research focus has shifted towards the transmitter with the aim of completely eliminating ISI using pre-equalization techniques. For example, Cao et al. [10] propose a point-by-point elimination adaptive pre-equalization algorithm that increases computational complexity but offers higher spectral efficiency and improved BER performance. Jana et al. [11] proposed two pre-equalization schemes to replace complex equalization algorithms in the receiver. These schemes enable the system to provide high spectral efficiency while maintaining optimal BER performance. And on this basis, Wen S. [12] introduced linear spectral precoding into FTN systems to mitigate signal spectrum widening by composite precoding.

On the other hand, deep learning (DL) has been extensively applied in wireless communications [13,14,15,16,17,18] due to its robust learning capabilities. DL-based approaches have gained significant popularity for enhancing the performance of FTN systems. For instance, in [19], a joint FTN signal detection algorithm that combines data-driven and model-driven approaches is proposed. By integrating a conventional channel equalizer with a neural network, the algorithm effectively mitigates ISI in FTN signals. In [20], the authors propose a DL-based method for estimating the symbol packing ratio of FTN signals, enabling an adaptive group ratio-based transmission without the need for a dedicated channel or control frame. A long short-term memory (LSTM) network-based algorithm is proposed in [21] to mitigate continuous ISI among neighboring signals. In [22], the authors proposed a DL-based signal detection method to improve signal recovery accuracy. Motivated by compensating for BER performance degradation using DL neural networks, we present a DL-based pre-equalization algorithm for the FTN-OWC system. By leveraging a deep neural network (DNN), nonlinear mappings within systems can be learned to alleviate ISI under Gamma-Gamma fading channels and enhance the reliability of FTN-OWC systems.

The rest of the paper is organized as follows: Section 1 provides a brief introduction to the study’s background and significance; Section 2 introduces DL-assisted pre-equalization for FTN-OWC system model; Section 3 depicts the proposed pre-equalization scheme and the training and application process of the pre-equalization neural network; Section 4 presents the simulation results and analysis; and finally, the paper concludes with a summary.

2. System Model

The schematic in Figure 1 illustrates the DL-assisted pre-equalization scheme for the FTN-OWC system. Initially, user data is modulated into on-off keying (OOK) and then shaped through FTN filtering before being input to the trained pre-equalization neural network. By processing with the network, almost complete elimination of ISI in the data is achieved. The processed signal is subsequently converted from digital to analog (DAC) and transmitted through the atmospheric channel. At the receiver end, optical signals are received and converted into electrical signals by optical antennas, which are then subjected to analog-to-digital conversion (ADC), matched filtering, and sampling processes. Finally, the signal undergoes OOK demodulation for data recovery.

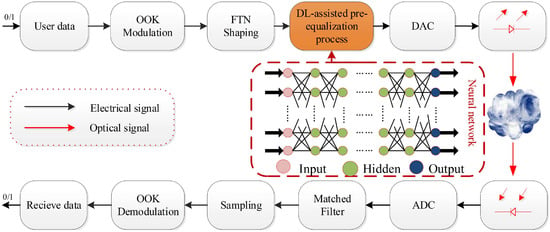
Figure 1. DL-assisted pre-equalization neural network for FTN-OWC system.

The OOK signal formed by the FTN shaping filter can be expressed as

$$S_{FTN}\left(t\right)=\sqrt{E\tau /2}{\displaystyle \sum _n{a}_{n}r\left(t-n\tau T\right)}$$

(1)

where $E$ is the pulse power, $r(\cdot )$ is the pulse shape of FTN, $\tau$ is the acceleration factor ($0<\tau <1$) that compresses adjacent pulses to break the Nyquist rate [23], $a_n$ is the data sequence, and $T$ is the symbol period.

After the implementation of the DL-assisted pre-equalization and DAC process, the transmitted signal through the atmospheric channel can be expressed as

$$S_{DL-OP}=\sqrt{P_{OC}}\cdot S_{DL}\cdot \exp \left[-\left({\omega }_{oc}t+{\varphi }_{oc}\right)\right]$$

(2)

where $P_{OC}$ is the average emitted laser power; ${\omega }_{oc}$ is the laser frequency; ${\varphi }_{oc}$ is the initial signal phase; and $S_{DL}$ is the signal after the DL-assisted pre-equalization process.

After traversing the atmospheric channel, the received signal can be expressed as

$$S_{RT}\left(t\right)=h\cdot S_{DL-OP}+n(t)$$

(3)

where $n(t)$ denotes the channel additive noise and $h$ denotes the channel fading coefficient which follows the Gamma-Gamma distribution. The probability density of the Gamma-Gamma channel can be expressed as [24]

$$\phi \left(h\right)={\displaystyle \frac{2{(\alpha \beta )}^{\frac{\alpha +\beta }{2}}}{\mathsf{\Gamma }(\alpha )\mathsf{\Gamma }(\beta )}}\cdot h^{{\displaystyle \frac{\alpha +\beta }{2}}-1}\cdot k_{\alpha -\beta }(2\sqrt{\alpha \beta h}), h>0$$

(4)

where $\mathsf{\Gamma }\left(·\right)$ denotes the Gamma function; $k_{\alpha -\beta }$ denotes the order of second class modified Bessel function; and $\alpha$ and $\beta$ denote the large and small scale scattering coefficient, respectively. $\alpha$ and $\beta$ can be, respectively, expressed as

$$\alpha ={\left\{\exp \left[{\displaystyle \frac{0.49{\sigma }^2}{(1+1.11{\sigma }^{12/5}{)}^{7/6}}}\right]-1\right\}}^{-1}$$

(5)

$$\beta ={\left\{\exp \left[{\displaystyle \frac{0.51{\sigma }^2}{(1+0.69{\sigma }^{12/5}{)}^{7/6}}}\right]-1\right\}}^{-1}$$

(6)

where ${\sigma }^2$ denotes the Rytov variance, ${\sigma }^2=1.23C_n^2{k}^{7/6}{L}^{11/6}$, $C_{\mathrm{n}}^2$ denotes the atmospheric refractive index structure constant, $L$ denotes the transmission distance, $k=2\pi /\lambda$, and $\lambda$ denotes the wavelength.

The received signal is subjected to ADC after passing through the matched filter, and its resulting output can be expressed as follows:

$$S_O={\displaystyle {\int }_{-\infty }^{+\infty }{S}_{RT}(t)\cdot r(t-n\tau T)}dt$$

(7)

The signal can be directly transmitted for hard decision. The decision rules are as follows:

$$\left\{\begin{array}{l}{S}_o>\delta output=1\\ S_o<\delta output=0\end{array}\right.$$

(8)

where $\delta$ denotes the decision threshold.

3. Pre-Equalization Algorithm

3.1. Proposed DNN-Assisted Pre-Equalization Algorithm

Building upon the second section, Figure 2 presents an overview of the proposed DNN-based pre-equalization scheme, which aims to eliminate the ISI induced by FTN. The neural network employed in this scheme is a fully connected DNN with six layers: one input layer, four hidden layers, and one output layer. The primary function of the input layer is to receive initial input data and transmit it to the network for processing. The hidden layers are pivotal in learning and extracting features from the input data. As the final layer of the DNN, the output layer is tasked with generating predictions or outputs based on the processed input data. These layers are interconnected, and their connection weights are learned through the training process, continuously adjusting the connection weights to achieve accurate processing and prediction of the input data. Furthermore, each complete hidden layer consists of a fully connected sublayer and a rectified linear unit (ReLU). The number of neurons initially increases and then decreases following the sequence M, 20, 40, 50, 20, N (where M and N represent the number of windows for input and the number of windows for output, respectively). The output layer solely contains an FC sublayer.

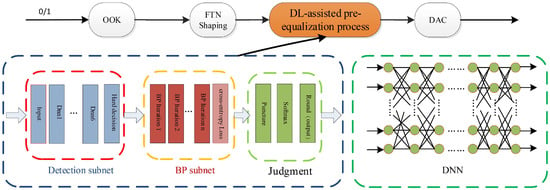
Figure 2. Pre-equalization neural network.

Figure 2 illustrates that the pre-equalization algorithm incorporates three distinct structures: the detection subnet, the backpropagation (BP) subnet, and the judgment subnet. The detection subnet is responsible for detecting data reaching the neural network and performing layer-by-layer operations to assess the signal significance. The BP subnet utilizes error backpropagation iterations to update parameters within the neural network, specifically neuron weights. The judgment subnet employs SoftMax function as an activation function at its output layer, enabling accurate judgments through probabilistic adjudication by classifying the signals from the BP subnet. The SoftMax function, serving as an activation function, uses probabilistic adjudication at the output layer to generate 0/1 signals, thus making accurate judgments.

Mathematically, the SoftMax function can be expressed as follows:

$$S_i={\displaystyle \frac{e^{V_i}}{{\displaystyle {\sum }_k^K{e}^{V_k}}}}$$

(9)

where $V$ denotes the set of output node values, $V_i$ and $V_k$ denote the i-th and k-th elements in $V$, $e$ is the natural constant, $K$ indicates the number of output nodes. Additionally, $S_i$ denotes the output of SoftMax while ${\displaystyle {\sum }_k^K{e}^{V_k}}$ denotes the sum of all values. It should be emphasized that $S_i$ also serves as a probability and acts as a judgment signal for DNN based on its value. For instance, when the probability of $S_0$ exceeds that of $S_1$, signal 0 will be assigned.

3.2. The Process of Training and Application

The training and application process of the pre-equalization neural network is depicted in Figure 3. Firstly, the pre-equalization neural network undergoes offline training on the FTN signal. This process includes labeling the FTN signals and feeding the prepared labels and FTN signals into the network for computation, until convergence of the loss function is achieved. Subsequently, the network parameters are saved. Once the network parameters are saved, the OOK-FTN signal can be fed into the network to eliminate the interference and recover the OOK signal. During online recovery, the OOK-FTN signal can be directly fed into the pre-equalization network to mitigate ISI and route the processed signal to the output layer.

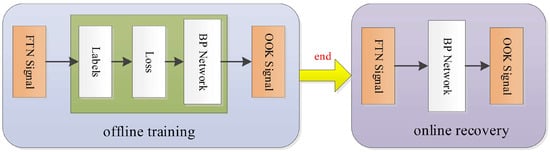
Figure 3. Offline training and online recovery.

The concrete FTN-ISI elimination process is illustrated in Figure 4. FTN signals are typically affected by the trailing from preceding and succeeding symbols, resulting in ISI. As shown in Figure 4, the input FTN signals, referred to as “symbols” are distorted by this trailing effect, leading to the appearance of “ISI” at both ends of the signal. In this case, the FTN signals are directly fed into the DL-based pre-equalization network to obtain the estimated output. For a well-trained pre-equalization network, the corrupted FTN signal can be used as input to recover the clean signal with ISI effectively mitigated.

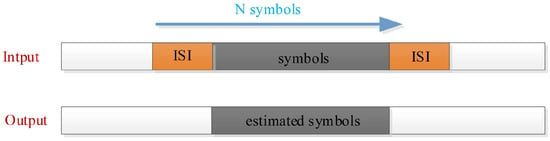
Figure 4. FTN-ISI elimination process.

4. Simulation and Analysis

To validate the effectiveness of the proposed DL-assisted pre-equalization scheme, we perform simulations to demonstrate its performance under various conditions, such as different acceleration factors, atmospheric turbulence intensity, and filter roll-off factors.

The proposed DL-assisted pre-equalization network is implemented in Python 3.8 using Keras, with TensorFlow serving as a backend for tensor operations. The training and test datasets are randomly generated in MATLAB, and each dataset consists of a specified number of symbols. The learning rate is set to 0.001, while the loss function employed is Cross Entropy Loss, and the optimizer utilized is stochastic gradient descent (SGD). The FTN signal is generated through OOK modulation and a root rising cosine (RRC) pulse-shaped filter. Otherwise, the up-sampling rate is 10 and the truncated RRC pulse length is 6. The photoelectric conversion efficiency is set to 0.5, and the receiver aperture diameter is set to 20 mm. More simulation parameter setting details are listed in Table 1.

Table 1. Simulation parameters.

Parameter	Value
size of data	2.0 × 106
training dataset	1.4 × 106
test dataset	6 × 105
epoch	80
batch size	100
learning rate	0.001
SNR range	0 dB–35 dB
optimizer	SGD
loss function	Cross Entropy Loss
activation function	SoftMax
layer	6
hidden neurons	20-40-50-20

The BER curves for different FTN shaping filter roll-off factors are depicted in Figure 5, under weak turbulence conditions with $\tau$ set to 0.8. The roll-off factor serves as a characterization of the trailing effect on the waveform and exhibits an inverse correlation with this phenomenon. Trailing effect results in ISI with adjacent signals, leading to increased noise levels, particularly after FTN is introduced. The figure clearly illustrates that the proposed DL-assisted scheme achieves significant improvements in BER performance, with enhancements of 3 dB, 4 dB, 7.3 dB, and 7 dB at BER = 10⁻³ for roll-off factors of 0.9, 0.7, 0.5, and 0.3, respectively, relative to the conventional system. It can be concluded that the DL-assisted pre-equalization scheme exhibits strong computing capability in mitigating signal trailing effects.

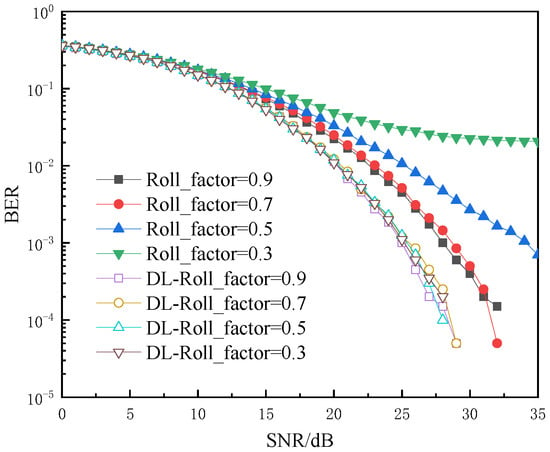
Figure 5. The influence of roll-off factors on BER.

Furthermore, the BER performance of our proposal remains almost unaffected by changes in the roll-off factor. It is evident from the figure that reducing the roll-off factor from 0.9 to 0.5 only leads to a marginal loss of 1 dB in performance. Conversely, without DL-assisted pre-equalization, there is a substantial degradation in BER performance, which fails to meet minimum communication requirements regarding BER values when the roll-off factor reaches 0.3.

The BER performance comparison in Figure 6 illustrates the impact of different atmospheric refractive index constants (${\mathrm{C}}_n^2$) on the system. It is well-known that atmospheric turbulence can significantly impact the performance of light propagation through the air. Notably, a higher refractive index constant indicates stronger turbulence, as clearly observed in Figure 6. When the BER is 10⁻³ and $\tau$ is set to 0.8, it is observed that the DL-assisted pre-equalization scheme significantly improves the BER performance by approximately 4.5 dB, 2 dB, and 2.3 dB as the atmospheric refractive index constants increase compared to the conventional system. This indicates that our proposal exhibits favorable anti-noise capability when encountering significant atmospheric turbulence.

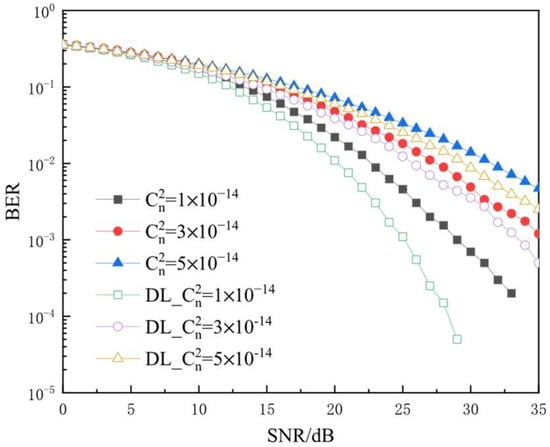
Figure 6. The BER at different atmospheric refractive index constants.

The BER curves in Figure 7 demonstrate the BER performance with different laser wavelengths under weak turbulence conditions with $\tau$ set to 0.8. It is evident that the BER performance of communication improves with increasing laser wavelength. Specifically, when BER = 10⁻³, employing the DL-assisted pre-equalization scheme with laser wavelengths at 1550 nm, 850 nm, 780 nm, and 675 nm results in BER performance enhancements of 4 dB, 4 dB, 3 dB, and 1.5 dB, respectively, compared to the conventional system. This observation highlights the favorable impact of longer laser wavelengths on the overall BER performance in the OWC system.

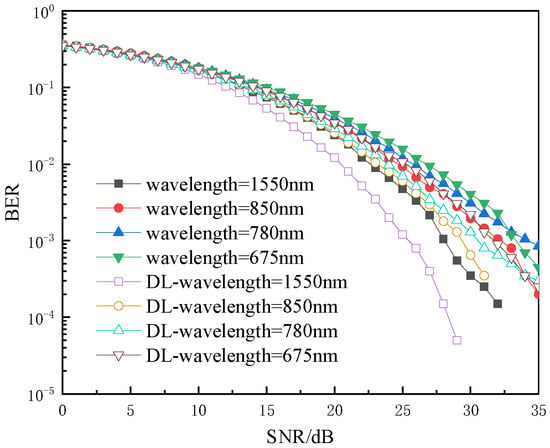
Figure 7. The influence of wavelength on BER.

The relationship between BER and transmission distance (TD) under weak turbulence conditions with $\tau$ set to 0.8 is illustrated in Figure 8. As the transmission distance increases, the laser energy decreases. It is evident that the BER performance exhibits an inverse proportionality to the transmission distance. Furthermore, our proposal demonstrates an approximate improvement of 4 to 5 dB in BER performance at the same transmission distance. Consequently, maintaining the desired BER performance will also extend the achievable transmission distance. This observation highlights the effectiveness of our proposal in enhancing the reliability and extending the reach of the OWC system.

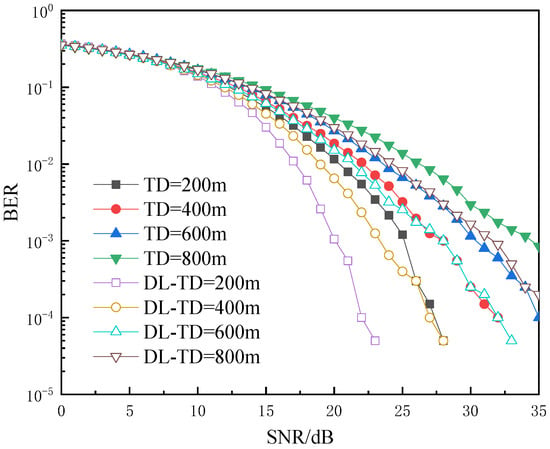
Figure 8. BER at different transmission distances.

The comparison of BER performance with and without the proposed method under weak turbulence conditions and different acceleration factors is illustrated in Figure 9. It can be observed from the figure that our proposal demonstrates greater superiority. As depicted in Figure 9a, when the BER is 10⁻⁴ and $\tau$ is set to 0.9, the DL-based algorithm outperforms the MMSE and ZF algorithms by a margin of 2 dB and 4 dB, respectively. In Figure 9b, when the BER is 10⁻³ and $\tau$ is set to 0.8, the DL-based algorithm exhibits an improvement in performance by approximately 2.9 dB compared to MMSE and an impressive enhancement of approximately 11.5 dB over the ZF algorithm’s performance level. Notably, as the acceleration factors decrease to values such as 0.7 and 0.6, both MMSE and ZF algorithms fail to optimize signal quality sufficiently to meet communication requirements effectively. In contrast, our proposed DL-assisted pre-equalization scheme provides reliable BER performance even when the system has severe interference.

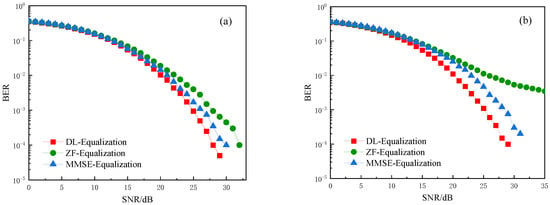
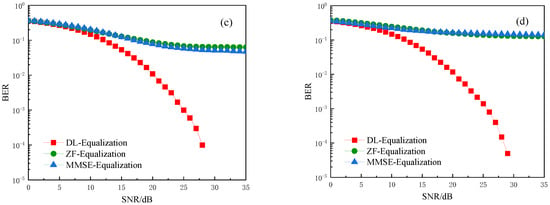
Figure 9. The BER curves with/without our proposal. (a) $\tau =0.9$; (b) $\tau =0.8$; (c) $\tau =0.7$; (d) $\tau =0.6$.

The impact of acceleration factors on the BER performance of the proposed pre-equalization algorithm under weak turbulence conditions is illustrated in Figure 10. With an SNR set at 25 dB, when $\tau$ exceeds 0.6, the proposed algorithm maintains a nearly stable performance. However, if $\tau$ drops below 0.6, the proposed algorithm becomes inadequate in eliminating ISI and results in a significant decline in performance. In FTN transmission, the acceleration factor $\tau$ fundamentally determines the extent of symbol interval compression: the smaller the value of $\tau$, the narrower the symbol interval, and the more severe the resulting ISI. When $\tau <0.6$, the symbol interval is significantly compressed, leading to multi-symbol overlapping interference characterized by substantially increased complexity. The proposed DNN-based algorithm is unable to effectively capture the interference features arising from such multi-symbol overlap, thereby experiencing a marked degradation in ISI mitigation capability and, consequently, a sharp deterioration in BER. This underscores the importance of appropriately selecting the acceleration factor to ensure optimal system operation.

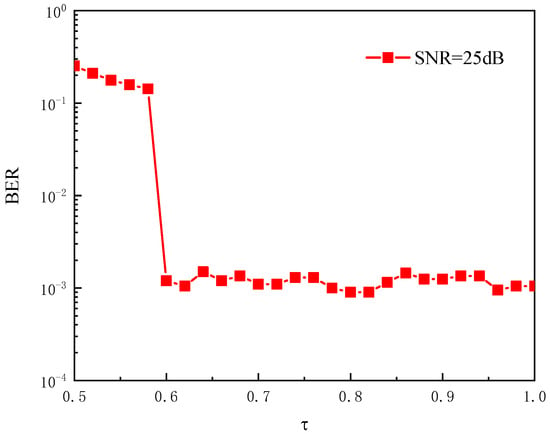
Figure 10. The BER curves with different acceleration factor $\tau$.

5. Conclusions

We propose a DNN-based pre-equalization algorithm for FTN-OWC systems to mitigate the ISI caused by FTN, leveraging the powerful capabilities of DNN. Simulation results demonstrate that the proposed method achieves performance gains of 2.9 dB and 11.5 dB compared to the conventional MMSE and ZF algorithms, respectively. This approach provides an effective solution for enabling more efficient and reliable OWC systems. The applicability of the algorithm will be further validated under complex scenarios, including dynamic channel conditions and sudden interference scenarios. Additionally, future work will focus on the development of hardware platforms for the relevant DL-based techniques to enhance the technical feasibility of practical implementation in communication systems.