Experimental Demonstration of High-Security and Low-CSPR Single-Sideband Transmission System Based on 3D Lorenz Chaotic Encryption

Abstract

Broadcast-style downlinks (e.g., PONs and satellites) expose physical waveforms despite transport-layer cryptography, motivating physical-layer encryption (PLE). Digital chaotic encryption is appealing for its noise-like spectra, sensitivity, and DSP-friendly implementation, but in low-CSPR KK-SSB systems, common embeddings disrupt minimum-phase requirements and raise PAPR/SSBI near 1 dB CSPR, while finite-precision effects can leak correlation after KK reconstruction. We bridge this gap by integrating 3D Lorenz-based PLE into our low-CSPR KK-SSB receiver. A KK-compatible embedding applies a Lorenz-driven XOR mapping to I/Q bitstreams before PAM4-to-16QAM modulation, preserving the minimum phase and avoiding spectral zeros. Co-design of chaotic strength and subband usage with the KK SSBI-suppression method maintains SSBI mitigation with negligible PAPR growth. We further adopt digitization settings and fractional-digit-parity-based key derivation to suppress short periods and remove key-revealing synchronization cues. Experiments demonstrate a 10⁹¹ key space without degrading transmission quality, enabling secure, key-concealed operation on shared downlinks and offering a practical path for chaotic PLE in near-minimum-CSPR SSB systems.

1. Introduction

With the rapid growth of multimodal communication, security is especially challenging in broadcast-style architectures where many receivers observe the same downlink (e.g., PONs and satellite group broadcasting) [1,2,3]. Transport-layer cryptography protects packets end-to-end but does not conceal the physical waveform or prevent signal-level interception. This motivates physical-layer encryption (PLE), which embeds confidentiality at signal generation and propagation and is inherently aligned with shared downlinks [4,5,6].

Within PLE, digital chaotic encryption is compelling: it leverages deterministic dynamical systems (e.g., Lorenz and hyperchaos) exhibiting pseudo-random behavior, strong parameter/initial-condition sensitivity, and broadband noise-like spectra to realize key-controlled masking, scrambling, or modulation mapping [7]. It offers (i) large key spaces that raise brute-force complexity; (ii) noise-like outputs that hinder interception and traffic analysis; (iii) DSP-friendly, low-cost implementations without specialized hardware; and (iv) compatibility with OFDM, FBMC/OQAM, and SSB/KK with modest adjustments. Practical deployment requires careful model selection and digitization to avoid short-period degradation, robust key management under known-/chosen-plaintext adversaries, embeddings co-designed for PAPR/BER/equalizer stability, synchronization aids that do not leak keys, and joint PHY processing [8].

In 2022, we proposed a low-carrier signal power ratio (CSPR) KK receiver that effectively eliminates SSBI [9], enabling single-sideband demodulation when the CSPR is close to 1 dB and attracting widespread attention. Yet most digital chaotic encryption schemes cannot be directly transplanted into low-CSPR KK-SSB systems despite their favorable secrecy properties. The main obstacles are that common chaotic embeddings—such as additive masking, symbol remapping, or amplitude/phase scrambling—tend to perturb the minimum-phase condition required by KK phase retrieval and thereby aggravate phase reconstruction errors; in addition, the induced envelope fluctuations and intermodulation components elevate PAPR and exacerbate SSBI at a low CSPR, undermining KK’s SSBI immunity. Conventional synchronization and key-aided training can also leave identifiable side features on shared downlinks, risking exposure of key structures, while finite-precision digitization of chaotic maps may introduce short-period artifacts that, after KK reconstruction, leak correlation and facilitate traffic analysis or known-/chosen-plaintext attacks. Together, these factors have impeded the use of chaotic PLE in KK-based SSB systems operating near the lowest CSPR regime.

In this work, we bridge this gap by integrating a 3D Lorenz-based PLE scheme into our previously proposed low-CSPR KK SSB system. We design a KK-compatible embedding that applies Lorenz-driven key generation to the I/Q streams via lightweight XOR mapping before PAM4-to-16QAM modulation, thereby preserving the signal’s minimum-phase property and avoiding spectral zeros detrimental to KK invertibility. We further co-design the chaotic strength and subband usage with the low-CSPR KK SSBI-suppression method in [10] to keep SSBI mitigation effective while keeping PAPR growth negligible. In parallel, we adopt digitization settings and a fractional-digit-parity-based key derivation that suppress short-period effects and eliminate key-revealing synchronization cues, enabling secure deployment in broadcast-style downlinks. Experimental demonstrations show that the scheme achieves a key space of 10⁹¹ without degrading transmission quality, ensuring that illegal users cannot crack the correct key in a short time and providing a secure transmission solution for further research and application of this single-sideband communication system.

2. Related Works

Currently, many scholars have proposed different chaotic encryption schemes for PONs. Liu, Zhao et al. proposed a 4D chaotic encryption scheme for orthogonal frequency division multiplexing (OFDM)–PON systems [11]; Liu, Ren et al. proposed a physical-layer encryption scheme based on a 4D hyperchaotic system for probabilistic shaping OFDM-PON systems [12]; Tang, Ren et al. proposed a filter-bank multicarrier/offset quadrature amplitude modulation (FBMC/OQAM) physical-layer encrypted transmission system based on chaotic encryption [13]. Wang, Zhiyi et al. proposed a PS-based constellation encryption system for OFDM–RoF. Hyperchaotic sequences and SHA–512 hashes drive two bit-level encryption steps. Probabilistic shaping is then applied using PS–16QAM. A constellation encryption stage maintains the shaping distribution while improving security. The encrypted signal was transmitted over a 50 km SSMF and a 5 m wireless link. The scheme achieves a key space of 10¹²¹, resisting brute-force attacks. It also provides a ~2.4 dB SNR gain at BER = 10⁻³ versus conventional OFDM [14]. Liu, L. et al. proposed a physical-layer encryption system for CO–OFDM based on disturbing data clusters via a color--seeking chaotic mechanism. The chaotic sequence is generated from key-driven Brownian motion, labeled with two primary colors, and reordered through sorting and seeking. Data disturbance follows this color-seeking process, and PAPR is optimized simultaneously. The scheme provides a key space of 10⁹⁰ and reduces PAPR by about 0.5 dB. In a 40 GHz 16QAM CO–OFDM system over an 80 km SSMF, authorized users decrypt successfully, while eavesdroppers see BER ≈ 0.5 [15]. Li, Y. et al. proposed a camera projection-based physical-layer encryption system for CO–OFDM. A camera projection module maps data to new positions and is driven by keys from a 5D hyperchaotic system. In a simulated 16QAM CO–OFDM over an 80 km SSMF, the scheme yields a key space of about 9 × 10⁹⁰, thwarting eavesdroppers. It also reduces PAPR by ~0.8 dB [16]. Chen, Q. et al. proposed dual chaotic encryption for OTFS–IM, securing both index and data bits. They also introduced a PAPR-optimized encryption system using random interleaved partitioning time segmentation (RIPTS) to lower autocorrelation and ICI. In B2B and 80 km SSMF PON tests, RIPTS improves PAPR by 4.3 dB over no optimization and by 0.8/0.6/0.5 dB over PTS/IPTS/RPTS, respectively. The dual-chaos system uses six parameters, yielding a key space up to 10⁹⁰ [17]. Wang, Zhang et al. proposed an efficient data security enhancement scheme for NOMA-PON, addressing primary-user interference and third-party eavesdropping by combining a fixed-point extended logistic chaotic map with a cascaded 2D cellular automata–Turing pattern scrambling (CA-TPCS) algorithm. The method uses FE chaos to construct 2D-CA for dynamic bit diffusion, extracts a Turing symbol substitution matrix via index sorting for 2D symbol scrambling, and employs a dual-key mechanism with uplink data as a private key [18]. Wang, Pan et al. proposed a 4D chaotic IM encryption system for CO-OFDM-PON, combining a 1D cubic map and a 3D T–S fuzzy chaotic system to generate four dynamic scrambling factors that secure index bits, data bits, intra-subcarrier blocks, and inter-subcarrier blocks. The design builds a chaotic many-to-many mapping between index bits and SAPs for index-bit encryption, as well as heterodynes data bits with chaotic bits for data encryption, and applies a chaotic shuffling algorithm to rearrange symbols within and across subcarrier blocks for secondary OFDM-IM encryption [19]. As shown in Table 1, we list and compare representative chaotic PLE schemes, highlighting the PAPR impact, BER/sensitivity performance, and implementation complexity.

Table 1. Comparative analysis of chaotic physical-layer encryption schemes in terms of PAPR impact, BER/sensitivity performance, and implementation complexity.

Scheme	PAPR Impact	BER/Sensitivity Performance	Complexity
This work: 3D Lorenz + low-CSPR KK-SSB	Negligible increase vs. non-encrypted baseline	B2B and 25 km: BER nearly overlaps non-encrypted for legitimate key; wrong/unknown keys >> HD-FEC	Low (fixed-point Lorenz + bitwise XOR; no PS/PTS/block shuffling)
4D hyperchaos + dimension coordination (Zhao et al., Optics Express 2020) [11]	Discussed, no explicit Δ reported	~1 dB sensitivity gain vs. uniform 16QAM-OFDM	Medium–high (4D factors + PS + coordination)
Chaotic-CCDM PS (Ren et al., Optics Express 2020) [12]	Not reported	~1.2 dB sensitivity improvement at BER = 1 × 10−3 vs. uniform	Medium (CCDM mapping/inverse)
PS-based constellation encryption (Wang et al., Optics Express 2021) [14]	Not reported	Focus on security/feasibility; key space ~10121	Medium (PS pipeline + encryption)
Color-seeking chaotic cluster disturbance (Liu et al., JLT 2023) [15]	PAPR ↓ ~0.5 dB	Sensitivity not reported (illegal BER ~0.5 shown)	Medium (clustering/sorting + search)
Camera-projection scrambler + 5D hyperchaos (Li et al., Mathematics 2024, sim.) [16]	PAPR ↓ ~0.8 dB	Mainly security and simulation feasibility	Medium–high (projection + 5D chaos)
Dual-chaos + RIPTS (Chen et al., Optics Express 2025) [17]	PAPR improvement 4.3 dB; 0.5–0.8 dB better than PTS/IPTS/RPTS	Reduces ICI with shaping–performance tradeoff	Medium–High (segmentation/interleaving + references)

Δ denotes the relative change with respect to the corresponding non-encrypted baseline under the same system settings (e.g., same modulation, bandwidth, and launch power). Arrows indicate qualitative trends when exact Δ values are not reported. ↓ denotes a decrease.

Meanwhile, in 2016, Mecozzi proposed the Kramer–Kronig (KK) receiver scheme, which theoretically proved that after adding a sufficiently large continuous wave, the KK receiver can eliminate the influence of signal–signal beat interference (SSBI) on single-sideband (SSB) signals [20]. Li, Erkılınç et al. evaluated DD-SSB 16QAM WDM systems with receiver-side electronic dispersion compensation plus DSP linearization (net O-ISD 2.8 b/s/Hz), showing that receiver-based compensation can match transmitter-based methods; the Kramers–Kronig receiver performed best [21]. Chen, Antonelli et al. demonstrated a 218 Gb/s direct-detection receiver using Kramers-Kronig phase reconstruction and chromatic-dispersion compensation with a single photodiode, enabling single-span 125 km SSMF transmission at 1550 nm [22]. Le, Schuh et al. show low-complexity SSB DD transmission by adding a digital (virtual) carrier with the complex signal using only two DACs. Combined with KK field reconstruction or two-stage SSBI cancelation, eight-channel WDM achieves 1.72 Tb/s net over 200 km at 1550 nm [23]. Kong, Da Silva et al. demonstrate KK detection of a 909.5 Tbit/s DSDM/WDM signal over a single-mode 37-core fiber [24]. Hoang, Sowailem et al. propose 4D modulation with direct detection via a Stokes-vector KK transceiver. Using a digital carrier plus KK detection enables polarization de-rotation without an LO [10]. Che, Sun, and Shieh propose an SSB Stokes-vector receiver to demultiplex 4D POL-MUX signals, fundamentally resolving carrier fading in direct detection. It was validated with 60 Gbaud POL–MUX 16QAM over an 80 km SSMF using digital post-compensation of dispersion [25]. Zhu, Zou et al. demonstrate 448 Gb/s single channels and 1.792 Tb/s WDM Nyquist PDM–16QAM using heterodyne detection with single-ended photodiodes [26]. Li, Galdino et al. present the first use of digital back-propagation for fiber nonlinearity compensation in KK direct-detection receivers, improving 112 Gb/s/λ WDM single-span SSMF transmission up to 160 km [27].

3. Principle

Three-dimensional Lorenz chaos is a three-dimensional chaotic phenomenon generated based on the Lorenz system, which is one of the most classic models in chaos theory. It was proposed by the American meteorologist Edward Lorenz in 1963 when he was studying atmospheric convection problems. It reveals the intrinsic randomness that may appear in deterministic systems and is a typical representative of the “butterfly effect”.

The Lorenz system is a dynamic system composed of three coupled nonlinear ordinary differential equations, and its expression is

$$\left\{\begin{array}{c}{\displaystyle \frac{dx}{dt}}=-\alpha x+\alpha y\\ {\displaystyle \frac{dy}{dt}}=\gamma x-xz-y\\ {\displaystyle \frac{dz}{dt}}=-\beta z+xy\end{array}\right.$$

(1)

where $\left\{x,y,z\right\}$ are the state variables of the system (which can be understood as physical quantities describing fluid motion, such as velocity, temperature, etc.); t is time, represented as a positive step value in this paper; and α (Prandtl number), γ (Rayleigh number), and β (geometric parameter) are the control parameters of the system. Among them, γ is the key to determining the transition of the system from order to chaos. Its chaotic range is related to the values of α and β, and the calculation formula of its critical value γ_c is as follows:

$${\gamma }_c={\displaystyle \frac{\alpha \left(\alpha +\beta +3\right)}{\alpha -\beta -1}}$$

(2)

Chaos begins to emerge when parameters take specific values (the classic values are α = 10 and β = 8/3). As ρ continues to increase (such as ρ = 28, 30, 100, etc.), the chaotic characteristics still exist, with only slight changes in the structure of the attractor (such as the degree of stretch of the “wings” and the frequency of trajectory jumps). α (Prandtl number) is a physical quantity describing the ratio of fluid viscosity to thermal diffusivity, and its value is usually related to specific physical scenarios, with a practical range of α ∈ [5,21]. (Ten, sixteen, etc., are commonly used in research). β is a parameter related to the geometric structure of the system (such as the thickness of the fluid layer), and its value is relatively fixed, with a classic practical range of β ∈ [1,12] (the most classic value is β = 8/3 ≈ 2.6667). When the parameters take specific values (the classic values are α = 10, γ = 28, and β = 8/3), the system will exhibit the optimal chaotic characteristics. The phase diagram of its chaotic mapping model is shown in Figure 1.

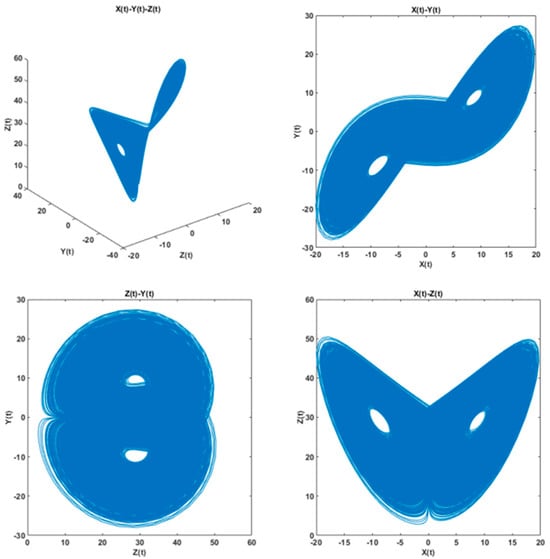
Figure 1. Phase diagram of the 3D Lorenz chaotic map model.

There are a total of 6 variables ($\left\{x_0,y_0,z_0,{\alpha }_0,{\beta }_0,{\gamma }_0\right\}$) in Equation (1). Different initial values $\left\{x_0,y_0,z_0\right\}$ and different control parameters $\left\{{\alpha }_0,{\beta }_0,{\gamma }_0\right\}$ will generate three different chaotic sequences $\left\{x,y,z\right\}$. To ensure the chaotic characteristics of the system, the value range of the control parameters in this paper does not exceed ±0.5 compared with the classic values.

In three-dimensional space, the trajectory of the Lorenz attractor behaves as follows: it winds repeatedly around two symmetric “vortex centers” and randomly “jumps” from one vortex region to another, with the timing and number of jumps being completely unpredictable. The overall trajectory never intersects or repeats itself, forming a complex yet ordered chaotic structure.

The encryption scheme proposed in this paper is as shown in Figure 2. First, we determine the initial values and control parameters $\left\{x_0,y_0,z_0,{\alpha }_0,{\beta }_0,{\gamma }_0\right\}$ of the transmission key for this transmission to generate chaotic sequences $\left\{x,y,z\right\}$. According to Equation (3), the parity of the 13th digit after the decimal point is used to generate corresponding perturbation sequences m/n and l. It should be noted that choosing k = 13 (the 13th fractional digit) balances stability and security: it lies beyond low-order digits that are susceptible to quantization/synchronization bias yet avoids the rounding-dominated tail near the precision limit, yielding stable, near-balanced bits across platforms. Then, m/n and l are generated into keys Key1 and Key2 according to Equation (4).

$$\left\{\begin{array}{c}m=floor\left[\mathrm{mod}\left(x\cdot {10}^{13},2\right)\right]\\ n=floor\left[\mathrm{mod}\left(y\cdot {10}^{13},2\right)\right]\\ l=floor\left[\mathrm{mod}\left(z\cdot {10}^{13},2\right)\right]\end{array}\right.$$

(3)

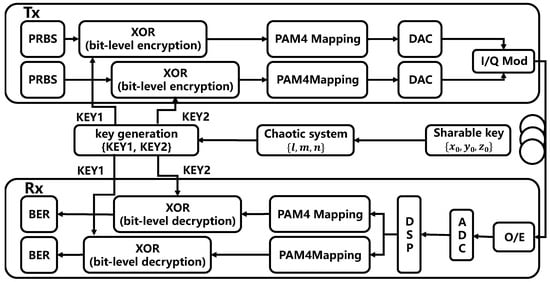
Figure 2. The encryption scheme proposed in this paper.

After the sender and receiver confirm the transmission of encrypted information, the sequences of the I and Q signals are XORed with the keys according to Equation (5).

$$\left\{\begin{array}{c}key1=m-n\\ key2=n-l\end{array}\right.$$

(4)

$$\left\{\begin{array}{c}sign\_I=xor\left(I,key1\right)\\ sign\_Q=xor\left(Q,key2\right)\end{array}\right.$$

(5)

The encrypted I and Q signals are modulated by PAM4, and then enter the IQ modulator to complete the modulation of 16QAM signals. After that, the encrypted signals are transmitted according to the method for generating and receiving low-CSPR SSB signals in reference [15]. After the receiver completes the equalization of the low-CSPR single-sideband signal, the legitimate ONU user will generate the correct keys Key1 and Key2 based on the initial values and control parameters of the transmission key and will obtain the information before encryption after performing the XOR operation with the I and Q signals.

4. Experiments and Result Analysis

4.1. Experiment Setup

Figure 3 shows the experimental setup of 3D Lorenz-encrypted SSB-16QAM coherent optical communication systems that remove SSBI to achieve low-CSPR detection. CWs are generated by external cavity lasers (ECLs) with a line width of less than 100 kHz and an output power of less than 15 dBm. The 1550 nm light source is then modulated by the I/Q modulator to realize photoelectric conversion. The I/Q modulator has a 3 dB bandwidth of 33 GHz and an insertion loss of 6 dB.

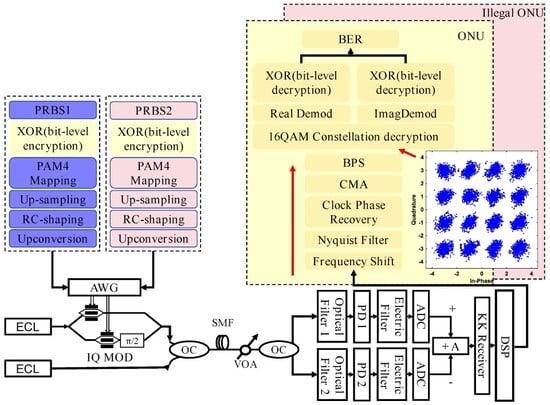
Figure 3. Experiment setup.

The input of initial values and control parameters for the chaotic sequence at the system’s transmitting end is $\left\{x_0=0,y_0=2,z_0=9,{\alpha }_0=10,{\beta }_0=8/3,{\gamma }_0=28\right\}$. A 64 GSa/s AWG is used to convert the two encrypted digital symbol sequences into I/Q analog 10 Gbaud PAM4 signals (with a raised cosine IQ filter and roll-off = 0.2), which are then converted into a 16QAM optical signal via an I/Q modulator. An EDFA with a noise value of 5.5 dB and a variable optical attenuator (VOA) is used to adjust the transmitted signal power into a 1 × 2 OC. CW light is generated by another external cavity laser (ECL 2) that can adjust the frequency to provide a guard band between the CW and 16QAM signals.

The output power of ECL 2 is adjusted by another VOA, and it is then coupled to the other side of the 1 × 2 coupler. The transmission link is composed of a 10 km SMF. The bandwidth of the OBPF1 is 20 GHz, including the 16QAM signal and CW. The bandwidth of OBPF2 is 12 GHz, and the center frequency domain is the same as that of the 16QAM signal. A four-channel digital phosphor oscilloscope with a bandwidth of 100 GSa/s and 20 GHz as ADC is used to receive the signal. The offline digital signal is then processed by MATLAB R2024b.

Offline DSP includes the KK algorithm, resampling, CD, a Nyquist filter, frequency shifts, clock phase recovery, MMA, and BPS. The KK chain is dominated by a block Hilbert transform implemented via two FFTs per $N$-sample block, yielding $\mathcal{O}(N\log N)$ complexity; timing recovery and equalization are $\mathcal{O}(N)$. The Lorenz-driven XOR mapping (and its inverse) is $\mathcal{O}(1)$ per symbol with no extra buffering, so end-to-end latency is governed by one DSP block ($N$ samples) plus filter transients, with negligible additional delay from the PLE layer. We have set up two types of Optical Network Units (ONUs) at the receiving end. One is a legitimate ONU that knows the initial values and control parameters, enabling it to generate the key at the receiving end and correctly decrypt the received information. The other is an illegal ONU that does not know the key but is aware of the encryption scheme and can use the exhaustive method to brute-force crack the encrypted signal.

4.2. Security Analysis Under Known-/Chosen-Plaintext and Side-Channel Models

We analyze the proposed scheme as a synchronous stream cipher acting on the I/Q bitstreams prior to PAM4-to-16QAM mapping. Let $P_{I,Q}[i]\in \{0,1\}$ denote the plaintext bits, and let

$$C_{I,Q}[i]\hspace{0.33em}=\hspace{0.33em}{P}_{I,Q}[i]\hspace{0.33em}\oplus \hspace{0.33em}{K}_{I,Q}[i],$$

(6)

denote the encrypted bits, where $K_{I,Q}[i]$ represents key stream bits derived from the Lorenz system by numerical integration with the secret seed

$${\mathsf{K}}_0\hspace{0.33em}=\hspace{0.33em}\{x_0,y_0,z_0,{\alpha }_0,{\beta }_0,{\gamma }_0\},$$

(7)

followed by burn-in, stride-$s$ sub-sampling, extraction of the 13th fractional-digit parity, and coordinate mixing, as shown in Equations (3)–(5). The adversary is passive, observes the broadcast downlink, and knows all algorithms (Kerckhoffs’s principle) but not ${\mathsf{K}}_0$. To preclude keystream reuse, we evolve the initial conditions across frames within the allowed parameter windows (Section 3), applying the same parity mechanism to derive small, deterministic offsets; extraction always follows a burn-in and sub-sampling stage. This design removes key-aided pilots or tones and avoids any key-dependent synchronization markers on the physical waveform.

Under known-plaintext or chosen-plaintext conditions, the attacker can recover $K_{I,Q}[i]$ for the queried positions within a frame via Equation (7). However, predicting unseen key stream bits or recovering ${\mathsf{K}}_0$ from such samples requires inverting highly nonlinear, quantized, and aliased observations—parities of deep fractional digits—of a continuous chaotic system at ${10}^{-15}$–${10}^{-16}$ precision across six dimensions. No efficient method is known for this inversion, and our per-frame evolution ensures statistical independence across frames. Consequently, KPA/CPA provide only instantaneous key stream exposure and do not compromise future symbols in the same frame or any subsequent frames when key stream reuse is avoided.

The residual attack reduces to a parameter-space search constrained by observed key stream bits. Even with optimistic pruning, discretizing four variables at ${10}^{-15}$ and $\beta$ at ${10}^{-16}$ within $\pm 0.5$ windows yields approximately $\mathcal{K}|\hspace{0.33em}\approx \hspace{0.33em}{10}^{91}$. We also consider side-channel avenues pertinent to low-CSPR KK-SSB. Because XOR is applied at the bit level before PAM4-to-16QAM modulation, the minimum-phase condition required by KK phase retrieval is preserved, spectral zeros are not introduced, and co-design with our SSBI mitigation maintains negligible PAPR growth. The absence of key-dependent pilots or tones eliminates simple spectral or timing markers on the downlink. Further, double-precision integration, burn-in, stride-$s$ sub-sampling, and coordinate mixing suppress finite-precision short-period effects that could otherwise re-emerge after KK reconstruction. These measures collectively raise the bar against side-channel exploitation while keeping transmission performance identical to the non-encrypted baseline shown in Figure 4 and Figure 5.

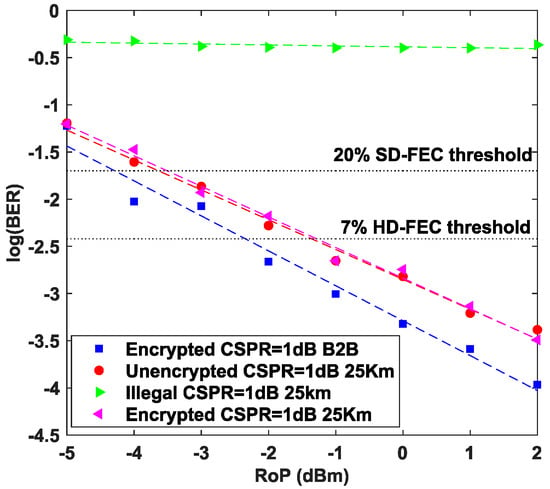
Figure 4. Comparison of transmission results among legitimate ONUs (using correct keys and incorrect keys), illegal ONUs, and non-encrypted systems.

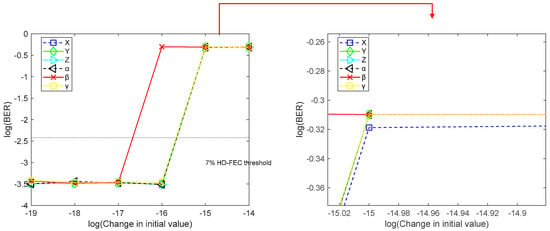
Figure 5. BER curve when there is a slight change in the initial value among the key parameters.

4.3. Results Analysis

Figure 4 shows a comparison between the proposed encrypted low-CSPR KK receiving system and the non-encrypted system. As can be seen from the experimental results in the figure, the ONU using the legitimate key achieves a bit error rate below the 7% HD-FEC threshold under the back-to-back condition with a received power of approximately −2.3 dBm. After 25 km of fiber transmission, the bit error rate curve of the ONU using the legitimate key nearly overlaps with that of the non-encrypted system. It can achieve a bit error rate below the 7% HD-FEC threshold at a received power of approximately −1.4 dBm and a bit error rate below the 20% SD-FEC threshold at a received power of approximately −3.7 dBm. Since the illegal ONU does not use the correct key (e.g., using $\left\{x_0=0+{10}^{-15},y_0=2,z_0=9,{\alpha }_0=10,{\beta }_0=8/3,{\gamma }_0=28\right\}$ or $\left\{x_0=0,y_0=2,z_0=9,{\alpha }_0=10,{\beta }_0=8/3+{10}^{-15},{\gamma }_0=28\right\}$), its bit error rate is much higher than 10⁻¹.

Figure 5 shows the BER curve when the initial values and initial parameters undergo slight changes at a received optical power of 0 dBm after 25 km of fiber transmission, verifying the initial value sensitivity of the chaotic system and the security of the proposed encryption system. Among them, the initial values and control parameters of the legitimate ONU user in the chaotic system are set as $\left\{x_0=0+{10}^{-15},y_0=2,z_0=9,{\alpha }_0=10,{\beta }_0=8/3,{\gamma }_0=28\right\}$. It can be found from the figure that when only a tiny change of 10–15 occurs in any of the above six parameters (such as $\left\{x_0=0,y_0=2,z_0=9,{\alpha }_0=10,{\beta }_0=8/3+{10}^{-15},{\gamma }_0=28\right\}$), the BER rises sharply, and the parameter β will have a significant change even with a 10⁻¹⁶ variation.

Since the control parameters of the chaotic model are generally selected around typical values, the considered value ranges of α, γ, and β are within ±0.5 of the typical values. If the above six parameters are taken into account, the step range of t is assumed to be [1, 103].

We bound the key space using the actual admissible domains and quantization applied in our system. Control parameters are restricted to robust-chaos windows around the canonical values, $\alpha \in [9.5,10.5],\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\beta \in [\frac{8}{3}-0.5,\frac{8}{3}+0.5],\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\gamma \in [27.5,28.5],$ and initial conditions to $x_0,y_0\in [-10,10],\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{z}_0\in [0,20].$ States are generated in single precision and deterministically quantized so that the parity of the 13th fractional digit is well-defined. Counting distinguishable seeds on these grids and including the time-step index $t\in \left\{1,\dots ,{10}^3\right\}$ and the per-segment counter (mixed into the seed) yield an effective brute-force space on the order of $N_{\mathrm{eff}}~{10}^{91}$ while retaining KK compatibility (no spectral zeros, negligible PAPR growth, and preserved SSBI mitigation).

5. Discussion

At higher symbol rates, the KK-SSB receiver remains computationally tractable because the FFT-based Hilbert transform and timing/equalization stages scale as O(N log N) and O(N), respectively. The dominant challenges arise from hardware and waveform margins: tighter analog front-end bandwidth, DAC/ADC ENOB limits, and increased sensitivity to laser phase noise and the excess phase. Preserving the minimum-phase condition over wider spectra requires careful CSPR tuning, digital pre-emphasis to manage PAPR, and consistent biasing of the modulator. The proposed PLE layer is rate-agnostic—its XOR mapping is O(1) per symbol and does not add buffering—so the principal rate-scaling risks are practical ones such as key/chaotic-seed synchronization at very short symbol periods, which we mitigate using lightweight frame markers and periodic seed re-alignment.

For longer fiber spans, chromatic dispersion and OSNR degradation become the primary constraints, followed by residual nonlinearities (SPM/XPM). KK detection is resilient to linear impairments when minimum-phase conditions hold, but accumulated dispersion broadens the signal spectrum and can shrink that margin if compensation is imperfect or if CSPR is set too low under amplified noise. Our DSP already includes CD compensation; for extended reaches, we anticipate modest enhancements—adaptive CD estimation per burst, tighter CSPR control versus OSNR, and, if needed, single-step digital back-propagation or a Volterra equalizer—to maintain performance without modifying the PLE layer. Since PLE operates on mapped bits rather than the analog waveform, it neither exacerbates fiber nonlinearity nor interferes with KK phase reconstruction; latency continues to be governed by one DSP block plus filter transients.

In multi-user settings such as WDM or PON, penalties are dominated by inter-channel crosstalk, relative frequency offsets, and timing skew, which appear as excess EVM and an increased cycle-slip risk in timing recovery. With independent seeds, the PLE masks are orthogonal across users, so interference manifests in the optical/electrical domains rather than through cryptographic coupling. Per-channel CSPR optimization, conventional guard-band planning, and narrowband optical filtering are effective in maintaining KK stability in the presence of adjacent-channel leakage typical of 50–100 GHz grids; for denser packing, slightly raised CSPR or sharper filters restore the minimum-phase condition at the cost of modest OSNR.

Overall, the scalability limits are governed by the familiar KK-SSB trade-offs among CSPR, OSNR, bandwidth, and front-end linearity and not by the PLE itself. Future work will report systematic measurements across baud rates (e.g., 32/64/96 Gbd), spans representative of metro–regional links with EDFA chains, and multi-user experiments in a WDM-PON emulator to map the operating envelope and quantify the minimal overhead introduced by the PLE under each regime.

6. Conclusions

We have experimentally demonstrated that the low-CSPR SSB transmission system, after adopting 3D Lorenz chaotic encryption, not only does not affect its transmission quality but also achieves a key space of 10⁹¹. This ensures that illegal users cannot crack the correct information in a short time, greatly enhancing its security. Chaotic encryption enables single-sideband systems to achieve extremely high security while maintaining high spectral resource utilization, which allows them to play a significant role in future applications such as large-capacity multi-user optical communication networks in data centers.