Abstract
We investigate the phenomenon of quantum interference in spontaneous emission pathways for a quantum emitter embedded in a two-dimensional photonic crystal composed of a square lattice of dielectric cylindrical rods. Using a V-type three-level system as a model, we demonstrate that the anisotropic Purcell effect inherent in such photonic structures can amplify quantum interference to its theoretical maximum, where the degree of interference p reaches unity. This results in the complete suppression of spontaneous emission for one polarization (directional suppression) and the emergence of coherent population trapping without the need for external coherent fields. By employing density matrix formalism, we derive analytical expressions for the population dynamics and identify conditions for indefinite or long-lived excited-state population. Our findings can find application in quantum technologies, including high-precision atomic clocks, magnetometry, and quantum information processing.
1. Introduction
Quantum interference (QI) in spontaneous emission arises when two or more decay channels from excited states of a quantum emitter (QE) interfere as they transition to a common ground state. This phenomenon is critically dependent on the relative orientation and coherence of the transition dipole moments, which must be nonorthogonal, a condition facilitated by the presence of the anisotropic Purcell effect [1,2]. The anisotropic Purcell effect modifies the spontaneous emission rate in a direction-dependent manner and can enhance QI by creating differences in the decay rates for orthogonal dipole moments [3]. This anisotropy is achievable through the interaction of QEs with structured electromagnetic environments, such as plasmonic nanostructures, dielectric nanostructures and microstructures, or metamaterials [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18], wherein these environments modify the local density of states (LDOS), providing control over spontaneous emission rates. The occurrence of QI in a QE can result in a variety of remarkable effects in quantum optics. These include ultranarrow spectral lines and controlled emission in resonance fluorescence spectra [19,20,21,22,23,24], coherent population trapping [25,26], lasing without inversion [27,28,29,30,31], modification of laser cooling [32], phase-dependent line shapes [2,33,34], optical transparency with slow light and enhanced Kerr nonlinearity [35,36,37,38], the latter being critical for quantum communication and computation technologies. Furthermore, the emergence of QI enables phase-controlled atom–photon entanglement [39,40,41] and the creation of controllable quantum optical limiters for optical devices [42]. Beyond these phenomena, QI provides a versatile toolset for quantum optoelectronics and photonics, enabling active control of light–matter interactions in nanophotonic circuits, low-threshold and inversionless lasers, switchable single-photon sources, and optically tunable quantum memories. It also underpins the design of quantum photonic devices such as modulators, sensors, and interferometers, where interference-based control over emission spectra and coherence directly translates into enhanced device performance and new functionalities.
Plasmonic nanostructures, in particular, are effective mediators of QI due to their ability to generate highly localized electromagnetic fields with strong polarization anisotropy. For instance, when a QE is placed near a metal–dielectric interface or a resonant plasmonic cavity, the decay rates associated with dipoles oriented parallel and perpendicular to the surface differ significantly, leading to enhanced QI [7,43,44,45]. Similarly, hyperbolic and negative-index metamaterials leverage periodic or anisotropic dielectric arrangements to support directional emission control and suppress specific decay pathways [4,5,6,10,11]. Notably, bismuth chalcogenide materials and other two-dimensional systems have emerged as promising platforms for QI, owing to their exceptionally large dielectric constant, which maximizes quantum-interference effects and enables the manipulation of the spontaneous emission spectra [15,16].
In the present work, we present an ideal framework for studying QI in spontaneous-emission pathways. Namely, we focus on 2D photonic crystals as a photonic environment that can amplify QI to its theoretical maximum (a degree of QI equal to unity, as detailed below) due to the presence of an anisotropic frequency band gap. The crucial characteristic of such an anisotropic gap is the complete suppression of the spontaneous emission rate for a specific polarization, due to the complete absence of photonic modes for this polarization. This unique property, which is not met in other photonic environments, enables the amplification of various quantum optical phenomena that depend on both maximal QI as well as on the complete suppression of the spontaneous emission rate for their manifestation. A characteristic example is coherent population trapping (CPT), where an excited state of a QE can stay populated almost indefinitely, as we will demonstrate below. The occurrence of CPT can find important application in areas of quantum technologies such as high-precision atomic clocks, magnetometry, and quantum information processing. It is therefore important to stress that, while other photonic environments such as plasmonic nanostructures and metamaterials can enhance QI by modifying decay rates, as we demonstrate below, only two-dimensional photonic crystals with anisotropic band gaps enable the complete suppression of one decay channel, thereby reaching the theoretical maximum degree of QI.
2. Quantum Interference in a Three-Level Quantum Emitter
Figure 1 illustrates a V-type three-level QE, which serves as a generic model system. This model consists of two closely spaced excited states, and , and a single ground state, . The atomic dipole moment operator for this system is expressed as:
where
and d is a real constant. The excited states and decay spontaneously to the ground state with decay rates and , respectively. The dynamics of the QE are analyzed using the density matrix formalism. By considering only spontaneous emission processes and applying the rotating-wave and Wigner–Weisskopf approximations, the time evolution of the system interacting with a photonic environment is governed by the following equations [5,6,7]:
subject to the constraints
and
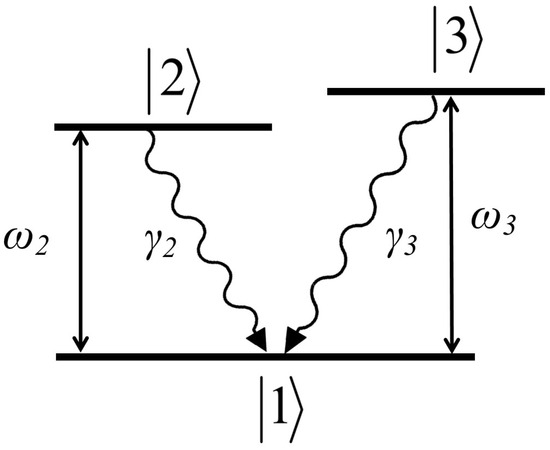
Figure 1.
A V-type three-level quantum emitter.
The dipole orientations for the transitions and are defined relative to a nearby material surface. The spontaneous emission rates for these transitions are given by
where ⊥ and ‖ refer to dipoles oriented perpendicular (along the z-axis) and parallel (within the -plane) to the material surface, respectively. Here, is the QE’s position, m is the dipole moment, and are components of the electromagnetic Green’s tensor. The terms and describe the QI between the spontaneous emission pathways and , and are given by:
Assuming that the two excited states and are nearly degenerate (), the decay rates and interference terms simplify to
where the perpendicular and parallel decay rates are defined as
The degree of QI, denoted as p, is defined as [5,6,7]
A degree of QI equal to indicates maximal interference, achievable by placing the QE near a structure that entirely suppresses . In order to assess the role of QI in the evolution of the population of the V-type system, we need to solve the density matrix equations, i.e., Equations (3)–(5). If one of the excited states is initially populated, for instance, , , and , the analytical solutions for the state populations can be obtained from Equations (3)–(5) as [43]
When no QI is accounted for, then and
We note that, according to Equations (12) and (13), the spontaneous emission rates are provided in terms of the EM Green’s tensor. However, they can be calculated by other means, as we will see below.
It should be noted that although QI can also occur in -type three-level systems, the V-type configuration provides a more natural platform for studying interference arising purely from spontaneous emission. In -type systems, such effects typically require external coherent driving, whereas in V-type systems CPT can emerge without any external field. In the present V-type system, coherence and interference arise intrinsically from the spontaneous emission channels rather than from external driving fields. The interference terms in the density matrix couple the excited states, forming a dark state that preserves coherence and suppresses spontaneous emission-induced decoherence. Experimental studies in photonic crystals have so far focused mainly on two-level QEs, while the V-type configuration remains largely unexplored and represents a promising direction for future investigations.
3. Anisotropic Purcell Effect in a 2D Photonic Crystal
We assume that the V-type three-level QE interacts with a 2D photonic crystal, as shown in Figure 2. The photonic crystal consists of a square lattice of infinitely long cylindrical rods with radius where a is the lattice constant. The dielectric constant of the rods is ( rods) and they are assumed to be surrounded by air (). This is a well-known system that has an anisotropic frequency band gap [46].

Figure 2.
2D photonic crystal composed of a square lattice of infinitely long cylindrical rods. The rods have a radius of , where a is the lattice constant. The rods are made of titanium dioxide () which corresponds to a dielectric constant of . The rods are embedded in air .
Figure 3 shows the frequency band structure of the photonic crystal of Figure 2 along the symmetry lines of the 2D first Brillouin zone (1BZ). The frequency bands are calculated via the plane wave (PW) method for EM waves [47,48]. Namely, we have included reciprocal lattice vectors up to order , resulting in a -dimensional basis set for the Fourier expansion of the inverse dielectric function. This choice provides converged results for the first 5–6 photonic bands, which are the frequency range of interest in this work. The band structures were computed along the high-symmetry directions , , and , with each path discretized into 100 equally spaced k-points, ensuring a fine resolution of the dispersion curves.
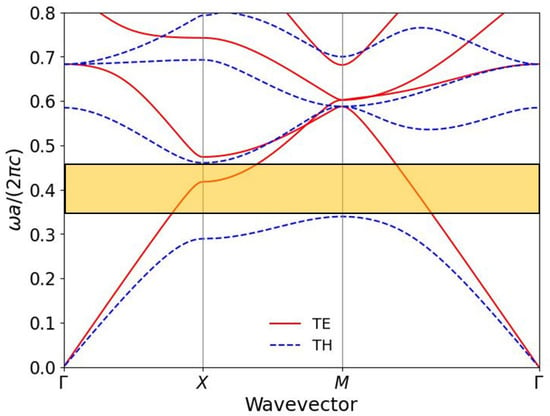
Figure 3.
Frequency band structure of the 2D photonic crystal of Figure 2 along the symmetry lines of the 1BZ of a square lattice. The solid (broken) lines correspond to the TE (TH) modes. The shaded region represents the full band gap for the TH modes.
We note that for 2D periodic crystals, the modes of the EM field are separated to two different polarizations, TE and TH waves, and are, thus, calculated separately. For the TE (TH) waves, the magnetic (electric) field H (E) is oriented parallel to the rods (z-axis in Figure 2). From Figure 3 it is evident that there exists a full (omnidirectional) band gap for the TH (E-polarization) waves from about to 0.45 (shaded region in Figure 3). At the same time, for H polarization, a directional band gap appears along the –X and X–M directions in the frequency range . Above this frequency, the gap closes along X–M, as shown in Figure 3. This anisotropy plays an important role in shaping the emission characteristics of dipole emitters embedded in the structure.
In order to confirm the existence of the full band gap for TH modes, in Figure 4 we present the first five frequency bands for Bloch wavevectors within the entire 1BZ. It is clear that an absolute frequency band gap for the TH waves exists for all directions in space. The QE, modeled as an electric dipole embedded in the photonic crystal and oriented along the z-axis, couples only to modes with non-zero , i.e., the TH manifold. In free space, such a dipole exhibits zero radiation along its axis of orientation () and radiates mainly in the plane with an angular dependence proportional to [49]. Inside the photonic crystal, however, the absolute TH band gap suppresses all in-plane propagation channels available to this dipole, effectively reducing its LDOS and thereby modifying the relative coupling strengths to different polarization channels, which in turn influences the achievable degree of QI. This polarization-dependent modification of the LDOS establishes a direct link between the photonic band structure and the coherence properties of the QE. In particular, the suppression of the TH modes and the persistence of the TE modes create an anisotropic photonic environment that induces unequal decay rates for the two optical transitions. This imbalance leads to strong interference between the corresponding spontaneous emission pathways, resulting in enhanced quantum coherence and facilitating the emergence of CPT within the photonic crystal, as will be demonstrated below.
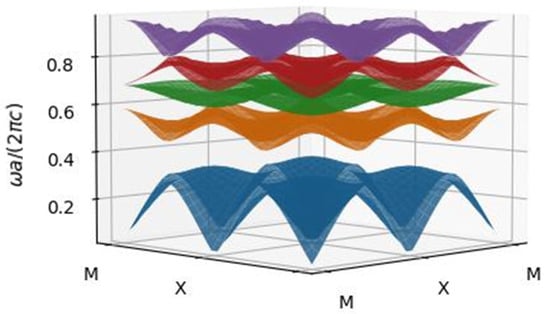
Figure 4.
Frequency band structure for TH waves.
For completeness, in Figure 5, we show the frequency band structure for the TE waves over the entire 1BZ. Evidently, in the spectral region of the absolute TH frequency gap, the TE bands intersect, and therefore there are EM modes available with which an electric dipole oriented in the -plane can couple with. For the case of the V-type three-level atom of Figure 1, the presence of a full band gap for TH waves translates into the optimal case of QI. That is, if we take a dipole parallel to the rod axis (along the z-plane), then the corresponding spontaneous emission rate due to the absence of EM modes for all wavevectors (TH wave). For a dipole vertically oriented to the rods (within the -plane), and the degree of QI is automatically equal to unity.
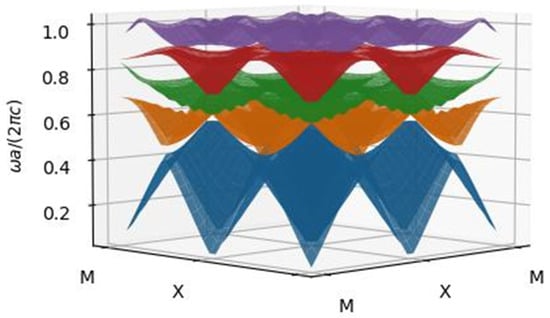
Figure 5.
Frequency band structure for TE waves.
In general, the spontaneous emission rate is proportional to the 3D local density of states (LDOS), which, in our case, is given by
where stands for the frequency bands (see Figure 4 and Figure 5), are the corresponding eigenmodes and where lies within the 1BZ of the 2D photonic crystal. lies in with determined by the calculated frequency region with [50].
A rigorous evaluation of the photonic density of states requires integration over the full two-dimensional Brillouin zone, with the number of sampled -points depending on the chosen numerical integration scheme and desired resolution. In this work we employ the effective-medium approximation, which is valid near the Brillouin zone center but does not capture the enhanced density of states near the zone boundaries. Importantly, however, our conclusions do not rely on the precise value of , since the interference effect we highlight arises from the exact condition . This ensures that the destructive interference channel remains robust even if the quantitative magnitude of is approximated.
The solid line in Figure 6 corresponds to the frequency bands along the line for the TE waves whilst the broken line corresponds to the frequency band taken by assuming the effective-medium approximation. The latter is applicable in the long-wavelength limit and replaces the actual photonic crystal with a homogeneous medium of average permittivity . For the case of TE waves, the average (effective) permittivity is provided by [51,52]
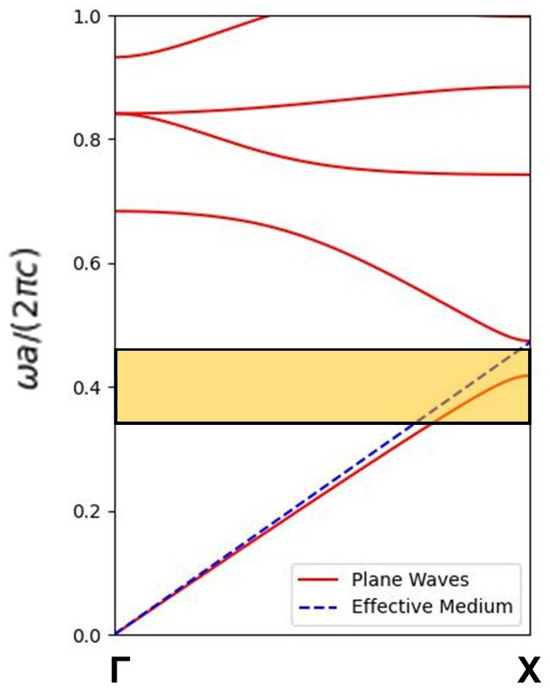
Figure 6.
Frequency band structure for TE waves along the direction of the 1BZ. The solid lines are calculated via the PW method whilst the broken lines are calculated by the effective-medium approximation. The shaded region corresponds to the frequency band gap for the TH waves.
Here, is the surface filling fraction of the photonic crystal, representing the ratio of the cross-sectional area of the dielectric cylinders to the area of the unit cell. The shaded region in Figure 6 corresponds to the absolute frequency gap for the TH waves. Evidently, the effective-medium frequency band reproduces fairly well the actual TE frequency band, mostly within the lowest half, , of the TH gap. This means that instead of employing the numerical implementation of Equation (18) we can use the spontaneous emission rate of a dipole placed within a homogeneous medium of permittivity provided by Equation (19), i.e.,
where
where is the dipole moment of the transition and c the light speed in vacuum. For the case of , i.e., a dipole within the -plane, we have
In Figure 7, we present the population dynamics of states and , represented by the functions and , respectively (for state , the population is given by ). These are plotted for various values of , while is calculated via Equation (22). Furthermore, we show and in the absence of QI, corresponding to , as described by Equation (17).
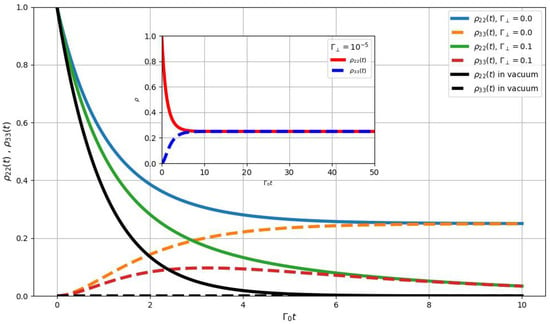
Figure 7.
Population dynamics of states (solid lines), and (broken lines), when the QE is initially in state , for different values of . We stress that in the legend of the plot the values of are given in units of .
Clearly, in the absence of QI, the population of the state decays exponentially with a rate . When the QE is embedded in the 2D photonic crystal depicted in Figure 2, the vanishing of results in the maximum theoretical degree of QI, i.e., . Specifically, for , the populations are given by and , in which case states and remain populated indefinitely, regardless of the value of .
In the same graph, we also show the populations of states and for , which represents a typical value of in a photonic environment such as a bismuth-chalcogenide microstructure [15,16], where the degree of QI is almost ideal, with . For , QI leads to CPT, as evidenced by the temporary population of the state . However, after a while, it eventually decays back to zero. In contrast, when the V-type QE is embedded in the 2D photonic crystal (), the states and remain populated indefinitely. This forms a dark state where the QE neither absorbs nor emits photons, rendering it effectively transparent to a probe laser, even when the laser is precisely resonant with the transition.
The case of corresponds to the ideal case of an infinite, perfectly periodic photonic crystal consisting of infinitely long cylindrical rods, for which . However, in realistic experimental conditions, the finite dimensions of the rods, the limited size of the photonic crystal slab, the fabrication imperfections and the material losses result in a non-zero . To account for these deviations, the inset of Figure 7 shows and for , representing the effects of such imperfections. Even under these conditions, the states and remain populated several hundred times the characteristic time scale (note that in the inset, the time window is five times larger than the time window in the main Figure 7).
As shown above, the CPT effect reported here arises directly from the anisotropic LDOS in the photonic crystal. In the ideal case of an infinite and perfectly periodic two-dimensional photonic crystal, this anisotropy is a bulk property and the emergence of CPT is not strongly dependent on the specific position of the QE within the unit cell. However, for finite photonic crystal slabs and when the emitter is placed near an edge, position-dependent variations in the LDOS may occur, which could influence the trapping efficiency.
The phenomenon of CPT via QI of spontaneous emission paths, especially with long-lived trapped states, can find important applications in quantum technology and precision measurement as the traditional CPT but without the need for excitation of coherent laser fields acting on the QE. CPT is widely applied in quantum engineering and metrology, with notable applications in atomic clocks [53,54,55] and atomic magnetometers [56,57,58,59,60,61]. Moreover, CPT facilitates electromagnetically induced transparency (EIT) for slow light and fast light [62], quantum memory for photons [63], nonlinear optics at the single-photon level [64], lasing without inversion for energy-efficient lasers [65,66], and ultranarrow spectral lines for high-resolution spectroscopy [67]. Additionally, it supports robust quantum communication by enabling entanglement [64] and low-noise quantum networks. It is easily understood that the emergence of CPT with only passive elements (the QE and a photonic crystal slab) without the need of external laser fields (active elements) constitutes a major advancement in the field of quantum technology.
It is important to emphasize that we have intentionally avoided specifying a particular spectral regime where QI and CPT occur. This deliberate choice reflects the fact that our findings are theoretically applicable across all spectral regions. This universality arises from the dimensionless representation of the frequency band structures shown in Figure 3, Figure 4 and Figure 5, which is a direct consequence of the scaling properties of macroscopic Maxwell’s equations when only dielectric materials with constant electric permittivity are considered [46]. As a result, the frequency band gap, and thus the region of maximum QI (), can be shifted throughout the electromagnetic spectrum. More specifically, this shift can align with the characteristic frequencies of any given QE, provided the dielectric permittivity remains constant in the relevant spectral range.
This tunability represents a major advantage of photonic crystals compared to metamaterials and plasmonic structures. In the latter, the region of maximum QI is confined to the resonance frequencies of the constituent materials, significantly limiting the selection of QEs that can resonate within those narrow spectral windows. Photonic crystals, by contrast, offer far greater flexibility, enabling their adaptation to a wide range of quantum systems.
We note that related anisotropy-induced QI effects have also been discussed in the context of quasi-two-dimensional photonic cavities and waveguides with quantum dots [12]. In those systems, the interference originates from dipole–dipole coupling between orthogonal excitonic states, mediated by the anisotropic Green’s function of the structured reservoir, and CPT typically requires additional external driving fields. In contrast, the present work highlights a different route to QI, where the anisotropy is inherent to the photonic crystal band structure and leads to the direct suppression of one decay pathway (). This mechanism enables CPT to emerge solely from spontaneous emission, without any external coherent pumping. The two approaches therefore represent complementary physical mechanisms—dipole–dipole coupling in quasi-2D nanostructures versus band-structure-induced channel suppression in 3D photonic crystals—both of which enrich the toolbox of structured photonic environments for controlling spontaneous emission and quantum coherence.
In this work we focused on a square lattice of TiO2 cylindrical rods as a prototypical two-dimensional photonic crystal exhibiting polarization-dependent band gaps. Nevertheless, we stress that the physical mechanism highlighted here, namely the suppression of spontaneous emission into one polarization channel due to anisotropy in the photonic density of states, is of more general validity. Similar effects can be expected in other two-dimensional photonic crystal lattices, such as triangular or honeycomb geometries, which are also known to exhibit complete or partial band gaps for selected polarizations [46,68]. In addition, various dielectric materials with high refractive indices, including silicon and GaAs, provide alternative platforms where polarization-selective band structures can be engineered. Consequently, while the square-lattice TiO2 system serves as a convenient demonstration, the predicted interference effects are broadly relevant across a wide class of photonic crystal structures.
Finally, it is worth discussing possible experimental platforms for the realization of the proposed scheme. The universality of our results, which stems from the scaling properties of Maxwell’s equations and the dimensionless form of the calculated band structures, allows for their applicability across the entire electromagnetic spectrum. In practice, the choice of spectral regime is dictated by both the QE employed and the available photonic crystal material. For example, TiO2-based two-dimensional photonic crystals with feature sizes in the range of a few hundred nanometers operate in the visible and near-infrared, which makes them compatible with semiconductor quantum dots and color centers in diamond [69,70]. In the near-infrared, silicon or GaAs photonic crystals can be used in combination with excitons in III–V quantum dots. At the same time, larger-scale photonic crystal slabs in the micron regime can be engineered to operate at microwave frequencies, thereby interfacing with atomic transitions in Rydberg states or superconducting qubits. Therefore, while our theoretical analysis has been presented in a dimensionless framework, the proposed effects can be realized in a broad variety of physical platforms by matching the band gap to the resonant frequency of the QE. Also, note that over the years, a series of important experiments [71,72,73,74,75,76,77] has demonstrated that placing QEs, primarily two-level-type QEs, inside photonic crystals modifies their spontaneous emission rates and the emission dynamics. In addition, there has been significant progress in the deterministic coupling and precise positioning of QEs within photonic structures, including photonic crystals [74,75,76,77].
4. Conclusions
We have demonstrated that utilizing 2D photonic crystals enables the realization of maximal QI in spontaneous emission pathways and the formation of long-lived CPT, which can be adjusted to match the energy spectrum of any given QE. Through analytical and numerical investigation of a V-type three-level QE embedded in a square lattice of titania rods, we demonstrated that the anisotropic Purcell effect can amplify QI to its maximum theoretical value (p = 1), suppressing spontaneous emission for a specific polarization. This unique property facilitates indefinite population trapping in the excited states under ideal conditions or long-lived trapping under experimental conditions. The above underscore the practical viability of leveraging 2D photonic crystals to eliminate the need for external coherent fields in QI-driven processes such as CPT.
Author Contributions
Methodology, V.Y. and E.P.; software, V.Y.; validation, V.Y. and E.P.; investigation, V.Y. and E.P.; resources, V.Y. and E.P.; data curation, V.Y.; writing—original draft preparation, V.Y.; writing—review and editing, V.Y. and E.P.; visualization, V.Y.; supervision, V.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Agarwal, G.S. Anisotropic vacuum-induced interference in decay channels. Phys. Rev. Lett. 2000, 84, 5500. [Google Scholar] [CrossRef] [PubMed]
- Paspalakis, E.; Keitel, C.H.; Knight, P.L. Fluorescence control through multiple interference mechanisms. Phys. Rev. A 1998, 58, 4868. [Google Scholar] [CrossRef]
- Ficek, Z.; Swain, S. Simulating quantum interference in a three-level system with perpendicular transition dipole moments. Phys. Rev. A 2004, 69, 023401. [Google Scholar] [CrossRef]
- Li, G.X.; Li, F.-L.; Zhu, S.-Y. Quantum interference between decay channels of a three-level atom in a multilayer dielectric medium. Phys. Rev. A 2001, 64, 013819. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, J.; Chen, H.; Zhu, S. Quantum interference enhancement with left-handed materials. Phys. Rev. Lett. 2008, 100, 043601. [Google Scholar] [CrossRef]
- Li, G.-X.; Evers, J.; Keitel, C.H. Spontaneous emission interference in negative-refractive-index waveguides. Phys. Rev. B 2009, 80, 045102. [Google Scholar] [CrossRef][Green Version]
- Yannopapas, V.; Paspalakis, E.; Vitanov, N.V. Plasmon-Induced Enhancement of quantum interference near metallic nanostructures. Phys. Rev. Lett. 2009, 103, 063602. [Google Scholar] [CrossRef]
- Xu, J.-P.; Yang, Y.-P. Quantum interference of V-type three-level atom in structures made of left-handed materials and mirrors. Phys. Rev. A 2010, 81, 013816. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, L.; Ren, P.; Zhang, J.-X.; Zhang, T.-C.; Martin, O.J.F.; Gong, Q.-H. Surface-plasmon-induced modification on the spontaneous emission spectrum via subwavelength-confined anisotropic Purcell factor. Nano Lett. 2012, 12, 2488. [Google Scholar] [CrossRef] [PubMed]
- Jha, P.K.; Ni, X.; Wu, C.; Wang, Y.; Zhang, X. Metasurface-enabled remote quantum interference. Phys. Rev. Lett. 2015, 115, 025501. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Jiang, C. Coherent control in plasmon–emitter coupled systems. Opt. Express 2016, 24, 7719. [Google Scholar] [CrossRef]
- Hughes, S.; Agarwal, G.S. Anisotropy-induced quantum interference and population trapping between orthogonal quantum dot exciton states in semiconductor cavity systems. Phys. Rev. Lett. 2017, 118, 063601. [Google Scholar] [CrossRef]
- Karanikolas, V.; Paspalakis, E. Plasmon-induced quantum interference near carbon nanostructures. J. Phys. Chem. C 2018, 122, 14788. [Google Scholar] [CrossRef]
- Fang, W.; Chen, Y.; Zeng, Y.; Ou, C.-J.; Li, G.-X.; Yang, Y.-P. Anisotropic mode excitations and enhanced quantum interference in quantum emitter-metasurface coupled systems. New J. Phys. 2022, 24, 093006. [Google Scholar] [CrossRef]
- Karaoulanis, D.; Paspalakis, E.; Yannopapas, V. Quantum interference near bismuth-chalcogenide microstructures. J. Opt. Soc. Am. B 2021, 38, 3301–3308. [Google Scholar] [CrossRef]
- Kyvelos, N.; Tsigaridas, G.; Paspalakis, E.; Yannopapas, V. Quantum interference in spontaneous decay of a quantum emitter placed in a dimer of bismuth-chalcogenide microparticles. Photonics 2022, 9, 596. [Google Scholar] [CrossRef]
- Liu, Q.; Shan, L.-X.; Jia, Y.; Ma, Y.; Gong, Q.-H.; Gu, Y. Quantum interference enhancement and fluorescence spectral linewidth narrowing of a four-level system via dielectric Mie resonances. Phys. Rev. A 2023, 108, 033702. [Google Scholar] [CrossRef]
- Thanopulos, I.; Karanikolas, V.; Paspalakis, E. Strong coupling spontaneous emission interference near a graphene nanodisk. Nanophotonics 2024, 13, 4545–4554. [Google Scholar] [CrossRef]
- Zhou, P.; Swain, S. Ultranarrow spectral lines via quantum interference. Phys. Rev. Lett. 1996, 77, 3995. [Google Scholar] [CrossRef]
- Keitel, C.H. Narrowing spontaneous emission without intensity reduction. Phys. Rev. Lett. 1999, 83, 1307. [Google Scholar] [CrossRef]
- Macovei, M.; Keitel, C.H. Quantum interference control of spontaneous emission. Phys. Rev. Lett. 2003, 91, 123601. [Google Scholar] [CrossRef]
- Wang, C.-L.; Kang, Z.-H.; Tian, S.-C.; Jiang, Y.; Gao, J.-Y. Effect of spontaneously generated coherence on absorption in a V-type system: Investigation in dressed states. Phys. Rev. A 2009, 79, 043810. [Google Scholar] [CrossRef]
- Asadpour, S.H.; Abbas, M.; Hamedi, H.R.; Ruseckas, J.; Paspalakis, E.; Asgari, R. Spatiospectral control of spontaneous emission. Phys. Rev. A 2024, 110, 033706. [Google Scholar] [CrossRef]
- Kosionis, S.G.; Yannopapas, V.; Paspalakis, E. Spectral narrowing in the resonance fluorescence of a driven V-type quantum emitter near a two-dimensional plasmonic nanostructure array. Results Phys. 2025, 68, 108084. [Google Scholar] [CrossRef]
- Zhu, S.-Y.; Chan, R.C.F.; Lee, C.P. Spontaneous emission from a three-level atom. Phys. Rev. A 1995, 52, 710. [Google Scholar] [CrossRef]
- Zhu, S.-Y.; Scully, M.O. Spectral line elimination and spontaneous emission cancellation via quantum interference. Phys. Rev. Lett. 1996, 76, 388. [Google Scholar] [CrossRef]
- Imamoglu, A. Interference of radiatively broadened resonances. Phys. Rev. A 1989, 40, 2835. [Google Scholar] [CrossRef]
- Zhou, P.; Swain, S. Quantum interference in probe absorption: Narrow resonances, transparency, and gain without population inversion. Phys. Rev. Lett. 1997, 78, 832. [Google Scholar] [CrossRef]
- Paspalakis, E.; Gong, S.-Q.; Knight, P.L. Quantum interference effects in driven atomic systems. Opt. Commun. 1998, 152, 293–296. [Google Scholar] [CrossRef]
- Menon, S.; Agarwal, G.S. Effects of spontaneously generated coherence on the pump-probe response of a Λ system. Phys. Rev. A 1998, 57, 4014. [Google Scholar] [CrossRef]
- Wu, J.H.; Zhang, H.F.; Gao, J.Y. Probe gain with population inversion in a four-level atomic system with vacuum-induced coherence. Opt. Lett. 2003, 28, 654. [Google Scholar] [CrossRef] [PubMed]
- Das, R.C.; Ravi, T.; Khan, S.; Pandey, K. Role of spontaneously transferred coherence in laser cooling. Phys. Rev. A 2024, 110, 033101. [Google Scholar] [CrossRef]
- Paspalakis, E.; Knight, P.L. Phase control of spontaneous emission. Phys. Rev. Lett. 1998, 81, 293–296. [Google Scholar] [CrossRef]
- Macovei, M.; Evers, J.; Keitel, C.H. Phase control of collective quantum dynamics. Phys. Rev. Lett. 2003, 91, 233601. [Google Scholar] [CrossRef]
- Paspalakis, E.; Kylstra, N.J.; Knight, P.L. Transparency induced via decay interference. Phys. Rev. Lett. 1999, 82, 2079. [Google Scholar] [CrossRef]
- Bortman-Arbiv, D.; Wilson-Gordon, A.D.; Friedmann, H. Phase control of group velocity: From subluminal to superluminal light propagation. Phys. Rev. A 2001, 63, 043818. [Google Scholar] [CrossRef]
- Gurudev Dutt, M.V.; Cheng, J.; Li, B.; Xu, X.; Li, X.; Berman, P.R.; Steel, D.G.; Bracker, A.S.; Gammon, D.; Economou, S.E.; et al. Stimulated and spontaneous optical generation of electron spin coherence in charged GaAs quantum dots. Phys. Rev. Lett. 2005, 94, 227403. [Google Scholar] [CrossRef]
- Niu, Y.-P.; Gong, S.-Q. Enhancing Kerr nonlinearity via spontaneously generated coherence. Phys. Rev. A 2006, 73, 053811. [Google Scholar] [CrossRef]
- Abazari, A.; Mortezapour, A.; Mahmoudi, M.; Sahrai, M. Phase-controlled atom-photon entanglement in a three-level V-type atomic system via spontaneously generated coherence. Entropy 2011, 13, 1541. [Google Scholar] [CrossRef]
- Sangshekan, B.; Sahrai, M.; Asadpour, S.H.; Poursamad Bonab, J. Controllable atom–photon entanglement via quantum interference near plasmonic nanostructure. Sci. Rep. 2022, 12, 677. [Google Scholar] [CrossRef] [PubMed]
- Batoo, K.M.; Naeem, Y.A.; Ali, E.; Abdulameer, M.K.; Ibrahim, A.A.; Abdulridui, H.A.; Zazoum, B.; Ramadan, M.F.; Kadhum, E.H.; Omran, A.A.; et al. Spatially hybrid control of entanglement between atom and photon. Phys. B Condens. Matter 2024, 695, 416561. [Google Scholar] [CrossRef]
- Silatan, A.; Ghaderi GoranAbad, M.; Mahmoudi, M. Optical limiting via spontaneously generated coherence. Sci. Rep. 2023, 13, 364. [Google Scholar] [CrossRef]
- Evangelou, S.; Yannopapas, V.; Paspalakis, E. Simulating quantum interference in spontaneous decay near plasmonic nanostructures: Population dynamics. Phys. Rev. A 2011, 83, 055805. [Google Scholar] [CrossRef]
- Evangelou, S.; Yannopapas, V.; Paspalakis, E. Transparency and slow light in a four-level quantum system near a plasmonic nanostructure. Phys. Rev. A 2012, 86, 053811. [Google Scholar] [CrossRef]
- Paspalakis, E.; Evangelou, S.; Yannopapas, V.; Terzis, A.F. Phase-dependent optical effects in a four-level quantum system near a plasmonic nanostructure. Phys. Rev. A 2013, 88, 053832. [Google Scholar] [CrossRef]
- Joannopoulos, J.D.; Meade, R.D.; Winn, J.N. Photonic Crystals: Molding the Flow of Light; Princeton University Press: Princeton, NJ, USA, 1995. [Google Scholar]
- Ho, K.M.; Chan, C.T.; Soukoulis, C.M. Existence of a photonic gap in periodic dielectric structures. Phys. Rev. Lett. 1990, 65, 3152. [Google Scholar] [CrossRef]
- Plihal, M.; Maradudin, A.A. Photonic band structure of two-dimensional systems: The triangular lattice. Phys. Rev. B 1991, 44, 8565. [Google Scholar] [CrossRef]
- Balanis, C.A. Antenna Theory: Analysis and Design, 4th ed.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Huang, Y.-G.; Fan, H.; Wang, X.-H. Exact calculation of local density of states in two-dimensional photonic crystals. Chin. Phys. Lett. 2010, 27, 104213. [Google Scholar] [CrossRef]
- Krokhin, A.A.; Halevi, P.; Arriaga, J. Long-wavelength limit (homogenization) for two-dimensional photonic crystals. Phys. Rev. B 2002, 65, 115208. [Google Scholar] [CrossRef]
- Arriaga, J.; Krokhin, A.A.; Halevi, P. Complete photonic band gap in two dimensions. Effective dielectric constant of 2D photonic crystals with high dielectric contrast. Phys. E Low-Dimens. Syst. Nanostr. 2003, 17, 436. [Google Scholar] [CrossRef]
- Vanier, J. Atomic clocks based on coherent population trapping: A review. Appl. Phys. B 2005, 81, 421. [Google Scholar] [CrossRef]
- Comparo, J. The rubidium atomic clock and basic research. Phys. Today 2007, 60, 33. [Google Scholar] [CrossRef]
- Fang, R.; Han, C.; Lu, B.; Huang, J.; Lee, C. Ramsey interferometry with arbitrary coherent-population-trapping pulse sequence. Phys. Rev. A 2023, 108, 043721. [Google Scholar] [CrossRef]
- Fleischhauer, M.; Scully, M.O. Quantum sensitivity limits of an optical magnetometer based on atomic phase coherence. Phys. Rev. A 1994, 49, 1973. [Google Scholar] [CrossRef] [PubMed]
- Schwindt, P.D.D.; Knappe, S.; Shah, V.; Hollberg, L.; Kitching, J.; Liew, L.-A.; Moreland, J. Chip-scale atomic magnetometer. Appl. Phys. Lett. 2004, 85, 6409. [Google Scholar] [CrossRef]
- Nagel, A.; Graf, L.; Naumov, A.; Mariotti, E.; Biancalana, V.; Meschede, D.; Wynands, R. Experimental realization of coherent dark-state magnetometers. Europhys. Lett. 1998, 44, 31. [Google Scholar] [CrossRef]
- Liang, S.-Q.; Yang, G.-Q.; Xu, Y.-F.; Lin, Q.; Liu, Z.-H.; Chen, Z.-X. Simultaneously improving the sensitivity and absolute accuracy of CPT magnetometer. Opt. Express 2014, 22, 6837. [Google Scholar] [CrossRef]
- Pati, G.S.; Tripathi, R.; Grewal, R.S.; Pulido, M.; Depto, R.A. Synchronous coherent population trapping and its magnetic spectral response in rubidium vapor. Phys. Rev. A 2021, 104, 033116. [Google Scholar] [CrossRef]
- Yuan, J.; Du, P.; Yang, F.; Quan, W.; Li, J. Simultaneous improvement of the sensitivity and resolution of CPT magnetometers based on phase delay and differential method. Opt. Lett. 2024, 49, 3858–3861. [Google Scholar] [CrossRef]
- Boyd, R.W.; Gauthier, D.J. Slow and fast light. In Progress in Optics; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 2002; Volume 43, pp. 497–530. [Google Scholar]
- Eisaman, M.D.; Fleischhauer, M.; Lukin, M.D.; Zibrov, A.S. Toward quantum control of single photons. Opt. Photonics News 2006, 17, 22. [Google Scholar] [CrossRef]
- Lukin, M.D.; Imamoglu, A. Nonlinear optics and quantum entanglement of ultraslow single photons. Phys. Rev. Lett. 2000, 84, 1419. [Google Scholar] [CrossRef] [PubMed]
- Peters, C.; Lange, W. Laser action below threshold inversion due to coherent population trapping. Appl. Phys. B 1996, 62, 221. [Google Scholar] [CrossRef]
- Kilin, S.Y.; Kapale, K.T.; Scully, M.O. Counterintuitive population dynamics in the transient regime. Phys. Rev. Lett. 2008, 100, 173601. [Google Scholar] [CrossRef]
- Lukin, M.D. Colloquium: Trapping and manipulating photon states in atomic ensembles. Rev. Mod. Phys. 2003, 75, 457. [Google Scholar] [CrossRef]
- Sakoda, K. Optical Properties of Photonic Crystals, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Lodahl, P.; Mahmoodian, S.; Stobbe, S. Interfacing single photons and single quantum dots with photonic nanostructures. Rev. Mod. Phys. 2015, 87, 347–400. [Google Scholar] [CrossRef]
- Atatüre, M.; Englund, D.; Vamivakas, N.; Lee, S.-Y.; Wrachtrup, J. Material platforms for spin-based photonic quantum technologies. Nat. Rev. Mater. 2018, 3, 38–51. [Google Scholar] [CrossRef]
- Schriemer, H.P.; van Driel, H.M.; Koenderink, A.F.; Vos, W.L. Modified spontaneous emission spectra of laser dye in inverse opal photonic crystals. Phys. Rev. A 2000, 63, 011801(R). [Google Scholar] [CrossRef]
- Lodahl, P.; van Driel, A.F.; Nikolaev, I.S.; Irman, A.; Overgaag, K.; Vanmaekelbergh, D.; Vos, W.L. Controlling the dynamics of spontaneous emission from quantum dots by photonic crystals. Nature 2004, 430, 654–657. [Google Scholar] [CrossRef] [PubMed]
- Englund, D.; Fattal, D.; Waks, E.; Solomon, G.S.; Zhang, B.; Nakaoka, T.; Arakawa, Y.; Yamamoto, Y.; Vučković, J. Controlling the spontaneous emission rate of single quantum dots in a two-dimensional photonic crystal. Phys. Rev. Lett. 2005, 95, 013904. [Google Scholar] [CrossRef]
- Jalali Mehrabad, M.; Foster, A.P.; Dost, R.; Clarke, E.; Patil, P.K.; Fox, A.M.; Skolnick, M.S.; Wilson, L.R. Chiral topological photonics with an embedded quantum emitter. Optica 2020, 7, 1690–1696. [Google Scholar] [CrossRef]
- Rao, M.; Shi, F.-L.; Rao, Z.-X.; Yang, J.-W.; Song, C.-K.; Chen, X.-D.; Dong, J.-W.; Yu, Y.; Yu, S.-Y. Single-photon emitter deterministically coupled to a topological corner state. Light Sci. Appl. 2024, 13, 19. [Google Scholar] [CrossRef] [PubMed]
- Schulz, A.S.; Kozoň, M.; Vancso, G.J.; Huskens, J.; Vos, W.L. Strongly inhibited spontaneous emission of PbS quantum dots covalently bound to 3D silicon photonic band gap crystals. J. Phys. Chem. C 2024, 128, 9142–9153. [Google Scholar] [CrossRef] [PubMed]
- Kala, A.; Sharp, D.; Choi, M.; Manna, A.; Deshmukh, P.; Kizhake Veetil, V.; Menon, V.; Pelton, M.; Waks, E.; Majumdar, A. Opportunities and challenges of solid-state quantum nonlinear optics. ACS Nano 2025, 19, 14557–14578. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).