Abstract
Suppressing the impact of atmospheric turbulence on laser beam propagation is a bottleneck problem in the application of free space optical communications, with the primary difficulty being the lack of a quantitative description of the effect of turbulence on a laser beam. In this paper, we propose a quantitative description of the effect of turbulence and express a quantitative analysis of the effect of atmospheric turbulence on Bessel–Gaussian beam based on the extended Huygens–Fresnel principle. The results of numerical analysis confirm the validity of the theoretical description. This study also shows that the influence of turbulence is stronger when the annular shape of the Bessel–Gaussian beam is more obvious. The method also provides theoretical guidance for reverse engineering the amplitude and phase distribution of the initial laser beam, thereby effectively reducing the impact of atmospheric turbulence on laser beam propagation.
1. Introduction
Long-distance propagation of laser beams in atmospheric turbulence has extensive application in science and technology such as laser communication, laser defense and remote sensing [1,2,3].
The propagation of lasers in the atmosphere is a complex process that involves several factors influencing the transmission and attenuation of laser beams. There are some key factors that affect the propagation of lasers in the atmosphere. Gases and particles in the atmosphere can absorb laser energy, causing a decrease in laser intensity. Particles or molecules in the atmosphere can scatter laser beams, leading to beam broadening and attenuation. Inhomogeneities and turbulent motion in the atmosphere can cause jitter and spreading of the laser beam, further affecting the quality of laser transmission, which seriously hinders the application of laser beams in these fields [4,5,6,7,8]. Adaptive optics systems can compensate for the deformation and spreading effects caused by atmospheric turbulence, which is considered one of the most effective methods to overcome the turbulence effect of the atmosphere [9,10,11,12,13]. However, due to the limitations of the environment and cost, adaptive optics technology has been applied in few fields, such as astronomical observation. In recent years, with the rapid development of optical field modulation technology, some researchers have proposed using the special structure and coherence control of laser beams to reduce the impact of turbulence on beams [14,15,16,17,18]. Recently, an “optical pin beam” which exhibits unusual properties in long-distance propagation compared with conventional Gaussian beams has been demonstrated [17]. Furthermore, true eigenmodes of atmospheric turbulence which are invariant under propagation through the atmosphere have been developed [18]. In addition, some non-diffracting beams, such as Bessel beams and Airy beams, are also considered ideal laser beam modes that can freely travel in turbulence [19,20]. It is important to note that quantitatively analyzing the turbulence effects on Gauss–Bessel beams is a challenging task. The specific impact of turbulence will depend on factors such as the strength and scale of the turbulence, the beam parameters and the propagation distance. However, to the best of my knowledge, there is no relevant research work that qualitatively analyzes the effects of turbulence on Gauss–Bessel beams.
Nevertheless, a large number of studies have found that these beams cannot maintain their polarization and optical field distribution during long-distance propagation [18]. The reason for this perception bias is that much attention has focused on which types of structured light are best with regard to turbulence, but with seemingly inconclusive results. Therefore, it is necessary to establish a scientific quantitative evaluation standard for the effect of atmospheric turbulence on a laser beam.
In this paper, we consider the quantitative description method with regard to the influence of turbulence on laser propagation. A quantitative evaluation method for the degree of influence of atmospheric turbulence on the distribution of laser intensity is given, using the degree of impact of atmospheric turbulence on light intensity as the judgment criterion. As an example, we quantitatively analyzed the relationship between the impact of turbulence on various parameters of the zero-order Bessel–Gauss beams based on this method.
2. Formulation
From the viewpoint of image processing, the influence of atmospheric turbulence on laser beam propagation depends on the ratio of the spectral radius of light intensity without turbulence to the atmospheric coherence length [21]. The larger the ratio, the greater the influence of atmospheric turbulence on the laser beam, and vice versa. In order to quantitatively describe the effect of turbulence on a laser beam, a criterion can be defined, namely [21]:
where can be seen as the atmospheric coherence length in the frequency domain with [22]:
is the structure constant of the refractive index fluctuations of the atmospheric turbulence which is used to describe the strength of turbulence. In Equation (2), L is the total propagation distance of the atmospheric turbulence. As we know, when using the traditional method, the effect of turbulence on the beam is only related to the atmospheric coherence length . In fact, the influence of turbulence with the same on different beams is different. The criterion defined in Equation (1) combines the turbulence strength and beam property.
It should be noted that there are inner scales and outer scales of turbulence which will affect the strength of turbulence. For simplicity, we only study the effect of atmospheric coherence length on the beam because inner scale and outer scale can be included in the atmospheric coherence length.
In Equation (1), is the second moment radius of the Fourier transform of the light intensity without turbulence, which can be written as:
where is the inverse Fourier transform of the , which can be expressed as:
In Equation (5), and with and are the transverse coordinates of two different points at the origin. Obviously, the is the light intensity under vacuum conditions.
As we know, the initial light field of the zero-order Bessel–Gaussian beam can be represented as [23,24]
where , is a constant that can modulate the size of the Bessel–Gaussian spot, is the waist radius of the Gaussian part of the zero-order Bessel–Gaussian beam. Using the Fresnel diffraction integral, the light intensity of the zero-order Bessel–Gaussian beam in the vacuum can be calculated as [24]:
where is the waist radius of the zero-order Bessel–Gaussian beam at the origin. The nth-order moments radius of the intensity can be derived from the relationship between the moment radius and Fourier transformation [25]
and the second-order semi-radius of the light intensity spectrum of a zero-order Bessel–Gaussian beam propagating in a vacuum is
To illustrate the relationship between our standards and the similarity of laser beam, we provide the definition of similarity. The definition of similarity is:
3. Numerical Results and Analysis
To quantitatively analyze the influence of atmospheric turbulence on the zero-order Bessel–Gaussian beam, we set the wavelength of the laser to be 1.06 microns, the waist radius w0 of Gaussian beam to be 0.1 m, and the refractive index structural constant does not change as the laser beam propagates in atmospheric turbulence. Since, under the condition that the waist of Gaussian is certain, different modulation factors correspond to different spot distributions, the a selected in this paper is 80/m, 60/m, 40/m and 20/m, respectively; the corresponding initial beam distributions are shown in Figure 1:
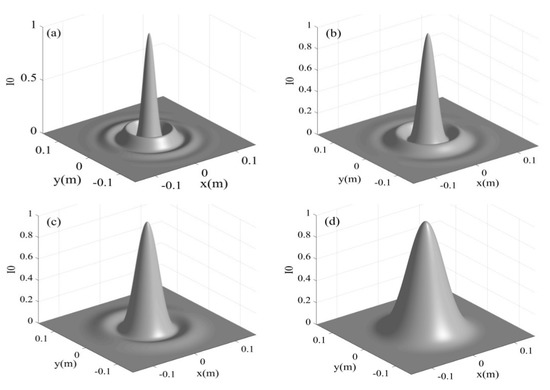
Figure 1.
Intensity distribution of initial Bessel–Gaussian beam with w0 = 0.1 m, where (a) a = 80/m, (b) a = 60/m, (c) a = 40/m, (d) a = 20/m.
From Figure 1, it can be seen that there are different intensity distributions with the different parameters a. As parameters a decreases, the ring spot of Bessel–Gaussian beam decreases gradually. This is because the ring spot of the Bessel–Gaussian beam is determined by the product of a and r. The smaller a is, the larger the ring spacing of Bessel–Gaussian beam is; that is to say, when the waist of the Gaussian part is certain, the smaller a is, the more similar the zero-order Bessel–Gaussian beam is to the Gaussian beam. The larger a is, the more similar the zero-order Bessel–Gaussian beam is to the Bessel beam.
In order to quantitatively study the effect of turbulence on different zero-order Bessel–Gaussian beams, we set the propagation distance of the beam to be 3 km. As a comparison, the spot distributions of different zero-order Bessel–Gaussian beams propagating 3 km in a vacuum are shown in Figure 2. Compared with Figure 1, after propagating 3 km in a vacuum, the spot of the corresponding zero-order Bessel–Gaussian beam basically maintains its original distribution characteristics.
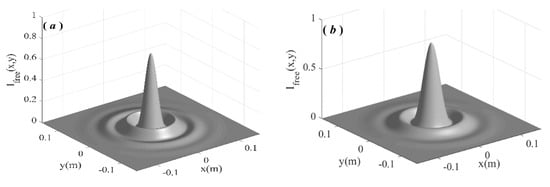
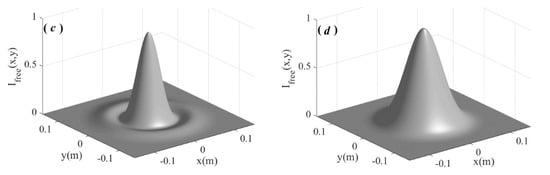
Figure 2.
Intensity distribution of the zero-order Bessel–Gaussian beam when it propagates 3000 m in vacuum, where (a) a = 80/m, (b) a = 60/m, (c) a = 40/m, (d) a = 20/m.
For the same propagating distance in turbulent atmosphere, that is, z = 3 km, the spot distributions with are shown in Figure 3. Compared with Figure 2, due to the influence of turbulence, the ring spots began to degrade. From Figure 3, it can be seen that the smaller the value of a, the less significant the effect of atmospheric turbulence. Correspondingly, the smaller the value of a, the fewer rings it corresponds to. This effect can also be seen from the change in peak value: the larger a is, the more obvious the drop in peak value.
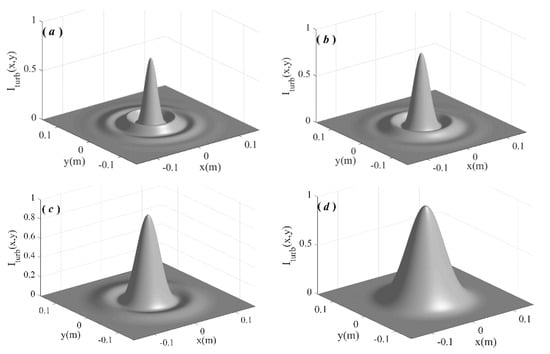
Figure 3.
Intensity distribution of the zero-order Bessel–Gaussian beam when it propagates 3000 m in turbulent atmosphere with , where (a) a = 80/m, (b) a = 60/m, (c) a = 40/m, (d) a = 20/m.
If the strength of turbulence is increased, that is, , the corresponding beam spot distributions propagated 3 km in turbulent atmosphere are shown in Figure 4. Similarly, the more obvious the initial ring spot is, the greater the impact of turbulence.
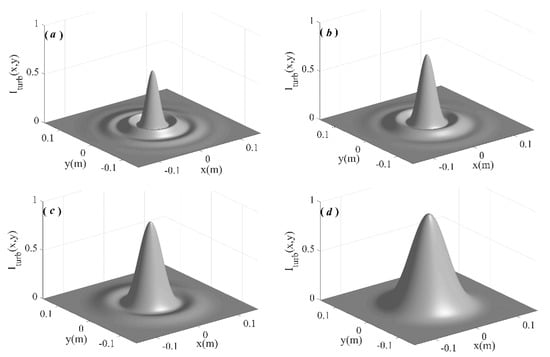
Figure 4.
Intensity distribution of the zero-order Bessel–Gaussian beam when it propagates 3000 m in turbulent atmosphere with , where (a) a = 80/m, (b) a = 60/m, (c) a = 40/m, (d) a = 20/m.
With a further increase in the turbulence intensity, the spot distributions of zero-order Bessel–Gaussian beam propagated 3 km with in turbulent atmosphere are shown in Figure 5. Similarly, the more obvious the initial ring spot is, the more it will be affected by turbulence.
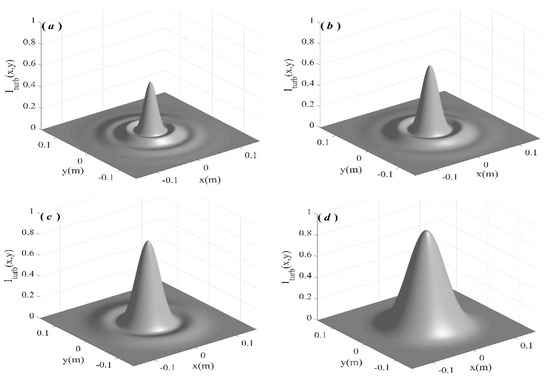
Figure 5.
Intensity distribution of the zero-order Bessel–Gaussian beam when it propagates 3000 m in turbulent atmosphere with , where (a) a = 80/m, (b) a = 60/m, (c) a = 40/m, (d) a = 20/m.
In order to illustrate the effectiveness of the judgment factor proposed in this paper, we calculate the similarity of beam spots corresponding to Figure 3, Figure 4 and Figure 5 with Figure 2, respectively. The smaller the similarity of light intensity, the greater the impact of turbulence on it.
The vacuum frequency domain radius for the different Bessel modulation factors, the coherence length of atmospheric turbulence in frequency domain, the ratio of and , namely the parameter τ which is used to quantitatively describe the turbulence influence, and the similarity S compared with Figure 2 are given in Table 1 for different atmospheric turbulence strengths.

Table 1.
The parameters of the zero-order Bessel–Gaussian beam after propagating 3000 m in atmosphere with different turbulence strengths.
It can be seen from Table 1 that the larger the parameter τ, the smaller the similarity of the beam, which means a laser beam with larger parameter τ is less affected by atmospheric turbulence. When the parameter τ is smaller than two, the similarity is approximately equal to one, which means the effect of atmospheric turbulence can be ignored. If the parameter τ is less than 6, the similarity can reach 0.99. That is to say, the parameter τ used to quantitatively describe the effect of atmospheric turbulence in this paper is effective and consistent with the change in similarity of the laser beam. At the same time, we can also see that the more obvious the ring, the greater the influence of atmospheric turbulence on the Bessel–Gaussian beam. The results can be explained as follows: micro vortex structure and turbulence-scale changes can play a similar role to the diffraction effect in optical systems, which can reduce the local intensity changes of the laser beam and achieve a certain degree of smoothness. When the laser beam passes through the turbulence, the irregular distribution of turbulence, changes in turbulence scale, and the interaction of vortices will smooth out the non-uniformity and fluctuations of the laser beam, making it more uniform and stable. A laser beam with more obvious rings has a higher frequency; thus, the influence of the beam affected by turbulence is more obvious.
4. Summary
Apart from adaptive optics technology, turbulence’s impact on laser propagation can also be reduced through light field modulation techniques and the design of initial light fields. This paper proposes a criterion for quantitatively describing the effect of turbulence on laser beam propagation in atmospheric turbulence. This criterion not only provides a quantitative description of turbulence’s impact but also offers a method for initial beam design. To illustrate its effectiveness, this paper uses Bessel–Gaussian beams as an example and conducts a quantitative study on the effect of atmospheric turbulence on the laser beam based on this criterion. The results indicate that the criterion is consistent with the description using the similarity of the laser beam. Based on this criterion, it can be inferred that under the same conditions, the more apparent the initial beam spot ring, the greater the impact of the atmospheric turbulence on the Bessel–Gaussian beams. The physical mechanism behind this phenomenon can be explained by the fact that laser beams with more pronounced ring structures have higher frequencies, and atmospheric turbulence has a more noticeable impact on them.
Funding
This work was supported by the Hunan Provincial Natural Science Foundation of China (2020JJ4491).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares that he has no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. The author declares no conflict of interest.
References
- Slusher, R.E. Laser technology. Rev. Mod. Phys. 1999, 71, S471–S479. [Google Scholar] [CrossRef]
- Kaushal, H.; Kaddoum, G. Optical communication in space: Challenges and mitigation techniques. IEEE Commun. Surv. Tutor. 2017, 19, 57–96. [Google Scholar] [CrossRef]
- Berge, L.; Skupin, S.; Nuter, R.; Kasparian, J.; Wolf, J.P. Ultrashort filaments of light in weakly ionized, optically transparent media. Rep. Prog. Phys. 2007, 70, 1633–1713. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Dissipation of energy in the locally isotropic turbulence. Dokl. Akad. Nauk SSSR 1941, 32, 16–18. [Google Scholar]
- Cai, Y.; He, S. Average intensity and spreading of an elliptical Gaussian beam propagating in a turbulent atmosphere. Opt. Lett. 2006, 31, 568–570. [Google Scholar] [CrossRef]
- Chu, X. Evolution of an Airy beam in turbulence. Opt. Lett. 2011, 36, 2701–2703. [Google Scholar] [CrossRef]
- Zhu, X.; Kahn, J.M. Free-space optical communication through atmospheric turbulence channels. IEEE Trans. Commun. 2002, 50, 1293–1300. [Google Scholar]
- Gu, Y.; Gbur, G. Scintillation of Airy beam arrays in atmospheric turbulence. Opt. Lett. 2010, 35, 3456–3458. [Google Scholar] [CrossRef]
- Xu, Y.; Lan, B.; Liu, C.; Chen, M.; Tang, A.; Xian, H. Adaptive optics pre-compensation for orbital angular momentum beams transmitting through simulated atmospheric turbulence. Opt. Express 2023, 31, 13665–13671. [Google Scholar] [CrossRef] [PubMed]
- Ricklin, J.C.; Davidson, F.M. Atmospheric turbulence effects on a partially coherent Gaussian beam: Implications for free-space laser communication. J. Opt. Soc. Am. A 2002, 19, 1794–1802. [Google Scholar] [CrossRef] [PubMed]
- Weyrauch, T.; Vorontsov, M.A. Free-space laser communications with adaptive optics: Atmospheric compensation experiments. J. Opt. Fiber. Commun. Rep. 2004, 1, 355–379. [Google Scholar] [CrossRef]
- Dayton, D.; Sandven, S.; Gonglewski, J.; Browne, S.; Rogers, S.; McDermott, S. Adaptive optics using a liquid crystal phase modulator in conjunction with a Shack-Hartmann wave-front sensor and zonal control algorithm. Opt. Express 1997, 1, 338–346. [Google Scholar] [CrossRef]
- Belousov, V.N.; Galaktionov, I.V.; Kudryashov, A.V.; Nikitin, A.N.; Otrubyannikova, O.V.; Rukosuev, A.L.; Samarkin, V.V.; Sivertceva, I.V.; Sheldakova, J.V. Adaptive optical system for correction of laser beam going through turbulent atmosphere. Proc. SPIE 2020, 11560, 1156026. [Google Scholar]
- Cox, M.A.; Mphuthi, N.; Nape, I.; Mashaba, N.; Cheng, L.; Forbes, A. Structured light in turbulence. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 7500521. [Google Scholar] [CrossRef]
- Nape, I.; Singh, K.; Klug, A.; Buono, W.; Rosales-Guzman, C.; McWilliam, A.; Franke-Arnold, S.; Kritzinger, A.; Forbes, P.; Dudley, A.; et al. Revealing the invariance of vectorial structured light in complex media. Nat. Photonics 2022, 16, 538–546. [Google Scholar] [CrossRef]
- Gbur, G. Partially coherent beam propagation in atmospheric turbulence. J. Opt. Soc. Am. A 2014, 31, 2038–2045. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Liang, X.; Goutsoulas, M.; Li, D.; Yang, X.; Yin, S.; Xu, J.; Christodoulides, D.N.; Efremidis, N.K.; Chen, Z. Robust propagation of pin-like optical beam through atmospheric turbulence. APL Photonics 2019, 4, 076103. [Google Scholar] [CrossRef]
- Klug, A.; Peters, C.; Forbes, A. Robust structured light in atmospheric turbulence. Adv. Photonics 2023, 5, 016006. [Google Scholar] [CrossRef]
- Durnin, J.; Miceli, J.J.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499–1501. [Google Scholar] [CrossRef] [PubMed]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of accelerating Airy beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Chu, X. Quantitative description of turbulence effect on a beam. J. Opt. 2023, 52, 63. [Google Scholar] [CrossRef]
- Yura, H.T.; Hanson, S.G. Optical beam wave propagation through complex optical systems. J. Opt. Soc. Am. A 1987, 4, 1931–1948. [Google Scholar] [CrossRef]
- Hwang, C.Y.; Kim, K.Y.; Lee, B. Bessel-like beam generation by superposing multiple Airy beams. Opt. Express 2011, 19, 7356–7364. [Google Scholar] [CrossRef] [PubMed]
- Chu, X. Analytical study on the self-healing property of Bessel beam. Eur. Phys. J. D 2012, 66, 259. [Google Scholar] [CrossRef]
- Testorf, M.E.; Hennelly, B.M.; Ojeda-Castaneda, J. Phase-Space Optics: Fundamentals and Applications; McGraw-Hill: New York, NY, USA, 2009; ISBN 978-0-07-159799-9. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).