Abstract
This study aims to apply the densitometry distribution analysis (DDA) method to study corneal densitometry depending on age and corneal region from Galilei Dual Scheimpflug Analyzer tomography. A total of 83 healthy participants aged 39.02 ± 18.34 years (range 9–81 years) were screened using a Ziemer Galilei G2. Images were analysed using the DDA, and two parameters, α (corneal transparency) and β (corneal homogeneity), were estimated. A two-way ANOVA analysis was performed to investigate whether α and β are influenced by age, corneal región (four concentric areas were considered), and their interaction. The parameters α and β statistically change with age and corneal region. A statistically significant interaction effect of 13% (α) and 11% (β) exists between age and corneal region. However, the corneal region plays a more significant role than aging in corneal densitometry; 31% (α) and 51% (β) of the variance can be attributed to the corneal region, while 28% (α) and 5% (β) can be attributed solely to aging. Corneal densitometry can be objectively assessed from Galilei G2 images using the DDA method. The corneal region plays a more significant role than aging in corneal densitometry. Consequently, general results on corneal densitometry and aging should be taken cautiously.
1. Introduction
Corneal densitometry consists of estimating corneal transparency automatically and objectively. Corneal transparency is of paramount importance to guarantee ocular integrity. Consequently, corneal densitometry is gaining interest as an indicator of ocular health. Investigating corneal densitometry has shown to be of use to assess corneal integrity in a large range of conditions, such as corneal infection [1,2], keratoconus [3,4,5,6], refractive surgery [7,8,9], contact lens wear [10,11,12,13], aging [14,15,16,17], and myopia [18], among others.
In the clinical environment, corneal densitometry has traditionally been restricted to Scheimpflug imaging with a single clinical device (Pentacam HR, Oculus GmbH, Wet-zlar, Germany), which made corneal densitometry a ‘black box’. However, due to the increasing interest in corneal densitometry, novel algorithms are being designed, tested, and shared to estimate corneal densitometry objectively. These have been applied to Scheimpflug images obtained from different devices [5,12,13,15,19]. Similar algorithms for corneal densitometry estimation are also applied to Optical Coherence Tomography (OCT) [20,21,22,23]. In this context, the Densitometry Distribution Analysis (DDA) was introduced [13,15]. The DDA is based on the statistical modeling of the pixel intensity distribution of Scheimpflug images [13,15]. The DDA has shown to be very well correlated with traditional densitometry estimated from Pentacam HR [15], while at the same time has shown to be repeatable and platform independent [15]. The DDA method provides two different parameters, α and β, accounting for corneal transparency (equivalent to corneal densitometry from Pentacam HR [15]) and corneal homogeneity, respectively. Corneal densitometry acquired from Pentacam HR represents an objective measure of corneal transparency. Additionally, the DDA has already been applied to Scheimpflug images acquired with a Galilei G2 Dual Scheimpflug Analyzer, overcoming the lack of proprietary software for corneal densitometry calculation [12].
From the wide range of parameters of corneal densitometry analysis, aging is one of the most controversial. The majority of reports based on Scheimpflug Pentacam HR support the idea of corneal densitometry being positively correlated with age [14,15,16,17], while other works contradict these findings [1,19,24,25]. The current work aims to apply the previously validated DDA method to Scheimpflug Galilei G2 Dual Scheimpflug Analyzer images corresponding to participants of different age and investigate potential changes in corneal transparency (α) and homogeneity (β) with corneal region and aging.
2. Materials and Methods
2.1. Participants and Protocol
This study was approved by the Ethics Committee for Clinical Research of Aragon (PI22/531) and adhered to the tenets of the Declaration of Helsinki. All subjects, or their legal guardian when applicable, gave written informed consent to participate after the nature and possible consequences of the study were explained.
This study included eighty-three healthy participants (36 men and 47 women; mean age 39.02 ± 18.34 years old, range 9–81 years old), resulting in data for 166 eyes. Participants were recruited into the study in the school of Optics and Optometry of the University of Zaragoza (Spain), and both eyes were assessed. Participants had no prior history of eye injury, history of cornea and intraocular surgery, corneal pathology (trauma, ectatic, and infections), or current use of topical ocular medications. Systemic conditions that were considered exclusion criteria were diabetes mellitus, multiple sclerosis, and uncontrolled hypertension. Patients were excluded on the basis of systemic medications if they were known to induce corneal changes. None of the subjects were rigid contact lens wearers. Regular soft contact lens wearers were asked not to wear them for at least 48 h prior to measurement day. Participant screening included subjective refraction, monocular visual acuity (VA) with the best-corrected distance refraction with glasses, and anterior pole evaluation with a slit-lamp biomicroscope.
Corneal Scheimpflug images were obtained for both eyes of each participant using the Galilei G2 Dual Scheimpflug Analyzer (Ziemer Ophthalmic Systems, Bellmund, Switzerland). This tomographer consists of two Scheimpflug cameras to decrease possible artefacts caused by movements. The measurements protocol takes a series of 26 images (i.e., 26 corneal meridians) with a uniform blue light source. The reproducibility and repeatability of the DDA method applied to Galilei G2 images have been reported previously [12]. Therefore, one measurement of good quality, as indicated by Galilei G2 Dual Scheimpflug Analyzer software, was captured in each eye. Measurements for all subjects took place in the morning, at least 3 h after the participant reported the time of awaking on that day.
2.2. Image Analysis
Corneal transparency and homogeneity were estimated in the overall cornea (up to 12 mm) using the DDA method [13,15]. Scheimpflug images corresponding to 26 corneal meridians (a fixed size of 1004 × 1004 pixels) were exported in .bin format for further analysis (i.e., 4316 images in total = 83 subjects × 2 eyes/subject × 26 images/measurement). The image analysis protocol applied to Galilei G2 Dual Scheimpflug Analyzer images is explained in detail in previous work [12]. In brief, the image analysis consists of three main stages: corneal registration, corneal segmentation, and statistical modelling of the pixel intensity distribution. The Galilei G2 Dual Scheimpflug Analyzer obtains two corneal images per meridian, each captured with one of the two available Scheimpflug cameras. Consequently, corneal registration is necessary to ensure that both corneal images captured per meridian share the same coordinate system.
Further, corneal segmentation is necessary to separate the pixels corresponding to the cornea from those from the background. Thus, in this stage, the segmentation method automatically extracts the anterior and posterior borders of the cornea. In short, traditional image processing techniques, including a median filter and Canny edge detection, were used to remove the noise, extract the boundaries of interest, and segment the corneal tissue.
Then, a region of interest (ROI) was extracted automatically for pixel statistical modelling, as in previous work [13]. In short, the anterior and posterior corneal boundaries delineated the vertical (axial) ROI dimension. Regarding the horizontal (lateral) dimension, a moving ROI of 11 pixels, with a one-pixel step, was applied across the cornea for each corneal image. The moving ROI covered the full corneal image—i.e., 12 mm of the cornea.
Further, for the statistical modelling of the pixel intensity distribution, pixels corresponding to a given ROI were modelled using the Weibull distribution function, as described in previous work [13]. From this function, two parameters are extracted (α and β), which account for tissue transparency and homogeneity, respectively. These are α (scale parameter) and β (shape parameter). In general, a change in scale parameter α (transparency) causes a shift in pixel intensity (x-axis), with higher α values corresponding to a brighter image (i.e., more scatter and less transparency), and vice versa. A change in shape parameter β (homogeneity) affects the width of the pixel intensity distribution. The smaller β is, the greater the spread of the pixel intensity distribution of a given image (i.e., lower homogeneity). In contrast, a large β indicates greater similarity in pixel intensities within a given image or ROI (i.e., greater homogeneity).
In order to build corneal α and β parameter maps, data were transformed from Cartesian (x, y) to polar coordinates (r, θ) and interpolated, as well as smoothened using second-order Zernike polynomials, in agreement with previous research [5,12,13]. For consistency with the previous literature on corneal densitometry based on the Pentacam densitometry add-on module [14,16,17], the DDA protocol was performed in four concentric corneal regions: the central cornea (2 mm diameter centered in the apex), the mid cornea (2–6 mm annulus), the mid-peripheral cornea (6–10 mm annulus), the peripheral cornea (10–12 mm annulus), and the entire cornea (up to 12 mm).
2.3. Statistical Analysis
The statistical analysis was performed using SPSS statistics software (SPSS Inc, Chicago, IL, USA). For statistical analysis, subjects were grouped into six different groups according to their age: from 9 to 17 years old (n = 15); from 18 to 29 years old (n = 15); from 30 to 39 years old (n = 13), from 40 to 49 years old (n = 13); from 50 to 59 years old (n = 15); and over 60 years old (n = 12). Two-way repeated measures ANOVA test was performed in α (i.e., transparency) and in β (i.e., homogeneity) independently to ascertain whether those parameters change depending on the age (6 levels corresponding to the 6 age groups previously defined) and on the corneal area (4 levels: central (0–2 mm), mid (2–6 mm), mid-peripheral (6–10 mm), and peripheral (10–12 mm) cornea). Shapiro–Wilk test, Mauchly’s test of sphericity, and Levene’s test indicated that the assumptions of normality, sphericity, and homogeneity of variances, respectively, had not been violated. The partial eta squared (ƞp2) was also calculated as a measure of the effect size of the different variables under analysis in the ANOVA model. The ƞp2, which can be also expressed as a percentage, represents the proportion of the variance that can be explained by a given variable in the model after accounting for variance explained by other variables in the model. The ƞp2 ranges from 0 (null effect size) to 1 (complete effect size). Additionally, the Pearson correlation was used to assess correlations of α and β against age, depending on the regional area considered. The level of significance was set to 0.05. The sample size was derived based on calculations from previously published data on DDA applied to age-related corneal densitometry changes [15]. The same methodology applied to the current work suggested that a sample size of at least 46 participants would yield a 90% power to distinguish corneal tissue changes between the youngest (mean age 25 yo) and oldest age (mean age 74 yo) groups at the 0.05 significance level.
3. Results
Table 1 shows the mean and standard deviation of age for the six different groups. As a part of a preliminary analysis, no statistically significant difference was found between left (OS) and right eyes (OD) in parameters α and β-OD vs. OS (paired t-test, overall cornea) α: p = 0.84, and β: p = 0.88. Similarly, a strong correlation was found between OD and OS eyes for both parameters (α: r = 0.96 and β: r = 0.96, both p < 0.001). Consequently, for simplicity, results are shown for the left eye only (83 eyes) unless otherwise stated. The monocular visual acuity, with the best-corrected distance refraction for all of them, was higher than 0.8 (decimal VA).

Table 1.
Group mean values ± standard deviation of parameters α and β, expressed in arbitrary units, in different corneal regions, for different age groups. Data for left eye only.
Group mean values of parameters α and β for different age groups and corneal areas are shown in Table 1. There is a statistically significant decrease in corneal transparency (parameter α) with age (two-way ANOVA, F(5405) = 23.95, p < 0.001, ƞp2 = 0.28) and with distance from the apex (two-way ANOVA, F(3243) = 44.61, p < 0.001, ƞp2 = 0.31). Additionally, there exists a statistically significant interaction effect between these two independent variables, i.e., age and distance from the apex (two-way ANOVA, F(15,1134) = 2.92, p < 0.001, ƞp2 = 0.13).
Similarly, there is a statistically significant change in corneal homogeneity (parameter β) with age (two-way ANOVA, F(5405) = 2.89, p = 0.015, ƞp2 = 0.05) and with distance from the apex (two-way ANOVA, F(3243) = 106.9, p < 0.001, ƞp2 = 0.51). Additionally, a statistically significant interaction effect exists between these two independent variables (two-way ANOVA, F(15,1134) = 2.50, p = 0.002, ƞp2 = 0.11).
The results from the corresponding Bonferroni post-hoc test for parameters α and β with age and with corneal area considered are shown in Table 2 and Table 3, respectively.

Table 2.
p-value for pairwise comparisons from ANOVA post-hoc test (adjustment for multiple comparisons: Bonferroni) for parameters α and β with age. The lack of statistical significance is marked with a cross (×).

Table 3.
p-value for pairwise comparisons from ANOVA post-hoc test (adjustment for multiple comparisons: Bonferroni) for parameters α and β with corneal area considered. The lack of statistical significance is marked with a cross (×).
Graphical representation of the distribution of the α and β parameters in the overall cornea depending on the age group for the 83 eyes is shown in Figure 1 and Figure 2, respectively.
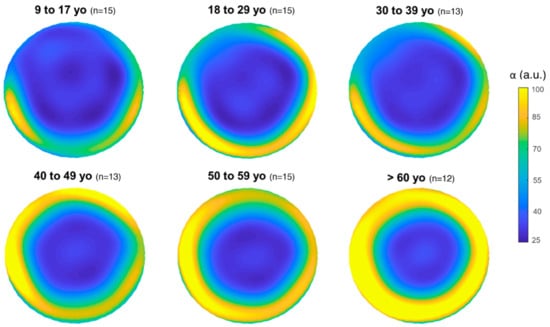
Figure 1.
Mean distribution of α (i.e., corneal transparency) for each age group in the overall cornea (12 mm diameter). The color bar (α) is expressed in arbitrary units (a.u.).
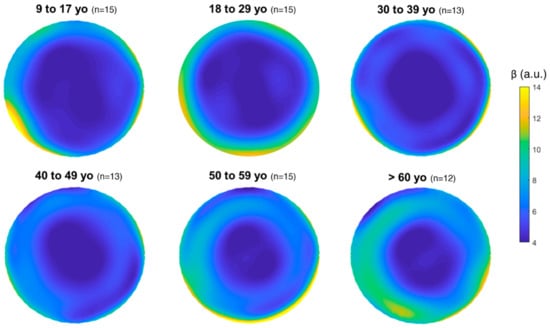
Figure 2.
Mean distribution of β (i.e., corneal homogeneity) for each age group in the overall cornea (12 mm diameter). The color bar (β) is expressed in arbitrary units (a.u.).
The relationship between corneal parameters (α and β) and age for different corneal areas of analysis is displayed in Figure 3. The corresponding results from the Pearson correlation coefficient along with their p-value are shown in Table 4.
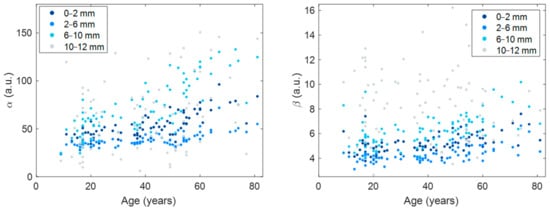
Figure 3.
Scatter plots of α (left) and β (right) against age for different corneal areas of analysis. α and β are expressed in arbitrary units (a.u.). Corresponding statistics are shown in Table 4.

Table 4.
The Pearson correlation coefficient and the corresponding p-value of the α and β with age, depending on the corneal area considered. The overall cornea is also considered. Corresponding scatter plots are shown in Figure 3.
4. Discussion
This work shows that corneal tomographies acquired with the Scheimpflug Galilei G2 Dual Scheimpflug Analyzer can be used to assess corneal densitometry objectively. The property software does not incorporate an objective module to such an end [12]. However, it is possible to obtain corneal densitometry by applying image processing and statistical modelling of the pixel intensity distribution (DDA method) to the acquired corneal tomographies.
This study investigates corneal densitometry obtained from a large group of healthy patients aged 9–81 years and its relationship with age and corneal region from Galilei Dual Scheimpflug Analyzer tomography. There is a statistically significant change in corneal transparency (α) and homogeneity (β) with age (Table 1 and Table 2). Apparently, corneal transparency (α) tends to increase with age (Table 1, Figure 1 and Figure 3), which translates into lower corneal transparency with age. This result is in agreement with previous works considering the overall cornea [14,16,17]. Seemingly, corneal homogeneity (β) tends to vary with age (Table 1, Figure 3), but more weakly than transparency (Table 2). In any case, the corneal region seems to play an important role in the relationship between corneal tissue parameters and age (Table 4). The two-way ANOVA statistical analysis results indicate that 28% of the variance of the dependent variable α can be attributed to aging, whilst only 5% of the variance of the dependent variable β can be attributed to aging. However, the corneal area analyzed (i.e., the distance from the apex) seems to play a more important role on its own than aging. The results from the statistical analysis indicate that 31% of the variance of the dependent variable α can be attributed to the corneal area analyzed, whilst 51% of the variance of the dependent variable β can be attributed to the corneal area analyzed, in both cases independently of aging. Additionally, stronger statistical significance was found in pairwise comparisons within corneal regions (Table 3) than within age groups (Table 2).
The corneal structure does not dramatically change from apex to limbus; however, the results from the current work point at the distance from the apex as a major contribution to corneal densitometry than aging. We consider this result might be an artifact caused by the spurious reflections originated at the limbal area. These reflections are inherent to Scheimpflug imaging and make the most peripheral cornea look white as if it were an opaque tissue, which in reality is not. The large spread observed in α and β at the most peripheral region (Figure 3) indicates a large variability in this area depending on the individual. The reason why some participants have stronger reflections in their corneoscleral transition is yet to be investigated. However, a previous report on normative corneal densitometry readings, in agreement with the current work, also found the peripheral area as the least repeatable and reproducible [14]. In the current work, to be in agreement with previous literature on corneal densitometry and aging [14,16,17], we decided to analyze the overall cornea (i.e., up to 12 mm). However, other works based on Scheimpflug imaging and the DDA method limited the analysis area to avoid those spurious reflections [5,12,13,15]. It would be interesting to analyze the whole corneal range with other technologies, such as OCT or confocal microscope, that would not be so strongly affected by this limitation inherent to Scheimpflug imaging. In that sense, OCT was used to objectively measure corneal light backscatter in patients who wear contact lenses [20]. Hillenaar et al. [26] evaluated the normative values in relation to sex and age measuring corneal bakscatter by in vivo confocal microscope.
Furthermore, there are novel reports investigating potential confounding factors affecting corneal densitometry. Anterior eye biometry changes with aging, and those changes in biometry might alter how light backscatters and consequently modify corneal densitometry readings. This is the thesis of the work of Miażdżyk et al. [19]. They developed a methodology based on image normalization applied to commercially available Scheimpflug images and eliminated the existing baseline correlation between age and corneal densitometry. Their work ponders whether the commonly accepted correlation of corneal densitometry with age is an artifact caused by intrinsic age-related biometry changes in anterior chamber depth or pupil size [19]. In the same line of work, Consejo et al. investigated whether corneal tilt might be a confounding factor affecting corneal densitometry readings [27]. They found a minor but statistically significant effect of corneal tilt on corneal densitometry readings [27]. The lack of perfect symmetry in Figure 1 might be a consequence of this effect. Furthermore, Garzon et al. [16] determined corneal densitometry values in relation to other parameters such as corneal thickness and keratometry using the Oculus Pentacam system. We found that neither corneal curvature nor corneal thickness affect corneal densitometry in normal subjects. Similar results were found by Wu et al. [28], i.e., corneal densitometry is not correlated with corneal thickness in healthy subjects. However, Lopes et al. [3] found that keratoconus patients had higher densitometry readings than healthy patients and there is a correlation with keratoconus severity, based on corneal keratometry and thickness.
It is well known that the cornea ages with time. In the corneal periphery, corneal limbal degenerations that do not significantly affect the subject’s visual ability, such as farinata, arcus senilus, Vogt’s white limbal girdle, and Hassal–Henle bodies, have been characterized clinically [29,30]. However, given the results of the current work and previous literature aiming to demystify corneal densitometry [19,30], whether corneal densitometry based on Scheimpflug imaging is a suitable platform to assess corneal aging changes remains elusive.
This study does not present substantial limitations. The DDA method allows a layer analysis. However, in the current work, corneal depth was not considered as it was previously evaluated that corneal densitometry in relation to aging is less affected by depth than by the corneal region analysed [14,15]. In the current study, only one measurement was acquired per person. However, this should not be considered a limitation of the current work because there is previous evidence of the excellent repeatability of the DDA method when applied to Galilei G2 Dual Scheimpflug Analyzer images [12].
In conclusion, the corneal region plays a greater role than aging in corneal densitometry. The influence of spurious reflections in the peripheral cornea, inherent to Scheimpflug corneal imaging, might confound the results. Consequently, results on corneal densitometry and aging should be taken with caution.
Author Contributions
A.C.: Conceptualization; data curation (equal); formal analysis (lead); investigation; methodology (lead); project administration (equal); resources (lead); software; supervision (equal); validation; visualization (lead); writing—original draft (equal); writing—review and editing. S.B.: Formal analysis; investigation (equal); validation (equal); visualization; writing—original draft (equal); writing—review and editing (equal). L.R.: Investigation (equal); methodology; project ad-ministration (equal); resources (lead); supervision (equal); validation (equal); writing—original draft (equal); writing—review and editing (equal). All authors have read and agreed to the published version of the manuscript.
Funding
Grant TED2021-130723A-I00 funded by MCIN/AEI/10.13039/501100011033 and by European Union “NextGenerationEU”/PRTR. Additionally supported by Cátedra SAMCA de Desarrollo Tecnológico de Aragón, Universidad de Zaragoza (III Premio a la Innovación Multidisciplinar).
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board (or Ethics Committee) of This study was approved by the Ethics Committee for Clinical Research of Aragon (PI22/531) for studies involving humans.
Informed Consent Statement
All subjects, or their legal guardian when applicable, gave written informed consent to participate after the nature and possible consequences of the study were explained.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Otri, A.; Fares, U.; Al-Aqaba, M.A.; Dua, H. Corneal densitometry as an indicator of corneal health. Ophthalmology 2012, 119, 501–508. [Google Scholar] [CrossRef] [PubMed]
- Orucoglu, F.; Talaz, S.; Aksu, A.; Muftuoglu, O. Corneal densitometry evaluation in archipelago keratitis. Int. Ophthalmol. 2014, 34, 99–102. [Google Scholar] [CrossRef] [PubMed]
- Lopes, B.; Ramos, I.; Ambrósio, R., Jr. Corneal densitometry in keratoconus. Cornea 2014, 33, 1282–1286. [Google Scholar] [CrossRef] [PubMed]
- Koc, M.; Tekin, K.; Tekin, M.I.; Uzel, M.M.; Kosekahya, P.; Ozulken, K.; Yilmazbas, P. An early finding of keratoconus: Increase in corneal densitometry. Cornea 2018, 37, 580–586. [Google Scholar] [CrossRef] [PubMed]
- Consejo, A.; Jiménez-García, M.; Issarti, I.; Rozema, J.J. Detection of subclinical keratoconus with a validated alternative method to corneal densitometry. Transl. Vis. Sci. Technol. 2021, 10, 32. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Han, T.; Jhanji, V.; Shang, J.; Zhao, J.; Li, M.; Zhou, X. Correlation between corneal topographic, densitometry, and biomechanical parameters in keratoconus eyes. Transl. Vis. Sci. Technol. 2019, 8, 12. [Google Scholar] [CrossRef] [PubMed]
- Fares, U.; Otri, A.M.; Al-Aqaba, M.A.; Faraj, L.; Dua, H.S. Wavefront-optimized excimer laser in situ keratomileusis for myopia and myopic astigmatism: Refractive outcomes and corneal densitometry. J. Cataract Refract. Surg. 2012, 38, 2131–2138. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, I.B.; Ivarsen, A.; Hjortdal, J. Changes in astigmatism, densitometry, and aberrations after SMILE for low to high myopic astigmatism: A 12-month prospective study. J. Refract. Surg. 2017, 33, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Shajari, M.; Wanner, E.; Rusev, V.; Mir Mohi Sefat, S.; Mayer, W.J.; Kohnen, T.; Priglinger, S.; Kook, D. Corneal densitometry after femtosecond laser-assisted in situ keratomileusis (Fs-LASIK) and small incision lenticule extraction (SMILE). Curr. Eye Res. 2018, 43, 605–610. [Google Scholar] [CrossRef]
- Ozek, D.; Karaca, E.E.; Kazanci, B.; Kemer, O.E. Evaluation of corneal densitometry and endothelial layer in soft contact lens users. Opt. Vis. Sci. 2021, 98, 592–596. [Google Scholar] [CrossRef]
- Doughty, M.J.; Jonuscheit, S. Corneal structure, transparency, thickness and optical density (densitometry), especially as relevant to contact lens wear—A review. Cont. Lens Anterior Eye 2019, 42, 238–245. [Google Scholar] [CrossRef] [PubMed]
- Consejo, A.; Trillo-Moreno, I.; Remon, L. Corneal tissue changes following short-term soft contact lens wear of different materials. Ophthalmic Physiol. Opt. 2022, 43, 35–45. [Google Scholar] [CrossRef] [PubMed]
- Consejo, A.; Alonso-Caneiro, D.; Wojtkowski, M.; Vincent, S.J. Corneal tissue properties following scleral lens wear using Scheimpflug imaging. Ophthalmic Physiol. Opt. 2020, 40, 595–606. [Google Scholar] [CrossRef] [PubMed]
- Dhubhghaill, S.N.; Rozema, J.J.; Jongenelen, S.; Hidalgo, I.R.; Zakaria, N.; Tassignon, M.J. Normative values for corneal densitometry analysis by Scheimpflug optical assessment. Investig. Ophthalmol. Vis. Sci. 2014, 55, 162–168. [Google Scholar] [CrossRef] [PubMed]
- Consejo, A.; Jiménez-García, M.; Rozema, J.J. Age-related corneal transparency changes evaluated with an alternative method to corneal densitometry. Cornea 2021, 40, 215–222. [Google Scholar] [CrossRef] [PubMed]
- Garzón, N.; Poyales, F.; Illarramendi, I.; Mendicute, J.; Jáñez, Ó.; Caro, P.; López, A.; Argüeso, F. Corneal densitometry and its correlation with age, pachymetry, corneal curvature, and refraction. Int. Ophthalmol. 2017, 37, 1263–1268. [Google Scholar] [CrossRef] [PubMed]
- Alzahrani, K.; Carley, F.; Brahma, A.; Morley, D.; Hillarby, M.C. Corneal clarity measurements in healthy volunteers across different age groups: Observational study. Medicine 2017, 96, e8563. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, Y.; Zhang, H.; Jia, Z.; Zhang, S.; Sun, B.; Han, Y.; Wang, X. Corneal densitometry in high myopia. BMC Ophthalmol. 2018, 18, 182. [Google Scholar] [CrossRef] [PubMed]
- Miażdżyk, M.; Consejo, A.; Iskander, D.R. Assessing and compensating for the confounding factors in Scheimpflug-based corneal densitometry. Biomed. Opt. Express 2022, 13, 6258–6272. [Google Scholar] [CrossRef]
- Wang, J.; Simpson, T.L.; Fonn, D. Objective measurements of corneal light-backscatter during corneal swelling, by optical coherence tomography. Investig. Ophthalmol. Vis. Sci. 2004, 45, 3493–3498. [Google Scholar] [CrossRef]
- Jesus, D.A.; Iskander, D.R. Assessment of corneal properties based on statistical modeling of OCT speckle. Biomed. Opt. Express 2017, 8, 162–176. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.Y.; Zhang, T.Q.; Rachwani, A.R.; Blanco-Domínguez, I.; Rocha de Lossada, C.; Adán-Civiera, A.M.; Peraza-Nieves, J. New algorithm for corneal densitometry assessment based on anterior segment optical coherence tomography. Eye 2022, 36, 1675–1680. [Google Scholar] [CrossRef] [PubMed]
- Niemczyk, M.; Iskander, D.R. Statistical analysis of corneal OCT speckle: A non-parametric approach. Biomed. Opt. Express 2021, 12, 6407–6421. [Google Scholar] [CrossRef] [PubMed]
- Patel, S.; Winter, E.J.; McLaren, J.W.; Bourne, W.M. Objective measurement of backscattered light from the anterior and posterior cornea in vivo. Investig. Ophthalmol. Vis. Sci. 2007, 48, 166–172. [Google Scholar] [CrossRef]
- Smith, G.; Brown, N.A.P.; Shun-Shin, G.A. Light scatter from the central human cornea. Eye 1990, 4, 584–588. [Google Scholar] [CrossRef] [PubMed]
- Hilllenaar, T.; Cals, R.H.; Eilers, P.H.; Wubbles, R.J.; van Cleynenbreeugel, H.; Remeijer, L. Normative database for corneal backscatter analysis by in vivo confocal microscope. Investig. Ophthalmol. Vis. Sci. 2011, 52, 7274–7281. [Google Scholar] [CrossRef] [PubMed]
- Consejo, A.; Jiménez-García, M.; Rozema, J.J.; Abass, A. Influence of eye tilt on corneal densitometry. Ophthalmic Physiol. Opt. 2022, 42, 1032–1037. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Y.; Zhang, L.; Wu, D.; Wei, S.; Su, X. Distribution of corneal densitometry and its correlation with ocular stray light in healthy eyes. Zhonghua Yan Ke Za Zhi 2014, 50, 20–26. [Google Scholar]
- Forstot, S. Marginal corneal degenerations. Int. Ophthalmol. Clin. 1984, 24, 93–106. [Google Scholar]
- Farragher, R.; Mulholland, B.; Tuft, S.J.; Sandeman, S.; Khaw, P.T. Aging and the cornea. Br. J. Ophthalmol. 1997, 81, 814–817. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).