A Lightweight Swin Transformer-Based Pipeline for Optical Coherence Tomography Image Denoising in Skin Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Swept-Source OCT and Data Acquisition
2.2. Definition of OCT Image Denoising
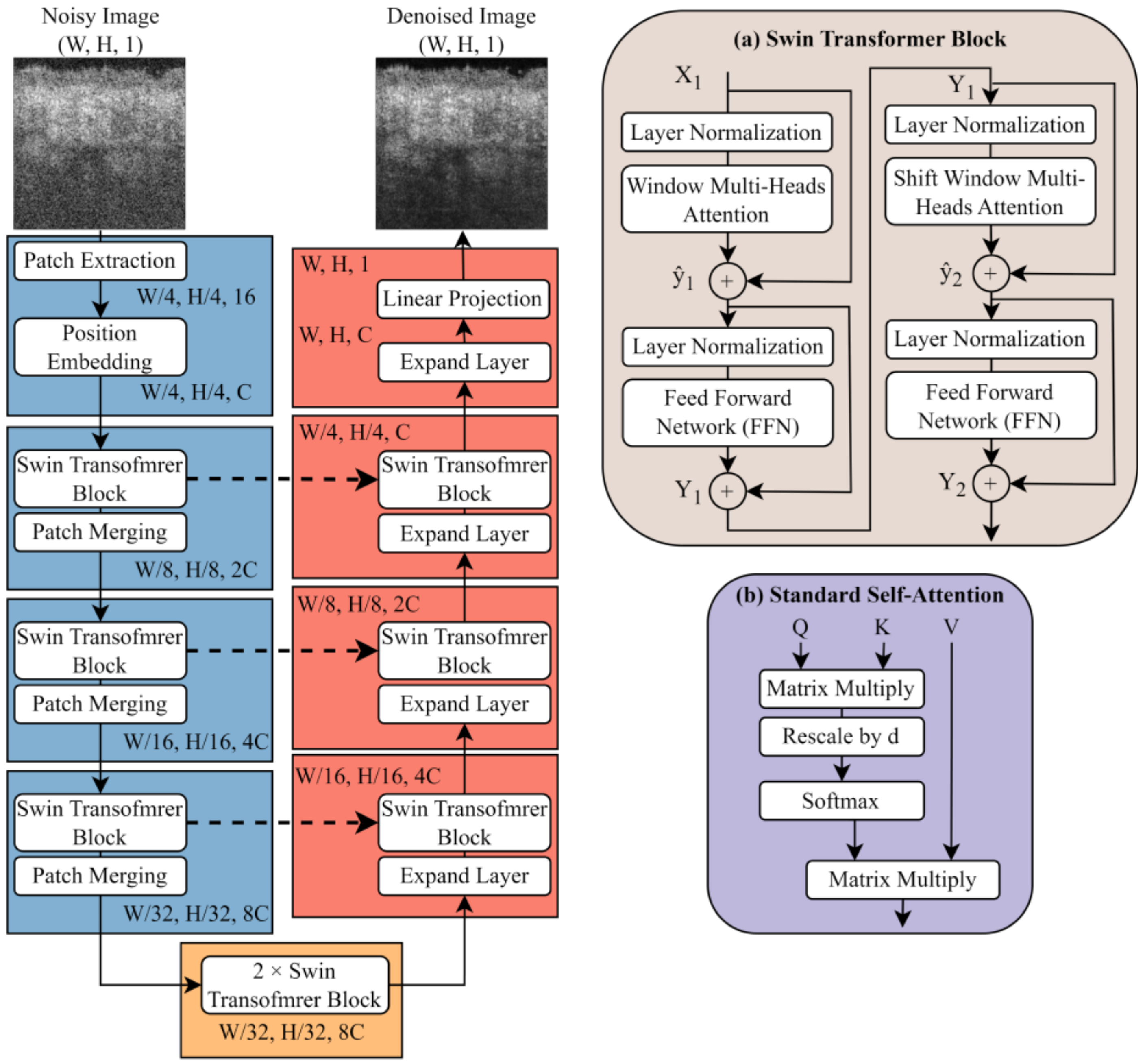
2.3. Lightweight U-Shape Swin Transformer
2.3.1. Swin Transformer Block
2.3.2. Patch Merging and Expand Layer
2.4. Loss Function
2.5. Implementation Details
2.6. Performance Comparison Methods
2.6.1. Comparison with the Neural Networks
2.6.2. Comparison of the Loss Function
2.6.3. Ablation Study on LUSwin Transformer
2.7. Quantitative Image Quality Assessment
3. Results
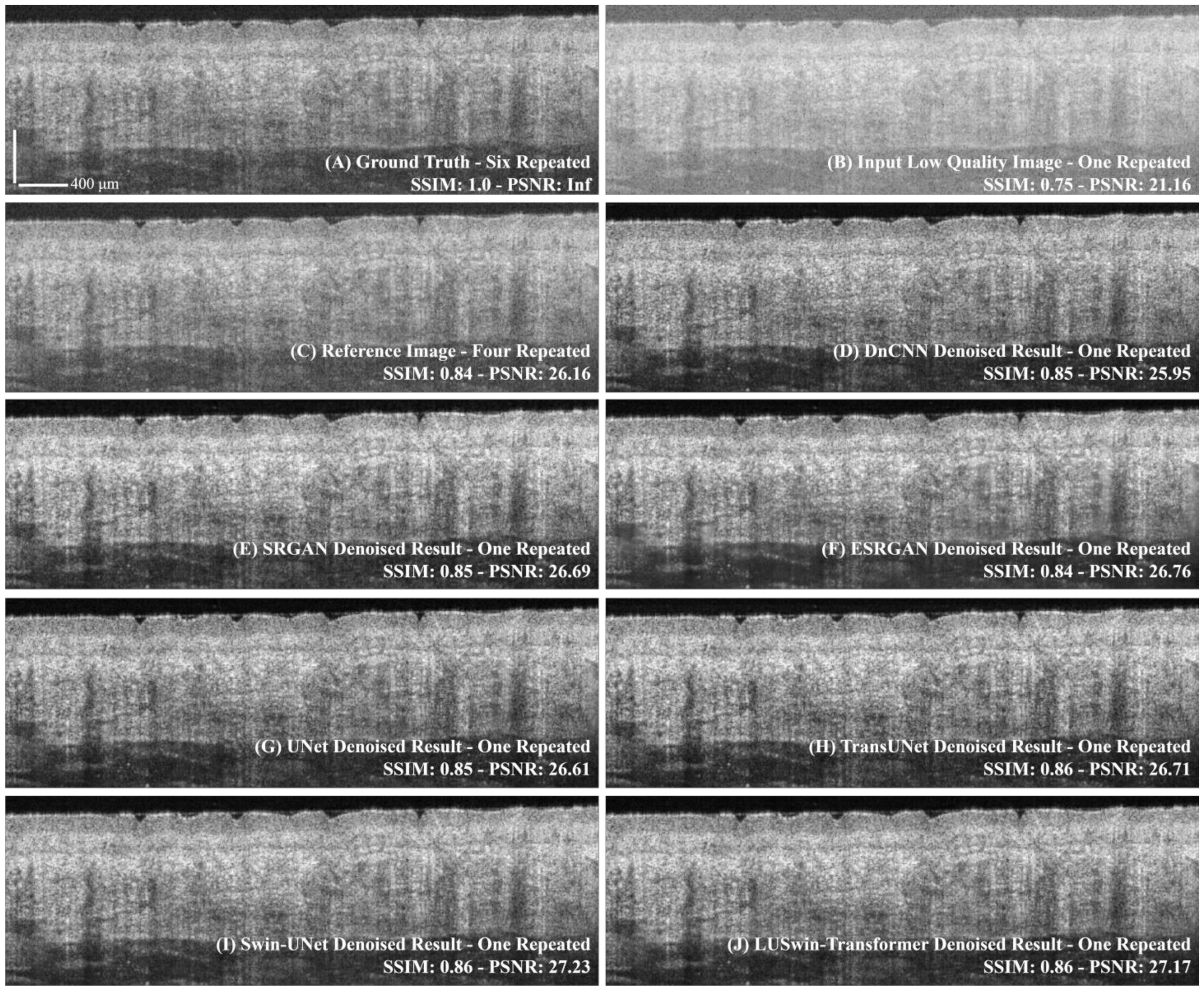
3.1. Comparison of the Different Networks
3.2. Comparison of the Different Loss Functions
3.3. Ablation Study Result
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Honari, G. Skin structure and function. In Sensitive Skin Syndrome; CRC Press: Boca Raton, FL, USA, 2017; pp. 16–22. [Google Scholar]
- Fujimoto, J.W.; Drexler, G. Introduction to OCT. In Optical Coherence Tomography: Technology and Applications; Fujimoto, J.G., Drexler, W., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 3–64. [Google Scholar] [CrossRef]
- Levine, A.; Wang, K.; Markowitz, O. Optical coherence tomography in the diagnosis of skin cancer. Dermatol. Clin. 2017, 35, 465–488. [Google Scholar] [CrossRef]
- Mogensen, M.; Thrane, L.; Jørgensen, T.M.; Andersen, P.E.; Jemec, G.B.E. Optical coherence tomography for imaging of skin and skin diseases. In Seminars in Cutaneous Medicine and Surgery; WB Saunders: Philadelphia, PA, USA, 2009; pp. 196–202. [Google Scholar]
- Kollias, N.; Stamatas, G.N. Optical non-invasive approaches to diagnosis of skin diseases. In Journal of Investigative Dermatology Symposium Proceedings; Elsevier: Amsterdam, The Netherlands, 2002; pp. 64–75. [Google Scholar]
- Wang, Y.-J.; Wang, J.-Y.; Wu, Y.-H. Application of Cellular Resolution Full-Field Optical Coherence Tomography in vivo for the Diagnosis of Skin Tumours and Inflammatory Skin Diseases: A Pilot Study. Dermatology 2021, 238, 121–131. [Google Scholar] [CrossRef]
- Chen, I.-L.; Wang, Y.-J.; Chang, C.-C.; Wu, Y.-H.; Lu, C.-W.; Shen, J.-W.; Huang, L.; Lin, B.-S.; Chiang, H.-M. Computer-aided detection (CADe) system with optical coherent tomography for melanin morphology quantification in melasma patients. Diagnostics 2021, 11, 1498. [Google Scholar] [CrossRef]
- Wu, W.; Tan, O.; Pappuru, R.R.; Duan, H.; Huang, D. Assessment of frame-averaging algorithms in OCT image analysis. Ophthalmic Surg. Lasers Imaging Retin. 2013, 44, 168–175. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Lin, S.; Ye, C.; Yu, D.; Qin, J.; An, L. Using a dual-tree complex wavelet transform for denoising an optical coherence tomography angiography blood vessel image. OSA Contin. 2020, 3, 2630–2645. [Google Scholar] [CrossRef]
- Huang, S.; Tang, C.; Xu, M.; Qiu, Y.; Lei, Z. BM3D-based total variation algorithm for speckle removal with structure-preserving in OCT images. Appl. Opt. 2019, 58, 6233–6243. [Google Scholar] [CrossRef] [PubMed]
- Bayhaqi, Y.A.; Hamidi, A.; Canbaz, F.; Navarini, A.A.; Cattin, P.C.; Zam, A. Deep-Learning-Based Fast Optical Coherence Tomography (OCT) Image Denoising for Smart Laser Osteotomy. IEEE Trans. Med. Imaging 2022, 41, 2615–2628. [Google Scholar] [CrossRef]
- Mehdizadeh, M.; MacNish, C.; Xiao, D.; Alonso-Caneiro, D.; Kugelman, J.; Bennamoun, M. Deep feature loss to denoise OCT images using deep neural networks. J. Biomed. Opt. 2021, 26, 046003. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, G.; Ni, G.; Jerwick, J.; Duan, L.; Zhou, C. Optical coherence tomography image denoising using a generative adversarial network with speckle modulation. J. Biophotonics 2020, 13, e201960135. [Google Scholar] [CrossRef]
- Qiu, B.; You, Y.; Huang, Z.; Meng, X.; Jiang, Z.; Zhou, C.; Liu, G.; Yang, K.; Ren, Q.; Lu, Y. N2NSR-OCT: Simultaneous denoising and super-resolution in optical coherence tomography images using semisupervised deep learning. J. Biophotonics 2021, 14, e202000282. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Nan, N.; Wang, X. Denoising algorithm of OCT images via sparse representation based on noise estimation and global dictionary. Opt. Express 2022, 30, 5788–5802. [Google Scholar] [CrossRef] [PubMed]
- Odena, A.; Dumoulin, V.; Olah, C. Deconvolution and checkerboard artifacts. Distill 2016, 1, e3. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Heigold, G.; Gelly, S.; Uszkoreit, J.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-unet: Unet-like pure transformer for medical image segmentation. arXiv 2021, arXiv:2105.05537. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Zhang, T.; Zhou, K.; Rocliffe, H.R.; Pellicoro, A.; Cash, J.L.; Wang, W.; Wang, Z.; Li, C.; Huang, Z. Windowed Eigen-Decomposition Algorithm for Motion Artifact Reduction in Optical Coherence Tomography-Based Angiography. Appl. Sci. 2022, 13, 378. [Google Scholar] [CrossRef]
- Brash, D.E.; Ziegler, A.; Jonason, A.S.; Simon, J.A.; Kunala, S.; Leffell, D.J. Sunlight and sunburn in human skin cancer: p53, apoptosis, and tumor promotion. J. Investig. Dermatol. Symp. Proc. 1996, 1, 136–142. [Google Scholar]
- Cheng, Y.; Chu, Z.; Wang, R.K. Robust three-dimensional registration on optical coherence tomography angiography for speckle reduction and visualization. Quant. Imaging Med. Surg. 2021, 11, 879. [Google Scholar] [CrossRef]
- Klein, S.; Staring, M.; Murphy, K.; Viergever, M.A.; Pluim, J.P.W. Elastix: A toolbox for intensity-based medical image registration. IEEE Trans. Med. Imaging 2009, 29, 196–205. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual losses for real-time style transfer and super-resolution. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016; pp. 694–711. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Loy, C.C. Esrgan: Enhanced super-resolution generative adversarial networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; p. 0. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In 12th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 16); USENIX: Berkely, CA, USA, 2016; pp. 265–283. [Google Scholar]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Lu, Y.; Yu, Q.; Luo, X.; Adeli, E.; Wang, Y.; Lu, L.; Yuille, A.L.; Zhou, Y. Transunet: Transformers make strong encoders for medical image segmentation. arXiv 2021, arXiv:2102.04306. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Huang, Z.; Wang, Z.; Wen, C.; Jiang, Z.; Yu, Z.; Liu, J.; Liu, G.; Huang, X.; Maier, A.; et al. A deep learning based pipeline for optical coherence tomography angiography. J. Biophotonics 2019, 12, e201900008. [Google Scholar] [CrossRef]
- Jolicoeur-Martineau, A. The relativistic discriminator: A key element missing from standard GAN. arXiv 2018, arXiv:1807.00734. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, Sydney, NS, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]



| Participant ID | Scan Positions | Number of Data | Biological Sex |
|---|---|---|---|
| #001 | Palm Thenar | 1 | Male |
| #002 | Palm Thenar | 2 | Male |
| #003 | Forearm (Arm) | 2 | Female |
| Neck | 2 | ||
| #004 | Palm Thenar | 1 | Female |
| #005 | Neck | 1 | Male |
| Face | 1 | ||
| #006 | Palm Thenar | 2 | Male |
| #007 | Palm Thenar | 1 | Male |
| #008 | Back of Palm | 2 | Female |
| Forearm (Arm) | 2 | ||
| #009 | Neck | 2 | Female |
| #010 | Face | 2 | Male |
| #011 | Face | 1 | Male |
| #012 | Palm Thenar | 2 | Male |
| #013 | Palm Thenar | 1 | Female |
| #014 | Palm Thenar | 1 | Female |
| Forearm (Arm) | 1 | ||
| #015 | Palm Thenar | 1 | Male |
| #016 | Palm Thenar | 1 | Female |
| Experiments | Channel Size (C) | Pairs of Downsample–Upsample Blocks |
|---|---|---|
| Control Group | 64 | 4 |
| Channel-48 | 48 * | 4 |
| Channel-32 | 32 * | 4 |
| Block-3 | 64 | 3 * |
| Method | Type | Repeat Scan | FLOPs * (G) | Params * (M) | PSNR | SSIM |
|---|---|---|---|---|---|---|
| Input Image | N/A | 1-Repeated | N/A | N/A | 21.28 ± 1.09 | 0.746 ± 0.047 |
| Reference | N/A | 4-Repeated | N/A | N/A | 26.19 ± 1.23 | 0.858 ± 0.035 |
| DnCNN [32] | CNN | 1-Repeated | 40.924 | 0.557 | 25.32 ± 0.01 | 0.787 ± 0.040 |
| SRGAN [28] | CNN | 41.684 | 0.567 | 26.42 ± 0.91 | 0.792 ± 0.038 | |
| ESRGAN [29] | CNN | 258.51 | 3.506 | 26.45 ± 1.15 | 0.765 ± 0.051 | |
| UNet [20] | CNN | 59.882 | 34.565 | 26.73 ± 0.63 | 0.789 ± 0.044 | |
| TransUNet [33] | Transformer | 23.014 | 52.351 | 26.68 ± 0.01 | 0.796 ± 0.037 | |
| Swin-UNet [19] | Transformer | 16.117 | 50.283 | 26.94 ± 0.58 | 0.795 ± 0.040 | |
| LUSwin Transformer | Transformer | 3.9299 | 11.922 | 26.92 ± 0.70 | 0.796 ± 0.040 |
| Loss Function | PSNR | SSIM | ||
|---|---|---|---|---|
| 1 | 0 | 26.77 ± 0.53 | 0.792 ± 0.04 | |
| 1 | 1 | 26.35 ± 0.54 | 0.793 ± 0.04 | |
| 1 | 0.1 | 26.71 ± 0.56 | 0.794 ± 0.04 | |
| (proposed) | 1 | 0.01 | 26.92 ± 0.70 | 0.796 ± 0.04 |
| 1 | 0.001 | 26.76 ± 0.48 | 0.792 ± 0.04 |
| Experiments * | FLOPs (G) | Params (M) | PSNR | SSIM |
|---|---|---|---|---|
| Control Group | 3.9299 | 11.922 | 26.77 ± 0.53 | 0.792 ± 0.04 |
| Channel (C)-48 | 2.2561 | 6.726 | 26.72 ± 0.57 | 0.791 ± 0.04 |
| Channel (C)-32 | 1.0447 | 3.013 | 26.61 ± 0.51 | 0.788 ± 0.04 |
| Block (B)-3 | 2.9267 | 2.985 | 26.71 ± 0.53 | 0.791 ± 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, J.; Li, C.; Huang, Z. A Lightweight Swin Transformer-Based Pipeline for Optical Coherence Tomography Image Denoising in Skin Application. Photonics 2023, 10, 468. https://doi.org/10.3390/photonics10040468
Liao J, Li C, Huang Z. A Lightweight Swin Transformer-Based Pipeline for Optical Coherence Tomography Image Denoising in Skin Application. Photonics. 2023; 10(4):468. https://doi.org/10.3390/photonics10040468
Chicago/Turabian StyleLiao, Jinpeng, Chunhui Li, and Zhihong Huang. 2023. "A Lightweight Swin Transformer-Based Pipeline for Optical Coherence Tomography Image Denoising in Skin Application" Photonics 10, no. 4: 468. https://doi.org/10.3390/photonics10040468
APA StyleLiao, J., Li, C., & Huang, Z. (2023). A Lightweight Swin Transformer-Based Pipeline for Optical Coherence Tomography Image Denoising in Skin Application. Photonics, 10(4), 468. https://doi.org/10.3390/photonics10040468





