Abstract
In this paper, the stabilization and high efficiency of an unstable Second Harmonic Generation (SHG) of an laser with a KTP intracavity is demonstrated. By using a passive Q-switching crystal () and a parametric modulation method (harmonic modulation), the stabilization of the laser is reached. An harmonic modulation was applied to the pumping of the -KTP laser to control the amplitude and frequency of the laser emission. The results were characterized by using power spectra analysis, optical spectrum, bifurcation diagrams, and temporal series of the laser intensity. The promising application of this green light source is materialized when such light is necessary for high-density optics, such as in the treatment materials industry or in some aesthetic applications.
1. Introduction
Currently, one of the most widely used solid-state lasers in industrial applications, such as materials processing, cutting, and welding, is the laser (yttrium orthovanadate crystal doped with neodymium) [1]. The is used due to its high absorption coefficient and its wide section of stimulated emission; in addition, it has a better performance as compared to an ( aluminum oxide and itrium oxide doped with neodymium ) laser. However, thermal effects (thermal lens) are more significant in the ; so, it is necessary to monitor the glass temperature to keep it low, as in [2] by using both acousto-optic modulator and GaAs saturable absorber. Mukhopadhyay et al. presented an analysis by incorporating a nonlinear loss term due to the intracavity second-harmonic generation to the general recurrence relation for the mode-locked pulses under the Q-switched envelope at the fundamental wavelength [3]. The use of a suturable absorber has also been demonstrated in a compact diode-pumped with Q-switched extracavity for frequency-doubled Nd:YVO4/KTP green-pulse laser generation [4,5]. Other researchers demonstrated that the diffusion bonding crystal method is an effective method to relieve the thermal lens for the end-pumping laser crystal, and opens the possibility to increase the optical power of the system [6,7].
Lasers doped with , such as Nd:YAG and , usually emit radiation at a wavelength of 1064 nm, supported by a crystal (potassium titanyl phosphate crystal or KTP). Inside the laser cavity, it is possible to double the frequency by converting the infrared light of 1064 nm into green light of 532 nm; this phenomenon is called Second Harmonic Generation (SHG) [8]. Due to the nonlinear coupling between modes in the SHG, the crystal causes irregular fluctuations in the laser output, which is amplified by a Q factor within the laser cavity due to the presence of the amplifying laser [9], also known as the green problem. This irregular behavior has been studied in detail and attributed to the destabilization of the relaxation of the oscillations, which has always been present in this type of lasers due to the nonlinear coupling of the longitudinal modes [10,11].
There are several approaches in order to stabilize the green light generated by SHG in a solid-state laser. One of them is the use of external modulation, where low emission power is achieved by using nonlinear waves for SHG. The stabilization of laser pulses with passive Q-switching has been studied [12,13]. This solution provides high conversion efficiency, and high power can be achieved by using flat waves [14]. In an laser, placement of the KTP crystal is fundamental to obtain green emission by folding the frequency. When the crystal is placed inside the cavity green radiation is emitted at high power, since the energy density of the radiation is higher inside the optical cavity. The green light intensity produced by the KTP crystal is proportional to the square of the fundamental wavelength intensity, but tends to be unstable. This instability is caused by the competition of modes in the cavity; if the KTP is placed outside the cavity, it is also possible to generate the second harmonic, and the emission, in this case, is stable, but with low power [15].
An approach to suppressing unwanted fluctuations is to control the injection current of the pump diode by means of electronic feedback. In 1992 [10], Rajarshi Roy et al. succeeded in stabilizing the output waveforms of the laser using a modification of the chaos control method proposed by Ott–Grebogy–Yorke (OGY) [16]; this control technique is known as Occasional Proportional Feedback (OPF), and in other systems, such as CO2 lasers, the method has been used to stabilize unstable periodic orbits [17]. A parametric modulation technique has been implemented by adding a sinusoidal signal to the system parameters in lasers made of erbium-doped fibers [18,19] to induce multistability and to stabilize the laser. A fast saturable absorber in a single-mode infrared laser induces a sequence of periodic orbits (P3, P4, P5, etc), which are stable. In the context of infrared lasers, this has been observed in simulations and studied via numerical continuation in bifurcation analysis in the CO2 laser with a saturable absorber [20,21]. The harmonic modulation technique consists in adding a periodic signal to the input of the system; in this case, it is a sinusoidal periodic signal to an accessible parameter of the laser system to obtain a modulated parameter.
There is a method to increase the output power of a laser by modulating losses. This method is known as Q-switching, and it is divided into two techniques: active and passive Q-switching. In active Q-switching, losses are modulated by active elements, such as acousto-optic or electro-optic modulators; in passive Q-switching, losses are automatically modulated by a saturable absorber, and the pulse is generated when the energy stored in the medium reaches the appropriate level [22]. Normally, the average power of lasers in Q-switch operation is lower than the optical power of a continuous wave laser and the instabilities are reduced by placing a Q-switch crystal inside the cavity [23,24,25,26]. Periodic modulation of the pump leads to different stable states in the experiment, for instance, another infrared laser (CO2 laser with modulated losses) where changing the periodic losses modulation depth “m” or frequency modulation leads to different chaotic and periodic attractors. This dependence on the losses modulation depth “m” and frequency has been studied for two different models in the CO2 laser: the two-level model and the four-level model [27,28].
In this paper, an experimental study of an laser with a KTP crystal intracavity emitting at 1064 nm is shown. In such case, the KTP crystal produces a laser emission at 532 nm, which tends to be unstable and gives rise to the so-called “green problem” treated in recent years [10,11]. By applying controlled external modulation and using passive Q-switching, it is possible to stabilize the emission and obtain a high conversion efficiency. The emission of the laser is analyzed based on the response in terms of optical power, optical spectra, frequency spectra, and time series by using the local maxima and Inter-Spike-Interval (ISI). This work focuses on stabilizing the green emission in frequency and pulse amplitude by adding harmonic modulation to the pumping current, where this modulation is applied by changing the amplitude and frequency. In Section 2, the experimental setup of an laser with a KTP crystal intracavity for second harmonic generation with external modulation is presented. Then, in Section 3, some results on stabilizing the frequency and amplitude of the SHG of the laser are shown. Finally, in Section 4, the results obtained and the conclusions are presented.
2. Preliminaries
There are a few methods to generate green light, but the best known is probably the second harmonic generation. The green problem arises when the cavity generates not only the second harmonic but also other frequencies due to the competition of longitudinal modes, which produce chaotic behavior [9]. The generation of those frequencies, as well as the generation of the second harmonic, are related to the polarization of the medium. This polarization occurs when an electric field is applied to the material as follows [29]:
where is the permittivity in the free space and is the linear susceptibility. If the electric field is small, the approximation is linear, but if the electric field is large, the best approximation is nonlinear; then, we can expand the equation of polarization in power series as:
note that , , ⋯, are the nonlinear susceptibilities of second, third, and nth-order, respectively, and is the polarization of order n. Next, suppose an electromagnetic wave
where and are frequencies, and are the amplitudes of the electromagnetic waves, while represents a complex conjugate term.
Substituting Equation (3) into the polarization of second order of Equation (2), the following equation is obtained:
By analyzing Equation (4), terms with different frequencies corresponding to the four non-linear effects of second order (Equations (5)–(8)) can be identified: Optical Rectification (OR), Second Harmonic Generation (SHG), Generation of Frequency Sum (GFS), and Generation of Difference Frequency (GDF):
In the cavity of a laser, it is possible to generate other longitudinal modes, creating more frequency combinations and making the behavior more unstable [30]. The first time this phenomenon was observed in a laser was in 1961, when it was reported that in addition to the laser’s natural wavelength (694.3 nm), a second harmonic (347.2 nm) had been generated [8]. With this finding, the study of nonlinear optics and the use of SHG in different areas of science began [31,32].
3. Experimental Setup
In Figure 1, the scheme of the experimental arrangement of an laser with a KTP crystal intracavity for second harmonic generation is shown. As can be seen, the arrangement is the simplest in order to find the easiest way to generate the SHG. To achieve Q-switching, a crystal is used, which generates short pulses from 10 to 50 ns. This experiment was carried out with a laser diode pumping at 808 nm (LD, Modulight ML2020), a current source (Bk-Precision 1696), and a lens (L) with focal length mm, which is used to focus the beam onto the . The cavity consists of the crystal and a KTP intracavity glass, which have special coatings that work as reflecting surfaces at the wavelengths used (Figure 1), and at the output there are two beam splitters: BS1 (BS010), designed for wavelengths from 400 to 700 nm, and BS2 (BS011), is designed for wavelengths of 700 to 1100 nm. The resulting beam of BS1 is filtered by a bandpass filter (FL532-10, FG) at 532 nm, and the BS2 beam is filtered by a bandpass filter (FL1064-10, IRF) at 1064 nm. Such filtering affects photo-detectors and , respectively, which convert the optical signal to an electrical voltage to be analyzed by the oscilloscope (DPO7104); the output of is also analyzed by a frequency spectrum analyzer (FSA Aeroflex). The unfiltered beam is introduced into an optical fiber to be analyzed in an optical spectrum analyzer (OSA MS9030A). All the technical specifications of the crystals and other optical components can be consulted in the Alphalas web page [33].

Figure 1.
Schematic arrangement of the -KTP laser with a KTP crystal intracavity for second harmonic generation and modulated by an external signal.
By carrying out the implementation of the experimental setup shown in Figure 1, it will be possible to know the unstable behavior that characterizes this type of laser and its output as a second harmonic. With this, we can analyze the original response of the -KTP laser which will serve as a starting point before applying the harmonic modulation to the system.
In order to analyze the emission of the -KTP laser with external modulation in the experimental setup shown in Figure 1, a sinusoidal modulation signal given by an arbitrary function generator (AFG) is added to the pump current. With the AFG device, the pump current is given as
where is the initial current parameter, and corresponds to the current obtained by the use of an Operational Amplifier (OA) that sums the signal that comes from the AFG as external harmonic modulation. In order to reach the desired control, the modulation signal, with a suitable gain and modulation frequency able to eliminate coexisting states, must be defined [11,12].
Using the same arrangement shown in Figure 1, it is possible to separate the green (532 nm) and infrared (1064 nm) emissions through the use of beam splitters (BS1 and BS2) at the output of the laser; then, we characterize the behavior of the laser when applying the modulation. The acquisition of data can be achieved through the use of and , that convert the optical signal to voltage amplitude; then, the signal is received by the oscilloscope (temporal series), the optical spectrum analyzer (optical spectra), and the frequency spectrum analyzer (frequency spectrum), to construct the figures of temporal series, optical spectrum, frequency spectrum, and other related with this measurements.
In order to obtain the laser emission from the it is necessary to feed the pump laser diode (LD) with an adequate voltage and current (Figure 1), these were fixed as V and A, respectively. The applied harmonic modulation was varied in frequency as 10 kHz < < 90 kHz in increments of 1 kHz, while modulation amplitude was increased in steps of 1 V within a range of 2 V < < 20 V. Figure 2a–e shows the emission of LD at 808 nm for and variable, and Figure 3a–e shows the emission of the laser diode with V and variable .
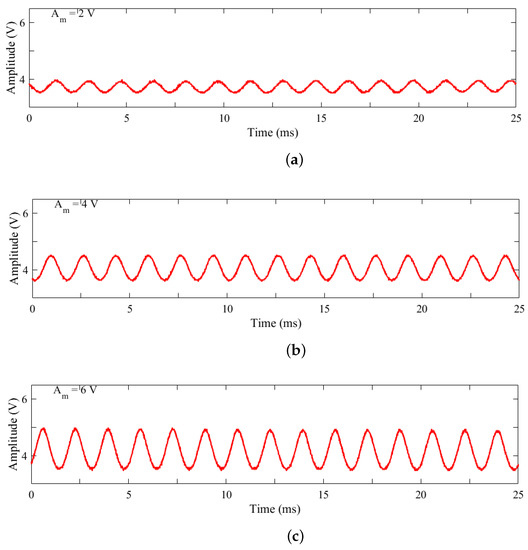
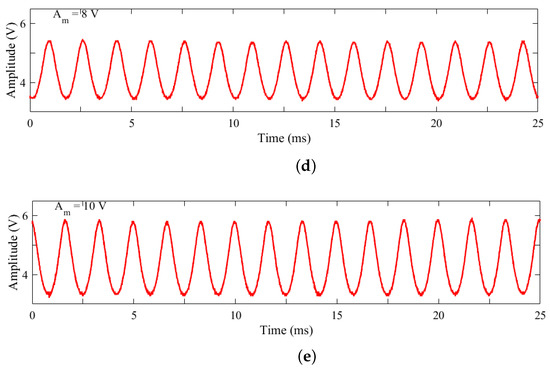
Figure 2.
Pump laser diode emission by varying the harmonic modulation amplitude for a fixed frequency and modulation amplitude : (a) 2 V, (b) 4 V, (c) V, (d) 8 V, (e) 10 V.
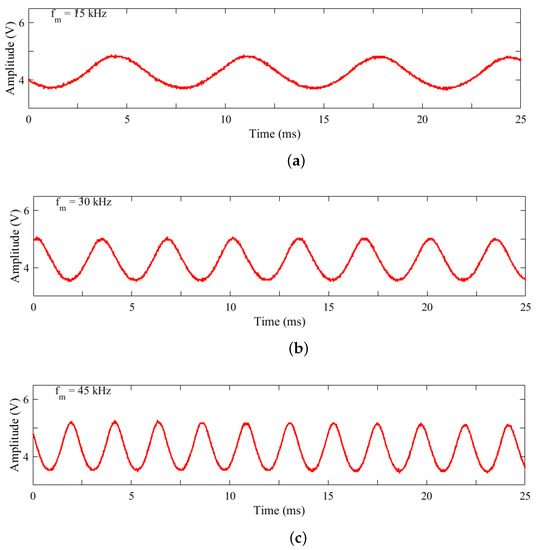
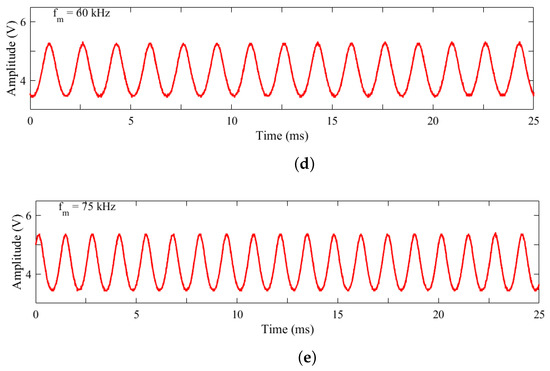
Figure 3.
Laser diode emission by varying the harmonic modulation frequency and with fixed amplitude = 7.5 V and modulation frequency : (a) 15 kHz, (b) 30 kHz, (c) 45 kHz, (d) 60 kHz, (e) 75 kHz.
Figure 4 shows the pump power necessary for the laser to emit at the 1064 nm wavelength and at 532 nm in continuous wave and with Q-switch. It is observed that the emission power in a continuous wave is higher than using Q-switch, also the emission threshold is lower in a continuous wave.
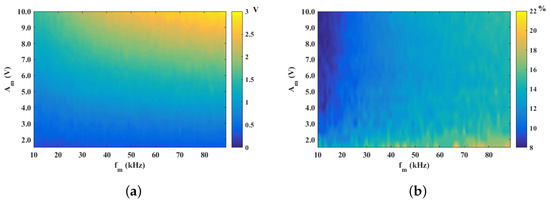
Figure 4.
(a) voltage map of the DL emission when modulated with signal . (b) percentage relationship of the voltage that presents the intensity of the emission of the LD with respect to the modulation amplitude .
In Figure 4, we can observe that the voltage of the emission increases by increasing or , but the intensity of the emission (Figure 4a vertical color bar, given in volts (V)), does not have the same amplitude to , and only a percentage is observed Figure 4b; this relationship between the amplitude of the modulation and the amplitude of the emission is shown in Figure 5. The peak-to-peak voltage of the LD emission was calculated by varying modulation amplitude (Figure 5a) and modulation frequency (Figure 5b).
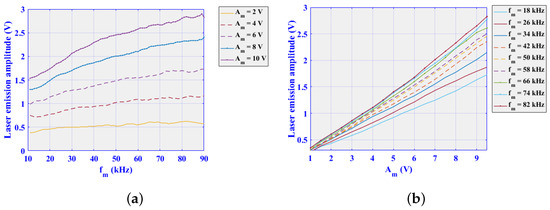
Figure 5.
Curves of the voltage of the emission of the LD varying: (a) amplitude (), and (b) frequency ().
4. Results of the Stabilization in Frequency and Amplitude of SHG of the
The stability of the intensity of the emission of the second harmonic in -KTP lasers is known to be normally irregular; so, in this experiment, it was worked to stabilize the intensity of the emission and also to achieve greater conversion efficiency. The wavelength of the second harmonic (532 nm) with respect to the emission at the fundamental wavelength (1064 nm). Passive Q-switching has been used to obtain an emission intensity with less stability, but it may present greater conversion efficiency of the laser power. It will be shown that, with the harmonic modulation , there is an emission intensity that has stability and greater conversion efficiency. In this section, the modulation parameters for amplitude () and frequency () are defined, for which the emission of the second harmonic has greater stability.
In order to know the behavior of the output power as a function of the pumping power, from the experimental arrangement shown in Figure 1, a sweep of 0 to W of optical pumping power was made, and the results can be seen in Figure 6, which shows the Nd:YVO4 laser output, as a continuous wave and in Q-Switching mode at 1064 nm, as well as the power output as a continuous wave and in Q-Switching mode at 532 nm.
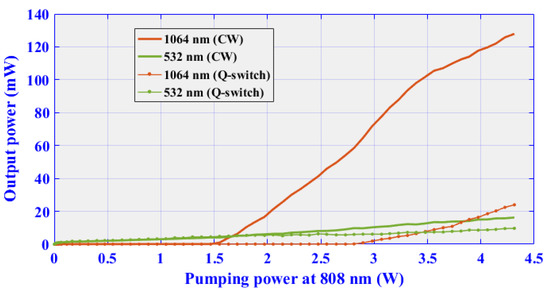
Figure 6.
Power of the laser with KTP intra-cavity.
The intracavity conversion efficiency was found by relating the optical power at 532 nm to the optical power at 1064 nm. In Table 1, we can see that if the laser set-up was in the Q-switching mode, efficiency was , higher than the results in previous works [34], whereas if the laser set-up was not in Q-switching mode, efficiency was only .

Table 1.
Optical efficiency conversion with intra-cavity configuration without modulation at V and A.
In order to analyze the laser emission, an optical spectrum analyzer was used, in which modulated and unmodulated laser measurements were made, and it was verified that, for the modulation ranges used, the laser emission lengths stay the same. Figure 7 shows the optical spectra amplitude at wavelength range 350 nm 1300 nm of the laser emission , with a modulation amplitude range 7 V < V and modulation frequency fixed to = 50 kHz to know the behavior of current output when modulating the diode current. The characteristic wavelengths of 808 nm of the pump laser diode, 1064 nm of the emission of and 532 nm of the second harmonic when using the KTP are observed. The wavelength of 350 nm corresponds to the frequency sums phenomenon of the fundamental wavelengths 1064 nm and second harmonic (532 nm).
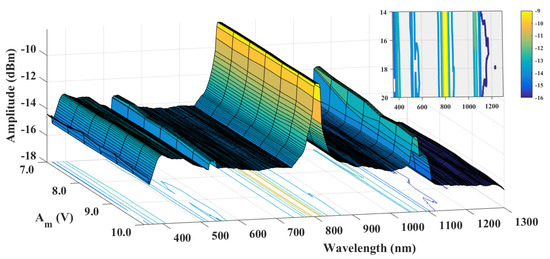
Figure 7.
Surface of optical spectra.
Using the experimental arrangement for the laser configuration shown in Figure 1, it was found that the pulse frequency without modulation is kHz; this is observed in Figure 8, where the parameters of the modulation signal were kept constant with voltage V and current A.
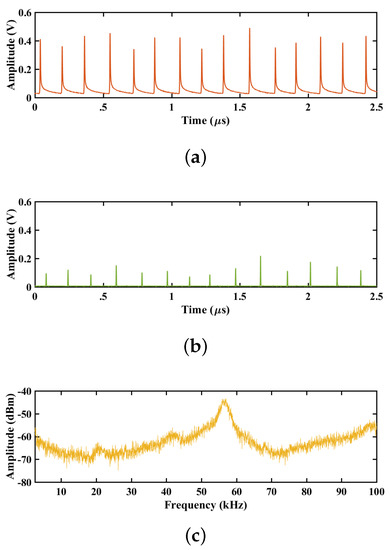
Figure 8.
Time series and frequency spectra of the emission laser without modulation. (a) Time series of the 1064 nm wavelength emission. (b) Time series of the wavelength radiation of 532 nm. (c) Spectrum frequency of the emission of 532 nm.
When a harmonic modulation is added to the pump, it is expected that there will be a harmonic resonance between the modulation signal and the relaxation frequency of the laser (). Figure 9 shows the emission at 1064 nm, 532 nm, and the frequency spectrum of the emission at 532 nm for the modulation parameters V and kHz, showing a conversion efficiency of 25% (Table 2). Table 2 shows the conversion efficiency obtained for a modulation sweep V with a fixed frequency kHz in the intracavity emission with Q-switching.
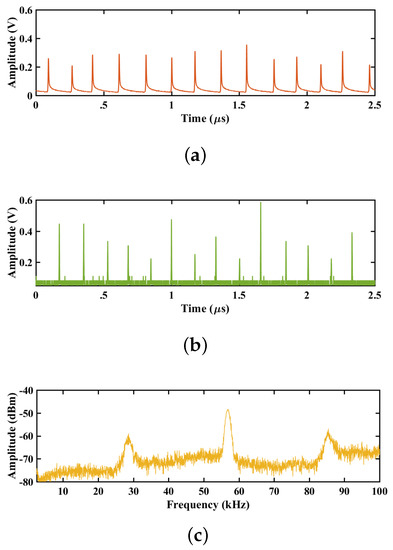
Figure 9.
Time series of the laser emission with the modulation parameters V and kHz. (a) Time series of the 1064 nm wavelength emission. (b) Time series of the wavelength radiation of 532 nm. (c) Spectrum frequency of the emission of 532 nm.

Table 2.
Optical efficiency conversion with intra-cavity configuration maintaining the pump of V and A, with modulation parameters 2 V V and kHz.
Here we can see that the frequency peak at 57 kHz is narrower, this can confirm harmonic resonance. An analysis of the frequency emission was carried out. As observed in the experimental setup, the emission at 532 nm was analyzed in frequency with a frequency spectrum analyzer, for each parameters variation (, ) ten spectra were taken and the average of these spectra was calculated. With the averaged spectra, frequency maps were built, one for each modulation amplitude. Figure 10 shows the frequency spectrum maps of the laser emission that were obtained by varying the modulation frequency 1 kHz < < 100 kHz while using a range of amplitude variation modulation of 2 V < V. In the maps, each row represents a frequency spectrum taken from 1 to 100 kHz, the y-axis represents the modulation frequency variation.
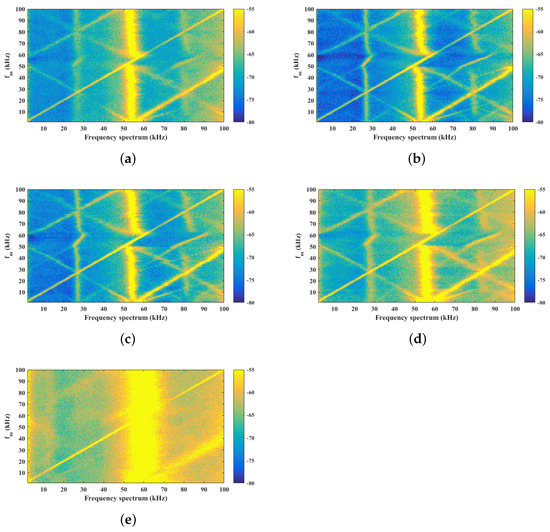
Figure 10.
Frequency spectrum maps obtained by varying harmonic modulation frequency 1 kHz < < 100 kHz and modulation amplitude: (a) V; (b) V; (c) V; (d) V; (e) V.
The local maxima of the time series obtained for each parameter set (, ) were determined and with this the standard deviation was calculated using an algorithm in Matlab. In Figure 11, we can see the standard deviation for each set of parameters. The black areas represent the minimums of the standard deviation: Figure 11a represents the standard deviation of the local maxima, Figure 11b represents the standard deviation of the interspike-interval (ISI), and Figure 11c represents the values of the parameters for which there are minimums of standard deviation of the ISI and of the local maxima of the emission at 532 nm.

Figure 11.
Stability zones for different amplitudes and frequencies . (a) represents the standard deviation of the local maxima, (b) represents the standard deviation of the interspike-interval (ISI), and (c) represents the values of the parameters for which there are minimums of standard deviation of the ISI and of the local maxima of the emission at 532 nm.
5. Conclusions
The implementation of an intracavity -KTP laser with passive Q-switching () was presented, using a harmonic modulation technique to stabilize the emission in amplitude and frequency of the laser.
For the optical emission without modulation, the relaxation frequency coincides with the peak of the frequency spectrum kHz, we observe in the Figure 8 that this peak is broad, which means that the frequency can have small variations with respect to the main peak. With respect to the optical power, it was found that the conversion efficiency between the fundamental wavelength 1064 nm and the wavelength of 532 nm, in pulsed emission (crystal for Q-switching) and using a saturable absorber () intracavity, resulted in conversion efficiency. Analyzing the time series of the laser emission when modulating signal is added to the pumping, the behavior of the laser emission is modified. In the frequency spectra, the relaxation frequency and the modulation frequency , in the maps Figure 10, the frequency locking or resonance can be observed. This resonance is achieved at the dominant frequency range 45 kHz < < 60 kHz, for the amplitude 5 V < < 10 V; under these conditions, the laser emission is stabilized in amplitude and frequency. The relaxation frequency of the Nd: YVO4 laser was found using a modulation amplitude of 7 V < V and a modulation frequency KHz. The best result appeared with the modulation parameters V and kHz, with this set of parameters, the frequency spectrum presents a narrower peak, with which it was possible to stabilize the emission laser in frequency. The standard deviation was calculated from local maxima of time series obtained for each parameter variation (, ), i.e., for each pair of fixed values of and , we obtain all the time series and take all the local maxima to construct the standard deviation maps. It can be said that, in order to stabilize the emission of the -KTP intracavity laser with passive Q-switching, a modulation frequency that is approximately equal to the oscillation frequency of the laser (), must be sought a harmonic resonance between the modulation frequency and the relaxation frequency of the laser. In addition, the conversion efficiency from 1064 nm to 532 nm in the laser with modulation was calculated, achieving an efficiency between 14% to 25%. Compared to the emission without modulation, the efficiency is lower, however, stable zones with greater frequency and amplitude are obtained.
Author Contributions
S.M.A.D.: Writing—Original Draft, Writing—Review and Editing, Methodology, Software, Validation, Data Curation, Visualization. J.H.G.L.: Writing—Review and Editing, Resources, Project administration. R.J.R.: Supervision, Funding acquisition, Writing—Review and Editing, Resources. V.A.: Writing—Review and Editing, Resources. J.L.E.M.: Writing—Review and Editing, Visualization, Conceptualization. G.H.C.: Writing—Original Draft, Writing—Review and Editing, Methodology, Software, Validation, Data Curation, Visualization, Project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This project was supported by CONACYT under project number 320597.
Acknowledgments
S.M.A.D. acknowledges support from National Council of Science and Technology -CONACyT-, Mexico, CONACYT. J.L.E.M. thanks CONACYT for financial support (CVU-706850, project: A1-S-26123, and project: 320597). R.J.R. thanks CONACYT for financial support, project No. 320597. G.H.C. acknowledges the State Council of Science and Technology of Jalisco (COECYTJAL), project number 10304-2022, with title “Control difuso aplicado a sistemas de tecnología solar térmica y fotovoltaica para implementación de planta piloto para pasteurización de leche” de la Convocatoriadel Fondo de Desarrollo Científico de Jalisco para Atender Retos Sociales “FODECIJAL 2022”.
Conflicts of Interest
The authors certify that they have NO affiliations with or involvement in any organization or entity with any financial interest (such as honoraria; educational grants; participation in speakers’ bureaus; membership, employment, consultancies, stock ownership, or other equity interest; and expert testimony or patent-licensing arrangements), or non-financial interest (such as personal or professional relationships, affiliations, knowledge, or beliefs) in the subject matter or materials discussed in this manuscript.
References
- Eichhorn, M. Laser Physics: From Principles to Practical Work in the Lab; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Zhang, Y.; Zhao, S.; Li, D.; Yang, K.; Li, G.; Zhang, G.; Cheng, K. Diode-pumped doubly Q-switched mode-locked YVO4/Nd: YVO4/KTP green laser with AO and GaAs saturable absorber. Opt. Mater. 2011, 33, 303–307. [Google Scholar] [CrossRef]
- Mukhopadhyay, P.; Alsous, M.; Ranganathan, K.; Sharma, S.; Gupta, P.; George, J.; Nathan, T. Analysis of laser-diode end-pumped intracavity frequency-doubled, passively Q-switched and mode-locked Nd: YVO4 laser. Appl. Phys. B 2004, 79, 713–720. [Google Scholar] [CrossRef]
- Wang, X.; Li, M. Continuous-wave passively mode-locked Nd:YVO4/KTP green laser with a semiconductor saturable absorber mirror. Laser Phys. 2010, 20, 733–736. [Google Scholar] [CrossRef]
- Liu, J.; Yang, J.; Fan, X.; Wang, G. Symmetric and short green-pulse generation by doubly Q-switched Nd:YVO4 laser. Laser Phys. 2010, 20, 222–225. [Google Scholar] [CrossRef]
- Zhuo, Z.; Li, T.; Li, X.; Yang, H. Investigation of Nd:YVO4/YVO4 composite crystal and its laser performance pumped by a fiber coupled diode laser. Opt. Commun. 2007, 274, 176–181. [Google Scholar] [CrossRef]
- Fields, R.; Birnbaum, M.; Fincher, C. Highly efficient Nd:YVO4 diode-laser end-pumped laser. Appl. Phys. Lett. 1987, 51, 1885–1886. [Google Scholar] [CrossRef]
- Franken, P.; Hill, A.E.; Peters, C.E.; Weinreich, G. Generation of optical harmonics. Phys. Rev. Lett. 1961, 7, 118. [Google Scholar] [CrossRef]
- McDonagh, L.; Wallenstein, R. Low-noise 62 W CW intracavity-doubled TEM 00 Nd: YVO 4 green laser pumped at 888 nm. Opt. Lett. 2007, 32, 802–804. [Google Scholar] [CrossRef]
- Roy, R.; Murphy, T., Jr.; Maier, T.; Gills, Z.; Hunt, E. Dynamical control of a chaotic laser: Experimental stabilization of a globally coupled system. Phys. Rev. Lett. 1992, 68, 1259. [Google Scholar] [CrossRef]
- Campos-Mejía, A.; Pisarchik, A.; Pinto-Robledo, V.; Sevilla-Escoboza, R.; Jaimes-Reátegui, R.; Huerta-Cuellar, G.; Vera-Avila, V. Synchronization of infrared and green components in a loss-modulated dual-cavity Nd:YAG laser with second harmonic generation. Eur. Phys. J. Spec. Top. 2014, 223, 2799–2806. [Google Scholar] [CrossRef]
- Villafana-Rauda, E.; Chiu, R.; Mora-Gonzalez, M.; Casillas-Rodriguez, F.; Medel-Ruiz, C.; Sevilla-Escoboza, R. Dynamics of a Q-switched Nd:YVO4/Cr:YAG laser under periodic modulation. Results Phys. 2019, 12, 908–913. [Google Scholar] [CrossRef]
- Tang, J.; Bai, Z.; Zhang, D.; Qi, Y.; Ding, J.; Wang, Y.; Lu, Z. Advances in All-Solid-State Passively Q-Switched Lasers Based on Cr4+:YAG Saturable Absorber. Photonics 2021, 8, 93. [Google Scholar] [CrossRef]
- Jensen, O.B.; Andersen, P.E.; Sumpf, B.; Hasler, K.H.; Erbert, G.; Petersen, P.M. 1.5 W green light generation by single-pass second harmonic generation of a single-frequency tapered diode laser. Opt. Express 2009, 17, 6532–6539. [Google Scholar] [CrossRef] [PubMed]
- Hitz, B. Generating High Green Power Without the Green Problem. Photonics Spectra 2007, 41, 92–93. [Google Scholar]
- Ott, E.; Grebogi, C.; Yorke, J.A. Controlling chaos. Phys. Rev. Lett. 1990, 64, 1196. [Google Scholar] [CrossRef]
- Pisarchik, A.; Corbalán, R.; Chizhevsky, V.; Vilaseca, R.; Kuntsevich, B. Dynamic stabilization of unstable periodic orbits in a CO2 laser by slow modulation of cavity detuning. Int. J. Bifurc. Chaos 1998, 8, 1783–1789. [Google Scholar] [CrossRef]
- Pisarchik, A.N.; Kir’yanov, A.V.; Barmenkov, Y.O.; Jaimes-Reátegui, R. Dynamics of an erbium-doped fiber laser with pump modulation: Theory and experiment. JOSA B 2005, 22, 2107–2114. [Google Scholar] [CrossRef]
- Sevilla-Escoboza, R.; Pisarchik, A.N.; Jaimes-Reátegui, R.; Huerta-Cuellar, G. Selective monostability in multi-stable systems. Proc. R. Soc. Math. Phys. Eng. Sci. 2015, 471, 20150005. [Google Scholar] [CrossRef]
- Doedel, E.J.; Pando L., C.L. Isolas of periodic passive Q-switching self-pulsations in the three-level:two-level model for a laser with a saturable absorber. Phys. Rev. E 2011, 84, 056207. [Google Scholar] [CrossRef]
- Doedel, E.J.; Pando, C.L. Multiparameter bifurcations and mixed-mode oscillations in Q-switched CO2 lasers. Phys. Rev. E 2014, 89, 052904. [Google Scholar] [CrossRef]
- Khanin, Y.I. Fundamentals of Laser Dynamics; Cambridge International Science Publishing: Cambridge, UK, 2008. [Google Scholar]
- Kee, H.H.; Lee, G.; Newson, T.P. Narrow linewidth CW and Q-switched erbium-doped fibre loop laser. Electron. Lett. 1998, 34, 1318–1319. [Google Scholar] [CrossRef]
- Yang, X.Q.; Wang, H.X.; He, J.L.; Zhang, B.T.; Huang, H.T. A compact passively Q-switched intra-cavity frequency doubled Nd: YAG/Cr4+: YAG composite crystal green laser. Laser Phys. 2009, 19, 1964. [Google Scholar] [CrossRef]
- Tsai, T.Y.; Fang, Y.C. A saturable absorber Q-switched all-fiber ring laser. Opt. Express 2009, 17, 1429–1434. [Google Scholar] [CrossRef]
- Degnan, J.J. Theory of the optimally coupled Q-switched laser. IEEE J. Quantum Electron. 1989, 25, 214–220. [Google Scholar] [CrossRef]
- Pando L, C.; Meucci, R.; Ciofini, M.; Arecchi, F. CO2 laser with modulated losses: Theoretical models and experiments in the chaotic regime. Chaos Interdiscip. J. Nonlinear Sci. 1993, 3, 279–285. [Google Scholar] [CrossRef]
- Pando, C.; Acosta, G.L.; Meucci, R.; Ciofini, M. Highly dissipative Hénon map behavior in the four-level model of the CO2 laser with modulated losses. Phys. Lett. A 1995, 199, 191–198. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Boyd, R.W. The nonlinear optical susceptibility. Nonlinear Opt. 2008, 3, 1–67. [Google Scholar]
- Alam, M.; Voravutinon, N.; Warycha, M.; Whiting, D.; Nodzenski, M.; Yoo, S.; West, D.P.; Veledar, E.; Poon, E. Comparative effectiveness of nonpurpuragenic 595-nm pulsed dye laser and microsecond 1064-nm neodymium: Yttrium-aluminum-garnet laser for treatment of diffuse facial erythema: A double-blind randomized controlled trial. J. Am. Acad. Dermatol. 2013, 69, 438–443. [Google Scholar] [CrossRef]
- Shen, Y. Surface properties probed by second-harmonic and sum-frequency generation. Nature 1989, 337, 519–525. [Google Scholar] [CrossRef]
- Alphalas-Inc. DPSS Laser Kit for Education and Research: LASKIT®-500. Available online: https://www.alphalas.com/products/lasers/dpss-laser-kit-for-education-and-research-laskit-500.html?etcc_med=SEA&etcc_par=Google&etcc_cmp=Laser%20Kit&etcc_grp=193189973&etcc_bky=laser%20kit&etcc_mty=p&etcc_plc=&etcc_ctv=304748847243&etcc_bde=c&etcc_var=CjwKCAjw0N6hBhAUEiwAXab-Talimf0tJ_9sk93ikW0uWykv7-2Aprbr6ObiFyslIHYJ9kw3AXmXIRoCbqoQAvD_BwE&gclid=CjwKCAjw0N6hBhAUEiwAXab-Talimf0tJ_9sk93ikW0uWykv7-2Aprbr6ObiFyslIHYJ9kw3AXmXIRoCbqoQAvD_BwE (accessed on 13 April 2023).
- Matía-Hernando, P.; Guerra, J.M.; Weigand, R. An Nd:YLF laser Q-switched by a monolayer-graphene saturable-absorber mirror. Laser Phys. 2013, 23, 025003. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).