A Family of Newton and Quasi-Newton Methods for Power Flow Analysis in Bipolar Direct Current Networks with Constant Power Loads
Abstract
1. Introduction
1.1. General Context
1.2. Motivation
1.3. Brief Literature Review
1.4. Contributions
- A unified power flow formulation for bipolar DC networks that considers monopolar and bipolar constant power loads. This model captures the nonlinear relationship between voltage and current via a generalized expression that integrates the effects of solidly grounded neutral wires. This formulation is suitable for both radial and meshed topologies and serves as the basis for Newton and quasi-Newton iterative solvers.
- A comparative study of multiple Newton and quasi-Newton power flow methods applied to two benchmark networks comprising 21 and 85 buses. The proposed methods demonstrate fast convergence and computational efficiency, with the Newton-based algorithms exhibiting quadratic convergence and the quasi-Newton methods offering lower computational costs through constant Jacobian approximations.
1.5. Article Structure
2. Power Flow Formulation for Bipolar DC Networks
2.1. General Power Flow Formula
2.2. Demanded Current Calculation
3. Theoretical Background and Power Flow Formulations
3.1. Multivariate Formulation and Taylor Expansion
3.2. Newton–Raphson Bipolar Power Flow Formulations
3.2.1. First Newton–Raphson Formulation
3.2.2. Second Newton–Raphson Formulation
3.2.3. Third Newton–Raphson Formulation
3.3. Quasi-Newton Methods with Constant Jacobians
3.4. Quasi-Newton Formulations
3.4.1. First Quasi-Newton Method
3.4.2. Second Quasi-Newton Method
3.4.3. Third Quasi-Newton Method
3.4.4. Fourth Quasi-Newton Method
3.5. Solution Procedure
| Algorithm 1: Newton and quasi-Newton power flow solver for bipolar DC networks. |
|
4. Test Feeder Characteristics
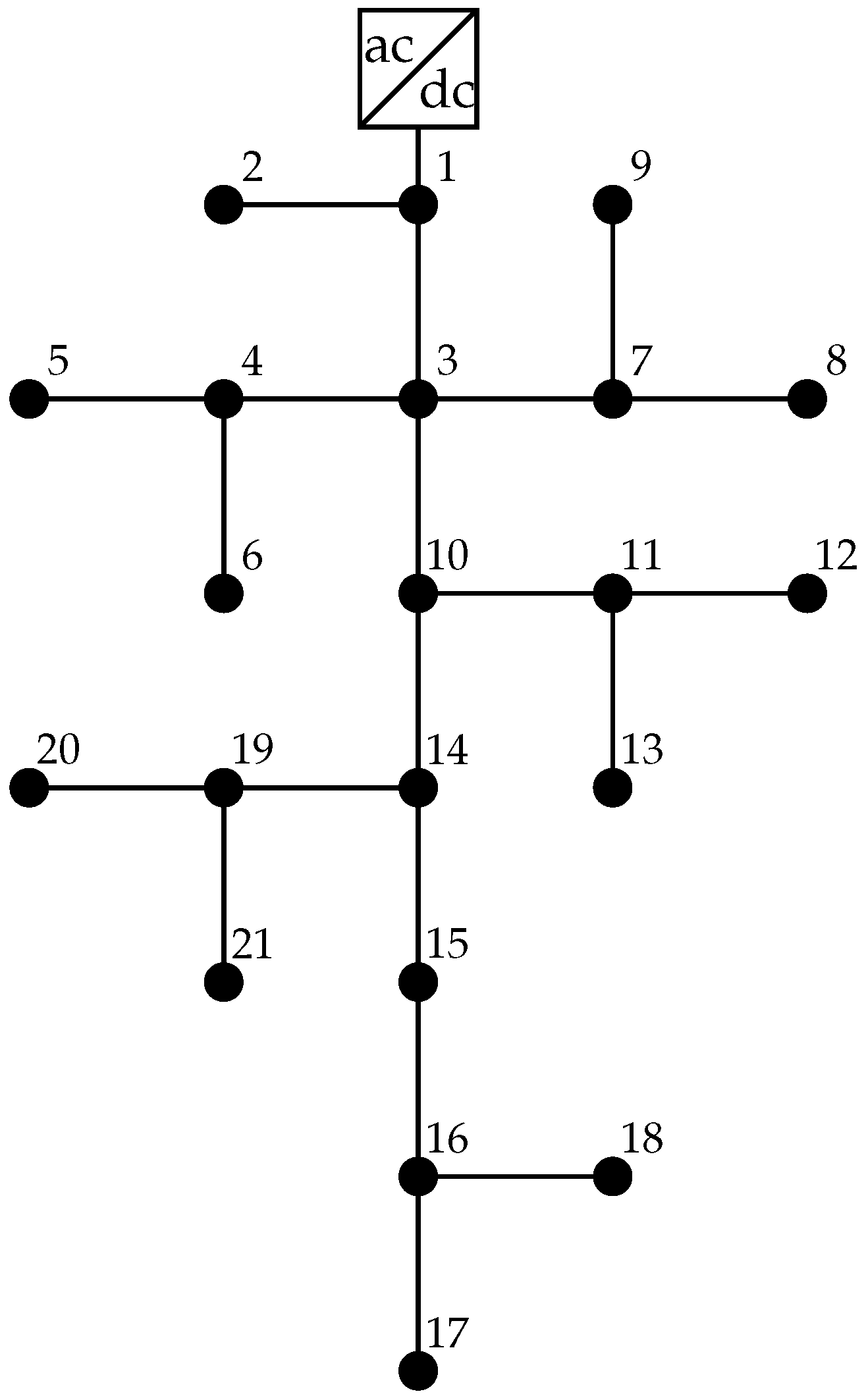
4.1. The 21-Bus Grid
4.2. The 85-Bus Grid
5. Computational Implementation
5.1. Voltage Performance and Power Loss Calculation
5.2. Rate of Convergence
5.3. Discussion
6. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vossos, V.; Gerber, D.L.; Gaillet-Tournier, M.; Nordman, B.; Brown, R.; Bernal Heredia, W.; Ghatpande, O.; Saha, A.; Arnold, G.; Frank, S.M. Adoption Pathways for DC Power Distribution in Buildings. Energies 2022, 15, 786. [Google Scholar] [CrossRef]
- Siraj, K.; Khan, H.A. DC distribution for residential power networks—A framework to analyze the impact of voltage levels on energy efficiency. Energy Rep. 2020, 6, 944–951. [Google Scholar] [CrossRef]
- Caballero-Peña, J.; Cadena-Zarate, C.; Parrado-Duque, A.; Osma-Pinto, G. Distributed energy resources on distribution networks: A systematic review of modelling, simulation, metrics, and impacts. Int. J. Electr. Power Energy Syst. 2022, 138, 107900. [Google Scholar] [CrossRef]
- Gelani, H.; Dastgeer, F.; Siraj, K.; Nasir, M.; Niazi, K.; Yang, Y. Efficiency Comparison of AC and DC Distribution Networks for Modern Residential Localities. Appl. Sci. 2019, 9, 582. [Google Scholar] [CrossRef]
- Hassan, S.J.U.; Mehdi, A.; Haider, Z.; Song, J.S.; Abraham, A.D.; Shin, G.S.; Kim, C.H. Towards medium voltage hybrid AC/DC distribution Systems: Architectural Topologies, planning and operation. Int. J. Electr. Power Energy Syst. 2024, 159, 110003. [Google Scholar] [CrossRef]
- Enomoto, M.; Sano, K.; Kanno, J.; Fukushima, J. Reconfiguration of Bipolar HVDC System for Continuous Transmission Under DC Line Fault. IEEE Trans. Power Electron. 2024, 39, 8622–8633. [Google Scholar] [CrossRef]
- Li, L.; Sun, K.; Liu, Z.; Wang, W.; Li, K.J. LVDC Bipolar Balance Control of I-M2C in Urban AC/DC Hybrid Distribution System. Front. Energy Res. 2022, 10, 809481. [Google Scholar] [CrossRef]
- Garces, A. Uniqueness of the power flow solutions in low voltage direct current grids. Electr. Power Syst. Res. 2017, 151, 149–153. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, Y.; Fan, B.; Liao, J.; Huang, T.; Zhang, X.; Zou, Y.; Zhou, N. Hierarchical optimal operation for bipolar DC distribution networks with remote residential communities. Appl. Energy 2025, 378, 124701. [Google Scholar] [CrossRef]
- Chew, B.S.H.; Xu, Y.; Wu, Q. Voltage Balancing for Bipolar DC Distribution Grids: A Power Flow Based Binary Integer Multi-Objective Optimization Approach. IEEE Trans. Power Syst. 2019, 34, 28–39. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Garcés, A. A successive approximations method for power flow analysis in bipolar DC networks with asymmetric constant power terminals. Electr. Power Syst. Res. 2022, 211, 108264. [Google Scholar] [CrossRef]
- Medina-Quesada, A.; Montoya, O.D.; Hernández, J.C. Derivative-Free Power Flow Solution for Bipolar DC Networks with Multiple Constant Power Terminals. Sensors 2022, 22, 2914. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.O.; Kim, Y.S.; Moon, S.I. Current Injection Power Flow Analysis and Optimal Generation Dispatch for Bipolar DC Microgrids. IEEE Trans. Smart Grid 2021, 12, 1918–1928. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, Q.; Huang, T.; Liao, J.; Chi, Y.; Zhou, N.; Xu, X.; Zhang, X. Convex optimal power flow based on power injection-based equations and its application in bipolar DC distribution network. Electr. Power Syst. Res. 2024, 230, 110271. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, Q.; Xu, X.; Huang, T.; Liao, J.; Chi, Y.; Zhang, X.; Zhou, N. Branch flow model based optimal power flow for bipolar dc distribution networks. CSEE J. Power Energy Syst. 2024, 11, 944–948. [Google Scholar]
- Wang, H.; Zhou, N.; Zhang, Y.; Liao, J.; Tan, S.; Liu, X.; Guo, C.; Wang, Q. Linearized power flow calculation of bipolar DC distribution network with multiple flexible equipment. Int. J. Electr. Power Energy Syst. 2024, 155, 109568. [Google Scholar] [CrossRef]
- Ahmed, H.M.; Eltantawy, A.B.; Salama, M. A generalized approach to the load flow analysis of AC–DC hybrid distribution systems. IEEE Trans. Power Syst. 2017, 33, 2117–2127. [Google Scholar] [CrossRef]
- Mackay, L.; Guarnotta, R.; Dimou, A.; Morales-Espana, G.; Ramirez-Elizondo, L.; Bauer, P. Optimal power flow for unbalanced bipolar DC distribution grids. IEEE Access 2018, 6, 5199–5207. [Google Scholar] [CrossRef]
- Lee, J.O.; Kim, Y.S.; Jeon, J.H. Optimal power flow for bipolar DC microgrids. Int. J. Electr. Power Energy Syst. 2022, 142, 108375. [Google Scholar] [CrossRef]
- Mackay, L.; Dimou, A.; Guarnotta, R.; Morales-Espania, G.; Ramirez-Elizondo, L.; Bauer, P. Optimal power flow in bipolar DC distribution grids with asymmetric loading. In Proceedings of the 2016 IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Lee, J.O.; Kim, Y.S.; Jeon, J.H. Generic power flow algorithm for bipolar DC microgrids based on Newton–Raphson method. Int. J. Electr. Power Energy Syst. 2022, 142, 108357. [Google Scholar] [CrossRef]
- Sepúlveda-García, S.; Montoya, O.D.; Garcés, A. Power Flow Solution in Bipolar DC Networks Considering a Neutral Wire and Unbalanced Loads: A Hyperbolic Approximation. Algorithms 2022, 15, 341. [Google Scholar] [CrossRef]
- Garces, A.; Montoya, O.D.; Gil-Gonzalez, W. Power Flow in Bipolar DC Distribution Networks Considering Current Limits. IEEE Trans. Power Syst. 2022, 37, 4098–4101. [Google Scholar] [CrossRef]
- Montoya, O.D.; Rocha, J.C.; Fontecha-Saboya, D. Development of an Application for Calculating the Power Flow of Bipolar DC Networks Using the MATLAB Environment. Rev. Fac. De Ing. 2024, 33, e17362. [Google Scholar]
- Enríquez, A.C.; Cardoso, Y.G. Chapter Four - Protective relay resiliency in an electric power transmission system. In Electric Power Systems Resiliency; Bansal, R.C., Mishra, M., Sood, Y.R., Eds.; Academic Press: Cambridge, MA, USA, 2022; pp. 87–148. [Google Scholar] [CrossRef]
- Garcés, A. On the Convergence of Newton’s Method in Power Flow Studies for DC Microgrids. IEEE Trans. Power Syst. 2018, 33, 5770–5777. [Google Scholar] [CrossRef]
- Petković, M.S.; Neta, B.; Petković, L.D.; Džunić, J. Multipoint methods for solving nonlinear equations: A survey. Appl. Math. Comput. 2014, 226, 635–660. [Google Scholar] [CrossRef]
- Abbasbandy, S. Improving Newton–Raphson method for nonlinear equations by modified Adomian decomposition method. Appl. Math. Comput. 2003, 145, 887–893. [Google Scholar] [CrossRef]
- Sereeter, B.; Vuik, C.; Witteveen, C. On a comparison of Newton–Raphson solvers for power flow problems. J. Comput. Appl. Math. 2019, 360, 157–169. [Google Scholar] [CrossRef]




| Current code version | V1.0 |
| Permanent link to code/repository used for this code version | https://github.com/odmontoya/Newton-Raphson-Family-Bipolar-DC-Networks, accessed on 4 May 2025 |
| Legal code license | MIT License |
| Code versioning system used | Git |
| Programming languages, tools, and libraries used | MATLAB R2024b |
| Compilation requirements and runtime environment | MATLAB (any OS with MATLAB R2024b or later) |
| Contact email for support | odmontoyag@udistrital.edu.co, accessed on 4 May 2025 |
| Node | Node | Node | Node | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| () | (kW) | (kW) | (kW) | () | (kW) | (kW) | (kW) | ||||
| 1 | 2 | 0.053 | 70 | 100 | 0 | 11 | 12 | 0.079 | 68 | 70 | 0 |
| 1 | 3 | 0.054 | 0 | 0 | 0 | 11 | 13 | 0.078 | 10 | 0 | 75 |
| 3 | 4 | 0.054 | 36 | 40 | 120 | 10 | 14 | 0.083 | 0 | 0 | 0 |
| 4 | 5 | 0.063 | 4 | 0 | 0 | 14 | 15 | 0.065 | 22 | 30 | 0 |
| 4 | 6 | 0.051 | 36 | 0 | 0 | 15 | 16 | 0.064 | 23 | 10 | 0 |
| 3 | 7 | 0.037 | 0 | 0 | 0 | 16 | 17 | 0.074 | 43 | 0 | 60 |
| 7 | 8 | 0.079 | 32 | 50 | 0 | 16 | 18 | 0.081 | 34 | 60 | 0 |
| 7 | 9 | 0.072 | 80 | 0 | 100 | 14 | 19 | 0.078 | 9 | 15 | 0 |
| 3 | 10 | 0.053 | 0 | 10 | 0 | 19 | 20 | 0.084 | 21 | 10 | 50 |
| 10 | 11 | 0.038 | 45 | 30 | 0 | 19 | 21 | 0.082 | 21 | 20 | 0 |
| Node | Node | Node | Node | Node | Node | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| () | (kW) | (kW) | (kW) | () | (kW) | (kW) | (kW) | () | (kW) | (kW) | (kW) | ||||||
| 1 | 2 | 0.108 | 0 | 0 | 10.075 | 20 | 21 | 0.819 | 17.64 | 70 | 152.5 | 40 | 41 | 1.002 | 10 | 0 | 0 |
| 2 | 3 | 0.163 | 50 | 0 | 40.35 | 21 | 22 | 1.548 | 17.64 | 17.995 | 30 | 41 | 42 | 0.273 | 17.64 | 25 | 17.995 |
| 3 | 4 | 0.217 | 28 | 28.565 | 0 | 19 | 23 | 0.182 | 28 | 75 | 28.565 | 41 | 43 | 0.455 | 17.64 | 17.995 | 0 |
| 4 | 5 | 0.108 | 100 | 50 | 0 | 7 | 24 | 0.910 | 0 | 17.64 | 17.995 | 34 | 44 | 1.002 | 17.64 | 17.995 | 0 |
| 5 | 6 | 0.435 | 17.64 | 17.995 | 25.18 | 8 | 25 | 0.455 | 17.64 | 17.995 | 50 | 44 | 45 | 0.911 | 50 | 17.64 | 17.995 |
| 6 | 7 | 0.272 | 0 | 8.625 | 0 | 25 | 26 | 0.364 | 0 | 28 | 28.565 | 45 | 46 | 0.911 | 25 | 17.64 | 17.995 |
| 7 | 8 | 1.197 | 17.64 | 17.995 | 30.29 | 26 | 27 | 0.546 | 110 | 75 | 175 | 46 | 47 | 0.546 | 7 | 7.14 | 10 |
| 8 | 9 | 0.108 | 17.8 | 350 | 40.46 | 27 | 28 | 0.273 | 28 | 125 | 28.565 | 35 | 48 | 0.637 | 0 | 10 | 0 |
| 9 | 10 | 0.598 | 0 | 100 | 0 | 28 | 29 | 0.546 | 0 | 50 | 75 | 48 | 49 | 0.182 | 0 | 0 | 25 |
| 10 | 11 | 0.544 | 28 | 28.565 | 0 | 29 | 30 | 0.546 | 17.64 | 0 | 17.995 | 49 | 50 | 0.364 | 18.14 | 0 | 18.505 |
| 11 | 12 | 0.544 | 0 | 40 | 45 | 30 | 31 | 0.273 | 17.64 | 17.995 | 0 | 50 | 51 | 0.455 | 28 | 28.565 | 0 |
| 12 | 13 | 0.598 | 45 | 40 | 22.5 | 31 | 32 | 0.182 | 0 | 175 | 0 | 48 | 52 | 1.366 | 30 | 0 | 15 |
| 13 | 14 | 0.272 | 17.64 | 17.995 | 35.13 | 32 | 33 | 0.182 | 7 | 7.14 | 12.5 | 52 | 53 | 0.455 | 17.64 | 35 | 17.995 |
| 14 | 15 | 0.326 | 17.64 | 17.995 | 20.175 | 33 | 34 | 0.819 | 0 | 0 | 0 | 53 | 54 | 0.546 | 28 | 30 | 28.565 |
| 2 | 16 | 0.728 | 17.64 | 67.5 | 33.49 | 34 | 35 | 0.637 | 0 | 0 | 50 | 52 | 55 | 0.546 | 38 | 0 | 48.565 |
| 3 | 17 | 0.455 | 56.1 | 57.15 | 50.25 | 35 | 36 | 0.182 | 17.64 | 0 | 17.995 | 49 | 56 | 0.546 | 7 | 40 | 32.14 |
| 5 | 18 | 0.820 | 28 | 28.565 | 200 | 26 | 37 | 0.364 | 28 | 30 | 28.565 | 9 | 57 | 0.273 | 48 | 35.065 | 10 |
| 18 | 19 | 0.637 | 28 | 28.565 | 10 | 27 | 38 | 1.002 | 28 | 28.565 | 25 | 57 | 58 | 0.819 | 0 | 50 | 0 |
| 19 | 20 | 0.455 | 17.64 | 17.995 | 150 | 29 | 39 | 0.546 | 0 | 28 | 28.565 | 58 | 59 | 0.182 | 18 | 28.565 | 25 |
| 21-Bus Grid | |||
| Method | Iter. | Proc. Time (ms) | Power Losses (kW) |
| Equation (17) | 4 | 0.6801 | |
| Equation (21) | 5 | 0.8269 | |
| Equation (25) | 5 | 0.8339 | |
| Equation (28) | 6 | 0.4252 | 92.2701 |
| Equation (30) | 13 | 0.5125 | |
| Equation (32) | 13 | 0.5123 | |
| Equation (34) | 10 | 0.4277 | |
| 85-Bus Grid | |||
| Method | Iter. | Proc. Time (ms) | Power Loss (kW) |
| Equation (17) | 4 | 8.3251 | |
| Equation (21) | 5 | 11.1240 | |
| Equation (25) | 5 | 11.2680 | |
| Equation (28) | 6 | 3.9778 | 452.2981 |
| Equation (30) | 13 | 4.5794 | |
| Equation (32) | 12 | 4.5075 | |
| Equation (34) | 10 | 3.5321 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montoya, O.D.; Pulgarín Rivera, J.D.; Grisales-Noreña, L.F.; Gil-González, W.; Andrade-Rengifo, F. A Family of Newton and Quasi-Newton Methods for Power Flow Analysis in Bipolar Direct Current Networks with Constant Power Loads. Math. Comput. Appl. 2025, 30, 50. https://doi.org/10.3390/mca30030050
Montoya OD, Pulgarín Rivera JD, Grisales-Noreña LF, Gil-González W, Andrade-Rengifo F. A Family of Newton and Quasi-Newton Methods for Power Flow Analysis in Bipolar Direct Current Networks with Constant Power Loads. Mathematical and Computational Applications. 2025; 30(3):50. https://doi.org/10.3390/mca30030050
Chicago/Turabian StyleMontoya, Oscar Danilo, Juan Diego Pulgarín Rivera, Luis Fernando Grisales-Noreña, Walter Gil-González, and Fabio Andrade-Rengifo. 2025. "A Family of Newton and Quasi-Newton Methods for Power Flow Analysis in Bipolar Direct Current Networks with Constant Power Loads" Mathematical and Computational Applications 30, no. 3: 50. https://doi.org/10.3390/mca30030050
APA StyleMontoya, O. D., Pulgarín Rivera, J. D., Grisales-Noreña, L. F., Gil-González, W., & Andrade-Rengifo, F. (2025). A Family of Newton and Quasi-Newton Methods for Power Flow Analysis in Bipolar Direct Current Networks with Constant Power Loads. Mathematical and Computational Applications, 30(3), 50. https://doi.org/10.3390/mca30030050










