Computational Modeling of Sodium-Ion-Channel-Based Glucose Sensing Biophysics to Study Cardiac Pacemaker Action Potential

Abstract

Elevated blood glucose levels, known as hyperglycemia, play a significant role in sudden cardiac arrest, often resulting in sudden cardiac death, particularly among those with diabetes. Understanding the internal mechanisms has been a challenge for healthcare professionals, leading many research groups to investigate the relationship between blood glucose levels and cardiac electrical activity. Our hypothesis suggests that glucose-sensing biophysics mechanisms in cardiac tissue could clarify this connection. To explore this, we adapted a single-compartment computational model of the human pacemaker action potential. We incorporated glucose-sensing mechanisms with voltage-gated sodium ion channels using ordinary differential equations. Parameters for the model were based on existing experimental studies to mimic the impact of glucose levels on pacemaker action potential firing. Simulations using voltage clamp and current clamp techniques showed that elevated glucose levels decreased sodium ion channel currents, leading to a reduction in the pacemaker action potential frequency. In summary, our mathematical model provides a cellular-level understanding of how high glucose levels can lead to bradycardia and sudden cardiac death.

1. Introduction

Cardiovascular disease is the leading global cause of death and imposes significant economic burdens due to healthcare costs and societal impacts. Effective prevention and management strategies are urgently needed for ischemic heart disease and stroke to mitigate their public health impact [1,2]. A heart attack is typically defined as the obstruction of oxygenated blood flow from the heart to a specific segment. Electrical signaling in cardiac muscle coordinates the heart’s contractions, regulating its rhythm and ensuring effective pumping. Sudden cardiac arrest (SCA), occurring abruptly due to irregular electrical activities of the heart, leads to sudden cardiac death (SCD) if the victim does not receive immediate treatment [3,4]. Bradycardia (heart rate of less than 60 beats per minute) and tachycardia (heart rate of more than 100 beats per minute) are two arrhythmic conditions that can lead to SCA and SCD [5,6]. Cardiac tissues are electrically excitable, initiating a series of electrical activities including depolarization, hyperpolarization, and the generation of action potentials (AP), which in turn generate mechanical forces responsible for pumping blood into various organs of the body [7,8,9,10]. The cardiac AP is a voltage change that propagates along the membrane of a myocyte, and it is an “all-or-nothing” event triggered by a sufficient depolarization reaching a threshold voltage [11]. In addition, the electrical signaling in different regions of the heart are not uniform as these sections generate a set of clearly distinguishable AP configurations [12,13]. Cardiac APs generated at the location of the sinoatrial node (pacemaker AP), atrioventricular node, and bundle of His and Purkinje fibers are major contributors to rhythmic function [14]. A diverse group of ion channels are present in the different regions of the cardiac tissue to generate and modulate all these electrical properties including the AP [15,16]. The most common ion channels in both excitable and non-excitable tissues are sodium, potassium, and calcium ion channels. Sodium channels initiate the rapid depolarization phase by allowing sodium influx, while potassium channels contribute to repolarization by facilitating potassium efflux. Calcium channels are involved in both depolarization and repolarization phases, maintaining the plateau phase and regulating contraction. These channels ensure the proper rhythmicity and contractility of the heart, essential for its normal function and circulation [17].

A set of clinical and experimental studies indicate that abnormal blood glucose concentrations are intricately linked to cardiac electrical properties, contributing significantly to SCD [18,19,20]. About one-third of SCD cases are associated with an interplay between abnormal blood glucose levels and cardiac electrical dysfunctions [21]. Hyperglycemia, characteristic of diabetes and glucose intolerance, can lead to non-enzymatic glycosylation and damage to cardiac tissues, affecting the heart’s electrical conductivity and predisposing individuals to fatal arrhythmias [19,21]. Elevated glucose levels are also correlated with increased arterial stiffness and microvascular damage, further exacerbating the risk of cardiac events [21]. These findings highlight the complex relationship between metabolic disturbances and cardiac function, underscoring the importance of managing blood glucose levels in preventing SCD. It is well known that elevated blood glucose levels are primary symptoms in people with both type 1 and type 2 diabetes due to a lack of sufficient insulin secretion from the pancreatic β cells [22,23,24]. Patients with type 2 diabetes are associated with an increased risk of SCA [25,26,27]. The scientific communities are exploring novel promising therapies to overcome the limitations of current exogenous insulin delivery for maintaining stable basal blood glucose concentrations. The ion channels are new medical research interests in finding novel pharmacological agents to maintain constant electrical properties in cardiac tissues [28,29,30]. In our body, the ion channels act as biological sensors by facilitating the flow of respective ions across the cell membrane after sensing several stimuli such as pH, light, force, hormones, chemicals, and electrical potentials [31,32]. In cardiac electrophysiology, voltage-gated sodium channels are the transmembrane proteins located across the cell membrane of cardiomyocytes. The influx of sodium ions through these ion channels is responsible for the initial fast upstroke of the cardiac AP [33]. Therefore, any dysfunction in this ion channel can alter the AP patterns and electrical signaling in the cardiomyocytes. It is demonstrated that extracellular glucose application inhibits the voltage-gated sodium channel current in the pancreatic β cells [34]. Therefore, we can predict a hypothesis that the cardiac voltage-gated sodium ion channels also act like glucose sensors and modulate the cardiac AP patterns concerning blood glucose concentrations. Therefore, any additional knowledge of the glucose-sensing mechanism by these sodium ion channels might be useful to explore new pharmacological targets for SCA. Unfortunately, the in-depth understanding of the relationship among cardiac ion channel biophysics, AP generation, and blood sugar levels is unexplored due to the complex nature of the cardiac electrophysiology experimental setup.

For several decades, computational, mathematical, and in silico techniques have significantly contributed to the understanding of complex biological signaling processes by simulating various scenarios, predicting outcomes, and providing insights that might be challenging to obtain through traditional experimental methods [35,36]. Computational simulations have contributed to understanding various types of muscle electrophysiology by exploring cellular biophysics, thus modulating cellular electrical activities [37,38]. These models provide insights into ion channel function, including conductance, ion selectivity, and channel opening, which are pivotal in pathological conditions [39,40]. Another positive aspect of biophysical modeling is that models directly simulate ion flux through membrane channels, aiding in understanding their behavior and contribution to disease processes [40]. Biophysical modeling of cardiac muscle electrophysiology plays a pivotal role in the discovery of novel therapies by providing a virtual platform to simulate the intricate electrical dynamics of the heart. Through these models, researchers can explore the effects of various pharmacological interventions and ion channel modulations on the cardiac AP, offering insights into potential therapeutic targets. By iteratively refining these models based on experimental data and clinical observations, researchers can identify promising drug candidates, predict their efficacy, and optimize treatment strategies for cardiovascular diseases [41]. Additionally, patient-specific models tailored to individual clinical measurements enable personalized medicine approaches, allowing for the development of precision therapies optimized for specific cardiac conditions [42]. Ultimately, biophysical modeling serves as a valuable tool in the translation of basic research findings into clinically relevant therapies, contributing to advancements in cardiovascular medicine and patient care [43]. Computational biophysical models are also continually enhanced by integrating new experimental data, refining parameters, and adjusting algorithms to better align with empirical findings [44]. This iterative process ensures that models accurately represent biological phenomena and facilitate deeper insights into complex systems [45]. Although there are numerous biophysical models for cardiac AP (detailed in the Methods section) aimed at understanding the underlying ion channel kinetics and signaling pathways, currently, there is no computational model describing the electrophysiological responses to blood glucose concentrations with ion channel kinetics in cardiac tissues, particularly for pacemaker action potential (PAP) electrophysiology. Here, we present a biophysically explained in silico model of PAP electrophysiology to examine the effect of glycemia on the PAP firing rate. Our objectives for establishing this model are threefold. First, supported by experimental data, we will simulate and validate the voltage-gated sodium ion channel kinetics concerning blood glucose concentration. Second, we will incorporate the ion channel into a single compartmental biophysical model to simulate the APs and investigate changes in AP parameters concerning blood glucose concentration. Third, we aim to draw new biological insights to support existing hypotheses from various experiments and propose new hypotheses for future research directions.

2. Materials and Methods

2.1. Model Adaptation

Biophysically detailed cell modeling made its debut in neuroscience 1952 thanks to the groundbreaking work of Hodgkin and Huxley on the squid giant axon. In the 1960s, Noble pioneered the first models of cardiac cellular activity [46]. Since then, an impressive array of mathematical models for cardiac muscle electrophysiology has emerged. The complexity of these models has steadily increased over the years as more experimental data has become available [47]. Recently, several models in cardiac cell electrophysiology have been mathematically designed to mimic the behavior of cardiac electrical activities [48,49,50,51,52,53,54,55,56]. These models also serve as a bridge between cellular-level models and organ-level function, offering a comprehensive understanding of cardiac electrical activity across different scales. In this study, we customized the Di Francesco model [55] to generate pacemaker action potentials. It should be noted that the Di Francesco model generates pacemaker AP, which originates from the sinoatrial (SAN) node. Key modifications involved adjusting ion channel kinetics and conductances to more closely represent the physiological conditions pertinent to our study. These changes were meticulously applied to ensure that the generated action potentials closely resemble the pacemaker activity of SAN cells, offering a robust basis for our subsequent analyses.

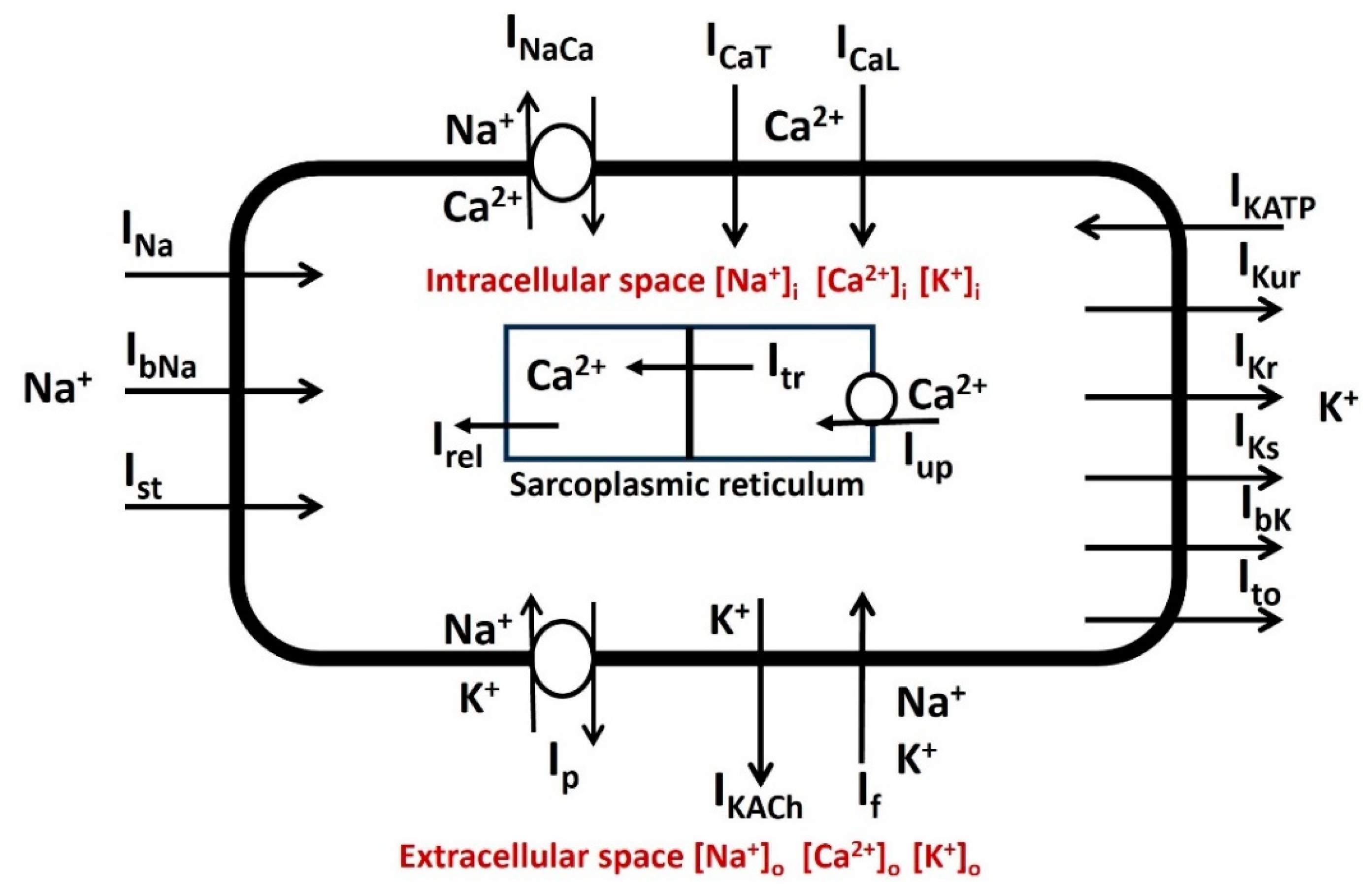
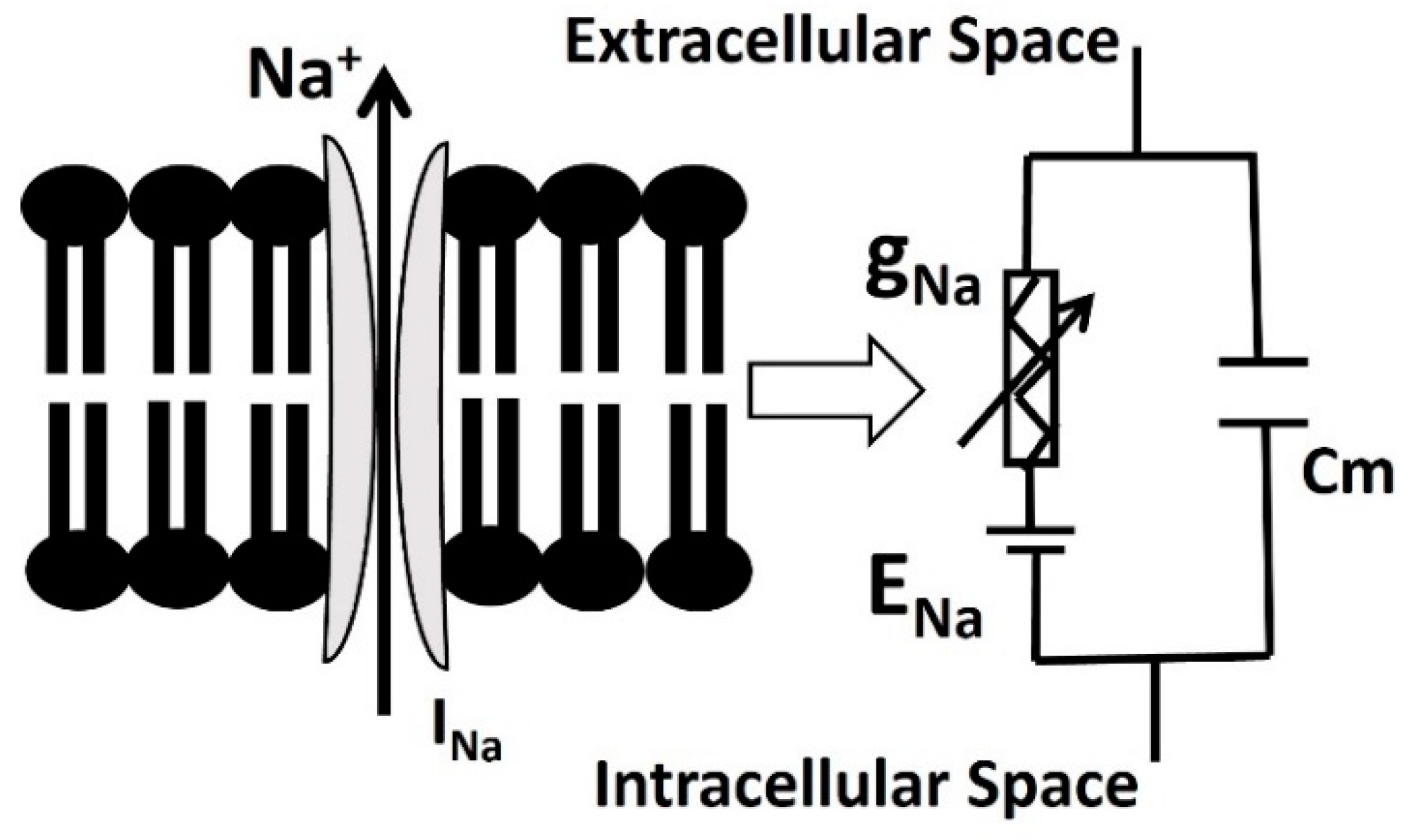
2.2. General Membrane Current Descriptions

The schematic diagram of Figure 1 shows all the ionic components in our model. It consists of L-type calcium current (I_CaL), T-type calcium current (I_CaT), sodium–calcium exchange current (I_NaCa), fast sodium current (I_Na), background sodium current (I_bNa), sustained inward current (I_st), ATP-dependent potassium current (I_KATP), ultrarapid component of delayed rectifying potassium current (I_Kur), rapid component of delayed rectifying potassium current (I_Kr), slow component of delayed rectifying potassium current (I_Ks), background potassium current (I_bK), transient outward current (I_to), hyperpolarizing-activated current (I_f), muscarinic potassium current (I_KACh), and sodium–potassium pump current (I_p). The sarcoplasmic reticulum, the internal storage of Ca²⁺, also consists of several components. I_tr is Ca²⁺ transfer current, I_up is Ca²⁺ uptake current, and I_rel is Ca²⁺ release current.

The single cell is electrically defined by a resistor-capacitor (RC) circuit, where the membrane capacitance C_m is parallel with the variable ion channel conductance g_ion. All active ion channel conductances g_ion are associated with respective Nernst potential E_ion in series. In addition, non-specific ionic currents are incorporated to compensate for any cellular leakage current. Figure 2. Illustrates the schematic overview of the parallel conductance model for ionic current (I_Na).

The time-dependent characteristics of the cell’s membrane potential V_m for Figure 1 are described by Equation (1).

$$\begin{array}{c}{\displaystyle \frac{d{V}_m\left(t\right)}{dt}}=-{\displaystyle \frac{1}{C_m}} (I_{CaL}+I_{CaT}+I_{NaCa}+I_{Na}+I_{bNa}+I_{st}+ I_l+I_{KATP}+I_{Kur}\\ +I_{Kr}+I_{Ks}+I_{bK}+I_{to}+I_f+I_{KACh}+I_p)\end{array}$$

(1)

Then, the individual ionic current is calculated by conventual Ohm’s law. It is described in Equation (2).

$$I_{ion}=\overline{g}{\left[m\right(V_m,t,{\left[{Ca}^{2+}\right]}_i\left)\right]}^x{\left[h\right(V_m,t,{\left[{Ca}^{2+}\right]}_i\left)\right]}^y(V_m-E_{\mathrm{N}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{s}\mathrm{t}})$$

(2)

where $\overline{g}$ and E_Nerrnst is the maximum channel conductance and Nernst potential of the respective ion channel.

The parameters m and h in Equation (2) are time/voltage/Ca²⁺ dependent dimensionless activation and inactivation gating variables respectively. For equation fitting purposes, another set of dimensionless parameters “x” and “y” are used. The m and h are computed by a set of first-order differential equations according to the classical Hodgkin–Huxley (HH) formulation mechanism [57]. For example, Equation (3) computes the instantaneous value of the activation variable “m” in our PAP model.

$${\displaystyle \frac{ dm(V_m, t)}{dt}}={\displaystyle \frac{m_{\infty }\left(V_m\right)-m(V_m,t)}{{\tau }_m}}$$

(3)

where m_∞, is the steady-state value and τ_m is the time constant, all being functions of voltage and/or ionic concentrations.

Here the state parameter dependence on V_m for ion channels is described by the Boltzmann equation.

$$m_{\infty }= \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$1+\mathrm{e}\mathrm{x}\mathrm{p}((V_m+V_{m\frac{1 }{2}})/S_m)$}\right.$$

(4)

where V_1/2 is the half activation potential and S is the slope factor.

Table 1. Model general constant parameters (–dapted from Courtemanche 1998 [50], Davies 2016 [54], Di Francesco 1985 [55], Fabbri 2017 [56]).

Parameter	Definition	Value
R	Gas constant	8.3143 J K−1 mol−1
T	Temperature	310 K
Cm	Membrane capacitance	100 pF
F	Faraday constant	96.4867 C/mmol
Vcell	Cell volume	20,100 μm3
Vi	Intracellular volume	13,668 μm3
Vup	SR uptake compartment volume	1109.52 μm3
Vrel	SR release compartment volume	96.48 μm3
[K+]o	Extracellular K1 concentration	5.4 mM
[Na+]o	Extracellular Na1 concentration	140 mM
[Ca2+]o	Extracellular Ca21 concentration	1.8 mM

consists of the general constant parameters used in this computational model

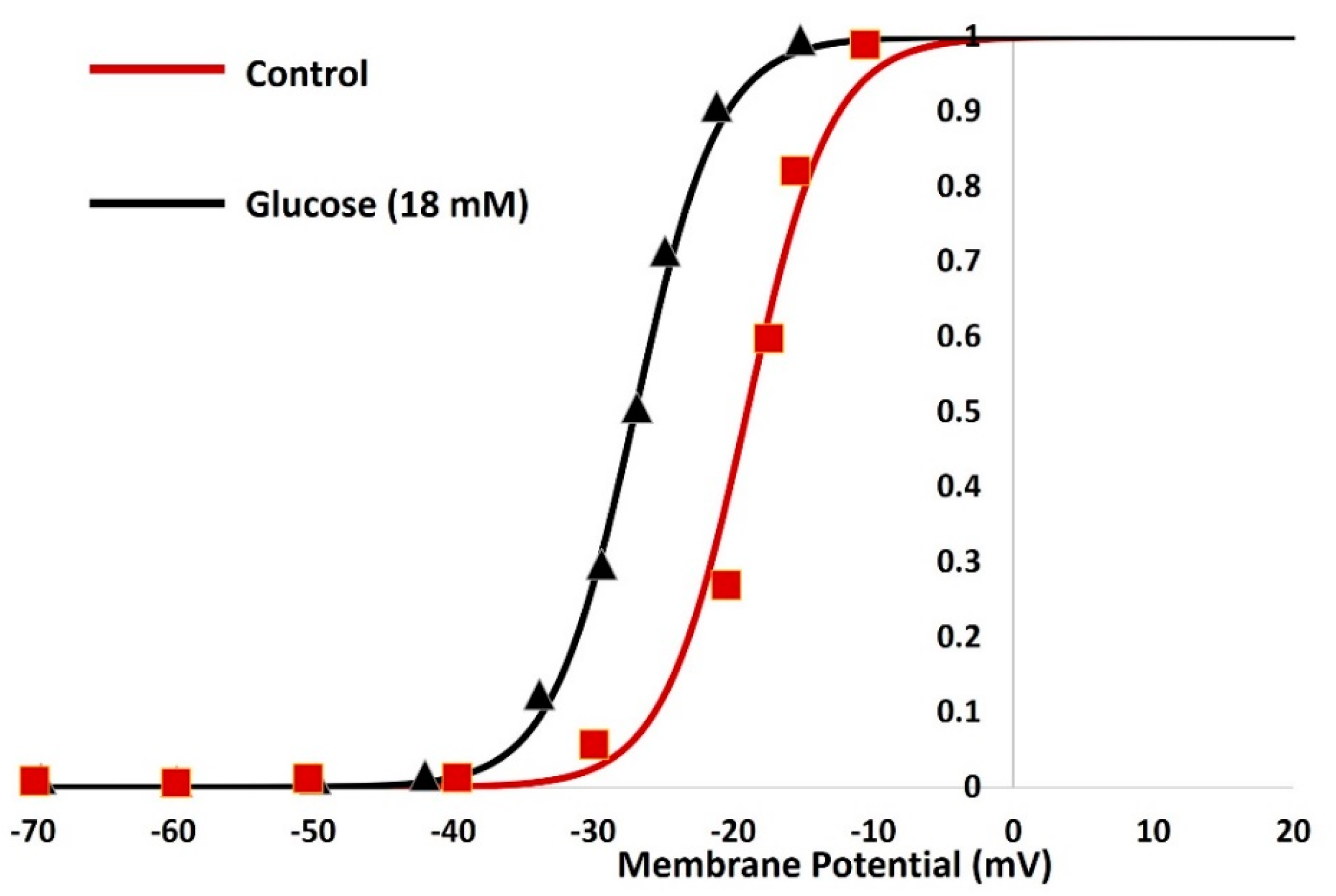
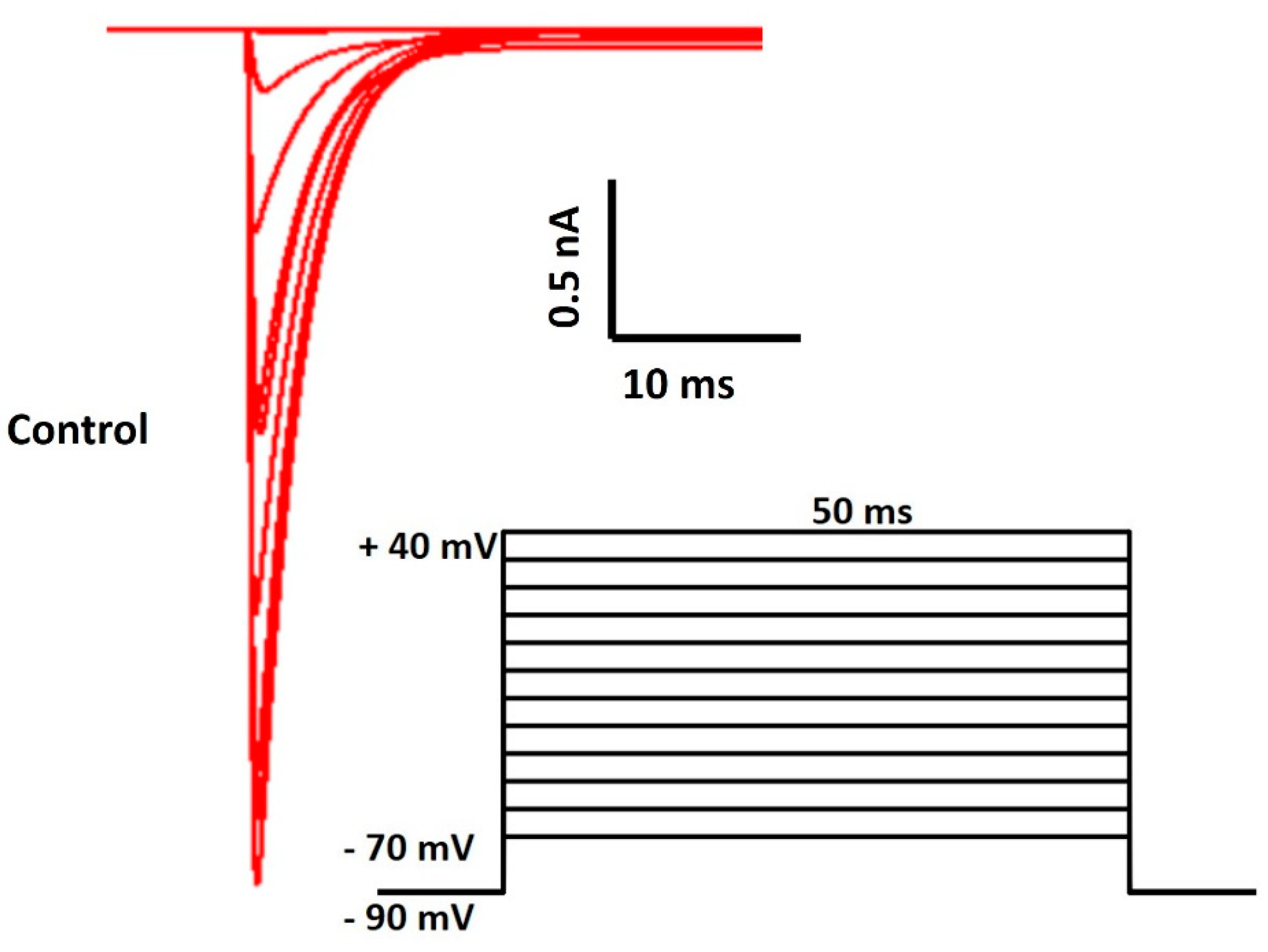
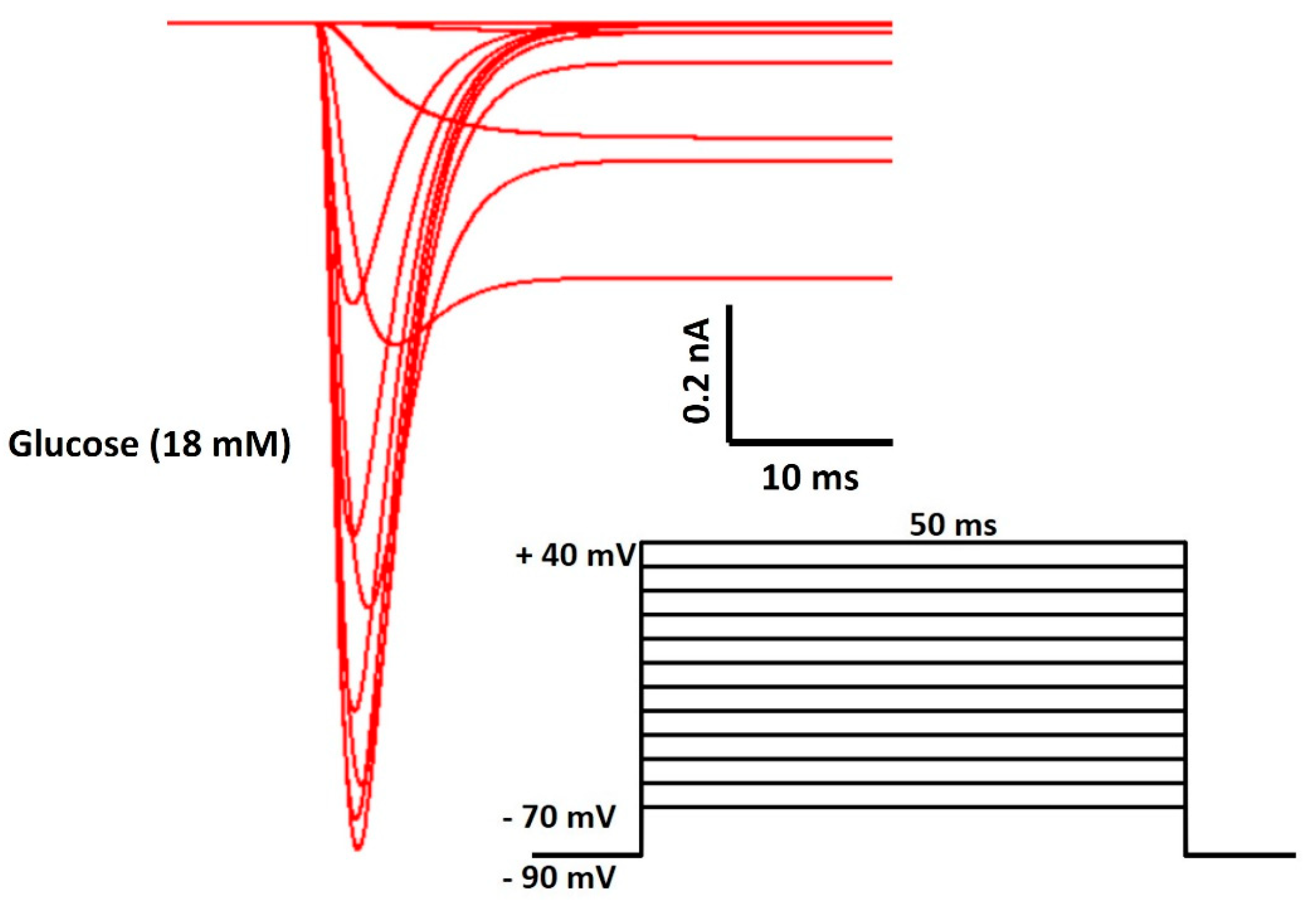
2.3. Na Channel with Blood Glucose Sensing Mechanism

$$I_{Na}=\overline{g_{Na}} n^{3}h(V-E_{Na})$$

(5)

$$n_{\infty }={\displaystyle \frac{1}{1+\mathit{exp}\left(\frac{-\left(V+9\right)}{8}\right)}}$$

(6)

$$\mathrm{s}{h}_{\infty }={\displaystyle \frac{1}{1+\mathit{exp}\left(\frac{\left(V+30\right)}{13}\right)}}$$

(7)

The blood glucose sensing mechanism is mimicked by changing the half activation potential for both normal and 18 mM glucose concentration according to the experimental data [34]. The slope value is tuned to match the experimental data. Observations were made of changes in the AP, total inward, and sodium ion channel current.

Simulations were conducted using a consistent time step of 0.04 ms via the Euler Method on a PC equipped with an Intel Core i7 CPU operating at 3.80 GHz and a dual-core setup. The NEURON simulation environment was employed for model creation, known for its accurate representation of excitable cells [58]. The Euler method is a primary numerical approach for solving ODEs. NEURON offers stability and adaptability in simulations of neuronal dynamics, making it suitable for ODE solutions due to its straightforwardness [58]. While NEURON primarily adopts implicit integration techniques like backward Euler and a version of Crank–Nicolson for stability, it also accommodates Euler’s method due to its efficiency and minimal memory footprint [58]. Post-modeling, stability, and consistency were assessed by varying the maximum conductance (g_max) of ionic conductances within +/− 30% of the default. Results showed stable action potentials, with expected responses to changes in conductance, such as increased g_max resulting in higher AP peak amplitudes, while maintaining the AP’s normal characteristics.

3. Results

The steady-state activation curve, current-voltage curve, and currents under the voltage-clamp protocol are generated for the voltage-gated sodium channel currents (I_Nav) under both control and application of glucose 18 mM) conditions. The I_Nav is formulated according to the Equations (5)–(7). The HH formalism consists of both activation and inactivation parameters. Active currents were induced by applying a series of +10 mV voltage steps ranging from −70 mV to 50 mV, each lasting 50 ms, starting from a holding potential of −120 mV. This protocol was used to assess the impact of glucose on I_Nav steady-state activation. The peak of each simulated current was recorded. Figure 3 displays the simulated and validated steady-state activation curves for the I_Nav. The red solid line represents the simulated curve from our model under control conditions, while the black solid line depicts the curve with 18 mM glucose application. The half activation potential for both control and 18 mM of glucose are −19.5 mV and −28.7 mV, respectively. The filled red squares and black triangles represent the combined experimental data sourced from Chen 2018 [34]. It also supports that our simulated curve has good matching with the experimental data.

Next, we simulated the I_Nav for 50 ms under the voltage clamp protocol. The holding potential was held at −90 mV and the membrane potential increased with 10 mV step voltage from −70 mV to 40 mV. Figure 4 illustrates the I_Nav under the voltage clamp protocol.

Then, the I_Nav was generated again under the same voltage clamp protocol with the application of 18 mM glucose. The simulated current is shown in Figure 5. When we compare the current amplitude (Y-axis) in Figure 4 and Figure 5, it is clearly illustrated that the glucose concentration reduces the I_Nav significantly.

The I_Nav model was integrated into a whole-cell, single-compartment cell model to simulate APs under both control conditions and the application of glucose. This approach allowed for a detailed examination of the effects of glucose on cardiac electrophysiology. To accurately assess the impact of glucose, we characterized the AP waveform using a comprehensive set of parameters that represent key experimental biomarkers. These parameters were calculated following standardized guidelines to ensure consistency and comparability with experimental data.

The parameters evaluated include:

• Cycle length (CL): The duration between the peaks of two consecutive APs, representing the pacemaker activity cycle.
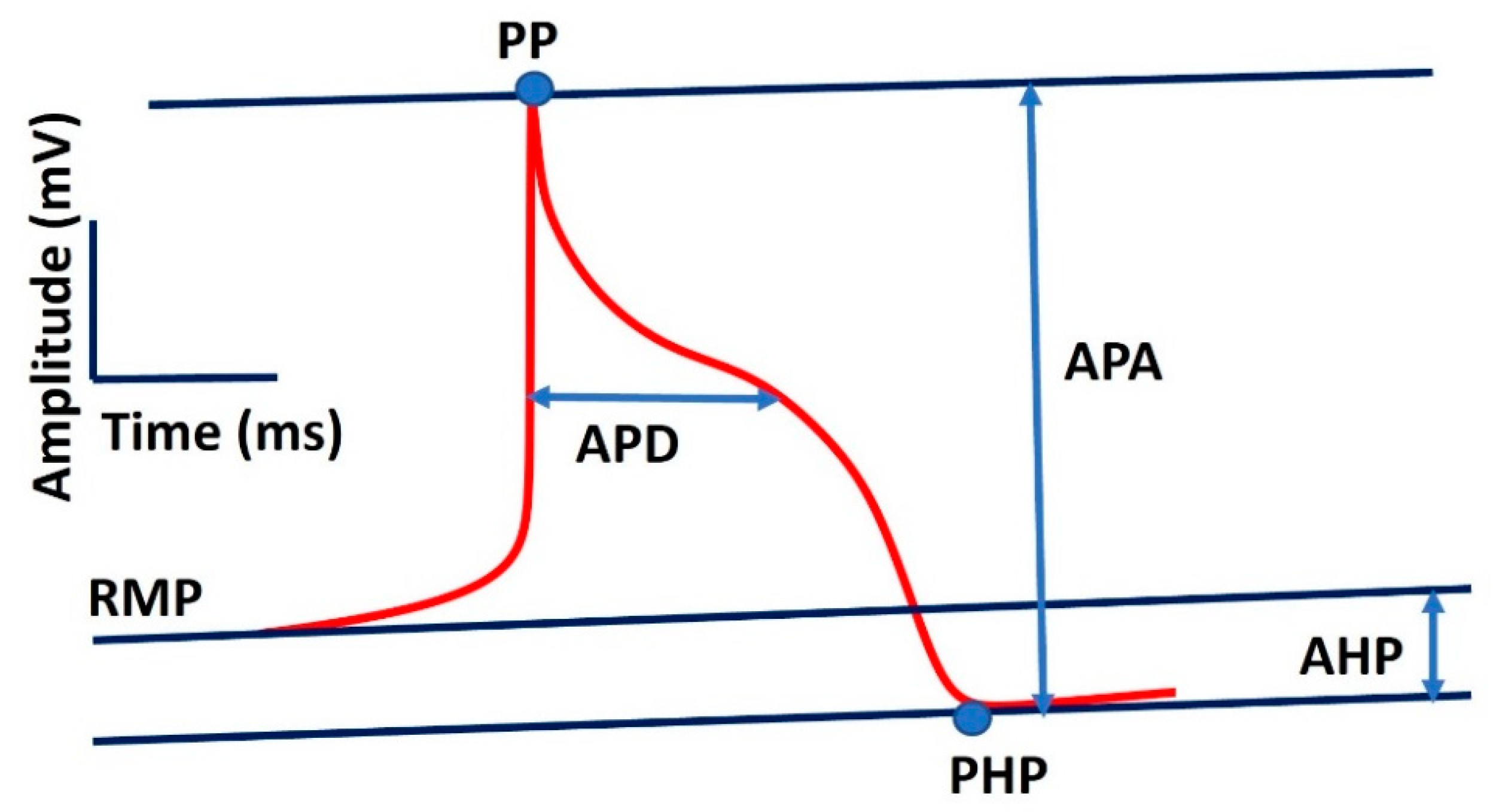
• Peak potential (PP): The maximum value reached during the AP.
• Action potential amplitude (APA): The difference between the peak potential and the most negative repolarization potential, reflecting the overall strength of the AP.
• Maximum diastolic potential (MDP): The most negative potential reached just before the peak potential, indicating the cell’s readiness for the next depolarization.
• Diastolic depolarization rate (DDR): The rate at which the membrane potential rises during diastole, indicative of the pacemaker cell’s automaticity.
• Diastolic depolarization rate over the first 100 ms (DDR100): A more specific measure of the initial depolarization rate during diastole.
• Action potential duration (APD): The time required for the membrane potential to repolarize to 90% of its peak value, providing insight into the refractory period and overall duration of the AP.

These parameters, illustrated in Figure 6, offer a comprehensive profile of the AP. Additional parameters, such as resting membrane potential (RMP), peak hyperpolarization (PHP) and after hyperpolarization (AHP), were also assessed. RMP is the baseline electrical potential of the cell in its quiescent state, while PHP and AHP describe the hyperpolarization phases following the AP peak. Together, these measurements provide a detailed understanding of the electrophysiological changes induced by glucose in PAPs, which are critical for interpreting the effects of hyperglycemia on cardiac function.

We conducted simulations to generate the PAPs under both control conditions and with a glucose concentration of 18 mM, as illustrated in Figure 7. The APs were simulated using a current clamp protocol in a single-cell model. In Figure 7a, a single AP was generated by injecting a 3 nA current for 100 ms, resulting in a significant reduction in all measured parameters for glucose concentration of 18 mM. Notably, the model did not produce any AP spikes when the injected current was below 3 nA. For further investigation of multiple APs, we injected the same 3 nA current over 11,000 ms. This longer stimulation, shown in Figure 7b, produced a pattern of AP firing that also demonstrated a reduced firing frequency for a glucose concentration of 18 mM.

We extended our simulation to investigate the modulation of conduction velocity (CV) by examining the AP propagation along a one-dimensional strand of sinoatrial cells. Initially, we simulated an AP in a single elongated cell with a length of 20 mm. The cell was divided into 101 interconnected compartments, treating it as a continuous cable where each compartment was considered spatially isopotential. The length constant, a key property for studying AP propagation in excitable tissues, is typically between 1 and 2 mm in sinoatrial cells [59]. Additionally, the CV in sinoatrial muscle is approximately 0.5 to 1.0 m/s [60]. A current stimulus was applied at the midpoint of the cell (x = 10 mm), and electrical activity was recorded at 10 mm and 14 mm (approximately twice the length constant). The resulting APs were compared, and the conduction velocity was calculated. Upon introducing glucose, the CV decreased from 0.85 m/s to 0.73 m/s.

We then compared all important parameters for both APs (from Figure 7a) listed in

Table 2. Comparison between simulated AP and experimental AP.

Parameter	Control	Glucose
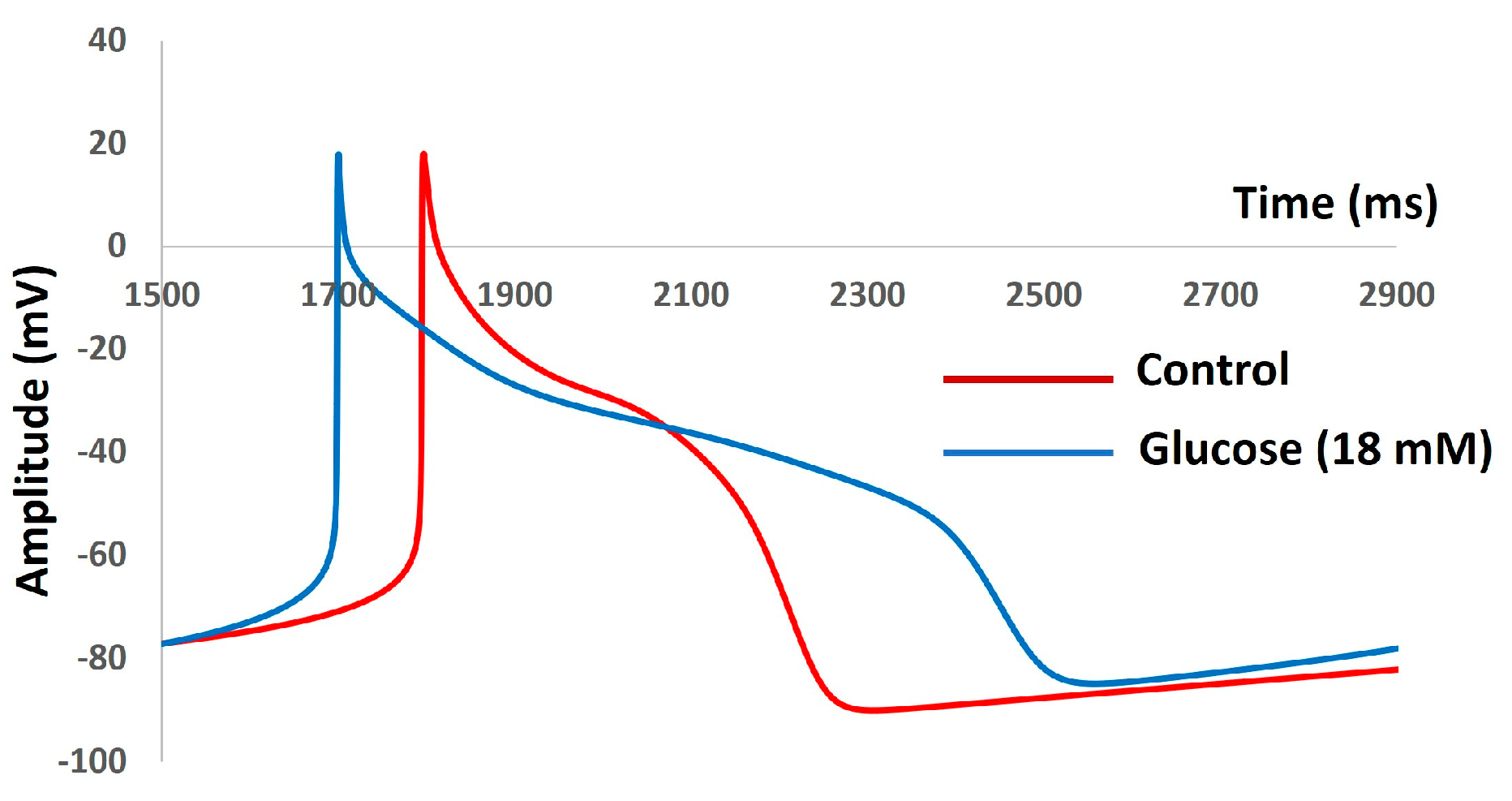
RMP (mV)	−79	−80
AP Peak (mV)	17	5
AHP peak (mV)	−83	−82
AP Duration (ms)	38	35
CV (m/s)	0.85	0.73

. We explored the changes induced by hyperglycemia and the main features of AP responsible for these changes.

Recent studies have indicated that hyperglycemia influences the activation and inactivation kinetics of various ion channels [61,62,63]. However, the precise relationship between glucose concentration and ion channel current electrophysiology has not been experimentally quantified. In one investigation, Yoshida’s group reported that glucose metabolism regulates voltage-gated K⁺ channels in pancreatic β-cells, with voltage-gated current modulation observed at glucose concentrations ranging from 2.8 to 16.6 mM [64]. To explore this effect in our model, we normalized the glucose concentration to the K⁺ channel’s maximum conductance and applied this to an 18 mM glucose concentration. While we anticipated an impact on excitability and APD duration, Figure 8 reveals a significant alteration (extended) in APD (without affecting peak amplitude), likely reducing the AP frequency.

4. Discussion

The human heart is the most delicate organ of the body and cardiac arrest is a common fatal crisis across the globe. Similarly, a large portion of the population in the world is affected by type 2 diabetes due to unhealthy diet. High blood glucose concentration or hyperglycemia can damage all major organs of the body including the heart, kidneys, eyes, and brain. Cardiac arrest leads to death immediately, so protecting the heart from the negative impact of hyperglycemia is the highest priority. Balancing the basal level of the blood glucose level with optimal insulin therapy is an invasive discomfort process. Therefore, researchers are investigating all kinds of alternative medication approaches to protect the heart. A plethora of experimental evidence has demonstrated the possible linking mechanism between the blood glucose concentration and the abnormal pacemaker rhythms of the cardiac tissue. Recent research has uncovered a novel approach to reducing blood glucose levels through the modulation of ion channel currents. Specific ion channels, when activated, can enhance glucose uptake into cells, thereby lowering blood glucose levels. These channels facilitate ion movement across cell membranes, triggering pathways that increase glucose transporter activity. This discovery offers new avenues for diabetes treatment, potentially providing alternatives to traditional insulin-based therapies. By targeting these ion channels, researchers aim to develop new drugs that efficiently manage blood glucose levels, offering a promising strategy to improve the lives of individuals with diabetes. In addition, understanding the blood glucose sensing mechanism to reduce cardiac ion channel current is also essential due to the interdependent nature of metabolic and cardiac functions. By using various cardiac ion channel agonists and antagonists, particularly for sodium and calcium channels, metabolic demand on cardiac cells can be recovered, membrane potential stabilized, and excessive excitability prevented. Modeling the blood glucose sensing mechanism by reducing sodium current conductance is particularly relevant for cardiac arrest due to the link between metabolic status and cardiac function. In comparison to modulating other ion channel currents, reducing sodium current conductance offers a unique perspective due to the pivotal role of sodium channels in cellular excitability and metabolic signaling. Sodium channels are integral to action potential initiation and propagation, influencing overall cellular electrical activity. Experimental studies are always complex and need a longer time to investigate any new biological process. To overcome these limitations, computational modeling approaches are substantially useful for expanding our knowledge in fundamental biological research. In this in silico study, we, therefore, established a computational model of the glucose sensing mechanisms in human PAP electrophysiology. First, the biophysically detailed voltage-gated sodium ion channel is built, and the ionic currents are simulated under the voltage clamp protocol. The simulation showed reduced current patterns for the high blood glucose concentration. Second, we integrated the sodium ion channel mechanism into a single compartmental PAP model, which was rebuilt from the published models. Under the current clamp protocols, we simulated the PAP under both control and high blood glucose concentration conditions. The simulation showed the changes in the AP shapes for RMP, APP, and APD. It supports the less excitability property of the PAP. That means the less numbers of AP are evoked for a current stimulus with a fixed duration. It will lead to bradycardia which is a reduced frequency of the pace-making activity. In the introduction part, we have discussed how bradycardia causes SCA. From these simulation results, we can conclude that the agonists of the voltage-gated sodium ion channel of a specific subtype might be useful to compensate for the high glucose concentration effects. An elaborate experimental study can support this hypothesis. It is important to recognize that bradycardia and tachycardia result from deviations in the ECG waveform, also known as the PQRSTU waveform. The ECG waveform is generated by integrating the action potentials from the sinoatrial node, atrial muscle, atrioventricular node, bundle of His, Purkinje fibers, and ventricular muscle. Investigating ventricular electrical activities is also essential for understanding bradycardia and tachycardia. Our simulation results extend the prediction of the effects of high glucose concentration on sinoatrial electrical activities. More rigorous and complex modeling approaches, combined with experimental data, are essential to explore the effects of high glucose concentration on all ion channels and action potentials, potentially identifying new pharmacological targets. Our findings also suggest that hyperglycemia significantly modulates K⁺ channel activity, leading to prolonged APD and potentially reduced action potential frequency. This underscores the importance of glucose regulation in maintaining normal cellular excitability, with implications for understanding diabetic complications.

It should be noted that while the glucose-sensing mechanism model for sodium ion channel biophysics has been experimentally validated with the rat heart, it is subsequently incorporated into a whole-cell model of the human heart. This approach is common in modeling studies, where it is often necessary to use parameters from different species, which is considered a limitation. We recognize that while we have carefully tailored the Di Francesco model [55] to meet our study’s goals, certain assumptions and modifications may have introduced limitations. Although our adaptation process was thorough, it may not fully replicate the complex details of pacemaker action potentials as they occur in vivo. Furthermore, the pacemaker action potential produced by our model, although similar to those of the SAN, does not exactly replicate the shape of atrial or SAN action potentials, which may restrict the broader applicability of our results to other cardiac tissues. Further experimental work and model refinement are needed to improve its precision and broader relevance. Another major limitation of this computational study is that we have not considered the effects of glucose upon other ion channels due to a lack of experimental data. Another limitation is the simulation of the single compartmental biophysical cell model. The electrical properties of the multi-cellular network model will be different from the single-cell model. However, this present model is flexible to integrate other ion channels and extend for a multi-compartmental network model by adding experimental data in the future.