Estimation of the Equivalent Circuit Parameters in Transformers Using Evolutionary Algorithms
Abstract
1. Introduction
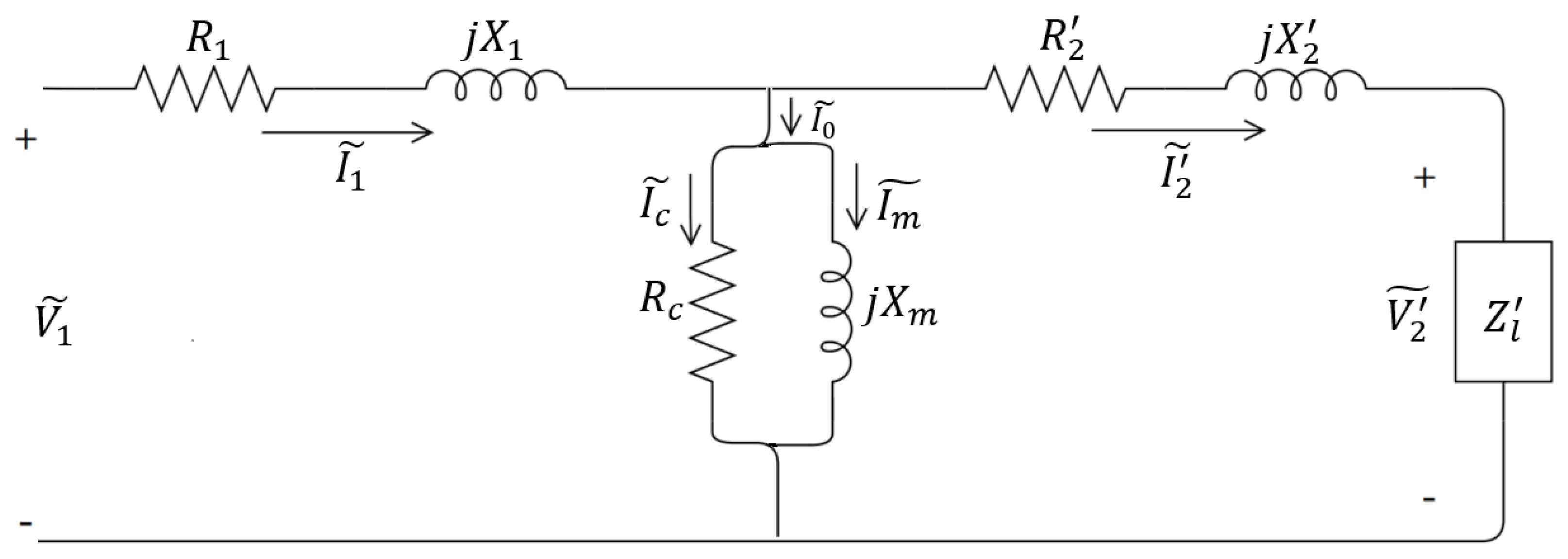
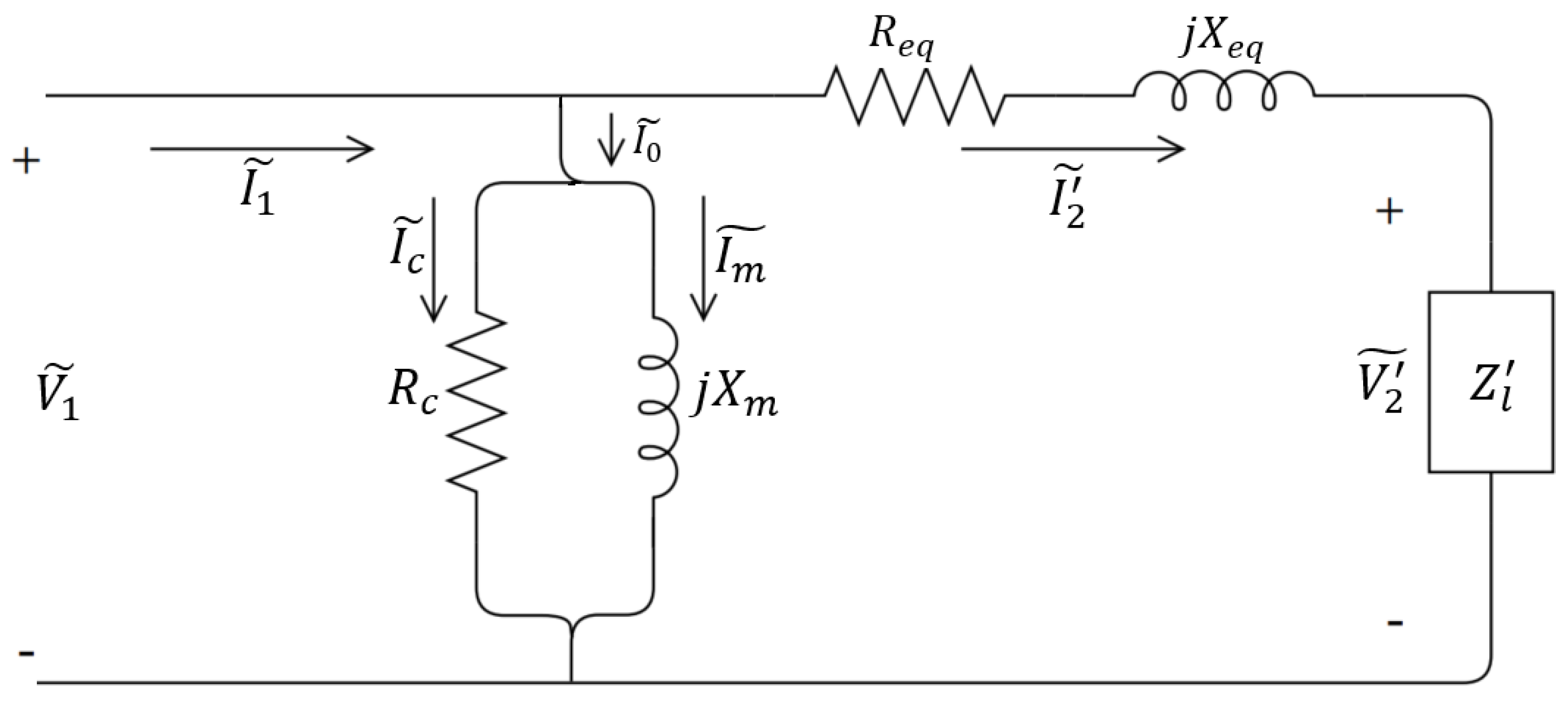
2. The Single-Phase Transformer Equivalent Circuit
| : primary winding resistance; |
| : primary winding reactance; |
| : secondary winding resistance with respect to the primary side; |
| : secondary leakage reactance with respect to the primary side; |
| : core resistance; |
| : magnetizing reactance. |
3. Optimization Algorithms
3.1. The Genetic Algorithm
| Algorithm 1: GA |
| Require: and ; 1: for i = 1 to NP do 2: Create ; 3: end for 4: for i = 1 to NP do 5: Evaluate (12); 6: end for 7: for gen = 1 to NG do 8: Select NP individuals based on fitness from X; 9: Apply crossover operator to individuals selected to generate NP children; 10: Apply mutation operator to the NP children; 11: Keep the NP children and discard the NP individuals in X, just keeping the best solution to replace the worst child; 12: end for Ensure: . |
3.2. Particle Swarm Optimization
| Algorithm 2: PSO |
| Require: and ; 1: for i = 1 to NP do 2: Create ; 3: end for 4: for i = 1 to NP do 5: Evaluate (12); 6: end for 7: while g < NGs do 8: for i = 1 to NP do 9: for j = 1 to D = (6) do 10: , = ; 11: Update velocity (13); 12: Update position (14); 13: end for 14: if then 15: ; 16: end if 17: end for 18: if then 19: ; 20: end if 21: end while Ensure: . |
3.3. The Gravitational Search Algorithm
| Algorithm 3: GSA |
| Require: and ; 1: for i = 1 to NP do 2: Create ; 3: end for 4: for i = 1 to NP do 5: Evaluate (12); 6: end for 7: for t = 1 to NGs do 8: ; 9: ; 10: ; 11: ; 12: ; 13: ; 14: for i = 1 to NP do 15: for j = 1 to Kbest do 16: if then 17: ; 18: end if 19: end for 20: end for 21: for i = 1 to NP do 22: for j = 1 to d = 6 do 23: ; 24: ; 25: ; 26: end for 27: end for 28: end for Ensure: . |
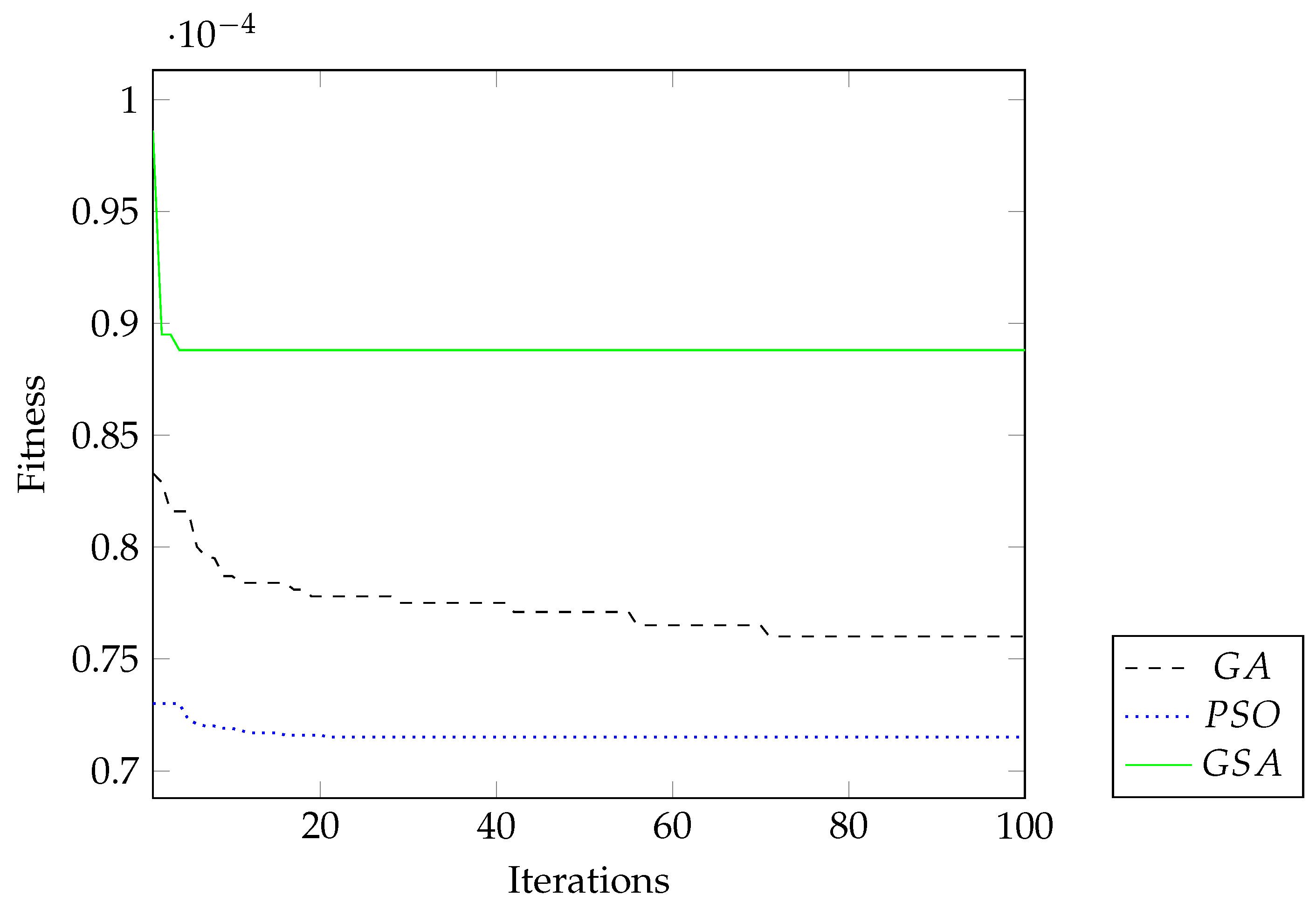
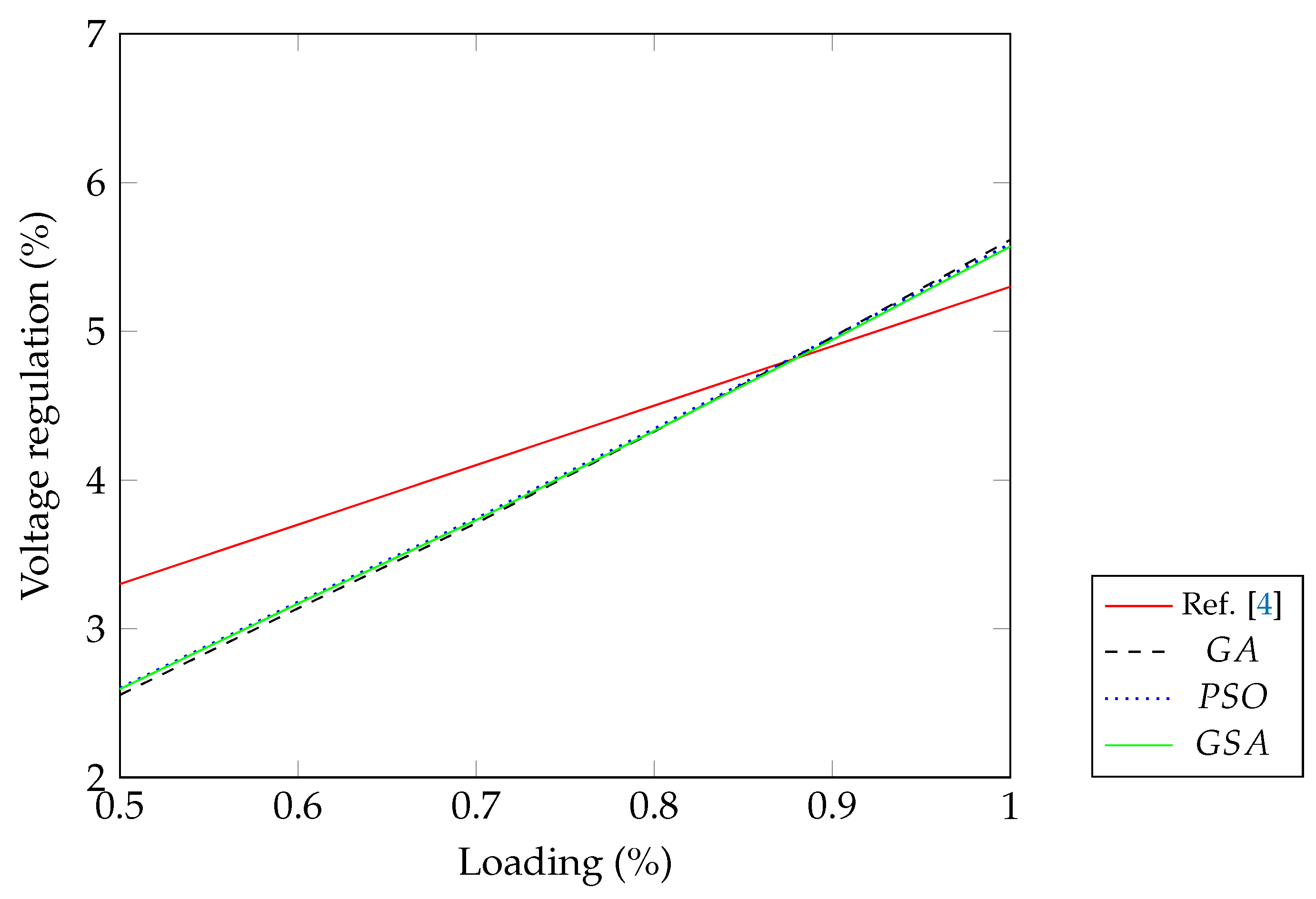
4. Simulation and Results
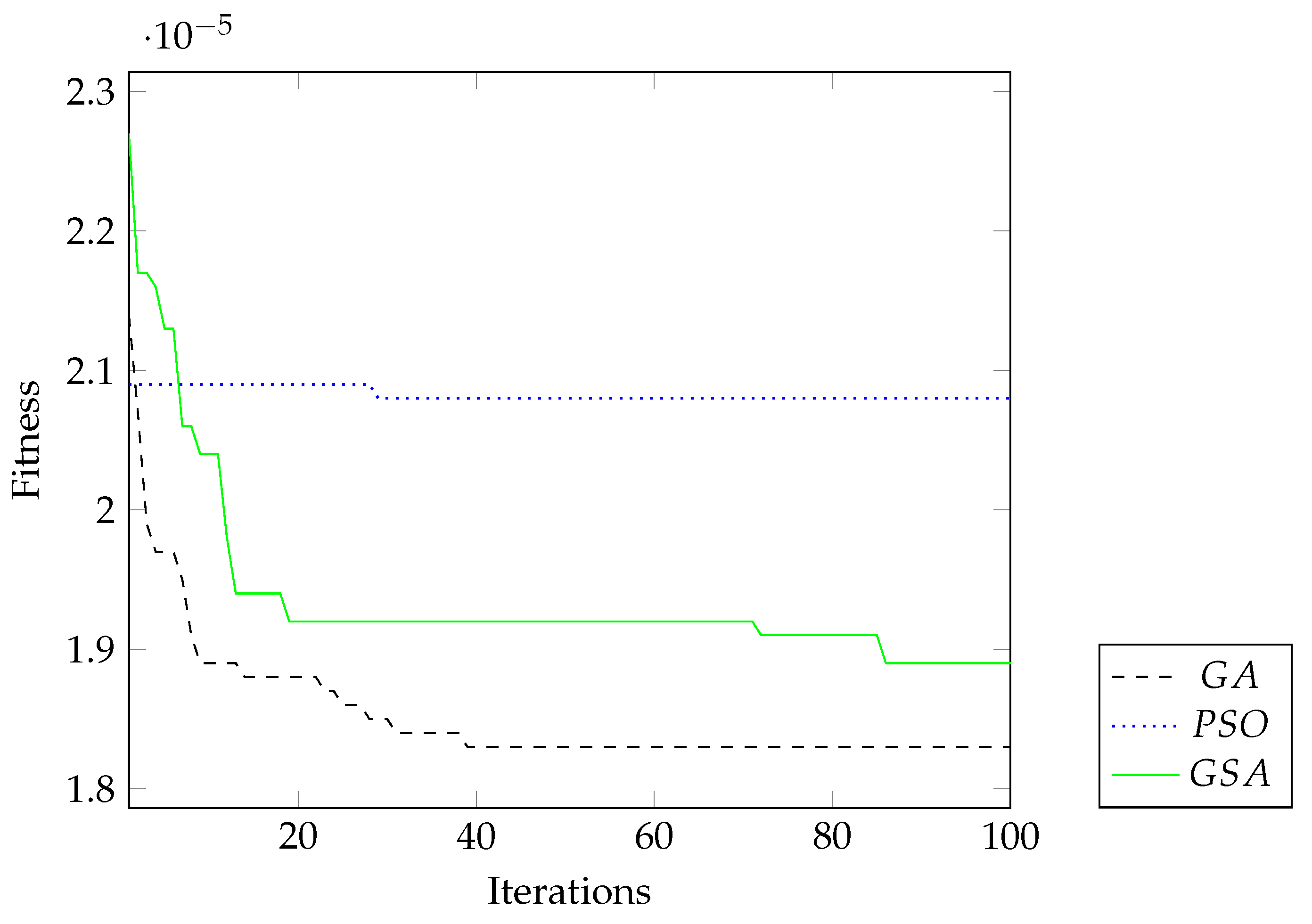
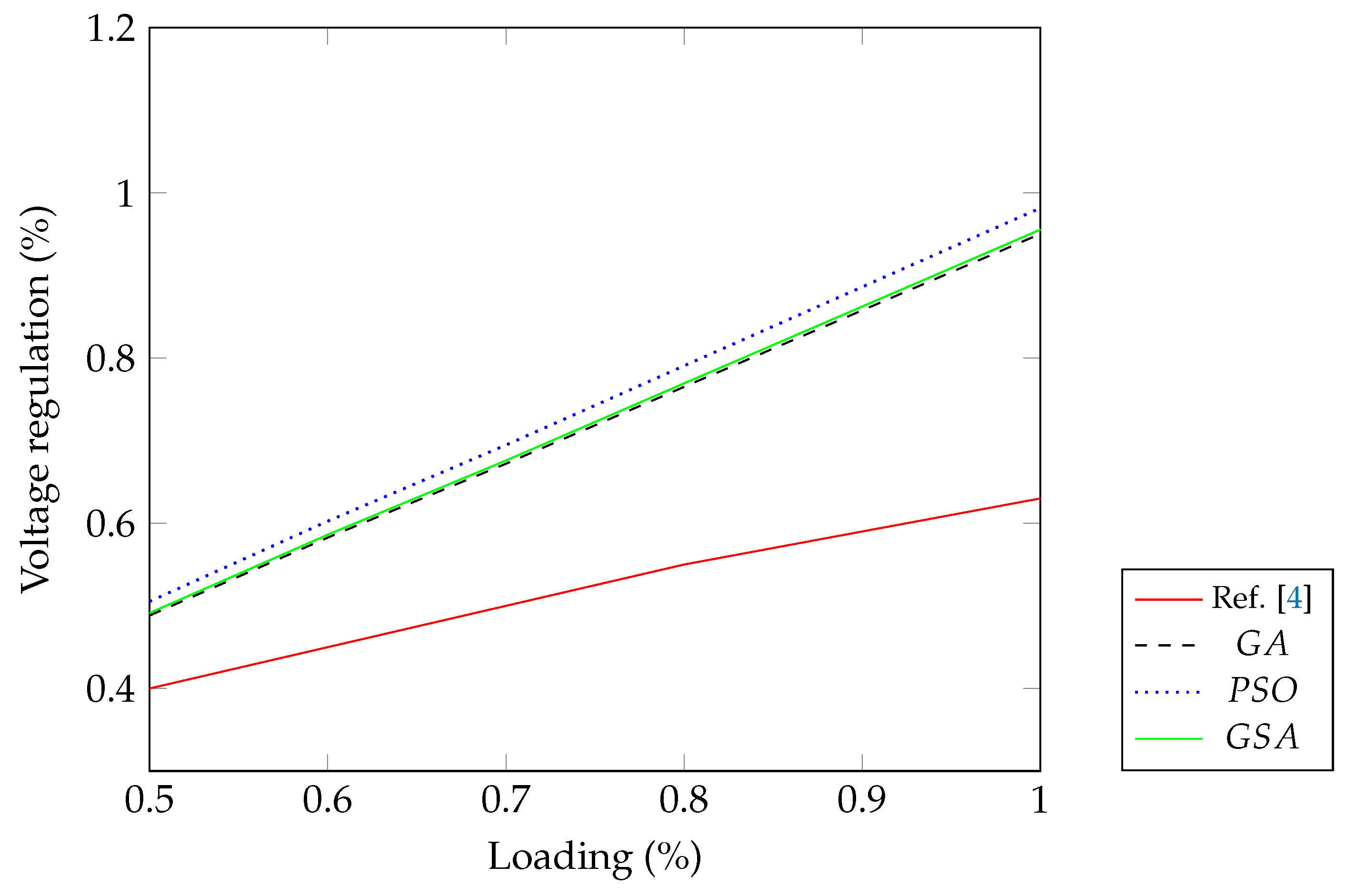
4.1. The Single-Phase Transformer: 4 kVA, 50 Hz, 250–125 V
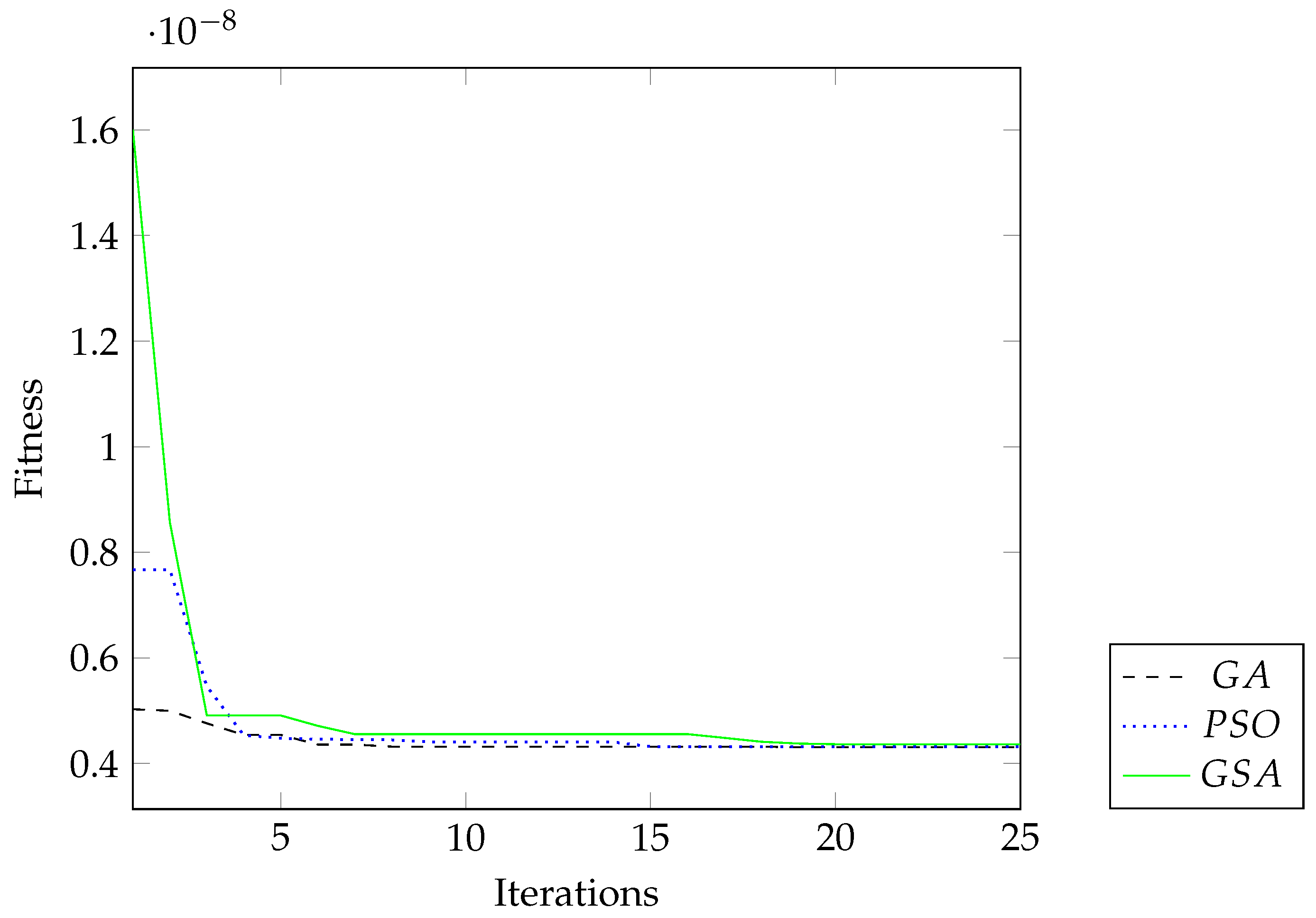
4.2. The Single-Phase Transformer: 15 kVA, 50 Hz, 2400–240 V
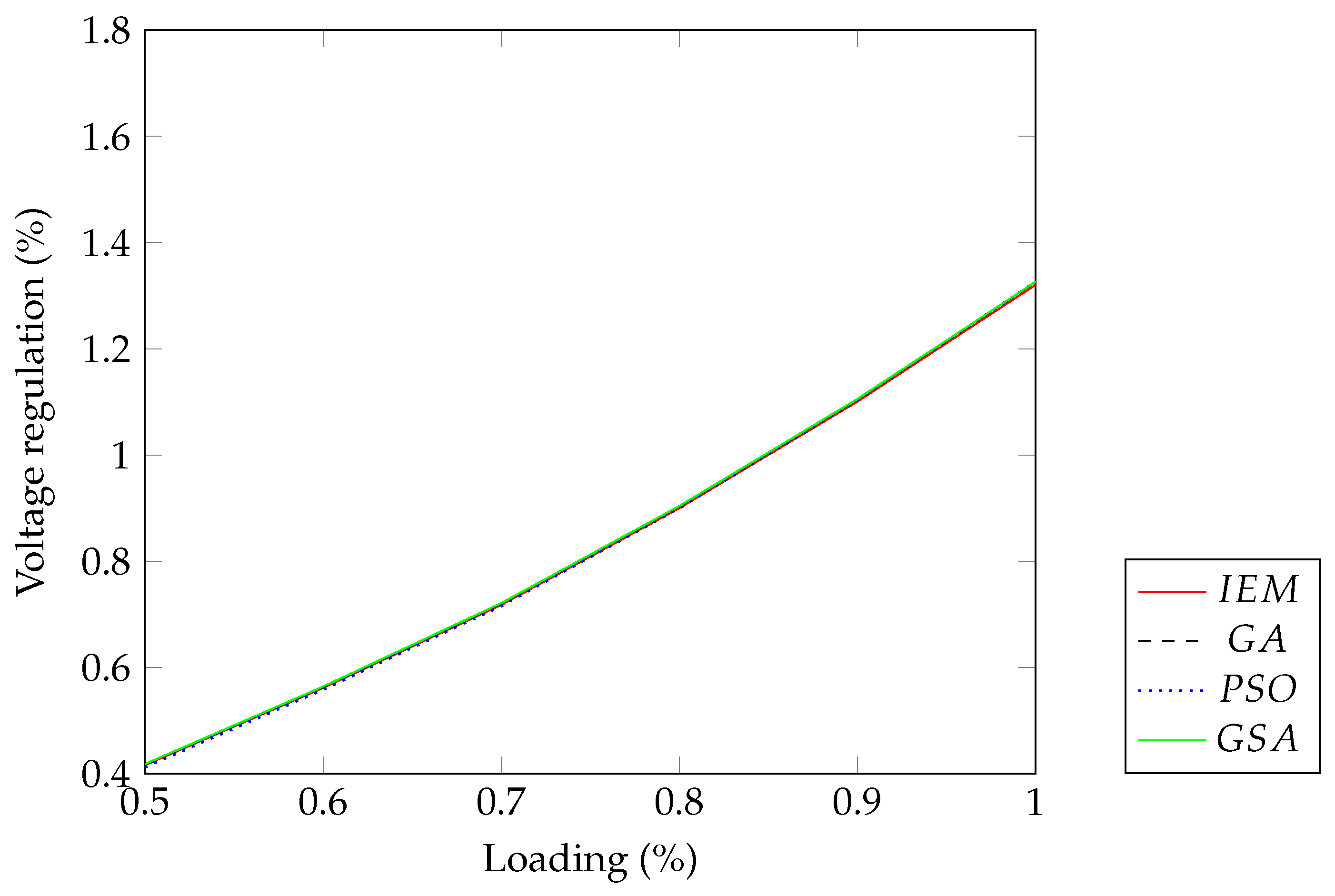
4.3. The Single-Phase Transformer: 33 MVA, 60 Hz, 230,000/–34,500 V
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GA | genetic algorithm; |
| PSO | particle swarm optimization; |
| GSA | gravitational search algorithm; |
| STPECP | single-phase transformer equivalent circuit parameters; |
| RMS | root mean square. |
References
- Bigdeli, M.; Azizian, D.; Bakhshi, H.; Rahimpour, E. Identification of transient model parameters of transformer using genetic algorithm. In Proceedings of the 2010 International Conference on Power System Technology, Zhejiang, China, 24–28 October 2010; pp. 1–6. [Google Scholar]
- Krishan, R.; Mishra, A.K.; Rajpurohit, B.S. Real-time parameter estimation of single-phase transformer. In Proceedings of the 2016 IEEE 7th Power India International Conference (PIICON), Bikaner, India, 25–27 November 2016; pp. 1–6. [Google Scholar]
- Soliman, S.; Alammari, R.; Mostafa, M. On-line estimation of transformer model parameters. In Proceedings of the 2004 Large Engineering Systems Conference on Power Engineering (IEEE Cat. No. 04EX819), Halifax, NS, Canada, 28–30 July 2004; pp. 170–178. [Google Scholar]
- Mossad, M.I.; Azab, M.; Abu-Siada, A. Transformer parameters estimation from nameplate data using evolutionary programming techniques. IEEE Trans. Power Deliv. 2014, 29, 2118–2123. [Google Scholar] [CrossRef]
- Illias, H.A.; Mou, K.; Bakar, A. Estimation of Transformer Parameters from Nameplate Data by Imperialist Competitive and Gravitational Search Algorithms; Elsevier: Amsterdam, The Netherlands, 2017; Volume 36, pp. 18–26. [Google Scholar]
- Padma, S.; Subramanian, S. Parameter estimation of single phase core type transformer using bacterial foraging algorithm. Engineering 2010, 2, 917. [Google Scholar] [CrossRef]
- Ćalasan, M.; Mujičić, D.; Rubežić, V.; Radulović, M. Estimation of equivalent circuit parameters of single-phase transformer by using chaotic optimization approach. Energies 2019, 12, 1697. [Google Scholar] [CrossRef]
- Golberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Boston, MA, USA, 2002. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Clerc, M.; Kennedy, J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Duarte, C.; Quiroga, J. PSO Algorithm for Parameter Identification in a DC Motor (Spanish); Universidad de Antioquia: Medellín, Colombia, 2010; Volume 55, pp. 116–124. [Google Scholar]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Darzi, S.; Islam, M.T.; Tiong, S.K.; Kibria, S.; Singh, M. Stochastic leader gravitational search algorithm for enhanced adaptive beamforming technique. PLoS ONE 2015, 10, e0140526. [Google Scholar] [CrossRef] [PubMed]
| Methods | PSO | GA | GSA | ||||
|---|---|---|---|---|---|---|---|
| Stats | Fitness | AE (%) | Fitness | AE (%) | Fitness | AE (%) | |
| Best | 6.4729 | 18.16 | 7.4670 | 10.93 | 7.9168 | 12.26 | |
| Mean | 7.1537 | 4.73 | 7.6007 | 10.00 | 8.8683 | 5.72 | |
| Medium | 7.1537 | 9.41 | 7.5987 | 10.91 | 8.8683 | 3.78 | |
| Worst | 7.9736 | 24.28 | 7.7175 | 7.43 | 9.6510 | 8.45 | |
| St. dev. | 3.2688 | - | 6.7636 | - | 4.7937 | - | |
| Wilcoxon rank-sum test with 95% confidence | + | + | |||||
| Parameters | AE (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| Methods | ||||||||
| Ref. [4] | 0.4 | 0.2 | 0.4 | 2 | 1500 | 750 | - | |
| GA | 0.3413 | 0.1879 | 0.4183 | 2.4543 | 1405 | 707.6 | - | |
| GA error (%) | 14.6783 | 6.0567 | 4.5633 | 22.7133 | 6.3222 | 5.6458 | 10.00 | |
| PSO | 0.3763 | 0.2150 | 0.4023 | 2.0256 | 1327 | 738.26 | - | |
| PSO error (%) | 5.9125 | 7.5183 | 0.5742 | 1.2815 | 11.5444 | 1.5653 | 4.7327 | |
| GSA | 0.3751 | 0.1904 | 0.3904 | 2.3839 | 1482.4333 | 745.9333 | - | |
| GSA error (%) | 6.225 | 4.785 | 2.3883 | 19.1983 | 1.1711 | 0.5422 | 5.7183 | |
| Variables | (A) | (A) | (V) | Efficiency (%) | AE (%) | |
|---|---|---|---|---|---|---|
| Methods | ||||||
| Ref. [4] | 14.0813 | 13.6893 | 235.8759 | 83.9990 | - | |
| GA | 13.9666 | 13.7435 | 236.7835 | 93.1954 | - | |
| GA error (%) | 0.8145 | 0.3958 | 0.3848 | 10.9483 | 3.1358 | |
| PSO | 13.9698 | 13.7410 | 236.7577 | 93.1524 | - | |
| PSO error (%) | 0.7921 | 0.3778 | 0.3738 | 10.8971 | 3.1102 | |
| GSA | 13.9558 | 13.7451 | 236.8283 | 93.3009 | - | |
| GSA error (%) | 0.8909 | 0.4077 | 0.4038 | 11.0738 | 3.1941 | |
| Methods | GA | PSO | GSA | ||||
|---|---|---|---|---|---|---|---|
| Stats | Fitness | AE (%) | Fitness | AE (%) | Fitness | AE (%) | |
| Best | 1.8178 | 12.3039 | 1.92 | 11.8855 | 1.8542 | 11.7523 | |
| Mean | 1.8299 | 11.8772 | 2.0875 | 7.8132 | 1.8936 | 9.8612 | |
| Medium | 1.8305 | 12.0800 | 2.0849 | 8.0294 | 1.8911 | 10.9429 | |
| Worst | 1.8500 | 11.7215 | 2.2897 | 8.8045 | 1.9326 | 9.6136 | |
| St. dev. | 7.4936 | - | 8.7936 | - | 1.8433 | - | |
|
Wilcoxon rank-sum test with 95% confidence | + | + | |||||
| Parameters | AE (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| Methods | ||||||||
| Ref. [4] | 2.45 | 3.14 | 2 | 2.2294 | 105,000 | 9106 | - | |
| GA | 2.0038 | 2.5440 | 1.5060 | 2.0531 | 105,730 | 9176 | - | |
| GA error (%) | 18.2121 | 18.9820 | 24.6983 | 7.9095 | 0.6952 | 0.7662 | 11.8772 | |
| PSO | 2.0568 | 2.9236 | 1.5504 | 2.2139 | 104,473 | 9130 | - | |
| PSO error (%) | 16.0503 | 6.8928 | 22.48 | 0.6953 | 0.5016 | 0.2595 | 7.8132 | |
| GSA | 2.0075 | 2.7198 | 1.5103 | 2.1694 | 104,453 | 9103 | - | |
| GSA error (%) | 18.0612 | 13.3811 | 24.4833 | 2.6913 | 0.5206 | 0.0297 | 9.8612 | |
| Variables | (A) | (A) | (V) | Efficiency (%) | AE (%) | |
|---|---|---|---|---|---|---|
| Methods | ||||||
| Ref. [4] | 6.2 | 6.2 | 2383.8 | 98.5 | - | |
| GA | 6.2128 | 6.1834 | 2377.4751 | 98.5928 | - | |
| GA error (%) | 0.2072 | 0.2673 | 0.2674 | 0.0920 | 0.2085 | |
| PSO | 6.2113 | 6.1815 | 2376.6855 | 98.5528 | - | |
| PSO error (%) | 0.1829 | 0.2983 | 0.2985 | 0.0536 | 0.2083 | |
| GSA | 6.2130 | 6.1864 | 2377.3001 | 98.5783 | - | |
| GSA error (%) | 0.2091 | 0.2187 | 0.2727 | 0.0795 | 0.1950 | |
| Methods | GA | PSO | GSA | ||||
|---|---|---|---|---|---|---|---|
| Stats | Fitness | AE (%) | Fitness | AE (%) | Fitness | AE (%) | |
| Best | 4.1138 | 8.3152 | 4.0597 | 4.5892 | 4.1520 | 4.5154 | |
| Mean | 4.2171 | 2.6105 | 4.3105 | 1.3703 | 4.3586 | 1.3415 | |
| Medium | 4.2202 | 2.5620 | 4.3196 | 3.3515 | 4.3646 | 3.0648 | |
| Worst | 4.3153 | 3.6331 | 4.5475 | 4.6009 | 4.5626 | 5.4431 | |
| St. dev. | 5.0994 | - | 1.0156 | - | 1.1556 | - | |
| Wilcoxon rank-sum test with 95% confidence | + | + | |||||
| Parameters | AE (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| Methods | ||||||||
| IEM-Condumex | 0.835 | 37.5 | 0.835 | 37.5 | 728,504 | 513,610 | - | |
| GA | 0.8724 | 38.99 | 0.8540 | 35.81 | 729,277 | 515,267 | - | |
| GA error (%) | 4.4790 | 3.9645 | 2.2754 | 4.5155 | 0.1061 | 0.3226 | 2.6105 | |
| PSO | 0.8105 | 37.15 | 0.8074 | 37.16 | 727,823 | 514,097 | - | |
| PSO error (%) | 2.9341 | 0.9184 | 3.2814 | 0.8995 | 0.0934 | 0.0948 | 1.3703 | |
| GSA | 0.8408 | 38.25 | 0.8002 | 37.13 | 727,743 | 514,170 | - | |
| GSA error (%) | 0.6946 | 1.992 | 4.1677 | 0.9741 | 0.1044 | 0.1090 | 1.3415 | |
| Variables | (A) | (A) | (V) | Efficiency (%) | AE (%) | |
|---|---|---|---|---|---|---|
| Methods | ||||||
| IEM-Condumex | 247.926 | 247.728 | 131,060 | 99.46 | - | |
| GA | 247.9332 | 247.7348 | 131,053.0316 | 99.4567 | - | |
| GA error (%) | 0.0025 | 0.0027 | 0.0053 | 0.0033 | 0.0035 | |
| PSO | 247.9329 | 247.7345 | 131,052.887 | 99.4765 | - | |
| PSO error (%) | 0.0028 | 0.0026 | 0.0054 | 0.0166 | 0.0069 | |
| GSA | 247.9347 | 247.7364 | 131,053.8826 | 99.4722 | - | |
| GSA error (%) | 0.0035 | 0.0034 | 0.0047 | 0.0123 | 0.0060 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ascencion-Mestiza, H.; Maximov, S.; Mezura-Montes, E.; Olivares-Galvan, J.C.; Ocon-Valdez, R.; Escarela-Perez, R. Estimation of the Equivalent Circuit Parameters in Transformers Using Evolutionary Algorithms. Math. Comput. Appl. 2023, 28, 36. https://doi.org/10.3390/mca28020036
Ascencion-Mestiza H, Maximov S, Mezura-Montes E, Olivares-Galvan JC, Ocon-Valdez R, Escarela-Perez R. Estimation of the Equivalent Circuit Parameters in Transformers Using Evolutionary Algorithms. Mathematical and Computational Applications. 2023; 28(2):36. https://doi.org/10.3390/mca28020036
Chicago/Turabian StyleAscencion-Mestiza, Hector, Serguei Maximov, Efrén Mezura-Montes, Juan Carlos Olivares-Galvan, Rodrigo Ocon-Valdez, and Rafael Escarela-Perez. 2023. "Estimation of the Equivalent Circuit Parameters in Transformers Using Evolutionary Algorithms" Mathematical and Computational Applications 28, no. 2: 36. https://doi.org/10.3390/mca28020036
APA StyleAscencion-Mestiza, H., Maximov, S., Mezura-Montes, E., Olivares-Galvan, J. C., Ocon-Valdez, R., & Escarela-Perez, R. (2023). Estimation of the Equivalent Circuit Parameters in Transformers Using Evolutionary Algorithms. Mathematical and Computational Applications, 28(2), 36. https://doi.org/10.3390/mca28020036








