An Efficient Two-Step Iterative Family Adaptive with Memory for Solving Nonlinear Equations and Their Applications

Abstract

We propose a new iterative scheme without memory for solving nonlinear equations. The proposed scheme is based on a cubically convergent Hansen–Patrick-type method. The beauty of our techniques is that they work even though the derivative is very small in the vicinity of the required root or $f^{\prime }\left(x\right)=0$. On the contrary, the previous modifications either diverge or fail to work. In addition, we also extended the same idea for an iterative method with memory. Numerical examples and comparisons with some of the existing methods are included to confirm the theoretical results. Furthermore, basins of attraction are included to describe a clear picture of the convergence of the proposed method as well as that of some of the existing methods. Numerical experiments are performed on engineering problems, such as fractional conversion in a chemical reactor, Planck’s radiation law problem, Van der Waal’s problem, trajectory of an electron in between two parallel plates. The numerical results reveal that the proposed schemes are of utmost importance to be applied on various real–life problems. Basins of attraction also support this aspect.

1. Introduction

Determining the zeros of a nonlinear function promptly and accurately has become a very crucial task in many branches of science and technology. The most used technique in this regard is Newton’s method [1], which converges linearly for multiple roots and quadratically for simple roots. Various higher order schemes have also been presented in [2,3,4,5,6,7,8]. One amongst them is the Hansen–Patrick’s family [9] of order 3 given by

$$x_{n+1}=x_n-\left[{\displaystyle \frac{\alpha +1}{\alpha \pm {(1-(\alpha +1)L_f\left(x_n\right))}^{1/2}}}\right]\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},n=0,1,2,\dots ,$$

(1)

where $L_f\left(x_n\right)={\displaystyle \frac{f^{″}\left(x_n\right)f\left(x_n\right)}{f^{\prime 2}\left(x_n\right)}}$ and $\alpha \in \mathbb{R}\backslash \{-1\}$. This family comprises of Euler’s method for $(\alpha =1)$, Ostrowski’s square-root method for $(\alpha =0)$, Laguerre’s method for $(\alpha =\frac{1}{\nu -1},\nu \ne 1)$ and Newton’s method as a limiting case. Despite the fact that it has cubic convergence, the involvement of second order derivative is limiting the applied region. This factor has inspired many researchers to concentrate on multipoint methods [10], since they overcome the drawbacks of one-point iterative methods with respect to the convergence order. The main motive in the development of new iterative methods is to achieve an order of convergence that is as high as possible with a certain number of functional evaluations per iteration.

Sharma et al. [11] had modified Equation (1), which is given as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{y}_n\hfill & =x_n-\alpha {\displaystyle \frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}},\hfill \\ x_{n+1}\hfill & =x_n-\left[{\displaystyle \frac{\beta +1}{\beta \pm {(1-(\beta +1)H_f\left(x_n\right))}^{1/2}}}\right]{\displaystyle \frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}},\hfill \end{array}\right.\end{array}$$

(2)

where $H_f\left(x_n\right)={\displaystyle \frac{f^{″}\left(y_n\right)f\left(x_n\right)}{f^{\prime 2}\left(x_n\right)}}$ and $\alpha$, $\beta$ are free parameters. Here, $\beta \ne -1$. Instead of $x_n$, the authors calculated a second-order derivative of f at $y_n$. Moreover, several developments of Hansen–Patrick-type methods have been presented and examined in [12] in order to eradicate the second-order derivative. Using some appropriate approximation for $f^{″}\left(x_n\right)$, authors in [12] presented the following method:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{y}_n\hfill & =x_n-{\displaystyle \frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}},\hfill \\ x_{n+1}\hfill & =x_n-\left[{\displaystyle \frac{\alpha +1}{\alpha \pm {\left({\displaystyle \frac{f{\left(x_n\right)}^2+(\beta -2\alpha -2)f\left(x_n\right)f\left(y_n\right)-\beta (\alpha +1)f{\left(y_n\right)}^2}{f{\left(x_n\right)}^2+\beta f\left(x_n\right)f\left(y_n\right)}}\right)}^{1/2}}}\right]{\displaystyle \frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}},\hfill \end{array}\right.\end{array}$$

(3)

where $\alpha$ and $\beta$ are free parameters. The prominent problem when using such types of methods is that they fail to work in the case where $f^{\prime }\left(x\right)=0$ and diverge or fail when the derivative is very small in the vicinity of the required root. That is why our main goal is to develop a method that is globally convergent.

On the other hand, it is sometimes possible to increase the convergence order with no further functional evaluation by making use of a self-accelerating parameter. Traub [1] referred these methods as schemes with memory as these methods use the previous information to calculate the next iterate. Traub was the first to introduce the idea of methods with memory. He made minute alterations in the already existing Steffensen method [13] and presented the first method with memory [1] as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & {\gamma }_0,x_0\mathrm{are}\mathrm{suitably}\mathrm{given},w_n=x_n+{\gamma }_{n}f\left(x_n\right),0\ne {\gamma }_n\in \mathbb{R},\hfill \\ \hfill & x_{n+1}=x_n-{\displaystyle \frac{f\left(x_n\right)}{f[x_n,w_n]}},n=0,1,2,\dots ,\hfill \end{array}\right.\end{array}$$

(4)

where ${\gamma }_n$ is a self-accelerating parameter given as

$${\gamma }_{n+1}={\displaystyle \frac{-1}{N_1^{\prime }\left(x_n\right)}},N_1\left(x\right)=f\left(x_n\right)+(x-x_n)f[x_n,w_n],n=0,1,2,\dots$$

This method has an order of convergence of 2.414. However, if we use a better self-accelerating parameter, there are apparent chances that the order of convergence will increase.

Using a secant approach, and by reusing information from the previous iteration, Traub refined a Steffensen-like method and presented the following method:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & {\gamma }_0\mathrm{is}\mathrm{given},{\gamma }_n={\displaystyle \frac{x_n-x_{n-1}}{f\left(x_n\right)-f\left(x_{n-1}\right)}},n\in \mathbb{N},\hfill \\ \hfill & x_{n+1}=x_n-{\displaystyle \frac{{\gamma }_{n}f{\left(x_n\right)}^2}{f(x_n+{\gamma }_{n}f\left(x_n\right))-f\left(x_n\right)}},\hfill \end{array}\right.\end{array}$$

(5)

having R-order of convergence [14] at least 2.414.

In addition, a new approach of hybrid methods is being adopted for solving nonlinear problems which can be seen in [15,16].

For finding the R-order of convergence of our proposed method with memory, we make use of the Theorem 1 given by Traub.

The rest of the paper is organized as follows. Section 2 contains the development of a new iterative method without memory and the proof of its order of convergence. Section 3 covers the inclusion of memory to develop a new iterative method with memory and its error analysis. Numerical results for the proposed methods and comparisons with some of the existing methods to illustrate our theoretical results are given in Section 4. Section 5 depicts the convergence of the methods using basins of attraction. Lastly, Section 6 presents conclusions.

Theorem 1.

Suppose that $\left(IM\right)$ is an iterative method with memory that generates a sequence $\left\{x_m\right\}$ (converging to the root ξ) of approximations to ξ. If there exists a nonzero constant ζ and nonnegative numbers $s_j$, $0\le j\le k$, such that the inequality

$$\mid {ϵ}_{m+1}\mid \le \zeta \prod _{j=0}^k\mid {ϵ}_{m-j}{\mid }^{s_j}$$

holds, then the R-order of convergence of the iterative method $\left(IM\right)$ satisfies the inequality

$$O_R(\left(IM\right),\xi )\ge t^{*},$$

where $t^{*}$ is the unique positive root of the equation

$$t^{k+1}-\sum _{j=0}^k{s}_j{t}^{k-j}=0.$$

(6)

2. Iterative Method without Memory and Its Convergence Analysis

We aim to construct a new two-point Hansen–Patrick-type method without memory in this section.

Suppose $y_n=x_n-{\displaystyle \frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}}$ be the Newton’s iterate. Expanding $f\left(y_n\right)$ about a point $x=x_n$ by Taylor series, we get

$$\begin{array}{c}f\left(y_n\right)\approx f\left(x_n\right)+f^{\prime }\left(x_n\right)(y_n-x_n)+\frac{1}{2}{f}^{″}\left(x_n\right){(y_n-x_n)}^2,\hfill \\ \hspace{1em}\Rightarrow f^{″}\left(x_n\right)\approx \frac{2f^{\prime }{\left(x_n\right)}^{2}f\left(y_n\right)}{f{\left(x_n\right)}^2}.\hfill \end{array}$$

Further, if we expand the function $f^{\prime }\left(y_n\right)=f^{\prime }\left(x_n-\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}\right)$ about $x=x_n$ by Taylor series, we have

$$f^{\prime }\left(y_n\right)\approx f^{\prime }\left(x_n\right)+f^{″}\left(x_n\right)(y_n-x_n),$$

$$\Rightarrow f^{″}\left(x_n\right)\approx \frac{f^{\prime }\left(x_n\right)}{f\left(x_n\right)}(f^{\prime }\left(x_n\right)-f^{\prime }\left(y_n\right)).$$

Using previous developments, we have

$$f^{″}\left(x_n\right)\approx \frac{{\left(\frac{2f^{\prime }{\left(x_n\right)}^{2}f\left(y_n\right)}{f{\left(x_n\right)}^2}\right)}^2+{\left(\frac{f^{\prime }\left(x_n\right)}{f\left(x_n\right)}(f^{\prime }\left(x_n\right)-f^{\prime }\left(y_n\right))\right)}^2}{\frac{2f^{\prime }{\left(x_n\right)}^{2}f\left(y_n\right)}{f{\left(x_n\right)}^2}+\frac{f^{\prime }\left(x_n\right)}{f\left(x_n\right)}(f^{\prime }\left(x_n\right)-f^{\prime }\left(y_n\right))}.$$

As we can see, this estimation for $f^{″}\left(x_n\right)$ uses 4 functional evaluations per iteration [8], $f\left(x_n\right)$, $f\left(y_n\right)$, $f^{\prime }\left(x_n\right)$ and $f^{\prime }\left(y_n\right)$. To decrease the number of functional evaluations, King’s approximation [17] may be used which is

$$f^{\prime }\left(y_n\right)=f^{\prime }\left(x_n\right)\frac{f\left(x_n\right)+\gamma f\left(y_n\right)}{f\left(x_n\right)+\beta f\left(y_n\right)},$$

when $\gamma =\beta -2$, where $\beta$ is a free parameter.

Now, using this new approximation for $f^{″}\left(x_n\right)$ in Equation (1), authors in [12] presented the following scheme:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{y}_n\hfill & =x_n-{\displaystyle \frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}},\hfill \\ x_{n+1}\hfill & =x_n-\left[{\displaystyle \frac{\alpha +1}{\alpha \pm {\left({\displaystyle \frac{f{\left(x_n\right)}^2+(\beta -2\alpha -2)f\left(x_n\right)f\left(y_n\right)-\beta (\alpha +1)f{\left(y_n\right)}^2}{f{\left(x_n\right)}^2+\beta f\left(x_n\right)f\left(y_n\right)}}\right)}^{1/2}}}\right]{\displaystyle \frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}},\hfill \end{array}\right.\end{array}$$

(7)

where $\alpha$ and $\beta$ are free parameters.

Now, in order to extend to the method with memory, we come up with an idea of introducing a parameter b in the scheme given by Equation (7) and we present a modification in this method as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{y}_n\hfill & =x_n-{\displaystyle \frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)+bf\left(x_n\right)}},\hfill \\ x_{n+1}\hfill & =x_n-\left[{\displaystyle \frac{\alpha +1}{\alpha \pm {\left({\displaystyle \frac{f{\left(x_n\right)}^2+(\beta -2\alpha -2)f\left(x_n\right)f\left(y_n\right)-\beta (\alpha +1)f{\left(y_n\right)}^2}{f{\left(x_n\right)}^2+\beta f\left(x_n\right)f\left(y_n\right)}}\right)}^{1/2}}}\right]{\displaystyle \frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)+bf\left(x_n\right)}},\hfill \\ \hfill & n=0,1,2,\dots ,\hfill \end{array}\right.\end{array}$$

(8)

where $\alpha$ and $\beta$ are free parameters.

Next, we establish the convergence results for our proposed method without memory given by Equation (8).

Convergence Analysis

Theorem 2.

Suppose that $f:D\subset \mathbb{R}\to \mathbb{R}$ be a real function suitably differentiable in a domain D. If $\xi \in D$ is a simple root of $f\left(x\right)=0$ and an initial guess $x_0$ is sufficiently close to ξ, then the iterative method given by Equation (8) converges to ξ with convergence order $p=3$ having the following error relation,

$$e_{n+1}=-\frac{1}{2}(b+a_2)(b(1+\alpha -\beta )+(-1+\alpha -\beta )a_2)e_n^3+O{\left(e_n\right)}^4,$$

where $e_n=x_n-\xi$ and $a_n={\displaystyle \frac{f^{\left(n\right)}\left(\xi \right)}{n!f^{\prime }\left(\xi \right)}},n=2,3,\dots$

Proof. 

Expanding $f\left(x_n\right)$ about $x_n=\xi$ by Taylor series, we have

$$\begin{array}{cc}\hfill f\left(x_n\right)& =f^{\prime }\left(\xi \right)(e_n+a_2{e}_n^2+a_3{e}_n^3+a_4{e}_n^4)+O{\left(e_n\right)}^5.\hfill \end{array}$$

(9)

Then,

$$\begin{array}{cc}\hfill f^{\prime }\left(x_n\right)& =f^{\prime }\left(\xi \right)(1+2a_2{e}_n+3a_3{e}_n^2+4a_4{e}_n^3)+O{\left(e_n\right)}^4.\hfill \end{array}$$

(10)

Using Equations (9) and (10), we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)+bf\left(x_n\right)}}& =e_n-(b+a_2)e_n^2+(b^2+2b{a}_2+2a_2^2-2a_3)e_n^3+O{\left(e_n\right)}^4.\hfill \end{array}$$

(11)

Using Equation (11) in the first step of Equation (8), we have

$$\begin{array}{cc}\hfill e_{n,y}& =y_n-\xi =(b+a_2)e_n^2+(-b^2-2b{a}_2-2a_2^2+2a_3)e_n^3+O{\left(e_n\right)}^4.\hfill \end{array}$$

(12)

Further, the Taylor’s expansion of $f\left(y_n\right)$ is

$$\begin{array}{cc}\hfill f\left(y_n\right)& =f^{\prime }\left(\xi \right)(e_{n,y}+e_{n,y}^2+e_{n,y}^3+e_{n,y}^4)+O{\left(e_{n,y}\right)}^5.\hfill \end{array}$$

(13)

Using Equations (9)–(13), we have

$$\begin{array}{c}\hfill \left[\frac{\alpha +1}{\alpha \pm {\left(\frac{f{\left(x_n\right)}^2+(\beta -2\alpha -2)f\left(x_n\right)f\left(y_n\right)-\beta (\alpha +1)f{\left(y_n\right)}^2}{f{\left(x_n\right)}^2+\beta f\left(x_n\right)f\left(y_n\right)}\right)}^{1/2}}\right]\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)+bf\left(x_n\right)}\end{array}$$

$$\begin{array}{c}\hfill =e_n+{\displaystyle \frac{1}{2}}(b+a_2)(a_2(-1+\alpha -\beta )+b(1+\alpha -\beta ))e_n^3+O{\left(e_n\right)}^4,\end{array}$$

(14)

Finally, putting Equation (14) in the second step of Equation (8), we get

$$\begin{array}{cc}\hfill e_{n+1}& =-\frac{1}{2}(b+a_2)(b(1+\alpha -\beta )+(-1+\alpha -\beta )a_2)e_n^3+O{\left(e_n\right)}^4,\hfill \end{array}$$

(15)

which is the error equation for the proposed scheme given by Equation (8) giving convergence order three. This completes the proof. □

3. Iterative Method with Memory and Its Convergence Analysis

Now, we present an extension to the method given by Equation (8) by inclusion of memory having improved convergence order without the addition of any new functional evaluation.

If we observe clearly, it can be seen from the error relation given in Equation (15), if $b=-a_2=-{\displaystyle \frac{f^{″}\left(\xi \right)}{2f^{\prime }\left(\xi \right)}}$, then the order of convergence of the presented scheme given by Equation (8) can possibly be improved, but this value can’t be reached because the values of $f^{\prime }\left(\xi \right)$ and $f^{″}\left(\xi \right)$ are not practically available. Instead, we can use approximations calculated by already available information [18]. So, to improve the convergence order, we give an estimation using first order divided difference [19], given by $b_n=-{\displaystyle \frac{1}{2}}{\displaystyle \frac{f^{\prime }[x_n,x_{n-1}]}{f[x_n,x_{n-1}]}}$, where $f[s,t]={\displaystyle \frac{f\left(s\right)-f\left(t\right)}{s-t}}$ denotes a first-order divided difference.

So, by replacing b by $b_n$ in the method given by Equation (8), we obtain a new family with memory using the two previous iterations $x_0,x_1$ as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{b}_n\hfill & =-{\displaystyle \frac{1}{2}}{\displaystyle \frac{f^{\prime }[x_n,x_{n-1}]}{f[x_n,x_{n-1}]}},\hfill \\ y_n\hfill & =x_n-{\displaystyle \frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)+b_{n}f\left(x_n\right)}},\hfill \\ x_{n+1}\hfill & =x_n-\left[{\displaystyle \frac{\alpha +1}{\alpha \pm {\left({\displaystyle \frac{f{\left(x_n\right)}^2+(\beta -2\alpha -2)f\left(x_n\right)f\left(y_n\right)-\beta (\alpha +1)f{\left(y_n\right)}^2}{f{\left(x_n\right)}^2+\beta f\left(x_n\right)f\left(y_n\right)}}\right)}^{1/2}}}\right]\hfill \\ \hfill & \times {\displaystyle \frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)+b_{n}f\left(x_n\right)}},n\in \mathbb{N},\hfill \end{array}\right.\end{array}$$

(16)

where $\alpha$ and $\beta$ are free parameters.

Next, we establish the convergence results for our proposed method with memory given by Equation (16).

Convergence Analysis

Theorem 3.

Suppose that $f:D\subset \mathbb{R}\to \mathbb{R}$ be a real function suitably differentiable in a domain D. If $\xi \in D$ is a simple root of $f\left(x\right)=0$ and an initial guess $x_0$ is sufficiently close to ξ, then the iterative method given by Equation (16) converges to ξ with convergence order at least $3.30$.

Proof. 

Using Taylor series expansion about $x_n=\xi$, we get

$$\begin{array}{cc}\hfill f\left(x_{n-1}\right)& =f^{\prime }\left(\xi \right)(e_{n-1}+a_2{e}_{n-1}^2+a_3{e}_{n-1}^3+a_4{e}_{n-1}^4+a_5{e}_{n-1}^5)+O{\left(e_{n-1}\right)}^6,\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill f\left(x_n\right)& =f^{\prime }\left(\xi \right)(e_n+a_2{e}_n^2+a_3{e}_n^3+a_4{e}_n^4+a_5{e}_n^5)+O{\left(e_n\right)}^6.\hfill \end{array}$$

(18)

Then,

$$\begin{array}{cc}\hfill f^{\prime }\left(x_{n-1}\right)& =f^{\prime }\left(\xi \right)(1+2a_2{e}_{n-1}+3a_3{e}_{n-1}^2+4a_4{e}_{n-1}^3+5a_5{e}_{n-1}^4)+O{\left(e_{n-1}\right)}^5,\hfill \end{array}$$

(19)

$$\begin{array}{c}\hfill f^{\prime }\left(x_n\right)=f^{\prime }\left(\xi \right)(1+2a_2{e}_n+3a_3{e}_n^2+4a_4{e}_n^3+5a_5{e}_n^4)+O{\left(e_n\right)}^5.\end{array}$$

(20)

Now, using previous developments, we have

$$\begin{array}{cc}\hfill b_n=& -\frac{1}{2}\frac{f^{\prime }[x_n,x_{n-1}]}{f[x_n,x_{n-1}]}\hfill \\ \hfill =& (-a_2+\left(a_2^2-\frac{3}{2}{a}_3\right)e_{n-1}+\left(-a_2^3+\frac{5a_2{a}_3}{2}-2a_4\right)e_{n-1}^2+(a_2^4-\frac{7}{2}{a}_2^2{a}_3+\frac{3a_3^2}{2}\hfill \\ & +3a_2{a}_4-\frac{5a_5}{2}\left)e_{n-1}^3\right)+(\left(a_2^2-\frac{3a_3}{2}\right)-2\left(a_2^3-2a_2{a}_3+a_4\right)e_{n-1}+(3a_2^4-\frac{17}{2}{a}_2^2{a}_3\hfill \\ & +3a_3^2+5a_2{a}_4-\frac{5a_5}{2}\left)e_{n-1}^2\right)e_n+(\left(-a_2^3+\frac{5a_2{a}_3}{2}-2a_4\right)+(3a_2^4-\frac{17}{2}{a}_2^2{a}_3+3a_3^2\hfill \\ & +5a_2{a}_4-\frac{5a_5}{2}\left)e_{n-1}\right)e_n^2+O_3\left(e_{n-1}{e}_n\right).\hfill \end{array}$$

(21)

Using Equations (18), (20) and (21) in the second step of Equation (16), we get

$$\begin{array}{cc}\hfill y_n-\xi & =\left(\left(a_2^2-\frac{3a_3}{2}\right)e_{n-1}+\left(-a_2^3+\frac{5a_2{a}_3}{2}-2a_4\right)e_{n-1}^2\right)e_n^2+\left(\right(\frac{a_3}{2}-2(a_2^3-2a_2{a}_3\hfill \\ \hfill & +a_4\left)\right)e_{n-1}+\frac{1}{4}\left(8a_2^4-22a_2^2{a}_3+3a_3^2+20a_2{a}_4-10a_5\right)e_{n-1}^2)e_n^3+O_4\left(e_{n-1}{e}_n\right).\hfill \end{array}$$

(22)

Then, using Equation (22) in Equation (18), we get

$$\begin{array}{cc}\hfill f\left(y_n\right)& =f^{\prime }\left(\xi \right)(\left(\left(a_2^2-\frac{3a_3}{2}\right)e_{n-1}+\left(-a_2^3+\frac{5a_2{a}_3}{2}-2a_4\right)e_{n-1}^2\right)e_n^2+(\frac{a_3}{2}-2(a_2^3\hfill \\ & -2a_2{a}_3+a_4)e_{n-1}+\frac{1}{4}\left(8a_2^4-22a_2^2{a}_3+3a_3^2+20a_2{a}_4-10a_5\right)e_{n-1}^2)e_n^3)+O_4\left(e_{n-1}{e}_n\right).\hfill \end{array}$$

(23)

Using Equations (18), (20)–(23) in the third step of Equation (16), we finally get

$$\begin{array}{cc}\hfill e_{n+1}& =\left(a_2^3-\frac{3a_2{a}_3}{2}\right)e_{n-1}{e}_n^3+\frac{a_2{a}_3}{2}{e}_n^4+O_5\left(e_{n-1}{e}_n\right)\hfill \end{array}$$

(24)

Now, we can see the lowest term of the error equation is $\left(a_2^3-{\displaystyle \frac{3a_2{a}_3}{2}}\right)e_{n-1}{e}_n^3$, therefore, by Theorem 1, the unique positive root of the polynomial $s^2-3s-1$ gives the R-order of the proposed scheme given by Equation (16), which is $s=\frac{3+\sqrt{13}}{2}\approx 3.30$. This completes our proof. □

4. Numerical Results

Now, we will investigate the numerical results of our proposed scheme. Further, we will be comparing those results with some existing schemes, both with and without memory. All calculations have been accomplished using Mathematica 11.1 in multiple precision arithmetic environment with the specification of a processor Intel(R) Pentium(R) CPU B960 @ 2.20 GHz (64-bit operating system) Windows 7 Ultimate @ 2009 Microsoft Corporation. We suppose that the initial value of $b_0$ must be selected prior to performing the iterations and a suitable $x_0$ be given. We have taken $b_0=0.01$ (or $b=0.01$) in our computations. In all the numerical values, $Ae-h$ refers to $A\times {10}^{-h}$.

We are using the following functions for our computations:

• $f_1\left(x\right)=x^2-e^x-3x+2=0$ having one of the real zero $0.2575$.
• $f_2\left(x\right)=sin\left(\pi x\right)e^{x^2+xcosx-1}+xlog(xsinx+1)=0$ having one of the real zero 0.
• $f_3\left(x\right)=(x-2)(x^{10}+x+2)e^{-5x}=0$ having one of the real zero 2.
• $f_4\left(x\right)=x^2-1=0$ having one of the real zero $-1$.
• $f_5\left(x\right)=sinx=0$ having one of the real zero $2\pi$.

The results are computed by using the initial guesses $0.7$, $0.5$, $2.2$, 0 and $1.69$ for functions $f_1$, $f_2$, $f_3$, $f_4$ and $f_5$ respectively. To check the theoretical order of convergence, we have calculated the computational order of convergence [20], ${\rho }_c$ (COC) using the following formula,

$${\rho }_c=\frac{log(\mid f\left(x_k\right)/f(x_{k-1}\mid )}{log(\mid f\left(x_{k-1}\right)/f(x_{k-2}\mid )},k=2,3,\dots ,$$

considering the last three approximations in the iterative procedure. The errors of approximations to the respective zeros of the test functions, $\mid x_n-\xi \mid$ and COC are displayed in Table 1 and Table 2.

Table 1. Comparison of different methods without memory.

Without Memory Methods	$\mid {\mathit{x}}_1-\mathit{\xi }\mid$	$\mid {\mathit{x}}_2-\mathit{\xi }\mid$	$\mid {\mathit{x}}_3-\mathit{\xi }\mid$	${\mathit{\rho }}_{\mathit{c}}$	CPU Time
$f_1\left(x\right)$
$P{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	1.1717 $\times {10}^{-4}$	$6.9442\times {10}^{-15}$	$1.8615\times {10}^{-35}$	3.0000	0.344
$P{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$1.0371\times {10}^{-4}$	$2.8730\times {10}^{-15}$	$1.8615\times {10}^{-35}$	3.0000	0.312
$P{M}_3$($\alpha =1,\beta =1$)	$1.1756\times {10}^{-4}$	$7.0128\times {10}^{-15}$	$1.8615\times {10}^{-35}$	3.0000	0.329
$HPF$($\alpha =\frac{1}{2}$)	$7.2409\times {10}^{-3}$	$2.0697\times {10}^{-8}$	$4.8653\times {10}^{-25}$	2.9993	0.343
$SHM$($\alpha =1,\beta =\frac{1}{2}$)	$1.1696\times {10}^{-2}$	$1.8718\times {10}^{-7}$	$7.6275\times {10}^{-22}$	3.0008	0.344
$HM$($\alpha =\frac{1}{2}$)	$7.2407\times {10}^{-3}$	$1.8148\times {10}^{-8}$	$2.8886\times {10}^{-25}$	2.9990	0.281
$f_2\left(x\right)$
$P{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$9.0357\times {10}^{-3}$	$3.6430\times {10}^{-7}$	$2.4171\times {10}^{-20}$	2.9961	0.578
$P{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$8.7353\times {10}^{-3}$	$1.5807\times {10}^{-7}$	$9.6730\times {10}^{-22}$	2.9946	0.656
$P{M}_3$($\alpha =1,\beta =1$)	$9.0033\times {10}^{-3}$	$3.5624\times {10}^{-7}$	$2.2602\times {10}^{-20}$	2.9950	0.749
$HPF$($\alpha =\frac{1}{2}$)	$1.4338\times {10}^{-1}$	$5.1439\times {10}^{-4}$	$6.3759\times {10}^{-11}$	2.7546	0.594
$SHM$($\alpha =1,\beta =\frac{1}{2}$)	$5.3590\times {10}^{-1}$	$1.7758\times {10}^{-1}$	$1.2161\times {10}^{-2}$	2.7518	0.843
$HM$($\alpha =\frac{1}{2}$)	$1.6294\times {10}^{-1}$	$3.4650\times {10}^{-3}$	$1.2247\times {10}^{-8}$	3.1314	0.751
$f_3\left(x\right)$
$P{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$7.5147\times {10}^{-5}$	$5.2354\times {10}^{-17}$	$1.7335\times {10}^{-53}$	3.0008	0.345
$P{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$3.0249\times {10}^{-4}$	$2.6407\times {10}^{-15}$	$1.8932\times {10}^{-48}$	2.9971	0.344
$P{M}_3$($\alpha =1,\beta =1$)	$1.8359\times {10}^{-4}$	$7.8639\times {10}^{-16}$	$5.8747\times {10}^{-50}$	3.0019	0.359
$HPF$($\alpha =\frac{1}{2}$)	$6.9350\times {10}^{-3}$	$3.9832\times {10}^{-7}$	$7.5926\times {10}^{-20}$	2.9994	0.358
$SHM$($\alpha =1,\beta =\frac{1}{2}$)	$2.3532\times {10}^{-2}$	$3.1713\times {10}^{-5}$	$7.6632\times {10}^{-14}$	3.0020	0.328
$HM$($\alpha =\frac{1}{2}$)	$9.4327\times {10}^{-3}$	$1.0017\times {10}^{-6}$	$1.2079\times {10}^{-18}$	2.9993	0.390
$f_4\left(x\right)$
$P{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$2.1991\times {10}^{-1}$	$1.01412\times {10}^{-3}$	$1.3014\times {10}^{-10}$	2.8943	0.250
$P{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$4.0446\times {10}^{-1}$	$2.5365\times {10}^{-3}$	$1.0552\times {10}^{-9}$	2.7963	0.266
$P{M}_3$($\alpha =1,\beta =1$)	$4.0439\times {10}^{-1}$	$4.4677\times {10}^{-3}$	$1.1047\times {10}^{-8}$	2.7547	0.328
$HPF$($\alpha =\frac{1}{2}$)	F	F	F	#	-
$SHM$($\alpha =1,\beta =\frac{1}{2}$)	F	F	F	#	-
$HM$($\alpha =\frac{1}{2}$)	F	F	F	#	-
$f_5\left(x\right)$
$P{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$2.4220\times {10}^{-1}$	$4.9246\times {10}^{-6}$	$5.9705\times {10}^{-21}$	3.1821	0.422
$P{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$4.3566\times {10}^{-1}$	$3.1927\times {10}^{-4}$	$2.4757\times {10}^{-15}$	3.5597	0.406
$P{M}_3$($\alpha =1,\beta =1$)	$4.7757\times {10}^{-1}$	$1.9651\times {10}^{-4}$	$3.7695\times {10}^{-16}$	3.4779	0.328
$HPF$($\alpha =\frac{1}{2}$)	C	C	C	$3.0017$ *	-
$SHM$($\alpha =1,\beta =\frac{1}{2}$)	C	C	C	$3.0000$ *	-
$HM$($\alpha =\frac{1}{2}$)	C	C	C	$5.1956$ *	-

F—Method fails; #—COC not required in case of failure; C—Converging to undesired root; *—COC in case of undesired root.

Table 2. Comparison of different methods with memory.

With Memory Methods	$\mid {\mathit{x}}_1-\mathit{\xi }\mid$	$\mid {\mathit{x}}_2-\mathit{\xi }\mid$	$\mid {\mathit{x}}_3-\mathit{\xi }\mid$	${\mathit{\rho }}_{\mathit{c}}$	CPU Time
$f_1\left(x\right)$
$PM{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$1.1718\times {10}^{-4}$	$4.9506\times {10}^{-15}$	$1.8615\times {10}^{-35}$	3.3435	0.407
$PM{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$1.0371\times {10}^{-4}$	$2.9246\times {10}^{-15}$	$1.8615\times {10}^{-35}$	3.3362	0.407
$PM{M}_3$($\alpha =1,\beta =1$)	$1.1756\times {10}^{-4}$	$4.9995\times {10}^{-15}$	$1.8615\times {10}^{-35}$	3.3434	0.344
$T{M}_1$(${\gamma }_0=0.01$)	$6.8591\times {10}^{-3}$	$2.0433\times {10}^{-7}$	$2.3938\times {10}^{-18}$	2.4151	0.343
$T{M}_2$(${\gamma }_0=0.01$)	$6.8591\times {10}^{-3}$	$9.0200\times {10}^{-6}$	$1.5202\times {10}^{-11}$	2.0037	0.312
$f_2\left(x\right)$
$PM{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$9.0357\times {10}^{-3}$	$3.1838\times {10}^{-7}$	$1.6192\times {10}^{-23}$	3.6558	0.859
$PM{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$8.7353\times {10}^{-3}$	$2.2053\times {10}^{-7}$	$5.2810\times {10}^{-24}$	3.6119	0.875
$PM{M}_3$($\alpha =1,\beta =1$)	$9.0033\times {10}^{-3}$	$3.1393\times {10}^{-7}$	$1.5492\times {10}^{-23}$	3.6550	0.938
$T{M}_1$(${\gamma }_0=0.01$)	$2.5974\times {10}^{-2}$	$2.2058\times {10}^{-4}$	$1.6454\times {10}^{-9}$	2.4624	0.672
$T{M}_2$(${\gamma }_0=0.01$)	$2.5974\times {10}^{-2}$	$1.1157\times {10}^{-3}$	$2.4553\times {10}^{-6}$	1.9291	0.657
$f_3\left(x\right)$
$PM{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$7.5147\times {10}^{-5}$	$2.6944\times {10}^{-14}$	$4.9147\times {10}^{-47}$	3.4661	0.516
$PM{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$3.0249\times {10}^{-4}$	$2.5479\times {10}^{-12}$	$1.6300\times {10}^{-40}$	3.4917	0.468
$PM{M}_3$($\alpha =1,\beta =1$)	$1.8359\times {10}^{-4}$	$3.9306\times {10}^{-13}$	$3.7470\times {10}^{-43}$	3.4628	0.422
$T{M}_1$(${\gamma }_0=0.01$)	$2.0344\times {10}^{-2}$	$1.4543\times {10}^{-7}$	$4.5676\times {10}^{-20}$	2.4298	0.313
$T{M}_2$(${\gamma }_0=0.01$)	$2.0344\times {10}^{-2}$	$4.8277\times {10}^{-5}$	$8.6971\times {10}^{-11}$	2.1886	0.297
$f_4\left(x\right)$
$PM{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$2.1991\times {10}^{-1}$	$2.5047\times {10}^{-3}$	$3.7120\times {10}^{-10}$	3.4326	0.250
$PM{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$4.0446\times {10}^{-1}$	$1.2232\times {10}^{-2}$	$6.8347\times {10}^{-8}$	3.2771	0.250
$PM{M}_3$($\alpha =1,\beta =1$)	$4.0439\times {10}^{-1}$	$1.1104\times {10}^{-2}$	$5.3550\times {10}^{-8}$	3.2331	0.296
$T{M}_1$(${\gamma }_0=0.01$)	$9.9000\times {10}^1$	$9.9010\times {10}^1$	$4.9012\times {10}^1$	$2.4357$	0.359
$T{M}_2$(${\gamma }_0=0.01$)	$9.9000\times {10}^1$	$6.5669\times {10}^1$	$3.7895\times {10}^1$	$1.9990$	0.282
$f_5\left(x\right)$
$PM{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$2.4220\times {10}^{-1}$	$3.8151\times {10}^{-3}$	$1.0165\times {10}^{-10}$	4.2117	0.360
$PM{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$4.3566\times {10}^{-1}$	$1.1013\times {10}^{-1}$	$1.1077\times {10}^{-5}$	6.8399	0.421
$PM{M}_3$($\alpha =1,\beta =1$)	$7.8773\times {10}^{-1}$	$8.7201\times {10}^{-2}$	$1.6415\times {10}^{-5}$	4.0907	0.485
$T{M}_1$(${\gamma }_0=0.01$)	C	C	C	$41.637$ *	-
$T{M}_2$(${\gamma }_0=0.01$)	C	C	C	$1.7991$ *	-

C—Converging to undesired root; *—COC in case of undesired root.

We have demonstrated results for our special cases without memory by taking $\left(\alpha =\frac{1}{2},\beta =\frac{1}{2}\right)$, $\left(\alpha =1,\beta =\frac{1}{2}\right)$ and $\left(\alpha =1,\beta =1\right)$ in Equation (8) denoted by $\left(P{M}_1\right)$, $\left(P{M}_2\right)$ and $\left(P{M}_3\right)$, respectively. Further, for our special cases with memory by taking $\left(\alpha =\frac{1}{2},\beta =\frac{1}{2}\right)$, $\left(\alpha =1,\beta =\frac{1}{2}\right)$ and $\left(\alpha =1,\beta =1\right)$ in Equation (16) denoted by $\left(PM{M}_1\right)$, $\left(PM{M}_2\right)$ and $\left(PM{M}_3\right)$, respectively.

For comparisons, we are considering the methods given below:

Hansen–Patrick’s family ($HPF$) [9]:

$$x_{n+1}=x_n-\left[\frac{\alpha +1}{\alpha \pm {(1-(\alpha +1)L_f\left(x_n\right))}^{1/2}}\right]\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},n=0,1,2,\dots ,$$

(25)

where $L_f\left(x_n\right)={\displaystyle \frac{f^{″}\left(x_n\right)f\left(x_n\right)}{f^{\prime 2}\left(x_n\right)}}$ and $\alpha \in \mathbb{R}\backslash \{-1\}$.

Sharma et al. method without memory ($SHM$) [11]:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & y_n=x_n-\alpha {\displaystyle \frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}},\hfill \\ \hfill & x_{n+1}=x_n-\left[{\displaystyle \frac{\beta +1}{\beta \pm {(1-(\beta +1)H_f\left(x_n\right))}^{1/2}}}\right]{\displaystyle \frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}},\hfill \end{array}\right.\end{array}$$

(26)

where $H_f\left(x_n\right)={\displaystyle \frac{f^{″}\left(y_n\right)f\left(x_n\right)}{f^{\prime 2}\left(x_n\right)}}$ and $\alpha$ and $\beta (\ne -1)$ are free parameters.

Halley’s method ($HM$) [3]:

$$x_{n+1}=x_n-\left[1+{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{L_f\left(x_n\right)}{1-\alpha L_f\left(x_n\right)}}\right)\right]\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)},n=0,1,2,\dots ,$$

(27)

where $L_f\left(x_n\right)={\displaystyle \frac{f^{″}\left(x_n\right)f\left(x_n\right)}{f^{\prime 2}\left(x_n\right)}}$ and $\alpha ={\displaystyle \frac{1}{2}}$.

Traub’s method with memory ($T{M}_1$) [1]:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & {\gamma }_0,x_0\mathrm{are}\mathrm{suitably}\mathrm{given},w_n=x_n+{\gamma }_{n}f\left(x_n\right),0\ne {\gamma }_n\in \mathbb{R},\hfill \\ \hfill & x_{n+1}=x_n-{\displaystyle \frac{f\left(x_n\right)}{f[x_n,w_n]}},n=0,1,2,\dots ,\hfill \end{array}\right.\end{array}$$

(28)

where ${\gamma }_n$ is a self-accelerating parameter given as

$${\gamma }_{n+1}={\displaystyle \frac{-1}{N_1^{\prime }\left(x_n\right)}},N_1\left(x\right)=f\left(x_n\right)+(x-x_n)f[x_n,w_n],n=0,1,2,\dots$$

Traub’s method with memory ($T{M}_2$) [1]:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & {\gamma }_0\mathrm{is}\mathrm{given},{\gamma }_n={\displaystyle \frac{x_n-x_{n-1}}{f\left(x_n\right)-f\left(x_{n-1}\right)}},n\in \mathbb{N},\hfill \\ \hfill & x_{n+1}=x_n-{\displaystyle \frac{{\gamma }_{n}f{\left(x_n\right)}^2}{f(x_n+{\gamma }_{n}f\left(x_n\right))-f\left(x_n\right)}}.\hfill \end{array}\right.\end{array}$$

(29)

Remark 1.

In Table 1, for the function $f_4\left(x\right)$, as the derivative of the function becomes zero, the existing methods $HPF$, $SHM$ and $HM$ fail. Further, for the function $f_5\left(x\right)$, $HPF$, $SHM$ and $HM$ converge to undesired root ‘$\pi$’. Further, in Table 2, for the function $f_4\left(x\right)$, $T{M}_1$ and $T{M}_2$ converge to the desired root but in 11 and 14 number of iterations, respectively as we can see the errors of approximations are large in these cases. Further, for the function $f_5\left(x\right)$, $T{M}_1$ and $T{M}_2$ both converge to undesired root ‘$3\pi$’.

Further, we are considering some real life problems which are as follows:

Example 1.

Firstly, we analyze the well-known Planck’s radiation law problem [21],

$$\begin{array}{c}\hfill \psi \left(\lambda \right)=\frac{8\pi c{h}_p{\lambda }^{-5}}{e^{\frac{c{h}_p}{\lambda B_{k}T}}-1},\end{array}$$

(30)

where λ is the wavelength of radiation, $h_p$ is the Planck’s constant, T is the absolute temperature of the blackbody, c is the speed of light and $B_k$ is the Boltzmann constant. It computes the energy density within an isothermal blackbody. We intend to obtain wavelength λ corresponding to maximum energy density $\psi \left(\lambda \right)$.

To obtain maximum value of ψ, we take ${\psi }^{\prime }\left(\lambda \right)=0$ which gives

$$\begin{array}{c}\hfill \frac{\frac{c{h}_p}{\lambda B_{k}T}{e}^{\frac{c{h}_p}{\lambda B_{k}T}}}{e^{\frac{c{h}_p}{\lambda B_{k}T}}-1}=5.\end{array}$$

(31)

Let $x={\displaystyle \frac{c{h}_p}{\lambda B_{k}T}}$. Then, Equation (31) becomes

$$\begin{array}{c}\hfill f_6\left(x\right)=e^{-x}+{\displaystyle \frac{x}{5}}-1=0.\end{array}$$

(32)

As we find the solutions of $f_6\left(x\right)=0$, we get the maximum wavelength of radiation λ. As stated in [22], the L.H.S. of Equation (32) is zero when $x=5$. Further, $e^{-5}\approx 6.738\times {10}^{-3}$. Thus, another root could appear close to $x=5$. The desired zero is $\xi \approx 4.9651142317442763$.

Example 2.

Van der Waal’s equation of state [4],

$$\begin{array}{c}\hfill \left(P+\frac{a{n}^2}{V^2}\right)(V-nb)=nGT.\end{array}$$

(33)

The following nonlinear equation needs to be solved to attain the volume V of the gas in terms of another parameters,

$$\begin{array}{c}\hfill P{V}^3-(nbP+nGT)V^2+a{n}^{2}V-a{n}^{2}b=0.\end{array}$$

(34)

Here, G is the universal gas constant, P is the pressure and T is the absolute temperature. If the parameters a and b of a specific gas are given, the values of n, P and T can be calculated. Using certain values, the following nonlinear equation can be obtained,

$$\begin{array}{c}\hfill f_7\left(x\right)=0.986x^3-5.181x^2+9.067x-5.289=0,\end{array}$$

(35)

having three roots, out of which one is real and two are complex. Though our required zero is $\xi \approx 1.9298462428478622$.

Example 3.

Fractional conversion in a chemical reactor [23],

$$\begin{array}{c}\hfill f_8\left(x\right)=\frac{x}{1-x}-5log\frac{0.4(1-x)}{0.4-0.5x}+4.45977=0.\end{array}$$

(36)

Here, x denotes the fractional conversion of quantities in a chemical reactor. If x is less than zero or greater than one, then the above fractional conversion will be of no physical meaning. Hence, x is taken to be bounded in the region of $0\le x\le 1$. Moreover, the desired root is $\xi \approx 0.7573962462537538$.

Example 4.

The path traversed by an electron in the air gap between two parallel plates considering the multi-factor effect is given by

$$\begin{array}{cc}\hfill u\left(t\right)=& u_0+\left({\nu }_0+c_0\frac{E}{m\omega }sin\omega t_0+\beta \right)(t-t_0)+c_0\frac{E_0}{m{\omega }^2}\left(cos(\omega t+\beta )+sin(\omega t+\beta )\right),\hfill \end{array}$$

(37)

where $u_0$ and ${\nu }_0$ are the position and velocity of the electron at time $t_0$, m and $c_0$ are the mass and the charge of the electron at rest and $E_{0}sin(\omega t+\beta )$ is the RF electric field between the plates. If particular parameters are chosen, Equation (37) can be simplified as

$$\begin{array}{c}\hfill f_9\left(x\right)=x-\frac{1}{2}cosx+\frac{\pi }{4}=0.\end{array}$$

(38)

The desired root of Equation (38) is $\xi \approx -0.3090932715417949$.

Example 5.

The following nonlinear equation results from the embedment x of a sheet-pile wall,

$$\begin{array}{c}\hfill f_{10}\left(x\right)=\frac{x^3+2.87x^2-10.28}{4.62}-x=0.\end{array}$$

(39)

The required zero of Equation (39) is $\xi \approx 2.0021$.

We have also implemented our proposed schemes given by Equations (8) and (16) on the above-mentioned problems. Table 3 and Table 4 demonstrate the corresponding results. Further, Table 1 demonstrates COC for our proposed method without memory given by Equation (8) ($P{M}_1$, $P{M}_2$ and $P{M}_3$), method given by Equation (25) denoted by $HPF$, the method given by Equation (26) denoted by $SHM$ and Halley’s method given by Equation (27) denoted by $HM$, respectively. Table 2 demonstrates COC for our proposed method with memory given by Equation (16) ($PM{M}_1$, $PM{M}_2$ and $PM{M}_3$), method given by Equation (28) denoted by $T{M}_1$ and the method given by Equation (29) denoted by $T{M}_2$, respectively.

Table 3. Comparison of different methods without memory for real-life problems.

Without Memory Methods	$\mid {\mathit{x}}_1-\mathit{\xi }\mid$	$\mid {\mathit{x}}_2-\mathit{\xi }\mid$	$\mid {\mathit{x}}_3-\mathit{\xi }\mid$	${\mathit{\rho }}_{\mathit{c}}$	CPU Time
$f_6\left(x\right)$
$P{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$2.4307\times {10}^{-6}$	$2.8490\times {10}^{-16}$	$2.8491\times {10}^{-16}$	3.0000	0.392
$P{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$2.2284\times {10}^{-6}$	$2.8491\times {10}^{-16}$	$2.8491\times {10}^{-16}$	3.0000	0.390
$P{M}_3$($\alpha =1,\beta =1$)	$2.5307\times {10}^{-6}$	$2.8491\times {10}^{-16}$	$2.8491\times {10}^{-16}$	3.0000	0.375
$HPF$($\alpha =\frac{1}{2}$)	$1.3952\times {10}^{-4}$	$1.6301\times {10}^{-14}$	$2.8491\times {10}^{-16}$	3.0000	0.313
$SHM$($\alpha =1,\beta =\frac{1}{2}$)	$2.4927\times {10}^{-4}$	$1.8505\times {10}^{-13}$	$2.8491\times {10}^{-16}$	3.0000	0.328
$HM$($\alpha =\frac{1}{2}$)	$1.4741\times {10}^{-4}$	$2.0063\times {10}^{-14}$	$2.8491\times {10}^{-16}$	3.0000	0.329
$f_7\left(x\right)$
$P{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$3.1479\times {10}^{-3}$	$5.5786\times {10}^{-7}$	$7.3448\times {10}^{-18}$	2.9887	0.234
$P{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$7.3066\times {10}^{-4}$	$3.5639\times {10}^{-9}$	$4.1118\times {10}^{-18}$	2.9976	0.218
$P{M}_3$($\alpha =1,\beta =1$)	$2.1500\times {10}^{-3}$	$1.7710\times {10}^{-7}$	$4.2152\times {10}^{-18}$	2.9912	0.250
$HPF$($\alpha =\frac{1}{2}$)	$4.0615\times {10}^{-4}$	$1.4098\times {10}^{-10}$	$4.1118\times {10}^{-18}$	3.0008	0.282
$SHM$($\alpha =1,\beta =\frac{1}{2}$)	$5.7189\times {10}^{-3}$	$5.6997\times {10}^{-6}$	$5.9525\times {10}^{-15}$	2.9774	0.234
$HM$($\alpha =\frac{1}{2}$)	$4.5561\times {10}^{-3}$	$2.3326\times {10}^{-6}$	$3.3202\times {10}^{-16}$	2.9830	0.234
$f_8\left(x\right)$
$P{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$8.0551\times {10}^{-4}$	$6.6259\times {10}^{-8}$	$8.8456\times {10}^{-17}$	3.0049	0.359
$P{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$5.9396\times {10}^{-4}$	$1.3586\times {10}^{-8}$	$8.8493\times {10}^{-17}$	3.0056	0.360
$P{M}_3$($\alpha =1,\beta =1$)	$1.0985\times {10}^{-3}$	$1.7216\times {10}^{-7}$	$8.7851\times {10}^{-17}$	3.0096	0.376
$HPF$($\alpha =\frac{1}{2}$)	$5.7969\times {10}^{-4}$	$4.0492\times {10}^{-8}$	$8.8506\times {10}^{-17}$	3.0000	0.344
$SHM$($\alpha =1,\beta =\frac{1}{2}$)	$2.8780\times {10}^{-3}$	$1.4099\times {10}^{-5}$	$1.6623\times {10}^{-12}$	3.0246	0.313
$HM$($\alpha =\frac{1}{2}$)	$1.9432\times {10}^{-5}$	$1.0029\times {10}^{-13}$	$8.8493\times {10}^{-17}$	3.0000	0.296
$f_9\left(x\right)$
$P{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$2.1183\times {10}^{-3}$	$3.7397\times {10}^{-10}$	$2.3650\times {10}^{-30}$	2.9998	0.390
$P{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$8.4057\times {10}^{-4}$	$1.0824\times {10}^{-11}$	$3.0466\times {10}^{-31}$	2.9999	0.375
$P{M}_3$($\alpha =1,\beta =1$)	$1.8511\times {10}^{-3}$	$2.4942\times {10}^{-10}$	$9.1594\times {10}^{-31}$	2.9998	0.376
$HPF$($\alpha =\frac{1}{2}$)	$1.2235\times {10}^{-3}$	$1.8468\times {10}^{-11}$	$3.0470\times {10}^{-31}$	2.9994	0.328
$SHM$($\alpha =1,\beta =\frac{1}{2}$)	$2.6486\times {10}^{-3}$	$1.4723\times {10}^{-9}$	$2.5407\times {10}^{-28}$	2.9996	0.406
$HM$($\alpha =\frac{1}{2}$)	$4.1975\times {10}^{-3}$	$3.6399\times {10}^{-9}$	$2.3630\times {10}^{-27}$	3.0001	0.375
$f_{10}\left(x\right)$
$P{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$1.1429\times {10}^{-3}$	$1.8779\times {10}^{-5}$	$1.8779\times {10}^{-5}$	3.0002	0.298
$P{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$6.2014\times {10}^{-4}$	$1.8779\times {10}^{-5}$	$1.8779\times {10}^{-5}$	3.0001	0.327
$P{M}_3$($\alpha =1,\beta =1$)	$1.3290\times {10}^{-3}$	$1.8779\times {10}^{-5}$	$1.8779\times {10}^{-5}$	3.0003	0.328
$HPF$($\alpha =\frac{1}{2}$)	$2.6168\times {10}^{-6}$	$1.8779\times {10}^{-5}$	$1.8779\times {10}^{-5}$	3.0000	0.313
$SHM$($\alpha =1,\beta =\frac{1}{2}$)	$1.5114\times {10}^{-3}$	$1.8778\times {10}^{-5}$	$1.8779\times {10}^{-5}$	3.0002	0.297
$HM$($\alpha =\frac{1}{2}$)	$1.6720\times {10}^{-3}$	$1.8778\times {10}^{-5}$	$1.8779\times {10}^{-5}$	3.0003	0.234

Table 4. Comparison of different methods with memory for real life problems.

With Memory Methods	$\mid {\mathit{x}}_1-\mathit{\xi }\mid$	$\mid {\mathit{x}}_2-\mathit{\xi }\mid$	$\mid {\mathit{x}}_3-\mathit{\xi }\mid$	${\mathit{\rho }}_{\mathit{c}}$	CPU Time
$f_6\left(x\right)$
$PM{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$2.4307\times {10}^{-6}$	$2.8491\times {10}^{-16}$	$2.8491\times {10}^{-16}$	3.3297	0.359
$PM{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$2.2284\times {10}^{-6}$	$2.8491\times {10}^{-16}$	$2.8491\times {10}^{-16}$	3.3318	0.344
$PM{M}_3$($\alpha =1,\beta =1$)	$2.5307\times {10}^{-6}$	$2.8491\times {10}^{-16}$	$2.8491\times {10}^{-16}$	3.3293	0.297
$T{M}_1$(${\gamma }_0=0.01$)	$1.5389\times {10}^{-3}$	$4.7636\times {10}^{-10}$	$2.8491\times {10}^{-16}$	2.4006	0.282
$T{M}_2$(${\gamma }_0=0.01$)	$1.5389\times {10}^{-3}$	$8.5688\times {10}^{-8}$	$5.5032\times {10}^{-16}$	2.0001	0.297
$f_7\left(x\right)$
$PM{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$3.1479\times {10}^{-3}$	$1.9881\times {10}^{-7}$	$4.1148\times {10}^{-18}$	3.2847	0.125
$PM{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$7.3066\times {10}^{-4}$	$2.3942\times {10}^{-9}$	$4.1118\times {10}^{-18}$	3.3337	0.187
$PM{M}_3$($\alpha =1,\beta =1$)	$2.1500\times {10}^{-3}$	$6.3764\times {10}^{-8}$	$4.1119\times {10}^{-18}$	3.3027	0.171
$T{M}_1$(${\gamma }_0=0.01$)	$1.8745\times {10}^{-2}$	$8.6076\times {10}^{-4}$	$6.4139\times {10}^{-7}$	2.2611	0.157
$T{M}_2$(${\gamma }_0=0.01$)	$1.8745\times {10}^{-2}$	$2.9838\times {10}^{-3}$	$9.9340\times {10}^{-5}$	1.7706	0.203
$f_8\left(x\right)$
$PM{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$8.0551\times {10}^{-4}$	$1.3900\times {10}^{-8}$	$8.8493\times {10}^{-17}$	3.2477	0.390
$PM{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$5.9396\times {10}^{-4}$	$5.4849\times {10}^{-9}$	$8.8493\times {10}^{-17}$	3.2580	0.374
$PM{M}_3$($\alpha =1,\beta =1$)	$1.0985\times {10}^{-3}$	$3.4510\times {10}^{-8}$	$8.8493\times {10}^{-17}$	3.2322	0.297
$T{M}_1$(${\gamma }_0=0.01$)	$1.7662\times {10}^{-3}$	$2.1922\times {10}^{-5}$	$1.2446\times {10}^{-10}$	2.7340	0.296
$T{M}_2$(${\gamma }_0=0.01$)	$1.7662\times {10}^{-3}$	$1.1307\times {10}^{-4}$	$3.9994\times {10}^{-7}$	2.0345	0.344
$f_9\left(x\right)$
$PM{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$2.1183\times {10}^{-3}$	$5.2782\times {10}^{-11}$	$3.0463\times {10}^{-31}$	3.3204	0.390
$PM{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$8.4057\times {10}^{-4}$	$3.2315\times {10}^{-12}$	$3.0463\times {10}^{-31}$	3.3363	0.391
$PM{M}_3$($\alpha =1,\beta =1$)	$1.8511\times {10}^{-3}$	$3.5214\times {10}^{-11}$	$3.0463\times {10}^{-31}$	3.3231	0.359
$T{M}_1$(${\gamma }_0=0.01$)	$3.9978\times {10}^{-2}$	$8.1932\times {10}^{-5}$	$2.4800\times {10}^{-11}$	2.4205	0.328
$T{M}_2$(${\gamma }_0=0.01$)	$3.9978\times {10}^{-2}$	$8.3312\times {10}^{-4}$	$3.8756\times {10}^{-7}$	1.9767	0.312
$f_{10}\left(x\right)$
$PM{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$1.1429\times {10}^{-3}$	$1.8779\times {10}^{-5}$	$1.8779\times {10}^{-5}$	3.2964	0.218
$PM{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$6.2014\times {10}^{-4}$	$1.8779\times {10}^{-5}$	$1.8779\times {10}^{-5}$	3.3102	0.187
$PM{M}_3$($\alpha =1,\beta =1$)	$1.3290\times {10}^{-3}$	$1.8779\times {10}^{-5}$	$1.8779\times {10}^{-5}$	3.2930	0.234
$T{M}_1$(${\gamma }_0=0.01$)	$2.3352\times {10}^{-2}$	$4.2977\times {10}^{-5}$	$1.8779\times {10}^{-5}$	2.5636	0.235
$T{M}_2$(${\gamma }_0=0.01$)	$2.3352\times {10}^{-2}$	$5.4260\times {10}^{-4}$	$1.9035\times {10}^{-5}$	2.0023	0.220

Remark 2.

The proposed scheme with memory given by Equation (16) has been compared with some other methods and it is noted that our proposed scheme with memory gives better outcomes in terms of COC and errors as depicted in Table 2 and Table 4. There is an obvious increase in the order of convergence.

5. Basins of Attraction

The basins of attraction of the root $t^{*}$ of $u\left(t\right)=0$ are the sets of all initial points $t_0$ in the complex plane that converge to $t^{*}$ on the application of the given iterative scheme. Our objective is to make use of basins of attraction to examine the comparison of several root-finding iterative methods in the complex plane in terms of convergence and stability of the method.

On this front, we have taken a $512\times 512$ grid of the rectangle $S=[-2,2]\times [-2,2]\subset \mathbb{C}$. A color is assigned to each point $t_0\in S$ on the basis of the convergence of the corresponding method starting from $t_0$ to the simple root and if the method diverges, a black color is assigned to that point. Thus, distinct colors are assigned to the distinct roots of the corresponding problem. It is decided that an initial point $t_0$ converges to a root $t^{*}$ when $\mid t^{*}-t_0\mid <{10}^{-4}$. The point $t_0$ is said to belong to the basins of attraction of $t^{*}$. Likewise, the method beginning from the initial point $t_0$ is said to diverge if no root is located in a maximum of 25 iterations. We have used MATLAB R2021a software [24] to draw the presented basins of attraction.

Furthermore, Table 5 and Table 6 list the average number of iterations denoted by Avg_Iter, percentage of non-converging points denoted by $P_{NC}$ and the total CPU time taken by the methods to generate the basins of attraction.

Table 5. Comparison of different methods without memory in terms of Avg_Iter, $P_{NC}$ and CPU time.

Without Memory Methods	Avg_Iter	${\mathit{P}}_{\mathit{N}\mathit{C}}$	CPU Time
$p_1\left(z\right)$
$P{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$2.7165$	0	$4.0501$
$P{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$2.2822$	0	$3.5181$
$P{M}_3$($\alpha =1,\beta =1$)	$2.6060$	0	$3.8734$
$HPF$($\alpha =\frac{1}{2}$)	$2.5187$	$0.004\times {10}^{-3}$	$2.7963$
$SHM$($\alpha =1,\beta =\frac{1}{2}$)	$2.5187$	$0.004\times {10}^{-3}$	$3.0479$
$p_2\left(z\right)$
$P{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$3.1603$	0	$5.6380$
$P{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$2.7433$	0	$4.9187$
$P{M}_3$($\alpha =1,\beta =1$)	$2.8910$	0	$5.0015$
$HPF$($\alpha =\frac{1}{2}$)	$2.2958$	$0.004\times {10}^{-3}$	$2.7867$
$SHM$($\alpha =1,\beta =\frac{1}{2}$)	$7.1570$	$1.505\times {10}^{-1}$	$7.9437$
$p_3\left(z\right)$
$P{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$3.9678$	$1.323\times {10}^{-2}$	$7.2858$
$P{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$3.4784$	$8.185\times {10}^{-3}$	$6.3408$
$P{M}_3$($\alpha =1,\beta =1$)	$3.6042$	$7.816\times {10}^{-3}$	$6.7897$
$HPF$($\alpha =\frac{1}{2}$)	$2.9863$	$0.004\times {10}^{-3}$	$3.4503$
$SHM$($\alpha =1,\beta =\frac{1}{2}$)	$8.9566$	$1.135\times {10}^{-1}$	$10.4044$
$p_4\left(z\right)$
$P{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$3.5381$	0	$6.2320$
$P{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$3.3973$	0	$6.0172$
$P{M}_3$($\alpha =1,\beta =1$)	$3.4684$	0	$6.0730$
$HPF$($\alpha =\frac{1}{2}$)	$3.4316$	0	$3.7895$
$SHM$($\alpha =1,\beta =\frac{1}{2}$)	$4.7686$	$0.304\times {10}^{-3}$	$6.3023$

Table 6. Comparison of different methods with memory in terms of Avg_Iter, $P_{NC}$ and CPU time.

With Memory Methods	Avg_Iter	${\mathit{P}}_{\mathit{N}\mathit{C}}$	CPU Time
$p_1\left(z\right)$
$PM{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$2.7089$	0	$5.2390$
$PM{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$2.4002$	0	$4.6904$
$PM{M}_3$($\alpha =1,\beta =1$)	$2.5916$	0	$5.1093$
$T{M}_1$(${\gamma }_0=0.01$)	$4.3642$	$1.949\times {10}^{-3}$	$3.2522$
$T{M}_2$(${\gamma }_0=0.01$)	$8.3338$	$1.390\times {10}^{-1}$	$5.6000$
$p_2\left(z\right)$
$PM{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$3.1132$	0	$6.8290$
$PM{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$2.7755$	0	$6.2775$
$PM{M}_3$($\alpha =1,\beta =1$)	$2.8498$	0	$6.3416$
$T{M}_1$(${\gamma }_0=0.01$)	$6.0252$	$1.110\times {10}^{-3}$	$5.2045$
$T{M}_2$(${\gamma }_0=0.01$)	$11.9211$	$2.765\times {10}^{-1}$	$9.6673$
$p_3\left(z\right)$
$PM{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$3.6980$	$0.030\times {10}^{-3}$	$8.2979$
$PM{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$3.3119$	0	$7.5358$
$PM{M}_3$($\alpha =1,\beta =1$)	$3.3200$	0	$7.7738$
$T{M}_1$(${\gamma }_0=0.01$)	$8.3110$	$4.734\times {10}^{-2}$	$6.7431$
$T{M}_2$(${\gamma }_0=0.01$)	$15.0794$	$4.084\times {10}^{-1}$	$11.8306$
$p_4\left(z\right)$
$PM{M}_1$($\alpha =\frac{1}{2},\beta =\frac{1}{2}$)	$3.7034$	0	$8.2241$
$PM{M}_2$($\alpha =1,\beta =\frac{1}{2}$)	$3.6684$	0	$8.2776$
$PM{M}_3$($\alpha =1,\beta =1$)	$3.6692$	0	$8.2856$
$T{M}_1$(${\gamma }_0=0.01$)	$5.4714$	$1.490\times {10}^{-3}$	$4.5927$
$T{M}_2$(${\gamma }_0=0.01$)	$9.1054$	$7.957\times {10}^{-2}$	$7.0686$

To carry out the desired comparisons, we have considered the test problems given below:

Problem 1.

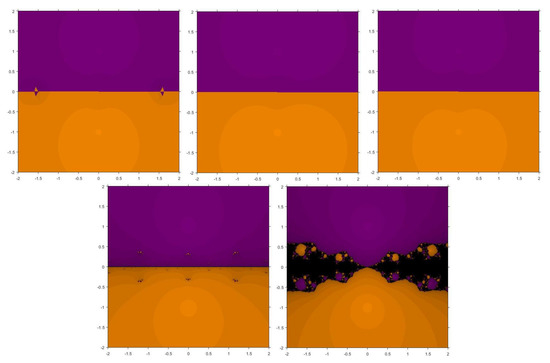
The first function considered is $p_1\left(z\right)=z^2+1$. The roots of this function are i, $-i$. The basins corresponding to our proposed method and the mentioned existing methods are shown in Figure 1 and Figure 2. It is observed that $P{M}_1$, $P{M}_2$, $P{M}_3$, $PM{M}_1$, $PM{M}_2$ and $PM{M}_3$ converge to the root with no diverging points but $HPF$, $SHM$, $T{M}_1$ and $T{M}_2$ have some points painted as black.

Figure 1. Basins of attraction for $P{M}_1$, $P{M}_2$, $P{M}_3$, $HPF$, $SHM$, respectively for $p_1\left(z\right)$.

Figure 2. Basins of attraction for $PM{M}_1$, $PM{M}_2$, $PM{M}_3$, $T{M}_1$, $T{M}_2$, respectively for $p_1\left(z\right)$.

Problem 2.

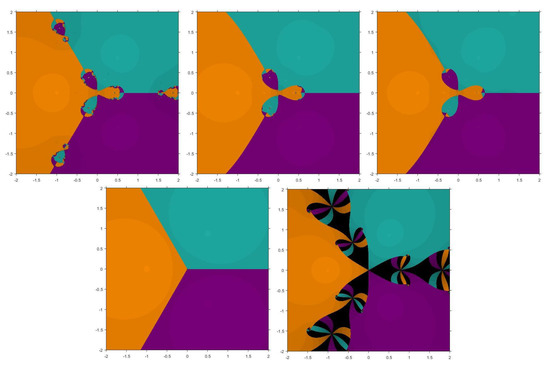
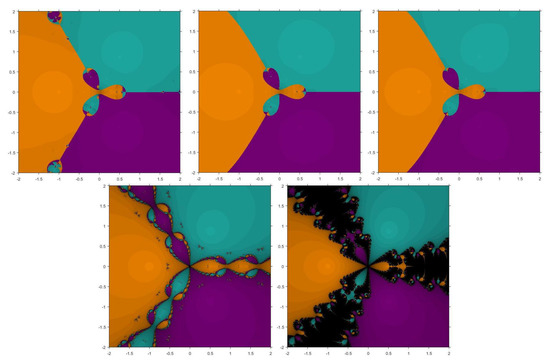
Second function taken is $p_2\left(z\right)=z^3+1$ having roots $-1$, $0.5+0.866i$, $0.5-0.866i$. Figure 3 and Figure 4 show the basins for $p_2\left(z\right)$ in which it can be seen that $SHM$, $T{M}_1$ and $T{M}_2$ have wider regions of divergence.

Figure 3. Basins of attraction for $P{M}_1$, $P{M}_2$, $P{M}_3$, $HPF$, $SHM$, respectively for $p_2\left(z\right)$.

Figure 4. Basins of attraction for $PM{M}_1$, $PM{M}_2$, $PM{M}_3$, $T{M}_1$, $T{M}_2$, respectively for $p_2\left(z\right)$.

Problem 3.

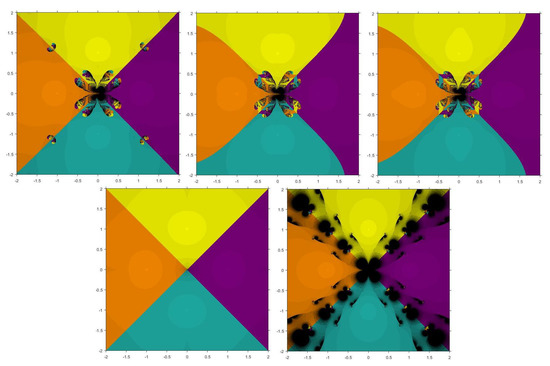
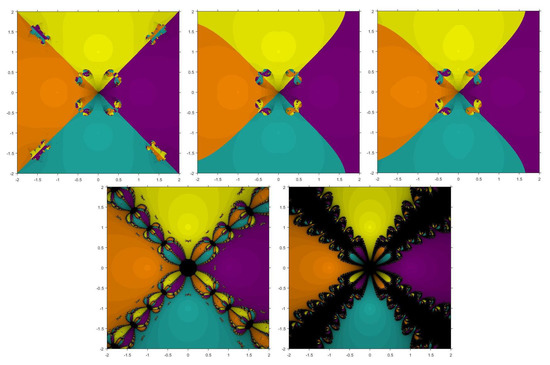
The third function considered is $p_3\left(z\right)=z^4-1$ having roots $\pm 1$, $\pm i$. Figure 5 and Figure 6 show that $SHM$ and $T{M}_2$ have smaller basins. Although $P{M}_1$, $P{M}_2$, $P{M}_3$ and $PM{M}_1$ have some diverging points, yet they converge faster than the existing methods.

Figure 5. Basins of attraction for $P{M}_1$, $P{M}_2$, $P{M}_3$, $HPF$, $SHM$, respectively for $p_3\left(z\right)$.

Figure 6. Basins of attraction for $PM{M}_1$, $PM{M}_2$, $PM{M}_3$, $T{M}_1$, $T{M}_2$, respectively for $p_3\left(z\right)$.

Problem 4.

The fourth function we have taken is $p_4\left(z\right)=z^5-z$ whose roots are 0, $\pm 1$, $\pm i$. Figure 7 and Figure 8 show that $P{M}_1$, $P{M}_2$, $P{M}_3$, $HPF$, $PM{M}_1$, $PM{M}_2$ and $PM{M}_3$ depict convergence to the root for any initial point as they have no diverging points.

Figure 7. Basins of attraction for $P{M}_1$, $P{M}_2$, $P{M}_3$, $HPF$, $SHM$, respectively for $p_4\left(z\right)$.

Figure 8. Basins of attraction for $PM{M}_1$, $PM{M}_2$, $PM{M}_3$, $T{M}_1$, $T{M}_2$, respectively for $p_4\left(z\right)$.

Remark 3.

One can see from Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 and Table 5 and Table 6 that there is a marginal increase in the average number of iterations per point of the existing methods, as they have more number of divergent points than that of the proposed method. Special mention to the fact that our proposed with memory method has negligible number of divergent points in the specified mesh of points and hence, larger basins of attraction. Consequently, our proposed method with memory shows faster convergence in comparison to the existing methods.

6. Conclusions

A new method with memory has been introduced. The proposed method has a higher order of convergence in comparison with the Hansen–Patrick and Traub methods. For verification, we have carried out numerical experiments on a few test functions and some real-life problems. It is clearly visible from our results that the proposed method improves the convergence order. This increase in the convergence order has been achieved with no additional functional evaluation. Furthermore, we have also presented the basins of attraction for the proposed, as well as some existing methods, and our results point to the very fact that our proposed method converges largely to the desired zeros over a specified region much faster. Finally, to conclude, we would say that the proposed method can be significantly used for solving nonlinear equations.