Abstract
The sparrow search algorithm (SSA) is a metaheuristic algorithm developed based on the foraging and anti-predatory behavior of sparrow populations. Compared with other metaheuristic algorithms, SSA also suffers from poor population diversity, has weak global comprehensive search ability, and easily falls into local optimality. To address the problems whereby the sparrow search algorithm tends to fall into local optimum and the population diversity decreases in the later stage of the search, an improved sparrow search algorithm (PGL-SSA) based on piecewise chaotic mapping, Gaussian difference variation, and linear differential decreasing inertia weight fusion is proposed. Firstly, we analyze the improvement of six chaotic mappings on the overall performance of the sparrow search algorithm, and we finally determine the initialization of the population by piecewise chaotic mapping to increase the initial population richness and improve the initial solution quality. Secondly, we introduce Gaussian difference variation in the process of individual iterative update and use Gaussian difference variation to perturb the individuals to generate a diversity of individuals so that the algorithm can converge quickly and avoid falling into localization. Finally, linear differential decreasing inertia weights are introduced globally to adjust the weights so that the algorithm can fully traverse the solution space with larger weights in the first iteration to avoid falling into local optimum, and we enhance the local search ability with smaller weights in the later iteration to improve the search accuracy of the optimal solution. The results show that the proposed algorithm has a faster convergence speed and higher search accuracy than the comparison algorithm, the global search capability is significantly enhanced, and it is easier to jump out of the local optimum. The improved algorithm is also applied to the Heating, Ventilation and Air Conditioning (HVAC) system control optimization direction, and the improved algorithm is used to optimize the parameters of the HVAC system Proportion Integral Differential (PID) controller. The results show that the PID controller optimized by the improved algorithm has higher control accuracy and system stability, which verifies the feasibility of the improved algorithm in practical engineering applications.
1. Introduction
Sparrow search algorithm (SSA) [1] is an emerging metaheuristic algorithm, first proposed in 2020, which belongs to the swarm intelligence algorithm based on the optimization of group socialization features. The algorithm is simple in structure, easy to implement and has the advantages of strong merit-seeking ability and fast convergence speed. However, the sparrow search algorithm, as with other swarm intelligence optimization algorithms, suffers from weak global comprehensive search ability, has reduced population diversity in the late stage of the search, and easily falls into local optimality and other defects.
The sparrow search algorithm itself possesses certain superiority, and to improve it with the same defects as other metaheuristics, many scholars have proposed a large number of improvement strategies to address the defects of the sparrow search algorithm. Reference [2] presents a literature based on the logarithmic spiral strategy and strategy of adaptive step chaotic sparrow search algorithm (CLSSA). The global search capability of the sparrow search algorithm is improved by the logarithmic spiral strategy and adaptive stepping strategy, and good results are achieved in structural engineering design problems. Reference [3] proposed an improved sparrow search algorithm based on sine cosine and firefly perturbation (SFSSA). The improved precision of algorithm convergence and optimization can solve the problem of the emergency supplies distribution center layout. Reference [4] proposed an improved sparrow search algorithm based on gold sine curve and adaptive strategies (GCSSA) through fusion, which increased the sparrow search algorithm convergence speed and global search ability. Reference [5] improves the ability of the sparrow search algorithm to jump out of local optima by mutation and greedy strategies (MSSA).
Numerous scholars in the above literature have made many improvements to the original sparrow search algorithm from different perspectives. The main improvement strategies can be summarized as four points: (1) improvement of the population initialization method of the sparrow search algorithm, which focuses on population initialization by replacing pseudo-random numbers with various chaotic mappings; (2) strategic position updating for individuals, such as individual position updating by sine cosine optimization, adaptive t-distribution, adaptive step size, etc. to improve the ability of the algorithm to jump out of the local optimum; (3) balancing the global search ability of the algorithm by weight adjustment; and (4) multi-algorithm integration improvement, such as combining the advantages of two algorithms for improvement.
The improvement strategies for the sparrow search algorithm are numerous but still in the exploration stage. In order to fully improve the convergence accuracy and merit-seeking performance of the sparrow search algorithm, based on the previous work, in this paper, an improved sparrow search algorithm PGL-SSA is proposed. The main work is as follows: (1) First, we analyze the influence of the population initialization method on the advantages and disadvantages of the initial solution and the convergence speed of the algorithm, consider the improvement of the performance of the algorithm by initializing the population with various chaotic mappings, and propose the population initialization of the sparrow search algorithm by the piecewise mapping instead of pseudo-random numbers to improve the population diversity of the algorithm. (2) Second, we address the problem of convergence of the algorithm into a local optimum, and we propose a Gaussian difference variation [6] strategy to update the individual positions and improve the ability of the algorithm to jump out of the local optimum through the optimal individual perturbation. (3) Third, we consider the balance between the early and late iterations of the algorithm to ensure that the global and local search capabilities of the algorithm are balanced. The proposed linear differential decreasing inertia weight [7] strategy enhances the global search ability of the algorithm in the early iteration, fully traverses the solution space to avoid the local optimum, and accurately searches for the optimal solution in the late iteration to improve the convergence accuracy of the algorithm. The optimization results for the CEC test function show that the improved algorithm in this paper has significant improvement in convergence accuracy, convergence speed and global search ability compared with the comparison algorithm, with obvious advantages. The simulation results of the PID controller for the HVAC system show that the PID controller optimized by this algorithm has high accuracy, fast response speed and strong robustness, which proves the effectiveness of this algorithm.
The Heating, Ventilation and Air Conditioning (HVAC) system has time-varying, time-lagging, strong coupling, non-linear and other characteristics, resulting in the application of traditional PID control methods in both engineering practice and theory being unable to achieve a good control effect, which leads to long-term inefficient operation of the HVAC system, as energy consumption is generally high [8,9]. At present, the parameter adjustment of the HVAC system PID controller is often carried out by empirical rules and trial and error. In order to make the system reach the preset temperature quickly, designers are used to setting higher parameters, which leads to unstable system operation and repeated changes of room temperature. The parameter adjustment of the HVAC system PID controller by an optimization algorithm [10,11] can greatly reduce the response time of the HVAC system, improve the control accuracy and loop control performance of the HVAC system and achieve the purpose of energy saving [12,13].
At present, the advanced control strategies and theoretical research of HVAC systems have been relatively mature, and various optimization algorithms have emerged [14]. Reference [15] proposed a method based on neural network optimization to optimize the PID controller of HVAC systems. Reference [16] proposed a PID parameter optimization method based on a Flower Pollination Algorithm (FPA) to obtain higher system control accuracy. Reference [17] proposed a Self-aggregating Moth Flame Optimization (SMFO) to optimize the PID parameters and introduced the light intensity attraction feature of the firefly algorithm into the conventional Moth Flame Optimization (MFO) to improve the optimization performance of the algorithm. Reference [18] proposed a new SOA-SSA hybrid algorithm based on the Seeker Optimization Algorithm (SOA) and the Salp Swarm Algorithm (SSA), which achieved better results in the optimization of PID parameters. In this paper, the improved sparrow search algorithm PGL-SSA is applied to the direction of HVAC system control optimization, which fully improves the system control accuracy and robustness.
The rest of this article is organized as follows: Section 2 introduces the principle and structure of SSA. Section 3 introduces the improvement strategy of PGL-SSA. Section 4 presents the overall structure and the flow chart of PGL-SSA. Section 5 and Section 6 introduce the experimental results and analysis based on benchmark functions and engineering problems. Section 7 summarizes the entire text.
2. Sparrow Search Algorithm
The sparrow search algorithm is a swarm intelligence optimization algorithm proposed based on the foraging and anti-predatory behavior of sparrow groups. The foraging process is a finder–follower model incorporating a reconnaissance warning mechanism. In the iterative process, the discoverer position is updated by the following equation:
Among them: represents the j-th dimensional position of the i-th individual in the t-th generation of the population; denotes a uniformly distributed random number within ; Q denotes a random number obeying normal distribution; L is a 1 × d matrix, where each element is 1; denotes the maximum number of iterations; and are the warning value and the safety threshold, respectively; takes the value 0.6. When , this means that there is no predator around and the discoverer can conduct a global search; if , this means that some sparrows have discovered the predator, and all sparrows have to take relevant actions.
A formula for updating the position of followers in sparrow populations:
where A is a 1 × D dimensional matrix with elements randomly assigned to 1 or ; denotes the location of the sparrow with the worst fitness value at the t-th iteration of the population; denotes the location of the sparrow with the best fitness value at the -th iteration of the population; when , it means that the i-th joiner has a low fitness value and needs to shift its foraging area to obtain more energy; when , the i-th joiner has the optimal fitness value and will search for a random location near the current optimal location to explore foraging.
Overall, – of individuals in the population act as scouts (SD), and its position update formula is as follows:
in which is the current global optimal position; is a standard normally distributed random number with mean 0 and variance 1; K is a uniformly distributed random number in the interval . represents the current individual fitness value, represents the current global optimal fitness value, represents the current global worst fitness value, and is the minimum constant to avoid the denominator being zero.
The analysis of the iterative process of the sparrow search algorithm reveals that the performance of the sparrow search algorithm is related to the quality of individuals in the initialized population and the location of individual updates. The initial population is randomized, which is likely to lead to low quality of the initial individuals and affect the performance of the algorithm. At the same time, the single way of updating the position of individuals in the population is easy to fall into the local optimum, which leads to the stagnation of the search.
3. Sparrow Search Algorithm Enhancement Strategy
In response to the above analysis, this paper adopts three strategies to improve the sparrow search algorithm. The strategies are as follows:
(1) Improving the population initialization by piecewise mapping to increase the population diversity, improve the initial solution quality, and enhance the convergence speed of the algorithm.
(2) Introducing the Gaussian difference variation into the individual position updating process, and perturbing the individual by Gaussian difference to improve the ability of the algorithm to jump out of the local optimum.
(3) Coordinating the global and local search ability of the algorithm by linear differential decreasing inertia weights. The algorithm is able to coordinate the global and local search capabilities by linear differential decreasing inertia weights to ensure the global search while accurately locking the optimal solution.
3.1. Piecewise Chaos Mapping
The current optimization algorithm often uses pseudo-random numbers for population initialization [19], and in most cases, using chaotic mappings instead of pseudo-random numbers in the population initialization process can achieve better results [20]. Piecewise chaotic mappings are typical representatives of chaotic mappings, which are ergodic and random, and their mathematical expressions are as follows:
Among them, P is the control parameter, and the values of P and X are in the range of .
This paper firstly analyzes some chaotic maps (logistic map, tent map, chebyshev map, piecewise map, iterative map, intermittency) commonly used in the field of swarm intelligence. The iterative distribution of six chaotic maps is shown in Figure 1.
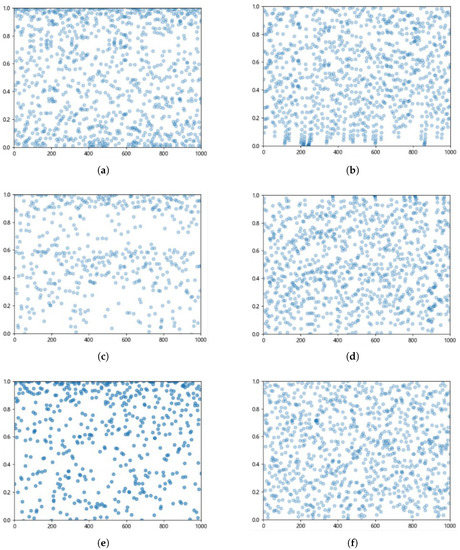
Figure 1.
The distribution of 1000 iterations of six chaotic mappings, (a) logistic mapping, (b) tent mapping, (c) iterative mapping, (d) intermittency mapping, (e) chebyshev mapping, and (f) piecewise mapping.
Secondly, the SSA algorithm is improved by six chaotic mappings for population initialization, and the improved algorithm is simulated and tested on some test functions with a population size of 50, dimension of 30, and the maximum number of iterations of 1000; the test results are shown in Figure 2.
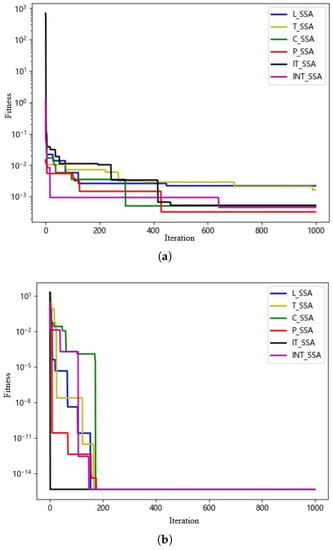
Figure 2.
Iteration curves of 6 chaotic mapping improved SSA algorithms for different types of test functions, (a) for high-dimensional single-peaked function, (b) for high-dimensional multi-peaked function.
From Figure 1, it can be seen that the piecewise chaos mapping has both ergodic and non-repeatable spatial distribution compared to the other five chaos mappings. From Figure 2, it can be seen that the SSA algorithm initialized by piecewise chaotic mapping has good performance in both test functions compared with other chaotic mapping initialized by the SSA algorithm. In a comprehensive analysis, the SSA algorithm with piecewise chaos mapping is used to improve the population initialization.
3.2. Gaussian Differential Variance
The application of traditional differential variation strategy can improve the convergence speed of the algorithm but also increase the possibility of the algorithm falling into the local optimum, while Gaussian differential variation can generate a larger perturbation in the vicinity of the current variant individual, making the algorithm more likely to jump out of the local optimum [21].
The position of individual sparrows is updated by applying the Gaussian difference variation strategy, the Gaussian difference between the position of the current optimal sparrow, the position of the current individual sparrow and the random individual in the sparrow population to generate a larger perturbation near the current variant individual to avoid the algorithm to fall into the local optimum, and the mathematical expression of Gaussian difference variation is as follows:
where and are the weight coefficients; and are the Gaussian distribution function coefficients that generate a Gaussian distribution random number function with mean 0 and variance 1; is the current optimal individual position; is the position vector of random sparrow individuals; and is the current sparrow individual position.
The individual perturbation of each sparrow by differential variables and Gaussian distribution function coefficients increases the individual diversity of the sparrow population, which ensures the convergence speed of the algorithm while avoiding the algorithm to fall into local optimum.
3.3. Linear Differential Decreasing Inertia Weights
A larger inertia weight has a good effect on the global search ability of the algorithm, while a smaller inertia weight is more beneficial to improve the local search ability of the algorithm [22,23]. In order to better balance the global and local search ability of the algorithm, a larger inertia weight is introduced in the early stage of the search to enhance the global search ability and fully traverse the solution space to avoid falling into the local optimum. In the later stage of the search, the local search capability is enhanced to improve the precision search capability. A typical Linear Decreasing Inertia Weight (LDIW) strategy is formulated as follows:
Among them, t is the number of current iterations; K is the total number of iterations; takes the value 0.9; and takes the value 0.4.
The disadvantage of linear decreasing inertia weights is that the slope is constant, which leads to premature local convergence of the algorithm, and if the initial iteration of the population is poorly positioned and the number of iterations keeps accumulating, it is very likely that the algorithm will fall into a local optimum at the end of the iteration. Therefore, a linear differential decreasing inertia weight is introduced in this paper, and the formula is as follows:
The inertia weight of this strategy is a quadratic function of time. At the beginning of the iteration, w changes slowly, which helps the algorithm to fully traverse the solution space at the beginning of the iteration and find the solution with better fitness. In the later iterations, w changes rapidly, and the algorithm can converge quickly after finding the optimal solution and lock the optimal solution precisely to improve the operation efficiency.
4. Improved Sparrow Search Algorithm
The original sparrow search algorithm will converge to the origin and the optimal value point; when the origin and the current optimal value point overlap, the algorithm performance is excellent, whereas when the optimal value point and the origin do not overlap, the sparrow population will wander between the two points, resulting in a significant decline in the performance of the algorithm. Therefore, the original sparrow search algorithm is eliminated to converge to the origin, while the jump search method is changed to move to the optimal value point.
The simplified formula for modifying discoverer location updates is as follows:
The discoverer position update formula with linear differential decreasing inertia weights is introduced as:
The original follower position update formula is modified by randomly assigning the sum of the difference between the location of the optimal sparrow and the optimal location in the full dimension to the original follower position update formula as follows:
The PGL-SSA algorithm increases the sparrow population diversity by introducing piecewise chaotic mapping, Gaussian difference variation and linear differential decreasing inertia weight strategy to enhance the ability of the algorithm to jump out of the local optimum, while balancing the global search and local search ability of the algorithm, and its specific implementation steps are as follows:
Step 1: The parameters are set; each parameter includes population size N, number of discoverers M, number of followers (), number of sparrows for reconnaissance warning , dimension of the objective function , upper and lower bounds , of initial values, and maximum number of iterations ;
Step 2: Apply the piecewise chaotic sequence in Equation (4) to initialize the population and generate N D-dimensional vectors;
Step 3: Calculate the fitness value of all individuals in the population, record the current best individual fitness value and the corresponding position , and record the current worst individual fitness value and the corresponding position ;
Step 5: Therandomly selected 10%–20% individuals in the species sparrow flock are used as scouts, and the scout positions are updated by Equation (3);
Step 6: During the iteration of the algorithm, the diversity of individuals is generated by perturbation of the difference variables to make the algorithm converge quickly. After one complete iteration, the fitness value and the population average fitness value are recalculated for each individual of the population, and when < , the Gaussian difference variation is performed according to Equation (5), and the pre-variation individual is replaced by the post-variation individual if it is better than the pre-variation individual;
Step 7: Update the historical optimal position and the corresponding fitness value of the sparrow population, and the worst position and the corresponding fitness value of the population;
Step 8: Determine whether the number of iterations of the algorithm reaches the maximum or the accuracy of the solution reaches the requirement, the loop ends if the requirement is reached; otherwise, return to Step 4.
The flow chart of PGL-SSA is shown in Figure 3.
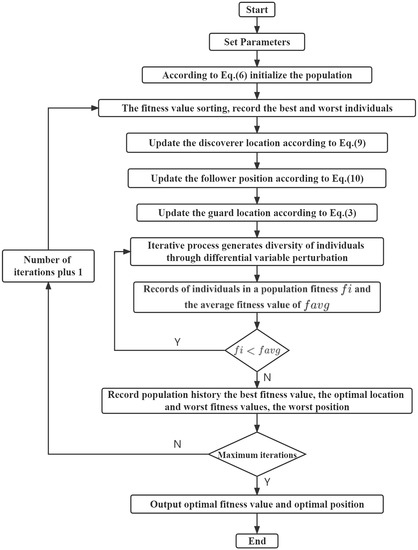
Figure 3.
Flow chart of PGL-SSA.
5. Simulation Experiments and Results Analysis
5.1. CEC Test Functions
In order to verify the feasibility of the algorithm in this paper, simulation tests are conducted by CEC benchmark functions. The CEC test functions [24,25] are shown in Table 1: F1–F5 are continuous single-peaked functions, which are used to test the convergence speed and accuracy of the algorithm, and F6–F11 are complex non-linear multi-peaked functions, which are used to test the global search ability and the ability to jump out of the local optimum. F12–F21 are fixed dimensional multi-peak test functions.

Table 1.
Test Functions.
5.2. Experimental Anvironment and Parameter Settings
The experimental platform is a PC with Win11 operating system, Intel(R) Core(TM) i7-8750H CPU@ 2.20 GHz, 8 GB RAM, PyCharm 2021.2.3 platform to simulate the algorithm in this paper.
The improved sparrow search algorithm (PGL-SSA) is compared with the original sparrow search algorithm (SSA), the particle swarm algorithm [26,27] (PSO), and the gray wolf optimization algorithm [28] (GWO). The population size , dimension , and the maximum number of iterations is 500. The parameters of each algorithm are set as Table 2.

Table 2.
Each algorithm parameter setting.
Due to the randomness of the algorithms, the four algorithms were run 30 times independently by the CEC benchmarking function to eliminate the chance error, and the experimental results of each algorithm are shown in Table 3 with the optimal values of each index bolded.

Table 3.
Results and comparison of different algorithms for 21 benchmark functions.
5.3. Comparative Analysis of Optimization Results
The experimental results show that PGL-SSA has good performance in finding the optimal results under the same conditions for both high-dimensional single-peak functions and high-dimensional multi-peak functions, and it shows good convergence accuracy and stability in 30 and 100 dimensions. In terms of mean and standard deviation, PGL-SSA has the best results for all tested functions, and in functions F1, F2, F3, and F4, PGL-SSA has improved the mean and standard deviation by several orders of magnitude compared with the comparison algorithm. In the index of optimal value, PGL-SSA has a significant advantage over PSO and GWO, and it also has a certain improvement over SSA. For functions F7 and F9, both PGL-SSA and SSA have good search performance, indicating that the algorithm itself has some superiority. For function F8, the algorithm is not applicable to function F8 due to its own limitation.
From the convergence curves in Figure 4 and Figure 5, PGL-SSA has the advantages of fast convergence speed and high convergence accuracy. The introduction of piecewise mapping in the initialization process of PGL-SSA effectively improves the population diversity of the algorithm, improves the quality of the initial solution, and lays the foundation for the global iterative optimization of the algorithm. The Gaussian difference variation strategy is introduced in the process of individual update, and the difference variation perturbation enables individuals to jump out of the local optimum effectively, which improves the algorithm’s optimization accuracy and ability to jump out of the local optimum. The introduction of linear differential decreasing inertia weights enables the algorithm to have good global search ability in the first iteration, and it improves the optimization accuracy in the second iteration. Under the same accuracy condition, PGL-SSA requires the least number of iterations and shorter time. The convergence curve of PGL-SSA is different from the flat curve of GWO and PSO due to the different optimization mechanism of the algorithm, and it shows a stepwise decrease, which indicates the advantage of PGL-SSA in moving away from local optimum.
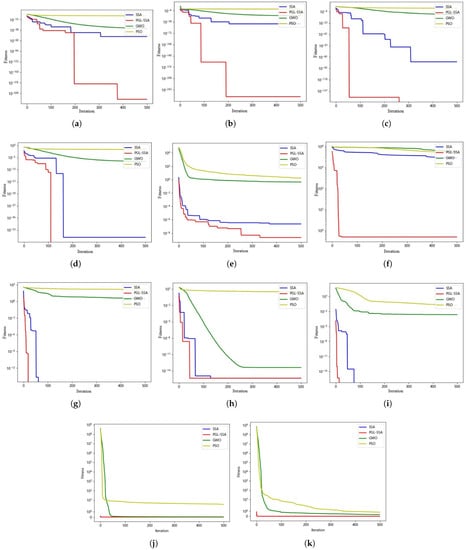
Figure 4.
Different algorithms convergence curves of F1–F11 with 30 dimensions. (a) F1 Convergence curve. (b) F2 Convergence curve. (c) F3 Convergence curve. (d) F4 Convergence curve. (e) F5 Convergence curve. (f) F6 Convergence curve. (g) F7 Convergence curve. (h) F8 Convergence curve. (i) F9 Convergence curve. (j) F10 Convergence curve. (k) F11 Convergence curve.
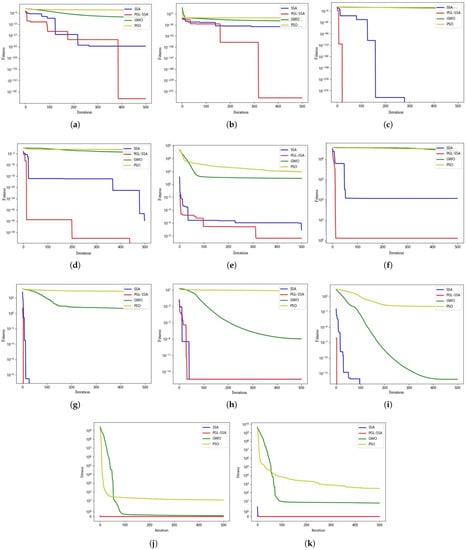
Figure 5.
Different algorithms convergence curves of F1–F11 with 100 dimensions. (a) F1 Convergence curve. (b) F2 Convergence curve. (c) F3 Convergence curve. (d) F4 Convergence curve. (e) F5 Convergence curve. (f) F6 Convergence curve. (g) F7 Convergence curve. (h) F8 Convergence curve. (i) F9 Convergence curve. (j) F10 Convergence curve. (k) F11 Convergence curve.
For the fixed-dimensional multi-peak functions F12–F21, from the convergence curves of each algorithm in Figure 6, it can be seen that PGL-SSA has a good comprehensive search performance. However, for the functions F15–F17, PGL-SSA’s search results are worse than GWO, ranking second. The PGL-SSA outperforms the SSA in all test functions in terms of finding the best results, which fully proves the effectiveness of the improvement strategy.
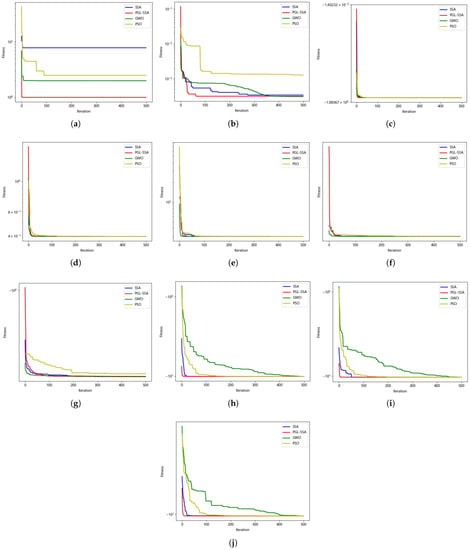
Figure 6.
Convergence curves of fixed-dimensional peak functions for different algorithms. (a) F12 Convergence curve. (b) F13 Convergence curve. (c) F14 Convergence curve. (d) F15 Convergence curve. (e) F16 Convergence curve. (f) F17 Convergence curve. (g) F18 Convergence curve. (h) F19 Convergence curve. (i) F20 Convergence curve. (j) F21 Convergence curve.
The comprehensive analysis shows that PGL-SSA outperforms other algorithms in the iterative search process for both high-dimensional single-peaked functions and high-dimensional multi-peaked functions. On the fixed-dimensional test function, the overall performance of PGL-SSA’s comprehensive merit-seeking ability is outstanding and has certain advantages. The 30- and 100-dimensional simulation results show that PGL-SSA can fully traverse the search space and precisely lock the optimal solution in the iterative search process, and its diversity improvement ensures excellent global search capability and the ability to jump out of the local optimum, reflecting the good searchability and stability that further determine the feasibility of its engineering applications.
5.4. Wilcoxon Rank-Sum Test
To further reflect the algorithm optimization performance, the P-values of the 21 benchmark test functions were analyzed using the Wilcoxon rank-sum test [29], and the four algorithms were run 30 times independently at a significant level of . The P-values of the rank-sum test for PGL-SSA and the other three compared algorithms are given in Table 4 (N/A means “not applicable”).

Table 4.
Wilcoxon rank sum test for the test function.
As can be seen from Table 4, compared with SSA, PGL-SSA’s search performance is significant for 18 test functions. Compared with GWO, the performance of PGL-SSA is significant on 14 test functions. In the fixed-dimensional test functions, the performance of PGL-SSA has a certain disadvantage compared with GWO due to the different algorithm-seeking mechanism. Compared with PSO, it is significant on 20 test functions and has an obvious advantage. In summary, it again shows the superiority of PGL-SSA in terms of the performance of the optimization search.
Figure 7 shows the comprehensive performance ranking of the four algorithms on the 21 tested functions. The smaller the curve area, the better the algorithm performance.
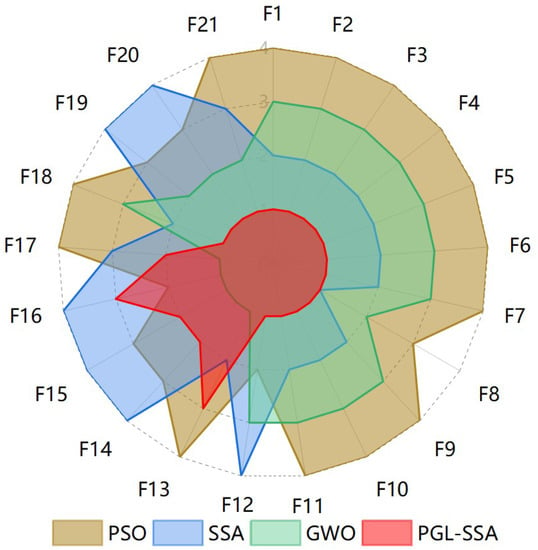
Figure 7.
Ranks of 4 algorithms.
5.5. Comparative Time Analysis
To further evaluate the performance of the improved algorithms, all algorithms were run 30 times independently on 21 test functions and the average running times were recorded. Figure 8 shows the average running time histogram of the four algorithms.
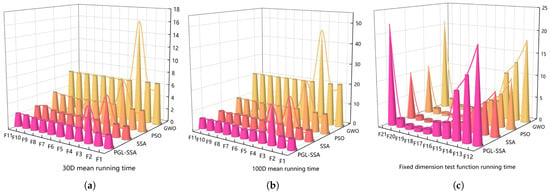
Figure 8.
Comparison of running time of different algorithms in each dimension. (a) 30D mean running time, (b) 100D mean running time, (c) Fixed dimension test function running time.
In terms of the running time of the high-dimensional single-peak function and the high-dimensional multi-peak function, PGL-SSA has obvious advantages over PSO and GWO, which reflects the good computational efficiency of the PGL-SSA optimization process to a certain extent. The improved strategy improves the performance of the algorithm without increasing the complexity of the algorithm. In terms of the running time of the fixed-dimensional test function, PGL-SSA has a significant increase in the running time of the algorithm compared with SSA due to the improved strategy of the optimization mechanism.
Overall, the results from the CEC benchmark test function show that the performance of PGL-SSA is significantly better than that of SSA. In the fixed-dimensional test function, PGL-SSA has a longer running time compared to SSA due to the optimization strategy. Compared with the other three algorithms, PGL-SSA improves the optimization accuracy by several orders of magnitude, which has obvious advantages. The superior performance and algorithmic feasibility of PGL-SSA are fully demonstrated.
5.6. Comparison of PGL-SSA with Different Improved SSA
To further verify the superiority of PGL-SSA, the test functions in Table 1 were compared with the improved sparrow search algorithms CLSSA, SFSSA, GCSSA, and CSSOA proposed in the References [2,3,4,20] for the optimization search experiments. The general conditions were based on the SSA parameter settings in Table 2, the sparrow population size was 50, the maximum number of iterations was 500, and each algorithm was run 30 times independently for each test function to obtain the search results, as shown in Table 5.

Table 5.
Results and comparison of different improved algorithms for 21 benchmark functions.
Figure 9 shows the comprehensive performance ranking of the SSA algorithm improved by different strategies on 21 test functions. The smaller the curve area, the better the algorithm performance.
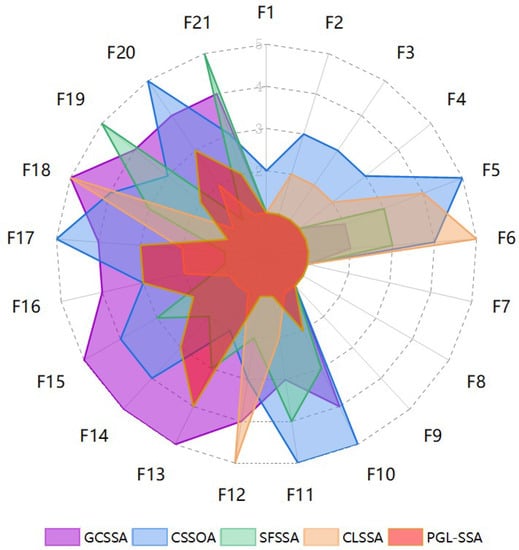
Figure 9.
Ranks of the SSA algorithm improved by different strategies.
Compared with other improvement algorithms, PGL-SSA proposes a more comprehensive fusion improvement strategy from three perspectives: population initialization, individual strategic position update, and global search ability balance. In the population initialization stage, PGL-SSA and CLSSA fully analyze the effects of different chaotic mapping initialized populations on the algorithm’s search performance. The strategy of initializing the population by piecewise mapping is finalized by testing the benchmark function on some chaotic mappings. In the process of individual iterative update, SFSSA uses a perturbation strategy for individual position update to obtain higher search accuracy. CSSOA uses a Gaussian variation strategy for individual position update, but the traditional Gaussian variation strategy increases the convergence speed of the algorithm while easily making the algorithm fall into local optimum. PGL-SSA uses a Gaussian difference variation strategy for individual perturbation, which enables the algorithm to obtain faster convergence speed while improving the ability of the algorithm to jump out of the local optimum. PGL-SSA proposes a linear differential decreasing inertia weighting strategy in balancing the global search ability and local search ability of the algorithm. By adjusting the weights in the early and late iterations of the algorithm, the algorithm can fully traverse the solution space in the early iterations while improving the convergence speed of the algorithm. The optimal solution is precisely locked in the late iteration to improve the algorithm operation efficiency.
From Table 5, among the 21 test functions, 13 of them can converge to the theoretical optimal solution and three are infinitely close to the optimal solution. Moreover, PGL-SSA has the best performance in 17 functions, which indicates that PGL-SSA has excellent overall optimization level and good accuracy in the 30 independent search. In terms of mean and standard deviation, PGL-SSA generally performs well, demonstrating high convergence accuracy and robustness.
From Figure 9, it can be seen that PGL-SSA ranks top in the overall ranking compared with other improved SSAs, which fully demonstrates the feasibility and superior performance of the PGL-SSA improvement strategy.
6. Application of PGL-SSA for HVAC Control
In the engineering field, most systems can be approximated as first-order inertial delay systems or second-order inertial delay systems [30,31]. Taking HVAC as an example, the HVAC indoor constant temperature system is modeled [32,33]. By the law of energy conservation, the rate of change of energy in the constant greenhouse is equal to the energy entering the constant greenhouse per unit time minus the energy exiting the constant greenhouse per unit time, and the mathematical model considering the enclosure structure and the transfer lag is:
where C is the constant room heat capacity; G is the air supply volume; c is the specific heat capacity of air; is the return air temperature; is the outdoor temperature; is the air supply temperature; is the indoor heat dissipation; and is the thermal resistance of the enclosure.
Collation formula:
Calculation of time constants for the constant temperature room:
Constant greenhouse thermal resistance:
Constant greenhouse magnification factor:
The amount of indoor and outdoor interference to convert the amount of air supply temperature change:
This leads to the mathematical model of the HVAC room thermostat system:
Laplace transform of Equation (17):
Therefore, the process control of the HVAC room thermostat system is a first-order inertial delay system with the transfer function:
6.1. Fitness Function
The fitness value is the only indicator to evaluate the merit of an individual or solution during the iterative process of the optimization algorithm, and it is used as the basis for updating the individual strategic position. The fitness function connects the optimization algorithm to the control system and allows the algorithm to evolve to reach the target value.
The PID control objective function using penalty control to avoid overshoot is as follows:
Among them: is the system error, is the controller output, , , are the weights, .
6.2. PID Parameter Tuning Simulation Experiment and Result Analysis
6.2.1. Optimal Tuning of PID Parameters for First-Order Inertia Delay Systems
The first-order inertial delay system transfer function is as follows:
The parameters were optimized by four algorithms, PGL-SSA, SSA, PSO and GWO, each with a population size of 50, a maximum number of iterations of 100, a unit step signal input, and a sampling time of 0.001 s. The optimized fitness curves and step response curves of the four algorithms are shown in Figure 10.
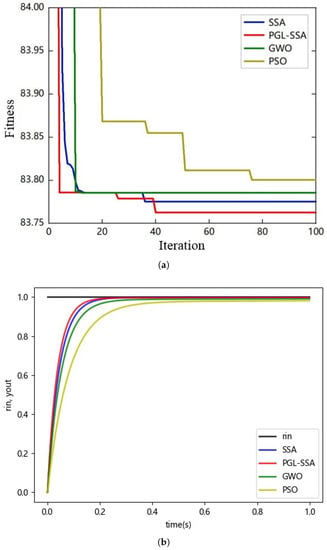
Figure 10.
Convergence curves and step response curves of different algorithms for first-order inertial delay systems. (a) Convergence curve. (b) Step response curve.
For the first-order inertial delay system, the PGL-SSA algorithm has a better finding accuracy as shown by the convergence curve of the adaptation degree. From the step response curves, it can be seen that the PSSA optimized system has a shorter adjustment time.
6.2.2. Optimal Tuning of PID Parameters for Second-Order Underdamped Delay Systems
The classical second-order time-delayed temperature control system transfer function is selected as follows:
The parameters were optimized by four algorithms, PGL-SSA, SSA, PSO and GWO, each with a population size of 50, a maximum number of iterations of 100, a unit step signal input, and a sampling time of 0.001 s. The optimized adaptation curves and step response curves of the four algorithms are shown in Figure 11.
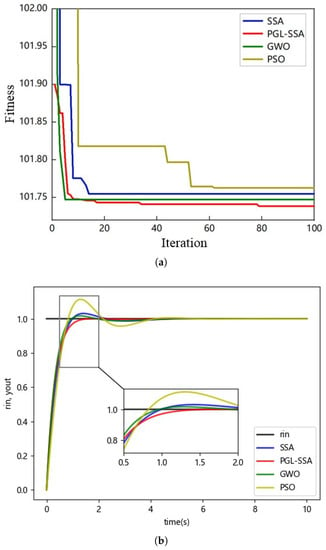
Figure 11.
Convergence curves and step response curves of different algorithms for second-order inertial delay systems. (a) Convergence curve. (b) step response curve.
The convergence curves and step response curves of the four algorithms can show that the PGL-SSA is more accurate than the other three algorithms for the second-order delay system. The overshoot and regulation time of the system adjusted by the PGL-SSA algorithm are better than those of the comparison algorithms, which proves the effectiveness of the PGL-SSA algorithm.
6.2.3. PMSM System PID Parameter Optimization
An inverter air conditioner has the characteristics of energy saving, high efficiency, low noise, stable temperature control, etc., and it has been rapidly developed in the field of HVAC [34]. Permanent Magnetic Synchronous Machine (PMSM) has the characteristics of fast dynamic response, high operating efficiency, safety and reliability, etc. [35]. Inverter air conditioners mostly use permanent magnet synchronous motors for inverter control. Traditional PID control is mostly used for permanent magnet synchronous motors, and the traditional PID controller parameter adjustment method is difficult to achieve fast and stable control effect for the increasingly complex control objects [36]. In this paper, the PID controller of a permanent magnet synchronous motor is parameterized by PGL-SSA. The mathematical model of PMSM established in the literature [37] is analyzed. The transfer function is selected as follows:
The four algorithms of PGL-SSA, SSA, PSO and GWO were used to optimize the parameters. The population size of each algorithm was 50, the maximum number of iterations was 100, the unit step signal was the input, and the sampling time was 0.001 s. The optimized adaptation curves and step response curves of the four algorithms are shown in Figure 12.
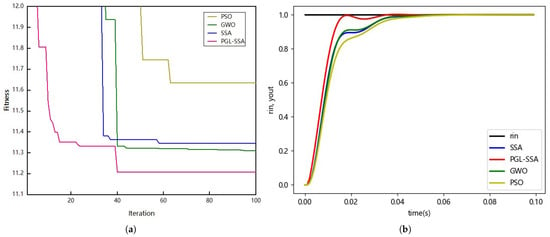
Figure 12.
Convergence curves and step response curves of different algorithms for PMSM systems. (a) Convergence curve. (b) Step response curve.
From the convergence curves of the different algorithms in Figure 12, we can see that the PGL-SSA algorithm has faster convergence speed and convergence accuracy than the comparison algorithms, which indicates that the PGL-SSA algorithm has better performance in finding the best performance. The step response curve shows that the error and the adjustment time of the PGL-SSA algorithm are smaller, which indicates that the PGL-SSA algorithm has better system stability.
7. Conclusions
In this paper, three strategies, piecewise mapping, Gaussian difference variation and linear differential decreasing inertia weights, are used to improve the basic SSA algorithm. Firstly, we analyze the effect of population initialization on the initial solution and the convergence speed of the algorithm, and we propose the population initialization of the sparrow search algorithm by piecewise mapping instead of pseudo-random numbers to improve the population diversity and the convergence speed and accuracy of the algorithm. Secondly, the individual position is updated by the Gaussian difference variation strategy, and the optimal individual is perturbed to improve the algorithm’s ability to jump out of the local optimum. In addition, the linear differential decreasing inertia weight strategy is used to solve the problem of balance between the early and late iterations of the algorithm, which enhances the global search ability of the algorithm in the early iteration, fully traverses the solution space to avoid the algorithm falling into local optimum, and accurately searches for the optimal solution in the late iteration to improve the convergence accuracy of the algorithm. In order to comprehensively evaluate the performance of the algorithm, 21 benchmark test functions are used for verification. The simulation results show that the hybrid improvement strategy proposed in this paper can effectively improve the performance of the algorithm. Compared with the basic metaheuristic algorithm and the advanced improvement algorithm, PGL-SSA has higher convergence accuracy and stability. In addition, PGL-SSA is applied to the direction of HVAC system control optimization, and the results show that PGL-SSA has higher control accuracy and robustness in the HVAC system control optimization problem. In future research, the group plans to further optimize the overall performance of PGL-SSA, improve the operation efficiency of the algorithm, and further consider applying the algorithm to more engineering fields, such as microgrid energy-scheduling problems.
Author Contributions
Strategy Algorithm Improvement and Application, X.L.; Overall Structure Guidance, X.W., Q.C., Y.B.; HVAC System Simulation, C.Y., H.Y., H.G. and J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Fundamental Research Fund Project of Hebei Provincial Department of Education (2021QNJS06) and the Youth Fund Project of Science and Technology Research Project of Hebei University (QN2021050).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xue, J.K.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Tang, A.D.; Zhou, H.; Han, T.; Xie, L. A Chaos Sparrow Search Algorithm with Logarithmic Spiral and Adaptive Step for Engineering Problems. Comput. Model. Eng. Sci. 2022, 130, 331–364. [Google Scholar] [CrossRef]
- Ren, X.Y.; Chen, S.; Wang, K.Y.; Tan, J. Design and application of improved sparrow search algorithm based on sine cosine and firefly perturbation. Math. Biosci. Eng. 2022, 19, 11422–11452. [Google Scholar] [CrossRef] [PubMed]
- Gao, C.F.; Chen, J.Q.; Shi, M.H. Multi-strategy sparrow search algorithm integrating golden sine and curve adaptive. Appl. Res. Comput. 2022, 39, 491–499. [Google Scholar]
- Gao, B.W.; Shen, W.; Guan, H.; Zheng, L.T.; Zhang, W. Research on Multistrategy Improved Evolutionary Sparrow Search Algorithm and its Application. IEEE Access 2022, 10, 62520–62534. [Google Scholar] [CrossRef]
- Pan, S.; Han, Y.; Wei, S.; Wei, Y.; Xia, L.; Xie, L.; Kong, X.; Yu, W. A model based on Gauss distribution for predicting window behavior in building. Build. Environ. 2019, 149, 210–219. [Google Scholar] [CrossRef]
- Wang, K.; Li, Z.B.; Cheng, H.; Zhang, K. Mutation Chicken Swarm Optimization Based on Nonlinear Inertia Weight. In Proceedings of the 3rd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 13–16 December 2017; pp. 2206–2211. [Google Scholar]
- Metzmacher, H.; Syndicus, M.; Warthmann, A.; van Treeck, C. Exploratory comparison of control algorithms and machine learning as regulators for a personalized climatization system. Energy Build. 2022, 255, 111653.1–111653.16. [Google Scholar] [CrossRef]
- Selamat, H.; Haniff, M.F.; Sharif, Z.M.; Attaran, S.M.; Sakri, F.M.; Razak, M.A.A. Review on HVAC System Optimization Towards Energy Saving Building Operation. Int. Energy J. 2020, 20, 345–357. [Google Scholar]
- Liao, G.C. Fusion of Improved Sparrow Search Algorithm and Long Short-Term Memory Neural Network Application in Load Forecasting. Energies 2021, 15, 130. [Google Scholar] [CrossRef]
- He, N.; Xi, K.; Zhang, M.; Li, S. A Novel Tuning Method for Predictive Control of VAV Air Conditioning System Based on Machine Learning and Improved PSO. J. Beijing Inst. Technol. 2022, 31, 350–361. [Google Scholar]
- Fayyaz, M.; Farhan, A.A.; Javed, A.R. Thermal Comfort Model for HVAC Buildings Using Machine Learning. Arab. J. Sci. Eng. 2022, 47, 2045–2060. [Google Scholar] [CrossRef]
- Yuan, X.L.; Pan, Y.Q.; Yang, J.R.; Wang, W.T.; Huang, Z.Z. Study on the application of reinforcement learning in the operation optimization of HVAC system. Build. Simul. 2021, 14, 75–87. [Google Scholar] [CrossRef]
- Puchta, E.D.P.; Bassetto, P.; Biuk, L.H.; Itaborahy, M.A.; Converti, A.; Kaster, M.D.; Siqueira, H.V. Swarm-Inspired Algorithms to Optimize a Nonlinear Gaussian Adaptive PID Controller. Energies 2021, 14, 3385. [Google Scholar] [CrossRef]
- Wang, M. HVAC Control System for Neural Network Optimization PID Controller. Mod. Electron. 2017, 40, 137–139, 143. [Google Scholar]
- He, S.Y.; Cao, Z.Q.; Yu, S.W. Optimization of PID Parameters Based on Flower Pollination Algorithm. Comput. Eng. Appl. 2016, 52, 59–62. [Google Scholar]
- Liu, W.Z.; An, D.; Xu, Y.; Shao, M.; Liu, Z.P.; Zou, D.F. Study on the Optimization of PID Parameters by Self-Polymerizing Moth Flame Optimization Algorithm. Mach. Tool Hydraul. 2021, 49, 24–28. [Google Scholar]
- Duan, S.M.; Luo, H.L.; Liu, H.P. Hybrid Algorithm of Population Search and Bottle Sea Sheath Group Optimizes PID Parameters. J. Syst. Simul. 2022, 34, 1230–1246. [Google Scholar]
- Kazimipour, B.; Li, X.D.; Qin, A.K. A Review of Population Initialization Techniques for Evolutionary Algorithms. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 2585–2592. [Google Scholar]
- Lv, X.; Mu, X.D.; Zhang, J.; Wang, Z. Chaos sparrow search optimization algorithm. J. Beijing Univ. Aeronaut. Astronaut. 2021, 47, 1712–1720. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CJFD&dbname=CJFDLAST2021&filename=BJHK202108024&uniplatform=NZKPT&v=VPpzCYKdySObbTY6_JlYuYqbd4mkg6i8M7MDATEvRlU26n4nq5mKeSlq3fpAm61m (accessed on 7 November 2022).
- Chen, L.; Yin, J.S. Whale swarm algorithm for Gaussian differential variation and logarithmic inertia weight optimization. Comput. Eng. Appl. 2021, 57, 77–90. [Google Scholar]
- Nagra, A.A.; Han, F.; Ling, Q.H. An improved hybrid self-inertia weight adaptive particle swarm optimization algorithm with local search. Eng. Optim. 2019, 51, 1115–1132. [Google Scholar] [CrossRef]
- Bai, Y.; Peng, Z.R. Bottle Sea Sheath Swarm Algorithm Based on Adaptive Inertia Weight. Control Decis. 2022, 37, 237–246. [Google Scholar]
- Shi, H.Q.; Hou, Q.; Xu, Z.; Li, K. Application Analysis of Optimization Algorithm Test Functions. Comput. Sci. Appl. 2021, 11, 2633–2645. [Google Scholar]
- Saeed, S.; Ong, H.C.; Sathasivam, S. Self-Adaptive Single Objective Hybrid Algorithm for Unconstrained and Constrained Test functions: An Application of Optimization Algorithm. Arab. J. Sci. Eng. 2019, 44, 3497–3513. [Google Scholar] [CrossRef]
- Cruz, L.M.; David, L.; Sumaiti, A.A.; Rivera, S. Load Curtailment Optimization Using the PSO Algorithm for Enhancing the Reliability of Distribution Networks. Energies 2020, 13, 3236. [Google Scholar] [CrossRef]
- Guo, J.X.; Lu, Y.J.; Li, Z.H. PID parameter tuning algorithm of rotor UAV Based on Improved Particle Swarm Optimization. In Proceedings of the 2022 IEEE 6th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 4–6 March 2022; pp. 1251–1255. [Google Scholar]
- Zhang, Z.; Rao, S.H.; Zhang, S.J. Gray Wolf Optimization Algorithm Based on Adaptive Normal Cloud Model. Control Decis. 2021, 36, 2562–2568. [Google Scholar]
- Derrac, J.; Garcia, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Kvascev, G.S.; Djurovic, Z.M. Water Level Control in the Thermal Power Plant Steam Separator Based on New PID Tuning Method for Integrating Processes. Energies 2022, 15, 6310. [Google Scholar] [CrossRef]
- Ozdemir, M.T.; Ozturk, D. Water Comparative Performance Analysis of Optimal PID Parameters Tuning Based on the Optics Inspired Optimization Methods for Automatic Generation Control. Energies 2017, 10, 2134. [Google Scholar] [CrossRef]
- Zhan, J.Y.; Zhang, Z.Z.; He, Y.Z. Modeling and simulation of building air conditioning system. Heat. Vent. Air Cond. 2021, 51, 271–275. [Google Scholar]
- Alipouri, Y.; Zhong, L.X. Multi-Model Identification of HVAC System. Appl. Sci. 2021, 11, 668. [Google Scholar] [CrossRef]
- Hui, H.X.; Ding, Y.; Chen, T.; Rahman, S.; Song, Y. Dynamic and Stability Analysis of the Power System With the Control Loop of Inverter Air Conditioners. IEEE Trans. Ind. Electron. 2020, 68, 2725–2736. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, C.; Zhang, L.; Wang, C. Multiobjective Optimization of PID Controller of PMSM. J. Control Sci. Eng. 2014, 2014, 471609. [Google Scholar] [CrossRef]
- Soundirarrajan, N.; Srinivasan, K. Performance Evaluation of Ant Lion Optimizer-Based PID Controller for Speed Control of PMSM. J. Test. Eval. 2019, 49, 1104–1118. [Google Scholar] [CrossRef]
- Gao, F.; Yu, L. Study on PID parameter optimization of PMSM drive system based on SOA. J. Hebei Univ. Technol. 2018, 47, 19–24, 31. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CJFD&dbname=CJFDLAST2018&filename=HBGB201801003&uniplatform=NZKPT&v=wgwYWMsY1TgzIAt1z5ErdR0uj-4rysj8G3GZ8w2D_H6tt0Edb0QduT_luii8oxeH (accessed on 7 November 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).