The Binomial–Natural Discrete Lindley Distribution: Properties and Application to Count Data

Abstract

In this paper, a new discrete distribution called Binomial–Natural Discrete Lindley distribution is proposed by compounding the binomial and natural discrete Lindley distributions. Some properties of the distribution are discussed including the moment-generating function, moments and hazard rate function. Estimation of the distribution’s parameter is studied by methods of moments, proportions and maximum likelihood. A simulation study is performed to compare the performance of the different estimates in terms of bias and mean square error. SO₂ data applications are also presented to see that the new distribution is useful in modeling data.

1. Introduction

Count data modeling is a challenging task in many areas, including, but not limited to, public health, medicine, epidemiology, applied science, sociology, and agriculture. In many situations, the life length of a device cannot be measured on a continuous scale and the survival function is assumed to be a function of a count random variable instead of being a function of a continuous-time random variable. Therefore, discrete distributions are somewhat meaningful to model lifetime data in situations where output may be of a discrete nature. The traditional discrete distributions have limited applicability as models for reliability, failure times, aggregate loss, etc., especially with the count data with over-dispersion in which the variance is greater than the mean. This has led to the development of some discrete distributions based on popular continuous models in reliability analysis, actuarial sciences survival analysis, etc. The discretization of continuous distributions has produced many discrete distributions in the last few decades in the statistical literature. However, the quest for a quintessential model remains the crux of the matter in the diverse scientific paradigm.

One of the many approaches to define new models is the discretization of distributions. Until recently, the majority of discrete lifetime distributions have been proposed in the statistical literature by discretizing the survival function $S\left(x\right)$ of continuous lifetime distributions (see the work of authors, for example, in references [1,2,3,4,5,6,7,8,9,10,11,12]).

The probability mass function (pmf) $P\left(X=x\right)$ is defined as follows

$$P\left(X=x\right)=S\left(x\right)-S\left(x+1\right) x=0, 1, 2, \dots$$

Away from this method, Afify [12] have introduced and studied a new discrete Lindley distribution by constructing a mixture of discrete analogs to the continuous components used in creating the continuous Lindley distribution.

In this paper, we propose and study a new probability mass function (pmf), denoted by $p_x$, by compounding the binomial and the NDL distributions. The basic principle of this method is stated as if $N$(input) and $X$(output) are two random variables denoting the number of particles entering and leaving an attenuator, then the probability functions $p\left(n\right)$ and $f\left(x\right)$ of these two random variables are connected by the binomial decay transformation

$$P\left(X=x\right)={\displaystyle \sum }_{n=x}^{\infty }\left(\begin{array}{c}n\\ x\end{array}\right)p^x{\left(1-p\right)}^{n-x}p\left(n\right); x=0,1,\dots , \infty$$

(1)

where $0\le p\le 1$ is the attenuating coefficient which is discussed by Hu et al. [7]. They considered $p\left(n\right)$ as a Poisson distribution with the parameter $\lambda >0$, and then they showed that $\mathrm{Pr}\left(X=x\right)$ is the Poisson distribution with the parameter $\lambda p$. For clarity, attenuators are electrical devices built to lower the amount of voltage flowing through them without severely compromising the signal’s integrity. They serve as a safeguard against systems being exposed to signals with power levels that are too high to be decoded. Déniz [13] introduced uniform Poisson distribution using the idea of Hu et al. [7] by interchanging in Equation (1) the binomial distribution and the discrete uniform distribution and maintaining $P\left(n\right)$ as the Poisson distribution. Some new discrete distributions also are proposed in the literature using the methodology of [7]. Akdoğan et al. [14] proposed uniform-geometric distribution and Coşkun et al. [15] constructed binomial–discrete Lindley distribution.

The rest of the paper is arranged as follows: Section 2 defines the natural discrete Lindley distribution and proposes the new binomial–natural discrete Lindley distribution with important properties, subsequently. In Section 3, various parameter estimation and simulation studies are given. Section 4 concerns the real data illustration of the findings. In Section 5, some conclusions are provided.

2. Natural Discrete Lindley Distribution

Recently, Al-Babtain et al. [16] proposed and studied a new natural discrete analog of the continuous Lindley distribution as a mixture of geometric and negative binomial distributions. The new distribution is called natural discrete Lindley (NDL) distribution and it has many interesting properties that make it superior to many other discrete distributions, particularly in analyzing over-dispersed count data. The NDL can be applied in the collective risk models and is competitive with the Poisson distribution to fit automobile-claim-frequency data. Let $N$ be a non-negative random variable obtained as a finite mixture of geometric ($p$) and negative binomial (2, $p$) with mixing probabilities $\frac{p}{p+1}$ and $\frac{1}{p+1}$, respectively, then the probability mass function of the NDL distribution is defined as

$$P\left(N=n\right)=\frac{p^2}{p+1}\left(2+n\right){\left(1-p\right)}^n ; n=0,1,2,\dots \mathrm{and} p\in \left(0,1\right)$$

(2)

One of the most important features of this distribution is that it has a single parameter and it has attractive properties, which makes it suitable for applications not only in insurance settings but also in other fields where over-dispersions are observed. For more details about this distribution, see Al-Babtain et al. [16]. Given the usefulness of NDL, the discrete analogue due to NDL known as the binomial NDL (BNDL) seems to be naturally interesting to explore.

2.1. The Proposed Discrete Analog

The probability mass function (1) can be expressed as

$$P\left(X=x\right)={\displaystyle \sum }_{n=x}^{\infty }P\left(X=x|N=n\right)P\left(N=n\right),$$

where $P\left(X|N=n\right)$ has the binomial $b\left(n,p\right)$ distribution. Suppose that $N$ is the random variable from NDL with parameter $p$ given in (2); then, the probability mass function of the discrete random variable $X$ is obtained as

$$\begin{array}{l}{p}_x\left(x;p\right)=P\left(X=x\right)={\displaystyle {\displaystyle \sum }_{n=x}^{\infty }}P\left(X=x|N=n\right)P\left(N=n\right)={\displaystyle {\displaystyle \sum }_{n=x}^{\infty }}\left(\begin{array}{c}n\\ x\end{array}\right)p^x{\left(1-p\right)}^{n-x}\frac{p^2}{p+1}\left(2+n\right){\left(1-p\right)}^n\\ ={\displaystyle {\displaystyle \sum }_{n-x=0}^{\infty }}\left(\begin{array}{c}n\\ x\end{array}\right)p^x{\left(1-p\right)}^{n-x}\frac{p^2}{p+1}\left(2+n\right){\left(1-p\right)}^n={\displaystyle {\displaystyle \sum }_{k=0}^{\infty }}\left(\begin{array}{c}x+k\\ x\end{array}\right)p^x{\left(1-p\right)}^k\frac{p^2}{p+1}\left(2+x+k\right){\left(1-p\right)}^{x+k}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{p^2}{p+1}{\displaystyle {\displaystyle \sum }_{k=0}^{\infty }}\left(\begin{array}{c}x+k\\ x\end{array}\right)p^x\left(2+x+k\right){\left(1-p\right)}^{x+2k}=\frac{{\left(1-p\right)}^x\left(1+x+2p-p^2\right)}{\left(p+1\right){\left(2-p\right)}^{x+2}}; x\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=0,1,2\dots \mathrm{and} p\in \left(0,1\right)\end{array}$$

(3)

If $X$ has the pmf (3), then it is called a binomial natural discrete Lindley (BNDL) random variable and it is denoted by $X~\mathrm{BNDL}\left(p\right).$ For $n=0$, this means that no particles enter into the attenuator and it will be termed as failure. Consequently, the corresponding cumulative distribution function (cdf) of BNDL distribution is given by

$$F\left(x;p\right)=P\left(X\le x\right)={\displaystyle \sum }_{t=0}^x{p}_x\left(t\right)={\displaystyle \sum }_{t=0}^x\frac{{\left(1-p\right)}^t\left(1+t+2p-p^2\right)}{\left(p+1\right){\left(2-p\right)}^{t+2}}=1-\frac{{\left(1-p\right)}^{x+1}\left(3+x+p-p^2\right)}{\left(p+1\right){\left(2-p\right)}^{x+2}}.$$

(4)

Figure 1 shows the probability mass function (pmf) plots of the proposed distribution for various values of parameter p. Thus, the pmf is always a decreasing function, and the new discrete random variable tends to take small values when p increases. The stochastic process tends to happen very quickly once the parameter value grows, which is implied quite strongly by the model’s behavior. Therefore, the BNDL model is a logical substitute for the traditional exponential distribution to characterize such phenomena. Additionally, the flexibility of the proposed BNDL can be tested for varied count data sources. For example, this model may be helpful for simulating aggregate losses that are typically limited to actuarial data by maximizing the overall garment fit for a particular number of sizes and accommodation rate, crucial to assessing the goodness of the scaling system. Furthermore, it may be helpful to overcome the problem of over-dispersed data in social sciences, as in anthropology where civilizations grew near the existence of a consistent water source, which is necessary for human survival. Figure 2 complements the results of Figure 1.

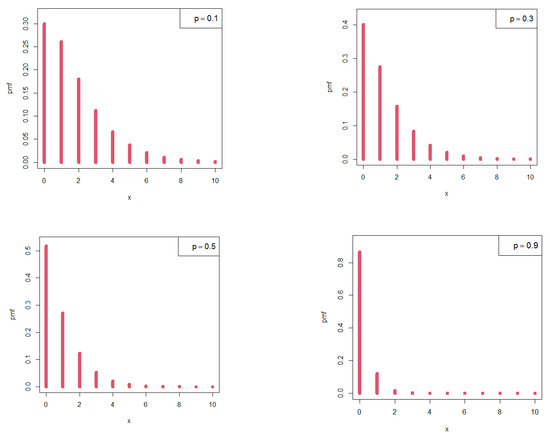
Figure 1. Pmf of BNDL distribution for some choices of p.

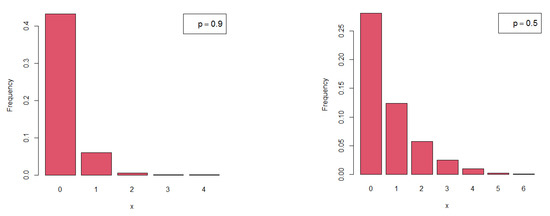
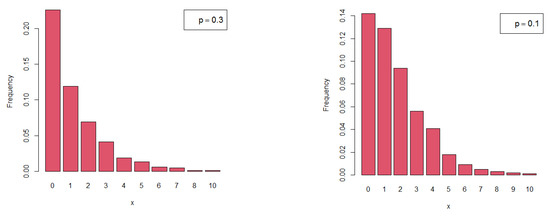
Figure 2. Histograms of the BNDL model for simulated data.

2.2. Statistical Properties of the BNDL Distribution

Primarily in this section, we provide some explicit results based on the mathematical properties of the BNDL distribution.

2.2.1. Moment-Generating Function

If $X~\mathrm{BNDL}\left(p\right)$ distribution, then the moment-generating function of $X$ is given as

$$M_X\left(t\right)=E\left(e^{tX}\right)={\displaystyle \sum }_{x=0}^{\infty }{e}^{tx}\frac{{\left(1-p\right)}^x\left(1+x+2p-p^2\right)}{\left(p+1\right){\left(2-p\right)}^{x+2}}=\frac{1-p\left(e^t-2\right)+p^2\left(e^t-1\right)}{{\left(2-e^t+p{e}^t-p\right)}^2\left(p+1\right)}.$$

For more on generating functions, see Yalcin and Simsek [17], Yalcin and Simsek [18] and Simsek [19].

2.2.2. Probability-Generating Function

The probability-generating function of the random variable $X~\mathrm{BNDL}\left(p\right)$ can be obtained using its moment-generating function which is equivalent to calculating $E\left(t^X\right)$; therefore, the probability-generating function of the random variable $X$ is

$$G_X\left(t\right)=E\left(t^X\right)=M_X\left(log\left(t\right)\right)=\frac{1-p\left(t-2\right)+p^2\left(t-1\right)}{{\left(2-t+p\left(t-1\right)\right)}^2\left(p+1\right)}.$$

Since,

$$G_X^{\left(k\right)}\left(t\right)=\frac{d^k{G}_X\left(t\right)}{d{t}^k}=E\left\{X\left(X-1\right)\left(X-2\right)\dots \left(X-k+1\right)t^{X-k}\right\}.$$

Therefore, at $t=1$, we can obatin

$$G_X^{\left(k\right)}\left(1\right)={\frac{d^k{G}_X\left(t\right)}{d{t}^k}|}_{t=1}=E\left\{X\left(X-1\right)\left(X-2\right)\dots \left(X-k+1\right)\right\},$$

where ${\mu }_{\left(k\right)}=E\left\{X\left(X-1\right)\left(X-2\right)\dots \left(X-k+1\right)\right\}$ is the $k$th factorial moment of $X$.

2.2.3. Non-Central Moments and Variance

If $X~\mathrm{BNDL}\left(p\right)$ distribution, then the kth moment about zero of X is given by

$${\mu }_k^{\prime }=E\left(X^r\right)={\displaystyle \sum }_{x=0}^{\infty }{x}^k{p}_x={\displaystyle \sum }_{x=0}^{\infty }{x}^k\frac{{\left(1-p\right)}^x\left(1+x+2p-p^2\right)}{\left(p+1\right){\left(2-p\right)}^{x+2}}.$$

The first four raw moments can be obtained as follows

$${\mu }_1^{\prime }=E\left(X\right)=\frac{\left(p+2\right)\left(1-p\right)}{p+1},$$

$${\mu }_2^{\prime }=E\left(X^2\right)=\frac{\left(1-p\right)\left(8-3p-2p^2\right)}{p+1},$$

$${\mu }_3^{\prime }=E\left(X^3\right)=\frac{\left(1-p\right)\left(44-53p+6p^2+6p^3\right)}{p+1},$$

and

$${\mu }_4^{\prime }=E\left(X^4\right)=\frac{\left(1-p\right)\left(308-516p+346p^2-12p^3-24p^4\right)}{p+1}.$$

The variance in the random variable $X$ is

$$Var\left(X\right)=E\left(X^2\right)-{\left[E\left(X\right)\right]}^2=\frac{\left(1-p\right)\left(4+5p-2p^2-p^3\right)}{{\left(p+1\right)}^2}.$$

2.2.4. Central Moments

The kth moment about the mean of X is

$${\mu }_r=E\left[{\left(X-{\mu }_1^{\prime }\right)}^k\right]={\displaystyle \sum }_{x=0}^{\infty }{\left(x-{\mu }_1^{\prime }\right)}^k{p}_x\left(x\right)={\displaystyle \sum }_{x=0}^{\infty }{\left(x-{\mu }_1^{\prime }\right)}^k\frac{{\left(1-p\right)}^x\left(1+x+2p-p^2\right)}{\left(p+1\right){\left(2-p\right)}^{x+2}}.$$

Therefore, the second, third and fourth central moments of the random variable $X$ are

$${\mu }_2=\frac{\left(1-p\right)\left(4+5p-2p^2-p^3\right)}{{\left(p+1\right)}^2},$$

$${\mu }_3=\frac{\left(1-p\right)\left(12+21p-7p^2-21p^3+5p^4+2p^5\right)}{{\left(p+1\right)}^3},$$

and

$${\mu }_4=\frac{\left(1-p\right)\left(100+181p-132p^2-285p^3+50p^4+137p^5-27p^6-9p^7\right)}{{\left(p+1\right)}^4}$$

2.2.5. Skewness and Kurtosis

The coefficient of skewness and the coefficient of kurtosis of the of BNDL distribution are, respectively,

$${\beta }_1=\frac{{\mu }_3}{\sqrt{{\mu }_2{}^3}}=\frac{\left(1-p\right)\left(12+21p-7p^2-21p^3+5p^4+2p^5\right)}{{\left(4+p-7p^2+p^3+p^4\right)}^{3/2}}.$$

$${\beta }_2=\frac{{\mu }_4}{{\mu }_2{}^2}=\frac{100+181p-132p^2-285p^3+50p^4+137p^5-27p^6-9p^7}{\left(1-p\right){\left(4+5p-2p^2-p^3\right)}^2}.$$

2.2.6. Index of Dispersion

The index of dispersion (ID) indicates whether a certain distribution is suitable for under- or over-dispersed datasets. For example, $\mathrm{ID}=1$ for the Poisson distribution where the variance is equal to the mean, for the geometric distribution and the negative binomial distribution $\mathrm{ID}>1$, while the binomial distribution has $\mathrm{ID}<1$.

Theorem 1.

If $X~BNDL\left(p\right)$, then $Var\left(X\right)>E\left(X\right)$ for all $p\in \left(0,1\right).$

Proof. 

We have

$$\mathrm{ID}\left(X\right)=\frac{Var\left(X\right)}{E\left(X\right)}=\frac{4+5p-2p^2-p^3}{p^2+3p+2}.$$

This function is a monotonic decreasing function as $p\in \left(0,1\right)$ increases. It converges to 2 when $p\to 0$, while it tends to 1 as $p\to 1$; therefore, $\mathrm{ID}\left(X\right)\in \left(1,2\right)$, which means that $\mathrm{ID}\left(X\right)>1$, and hence, $Var\left(X\right)>E\left(X\right)$. □

From Theorem 1, BNDL distribution should only be used in the count data analysis with over-dispersion. In Table 1, some of the empirical findings of these measured are due for considerations.

Table 1. Mean, Variance, Skewness, kurtosis and ID of the BNDL distribution for different values of the parameter p.

p	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
Mean	1.71818	1.4666	1.2384	1.0285	0.8333	0.6500	0.4764	0.3111	0.1526
Variance	3.3314	2.7288	2.1923	1.7191	1.3055	0.9475	0.6412	0.3832	0.1703
Skewness	1.5578	1.6186	1.6831	1.7542	1.8372	1.9427	2.0935	2.3522	2.9813
Kurtosis	7.7069	9.4991	11.8378	15.0902	19.9488	27.8656	42.3746	74.4447	180.1786
ID	1.9389	1.8606	1.770268	1.6714	1.5666	1.4576	1.3459	1.2317	1.1159

2.2.7. Log-Concavity

A necessary and sufficient condition that $p_x$ be strongly unimodal is that it has to be log-concave, i.e., $p_{x+1}^2\ge p_x{p}_{x+2}$ for all $x$ (see Keilson and Gerber [20])).

Theorem 2.

The pmf of the BNDL distribution in (3) is log-concave.

Proof. 

From (3), we can directly reach

$$p_{x+1}^2=\frac{{\left(1-p\right)}^{2x+2}{\left(2+x+2p-p^2\right)}^2}{{\left(p+1\right)}^2{\left(2-p\right)}^{2x+6}},$$

and

$$p_x{p}_{x+2}=\frac{{\left(1-p\right)}^{2x+2}\left(1+x+2p-p^2\right)\left(3+x+2p-p^2\right)}{{\left(p+1\right)}^2{\left(2-p\right)}^{2x+6}}.$$

After some algebraic operations, we find that

$$p_{x+1}^2-p_x{p}_{x+2}=\frac{{\left(1-p\right)}^{2x+2}}{{\left(p+1\right)}^2{\left(2-p\right)}^{2x+6}}>0,$$

for all $x$ and for all choices $p\in \left(0,1\right)$.

Theorem 2 confirms that the BNDL distribution is strongly unimodal. □

2.3. Reliability Properties of the BNDL Distribution

2.3.1. Survival Function

If $X~\mathrm{BNDL}\left(p\right)$ distribution, then from (4), the survival function of $X$ is

$$S\left(x;p\right)=P\left(X\ge x\right)=\frac{{\left(1-p\right)}^{x+1}\left(3+x+p-p^2\right)}{\left(p+1\right){\left(2-p\right)}^{x+2}}.$$

2.3.2. Hazard Rate and Mean Residual Life Functions

The hazard (failure) rate function is the probability that an item has survived time $x$, given that it has survived to at least time $x$. If $X~\mathrm{BNDL}\left(p\right)$ distribution, then its hazard rate (failure rate) function is given as

$$r\left(x;p\right)=P\left(X=x|X>x\right)=\frac{p_x\left(x;p\right)}{S\left(x;p\right)}=\frac{1+x+2p-p^2}{\left(1-p\right)\left(3+x+p-p^2\right)}.$$

Obviously, the upper limit of the failure rate function is $\frac{1}{1-p}$, i.e., $\underset{x\to \infty }{\lim }r\left(x;p\right)=\frac{1}{1-p}$. Graphical illustrations of hazard rate function are presented in Figure 3 while descriptive measures are presented in Figure 4.

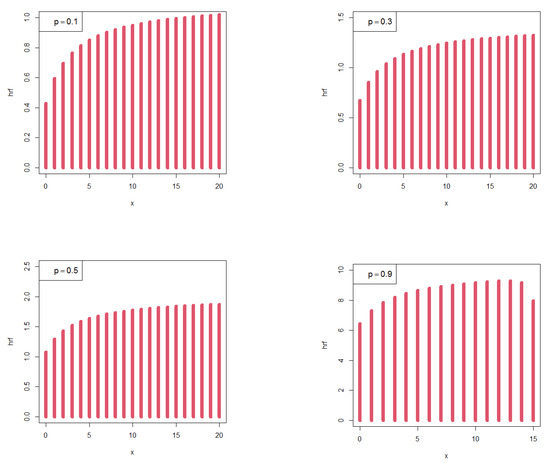
Figure 3. Plots of hazard rate of BNDL distribution for some choices of p.

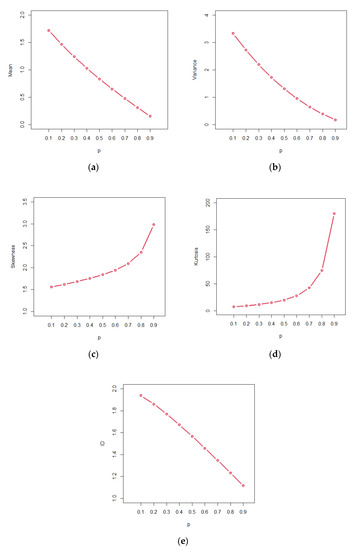
Figure 4. Plots of the BNDL model for (a) Mean, (b) Variance, (c) Skewness, (d) Kurtosis and (e) ID.

The mean residual life function of $X$ is given by

$$m\left(x;p\right)=P\left(X-x|X>x\right)=\frac{{{\displaystyle \sum }}_{t=x+1}^{\infty }S\left(t;p\right)}{S\left(x;p\right)}=\frac{\left(p-1\right)\left(p^2-x-5\right)}{3+p-p^2+x}.$$

Corollary 1.

If $X~BNDL\left(p\right)$ distribution, then it has an increasing failure rate and decreasing mean residual life.

As we explained through Theorem 2, the BNDL distribution has a property of log-concavity; therefore, according to Gupta et al. [21], the BNDL distribution has an IFR property. According to Kemp [22], the next chain is verified

$$\mathrm{IFR}\Rightarrow \mathrm{IFRA}\Rightarrow \mathrm{NBU}\Rightarrow \mathrm{NBUE}\Rightarrow \mathrm{DMRL}.$$

So, the BNDL distribution is

• IFR (increasing failure rate).
• IFRA(increasing failure rate average).
• NBU (new better than used).
• NBUE(new better than used in expectation).
• DMRL (decreasing mean residual lifetime).

2.4. Stochastic Orderings

Stochastic orders are important measures to judge comparative behaviors of random variables. Shaked and Shanthikumar [8] showed that many stochastic orders exist and have various applications. Given two random variables $X$ and $Y,$ we say that $X$ is smaller than $Y$ in the

• Usual stochastic order, denoted by $X{\le }_{st}Y$, if $F_X\left(x\right)\ge F_Y\left(x\right)$, for all $x$.
• Hazard rate order, denoted by $X{\le }_{hr}Y$, if $h_X\left(x\right)\ge h_Y\left(x\right)$, for all $x$.
• Reversed hazard rate order, denoted by $X{\le }_{rh}Y$, if $F_X\left(x\right)/F_Y\left(x\right)$ decreases in $x$.
• Mean residual life order, denoted by $X{\le }_{mrl}Y$, if $m_X\left(x\right)\le m_Y\left(x\right)$, for all x.
• Likelihood ratio order, denoted by $X{\le }_{lr}Y$, if $f_X\left(x\right)/f_Y\left(x\right)$ decreases in $x$.

For all the previous orders, we have the following chains of implications:

$$X{\le }_{lr}Y\Rightarrow X{\le }_{hr}Y\Rightarrow X{\le }_{st}Y,$$

and

$$X{\le }_{lr}Y\Rightarrow X{\le }_{rh}Y\Rightarrow X{\le }_{st}Y$$

also,

$$X{\le }_{hr}Y\Rightarrow X{\le }_{mrl}Y.$$

Theorem 3.

Let $X~BNDL\left(p_1\right)$ and $Y~BNDL\left(p_2\right)$; then, $X{\le }_{lr}Y$ for all $p_1>p_2.$

Proof. 

Let

$$L\left(x;p_1,p_2\right)=\frac{p_X\left(x;p_1\right)}{p_Y\left(x;p_2\right)}.$$

Now,

$$L\left(x;p_1,p_2\right)=\frac{\left(p_2+1\right){\left(2-p_2\right)}^{x+2}{\left(1-p_1\right)}^x\left(1+x+2p_1-p_1^2\right)}{\left(p_1+1\right){\left(2-p_1\right)}^{x+2}{\left(1-p_2\right)}^x\left(1+x+2p_2-p_2^2\right)},$$

and

$$L\left(x+1; p_1,p_2\right)=\frac{\left(p_2+1\right){\left(2-p_2\right)}^{x+3}{\left(1-p_1\right)}^{x+1}\left(2+x+2p_1-p_1^2\right)}{\left(p_1+1\right){\left(2-p_1\right)}^{x+3}{\left(1-p_2\right)}^{x+1}\left(2+x+2p_2-p_2^2\right)}.$$

Therefore,

$$\frac{L\left(x+1; p_1,p_2\right)}{L\left(x;p_1,p_2\right)}=\frac{\left(2-p_2\right)\left(1-p_1\right)\left(2+x+2p_1-p_1^2\right)\left(1+x+2p_2-p_2^2\right)}{\left(2-p_1\right)\left(1-p_2\right)\left(2+x+2p_2-p_2^2\right)\left(1+x+2p_1-p_1^2\right)}$$

(5)

Let $p_1=1-\delta$ and $p_2=1-\delta -\epsilon$, where $0<\delta <1$ and $0<\epsilon <1-\delta .$

After substitution of the values $p_1$ and $p_2$ in (5), we obtain

$$\frac{L\left(x+1; p_1,p_2\right)}{L\left(x;p_1,p_2\right)}=\frac{{\eta }_1\left(\delta +{\delta }^2+\delta \epsilon \right)}{{\eta }_2\left(\delta +\delta \epsilon +{\delta }^2+\epsilon \right)},$$

where

$${\eta }_1=\left(3+x-{\delta }^2\right)\left(2+x-{\left(\delta +\epsilon \right)}^2\right),$$

and

$${\eta }_2=\left(3+x-{\left(\delta +\epsilon \right)}^2\right)\left(2+x-{\left(\delta \right)}^2\right).$$

After some algebraic operations, we find that

$${\eta }_1-{\eta }_2=-\epsilon \left(2\delta +\epsilon \right)<0\Rightarrow {\eta }_1<{\eta }_2.$$

Therefore,

$${\eta }_1\left(\delta +{\delta }^2+\delta \epsilon \right)<{\eta }_2\left(\delta +\delta \epsilon +{\delta }^2+\epsilon \right).$$

This implies that

$$\frac{L\left(x+1; p_1,p_2\right)}{L\left(x;p_1,p_2\right)}<1\Rightarrow L\left(x+1; p_1,p_2\right)<L\left(x;p_1,p_2\right).$$

□

2.5. Entropy

Entropy is a measure of uncertainty of a random variable. The entropy of a discrete random variable $X$ with pmf $p\left(x\right)$ and alphabet $\mathcal{X}$ is given by

$$ℍ\left(X\right)=-E(logp\left(X\right))=-{\displaystyle \sum }_{x\in \mathcal{X}} p\left(x\right)log\left(p\left(x\right)\right).$$

Entropy can be interpreted as the measure of average uncertainty in $X$ or the average number of bits needed to describe $X$. For more details on entropy and information theory, we refer the reader to Gray [23].

Now, if $X~\mathrm{BNDL}\left(p\right)$, then the entropy of the random variable $X$ can be calculated by the following formula

$$ℍ\left(X\right)=\frac{1}{{\left(2-p\right)}^2\left(1+p\right)}\left\{{\left(2-p\right)}^2\left[\left(-2+p+p^2\right)log\left(1-p\right)+\left(4+p-p^2\right)log\left(2-p\right)+\left(1+p\right)log\left(1+p\right)\right]+\mathrm{LerchPhi}{ }^{\left(0,1,0\right)}\left[\frac{1-p}{2-p},-1,1+2p-p^2\right]\right\},$$

where ${\mathrm{LerchPhi}}^{\left(0,1,0\right)}\left[z,s,a\right]$ gives the Lerch transcendent $\Phi \left(z,s,a\right)={\displaystyle \sum }_{k=0}^{\infty }\frac{z^k}{{\left(a+k\right)}^s}$. Table 2 presents some numerical values of the entropy of $X~\mathrm{BNDL}\left(p\right)$ for different choices of $p$. From Table 2, one can observe that $ℍ\left(X\right)$ is monotonically decreasing in $p\in \left(0,1\right)$ with its limits tending to be 1.88 as $p$ tends to 0 as $p\to 1.$

Table 2. Numerical results of $ℍ\left(X\right)$ for different values of the parameter p.

p	$ℍ\left(\mathit{X}\right)$	p	$ℍ\left(\mathit{X}\right)$
0.0001	1.87934	0.5	1.25943
0.01	1.86852	0.55	1.18391
0.03	1.84654	0.6	1.10402
0.05	1.82437	0.65	1.01888
0.07	1.80201	0.7	0.927315
0.09	1.77948	0.75	0.827736
0.11	1.75675	0.8	0.717861
0.14	1.72231	0.85	0.594157
0.17	1.6874	0.9	0.450497
0.2	1.652	0.95	0.273684
0.25	1.59181	0.96	0.231718
0.3	1.52994	0.97	0.186252
0.35	1.46611	0.98	0.135994
0.4	1.40002	0.99	0.078212
0.45	1.33128	0.999	0.0112562

Figure 5 relates the $ℍ\left(X\right)$ to the values of parameter p. One may note that (X) is monotonically decreasing in p ∈ (0, 1) with its limit inclining to zero as p tends to 1.

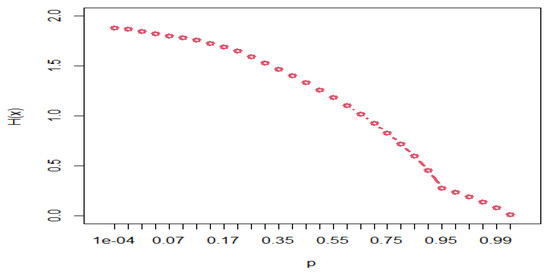
Figure 5. $ℍ\left(X\right)$ of X versus p.

3. Estimation and Simulation

In this section, we determine the estimation of unknown parameter $p$ by the maximum likelihood, moment and proportion methods.

3.1. Method of Maximum Likelihood Estimation

Let $x_1, x_2,\dots , x_n$ be the observed values from the BNDL distribution with parameter $p$. The likelihood and log-likelihood function are given, respectively, as

$$L\left(p\right)={\displaystyle \prod }_{i=1}^{n}f\left(x_i\right)={\displaystyle \prod }_{i=1}^n\frac{{\left(1-p\right)}^{x_i}\left(1+x_i+2p-p^2\right)}{\left(p+1\right){\left(2-p\right)}^{x_i+2}},$$

and

$$l\left(p\right)=log\left(1-p\right){\displaystyle \sum }_{i=1}^n{x}_i+{\displaystyle \sum }_{i=1}^{n}log\left(1+x_i+2p-p^2\right)-nlog\left(p+1\right)-2nlog\left(2-p\right)-log\left(2-p\right){\displaystyle \sum }_{i=1}^n{x}_i.$$

The maximum likelihood estimate (MLE) of the parameter $p$ can be obtained by solving the following equation using some numerical procedures.

$$\frac{\partial l\left(p\right)}{\partial p}=\frac{3pn}{2+p-p^2}-\frac{{{\displaystyle \sum }}_{i=1}^n{x}_i}{2-3p+p^2}+2{\displaystyle \sum }_{i=1}^n\frac{1-p}{1+2p-p^2+x_i}=0$$

3.2. Method of Moments Estimation

Let $X_1, X_2,\dots , X_n$ be a random sample from the BNDL distribution with parameter $p$. The moment estimate (ME) of the parameter $p$ can be obtained by solving the following equation.

$$\frac{\left(p+2\right)\left(1-p\right)}{p+1}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{X}_i.$$

3.3. Method of Proportions Estimation

Let $X_1, X_2,\dots , X_n$ be a random sample from the BNDL distribution with parameter $p$. For $i=1,2,\dots ,n$, we define the indicator functions

$$I\left(X_i\right)=\{\begin{array}{c}1 if X_i=0\\ 0 if X_i>0\end{array}$$

.

Therefore, the proportion of 0s in the sample $\mathsf{\Pi }=\frac{1}{n}{\displaystyle \sum }_{i=1}^{n}I\left(X_i\right)$. The proportion estimate (PE) of the parameter $p$ can be obtained by solving the following equation with respect to $p$

$$\mathsf{\Pi }=\frac{1+2p-p^2}{\left(p+1\right){\left(2-p\right)}^2}.$$

3.4. Simulation Study

In this section, we assess the behavior of the maximum likelihood estimators for a finite sample of size n. Based on BNDL distribution, a simulation study is carried out. The simulation study is based on the following steps: firstly, generate N = 1000 samples of sizes n = 25, 50, …, 500 from the BNDL distribution. Then, compute the maximum likelihood estimators for the model parameters. Lastly, compute the MSEs given by

$$\mathrm{MSE}\left(p\right)=\frac{1}{1000}{\displaystyle \sum }_{i=1}^{1000}{\left(\widehat{p}-p\right)}^2$$

For various parameters’ values, the simulation’s results provided in Figure 6 indicate that the estimated MSEs fall off toward zero when the sample size n increases. Hence, we have conclusive evidence to claim that the maximum likelihood estimation of p satisfies the asymptotic convergence of normality. The asymptotic normality of the MLE is a very well-known classic property given as follows. In a parametric model, we say that an estimator $\widehat{p}$ based on $X_1, X_2, X_3, \dots , X_n$ is consistent if $\widehat{p}\to p$ in probability as $n \to \infty$. We say that it is asymptotically normal if $\sqrt{n}\left(\widehat{p}-p\right)$ converges in distribution to a normal distribution. So $\widehat{p}$ above is consistent and asymptotically normal.

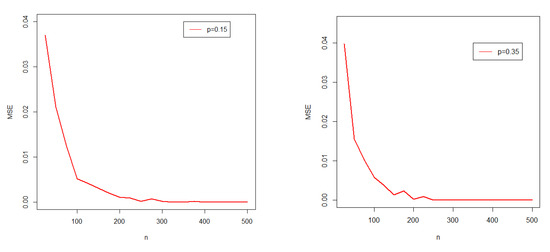
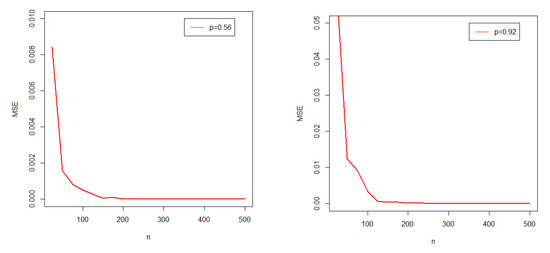
Figure 6. Plots of the estimated parameter and MSEs for various values of p.

4. Applications to Count Data

In this section, to show the application, we used a real-life data set to examine the efficiency and superiority of the BNDL distribution in modeling real data practice, recently studied by Balakarishnan et al. [24], consisting of 744 discrete observations. Santiago, Chile is recognized as one of the most environmentally contaminated cities in the world. In order to obtain the level of air pollution and its associated adverse effects on humans in Santiago, the National Commission of Environment (CONAMA) of the government of Chile collects data on sulfur dioxide (SO₂) concentrations in the air. The data corresponding to the hourly SO₂ concentrations (in ppm) observed at a monitoring station located in Santiago city are:

x	1	2	3	4	5	6	7	8	9	10 and above
f	86	235	120	119	35	15	11	9	4	10

The descriptive statistics of the data sets are, Mean = 2.93, Median = 2, Mode = 3, SD = 2.02, Coefficient of Variation = 0.69, Skewness = 4.32, Kurtosis = 34.57, Range = 24, Min value = 1 and Max value = 25.

We compare BNDL to Binomial–Discrete Lindley Distribution (BDLD) by Kuş et al. [15] and Negative Binomial distribution. The pmf of BDLD is given as

$$p_x\left(x;p\right)=\frac{p^{2x}\left[\left\{p^3-\left(1-p\right)\left(1-p-x\right)\right\}log\left(p\right)+\left(1-p\right)\left\{1-p\left(1-p\right)\right\}\right]}{\left\{1-log\left(p\right)\right\}{\left\{1-p\left(1-p\right)\right\}}^{x+2}}$$

We considered the AIC (Akaike Information Criterion), CAIC (Consistent Akaike Information Criterion), BIC (Bayesian Information Criterion) and HQIC (Hannan–Quinn Information Criterion). The model with minimum values for these statistics could be chosen as the best model to fit the data. All results in Table 3 were obtained using the R PROGRAM.

Table 3. MLEs and their standard errors (in parentheses) with statistics AIC, BIC, HQIC and CAIC values for given data.

Distribution	MLE (SE)	MEASURES
		AIC	CAIC	BIC	HQIC
BNDL (p)	0.6283 (0.0129)	2681.839	2681.844	2686.451	2683.616
BDLD (p)	0.6922 (0.0055)	3092.3700	3092.3760	3096.9820	3094.1480
Negative Binomial (n, k)	17.2957, 2.9262 (4.7378, 0.0678)	2824.156	2849.44	2833.38	2818.69

Figure 7 gives the quantile–quantile plot (Q-Q plot) and box plot and Figure 8 gives TTT plot versus the EHRF for the given data set. Total Time on Test (TTT plots) showed that the data set has an increasing hazard rate shape which is confirmed by EHRF. Figure 9 and Figure 10 show the fitted model against its comparative distributions. These plots clearly show that the BNDL model is superior to well-known BDLD and Negative Binomial models.

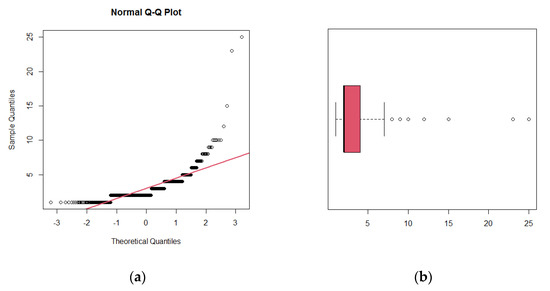
Figure 7. (a) QQ plot and (b) box for the given data.

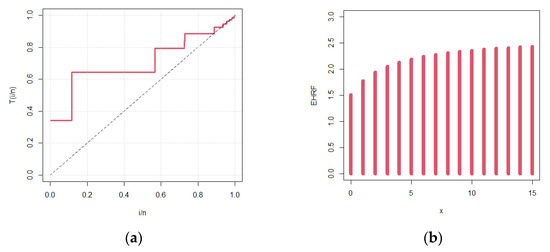
Figure 8. (a) TTT plot and (b) Expected Hazard Rate Function (EHRF) for the BDLD model for the dataset.

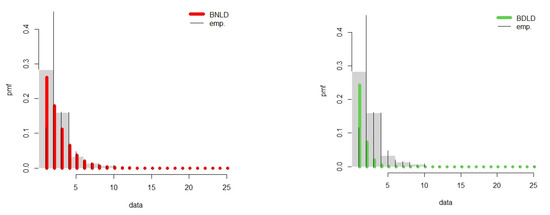
Figure 9. Fitted plots of BNDL and BDLD distribution for given data set.

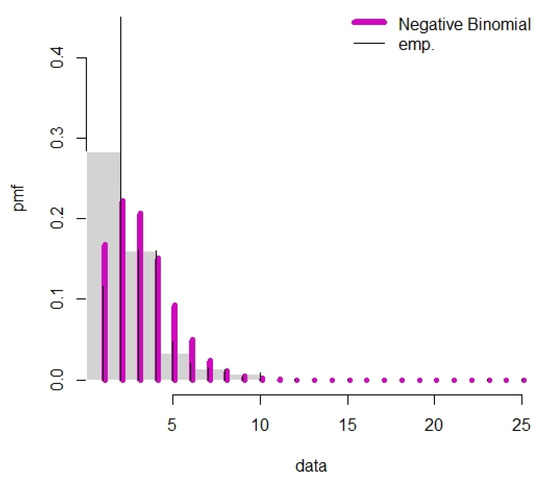
Figure 10. Fitted plot of Negative Binomial distributions for given data set.

5. Concluding Remarks

A new one-parameter discrete distribution was proposed and its important distributional, monotonic, and reliability characteristics were explored. Some statistical and reliability properties of the proposed discrete model were derived. Various estimating approaches were discussed. A simulation study was conducted to determine the MLEs’ accuracy and precision. The applicability of the proposed distribution in modeling a real-life discrete data set was demonstrated. It is clear from the comparison that the new distribution is the best distribution for fitting the data sets from among the all-tested distributions and it will be a useful contribution to the field of count data modeling.