In this section, supporting numerical results are presented to show the performance of our proposed learning adaptive BDDC algorithm. We will consider various choices of permeability coefficients with two major stochastic behaviors. As the concern of our numerical tests are on the learning algorithm, we fix all the parameters that are not related. In most of the experiments, is chosen to be a unit square spatial domain, and it is partitioned into 16 uniform square subdomains with as the coarse grid size. Each subdomain is then further divided into uniform grids with a fine grid size . We will state clearly if other grid sizes are used. In the following, we will first describe the considered stochastic coefficients and training conditions.
3.2. Adaptive BDDC Parameters and Training Conditions
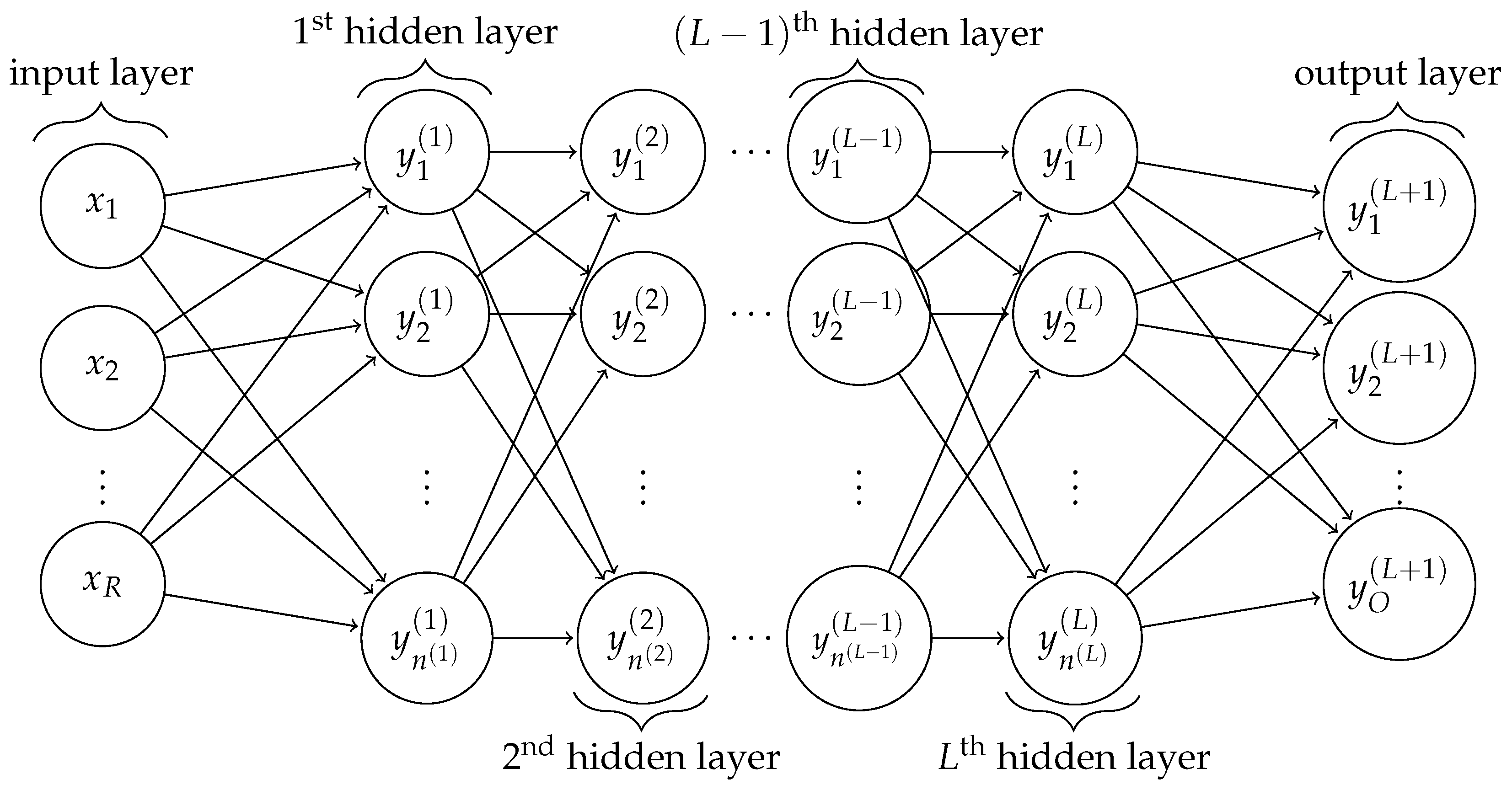
In the setting of BDDC parameters, we fix the number of dominant eigenvectors on every coarse edge to be 2 and deluxe scaling is always considered. We remark that we have fixed the number of coarse basis functions on each edge. In general, one should vary the number of coarse basis functions according to the local heterogeneities. If the number of coarse basis function is too large, then the coarse problem is more expensive to solve. On the other hand, if the number of coarse basis function is too small, then the number of iteration will increase. It is worth note that, the output layer of neural network is composed by the total dominant eigenvectors on all the coarse edges, so the output layer size O is determined by the coarse grid size H, fine grid size h, and also the number of dominant eigenvectors on every coarse edge. When solve the system by the conjugate gradient method, the iteration is stopped when the relative residual is below .
In the training, there are different sets of hyperparameter that could affect the training performance of the neural network. Unless specified, the following training conditions are considered:
Number of truncated terms in KL expansion: ;
Number of hidden layers: ;
Number of neurons in the hidden layer: 10;
Number of neurons in the output layer: ;
Activation function in hidden layer: hyperbolic tangent function;
Activation function in output layer: linear function;
Stopping criteria:
- -
Minimum value of the cost function gradient: ; or
- -
Maximum number of training epochs: 1,000,000;
Sample size of training set: 10,000;
Sample size of testing set: .
After we obtain an accurate neural network from the proposed algorithm, besides the NRMSE of testing set samples, we also present some characteristics of the pre-conditioner based on the approximate eigenvectors from the learning adaptive BDDC algorithm, which include the number of iterations required, minimum and maximum eigenvalues of the pre-conditioner. To show the performance of pre-conditioning on our predicted dominant eigenvectors, we will use the infinity norm to measure the largest difference and also the following symmetric mean absolute percentage error (sMAPE), proposed in [
34], to show a relative error type measure with an intuitive range between 0% and 100%:
where
are some target quantities from pre-conditioning and
is the same type of quantity as
from pre-conditioning using our predicted eigenvectors. In the following subsections, all the computation and results were obtained using MATLAB R2019a with Intel Xeon Gold 6130 CPU and GeForce GTX 1080 Ti GPU in parallel.
3.3. Brownian Sheet Covariance Function
The first set of numerical tests bases on the KL expansion of Brownian sheet covariance function with the following expected functions :
- ()
- ()
.
Expected function
is a random coefficient as
is randomly chosen for each fine grid element, and expected function
is a smooth trigonometric function with values between
. The common property between these two choices is that the resulting permeability function
is highly oscillatory with magnitude order about
to
, which are good candidates to test our method on oscillatory and high contrast coefficients. Here, we show the appearance of mean functions
and
and the corresponding permeability function
in
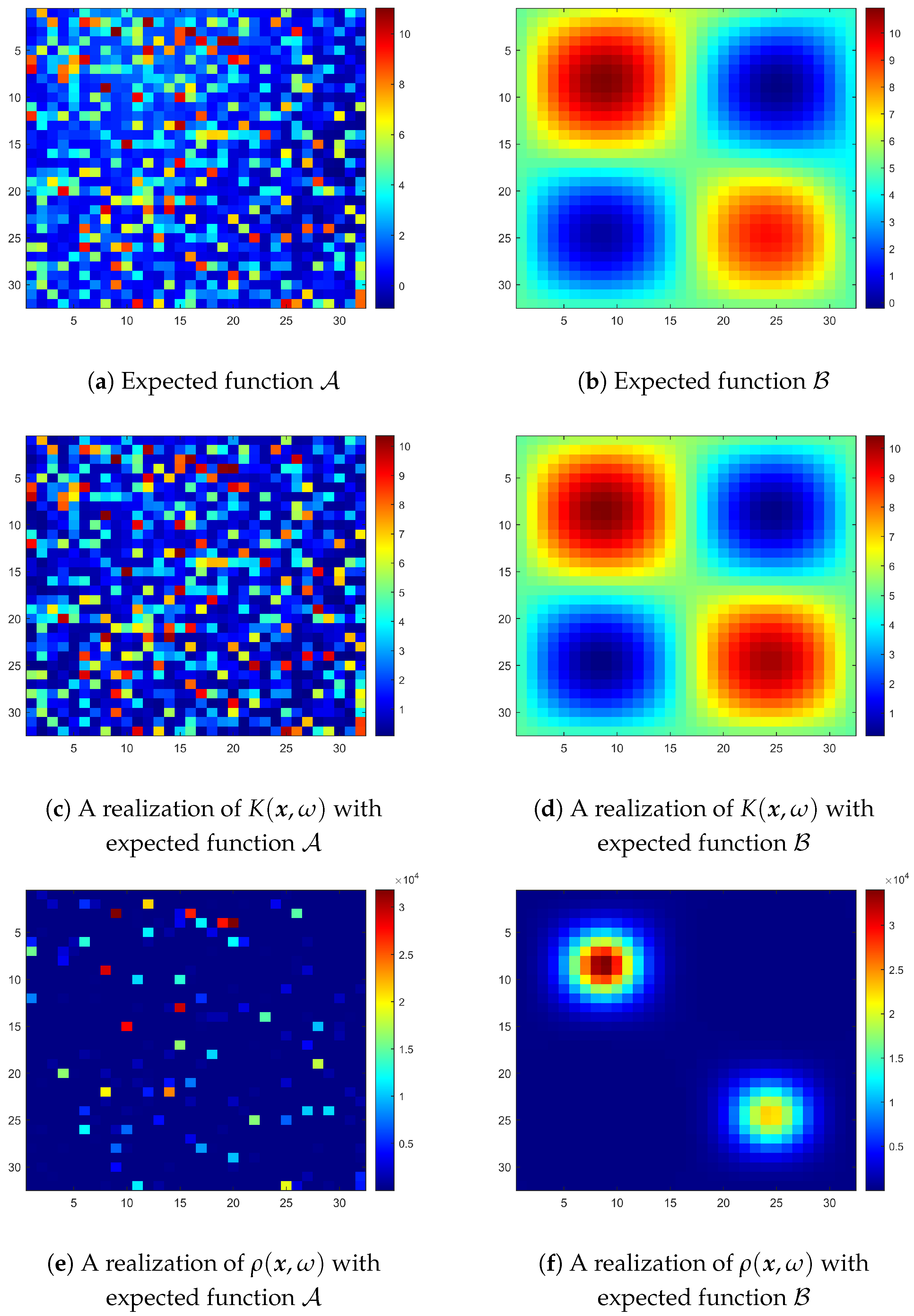
Figure 3. We can observe that from the first row of
Figure 3 to the second row, that is, from the appearances of expected function
to the logarithmic permeability coefficient
, there are no significant differences except only a minor change on the values on each fine grid element. Nevertheless, these small stochastic changes cause a high contrast
after taking exponential function as in the third row of
Figure 3.
In
Table 1, the training results of these two expected functions
and
under the training conditions mentioned are presented. Although the random initial choice of conjugate gradient algorithm for minimization may have influences, in general, the neural network of expected function
usually needs more epochs until stopping criterion is reached and, thus, the training time is also longer. However, this increase in training epochs does not bring a better training NRMSE when compared with expected function
. We can see the same phenomenon when the testing set is considered. The main reason is due to the smoothness of expected function
, the neural network can capture its characteristics easier than a random coefficient.
In the testing results, we consider another set of data containing
samples as a testing set. After obtaining the predicted eigenvectors from neural network, we plug it into the BDDC pre-conditioned solver and obtain an estimated pre-conditioner. For the estimated pre-conditioner, we report several properties such as the number of iteration needed for the iterative solver, the maximum and minimum eigenvalues of the pre-conditioned system. Therefore, to better show the performance of network, besides the testing error NRMSE, we also use the sMAPE and
norm of difference of the iteration numbers, the maximum and minimum eigenvalues of the estimated pre-conditioner and the target pre-conditioner. The comparison results are listed in
Table 2 below.
It is clear that the testing NRMSE of expected function is also much smaller than expected function . One possible reason is because the function used is smooth, and the neural network can better capture the property of the resulting stochastic permeability function. We can see that values of the testing NRMSE of both expected function and expected function are just a bit larger than the training NRMSE. This suggests that the neural network considered is capable to give a good prediction on dominant eigenvectors in the coarse space even when the magnitude of coefficient function value changes dramatically across each fine grid element. Nevertheless, even though a more accurate set of eigenvectors can be obtained for the expected function , but its performance after the BDDC pre-conditioning is not always better than that of expected function . Obviously, errors in the aspects of and are larger for the expected function .
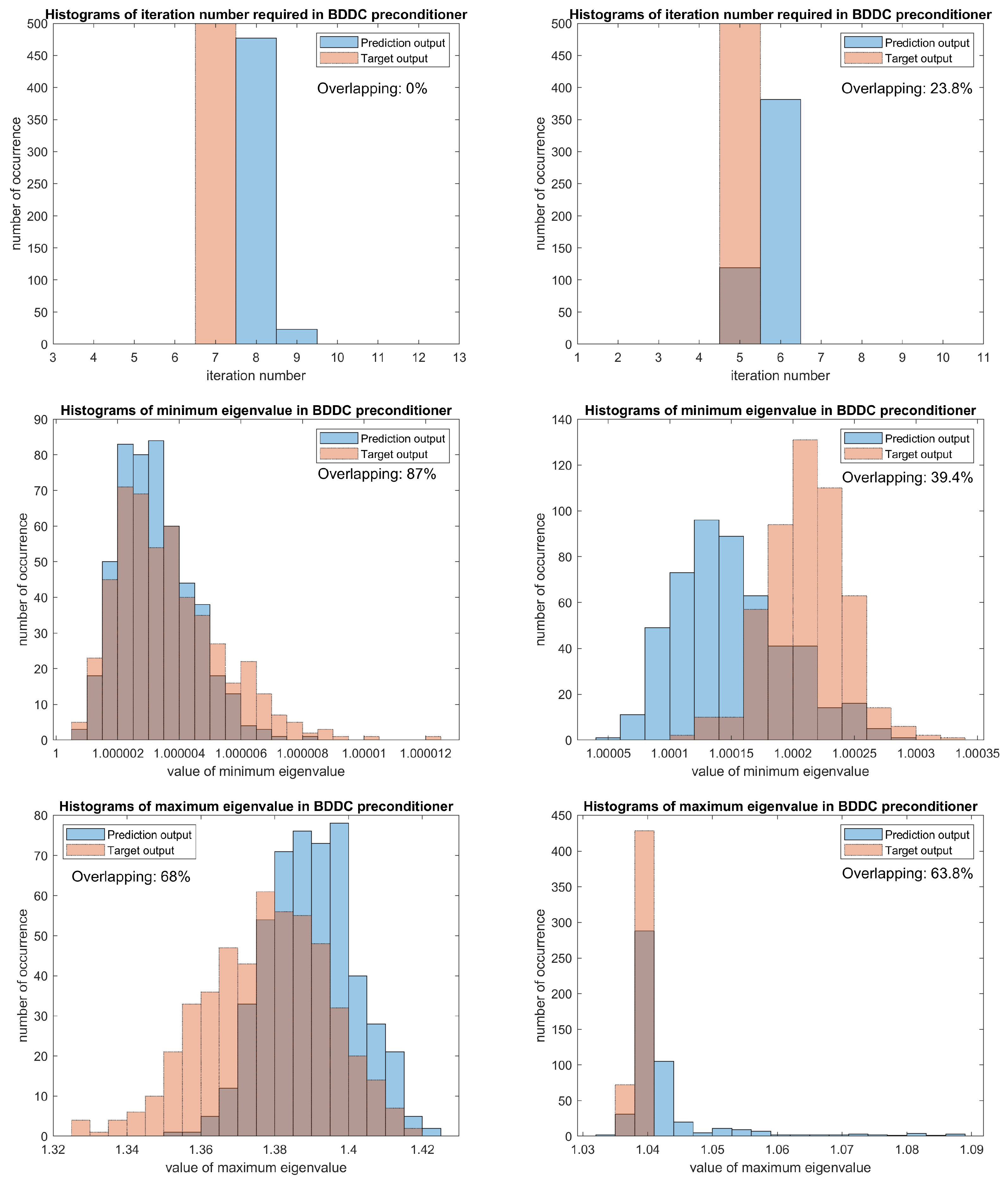
Detailed comparisons can be found in
Figure 4, where the area of overlapping represents how close the specified quantity of the estimated pre-conditioner is compared to the target pre-conditioner. In the first row of figures, we can see the number of iteration required for the predicted eigenvectors is usually more than the target iteration number, however, the differences in the iteration number is not highly related to the difference in minimum and maximum eigenvalues. We can see more examples to verify it in this and later results. The bin width of the histogram of minimum eigenvalues for expected function
is about
, which is in coherence with the
error, but we eliminate this small magnitude effect and the sMAPE is considered. The high ratio of overlapping area for expected function
confirms the usage of sMAPE as a good measure, as the resulting sMAPE 2.58
of expected function
is much smaller than 3.19
of expected function
.
For the last column of errors in
Table 2, the
norm of maximum eigenvalues is larger for expected function
. Nevertheless, it does not mean that the neural network of expected function
performs worse. From its histogram, we can see an extremely concentrated and overlapping area at the bin around 1.04, moreover, there are some outliers for the prediction results, which is one of the source for a larger
norm. Therefore, the sMAPE can well represent the performance of preconditioning on the estimated results, and we can conclude that both neural networks show a good results on oscillatory and high contrast coefficients, which can be represented by NRMSE and sMAPE. In
Section 3.4, besides an artificial coefficient, we will consider one that is closer to a real life case.
Although the norm seems not describe the characteristics of performance in a full picture, it is still a good and intuitive measure, for example, in the difference of iteration number, we can immediately realize how large will be the worst case.
Further Experiments on Different Training Conditions
To emphasize the changes of using different training conditions, we display the results of increasing the truncated terms
R in KL expansion and using less training samples. The expected functions and stochastic property considered are the same as above to show the effect of changing conditions only. For clarification, there are two experiments each with only one condition is modified and other conditions are the same as stated in
Section 3.2. We state the new conditions as the follows:
When
R is increased, we can see in
Table 3, the training time increases as the total number of parameters increases with the input layer. In
Table 4, the testing results of expected function
clearly have better performance than in
Table 2, which suggests that a larger
R could bring a smaller NRMSE.
The training and testing results of modified experiment 2 are shown in
Table 5 and
Table 6, respectively. Obviously, the testing results in
Table 6 are worse than when 10,000 training samples are used. Moreover, as the training time does not have a distinct reduction, and with the aid of parallel computation, more training samples can be easily obtained. Therefore, using less samples is not always a good choice, we should use appropriate number of samples.
3.4. Exponential Covariance Function
To test our method on realistic highly varying coefficients, we consider expected functions that come from the second model of the 10th SPE Comparative Solution Project (SPE10), with the KL expanded exponential covariance function as the stochastic source. For clarification, in this set of experiment, we first use the modified permeability of Layer 35 in the x-direction of SPE10 data as the expected function with in the exponential covariance function . We then train the neural network, and the resulting neural network is used to test its generalization capacity on the following different situations:
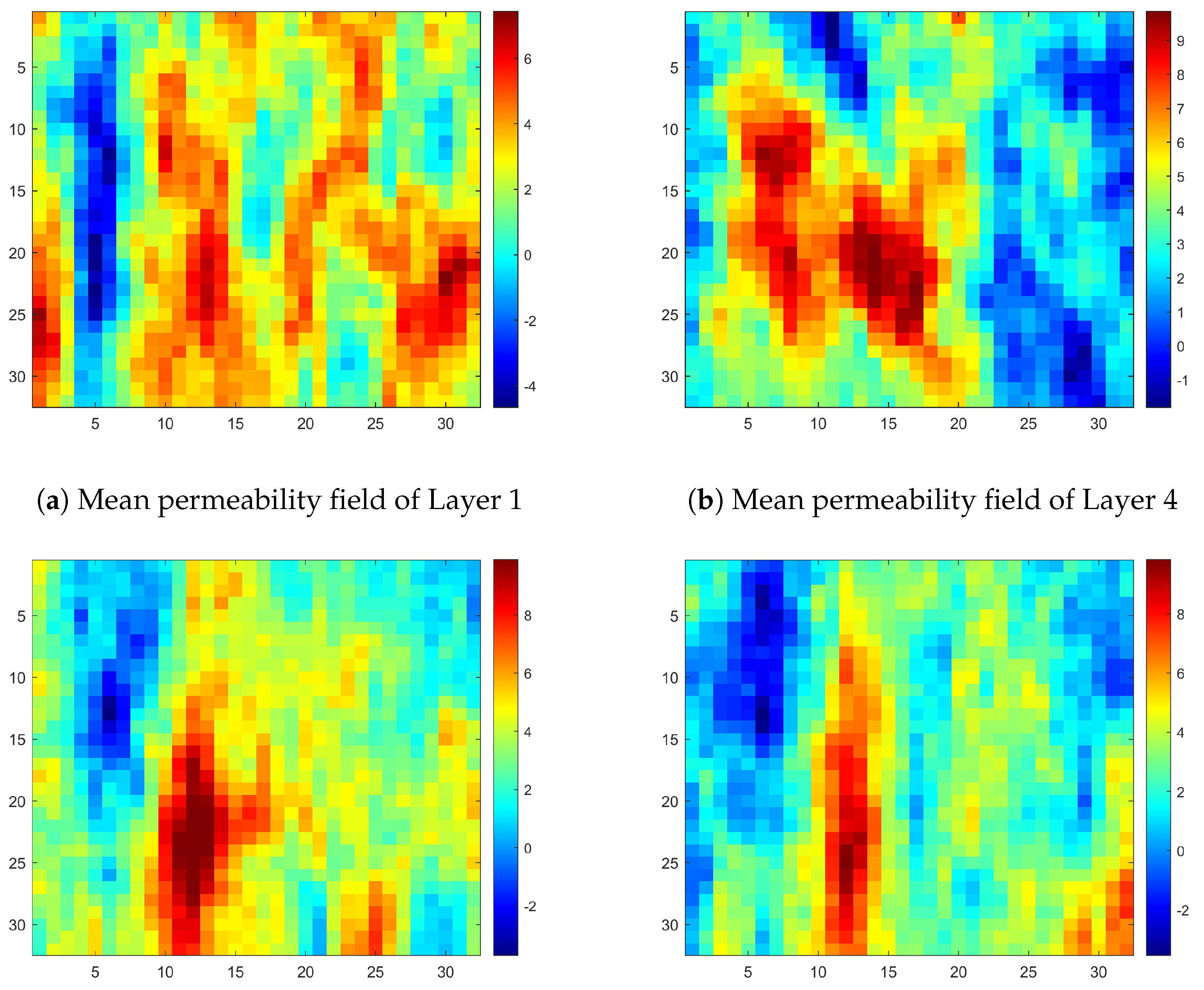
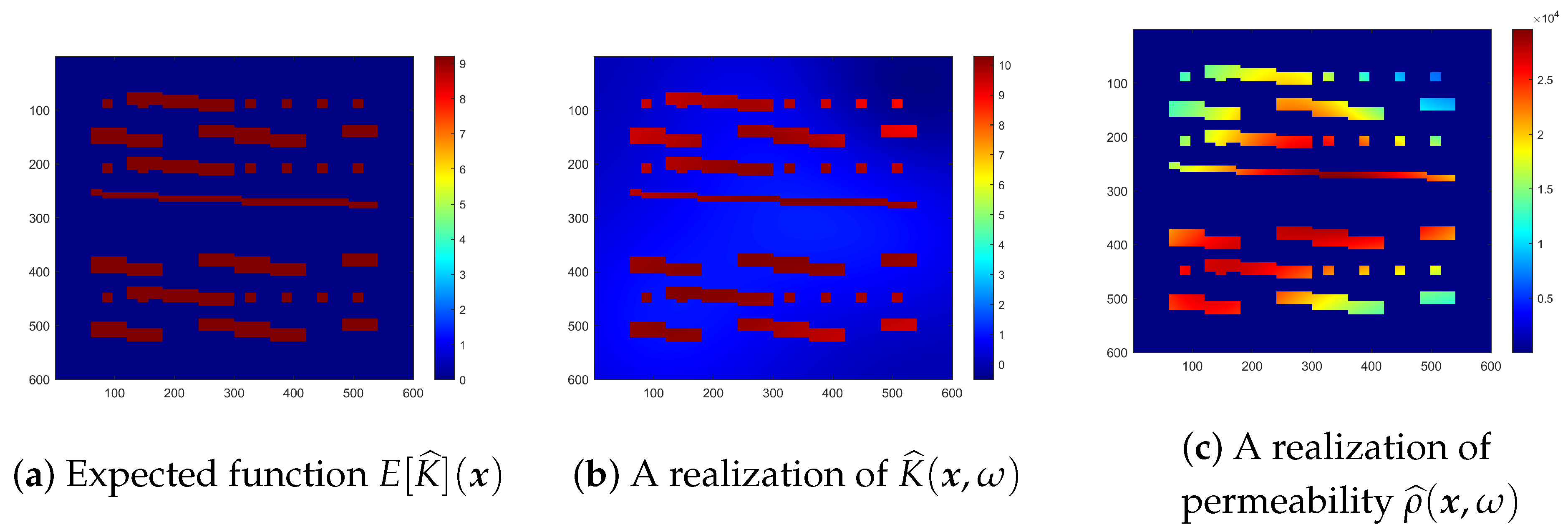
It is of note that, all the permeability fields used are modified into our computational domain and shown in
Figure 5 for a clear comparison. In the Layer 35 permeability field, four sharp properties can be observed. There are one blue strip on the very left side, and a reversed but narrower red strip is next to it. In the top right corner, a low permeability area is shown and just below it, a small high permeability area is located in the bottom right corner. So a similar but with slightly different properties of Layer 34, and two Layers 1, 4 with more distinct differences are chosen to test the generalization capacity of our neural network.
Before showing the training and testing records of neural network, we further present the logarithmic permeability
, and permeability
when
,
and
in
Figure 6. The sets of
used in these three rows of realizations are the same. We can thus see the change in parameters does cause the stochastic behavior to change, too. We present the training and testing records of neural network as below in
Table 7 and
Table 8, where we specify the expected functions considered in the first column.
In
Table 8, we clarify that the results of Layer 35 * also use Layer 35 permeability as the expected function but with
. Similarly, Layer 35 ** is with another set of parameters
. Each row corresponds to the results of different testing sets, however, all the results are obtained using the same neural network of Layer 35 in
Table 7. Therefore, the testing results of Layer 35 are used as a reference to decide whether the results of other testing sets are good or not.
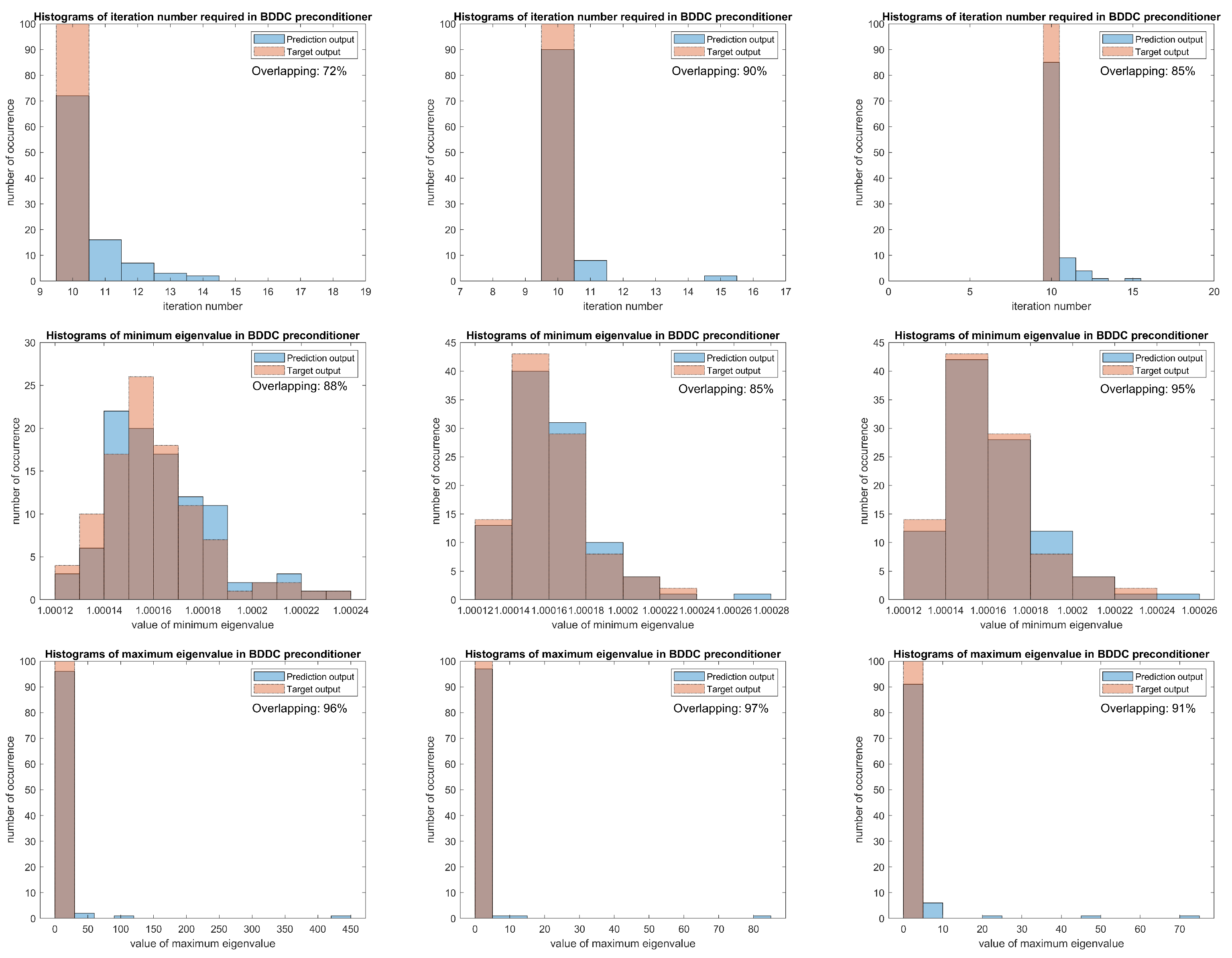
We first focus on the testing results of Layer 35. From the corresponding histograms in the left column of
Figure 7, besides the iteration number required for predicted eigenvectors are still usually larger by 1, we can observe a large area of overlapping, in particular, there is only 8.4% of data that are not overlapped in the histogram of maximum eigenvalues. Moreover, the small NRMSE and sMAPE again confirm with the graphical results. For generalization tests, we then consider other testing sets with different stochastic behaviors and expected functions.
When the stochastic behavior of Layer 35 is changed to
and
, we list the corresponding sMAPE and
norms of differences in iteration numbers, maximum eigenvalues and minimum eigenvalues of pre-conditioners in the last two rows of
Table 8. We can see the values of errors are very similar to the row of Layer 35 and the NRMSE are very close. Therefore, we expect that the Layer 35 neural network can generalize the coefficient functions with similar stochastic properties, and give a good approximation on dominant eigenvectors for the BDDC pre-conditioner. It is then verified by the histograms in the middle column of
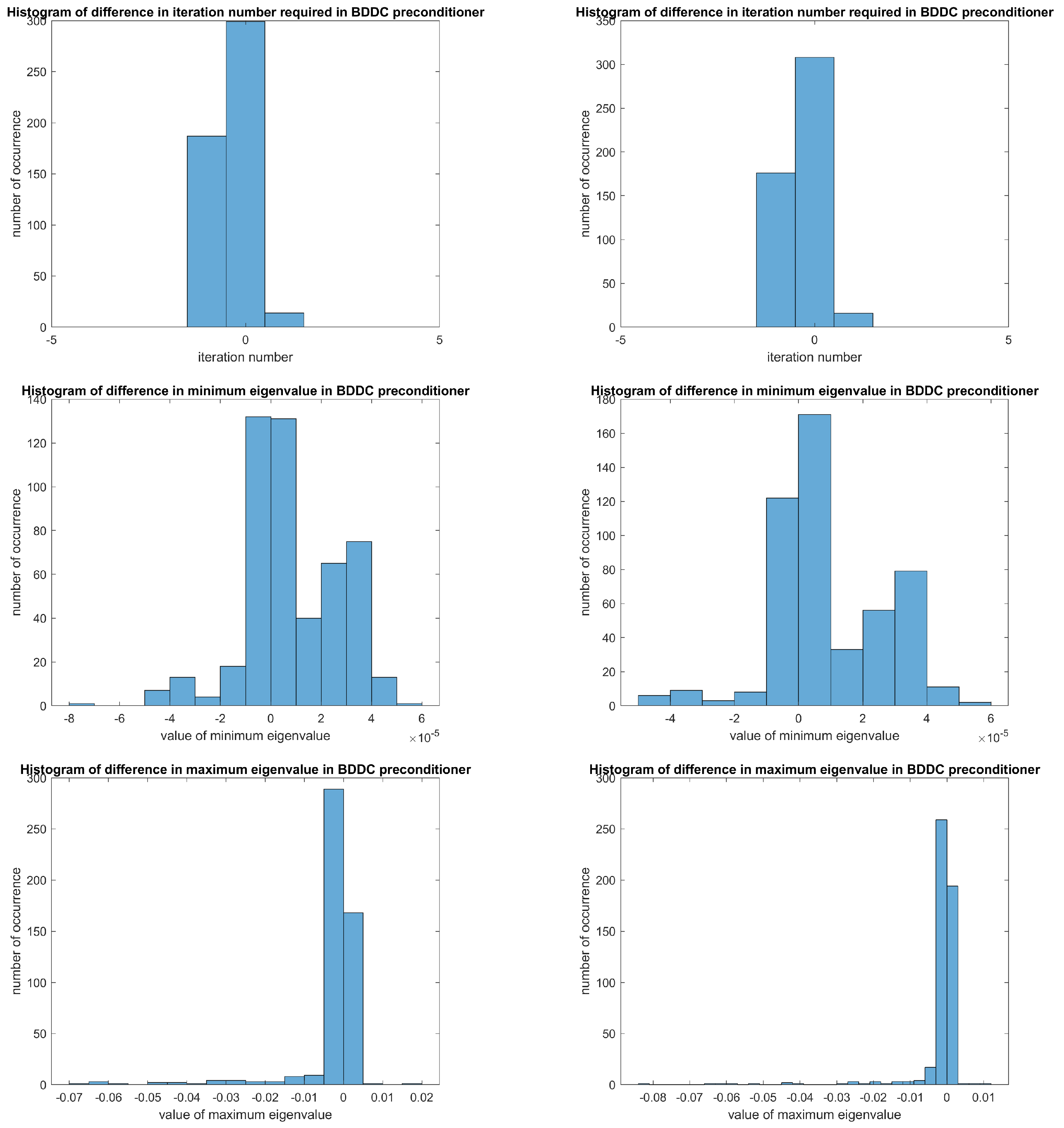
Figure 7. Moreover, a large population of samples are concentrated around 0 in the histograms of difference between the estimated pre-conditioner and target pre-conditioner in
Figure 8. All these show our method performs well with stochastic oscillatory and high contrast coefficients, and also coefficient functions with similar stochastic properties.
Finally, we compare the performances when the expected function is changed to Layer 1, 4, and 34. Note, the NRMSE, sMAPE and
errors of the three layers are almost all much higher than those of Layer 35, which are crucial clues for a worse performance. It is clear that when the permeability fields do not have many similarities such as Layer 1 and 4, the testing NRMSE increases distinctly. Even though the permeability fields of Layer 34 and Layer 35 share some common properties and have a near magnitude, unlike previous results for Layer 35 and Layer 35 *, we can see in the right column of
Figure 7, the prediction output and target output on maximum and minimum eigenvalues of pre-conditioners are even two populations with different centres and only a little overlapping area. The main reason is a minor difference in
can already cause a huge change after taking exponential function. Therefore, when
is changed to another entirely different mean permeability with just some common properties, the feed-forward neural network may not be able to capture these new characteristics, which will be part of our future research.
3.5. Exponential Covariance Function with Multiple Hidden Layers
It is noted that after taking exponential function, the permeability fields in previous experiments only show some global peaks, the single layer structure of neural network may then suffice to give an accurate prediction. Therefore, in this subsection, we illustrate an example with a high contrast coefficient cutting more interfaces and a realization of this new coefficient function
is displayed in
Figure 9. It is of note that, the stochastic properties considered are still the exponential covariance function with
.
To extract more features and details from the new coefficient, we consider a much finer grid sizes, which are and , and the spatial domain is still the unit square . With respect to this change, we change the following training conditions accordingly:
Number of hidden layers: or ;
Number of neurons in the hidden layers: and or 7;
Number of neurons in the output layer: 21,240;
Sample size of training set: ;
Sample size of testing set: .
Other conditions are kept to be unchanged as in
Section 3.2. We show the new training and testing records in
Table 9 and
Table 10.
On one hand, when the number of neurons in the second hidden layer increases, the training results do not show a distinct difference, the three training NRMSE are all around with a much longer training time than previous experiments. However, on the other hand, the testing results do show some improvements when increases. Obviously, the testing NRMSE and pre-conditioner errors improve when a second hidden layer is introduced. Moreover, the testing NRMSE also decreases when increases. We can see the testing NRMSE of multiple hidden layers are slightly lower than the corresponding training NRMSE.
This indicates that for more complicated coefficient functions, introduction of multiple hidden layers could help to bring better performance. However, as it also increases the complexity of neural network and the training time, thus, a single layer of neural network should be considered first if the problem is not complicated. In
Figure 10, comparisons of the iteration number, maximum and minimum eigenvalues are illustrated in histograms for easy observation. Unlike the histograms in
Figure 7, we can see more iterations are needed for solving the problem and more outliers exist in the maximum eigenvalue comparison as the problem itself becomes more complicated than previous experiments.