A 5(4) Embedded Pair of Explicit Trigonometrically-Fitted Runge–Kutta–Nyström Methods for the Numerical Solution of Oscillatory Initial Value Problems

Abstract

A 5(4) pair of embedded explicit trigonometrically-fitted Runge–Kutta–Nyström (EETFRKN) methods especially designed for the numerical integration of second order initial value problems with oscillatory solutions is presented in this paper. Algebraic order analysis and the interval of absolute stability for the new method are also discussed. The new method is capable of integrating the test equation $y^{″}=-w^{2}y$. The new method is much more efficient than the other existing Runge–Kutta and Runge–Kutta–Nyström methods.

1. Introduction

In this study, our focus is on the numerical solution of the initial value problems (IVPs) of second-order differential equations; whose first derivative does not appear explicitly of the form :

$$\begin{array}{c}{y}^{″}=f(x,y),x\in [x_0,X],\\ y\left(x_0\right)=y_0,y^{\prime }\left(x_0\right)=y_0^{\prime },\end{array}$$

(1)

whose solutions have a noticeable oscillatory character, where $y\in {\Re }^d$ and $f:{\Re }^d\to {\Re }^d$ are sufficiently differentiable. Such problems frequently occur in several areas of applied sciences such as: theoretical physics, celestial mechanics, nuclear chemistry, nuclear physics, electronics, molecular dynamics and elsewhere. Many numerical methods have been developed for the numerical integration of Equation (1), among them are Runge–Kutta–Nyström (RKN) methods. Exponentially/trigonometrically-fitted RKN methods have been studied by Simos in [1],Van de Vyver in [2], Kalogiratou and Simos in [3] and Shiwei Liu et al. in [4]. Franco in [5] proposed a 5(3) pair of explicit adapted Runge–Kutta–Nyström methods for the numerical integration of perturbed oscillators, Van de Vyver in [6,7] proposed a Runge–Kutta–Nyström pair for the numerical integration of perturbed oscillators, a 5(3) pair of explicit RKN methods for oscillatory problems. Senu et al. in [8] proposed an embedded explicit RKN method for solving oscillatory problems. Recently, Tsitouras in [9] proposed fitted modifications of RKN pairs, Franco et al. in [10] proposed two new embedded pair of explicit Runge-Kutta methods adapted to the numerical solution of oscillatory problems, and Anastassi and Kosti in [11] proposed a 6(4) optimized embedded Runge–Kutta–Nyström pair for the numerical solution of periodic problems.

In this paper, we develop a new efficient embedded explicit trigonometrically-fitted RKN method based on the technique proposed by Simos in [12] for Runge–Kutta (RK) methods. The constructed method can exactly integrate the test equation $y^{″}=-w^{2}y$ and the numerical results show the efficacy of the new method. The remaining part of this paper is arranged as follows: in Section 2, we give the basic theory of an explicit Runge–Kutta–Nyström pair, the basic definition of trigonometrically-fitted RKN method and the derivation of an explicit trigonometrically-fitted RKN method. Section 3 deals with the derivation of the proposed method. In Section 4, we analyze the algebraic order of the new pair from their local truncation errors and give the interval of absolute stability of the new pair. In Section 5, we present the numerical results. In Section 6, we give a brief discussion about the graphs and the last section deals with the conclusions.

2. Basic Theory

The general form of an explicit k-stage RKN method is given by:

$$y_{n+1}=y_n+h{y}_n^{\prime }+h^2\sum _{i=1}^k{b}_{i}f(x_n+c_{i}h,Y_i),$$

(2)

$$y_{n+1}^{\prime }=y_n^{\prime }+h\sum _{i=1}^k{d}_{i}f(x_n+c_{i}h,Y_i),$$

(3)

$$Y_i=y_n+c_{i}h{y}_n^{\prime }+h^2\sum _{j=1}^{i-1}{a}_{ij}f(x_n+c_{i}h,Y_j),$$

(4)

where $y_{n+1}$ and $y_{n+1}^{\prime }$ represent the approximation of $y\left(x_{n+1}\right)$ and $y^{\prime }\left(x_{n+1}\right)$, respectively, where $x_{n+1}=x_n+h,n=0,1,...,$ or in Butcher Tableau as :

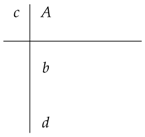where A is a matrix ${\left(a_{ij}\right)}_{k\times k},$ $c={(c_1,c_2,...,c_k)}^T$, $b=(b_1,b_2,...,b_k)$, $d=(d_1,d_2,...,d_k).$

An embedded $p\left(q\right)$ pair of RKN methods is based on the method $(c,A,b,d)$ of order p and the other RKN method ($c,A,\widehat{b},\widehat{d}$) of order q($q<p$). The higher order produces the solution ($y_{n+1}$, $y_{n+1}^{\prime }$), while the lower order method produces the solution ${\widehat{y}}_{n+1}$ and ${\widehat{y}}_{n+1}^{\prime }$, which is used for the estimation of local truncation error only. An embedded pair is characterized by the Butcher tableau below:

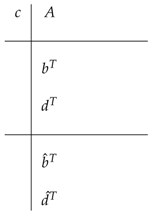
In this work, a variable step size algorithm using the embedded technique is used because it provides cheap local error estimation. Local error estimation at the point $x_{n+1}=x_n+h$ is determined by ${\delta }_{n+1}={\widehat{y}}_{n+1}-y_{n+1}$ and ${\delta }_{n+1}^{{}^{\prime }}={\widehat{y}}_{n+1}^{{}^{\prime }}-y_{n+1}^{{}^{\prime }}.$

Let ${\mathrm{Est}}_{n+1}=\max ({∥{\delta }_{n+1}∥}_{\infty },\parallel {\delta }_{n+1}^{{}^{\prime }}{\parallel }_{\infty })$ represent local error estimation to control the step size h. For the numerical integration of the oscillatory problems, we use the step-size control procedure given by Shiwei in [4]:

• if $Es{t}_{n+1}<Tol/100,h_{n+1}=2h_n$,
• if $Tol/100\le Es{t}_{n+1}<Tol,h_{n+1}=h_n,$
• if $Es{t}_{n+1}\ge Tol,h_{n+1}=h_n/2$ and repeat the step,

where $Tol$ is the tolerance (requested local error). It should be noted that the N th order approximation $y_n$ is used as the initial value for the (n+1)th step, that is to say, the embedded pair is applied in local extrapolation mode or higher order mode.

Definition 1.

Runge–Kutta–Nyström method (2)–(4) is said to be trigonometrically-fitted if it integrates exactly the function $e^{iwx}$ and $e^{-iwx}$ or equivalently $sin\left(wx\right)$ and $cos\left(wx\right)$ with $w>0$ the principal frequency of the problem when applied to the test equation $y^{{}^{″}}=-w^{2}y$; Leading to a system of equations as derived below:

When an explicit Runge–Kutta–Nyström method (2)–(4) is applied to the test equation $y^{″}=-w^{2}y$, the method becomes:

$$y_{n+1}=y_n+hy{{}^{\prime }}_n+h^2\sum _{i=1}^k{b}_i(-w^2{Y}_i),$$

(5)

$$y_{n+1}^{\prime }=y_n^{\prime }+h\sum _{i=1}^k{d}_i(-w^2{Y}_i),$$

(6)

where

$$Y_1=y_n,$$

(7)

$$Y_i=y_n+c_{i}h{y}_n^{\prime }+h^2\sum _{j=1}^{i-1}{a}_{ij}(-w^2{Y}_j),i=2,3,...,k.$$

(8)

Let $y_n=e^{Iwx}$. By computing the value of $y_{n+1}$, $y_n^{\prime }$ and $y_{n+1}^{\prime }$ and substituting in the Equations (5)–(8) and by using $e^{Iv}=cos\left(v\right)+Isin\left(v\right)$ and comparing the real and imaginary part, we obtain the following system of equations:

$$cos\left(v\right)=1-v^2\sum _{i=1}^k{b}_i(1-v^2\sum _{j=1}^{i-1}{a}_{ij}{Y}_j{e}^{-Iwx}),$$

(9)

$$sin\left(v\right)=v-v^2\sum _{i=1}^k{b}_i{c}_{i}v,$$

(10)

$$sin\left(v\right)=v\sum _{i=1}^k{d}_i(1-v^2\sum _{j=1}^{i-1}{a}_{ij}{Y}_j{e}^{-Iwx}),$$

(11)

$$cos\left(v\right)=1-v^2\sum _{i=1}^k{d}_i{c}_i,$$

(12)

where $v=wh.$

3. Derivation of the Proposed Method

In this section, we will construct a new efficient embedded explicit trigonometrically-fitted RKN method.

In this study, Embedded Runge–Kutta–Nyström 5(4)M pair (ERKN5(4)M) is used as given by Senu in [13]. The coefficients of the method are given in Table 1.

Table 1. The Embedded Runge–Kutta–Nyström 5(4)M (ERKN5(4)M) Method in [13].

0
$\frac{1}{2}$	$\frac{1}{8}$
$\frac{19}{70}$	$\frac{2907}{343000}$	$\frac{1216}{42875}$
$\frac{44}{51}$	$\frac{6624772}{128538819}$	$\frac{6273905}{54121608}$	$\frac{210498365}{1028310552}$
	$\frac{479}{5016}$	$\frac{235}{1776}$	$\frac{145775}{641744}$	$\frac{309519}{6873416}$
	$\frac{479}{5016}$	$\frac{235}{888}$	$\frac{300125}{962616}$	$\frac{2255067}{6873416}$
	$\frac{184883}{2021250}$	$\frac{411163}{3399375}$	$\frac{6}{25}$	$\frac{593028}{12464375}$
	$\frac{479}{5016}$	$\frac{235}{888}$	$\frac{300125}{962616}$	$\frac{2255067}{6873416}$

Solving the above system of Equations (9)–(12) using the coefficients of the lower order method (order 4) for $b_2,b_3,d_2,d_3$, we obtain the solution as given in Equation (13).

$$\begin{array}{ccc}{b}_2\hfill & =\hfill & -\frac{-5,380,190,812,500cos\left(v\right)v-14,441,564,812,500v+514,613,717,975v^3+19,821,755,625,000sin\left(v\right)}{462,315,000v^3\left(1273v^2+9800\right)}\hfill \\ & & -\frac{72,954,403,664v^5-1,050,695,364v^7-730,168,753,125sin\left(v\right)v^2+281,087,520,000v^{3}cos\left(v\right)+70,271,880,000v^{4}sin\left(v\right)}{462,315,000v^3\left(1273v^2+9800\right)},\hfill \\ \\ b_3\hfill & =\hfill & -\frac{18,586,312,500cos\left(v\right)v+18,586,312,500v-3,588,043,375v^3-37,172,625,000sin\left(v\right)+62,403,600v^5}{867,000v^3\left(1273v^2+9800\right)}\hfill \\ & & -\frac{10,749,212v^7+4,646,578,125sin\left(v\right)v^2}{867,000v^3\left(1273v^2+9800\right)},\hfill \\ \\ d_2\hfill & =\hfill & -\frac{82,672,800sin\left(v\right)v-111,333v^6-3,675,956v^4+62,415,080v^2-11,219,880v^{2}cos\left(v\right)}{7104v^2\left(1273v^2+9800\right)}\hfill \\ & & +\frac{304,584,000cos\left(v\right)-304,584,000-4,319,232v^{3}sin\left(v\right)+1,079,808v^{4}cos\left(v\right)}{7104v^2\left(1273v^2+9800\right)},\hfill \\ \\ d_3\hfill & =\hfill & -\frac{245(-673,831,200sin\left(v\right)v-2,687,303v^6+15,600,900v^4-264,497,800v^2+168,457,800v^{2}cos\left(v\right)}{7,700,928v^2\left(1273v^2+9800\right)}\hfill \\ & & -\frac{1,347,662,400cos\left(v\right)+1,347,662,400)}{7,700,928v^2\left(1273v^2+9800\right)}.\hfill \end{array}$$

(13)

The corresponding Taylor series expansion of the solution is given in Equation (14):

$$\begin{array}{ccc}{b}_2\hfill & =\hfill & \frac{411,163}{3,399,375}+\frac{206,089}{99,960,000}{v}^2+\frac{32,195,419}{61,225,500,000}{v}^4-\frac{16,326,175,118,467}{129,602,138,400,000,000}{v}^6+\frac{253,277,042,450,924,651}{13,971,110,519,520,000,000,000}{v}^8\hfill \\ \\ & & -\frac{4,241,152,320,070,814,549,399}{1,779,919,480,186,848,000,000,000,000}{v}^{10}+\frac{3,741,076,822,521,180,957,593,411}{12,076,069,088,652,307,200,000,000,000,000}{v}^{12}\hfill \\ \\ & & -\frac{61,913,938,732,739,966,085,182,108,639}{1,538,491,201,894,303,937,280,000,000,000,000,000}{v}^{14}+...,\hfill \\ \\ b_3\hfill & =\hfill & \frac{6}{25}-\frac{206,089}{99,960,000}{v}^2-\frac{2,667,305,573}{3,122,500,500,000}{v}^4+\frac{390,570,720,145,763}{2,203,236,352,800,000,000}v6-\frac{5,709,954,829,720,650,539}{237,508,878,831,840,000,000,000}{v}^8\hfill \\ \\ & & +\frac{284,375,014,038,527,074,809,733}{90,775,893,489,529,248,000,000,000,000}{v}^{10}-\frac{98,745,865,792,553,965,577,692,757}{242,619,206,235,650,899,200,000,000,000,000}{v}^{12}\hfill \\ \\ & & +\frac{1,382,746,883,790,630,905,277,400,426,271}{26,154,350,432,203,166,933,760,000,000,000,000,000}{v}^{14}+...,\hfill \\ \\ d_2\hfill & =\hfill & \frac{235}{888}+\frac{11}{5760}{v}^4-\frac{26,759}{56,448,000}{v}^6+\frac{30,179,399}{414,892,800,000}{v}^8-\frac{974,755,501,787}{100,632,248,640,000,000}{v}^{10}+\frac{32,337,223,905,299,251}{25,641,096,953,472,000,000,000}{v}^{12}\hfill \\ \\ & & -\frac{41,171,207,949,008,915,273}{251,282,750,144,025,600,000,000,000}{v}^{14}+...,\hfill \\ \\ d_3\hfill & =\hfill & \frac{300,125}{962,616}-\frac{11}{5760}{v}^4+\frac{38,503}{56,448,000}{v}^6-\frac{121161749}{1,244,678,400,000}{v}^8+\frac{1,283,041,005,779}{100,632,248,640,000,000}{v}^{10}\hfill \\ \\ & & -\frac{42,487,644,873,726,467}{25,641,096,953,472,000,000,000}{v}^{12}+\frac{162,263,941,292,140,283,723}{753,848,250,432,076,800,000,000,000}{v}^{14}+.....\hfill \end{array}$$

(14)

As $v\to 0,$ the coefficients $b_2$, $b_3$, $d_2$ and $d_3$ of the lower order method reduces to the coefficients of the original method (lower order ). That is to say, $b_2\left(0\right)$, $b_3\left(0\right)$, $d_2\left(0\right)$ and $d_3\left(0\right)$ are identical to $b_2$, $b_3$, $d_2$ and $d_3$ of the lower order method in ERKN5(4)M.

In a similar way, solving the above system of Equations (9)–(12) using the coefficients of the higher order method (order 5) for $b_1,b_2,d_1,d_2$, we obtain the solution as given in Equation (15):

$$\begin{array}{ccc}{\widehat{b}}_1\hfill & =\hfill & -\frac{25,581,600cos\left(v\right)v+25,581,600v-51,163,200sin\left(v\right)+426360v^5-4,574,700v^3-14,003v^7+6,395,400sin\left(v\right)v^2}{25,581,600v^3},\hfill \\ \\ {\widehat{b}}_2\hfill & =\hfill & -\frac{4,528,800sin\left(v\right)-4,528,800v-37,740v^5+455175v^3+592v^7}{2,264,400v^3},\hfill \\ \\ {\widehat{d}}_1\hfill & =\hfill & -\frac{-3,511,200sin\left(v\right)v-14,003v^6+146,300v^4-1,213,100v^2+7,022,400+877,800v^{2}cos\left(v\right)-7,022,400cos\left(v\right)}{3,511,200v^2},\hfill \\ \\ {\widehat{d}}_2\hfill & =\hfill & -\frac{310,800cos\left(v\right)-310,800-12,950v^4+114,275v^2+296v^6}{155,400v^2}.\hfill \end{array}$$

(15)

The corresponding Taylor series expansion of the solution is given in Equation (16):

$$\begin{array}{ccc}{\widehat{b}}_1\hfill & =\hfill & \frac{479}{5016}-\frac{233}{428,400}{v}^4+\frac{11}{362,880}{v}^6-\frac{37}{79,833,600}{v}^8+\frac{1}{222,393,600}{v}^{10}-\frac{79}{2,615,348,736,000}{v}^{12}+\frac{53}{355,687,428,096,000}{v}^{14}+...,\hfill \\ \\ {\widehat{b}}_2\hfill & =\hfill & \frac{235}{1776}+\frac{29}{214,200}{v}^4-\frac{1}{181,440}{v}^6+\frac{1}{19,958,400}{v}^8-\frac{1}{3,113,510,400}{v}^{10}+\frac{1}{653,837,184,000}{v}^{12}-\frac{1}{177,843,714,048,000}{v}^{14}+...,\hfill \\ \\ {\widehat{d}}_1\hfill & =\hfill & \frac{479}{5016}-\frac{11}{12,600}{v}^4+\frac{1}{5040}{v}^6-\frac{29}{7,257,600}{v}^8+\frac{23}{479,001,600}{v}^{10}-\frac{67}{174,356,582,400}{v}^{12}+\frac{23}{10,461,394,944,000}{v}^{14}+...,\hfill \\ \\ {\widehat{d}}_2\hfill & =\hfill & \frac{235}{888}+\frac{11}{12,600}{v}^4-\frac{1}{20,160}{v}^6+\frac{1}{1,814,400}{v}^8-\frac{1}{239,500,800}{v}^{10}+\frac{1}{43,589,145,600}{v}^{12}-\frac{1}{10,461,394,944,000}{v}^{14}+....\hfill \end{array}$$

(16)

As $v\to 0,$ the coefficients ${\widehat{b}}_1$, ${\widehat{b}}_2$, ${\widehat{d}}_1$ and ${\widehat{d}}_2$ of the higher order method reduces to the coefficients of the original method (higher order ). That is to say, ${\widehat{b}}_1\left(0\right)$, ${\widehat{b}}_2\left(0\right)$, ${\widehat{d}}_1\left(0\right)$ and ${\widehat{d}}_2\left(0\right)$ are identical to ${\widehat{b}}_1,{\widehat{b}}_2,{\widehat{d}}_1$ and ${\widehat{d}}_2$ of the higher order method in ERKN5(4)M.

The above two solutions found resulted in the new Embedded explicit trigonometrically-fitted Runge–Kutta–Nyström 5(4) pair (EETFRKN5(4)).

4. Algebraic Order and Error Analysis

In this section, we will find the local truncation error of the new methods and verify their algebraic order. We first find the Taylor series expansion of the actual solution $y(x_n+h)$, the first derivative of the actual solution $y^{\prime }(x_n+h)$, the approximate solution $y_{n+1}$, and the first derivative of the approximate solution $y_{n+1}^{\prime }$. The local truncation error (LTE) of y and its first derivative $y^{\prime }$ is given as:

$$\begin{array}{c}LTE=y_{n+1}-y(x_n+h),\\ LT{E}_{der}=y_{n+1}^{\prime }-y^{\prime }(x_n+h).\end{array}$$

(17)

The $LTE$ and $LT{E}_{der}$ of the lower order method (order 4) are:

$$\begin{array}{cc}\hfill LTE=& -\frac{206,089h^5}{2,623,950,000}(3y^{\prime }{f}_{yy}{y}^{″}+6w^2{f}_x+6f_y{f}_x+{\left(y^{\prime }\right)}^3{f}_{yyy}+3y^{″}{f}_{xy}\hfill \\ & +6{\left(f_y\right)}^2{y}^{\prime }+3y^{\prime }{f}_{yxx}+3{\left(y^{\prime }\right)}^2{f}_{xyy}+6w^2{f}_y{y}^{\prime }+f_{xxx})+O\left(h^6\right),\hfill \\ \hfill LT{E}_{der}=& \frac{h^5}{120}(4{\left(y^{\prime }\right)}^3{f}_{xyyy}+{\left(y^{\prime }\right)}^4{f}_{yyyy}+6{\left(y^{\prime }\right)}^2{f}_{xxyy}+3{\left(y^{″}\right)}^2{f}_{yy}+4f_{xy}{f}_x\hfill \\ & +y^{″}{f}_{yxx}+{\left(f_y\right)}^2{y}^{″}+f_y{f}_{xx}+4y^{\prime }{f}_{xxxy}+f_{xxxx}+6{\left(y^{\prime }\right)}^2{f}_{yyy}{y}^{″}\hfill \\ & +5{\left(y^{\prime }\right)}^2{f}_{yy}{f}_y+12y^{\prime }{f}_{xyy}{y}^{″}+6f_y{y}^{\prime }{f}_{xy}+4y^{\prime }{f}_{yy}{f}_x)+O\left(h^6\right).\hfill \end{array}$$

(18)

From Equation $\left(18\right)$, we can see that the algebraic order of the lower order method is 4 because all of the coefficients up to $h^4$ vanished. Similarly, the $LTE$ and $LT{E}_{der}$ of the higher order method (order 5) are :

$$\begin{array}{cc}\hfill LTE=& -\frac{479h^6}{10,281,600}(6{\left(y^{\prime }\right)}^2{f}_{yyy}{y}^{″}+\frac{1416}{479}{\left(y^{\prime }\right)}^2{f}_{yy}{f}_y+12y^{\prime }{f}_{xyy}{y}^{″}+\frac{5616}{479}{f}_y{y}^{\prime }{f}_{xy}-\frac{2784}{479}{y}^{\prime }{f}_{yy}{f}_x-\frac{4200}{479}{w}^4{y}^{″}\hfill \\ \\ & +6{\left(y^{\prime }\right)}^2{f}_{xxyy}-\frac{2784}{479}{f}_{xy}{f}_x+4y^{\prime }{f}_{xxxy}+{\left(y^{\prime }\right)}^4{f}_{yyyy}+\frac{4200}{479}{\left(f_y\right)}^2{y}^{″}+4{\left(y^{\prime }\right)}^3{f}_{xyyy}+3{\left(y^{″}\right)}^2{f}_{yy}+6y^{″}{f}_{yxx}\hfill \\ \\ & +\frac{4200}{479}{f}_y{f}_{xx}+f_{xxxx})+O\left(h^7\right),\hfill \\ \hfill LT{E}_{der}=& \frac{h^6}{720}(10y^{″}{f}_{xxxy}+5y^{\prime }{f}_{xxxxy}+{\left(f_y\right)}^3{y}^{\prime }+10f_{yxx}{f}_x+{\left(y^{\prime }\right)}^5{f}_{yyyyy}+10y^{\prime }{\left(f_{xy}\right)}^2+10{\left(y^{\prime }\right)}^2{f}_{xxxyy}+5{(y^{{}^{\prime }})}^4{f}_{xyyyy}\hfill \\ \\ & +{\left(f_y\right)}^2{f}_x+5f_{xx}{f}_{xy}+f_y{f}_{xxx}+18y^{\prime }{f}_{yy}{f}_y{y}^{″}+f_{xxxxx}+5{\left(y^{\prime }\right)}^3{\left(f_{yy}\right)}^2+10{\left(y^{\prime }\right)}^3{f}_{xxyyy}+15{\left(y^{″}\right)}^2{f}_{xyy}+10{\left(y^{\prime }\right)}^2{f}_{yyy}{f}_x\hfill \\ \\ & +11{\left(y^{\prime }\right)}^3{f}_{yyy}{f}_y+15y^{\prime }{f}_{yyy}{\left(y^{″}\right)}^2+15{\left(y^{\prime }\right)}^2{f}_{yy}{f}_{xy}+30y^{\prime }{f}_{xxyy}{y}^{″}+8f_y{y}^{″}{f}_{xy}+10y^{″}{f}_{yy}{f}_x+13f_y{y}^{\prime }{f}_{yxx}+5y^{\prime }{f}_{yy}{f}_{xx}\hfill \\ \\ & +30{\left(y^{\prime }\right)}^2{f}_{xyyy}{y}^{″}+20y^{\prime }{f}_{xyy}{f}_x+10{\left(y^{\prime }\right)}^3{f}_{yyyy}{y}^{″}+23{\left(y^{\prime }\right)}^2{f}_y{f}_{xyy})+O\left(h^7\right).\hfill \end{array}$$

(19)

From Equation $\left(19\right)$, the higher order method has order 5 because all of the coeffients up to $h^5$ vanished.

Absolute Stability Analysis of the New Embedded Pair

The linear stability of the RKN method (2)–(4) is derived by applying it to the test equation $y^{″}=-w^{2}y$. Setting $H=-{\left(wh\right)}^2$, the numerical solution satisfies the following:

$$Z_{n+1}=P\left(H\right)Z_n,$$

where $Z_{n+1}=\left[\begin{array}{c}{y}_{n+1}\\ h{y}_{n+1}^{\prime }\end{array}\right]$, $Z_n=\left[\begin{array}{c}{y}_n\\ h{y}_n^{\prime }\end{array}\right]$, $P\left(H\right)=\left[\begin{array}{cc}1+H{b}^T{N}^{-1}e& wh(1+H{b}^T{N}^{-1}c)\\ -wh{d}^T{N}^{-1}e& 1+H{d}^T{N}^{-1}c\end{array}\right]$, $N=I-HA$, $A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& a_{13}& a_{14}\\ a_{21}& a_{22}& a_{23}& a_{24}\\ a_{31}& a_{32}& a_{33}& a_{34}\\ a_{41}& a_{42}& a_{43}& a_{44}\end{array}\right]$, $I=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right],$ $b={[b_1,b_2,b_3,b_4]}^T$, $d={[d_1,d_2,d_3,d_4]}^T$, $e={[1,1,1,1]}^T$, $c={[c_1,c_2,c_3,c_4]}^T$. It is assumed that $P\left(H\right)$ has complex conjugate eigenvalues for sufficiently small values of v [14]. With this assumption, a periodic numerical solution is obtained whose characteristic depends on the eigenvalues of $P\left(H\right)$, which is called the stability matrix and its characteristic equation can be written as

$${\lambda }^2-tr\left(P\left(H\right)\right)\lambda +det\left(P\left(H\right)\right)=0.$$

Definition 2.

An interval $(-H_b,0)$ of the RKN method (2)–(4) is said to be absolutely stable if for all $H\in (-H_b,0)$, $|{\lambda }_{1,2}|<1$, where ${\lambda }_{1,2}$ are the roots of $P\left(H\right)$.

Hence, we obtain the approximate interval of absolute stability of the higher order method (order 5) of our new embedded pair as $(-36.99,0)$ and the lower order method (order 4) has no interval of absolute stability.

5. Numerical Results

In order to show the efficiency of the new method, we use the following RK and RKN pairs for the numerical comparison:

• EETFRKN5(4)M: The new embedded explicit trigonometrically-fitted Runge–Kutta–Nyström pair (EETFRKN5(4)) derived in this paper,
• ERKN6(4)6ER: A 6(4) optimized embedded Runge–Kutta–Nyström pair derived by Anastassi and Kosti in [11],
• ERKN4(3): The embedded Runge–Kutta–Nyström method obtained by Van de Vyver in [6],
• ARKN5(3)S: A 5(3) pair of explicit adapted Runge–Kutta–Nyström method derived by Franco in [5],
• DOP5(4): A 5(4) Dormand and Prince embedded Runge–Kutta method given by Butcher in [15],

and by considering the following problems.

Problem 1.

(Almost Periodic Orbit Problem) Senu et al. in [8]

$$\begin{array}{ccc}\hfill y_1^{″}& =& -y_1+0.001cos\left(x\right),y_1\left(0\right)=1,y_1^{\prime }\left(0\right)=0,\hfill \\ \hfill y_2^{″}& =& -y_2+0.001sin\left(x\right),y_2\left(0\right)=0,y_2^{\prime }\left(0\right)=0.9995,x_{end}=100.\hfill \end{array}$$

The exact solution is

$$y_1\left(x\right)=cos\left(x\right)+0.0005xcos\left(x\right),$$

$$y_2\left(x\right)=sin\left(x\right)-0.0005xsin\left(x\right).$$

Problem 2.

(Nonlinear System) Fang et al. in [16]

$$\begin{array}{ccc}\hfill y_1^{″}& =& -4x^2{y}_1-\frac{2y_2}{{(y_1^2+y_2^2)}^{1/2}},y_1\left(0\right)=1,y_1^{\prime }\left(0\right)=0,\hfill \\ \hfill y_2^{″}& =& -4x^2{y}_2+\frac{2y_1}{{(y_1^2+y_2^2)}^{1/2}},y_2\left(0\right)=0,y_2^{\prime }\left(0\right)=0,x_{end}=10.\hfill \end{array}$$

The exact solution is

$$\begin{array}{ccc}\hfill y_1\left(x\right)& =& cos\left(x^2\right),\hfill \\ \hfill y_2\left(x\right)& =& sin\left(x^2\right).\hfill \end{array}$$

Problem 3.

(Nonhomogeneous System) Senu et al. in [8]

$$\begin{array}{ccc}\hfill y_1^{″}& =& -v^2{y}_1\left(x\right)+v^{2}f\left(x\right)+f^{″}\left(x\right),y_1\left(0\right)=a+f\left(0\right),y_1^{\prime }\left(0\right)=f^{\prime }\left(0\right),\hfill \\ \hfill y_2^{″}& =& -v^2{y}_2\left(x\right)+v^{2}f\left(x\right)+f^{″}\left(x\right),y_2\left(0\right)=f\left(0\right),y_2^{\prime }\left(0\right)=av+f^{\prime }\left(0\right),x_{end}=100.\hfill \end{array}$$

The exact solution is

$$\begin{array}{ccc}\hfill y_1\left(x\right)& =& acos\left(vx\right)+f\left(x\right),\hfill \\ \hfill y_2\left(x\right)& =& asin\left(vx\right)+f\left(x\right),\hfill \end{array}$$

where $v=1.0$, $a=0.1$ are parameters and $f\left(x\right)=e^{-10x}$.

Problem 4.

(Almost Periodic Problem) Van de Vyver in [6]

$$\begin{array}{ccc}\hfill y_1^{″}& =& -y_1+ϵcos\left(\mathrm{\Psi }x\right),y_1\left(0\right)=1,y_1^{\prime }\left(0\right)=0,\hfill \\ \hfill y_2^{″}& =& -y_2+ϵsin\left(\mathrm{\Psi }x\right),y_2\left(0\right)=0,y_2^{\prime }\left(0\right)=1.\hfill \end{array}$$

The exact solution is

$$y_1\left(x\right)=\frac{(1-ϵ-{\mathrm{\Psi }}^2)}{(1-{\mathrm{\Psi }}^2)}cos\left(x\right)+\frac{ϵ}{(1-{\mathrm{\Psi }}^2)}cos\left(\mathrm{\Psi }x\right),$$

$$y_2\left(x\right)=\frac{(1-ϵ\mathrm{\Psi }-{\mathrm{\Psi }}^2)}{(1-{\mathrm{\Psi }}^2)}sin\left(x\right)+\frac{ϵ}{(1-{\mathrm{\Psi }}^2)}sin\left(\mathrm{\Psi }x\right),$$

where $ϵ=0.001$, $\mathrm{\Psi }=0.1$ and $x_{end}=100$.

The numerical results are shown in Table 2, Table 3, Table 4 and Table 5.

Table 2. Numerical results for Problem 1.

TOL	METHOD	STEP	FCN	FSTEP	MAXE	TIME (s)
${10}^{-2}$	EETFRKN5(4)M	63	252	0	1.589499(-4)	0.312
	ARKN5(3)S	242	968	0	9.829659(-1)	0.812
	ERKN6(4)6ER	215	1290	0	7.375736(-1)	1.063
	ERKN4(3)	578	2315	1	2.175738(-1)	1.031
	DOP5(4)	121	726	0	7.747317(-3)	0.531
${10}^{-4}$	EETFRKN5(4)M	132	528	0	3.336685(-6)	0.359
	ARKN5(3)S	1044	4179	1	6.406274(-2)	1.547
	ERKN6(4)6ER	825	4955	0	5.685758(-2)	1.531
	ERKN4(3)	2901	11,610	2	8.650517(-3)	2.000
	DOP5(4)	262	1572	0	1.273632(-4)	1.531
${10}^{-6}$	EETFRKN5(4)M	283	1132	0	7.329552(-8)	1.230
	ARKN5(3)S	4491	17,970	2	3.460856(-3)	3.044
	ERKN6(4)6ER	3180	19,090	2	3.817832(-3)	2.904
	ERKN4(3)	29,131	116,536	4	8.569318(-5)	14.371
	DOP5(4)	561	3366	0	2.521377(-6)	2.531
${10}^{-10}$	EETFRKN5(4)M	654	2616	0	1.089911(-9)	1.250
	ARKN5(3)S	83,362	333,460	4	1.003239(-5)	41.557
	ERKN6(4)6ER	94,782	568,717	5	4.291853(-6)	41.977
	ERKN4(3)	2,940,668	11,762,696	8	8.077835(-9)	1347.362
	DOP5(4)	5210	31,260	0	3.630829(-11)	4.531

EETFRKN5(4)M: The new embedded explicit trigonometrically-fitted Runge–Kutta–Nyström pair derived in this paper; ARKN5(3)S: A 5(3) pair of explicit Adapted Runge–Kutta–Nyström method derived by Franco in [5]; ERKN4(3): The embedded Runge–Kutta–Nyström method obtained by Van de Vyver in [6]; ERKN6(4)6ER: A 6(4) optimized embedded Runge–Kutta–Nyström pair derived by Anastassi and Kosti in [11]; DOP5(4): A 5(4) embedded Runge–Kutta method given by Butcher in [15]; TOL: The tolerance used; STEP: Execution steps; FCN: Function evaluation; FSTEP: Are the failed steps; MAXE: Maximum global error; TIME (s): Execution time in seconds.

Table 3. Numerical results for Problem 2.

TOL	METHOD	STEP	FCN	FSTEP	MAXE	TIME (s)
${10}^{-2}$	EETFRKN5(4)M	77	320	4	1.868952(-2)	0.500
	ARKN5(3)S	391	1579	5	7.585297(-2)	1.297
	ERKN6(4)6ER	412	2502	6	2.409650(-1)	1.685
	ERKN4(3)	1391	5585	7	4.620804(-2)	1.984
	DOP5(4)	148	908	4	1.003445(-1)	0.703
${10}^{-4}$	EETFRKN5(4)M	203	824	4	1.883175(-4)	0.844
	ARKN5(3)S	1768	7090	6	3.050204(-3)	2.250
	ERKN6(4)6ER	2119	12,749	7	1.047787(-2)	2.188
	ERKN4(3)	6278	25,136	8	2.250399(-3)	5.234
	DOP5(4)	369	2234	4	8.921876(-4)	1.020
${10}^{-6}$	EETFRKN5(4)M	507	2040	4	1.389967(-6)	1.609
	ARKN5(3)S	8001	32,025	7	1.295624(-4)	5.636
	ERKN6(4)6ER	9744	58,504	8	4.798031(-4)	6.125
	ERKN4(3)	30,571	122,311	9	8.727528(-5)	15.296
	DOP5(4)	915	5510	4	7.372093(-6)	2.703
${10}^{-8}$	EETFRKN5(4)M	1208	4844	4	1.809555(-8)	1.844
	ARKN5(3)S	36,949	147,823	9	6.030980(-6)	19.549
	ERKN6(4)6ER	42,606	255,681	9	2.359393(-5)	20.213
	ERKN4(3)	300,521	120,214	10	8.837019(-7)	134.762
	DOP5(4)	2202	13,232	4	7.347484(-8)	3.124
${10}^{-10}$	EETFRKN5(4)M	2968	11,887	5	1.891552(-10)	3.584
	ARKN5(3)S	180,503	722,042	10	3.607369(-7)	86.196
	ERKN6(4)6ER	202,603	1,215,673	11	1.132031(-6)	86.814
	ERKN4(3)	3,017,354	12,069,452	12	1.646494(-8)	1620.306
	DOP5(4)	5378	32,293	5	1.071751(-9)	5.223

Table 4. Numerical results for Problem 3.

TOL	METHOD	STEP	FCN	FSTEP	MAXE	TIME (s)
${10}^{-2}$	EETFRKN5(4)M	65	263	1	2.665158(-3)	0.250
	ARKN5(3)S	133	541	3	1.336913(-1)	0.328
	ERKN6(4)6ER	219	1324	2	6.973318(-2)	0.422
	ERKN4(3)	588	2361	3	2.107025(-2)	0.719
	DOP5(4)	127	772	2	1.107309(+1)	0.344
${10}^{-4}$	EETFRKN5(4)M	138	555	1	7.897400(-5)	0.359
	ARKN5(3)S	551	2213	3	2.752336(-2)	0.828
	ERKN6(4)6ER	429	2589	3	2.187558(-2)	0.609
	ERKN4(3)	3005	12,035	5	8.461092(-4)	1.703
	DOP5(4)	529	3184	2	1.1000002(+1)	1.030
${10}^{-6}$	EETFRKN5(4)M	164	662	2	5.757119(-7)	0.422
	ARKN5(3)S	4523	18,137	15	9.530356(-4)	2.188
	ERKN6(4)6ER	1688	10,153	5	1.495030(-3)	1.047
	ERKN4(3)	15,709	62,857	7	3.359187(-5)	6.748
	DOP5(4)	1143	6868	2	1.099999(+1)	2.344
${10}^{-8}$	EETFRKN5(4)M	355	1426	2	8.919276(-9)	0.625
	ARKN5(3)S	9943	39,796	8	1.652088(-4)	4.453
	ERKN6(4)6ER	6550	39,330	6	1.003134(-4)	3.069
	ERKN4(3)	85,151	340,631	9	1.337546(-6)	36.152
	DOP5(4)	2483	14,913	3	1.100000(+1)	3.031
${10}^{-10}$	EETFRKN5(4)M	774	3102	2	1.223295(-10)	0.781
	ARKN5(3)S	43,042	172,186	6	4.372055(-6)	17.310
	ERKN6(4)6ER	48,932	293,632	8	1.680967(-6)	20.141
	ERKN4(3)	855,349	3,421,429	11	1.314822(-8)	356.970
	DOP5(4)	5379	32,289	3	1.100000(+1)	4.344

Table 5. Numerical results for Problem 4.

TOL	METHOD	STEP	FCN	FSTEP	MAXE	TIME (s)
${10}^{-2}$	EETFRKN5(4)M	122	488	0	5.791290(-4)	0.424
	ARKN5(3)S	242	968	0	2.111440(-1)	0.453
	ERKN6(4)6ER	215	1290	0	7.335990(-1)	0.453
	ERKN4(3)	578	2315	1	2.168852(-1)	0.844
	DOP5(4)	121	726	0	7.766793(-3)	0.429
${10}^{-4}$	EETFRKN5(4)M	262	1048	0	1.294696(-5)	0.578
	ARKN5(3)S	1044	4179	1	1.141697(-2)	1.109
	ERKN6(4)6ER	825	4955	1	5.673723(-2)	0.781
	ERKN4(3)	2901	11,610	2	8.642825(-3)	1.547
	DOP5(4)	262	1572	0	1.275701(-4)	1.422
${10}^{-6}$	EETFRKN5(4)M	562	2248	0	2.671335(-7)	0.656
	ARKN5(3)S	4491	17,970	2	6.156293(-4)	2.219
	ERKN6(4)6ER	3180	19,090	2	3.814429(-3)	1.656
	ERKN4(3)	29,131	116,536	4	8.562316(-5)	12.500
	DOP5(4)	561	3366	0	2.521051(-6)	2.422
${10}^{-8}$	EETFRKN5(4)M	1211	4844	0	5.680715(-9)	0.859
	ARKN5(3)S	19347	77,397	3	3.316106(-5)	8.094
	ERKN6(4)6ER	24,548	147,308	4	6.394316(-5)	10.047
	ERKN4(3)	292,676	1,170,722	6	8.477710(-7)	123.098
	DOP5(4)	1210	7260	0	5.343219(-8)	3.422
${10}^{-10}$	EETFRKN5(4)M	2622	10488	0	1.301748(-10)	1.500
	ARKN5(3)S	83,362	333,460	4	1.785978(-6)	34.359
	ERKN6(4)6ER	94,782	568,717	5	4.2883486(-6)	37.406
	ERKN4(3)	2,940,668	11,762,696	8	8.074738(-9)	1164.595
	DOP5(4)	5210	31,260	0	3.620826(-11)	4.422

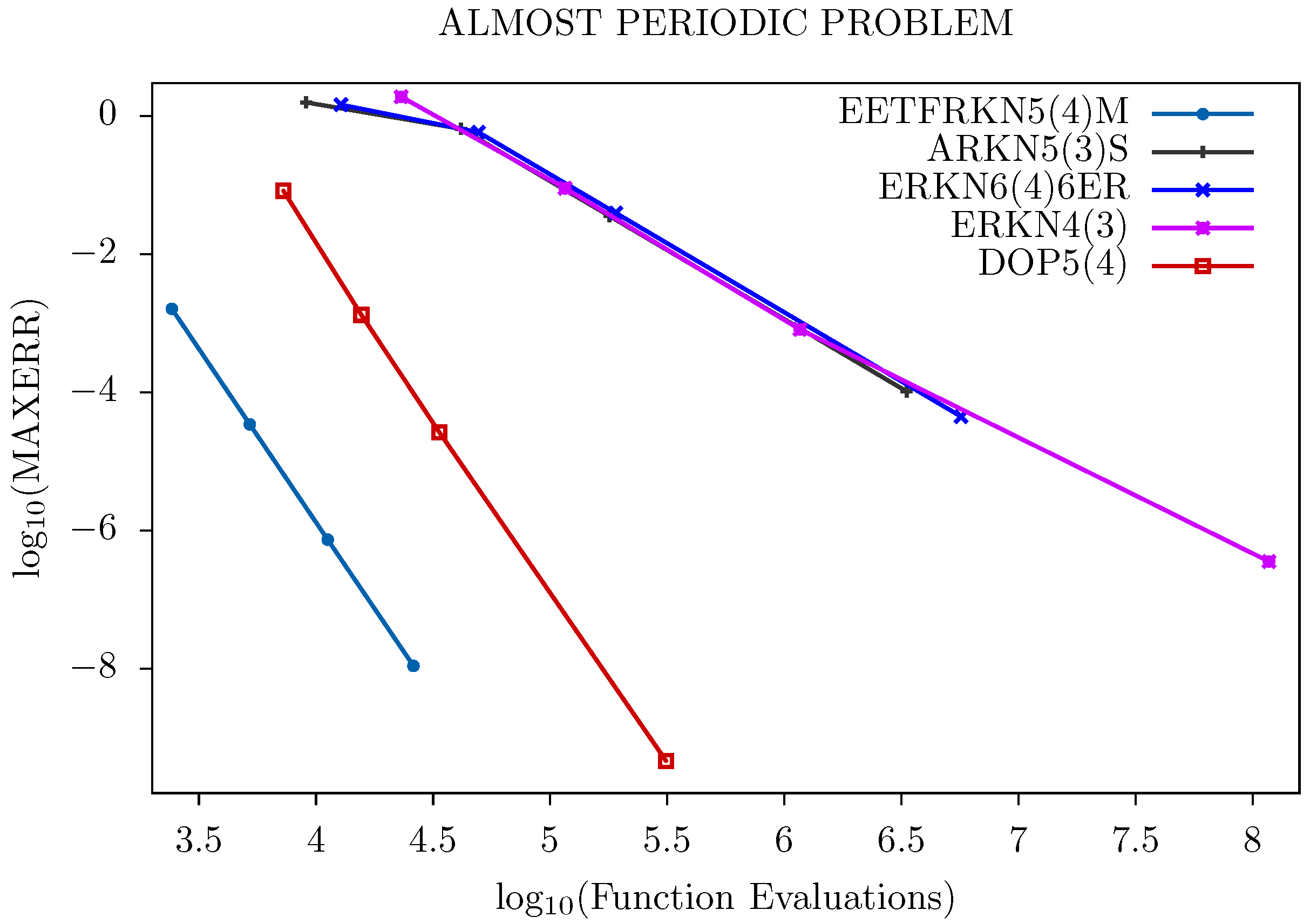
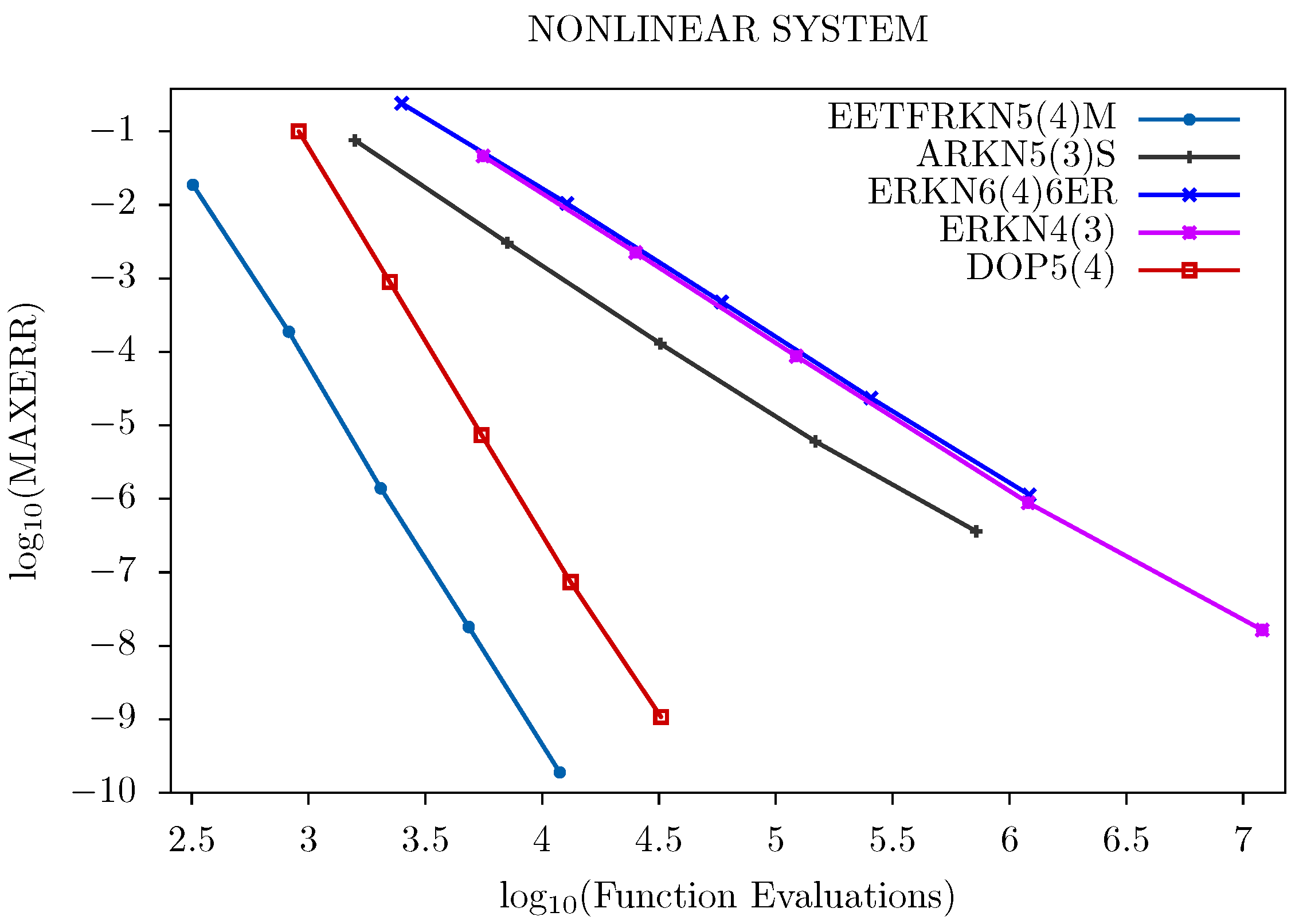
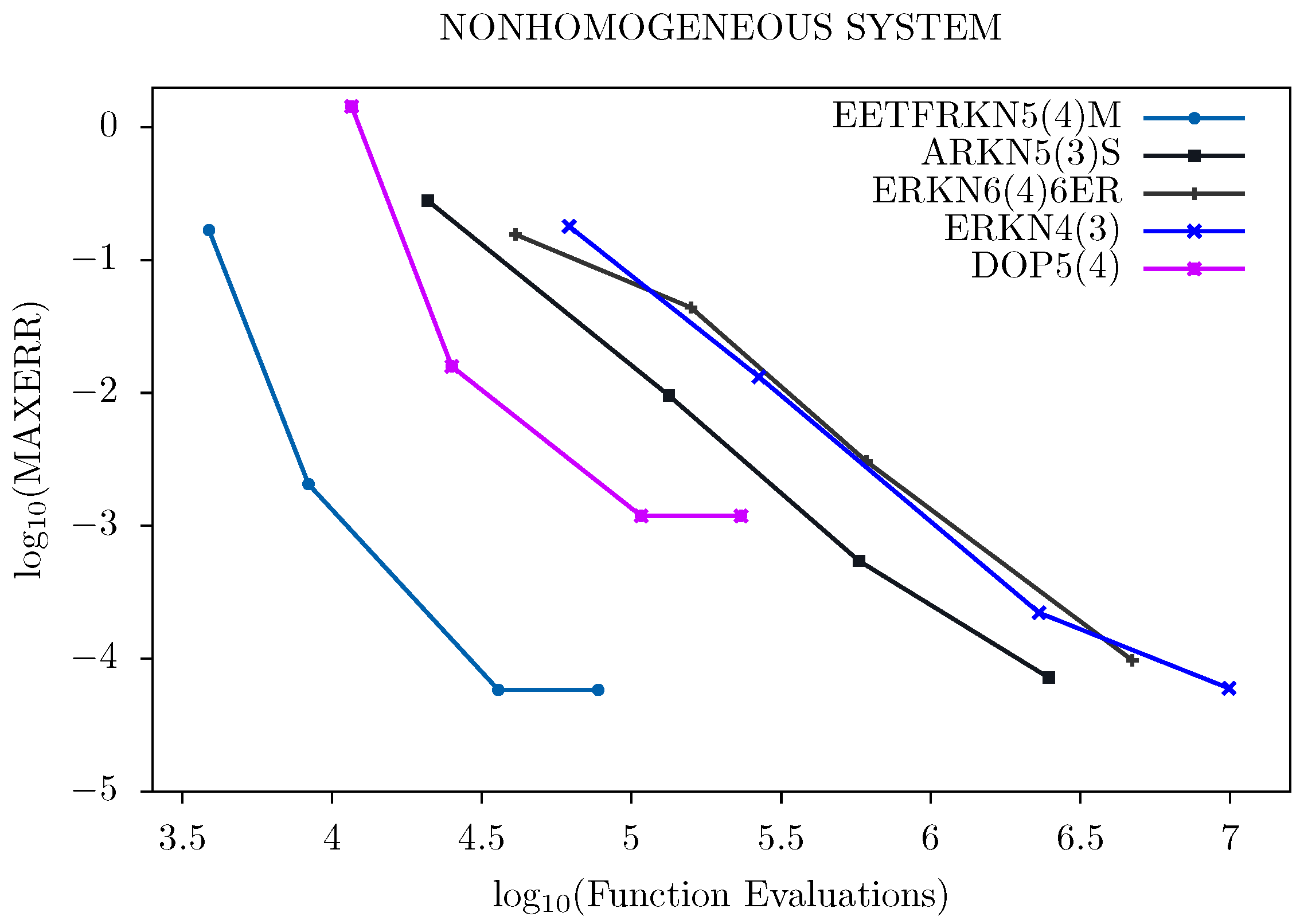
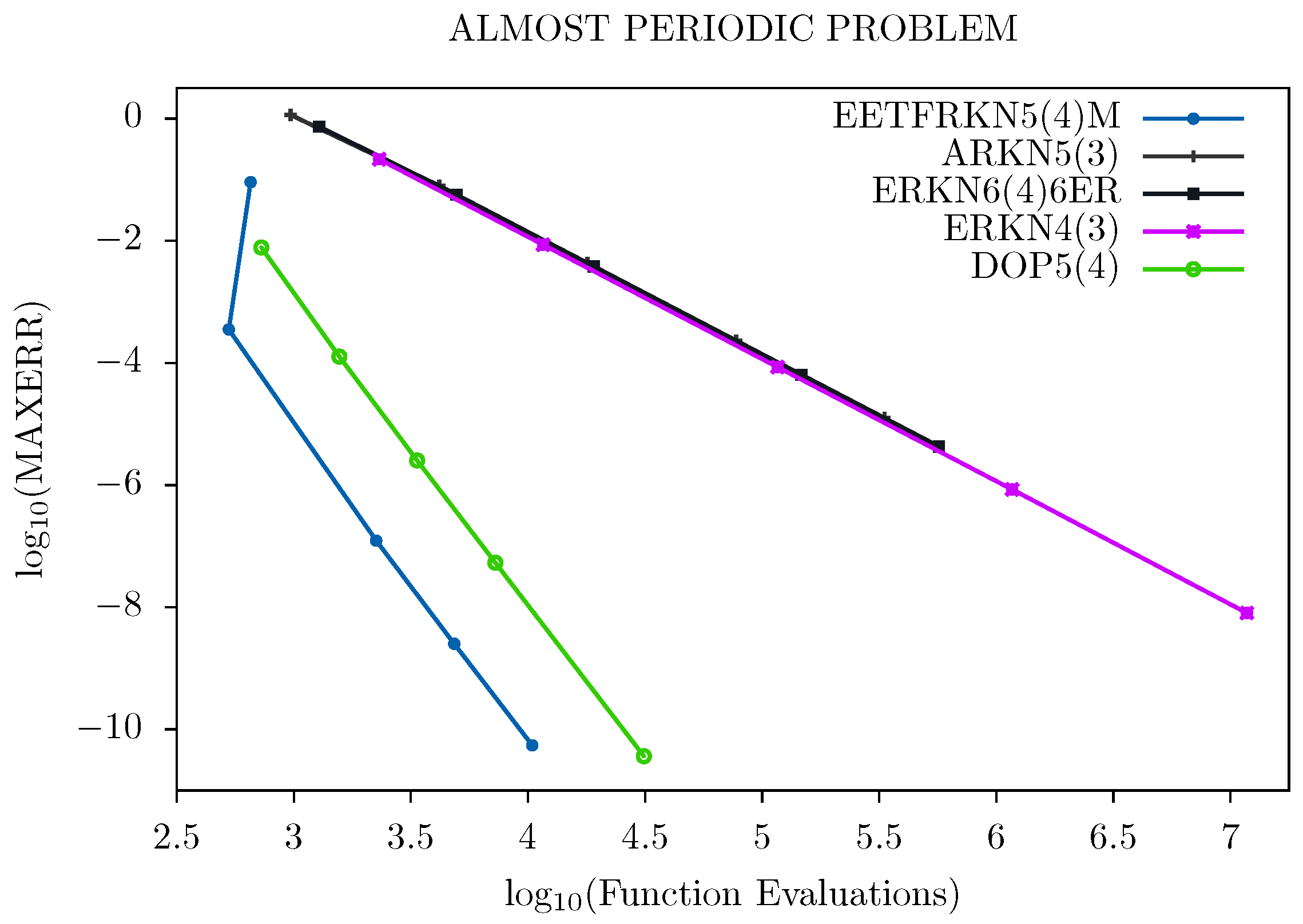
We further display the performance of these methods graphically in Figure 1, Figure 2, Figure 3 and Figure 4. The tolerances used for Problem 1 are: Tol = ${10}^{-2i},i=1,2,3,5,$ and that of Problems 2–4 are: Tol = ${10}^{-2i}$, $i=1,2,3,4,5$.

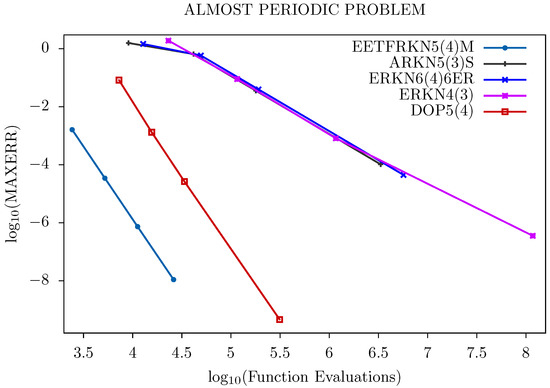
Figure 1. Efficiency curves for Problem 1.

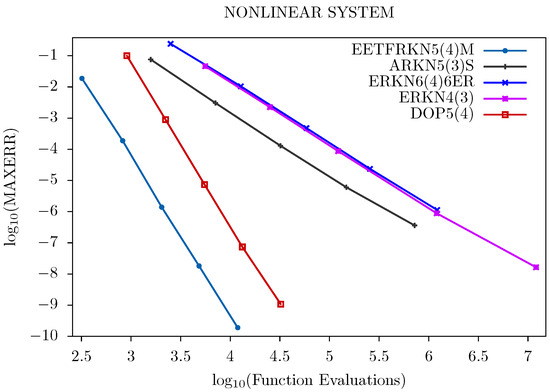
Figure 2. Efficiency curves for Problem 2.

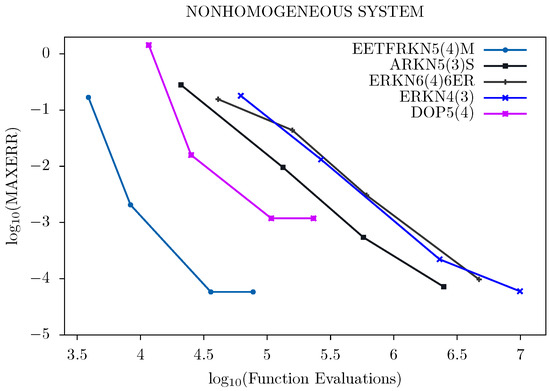
Figure 3. Efficiency curves for Problem 3.

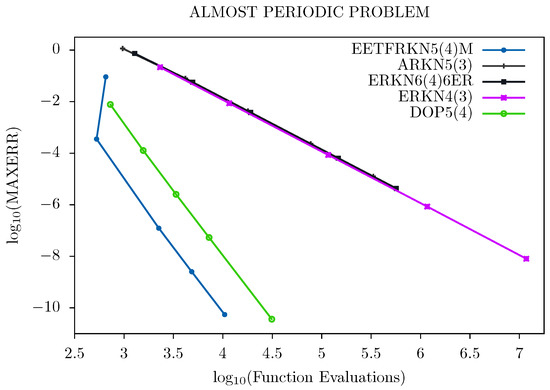
Figure 4. Efficiency curves for Problem 4.

6. Discussion

For all of the problems tested and from Figure 1, Figure 2, Figure 3 and Figure 4, we can deduce that our new method has a lower number of function evaluations per step, which signifies that our new method has less computational costs than the other existing methods, and is therefore more suitable for solving second order ordinary differential equations with oscillatory solutions than the other existing methods in the literature.

7. Conclusions

In this study, we have derived a new efficient 5(4) embedded pair of explicit trigonometrically-fitted Runge–Kutta–Nyström methods for the solution of oscillatory initial value problems. The numerical results obtained indicate that the function evaluations per step of the new method are less when compared with the other existing embedded pairs. Hence, the new method has less computational costs than the other existing methods, and, therefore, the efficiency of the new method is higher than the other existing methods.