Abstract
Operating in unstable and competitive globalized markets, management of today’s transnational enterprises continually searches for different alternatives to maintain product quality, streamline production activities, and reduce overall operating costs, particularly in their internal supply chain system. With the aim of revealing and offering insight information to support managerial decision making, this study explores the optimal replenishment lot-size and shipping frequency problem for an intra-supply chain system with a partial outsourcing policy and random scrap. In this study, the demand of a product is partially outsourced and partially fabricated by the production units, to release the workload of machine and smooth production schedule. During the fabrication process, a portion of random scrap items is produced, and finished products are distributed to sales locations using a multiple-shipment policy. The objective is to simultaneously determine an optimal fabrication lot-size and shipping frequency decisions that minimize the overall expected costs for such an intra-supply chain system. Mathematical modeling and optimization methods are used to solve the problem. Moreover, through the use of a numerical example and sensitivity analyses, various important insights with regard to the joint effects of the partial outsourcing policy and random scrap on the optimal solutions are revealed to support managerial decision making.
1. Introduction
Operating in competitive globalized markets, management of today’s transnational enterprises constantly searches for different alternatives in order to maintain product quality, streamline production activities, and reduce overall operating costs, particularly in their internal supply chain system. Moreover, due to the existence of production capacity constraint in most real manufacturing environments, sometimes adoption of a partial outsourcing policy can help managers to partially release a portion of workloads from the production equipment, hence smoothing machine utilization and production operation/schedule, and reducing the potential overtime cost.
With the aim of providing sound analytical information to help managerial decision making on the optimal outsourcing policy, this study constructs a hybrid production-outsourcing model to explore the optimal replenishment lot-size and shipment problem for an intra-supply chain system with a partial outsourcing policy and random scrap. The objective of this study is to simultaneously determine an optimal fabrication lot size and shipping frequency decisions that minimize the overall expected costs for such an intra-supply chain system. Mathematical modeling and optimization methods are used to solve the problem, and through the use of a numerical example and sensitivity analyses various important insights with regard to the joint effects of the partial outsourcing policy and random scrap on the optimal solutions are revealed to support managerial decision makings.
2. Literature Review
In contrast to the conventional economic production quantity (EPQ) model, Taft [1] used a mathematical approach to portray a simplified production system, wherein a perfect fabrication process and continuous inventory issuing policy was assumed. The real-life vendor-buyer integrated systems consider practical situations, such as adoption of an outsourcing policy, action for defective products, and a discontinuous periodic multiple shipments of end products. Due to the existence of production capacity constraint in most real manufacturing environments, sometimes adoption of a partial outsourcing policy can help managers to partially release a portion of workloads from the production equipment, hence smoothing machine utilization and production operation/schedule, and reducing the potential overtime cost. However, some efforts are required toward selection of qualified outsourcing contractors/vendors and an extra percentage of the cost is associated with unit purchase expense compared to that of unit in-house production cost. Coman and Ronen [2] analyzed an outsourcing problem and identified the pertinent variables and their relationships. They used a linear programming approach to solve the problem, including examinations of models with standard cost accounting and standard theory of constraints, as well as a model proposed by them. Different results enable managers to determine which products to manufacture and which to outsource. An operational ratio is proposed to the problem, which avoids solving a linear programming problem. They claimed that their proposed model is simpler to apply and requires the computation of fewer variables than other prevalent models. Cachon and Harker [3] examined a competition and outsourcing problem with scale economies. They assumed that the cost per unit of demand is decreasing in demand, two vendors with price- and time-sensitive demand, and competition between two retailers with fixed order costs and price-sensitive buyers. They showed that for the case of two vendors, there was an enviable situation where the lower cost firm has a higher market share and a higher price. When allowing the firms to outsource their production process to a supplier, their study showed that the firms strictly prefer to outsource. They revealed that scale economies provide a strong motivation for outsourcing. Fu et al. [4] studied the inventory and production problem for an assemble-to-order system with uncertain demand and limited assembly capacity. Profit maximization models with outsourcing option are examined, and their objectives were to derive the optimal inventory and production decisions for their studied models. They presented the structural properties of optimal solutions, developed the efficient solution procedures to the problems, and provided sensitivity analysis and managerial insights of the optimal decisions. Narayanan et al. [5] studied the role of integration in business process outsourcing (BPO) and its effect on BPO firm performance. Both the internal process integration to effective integration of task execution within the BPO and the external process integration to effective integration between the BPO and their clients were are examined. The survey data from 205 Indian BPO service providers was use to analyze the antecedents of process integration and its impact on BPO performance, wherein task complexity, task security, end customer orientation of the client, and information technology capability of the BPO were investigated. They found that both internal and external process integration partially mediate the impact of the antecedents on performance. Managerial implications on how to successfully implementing the BPO were provided. Additional studies that related to various aspects of fabrication systems with an outsourcing option can also be found elsewhere [6,7,8,9,10,11,12].
During the manufacturing process, a variety of uncontrollable factors may cause unexpected defective items to be produced. Porteus [13] determined the optimal lot size for a production process with quality improvement and reduction of setup cost. It was assumed that the status of in-control process may shift to out-of-control status. Accordingly, a two-state Markov chain is developed to derive the optimal lot size that minimized the overall costs. Makis [14] simultaneously derived the optimal lot-size and inspection policy for an economic manufacturing quantity (EMQ) model with imperfect inspections. It was assumed that through inspections the production process could be monitored, the in-control periods are generally distributed, and the inspections are imperfect. Lagrange’s method was used to solve the nonlinear equations. Additionally, a two-dimensional search procedure for the optimal lot-size and inspection policy were proposed. Sana [15] examined an imperfect production-inventory model with the objectives of determining the optimal product reliability and production rate so that total integrated profit of the system can be maximized. An optimal control formulation of the problem was provided and the necessary and sufficient conditions for optimality of the dynamic variables were developed. Using the Euler-Lagrange method, the optimal solutions for product reliability parameter and dynamic production rate were obtained. Other papers that addressed various aspects of fabrication systems with defective items or quality improvement issues can also be found elsewhere [16,17,18,19,20,21,22,23,24,25,26,27,28].
In real-life vendor–buyer integrated inventory systems, finished products often are delivered by a periodic multi-shipment policy. Schwarz [29] examined a single-warehouse multi-retailer inventory system with the objectives of deciding the optimal stocking policy and revealing some necessary properties for the optimal policy. For the general problem, he proposed heuristic solutions and tested against their analytical lower bounds. Sarker and Parija [30] derived an optimal batch size for a production system with a fixed quantity periodic delivery policy. They considered that the raw materials of a fabrication system are purchased from suppliers and then these materials are manufactured for conversion to finished products. A model was proposed to portray such a system, and a minimum-cost solution procedure was provided to decide an optimal raw materials ordering policy and optimal in-house fabrication lot size for the system operating under an equal-shipment delivery plan. Ertogral et al. [31] examined a production and shipment lot sizing problem in a vendor–buyer supply chain with transportation cost, wherein the finished products are delivered under an equal-size shipment policy. Transportation cost was explicitly incorporated into their system and its cost minimization solution process to obtain the optimal operating policy. Additional studies related to different aspects of supply-chain systems with multi-shipment policy can also be referred elsewhere [32,33,34,35,36,37,38,39,40]. With the aim of providing managers of intra-supply chain systems with insight information to support their decision makings, this study incorporates a beneficial outsourcing option into a prior work [18], and explores the optimal replenishment lot-size and shipping frequency problem with a partial outsourcing policy and random scrap. The objective is to simultaneously decide the optimal fabrication lot size and number of shipments per cycle to minimize the expected system cost for the problem. As little attention has been paid to this particular area, the present study is intended to fill the gap.
3. Methods
Problem Statement and Mathematical Modeling
This study explores the optimal replenishment lot-size and shipping frequency problem for an intra-supply chain system with a partial outsourcing policy and random scrap. Consider a product that has a demand of λ units per year and this item can be fabricated at a rate of P units per year. The fabrication process randomly produces an x portion of scrap items at a rate of d, hence, d = Px. Under the ordinary operating policy of the EPQ model, the production rate P must be larger than the sum of demand rate λ and production rate of scrap items d. Hence, (P − d − λ) > 0 is required to avoid a stock-out situation. It is further assumed that in any production cycle there is a π portion (where 0 ≤ π ≤ 1) of batch size Q that is supplied by outside vendor and the other (1 − π) portion of Q is produced in-house. Outsourcing items are received at the time when the in-house production uptime ends (see Figure 1) and they are of perfect quality as guaranteed by the vendor. It is noted that when π = 0, the studied EPQ-based system becomes a 100% in-house fabrication system and on the contrary, if π = 1 then all items are supplied by outside vendor—it becomes a pure ‘buy’ rather than ‘make’ situation. Upon receipt of the outsourcing items, fixed quantity n installments of the entire batch are transported to the customer, at a fixed interval of time during the production downtime t2π.
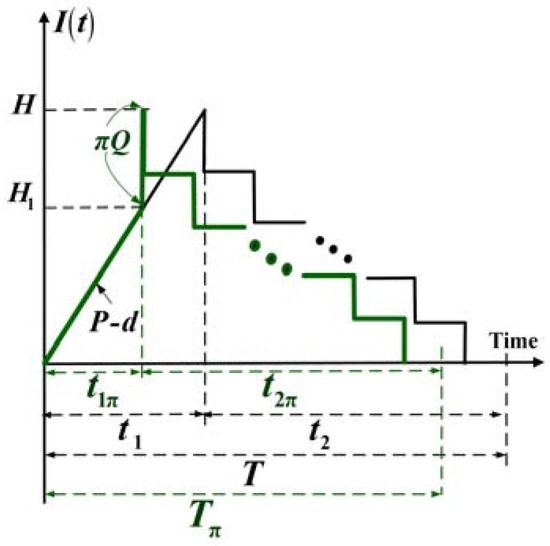
Figure 1.
The on-hand inventory level of perfect quality items in the proposed model (in green) as compared to that in the same model without outsourcing (in black).
Other notation used in this study includes the following:
- Tπ = the replenishment cycle time of the proposed system,
- T = the replenishment cycle time for a production system without outsourcing,
- πQ = outsourcing quantity per replenishment cycle,
- K = in-house production setup cost per cycle,
- C = unit fabrication cost, which includes unit cost of inspection,
- h = holding cost per item per unit time,
- CS = unit disposal cost,
- Kπ = fixed order (setup) cost of outsourcing items per cycle,
- Cπ = unit purchasing cost of outsourcing items,
- β1 = the relating parameter between Kπ and K, that is Kπ = (1 + β1)K where 0 ≤ β1 ≤ 1,
- β2 = the relating parameter between Cπ and C, that is Cπ = (1 + β2)C where β2 ≥ 0,
- H1 = on-hand inventory in units at the time in-house production ends,
- H = maximum level of on-hand inventory in units after receiving outsourcing items,
- t1π = production uptime for the proposed system,
- t2π = time required for transporting all items,
- t1 = uptime of the conventional EPQ model,
- t2 = delivery time of the conventional EPQ model,
- I(t) = on-hand inventory of perfect quality items at time t,
- Id(t) = on-hand inventory of scrap items at time t,
- K1 = fixed transportation cost per shipment,
- CT = unit transportation cost,
- n = number of fixed quantity installments of the finished batch to be delivered per cycle,
- tn = the fixed interval of time between each installment delivered during downtime t2π,
- h2 = unit stock holding cost per unit time at the customer’s side,
- Ic(t) = on-hand inventory of stocks at the customer’s side at time t,
- TC(Q,n) = total production-inventory-delivery cost per cycle for the proposed system,
- E[TCU(Q,n)] = the long-run average costs per unit time for the proposed system.
The maximum level of scrap items is:
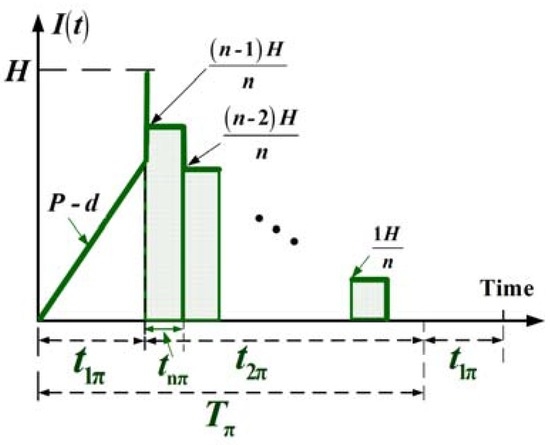
Figure 2.
The on-hand inventory of the perfect quality items in delivery time t2π.
Transportation cost per shipment is:
Total transportation costs per cycle are:
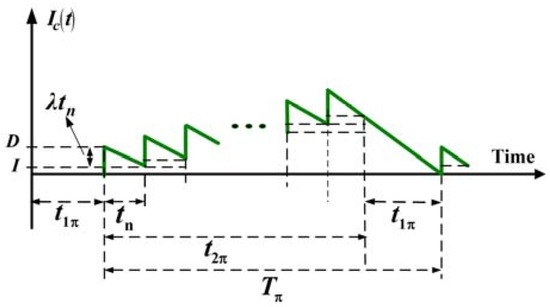
Figure 3.
The on-hand inventory of products stored at the customer’s side Ic(t) in the proposed model (where D is the quantity per shipment, and I is the left-over quantity after demand λtn is satisfied [18]).
Total production-inventory-delivery costs per cycle TC(Q, n), consists of fixed and variable outsourcing costs, setup and variable in-house production costs, disposal cost for scrap items, fixed and variable delivery costs, holding cost during uptime t1π and downtime t2π, and stock holding cost at the customer’s side. Hence, TC(Q, n) is as follows:
Substituting Kπ and Cπ in Equation (12), we have:
We use the expected values of x in the cost analysis to cope with the randomness of scrap rate, by substituting all related variables from Equations (1) to (7) into TC(Q, n) (i.e., Equation (13)), the long-run average system costs per unit time, E[TCU(Q, n)] becomes:
4. Results
4.1. The Convexity of E[TCU(Q, n)]
Since the number of shipments n is integer. For the proof of convexity of E[TCU(Q, n)], we first show that given n, E[TCU(Q, n)] is convex with respect to Q as follows:
Equation (16) results positive, because (2 + β1), K, n, K1, λ, [1 − E[x](1 − π)], and Q are all positive. Hence, E[TCU(Q, n)] is convex with respect to all Q different from zero.
Then, given Q, we need to show that the optimal n exists, or E[TCU(Q, n + 1)] + E[TCU(Q, n − 1)] − 2{E[TCU(Q, n)] ≥ 0. Let δn+1 = E[TCU(Q, n + 1)], δn = E[TCU(Q, n)], and δn−1 = E[TCU(Q, n − 1)]. By applying Equation (14), we have (δn+1 − δn) and (δn−1 − δn) as follows:
and:
or:
In general, the holding cost at the customer’s side is greater than or equal to that in the producer’s factory, i.e., (h2 − h) ≥ 0; also, based on the assumption EPQ model, annual production rate is much greater than annual demand rate, hence P[1 − E[x]] − λ ≥ 0. Therefore, for n ≥ 2, Equation (20) is resulting greater than or equal to zero. A computational verification is provided in Table A1 (refer to Appendix A for details).
4.2. Deriving the Optimal Operating Policy
Given n, to derive the optimal lot size, we can set Equation (15) equal to zero, and solve the optimal lot size Q* as follows:
Then, in order to find the optimal number of shipments n, we propose the following searching procedure:
- (1)
- Let n = 1 initially, and apply Equations (14) and (21) to compute the values of Q, δn, δn+1, and (δn+1 − δn).
- (2)
- Let n = n + 1, and calculate the values of Q, δn, δn−1, δn+1, (δn−1 − δn), and (δn+1 − δn).
- (3)
- If both (δn−1 − δn) ≥ 0 and (δn+1 − δn) ≥ 0, then go to step (4); otherwise, go to step (2).
- (4)
- Stop. The optimal number of shipments n* and optimal lot size Q* are obtained.
A step-by-step demonstration of the aforementioned searching procedure is presented in Table 1 (see Section 5.1 for details).

Table 1.
Iterations of the proposed searching procedure for optimal n* (please refer to Section 4.1 for definition for δn, δn−1, and δn+1).
5. Implications
5.1. Numerical Example
Consider a product that has an annual demand rate λ = 4000 and this item can be fabricated at a rate of P = 20,000 units per year. The setup cost K is $5,000 per production run and all items produced are screened and the inspection cost per unit is included in the production cost C = $100 per unit. A portion π is supplied by an outside vendor with a fixed outsourcing cost Kπ = $30 (i.e., β1 = −0.7) and unit outsourcing cost Cπ = $130 (i.e., β2 = 0.3). The in-house production process may randomly produce an x portion of scrap items which follows a uniform distribution over the interval [0, 0.2]. Other values of system parameters include the following:
- h = $30 per item per year,
- CS = $20, disposal cost per scrap item,
- K1 = $800, fixed transportation cost per shipment,
- CT = $0.5, transportation cost per item.
First, by applying Equation (14), we conducted a computational verification on that given Q, (δn−1 + δn+1) − 2(δn) ≥ 0 (please refer to Table A1 in Appendix A for details). Then, for the optimal operating policy, we apply the searching procedure presented in Section 4.2 and obtain the optimal number of shipments n* = 3, optimal replenishment batch size per cycle Q* = 1229, and the long-run average system cost per unit time E[TCU(Q*, n*)] = $545,344 (see Table 1 for details).
For π = 0.4, the behavior of E[TCU(Q, n)] with respect to the lot size Q is illustrated in Figure 4.
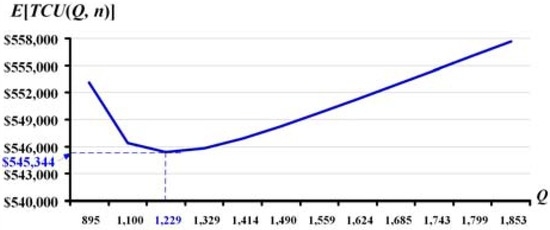
Figure 4.
The behavior of E[TCU(Q, n)] with respect to the lot size Q.
5.2. Sensitivity Analysis with Respect to the Scrap Rate x
Since during the production process a portion of scrap items may be produced randomly, the joint effects of various scrap rates and lot sizes are specifically analyzed, and the results are demonstrated in Figure 5. It is noted that as scrap rate x increases, the expected system cost E[TCU(Q, n)] increases notably.
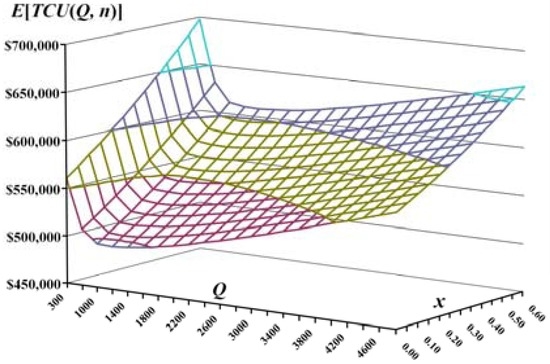
Figure 5.
The joint effects of different lot size Q and scrap rate x on the expected system cost E[TCU(Q, n)].
Further analysis indicates that a critical scrap rate exists at x = 0.339 (see Figure 6). Meaning that if the scrap rate of a production system exceeds this critical point, then the completely outsourcing policy (i.e., π = 1) becomes the better choice than a partial or no outsourcing option, in terms of cost savings.
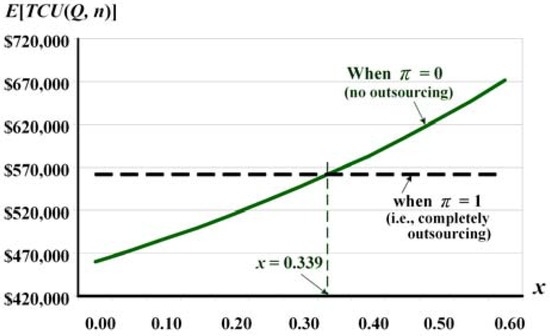
Figure 6.
Analysis of the critical scrap rate x in production in the proposed model.
5.3. Sensitivity Analysis with Respect to Outsourcing Proportion π
A further analysis reveals that a critical outsourcing cost factor β2 exists (see Figure 7) at β2 = 0.188, in the numerical example with a uniformly distributed scrap rate range of [0, 0.2]. This represents that if the outsourcing cost factor β2 is less than the critical point (i.e., Cπ < $118.80), then the completely outsourcing policy (i.e., π = 1) turns into the better choice than a partial or no outsourcing option, in terms of cost savings.
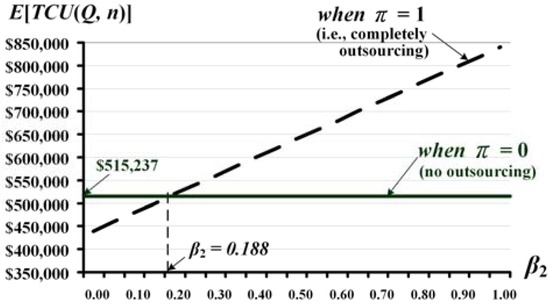
Figure 7.
Analysis of the breakeven point of outsourcing cost factor β2 in the proposed model.
Figure 8 depicts the effect of variations in outsourcing proportion π on the machine utilization ratio (i.e., t1π/E[Tπ]). It demonstrates that as the outsourcing proportion π increases, the in-house machine utilization ratio declines accordingly. This information can assist production managers in scheduling the multi-product fabrication plan.
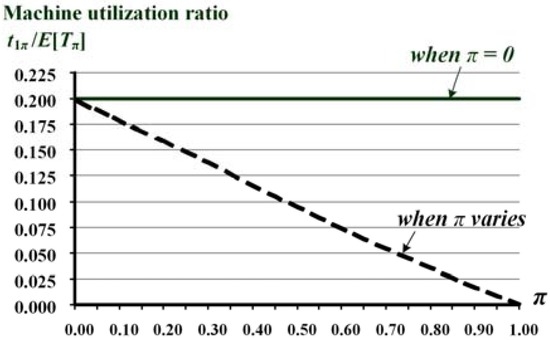
Figure 8.
The effect of variation in outsourcing proportion π on the machine utilization ratio (t1π/E[Tπ]).
Furthermore, Table 2 exhibits the analytical result of the effects of variations in outsourcing proportion π on optimal production–shipment policy and on major system cost components. It provides not only information of the optimal (Q*, n*) operating policy and optimal expected cost E[TCU(Q*, n*)], but also detailed costs and percentages information of partial outsourcing and in-house fabrication as compared to the expected total system cost.

Table 2.
The effects of variations in outsourcing ratio π on optimal production–shipment policy and on major system cost components (where Q* and n* denote the optimal replenishment batch size and number of shipments, respectively).
From Table 2, for π = 0.4, we can find (Q*, n*) = (1229, 3) and E[TCU(Q*, n*)] = $545,344, as shown earlier in the example. A further analytical result reveals that a critical outsourcing proportion π = 0.658 exists (see Figure 9). It means that in the numerical example, if the outsourcing proportion π is greater than the critical point (i.e., π > 65.8%), then the completely outsourcing policy (i.e., π = 1) becomes the better choice than a partial or no outsourcing option, in terms of cost savings.
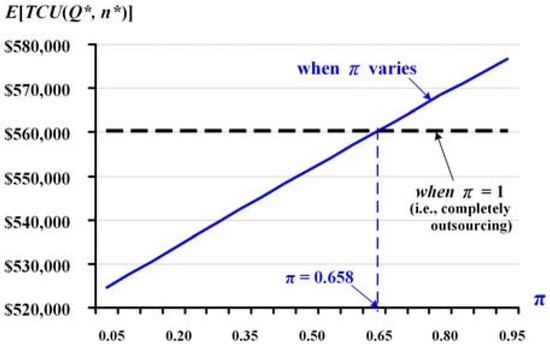
Figure 9.
Analysis of the breakeven point of outsourcing proportion π in the proposed model.
6. Conclusions
With the intention of providing managers of intra-supply chain systems with insight information to support their decision making, this study incorporated a beneficial outsourcing option into a prior work [18] and explored the optimal replenishment lot-size and shipping frequency problem with a partial outsourcing policy and random scrap. An exact mathematical model to the problem is developed, and with the help of optimization techniques the optimal operating decisions that minimize the expected system costs are obtained. Furthermore, through the use of a numerical example and sensitivity analyses, various important insight system information with regard to the joint effects of the partial outsourcing policy and random scrap on the optimal solutions are revealed (Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9) to support managerial decision making. For future research, an interesting area will be to examine the effect of stochastic demand on the optimal solutions of the same problem.
Acknowledgments
Authors truly appreciate the Ministry of Science and Technology of Taiwan for sponsoring this project under grant number: MOST 104-2410-H-324-008-MY2.
Author Contributions
Y-S.P.C. and S.W.C. gave the idea and developed the initial model; G.-M.L. and S.W.C. carried out mathematical derivations and obtained the optimal solutions to the problem, and Y-S.P.C. and S.W.C. verified the research results and conducted the numerical demonstration.
Conflicts of Interest
(1) Authors declare no conflict of interest; (2) The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Appendix A

Table A1.
Computational verification of that given Q, (δn−1 + δn+1) − 2(δn) ≥ 0.
| Q | n | δi | δn−1 − δn | δn+1 − δn | (δn−1 + δn+1) − 2(δn) |
|---|---|---|---|---|---|
| 600 | 1 | δn−1 = $558,725 | $476 > 0 | $3,624 > 0 | $4,100 > 0 |
| 2 * | δn = $558,248 | ||||
| 3 | δn+1 = $561,872 | ||||
| 1000 | 2 | δn−1 = $546,669 | $12 > 0 | $1,696 > 0 | $1,708 > 0 |
| 3 * | δn = $546,657 | ||||
| 4 | δn+1 = $548,353 | ||||
| 1400 | 2 | δn−1 = $548,221 | $2,352 > 0 | $40 > 0 | $2,392 > 0 |
| 3 * | δn = $545,869 | ||||
| 4 | δn+1 = $545,909 | ||||
| 1800 | 3 | δn−1 = $549,890 | $1,184 > 0 | $46 > 0 | $1,230 > 0 |
| 4 | δn = $548,707 | ||||
| 5 | δn+1 = $548,753 | ||||
| 2200 | 4 | δn−1 = $553,887 | $708 > 0 | $44 > 0 | $752 > 0 |
| 5 * | δn = $553,179 | ||||
| 6 | δn+1 = $553,223 | ||||
| 2600 | 5 | δn−1 = $558,994 | $467 > 0 | $40 > 0 | $508 > 0 |
| 6 * | δn = $558,527 | ||||
| 7 | δn+1 = $558,567 | ||||
| 3000 | 6 | δn−1 = $564,727 | $330 > 0 | $37 > 0 | $366 > 0 |
| 7 * | δn = $564,398 | ||||
| 8 | δn+1 = $564,434 | ||||
| 3400 | 7 | δn−1 = $570,850 | $243 > 0 | $33 > 0 | $277 > 0 |
| 8 * | δn = $570,606 | ||||
| 9 | δn+1 = $570,639 | ||||
| 3800 | 8 | δn−1 = $577,231 | $186 > 0 | $30 > 0 | $216 > 0 |
| 9 * | δn = $577,045 | ||||
| 10 | δn+1 = $577,075 | ||||
| 4200 | 9 | δn−1 = $583,795 | $146 > 0 | $28 > 0 | $174 > 0 |
| 10 * | δn = $583,649 | ||||
| 11 | δn+1 = $583,676 | ||||
| 4600 | 10 | δn−1 = $590,491 | $117 > 0 | $26 > 0 | $143 > 0 |
| 11 * | δn = $590,374 | ||||
| 12 | δn+1 = $590,399 | ||||
| 5000 | 11 | δn−1 = $597,286 | $96 > 0 | $24 > 0 | $119 > 0 |
| 12 * | δn = $597,191 | ||||
| 13 | δn+1 = $597,214 | ||||
| 5400 | 12 | δn−1 = $604,159 | $79 > 0 | $22 > 0 | $101 > 0 |
| 13 * | δn = $604,079 | ||||
| 14 | δn+1 = $604,102 |
*: denotes the optimal number of n
References
- Taft, E.W. The most economical production lot. Iron Age 1918, 101, 1410–1412. [Google Scholar]
- Coman, A.; Ronen, B. Production outsourcing: A linear programming model for the theory-of-constraints. Int. J. Prod. Res. 2000, 38, 1631–1639. [Google Scholar] [CrossRef]
- Cachon, G.P.; Harker, P.T. Competition and outsourcing with scale economies. Manag. Sci. 2002, 48, 1314–1333. [Google Scholar] [CrossRef]
- Fu, K.; Hsu, V.N.; Lee, C.-Y. Inventory and production decisions for an assemble-to-order system with uncertain demand and limited assembly capacity. Oper. Res. 2006, 54, 1137–1150. [Google Scholar] [CrossRef]
- Narayanan, S.; Jayaraman, V.; Luo, Y.; Swaminathan, J.M. The antecedents of process integration in business process outsourcing and its effect on firm performance. J. Oper. Manag. 2011, 29, 3–16. [Google Scholar] [CrossRef]
- Leavy, B. Outsourcing strategy and a learning dilemma. Prod. Invent. Manag. 1996, 37, 50–54. [Google Scholar]
- Amaral, J.; Billington, C.A.; Tsay, A.A. Safeguarding the promise of production outsourcing. Interfaces 2006, 36, 220–233. [Google Scholar] [CrossRef]
- De Fontenay, C.C.; Gans, J.S. A bargaining perspective on strategic outsourcing and supply competition. Strateg. Manag. J. 2008, 29, 819–839. [Google Scholar] [CrossRef]
- Gray, J.V.; Roth, A.V.; Tomlin, B. The influence of cost and quality priorities on the propensity to outsource production. Decis. Sci. 2009, 40, 697–726. [Google Scholar] [CrossRef]
- Lee, K.; Choi, B.-C. Two-stage production scheduling with an outsourcing option. Eur. J. Oper. Res. 2011, 213, 489–497. [Google Scholar] [CrossRef]
- Ciliberto, F.; Panzar, J.C. Outsourcing and vertical integration in a competitive industry. South. Econ. J. 2011, 77, 885–900. [Google Scholar] [CrossRef]
- Balachandran, K.R.; Wang, H.-W.; Li, S.-H.; Wang, T. In-house capability and supply chain decisions. Omega 2013, 41, 473–484. [Google Scholar] [CrossRef]
- Porteus, E.L. Optimal lot sizing, process quality improvement and setup cost reduction. Oper. Res. 1986, 34, 137–144. [Google Scholar] [CrossRef]
- Makis, V. Optimal lot sizing and inspection policy for an EMQ model with imperfect inspections. Nav. Res. Logist. 1998, 45, 165–186. [Google Scholar] [CrossRef]
- Sana, S.S. A production–inventory model in an imperfect production process. Eur. J. Oper. Res. 2010, 200, 451–464. [Google Scholar] [CrossRef]
- Mak, K.L. Inventory control of defective products when the demand is partially captive. Int. J. Prod. Res. 1985, 23, 533–542. [Google Scholar] [CrossRef]
- Berg, M.; Posner, M.J.M.; Zhao, H. Production-inventory systems with unreliable machines. Oper. Res. 1994, 42, 111–118. [Google Scholar] [CrossRef]
- Chiu, S.W.; Lin, H.-D.; Cheng, C.-B.; Chung, C.-L. Optimal production-shipment decisions for the finite production rate model with scrap. Int. J. Eng. Model. 2009, 22, 25–34. [Google Scholar]
- Ma, W.-N.; Gong, D.-C.; Lin, G.C. An optimal common production cycle time for imperfect production processes with scrap. Math. Comput. Model. 2010, 52, 724–737. [Google Scholar] [CrossRef]
- Lin, G.C.; Gong, D.-C.; Chang, C.-C. On an economic production quantity model with two unreliable key components subject to random failures. J. Sci. Ind. Res. India 2014, 73, 149–152. [Google Scholar]
- Koley, E.; Verma, K.; Ghosh, S. An improved fault detection classification and location scheme based on wavelet transform and artificial neural network for six phase transmission line using single end data only. SpringerPlus 2015, 4, 551. [Google Scholar] [CrossRef] [PubMed]
- Ocampo, L.A. A hierarchical framework for index computation in sustainable manufacturing. Adv. Prod. Eng. Manag. 2015, 10, 40–50. [Google Scholar] [CrossRef]
- Chiu, S.W.; Sung, P.-C.; Tseng, C.-T.; Chiu, Y.-S.P. Multi-product FPR model with rework and multi-shipment policy resolved by algebraic approach. J. Sci. Ind. Res. India 2015, 74, 555–559. [Google Scholar]
- Koren, R.; Palčič, I. The impact of technical and organisational innovation concepts on product characteristics. Adv. Prod. Eng. Manag. 2015, 10, 27–39. [Google Scholar] [CrossRef]
- Kiron, K.R.; Kannan, K. Prioritizing the factors affecting innovation capability of steel manufacturing SMEs using fuzzy logic. J. Sci. Ind. Res. India 2015, 74, 665–669. [Google Scholar]
- Chiu, Y.-S.P.; Sung, P.-C.; Chiu, S.W.; Chou, C.-L. Mathematical modeling of a multi-product EMQ model with an enhanced end items issuing policy and failures in rework. SpringerPlus 2015, 4, 679. [Google Scholar] [CrossRef] [PubMed]
- Vadali, S.; Chandra, S. Buyer-supplier transport access measures for industry clusters. J. Appl. Res. Technol. 2014, 12, 839–849. [Google Scholar] [CrossRef]
- Safaei, M. An integrated multi-objective model for allocating the limited sources in a multiple multi-stage lean supply chain. Econ. Model. 2014, 37, 224–237. [Google Scholar] [CrossRef]
- Schwarz, L.B. A simple continuous review deterministic one-warehouse N-retailer inventory problem. Manag. Sci. 1973, 19, 555–566. [Google Scholar] [CrossRef]
- Sarker, B.R.; Parija, G.R. An optimal batch size for a production system operating under a fixed-quantity, periodic delivery policy. J. Oper. Res. Soc. 1994, 45, 891–900. [Google Scholar] [CrossRef]
- Ertogral, K.; Darwish, M.; Ben-Daya, M. Production and shipment lot sizing in a vendor–buyer supply chain with transportation cost. Eur. J. Oper. Res. 2007, 176, 1592–1606. [Google Scholar] [CrossRef]
- Chen, K.-K.; Chiu, S.W. Replenishment lot size and number of shipments for EPQ model derived without derivatives. Math. Comput. Appl. 2011, 16, 753–760. [Google Scholar] [CrossRef]
- Grunder, O.; Wang, D.; El Moudni, A. Production scheduling problem with delivery considerations in a mono-product supply chain environment to minimize the total joint cost. Eur. J. Ind. Eng. 2013, 7, 615–634. [Google Scholar] [CrossRef]
- Chiu, S.W.; Huang, C.-C.; Chiang, K.-W.; Wu, M.-F. On intra-supply chain system with an improved distribution plan, multiple sales locations and quality assurance. SpringerPlus 2015, 4, 687. [Google Scholar] [CrossRef] [PubMed]
- Herui, C.; Xu, P.; Yuqi, Z. Co-Evolution Analysis on Coal-Power Industries Cluster Ecosystem Based on the Lotka-Volterra Model: A Case Study of China. Math. Comput. Appl. 2015, 20, 121–136. [Google Scholar] [CrossRef]
- Chiu, S.W.; Kuo, J.-S.; Chiu, V.; Chiu, Y.-S.P. Cost minimization for a multi-product fabrication-distribution problem with commonality, postponement, and quality assurance. Math. Comput. Appl. 2016, 21, 38. [Google Scholar] [CrossRef]
- Chiu, Y.-S.P.; Chiang, K.-W.; Chiu, S.W.; Song, M.-S. Simultaneous determination of production and shipment decisions for a multi-product inventory system with a rework process. Adv. Prod. Eng. Manag. 2016, 11, 141–151. [Google Scholar] [CrossRef]
- Sarkar, B. Supply chain coordination with variable backorder, inspections, and discount policy for fixed lifetime products. Math. Probl. Eng. 2016, 2016, 6318737. [Google Scholar] [CrossRef]
- Sarkar, B. A production-inventory model with probabilistic deterioration in two-echelon supply chain management. Appl. Math. Model. 2013, 37, 3138–3151. [Google Scholar] [CrossRef]
- Sarkar, B. An inventory model with reliability in an imperfect production process. Appl. Math. Comput. 2012, 218, 4881–4891. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).