A Complete Heterogeneous Model for the Production of n-Propyl Propionate Using a Simulated Moving Bed Reactor
Abstract
:1. Introduction
2. Methodology
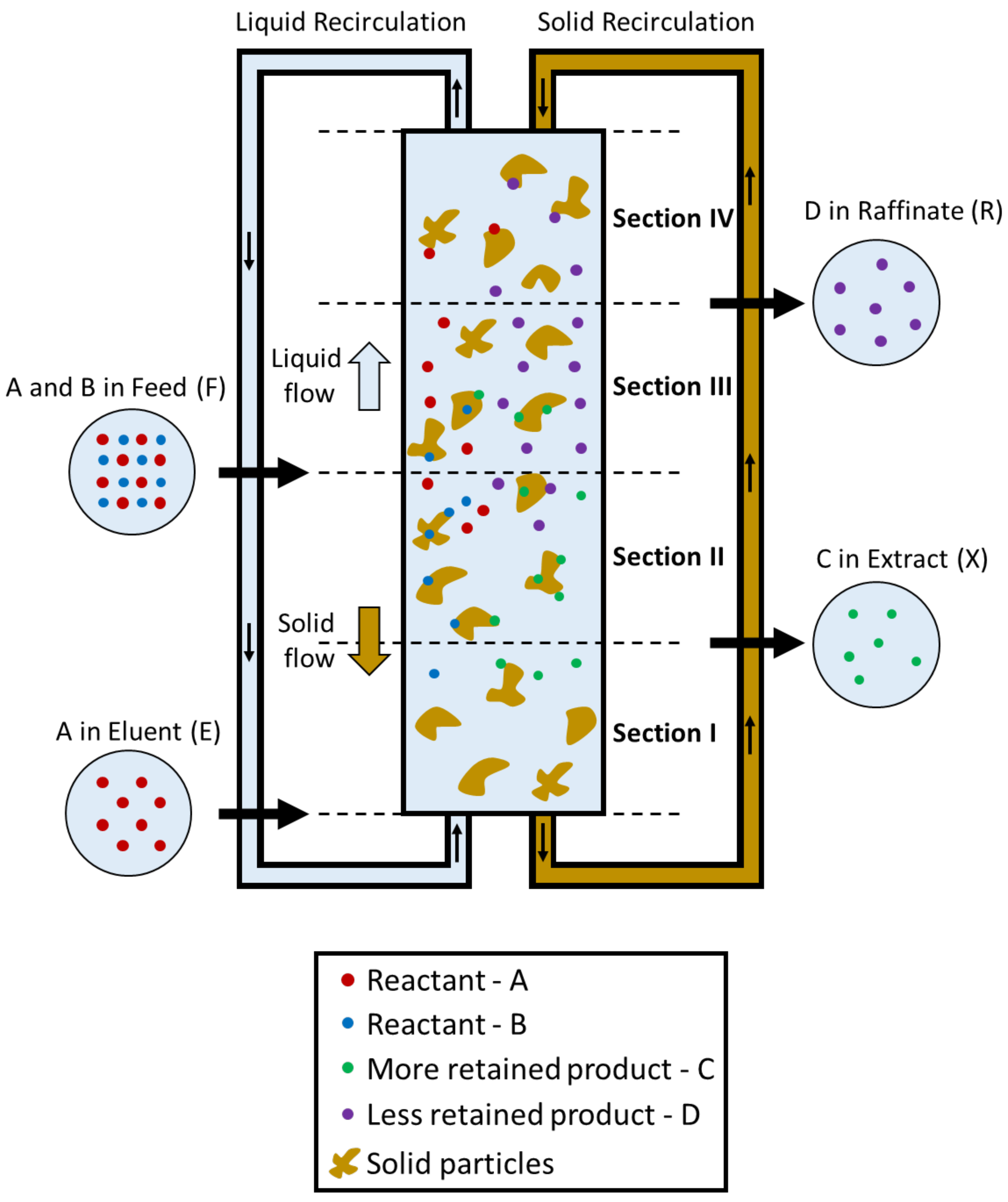
2.1. TMBR Model
- A heterogeneous reaction system;
- Isothermal process;
- The bed length and porosity are constant;
- External mass transfer to the particle and internal mass transfer are negligible;
- A plug flow model with axial dispersion;
- Dispersion along radius is negligible;
- Velocity changes along the column because of composition variation and a linear driving force for the mass transfer rate.
2.2. Parameter Estimations
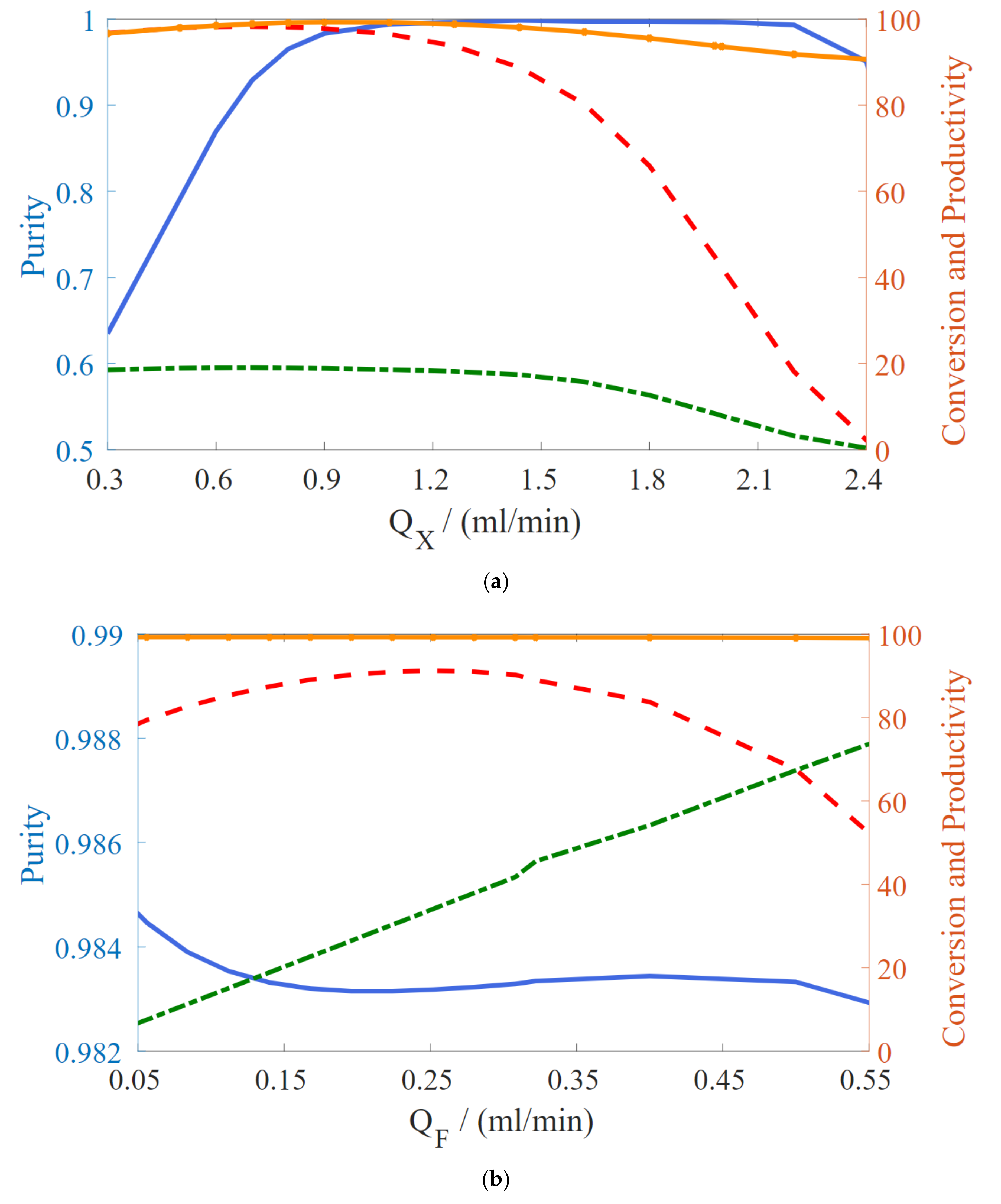
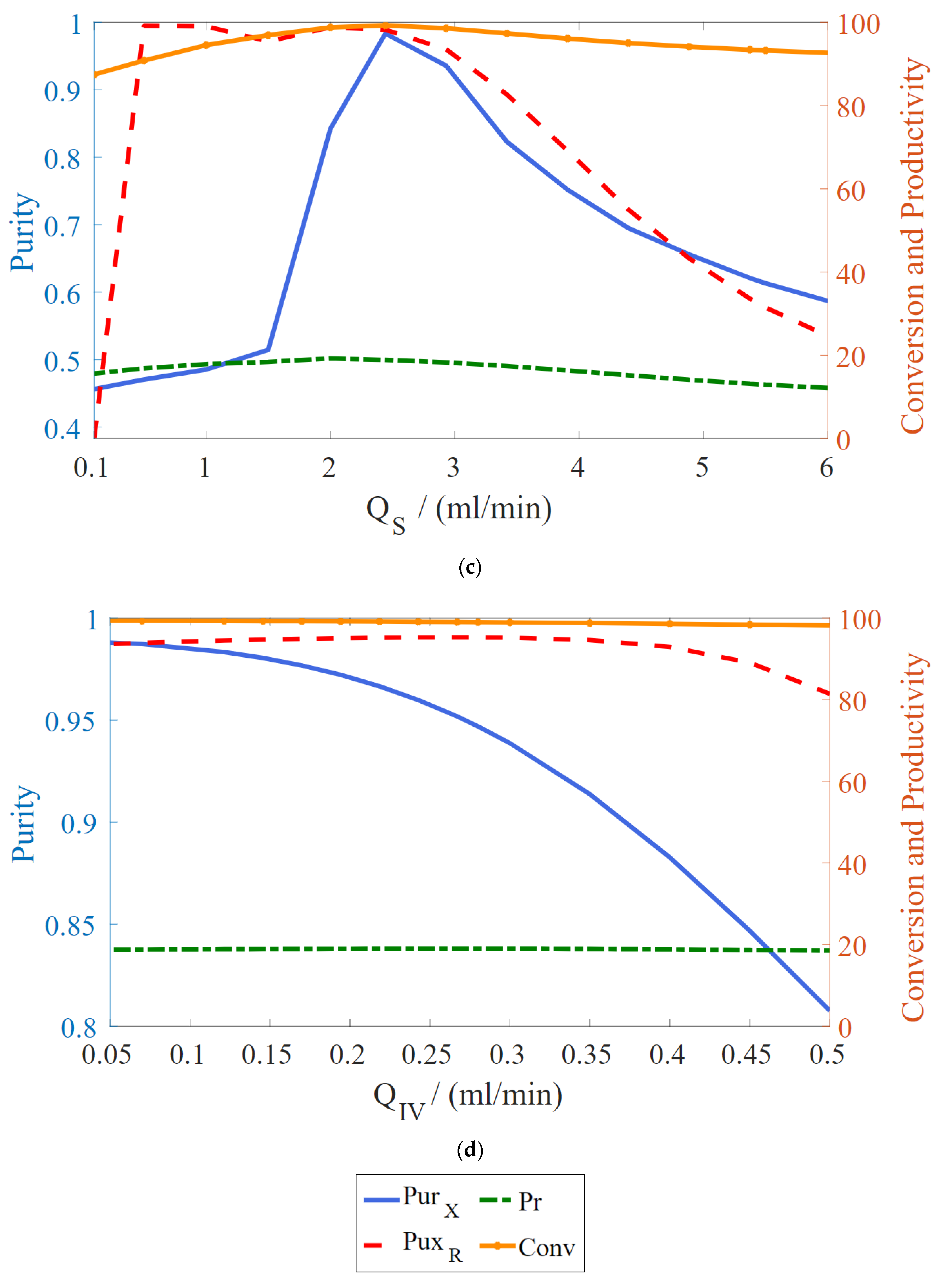
2.3. Unit Design and Optimization
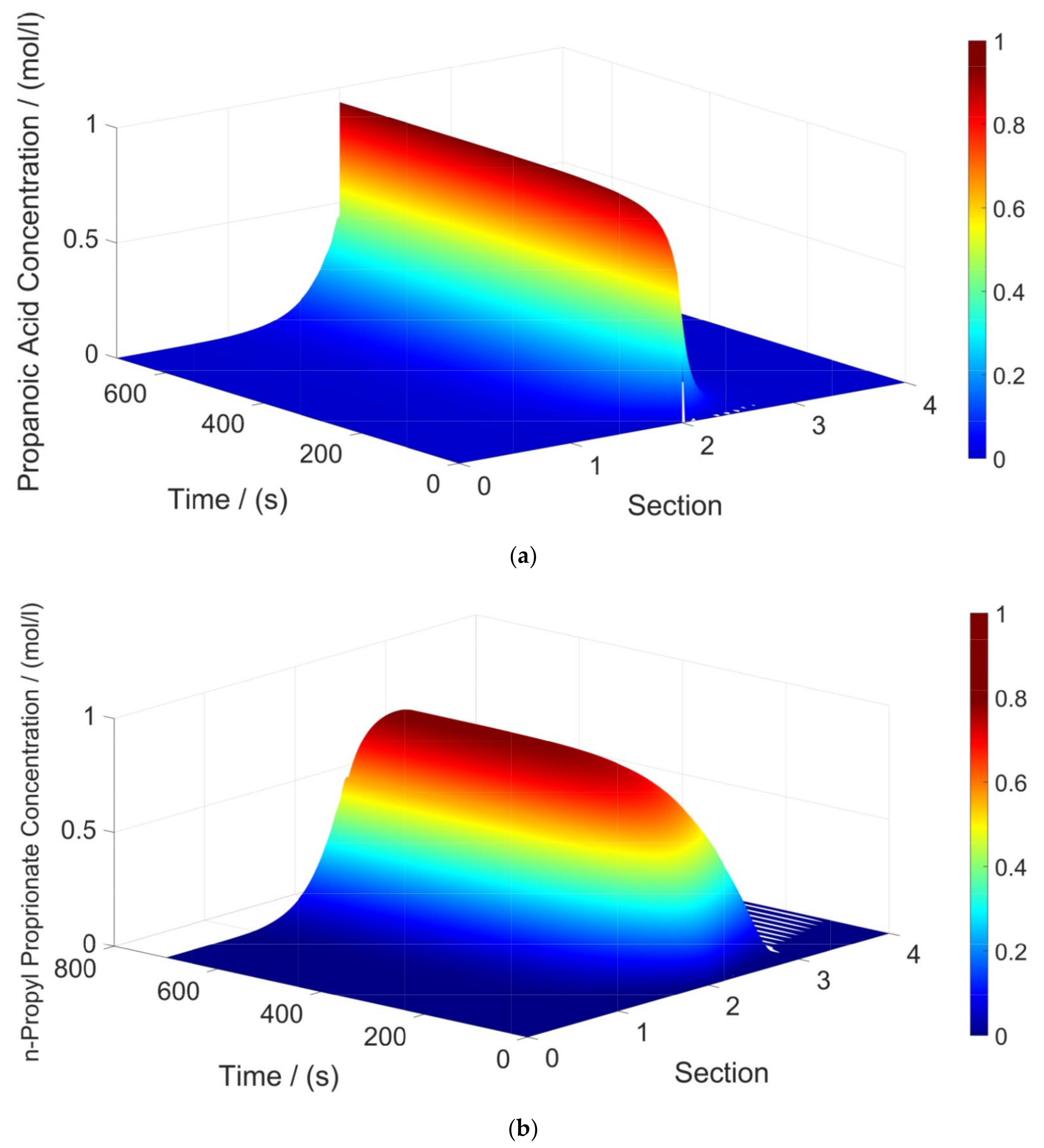
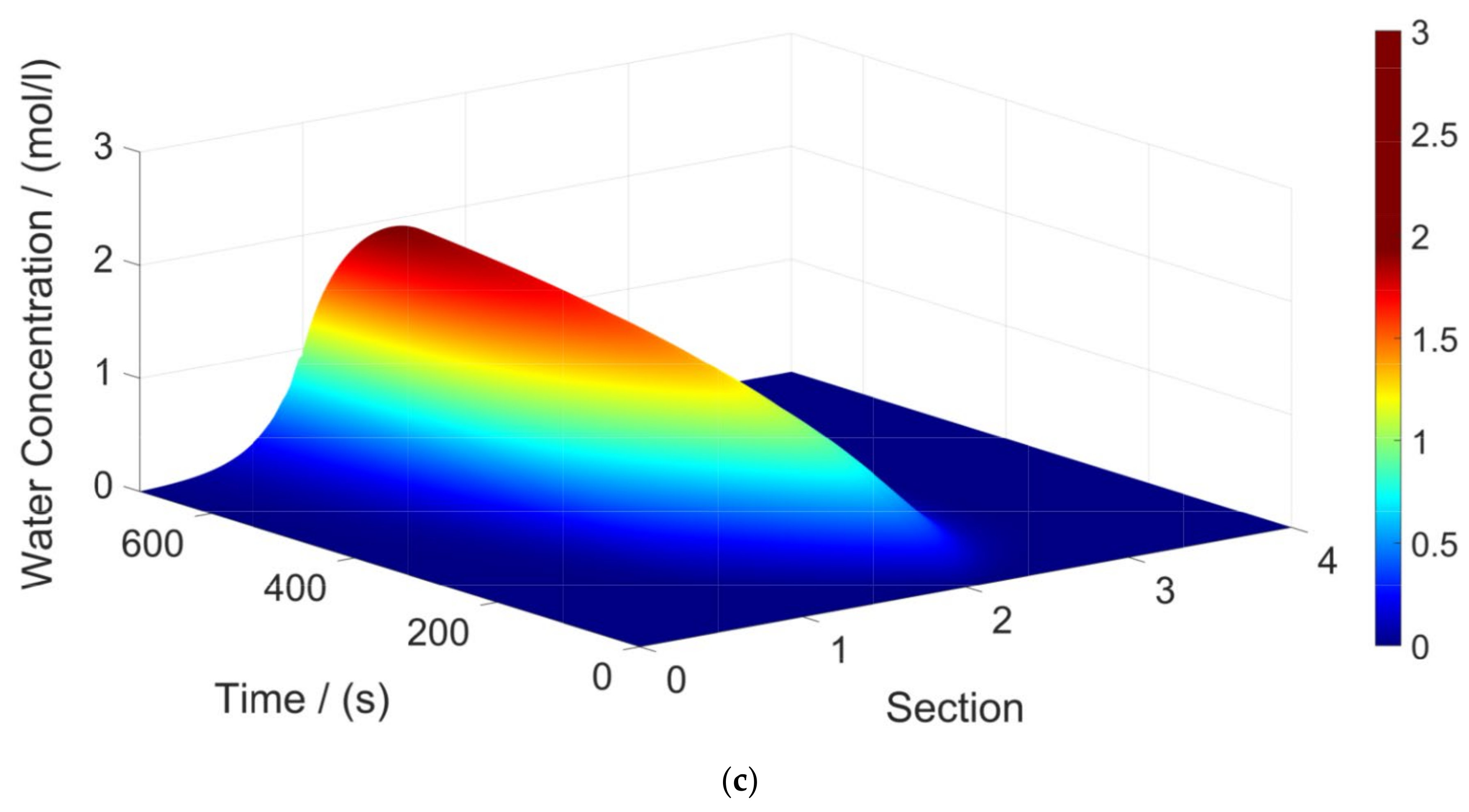
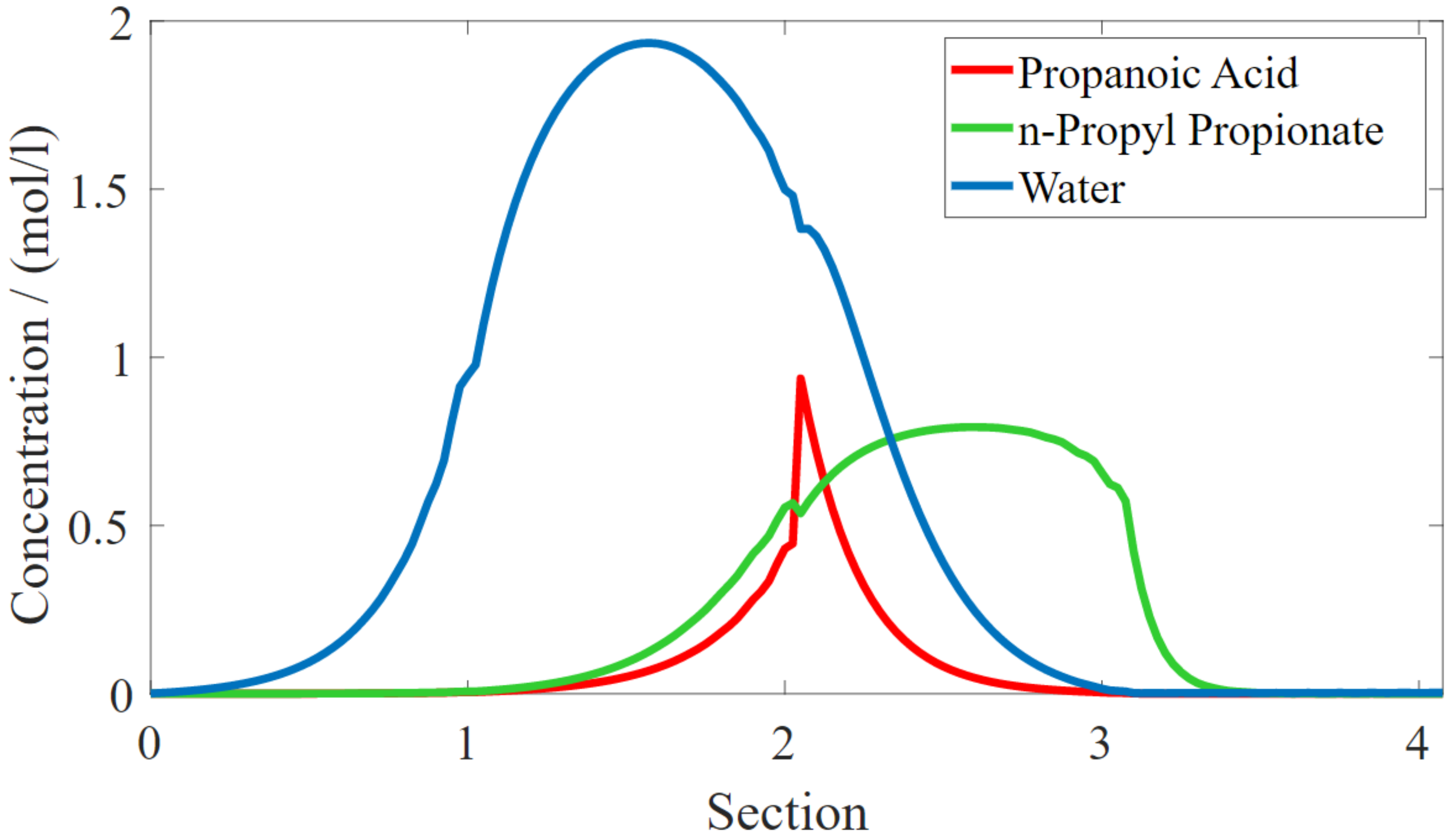
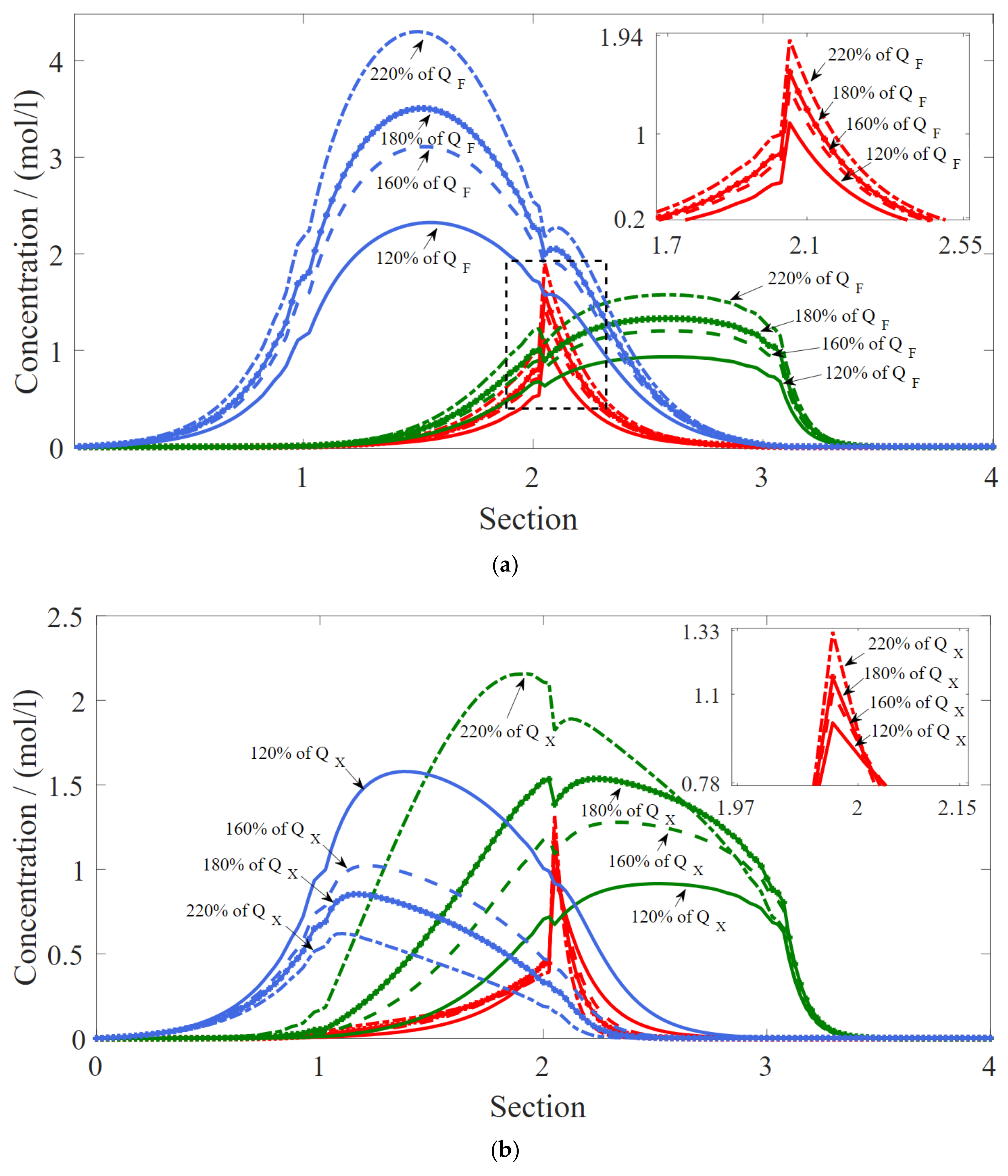
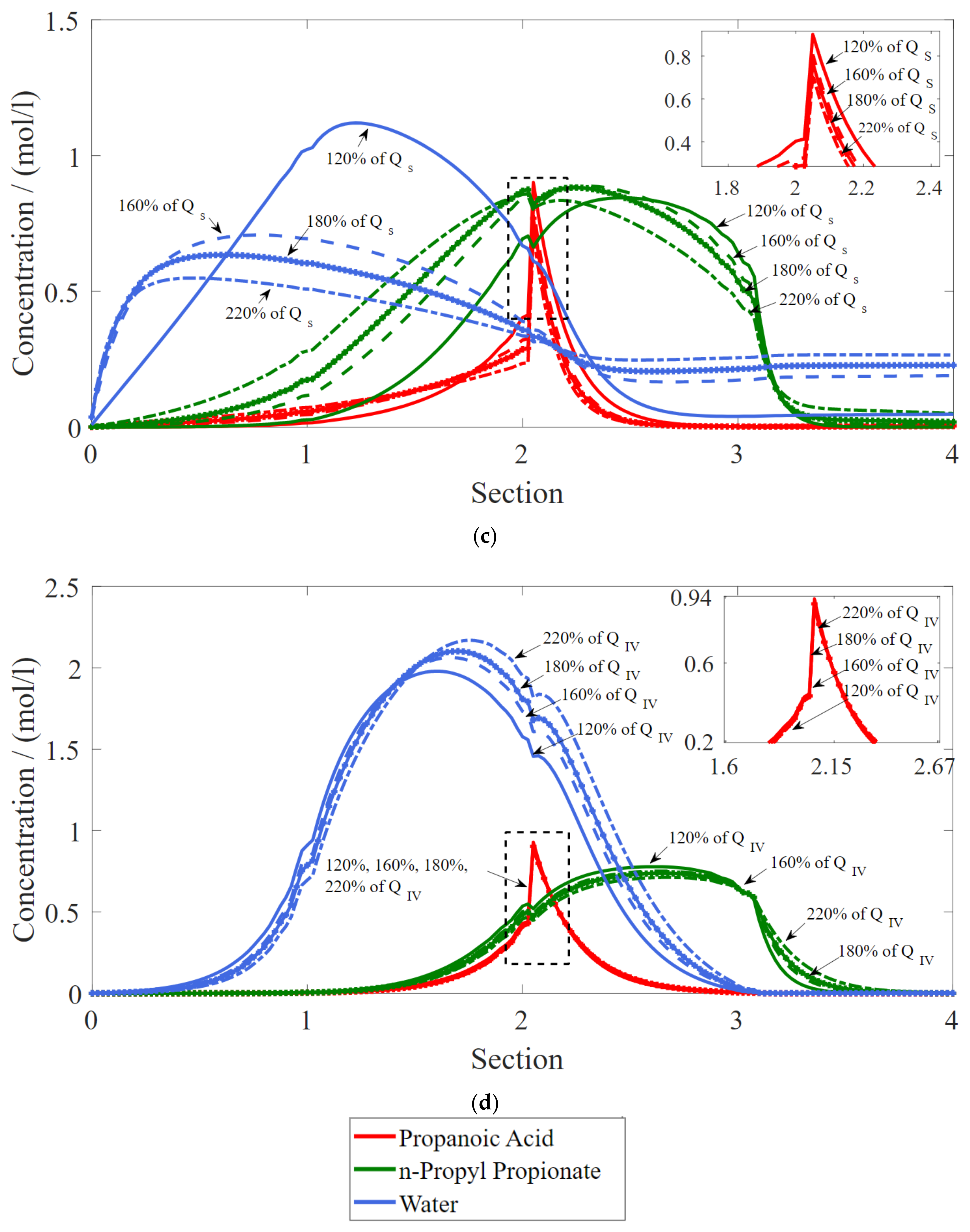
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Activity (dimensionless)/ 1-propanol stoichiometric coefficient | |
| Reactant 1-propanol | |
| Propionic acid stoichiometric coefficient | |
| Reactant propionic acid | |
| ) / Water stoichiometric coefficient | |
| Product water | |
| ) | |
| Conversion () | |
| n-propyl propionate stoichiometric coefficient | |
| Diffusivity coefficient () | |
| Particle diameter () | |
| Axial dispersion coefficient () | |
| Activation energy () | |
| EC | Eluent consumption () |
| Thermodynamic parameter () | |
| NRTL model parameter (dimensionless) | |
| Reaction enthalpy () | |
| Kinetic constants () | |
| Langmuir adsorption parameter ()/Adsorption equilibrium constants () | |
| Pre-exponential factor () | |
| Equilibrium constant (dimensionless) | |
| External mass transfer coefficient () | |
| Pre-exponential factor for equilibrium reaction (dimensionless) | |
| Length () | |
| Lower bound (dimensionless) | |
| Number of components | |
| Purity (%) | |
| Productivity () | |
| Adsorbed phase concentration () | |
| Adsorbed phase concentration in equilibrium with c () | |
| n-Propyl Propionate | |
| Flow rate () | |
| Langmuir adsorption parameter (mol/l) | |
| Reaction rate () | |
| Universal gas constant () | |
| Particle radius (dm) | |
| Temperature (K) | |
| Time () | |
| Velocity () | |
| Upper bound (dimensionless) | |
| Stoichiometric coefficient | |
| Molar volume () | |
| Volume of the bed () | |
| Dimensionless axial position in the bed / Molar fraction (Dimensionless) | |
| Axial position in the bed () | |
| Subscripts and Superscripts | |
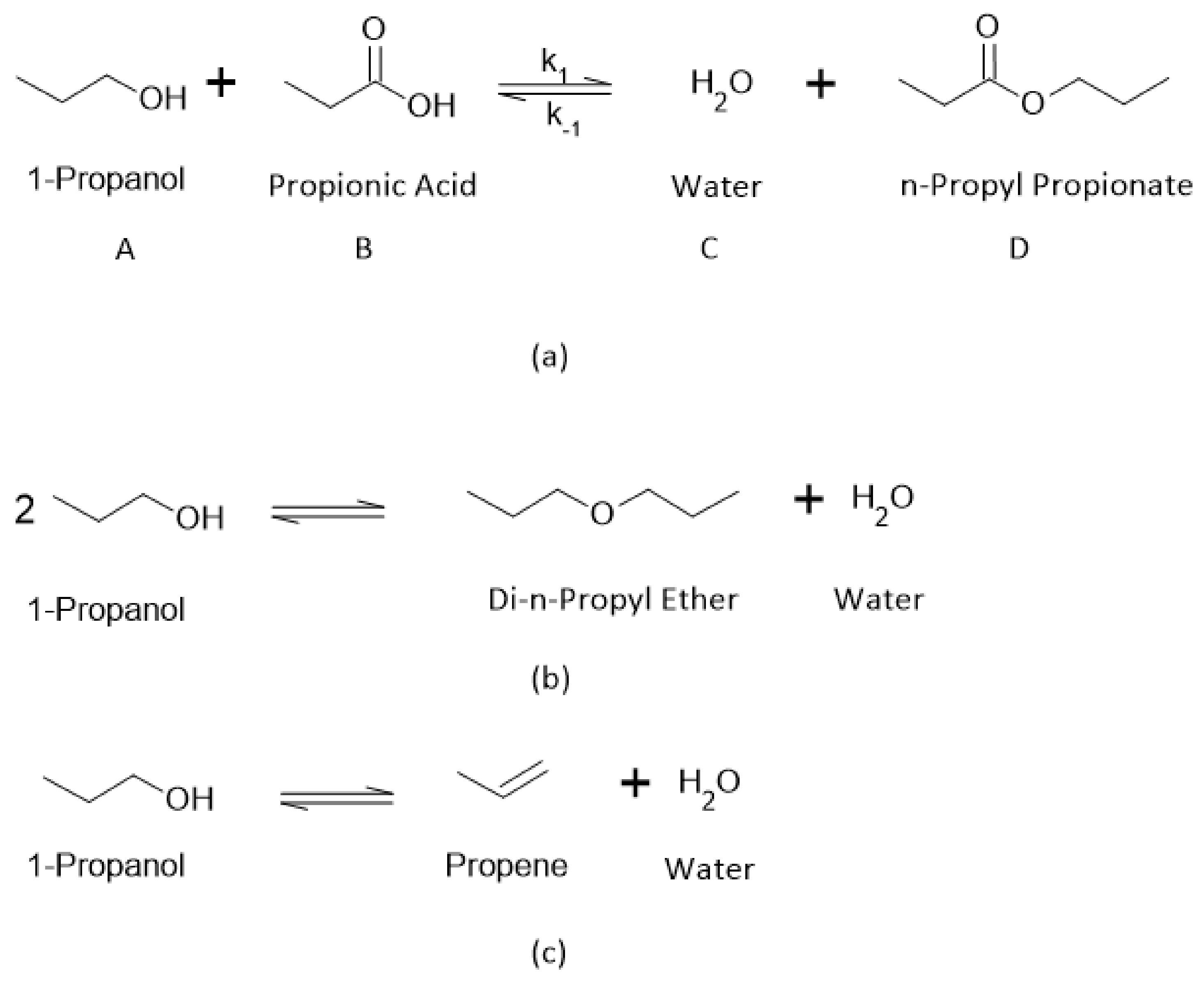
| A | Reactant 1-propanol |
| B | Reactant propionic acid |
| C | Product water |
| D | Product n-propyl propionate |
| Eluent stream | |
| Feed stream | |
| Component | |
| I | Section 1 |
| II | Section 2 |
| III | Section 3 |
| IV | Section 4 |
| Component | |
| TMBR section | |
| Mixture | |
| Raffinate stream | |
| Solid | |
| Extract stream | |
| 0 | Diluted component |
| Greek Symbols | |
| Number of non-randomness in the systems (dimensionless) | |
| Bed porosity (dimensionless) | |
| Activity coefficients (dimensionless) | |
| Fluid viscosity () | |
| Bulk density () | |
| NRTL model parameter (dimensionless) | |
References
- Nogueira, I.B.R.; Faria, R.P.V.; Rodrigues, A.E.; Loureiro, J.M.; Ribeiro, A.M. Chromatographic Studies of N-Propyl Propionate, Part II: Synthesis in a Fixed Bed Adsorptive Reactor, Modelling and Uncertainties Determination. Comput. Chem. Eng. 2019, 128, 164–173. [Google Scholar] [CrossRef]
- Pereira, C.S.M.; Gomes, P.S.; Gandi, G.K.; Silva, V.M.T.M.; Rodrigues, A.E. Multifunctional Reactor for the Synthesis of Dimethylacetal. Ind. Eng. Chem. Res. 2008, 47, 3515–3524. [Google Scholar] [CrossRef]
- Santana, V.V.; Martins, M.A.F.; Rodrigues, A.E.; Loureiro, J.M.; Ribeiro, A.M.; Nogueira, I.B.R. Transient Analysis of True/Simulated Moving Bed Reactors: A Case Study on the Synthesis of n-Propyl Propionate. Comput. Chem. Eng. 2020, 137, 106820. [Google Scholar] [CrossRef]
- Wang, J.; Tian, Y.; Li, Y.; Xu, J.; Yu, W.; Ray, A.K. Multi-Objective Optimization of Non-Isothermal Simulated Moving Bed Reactor: Methyl Acetate Synthesis. Chem. Eng. J. 2020, 395, 125041. [Google Scholar] [CrossRef]
- Shi, Q.; Gonçalves, J.C.; Ferreira, A.F.P.; Rodrigues, A.E. Simulated Moving Bed Reactor for P-Xylene Production: Modeling, Simulation, and Optimization. Chem. Eng. Sci. 2020, 225, 115802. [Google Scholar] [CrossRef]
- Nogueira, I.B.R.; Viena, V.; Rodrigues, A.E.; Loureiro, J.M.; Ribeiro, A.M. Dynamics of a True Moving Bed Reactor: Synthesis of n-Propyl Propionate and an Alternative Optimization Method. Chem. Eng. Process.-Process Intensif. 2020, 148, 107821. [Google Scholar] [CrossRef]
- Duarte, C.F.M. Production of TAME and N-Propyl Propionate by Reactive Distillation; University of Porto: Porto, Portugal, 2006. [Google Scholar]
- The Dow Chemical Company. Amberlyst 46 ®. No. 177, 3028. 2014. Available online: https://www.lenntech.com/Data-sheets/Dow-Amberlyst-46-L.pdf (accessed on 15 September 2021).
- Cruz-Díaz, M.; Buchaly, C.; Kreis, P.; Pérez-Cisneros, E.S.; Lobo-Oehmichen, R.; Górak, A. Synthesis of N-Propyl Propionate in a Pilot-Plant Reactive Distillation Column: Experimental Study and Simulation. Comput. Chem. Eng. 2012, 39, 118–128. [Google Scholar] [CrossRef]
- Lundquist, E.G. Catalyzed Esterification Process. U.S. Patent 5,426,199, 20 June 1995. [Google Scholar]
- Dai, X.; Ye, Q.; Yu, H.; Suo, X.; Li, R. Design and Control of Dividing-Wall Column for the Synthesis of n-Propyl Propionate by Reactive Distillation. Ind. Eng. Chem. Res. 2015, 54, 3919–3932. [Google Scholar] [CrossRef]
- Xia, H.; Dai, X.; Ye, Q.; Feng, S.; Li, R.; Suo, X. Design and Control of Entrainer-Assisted Reactive Distillation for N-Propyl Propionate Production. Comput. Chem. Eng. 2017, 106, 559–571. [Google Scholar] [CrossRef]
- Constantino, D.S.M.; Pereira, C.S.M.; Faria, R.P.V.; Loureiro, J.M.; Rodrigues, A.E. Simulated Moving Bed Reactor for Butyl Acrylate Synthesis: From Pilot to Industrial Scale. Chem. Eng. Process. Process Intensif. 2015, 97, 153–168. [Google Scholar] [CrossRef]
- Constantino, D.S.M.; Faria, R.P.V.; Pereira, C.S.M.; Loureiro, J.M.; Rodrigues, A.E. Enhanced Simulated Moving Bed Reactor Process for Butyl Acrylate Synthesis: Process Analysis and Optimization. Ind. Eng. Chem. Res. 2016, 55, 10735–10743. [Google Scholar] [CrossRef]
- Azevedo, D.C.S.; Rodrigues, A.E. Design Methodology and Operation of a Simulated Moving Bed Reactor for the Inversion of Sucrose and Glucose-Fructose Separation. Chem. Eng. J. 2001, 82, 95–107. [Google Scholar] [CrossRef]
- Santos, R.V.A.; Prudente, A.N.; Ribeiro, A.M.; Rodrigues, A.E.; Loureiro, J.M.; Martins, M.A.F.; Pontes, K.V.; Nogueira, I.B.R. Global Approach for Simulated Moving Bed Model Identification: Design of Experiments, Uncertainty Evaluation, and Optimization Strategy Assessment. Ind. Eng. Chem. Res. 2021, 60, 7904. [Google Scholar] [CrossRef]
- Lilja, J.; Murzin, D.Y.; Salmi, T.; Aumo, J.; Maäki-Arvela, P.; Sundell, M. Esterification of Different Acids over Heterogeneous and Homogeneous Catalysts and Correlation with the Taft Equation. J. Mol. Catal. A Chem. 2002, 182, 555–563. [Google Scholar] [CrossRef]
- Nogueira, I.B.R.; Faria, R.P.V.; Requião, R.; Koivisto, H.; Martins, M.A.F.; Rodrigues, A.E.; Loureiro, J.M.; Ribeiro, A.M. Chromatographic Studies of N-Propyl Propionate: Adsorption Equilibrium, Modelling and Uncertainties Determination. Comput. Chem. Eng. 2018, 119, 371–382. [Google Scholar] [CrossRef]
- Prudente, A.N.; Santana, D.D.; Pontes, K.V.; Loureiro, J.M.; Ribeiro, A.M.; Nogueira, I.B.R. Engineering: Parameter Estimation of a Liquid-Liquid Equilibrium for the Quaternary System n-Propanol, Propanoic Acid, Propyl Propionate and Water Though the Exploration and Exploitation Technique. In Proceedings of the Congresso de Métodos Numéricos em Engenharia, Guimarães, Portugal , 1–3 July 2019; pp. 1097–1107. [Google Scholar]
- Samarov, A.; Toikka, M.; Trofimova, M.; Toikka, A. Liquid-Liquid Equilibrium for the Quaternary System Propionic Acid + n-Propanol + n-Propyl Propionate + Water at 293.15, 313.15 and 333.15 K. Fluid Phase Equilib. 2016, 425, 183–187. [Google Scholar] [CrossRef] [Green Version]
- Constantino, D.S.M.; Pereira, C.S.M.; Faria, R.P.V.; Ferreira, A.F.P.; Loureiro, J.M.; Rodrigues, A.E. Synthesis of Butyl Acrylate in a Fixed-Bed Adsorptive Reactor over Amberlyst 15. AIChE J. 2015, 61, 1263–1274. [Google Scholar] [CrossRef]
- Buchaly, C.; Kreis, P.; Górak, A. Hybrid Separation Processes-Combination of Reactive Distillation with Membrane Separation. Chem. Eng. Process. Process Intensif. 2007, 46, 790–799. [Google Scholar] [CrossRef]
- Xu, H.; Ye, Q.; Zhang, H.; Qin, J.; Li, N. Design and Control of Reactive Distillation-Recovery Distillation Flowsheet with a Decanter for Synthesis of N-Propyl Propionate. Chem. Eng. Process. Process Intensif. 2014, 85, 38–47. [Google Scholar] [CrossRef]
- Lode, F.; Houmard, M.; Migliorini, C.; Mazzotti, M.; Morbidelli, M. Continuous Reactive Chromatography. Chem. Eng. Sci. 2001, 56, 269–291. [Google Scholar] [CrossRef]
- Sporti, G.; Masi, M.; Carrà, S. Optimal Desgin of Multicomponent Cuntercurrent Adsorption Separation Processes Involving Nonlinear Equilibria. Chem. Eng. Sci. 1989, 44, 1329–1345. [Google Scholar]
| Unit Condition | |
|---|---|
| Column length | 4.6 dm |
| Column diameter | 0.26 dm |
| Temperature | 313 K |
| Bed porosity | 0.4 |
| Peclet number | 166 |
| Particle diameter | 245.5 µm |
| Feed composition | 40% A/60% B |
| Adsorption Equilibrium Constants | |
|---|---|
| ) | 11.67 |
| 9.06 | |
| 2.36 | |
| 5.1 | |
| Operating Conditions | |
|---|---|
| 0.14 | |
| 2.56 | |
| 0.12 | |
| 0.90 | |
| 2.45 | |
| Kinetic Parameter | Estimated | Literature |
|---|---|---|
| / ( | ||
| ( |
| j | A | B | C | D | ||||
|---|---|---|---|---|---|---|---|---|
| i | Estimated | Literature | Estimated | Literature | Estimated | Literature | Estimated | Literature |
| A | 0.0 | 0.0 | 674.9 | 1754.0 | 704.0 | 1744.7 | 391.7 | 566.0 |
| B | −712.0 | 1120.8 | 0.0 | 0.0 | 672.6 | 1 631.9 | 384.5 | 590.0 |
| C | 766.6 | −93.5 | 4 244.0 | −182.3 | 0.0 | 0.0 | 3 302.4 | 1 142.5 |
| D | −677.4 | 236.9 | 224.6 | 32.1 | 2 237.8 | 3 505.0 | 0.0 | 0.0 |
| Parameter | Estimated | Literature |
|---|---|---|
| Kinetic | 6.7% | 20.3% |
| Thermodynamic | 0.2% | 2.9% |
| Performance Parameters | |
|---|---|
| (%) | 98.30 |
| (%) | 98.90 |
| (%) | 99.28 |
| 18.88 | |
| 10.40 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, R.; Rebello, C.; Prudente, A.; Ribeiro, A.M.; Rodrigues, A.E.; Loureiro, J.M.; Pontes, K.V.; Nogueira, I.B.R. A Complete Heterogeneous Model for the Production of n-Propyl Propionate Using a Simulated Moving Bed Reactor. Separations 2022, 9, 43. https://doi.org/10.3390/separations9020043
Santos R, Rebello C, Prudente A, Ribeiro AM, Rodrigues AE, Loureiro JM, Pontes KV, Nogueira IBR. A Complete Heterogeneous Model for the Production of n-Propyl Propionate Using a Simulated Moving Bed Reactor. Separations. 2022; 9(2):43. https://doi.org/10.3390/separations9020043
Chicago/Turabian StyleSantos, Rodrigo, Carine Rebello, Anderson Prudente, Ana M. Ribeiro, Alírio E. Rodrigues, José M. Loureiro, Karen V. Pontes, and Idelfonso B. R. Nogueira. 2022. "A Complete Heterogeneous Model for the Production of n-Propyl Propionate Using a Simulated Moving Bed Reactor" Separations 9, no. 2: 43. https://doi.org/10.3390/separations9020043
APA StyleSantos, R., Rebello, C., Prudente, A., Ribeiro, A. M., Rodrigues, A. E., Loureiro, J. M., Pontes, K. V., & Nogueira, I. B. R. (2022). A Complete Heterogeneous Model for the Production of n-Propyl Propionate Using a Simulated Moving Bed Reactor. Separations, 9(2), 43. https://doi.org/10.3390/separations9020043









