Abstract
Optimal oxygen supply is vitally important for the cultivation of aerobically growing cells, as it has a direct influence on cell growth and product formation. A process engineering parameter directly related to oxygen supply is the volumetric oxygen mass transfer coefficient . It is the influences on and computing time of different interfacial force and population balance models in stirred bioreactors that have been evaluated in this study. For this investigation, the OpenFOAM 7 open-source toolbox was utilized. Firstly, the Euler–Euler model with a constant bubble diameter was applied to a 2 scale bioreactor to statistically examine the influence of different interfacial models on the value. It was shown that the model and the constant bubble diameter have the greatest influence on the calculated value. To eliminate the problem of a constant bubble diameter and to take effects such as bubble breakup and coalescence into account, the Euler–Euler model was coupled with population balance models (PBM). For this purpose, four coalescence and five bubble breakup models were examined. Ultimately, it was established that, for all of the models tested, coupling computational fluid dynamics (CFD) with PBM resulted in better agreement with the experimental data than using the Euler–Euler model. However, it should be noted that the higher accuracy of the PBM coupled models requires twice the computation time.
1. Introduction
Due to the vast potential of biopharmaceuticals, the market is growing rapidly [1]. To produce biopharmaceuticals, either cell cultures or microorganisms are used as production hosts, which, among other things, has an impact on bioreactor design and oxygen consumption [2]. As oxygen supply has a significant influence on cell growth and product yield, manufacturers are very interested in establishing how to achieve an optimal oxygen supply for specific organisms as early as the process development stage. The most commonly used bioreactors in both process development and commercial production are stirred bioreactors with forced aeration. Both computational fluid dynamics (CFD) and classical process engineering approaches are used for optimization and scaling-up of stirred bioreactor processes [3,4,5,6]. CFD is based on the laws of conservation of energy, mass, and momentum. Multiphase systems, such as aerated bioreactors, pose a particular challenge in terms of modeling, but they can be modeled with different degrees of abstraction. A promising approach to modeling polydisperse systems is to couple CFD with population balance models (PBM) [7]. This allows size distributions of gas bubbles that occur due to break-up and coalescence to be modeled. The polydisperse approach makes it possible to model a realistic oxygen supply in bioreactors. A process parameter that describes the efficiency of the oxygen supply in a bioreactor is the volumetric oxygen mass transfer coefficient .
1.1. Oxygen Demand of Cells
Oxygen plays a central role in aerobic bioprocesses, as it is constantly required by the cells for growth, maintenance, and other metabolic processes, such as product synthesis [8]. For example, Losen et al. [9] point out that in Escherichia coli, the expression of more than 200 genes depends on oxygen availability. The amount of oxygen required is characteristic for each organism and can be described by the specific oxygen uptake rate . An overview of different specific oxygen uptake rates can be found in [7,10]. Garcia-Ochoa and Gómez were able to show that this rate can change in the course of cultivation, nevertheless, it is typically assumed to be constant [11]. The specific oxygen consumption rate is influenced by different factors, such as cultivation temperature, medium, carbon source, pH value, and fluid mechanical stress [12,13,14,15]. To achieve targeted cell densities and product titers, sufficient oxygen must be available. However, the addition of arbitrary amounts of air or oxygen should be avoided, as the bursting of bubbles causes fluid mechanical stress, which can irreversibly damage the cells [16]. Additionally, increased sparging may also influence the pH value in buffered cell culture media, as it strips the solved carbon dioxide. Oxygen input can be achieved using various techniques that include surface gassing, hollow stirrer gassing, forced gassing, as well as external, bubble-free gassing [17,18]. Surface gassing is only used in cell culture technologies with high surface-to-volume ratios (e.g., spinner or shake flasks) or in wave-mixed bioreactors [19,20]. The most common method is forced gassing through a sparger. To be able to vary gas bubble size distribution and the point of entry, a variety of spargers exist, which are described in [21].
To avoid oxygen limitation, the amount of oxygen introduced into a reactor must be greater or equal to the oxygen that is consumed by the cells [22]. The oxygen supply capacity of a bioreactor can be described by the oxygen transfer rate (OTR), which is the product of the value and the difference between the concentrations of dissolved oxygen at the gas–liquid interphase and the liquid phase (Equation (1)). The OTR depends on the reactor geometry, the operating parameters, and the physical properties of the fluid [23,24]. The volumetric oxygen mass transfer coefficient is the product of the liquid-side mass transfer coefficient and the specific interfacial area a. The specific interfacial area corresponds to the surface area of all gas bubbles and the free liquid surface per volume and can be calculated via the relative gas fraction and the Sauter mean diameter (Equation (2)). A large number of empirical and dimensionless formulae exist to describe the individual factors , a and [23,25,26,27,28]. On the biological side, the oxygen uptake rate (OUR) can be calculated as the product of cell concentration and the specific oxygen uptake rate (Equation (3)). By combining OTR and OUR calculations, a sufficient oxygen supply can be ensured.
1.2. Breakup and Coalescence
In forced aeration, gas bubbles rise from the sparger through the medium to the liquid surface. The behavior of gas bubbles in the often turbulent flows is difficult to describe precisely, as it is a very complex phenomenon. Gas bubbles are deformable, which affects their specific surface area, they can break apart into two or more gas bubbles, or they can coalesce [29]. Four different mechanisms of gas bubble breakage (turbulent fluctuations and collisions, viscous shear stress, shearing-off processes and interfacial instability) are described in the literature [7,30]. Liao and Lucas [30] provide an overview of different breakup frequency models and daughter size distribution (DSD) models. In addition to bubble–liquid interaction, bubble-bubble interaction is also involved in the process of coalescence [31]. Three different theories describing the coalescence process are mentioned in the literature, with Lehr’s theory being the most recent [32,33,34]. An overview of different coalescence models can be found in [35].
1.3. Population Balance Modeling
PBM, which is based on the population balance equation (PBE), can be used to describe the temporal and spatial development of a population [36,37,38]. As particles can be described as individuals within a population, PBM is suitable for modeling gas bubble size distributions in polydisperse gas-liquid systems, such as aerated bioreactors [39,40]. The PBE describes the change in the number density function (NDF) of one or more inner coordinates. A distinction can be made between inner and outer coordinates, with space and time considered as outer coordinates and the characteristics of an individual in the population as inner coordinates. However, due to exponentially increasing computational costs, typically only one inner coordinate is considered. In polydisperse gas-liquid systems, this is the gas bubble diameter [41]. Different PBEs exist, which typically include accumulation, convection, and diffusion terms for each spatial coordinate, as well as a source term that accounts for the birth and death of individuals (Equation (4)) [42,43,44]. The source term for gas bubble size distribution is calculated using the following four individual terms: Death by coalescence , Birth by coalescence , Death by breakup , Birth by breakup (Equations (5)–(8)). The differential equation and the four source terms cannot be determined directly and have to be closed using the coalescence and breakup model described in Section 1.2 [45]. Different approaches can be used to solve the PBE, and the most frequently used algorithms can be found in [39,46]. These approaches can then be coupled with CFD [43]. The most commonly used method is the method of moments (MOM) and its various modifications. The fixed pivot method, which belongs to the class method, is also frequently used and is the standard method in OpenFOAM 7. In the class method, the continuous NDF is approximated by a discrete distribution. The number of classes has a direct influence on accuracy and must be defined manually, just like the class size. The discretised function of the NDF for breakup and coalescence can be represented and solved according to Equations (9) and (10) [47].
1.4. Computational Fluid Dynamics
Models and methods used for continuous and disperse multiphase systems and their numerical solution are summarised in [7]. The segment, marker-and-cell, level set, and volume of fluid (VOF) methods are suitable for surface aerated bioreactors, although only the latter is of practical relevance. To solve the balance equations, a type of mixed fluid is assumed for this method.
For dispersing systems, the Euler–Euler and Euler–Lagrange methods are widely used [48]. In the Euler–Euler method, a mixed fluid is no longer used. Instead the balance equations are solved individually for each fluid and are coupled via the phase fraction (Equation (11)) [3]. This implies that the equations have to be solved iteratively for the different fluids. The continuity equations without phase transition for two fluids correspond to Equation (12). If the phase transition is to be taken into account, the volume-related mass flow would have to be considered on the right-hand side of the equation. The momentum equation for two fluids without phase transition is shown in Equation (13) [49]. corresponds to the sum of the volume-related interfacial forces [50]. The forces acting from the gas phase on the liquid phase are equal to the forces acting from the liquid phase on the gas phase (with reversed sign).
Momentum transfer is mainly caused by drag force (Equation (14)) [51,52,53,54]. Other forces are lift force [55,56] (Equation (15)), virtual mass force [52,56,57,58] (Equation (16)), wall lubrication force (Equation (17)) [59,60,61], turbulent dispersion force (Equation (18)) [62,63,64,65,66], basset force [67] and Brownian force [68]. A detailed description of these interfacial forces can be found in [7].
2. Materials and Methods
The laboratory-scale case study experiments were performed using a 3 HyPerformaTM glass bioreactor with 2 working volume from Thermo Fisher Scientific, San José, USA (Figure 1). A pitched four-blade stirrer with a 45 angle (diameter 50 ) was used together with an open pipe sparger (inner diameter 6 ). The Euler–Euler model with and without PBM was applied for the CFD simulations. Validation of CFD simulations was performed using measurements.
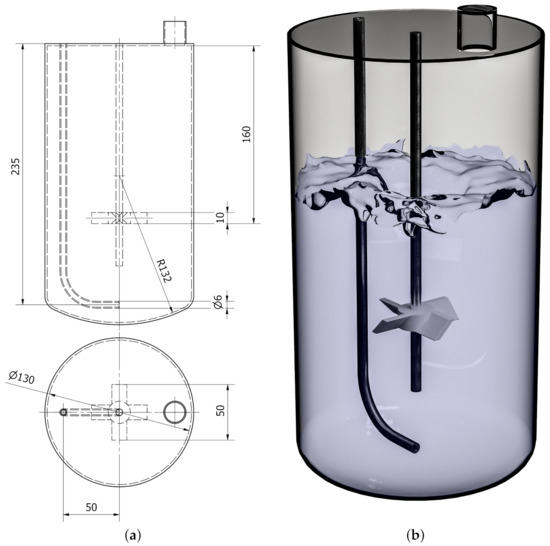
Figure 1.
Modified HyPerformaTM glass bioreactor with a pitched four-blade stirrer used for measurements and CFD simulations. (a) Technical drawing; (b) 3D rendered bioreactor.
2.1. CFD Simulations
The geometry used in this study was drawn with Autodesk® Inventor® Professional 2020.2 (Autodesk, Inc., San Rafael, USA) [69]. Mesh generation was carried out in two steps, both of which was performed using OpenFOAM 7 [70]. The background mesh was created with the blockMesh application. Emphasis was placed on creating regular hexahedrons and thus a mesh that is as orthogonal as possible. Using the surfaceFeatures application, the required features were extracted from the respective geometry files that are used to generate the mesh using the octree algorithm (snappyHexMesh). The mesh quality was checked using the checkMesh application, with higher mesh quality requirements than the default OpenFOAM 7 settings. The reason for the higher mesh quality is that the two solvers used, twoPhaseEulerFoam and reactingTwoPhaseEulerFoam, are prone to poor mesh quality. After successfully checking the mesh quality, the mesh was renumbered to reduce the bandwidth (renumberMesh). A special feature of stirred bioreactors is that part of the geometry rotates. To consider the stirrer movement, the moving reference frame (MRF) approach was used for all of the simulations. In the MRF zone, the conservation equations were solved in a rotating reference frame involving Coriolis and centrifugal forces. For all two-phase simulations, the PIMPLE algorithm for pressure-velocity coupling was used [71]. For the transient calculation, an adaptive time step size was used, with a maximum Courant–Friedrichs–Lewy-number (CFL-number) of in each case [72]. The Gauss linear method was generally used for discretization. For all simulations in the turbulent range, turbulence was modeled using the Reynolds-averaged Navier–Stokes (RANS) approach. The standard k- model of Launder and Spalding [73], which is the most commonly used in the industry, was applied (Equations (19) and (20)) [74]. The physical properties listed in Table 1 were taken for all of the simulations. The boundary conditions are listed in the Appendix A Table A1.

Table 1.
Physical properties for all CFD simulations based on [75].
To scrutinize the interfacial force models, the standard Euler–Euler model was selected, with the twoPhaseEulerFoam The OpenFOAM solver being utilized for this purpose. The interfacial force models examined are listed in Table 2.

Table 2.
Examined interfacial force, breakup and coalescence models.
The constant bubble diameter, with an aspect ratio of 1, was varied for the different investigations. For the coupling of CFD with PBM, the reactingTwoPhaseEulerFoam solver was used, and the class method applied. The number of classes and the associated initial gas bubble size distribution were varied for the studies. The coalescence and breakup models used and compared are listed in Table 2.
The high-performance computing (HPC) system at the ZHAW was used to parallelize the calculations on up to 32 physical cores. The HPC system consists of a total of 880 physical central processing units (CPU) with a total of RAM (HPE ProLiant XL230k Gen. 10 HPC servers with Xeon-Gold 6142). An enhanced data rate InfiniBandTM interface is available to manage the high data transfer for parallel computing. The interface allows a data throughput of up to 100 s−1 and a latency of . A Linux CentOS 7 operating system (release 7.5.1804) was installed on the cluster. All fluid dynamics simulations were performed using the OpenFOAM 7 open-source C++ toolbox (OpenFOAM Foundation version). The calculation on the HPC system used, Open MPI 3.1.3 [89] (The Open MPI Project), as recommended by the OpenFOAM foundation for parallelization. Slurm 17.11.8 (SchedMD LLC) was used to manage the jobs on the HPC system [90]. Post-processing of the simulations was performed with Paraview 5.4.1 [91] and Python® 3.8.0 [92].
2.2. Richardson Extrapolation
A widely used method to estimate the discretization error of the mesh is the Richardson extrapolation [93,94,95]. Simulations are performed with at least three meshes of different refinements that are already so fine that asymptotic convergence can be assumed. Asymptotic convergence can be assumed if the pointwise error for each grid cell j can be described according to Equations (21) and (22) [96], where is a cell-specific constant. The discretisation error for the individual meshes can then be estimated with Equations (23)–(27), where the three meshes with descending mesh numbers correspond to the indices 1,2 and 3. It should be noted that for the mesh study, the CFL-number was kept constant for all meshes [3], with CFL-numbers of chosen for all of the meshes. The goal of the mesh study was to select a computational mesh that causes as small a discretization error as possible and results in economic computing time (as computing time increases exponentially as mesh size increases).
2.3. Statistical Analysis
To determine whether an interface, a coalescent, or a breakup model has a statistically significant influence on the calculation of the value, an analysis of variance (ANOVA) was performed. To perform a one-way ANOVA, both the normal distribution of the residuals and homoscedasticity must be ensured [97]. Using Shapiro–Wilk tests and quantile-quantile plots, the residuals were tested for a normal distribution () [98]. If the hypothesis of a normal distribution had to be rejected, a Box–Cox transformation was carried out and a normal distribution of the residuals was achieved [99] (Equation (28)). Homoscedasticity was tested according to Bartlett [100], Levene [101] and Fligner-Killeen [102]. If the hypothesis of homoscedasticity () had to be rejected, the non-parametric Kruskal–Wallis test was used for the analysis of variance, which has a lower power, but does not depend on the normal distribution of the residuals and homoscedasticity [103]. As ANOVA and the Kruskal–Wallis test only provide a statistical statement about all mean values, post-hoc analysis was also carried out in each case. With the help of post-hoc analysis, the mean values can be compared pairwise. For this purpose, post-hoc analysis according to Conover [104] was used, which is also parameter-free and performs multiple comparisons using rank sums. To counteract the problem of multiple comparisons, the p values were adjusted according to the Bonferroni–Holm method [105].
2.4. Validation
To validate the CFD results, the value was determined experimentally. The gassing-out method according to the recommendation from the DECHEMA expert group for single-use technology was used [106]. The following points were changed from the guidelines: a temperature of was set, as in the simulations, and ultrapure water with a conductivity of cm−1 was used instead of phosphate-buffered saline. To perform the measurement, nitrogen was injected into the bioreactor via the sparger for gassing-out, followed by air gassing. The value was determined for an oxygen saturation range of 10–90%. The base case was measured at a stirrer speed of 600 and an aeration rate of , resulting in a value of (11.1 ± 0.2) h−1, which served as a reference value for the subsequent CFD simulations. The measurements were performed eight times, using a POF-L2-5-OIM-L215 (polymer optical fiber) oxygen sensor from PreSens Precision Sensing GmbH (Regensburg, Germany). The stirrer was printed of polylactic acid using the fused filament fabrication process (Ultimaker S5, Ultimaker B.V., Utrecht, The Netherlands).
3. Results and Discussion
The investigations focus mainly on the statistical evaluation of the values achieved by the different models and their required computing time. To examine the influence of different interfacial force models, the classical Euler–Euler model was used in the first step after the mesh analysis. In the second step, the influence of different population balance models was investigated. All results were compared with the experiments described in Section 2.4.
3.1. Mesh Study
To estimate the discretization error caused by the computational mesh, four meshes of different resolutions were created (Table 3). The mesh study was evaluated qualitatively by considering the velocity field and the turbulent energy dissipation field, while quantitative analysis was performed using a Richardson extrapolation. For the quantitative examination, the value dependent on the energy dissipation rate was used. The Richardson extrapolation yielded an estimated discretization error for the value of % for the coarsest mesh. The discretization errors are summarised in Table 3. While it is desirable to keep the discretization error as small as possible, this results in an increased number of meshes and an associated exponential increase in computing time. As will be shown in the following sections, a discretization error of % is negligibly small compared to the model errors. Therefore, for economic reasons, the computational mesh with 256,253 mesh cells was used for all further simulations.

Table 3.
Discretisation error calculated by the Richardson extrapolation for the mass transfer coefficient .
3.2. Euler–Euler Simulations
As in the experiments, a stirrer speed of 600 and an aeration rate of was used for the basic simulation. The maximum velocity can be seen on the contour plot with unscaled velocity vectors for a stirrer circumference of 1.57 m s−1 (Figure 2a). This corresponds to the theoretical tip speed of the stirrer. The flow velocity then decreases radially until it approaches 0 m s−1 at the bioreactor wall through the no-slip boundary condition (Figure 2b). Due to the counterclockwise rotation, the pitched blade stirrer has a downward pumping effect (Figure 2a,b). The resulting flow pattern corresponds to that described by Aubin et al. [107]. The stirring creates a turbulent flow with a Reynolds number of 2.8 · 104. The gas flowing in at 1.32 m s−1 also influences the fluid flow in the bioreactor, particularly in the area around the sparger (Figure 2c). The turbulent energy dissipation rate, which is particularly interesting for the calculation of the mass transfer coefficient , is at its maximum at the stirrer tip at 259.4 m2 s−3 and then decreases radially (Figure 2d). As energy is also introduced into the system via the aeration process, a higher energy dissipation rate, compared to the bulk liquid, of 25.1 m2 s−3 to 31.8 m2 s−3 occurs at the sparger outlet (Figure 2c). A further increase in the energy dissipation rate can also be seen at the phase transition. The distribution of the gas fraction in the bioreactor is important for determining both the value and a. Figure 2e and f show the logarithmic gas fraction at a simulation time of 30 . As expected, the air rises centrally below the stirrer and after passing the stirrer, radial distribution increases significantly. This remains almost constant until it reaches the liquid surface.
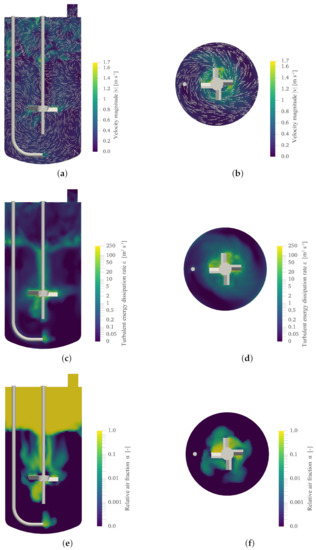
Figure 2.
Flow field overview of the base simulation ( 600 and 2 ) after 30 simulation time. (a,b) Velocity field laterally and from above on the stirrer plane, respectively. (c,d) Logarithmic representation of the turbulent energy dissipation rate in the same planes, and (e,f) relative air fraction in the bioreactor system.
The simulation was divided into three steps. In the first 10 s, the flow field was built up without gassing. This served as a starting point for all further investigations (with the same speeds and gassing rates). For the last two steps, gassing was switched on and the last 10 s were evaluated for the . It is assumed that there is a constant value that fluctuates around an average value. Figure 3a shows the temporal progression of and a after aeration was switched on. Both values rise rapidly and begin to level off after two to three seconds. The resulting product, the value, is shown in Figure 3b, with the evaluated area marked in grey.
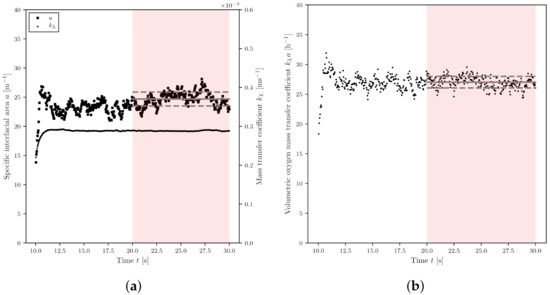
Figure 3.
Temporal progression of (a) the , a and (b) values for the base simulation. The gas supply was switched on at time . For the value, the time interval 20 to 30 was evaluated (red highlighted). The mean value and the standard deviation are shown in grey.
The two terms and a must be calculated individually and at each time step in each cell to determine the value. The specific interface a can be calculated according to Equation (2) [108]. A variety of semi-empirical formulae exist for calculating the mass transfer coefficient that include different coefficients for the individual terms. Seven different models were tested to choose a -model. Table 4 shows , a and for the base simulation after 30 . The choice of -model had a significant influence on the resulting value, resulting in values that differ by two powers of ten. A value ten times lower than the experimentally determined one was predicted by the model of Prasher and Wills [109] (1.2 h−1). The models of Perez and Sandall [110] and of Garcia-Ochoa and Gómez [111], on the other hand, predicted significantly higher values (480.4 h−1 and 80.9 h−1, respectively). However, it must be taken into account that the former was developed for non-Newtonian fluids. The only model that is not based on the energy dissipation rate is the model of Akita and Yoshida [112]. This model takes into account gravitational acceleration, diffusivity, density of the liquid, surface tension and the bubble diameter, which is not appropriate for the Euler–Euler simulation with its constant bubble diameter. The model of Johnson and Huang [113] is rather uninteresting for CFD applications, as only an average value can be calculated. Both the models of Brüning [114] and Kawase and Moo-Young [115] achieve good agreements with the experimental data. The Brüning model showed the best agreement across all of the simulations performed and was therefore used for all further simulations ( 100 to 1200 and to 2 ). No consideration was given to adjusting the factors of the model to fit the results, as this may have resulted in a loss of generality.

Table 4.
Overview of different mass transfer coefficient models and their effect on the calculation for the base simulation. The relative difference refers to the experimentally measured value of 11.1 h−1.
3.2.1. Influence of the Bubble Diameter
The simulations with the standard Euler–Euler model were carried out assuming a constant gas bubble diameter. As the gas bubble surface and thus the specific interface area a is directly dependent on the gas bubble diameter , it was assumed that this has a large influence on the value. Figure 4 shows the relationship between the calculated value and the assumed gas bubble diameter. The decrease in the value can be described by a power function as the bubble diameter increases. Thus, the value is (125.7 ± 3.8) h−1 for a bubble diameter of 1 and decreases to (8.7 ± 0.3) h−1 for a bubble diameter of 7 . For all further simulations, a bubble diameter of 3 was assumed, which corresponds to the theoretical diameter calculated according to Garcia-Ochoa and Gómez (Equation (29)) [23].
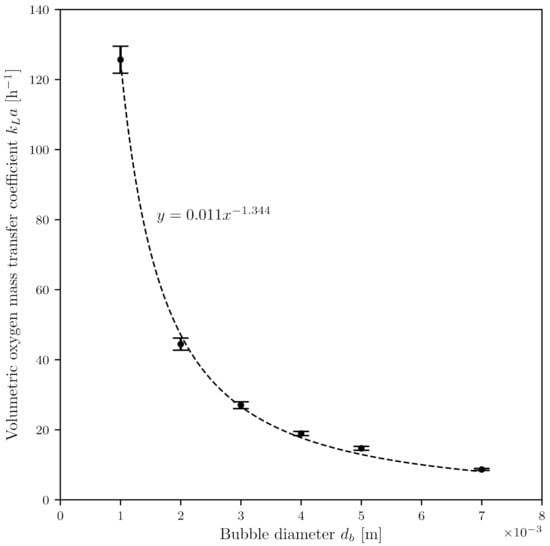
Figure 4.
Influence of a constant bubble diameter on the value.
3.2.2. Influence of Drag Force
To study the influence of the drag force coefficient model on the value, seven different models were evaluated, one of which included a bubble swarm correction. The violin plot in Figure 5 shows the mean values and their probability density function. The ranged from (25.6 ± 0.9) h−1 when using the model of Gidaspow [80] to (33.5 ± 1.5) h−1 for the Ergun model [77]. Statistical analysis was performed according to Section 2.3, rejecting the hypothesis of a normal distribution for Ergun’s [77], Tomiyama’s [79] and Lain’s models [116]. All of the tests rejected the hypothesis of homoscedasticity (). The Kruskal–Wallis test also rejected the hypothesis with · 10−211 (). It is thus assumed that the choice of model for the drag force coefficient has a statistically significant influence on the CFD predicted value. The hypothesis was rejected with for all of the pairwise tests. The choice of model for the drag force coefficient had a statistically significant influence on the value, whereby the specific interface a, with a coefficient of variation of , is significantly more influenced than the mass transfer coefficient (). Besides the statistical influence, the change in computing time due to the choice of model is also of interest from an economic point of view. The models were ordered in the violin plot (Figure 5) according to ascending computation time. The shortest computation time, for 20 s of aeration, resulted from the Schiller Naumann [76] drag force coefficient model with a swarm correction function. The computation time (calculated for a single CPU unit) was 1243 . The maximum computing time required for the Lain [116] model was times longer and amounted to 2000 CPU time.
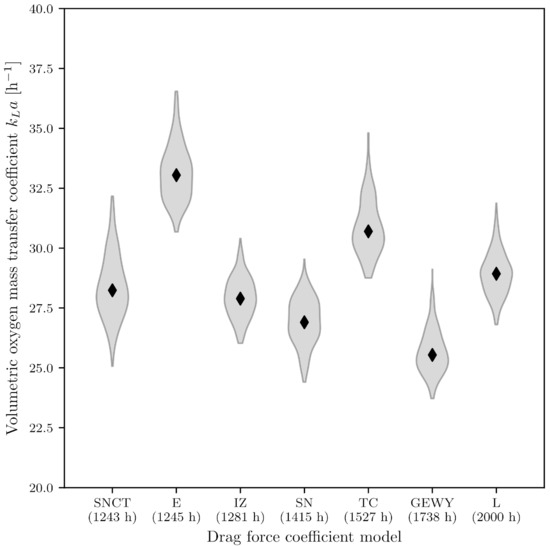
Figure 5.
Influence of the drag force coefficient model on the value. The mean values and the corresponding probability density function are shown in violin form. The time corresponds to the CPU time for the simulation of 20 s (SNCT = Schiller and Naumann [76] with swarm correction, E = Ergun [77], IZ = Ishii and Zuber [78], SN = Schiller and Naumann [76], TC = Tomiyama correlated [79], GEWY = Gidaspow, Ergun, Wen, and Yu [80], L = Lain [116]).
Several authors have already indicated that drag force has a greater influence on the flow field and other parameters than other interfacial forces [53,54]. This statement is consistent with the investigations made in this study. The most frequently used models for the drag force coefficient are those of Schiller Naumann [76] and Ishii Zuber [7,78,117]. A disadvantage of both models is that they neglect the influence of turbulence. While this reduces the computational effort, it could also explain why these models often do not agree with experiments [53,118,119]. Ergun’s [77] model delivers the highest value of (33.5 ± 1.5) h−1. This model was empirically derived for Newtonian fluids in packed columns with a porosity of about . As described by Halverson et al. [120], this model has a very small range of applications and is therefore unsuitable for use in stirred bioreactors which is consistent with the results of this work. By combining the models of Ergun [77] and Wen Yu, the model of Gidaspow [80] can be used for a wider range of applications [121]. The longer computation time described by Dey et al. [122] could be confirmed by the results of this study. This model has the second-longest calculation time of 1738 and also takes the influence of turbulence into account. Lain’s model, which had the longest computing time, is also suitable for stirred bioreactors, as it also takes turbulence into account [116]. Tomiyama’s [79] model addresses both the aspect ratio of bubbles and turbulence. However, Lote et al. [117] and Colombo et al. [123] showed that this model is only suitable for high Reynolds numbers. The drag force study was carried out for a stirrer speed of 600 . Turbulence was generated, but the Reynolds number was with 2.80 · 104 not very high. For this reason, it can be assumed that the correlated Tomiyama [79] model is unsuitable in this particular case, but would be suitable for simulations with higher Reynolds numbers. Several authors have been able to show that Lane’s model agreed best with the experimental results [53,119,124]. This model is currently not standard in OpenFOAM 7 and would need to be implemented for further studies.
3.2.3. Influence of Lift Force
To examine the lift force coefficients, three simulations were carried out using different lift force coefficient models, one that neglected the lift force () and two with constant lift force coefficients ( and ). The resulting values are shown in the form of a violin plot in Figure 6a. Depending on the model, the values vary from (23.4 ± 0.8) h−1 (Morgan model) to (31.5 ± 1.3) h−1 (Legendre and Magnaudet model [82]). The models were also plotted based on increasing CPU time. Morgan’s model required only 1278 for 20 s of aerated simulation, while the Legendre and Magnaudet model [82] required fold more time to perform the same computation.
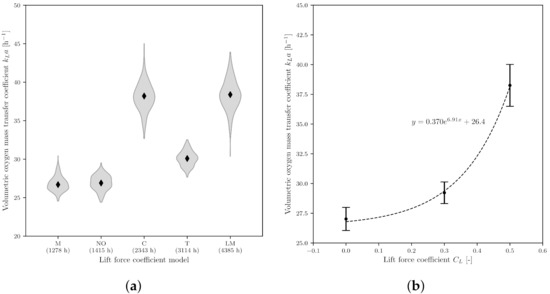
Figure 6.
Influence of the lift force coefficient on the value. (a) Effect of different lift force coefficient model on the value. The mean values and the corresponding probability density function are shown in violin form. The time corresponds to the CPU time for the simulation of 20 s (M = Moraga, NO = no lift coefficient, C = constant lift coefficient 0.5, T = Tomiyama [81], LM = Legendre and Magnaudet [82]); (b) Influence of different constant lift force coefficient on the value.
To obtain statistical information about the influence of the lift force coefficient model on the value, the same procedure as the drag force coefficient was chosen. Except for Morgan’s model, the hypothesis of a normal distribution could not be rejected by the Shapiro–Wilk test. The homoscedasticity tests all rejected the hypothesis of homoscedasticity. The Conover post-hoc analysis showed that there is no statistically significant difference between the Morgan model and the neglection of lift force (, ). There was also no statistically significant difference between the Legendre and Magnaudet [82] model and a constant lift force coefficient of (, ). Similar to drag force, the variability coefficient of the specific interfacial area was and therefore times higher than the variability coefficient of the mass transfer coefficient. Several authors have been able to show that the lift force is significantly smaller or even negligible compared to the drag force [54,125]. For small () spherical gas bubbles, the lift force coefficient is , but the coefficient is strongly influenced by the shape of the gas bubble and decreases as bubble size increases. As the simulations were performed assuming a bubble diameter of 3 , the constant lift force coefficient of tends to be too high. As shown in Figure 6b, the value increases exponentially as the lift force coefficient () increases. The Legendre and Magnaudet model [82] was developed for laminar systems and is therefore not particularly suitable for stirred bioreactor applications. Lucas et al. [65] describe the lift force as a not yet fully understood phenomenon and recommend further numerical and experimental investigations, especially for simulations with many particles like those found in bioreactors. Nevertheless, Lucas et al. [65] were able to achieve good agreement with experimental findings using Tomiyama’s [81] model, which cannot be refuted in this study.
3.2.4. Influence of the Virtual Mass Force
To study the influence of virtual mass force on the value, three simulations were carried out. One simulation with a constant virtual mass force coefficient , one with Lamb’s [83] virtual mass coefficient model, and one that did not consider the virtual mass force. The results are shown graphically in Figure 7. The highest value of (27.0 ± 1.0) h−1 was calculated with the constant virtual mass force coefficient, the lowest value of (15.6 ± 0.3) h−1 was calculated without considering virtual mass force. The CPU time for the calculation of 20 of aeration differed by a maximum of 20% and ranged from 1290 for the Lamb model [83] to 1543 for the calculation that did not consider virtual mass force. As shown in Figure 7, the simulation that did not consider virtual mass differed significantly from the other two simulations and resulted in the lowest value of all the Euler–Euler simulations without PBM. As only the residuals of from the simulation with the constant virtual mass force coefficient were normally distributed and all tests rejected the hypothesis of homoscedasticity, the Kruskal–Wallis test was performed. As expected, the null hypothesis was rejected with a p value of 3.4 · 10−80 (). The Conover post-hoc analysis also showed that there is a statistically significant difference between the calculated values for all of the models examined.

Figure 7.
Influence of the virtual mass force coefficient model on the value. The mean values and the corresponding probability density function are shown in violin form. The time corresponds to the CPU time for the simulation of 20 s (L = Lamb [83], C = constant virtual mass coefficient 0.5, NO = no virtual mass).
The simulations assumed a constant aspect ratio of 1, which is justifiable for small bubbles. For spherical particles, the virtual mass force coefficient is . As the Lamb [83] model takes the aspect ratio into account when modeling the [126], similar values were expected for the simulation with constant and when using Lamb’s [83] model. Although these exhibited a statistically significant difference, the practical relevance is questionable. Lamb’s [83] model is of great interest, especially for variable aspect ratios, and is preferred over a constant of . Nevertheless, in the literature the virtual mass force coefficient is often not modeled and is assumed to be a constant [127]. The value calculated without taking the virtual mass force into account differed significantly from the other two simulations. The reason for this difference could be that the phenomenon of virtual mass force is omnipresent and is of great importance especially in the vicinity of spargers [125,128]. Due to the large difference in density between gas bubbles and the continuous phase, it is possible that the virtual mass is greater than the actual mass of the dispersed particles [129]. Besides Lamb’s [83] model, there are several other available models, of which Pudasaini’s [130] is a promising one, as it is a completely analytical model. However, this model is not yet available in OpenFOAM 7 and would need to be implemented for further research.
3.2.5. Influence of Turbulent Dispersion Force
Two simulations were carried out to examine the influence of the force caused by the turbulent fluctuation of the flow velocity on the value. A simulation without taking the turbulent dispersion force into account and one with the model according to Gosman [64] were performed. The first simulation delivered a value of (27.0 ± 1.0) h−1 and the second a value of (26.6 ± 0.8) h−1, with the Gosman [64] model requiring 10% less computational time (Figure 8). As the hypothesis of the Shapiro–Wilk test could not be rejected for both models, but the hypothesis of the homoscedasticity test had to be rejected, a t-test with unequal variance was performed. The two models were statistically shown to be significantly different, with a p value of 1.49 · 10−5 ().
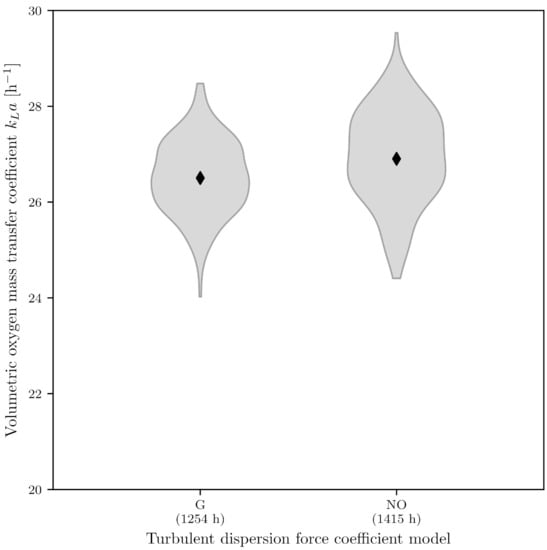
Figure 8.
Influence of the turbulent dispersion force coefficient model on the value. The mean values and the corresponding probability density function are shown in violin form. The time corresponds to the CPU time required for the simulation of 20 s (G = Gosman [64], NO = no turbulent dispersion force).
The turbulent dispersion force is often neglected in the literature, Nevertheless, even though there was a statistically significant difference in the calculated values, this approach has been confirmed. However, when turbulent dispersion force is modeled, the Gosman [64] model is usually applied because of its relative simplicity and robustness [131]. Although more complex models exist, these have not yet been implemented in OpenFOAM 7 [132].
3.3. Population Balance Modelling
As described in Section 3.2.1, in the classical Euler–Euler simulation, the selected bubble diameter has the greatest influence on the value. Coupling the CFD simulation with PBM can eliminate the problem of a constant bubble diameter. This allows the two phenomena of bubble coalescence and bubble breakup to be modeled, which makes the simulations more complex, but reduces the degree of abstraction. For the following investigations, the class method was used to solve the PBE, as it is implemented in OpenFOAM 7 by default.
3.3.1. Influence of Initial Gas Bubble Size Distribution
The class method is characterized by the fact that the gas bubble size distribution is discretized into classes. This allows the size distribution to be more accurately approximated as the number of classes increases. To study this effect and to obtain an optimum balance between economy and accuracy, four simulations with different numbers of classes were carried out (16, 24, 32, and 64 classes). For all simulations, the classes were chosen for a range of 1 to 5 and an initial bubble diameter of 3 . The calculated value initially decreased slightly as the number of classes increased and then slightly increased again at 64 classes, with values between (15.1 ± 0.4) h−1 and (16.0 ± 0.5) h−1 (Figure 9a). As, in addition to accuracy, the economy is also of great interest, simulation duration was also taken into account. As shown in Figure 9b, the computing time increased exponentially as the number of classes increased, matching the conclusions of other authors [133,134]. The literature recommends using between 12 and 25 classes [133,134]. As the value only changes minimally as the class number increased, but the computing time increased exponentially, 24 classes were used for the further simulations. 24 classes were preferred over 16 classes because, although the computation time increases, the value is closer to the experimental data. Furthermore, five simulations with different initial bubble diameters were also carried out ( 1 to 5 ). In contrast to the free and constant bubble diameters of the Euler–Euler model (Figure 4), the influence on was minimal. This is due to the fact that the gas bubble size distribution in the system adjusts itself when solving the PBE (Figure A1).
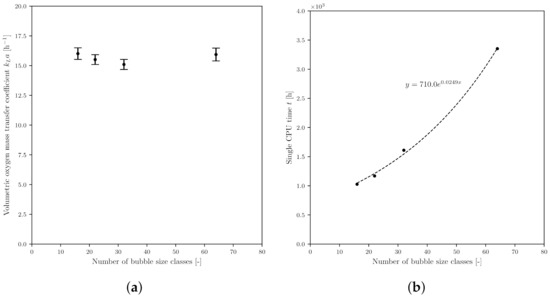
Figure 9.
Results of the class method PBM simulations. (a) Influence of the number of bubble size classes on the value; (b) relationship between the number of bubble size classes and CPU time.
3.3.2. Influence of the Coalescence Model
To scrutinize the effect of coalescence modeling on the value, four models were compared, including Luo’s model, which is widely used in the literature [135]. The calculated values are shown in Figure 10 and range from (14.8 ± 0.8) h−1 for Luo’s [87] model to (17.0 ± 0.9) h−1 for the model proposed by Lehr et al. [32]. The procedure described in Section 2.3 was also used for statistical analysis. The post-hoc analysis showed that there is a statistically significant difference between all of the models (). It should be noted that all of the values were significantly lower and thus closer to the measured than the values from the standard Euler–Euler simulations. In terms of computing time, the models of Coulaloglou and Tavlarides [86], Luo [87] and Prince & Blanch [88] hardly differed, whereas the model of Lehr et al. [32] required about twice as long for the same simulation, making it of little interest for practical applications. Other authors, who also examined the influence of different coalescence models, came to the same conclusion that the models of Coulaloglou and Tavlarides [86], Luo [87] and Prince & Blanch [88] hardly differed [135]. Kaiser [136] was able to show in his research that the Lehr et al. [32] model overestimates the value, which is also in line with the results presented here. Luo’s [87] model, which is used most frequently, showed the best agreement with the experimental investigations and is characterized by an economic calculation time.
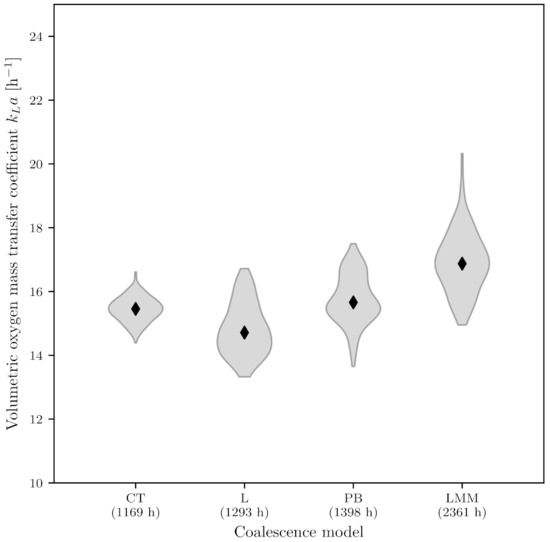
Figure 10.
Influence of different coalescence models on the value. The mean values and the corresponding probability density function are shown in violin form. The time corresponds to the CPU time required for the simulation of 20 s (CT = Coulaloglou and Tavlarides [86], L = Luo [87], PB = Prince and Blanch [88], LMM = Lehr, Millies and Mewes [32]).
3.3.3. Influence of the Breakup Model
In addition to the four coalescence models investigated, four breakup models were also examined to determine their influence on the . An exponential kernel [137] was tested, which often serves as a basis for other models, as well as the models of Luo and Svendsen [85], Laakkonen et al. [84] and Lehr et al. [32]. Binary bubble breakup was modelled in each case. In addition, a simulation was also carried out using the model of Laakkonen et al. [84] that modeled the daughter gas bubble size distribution. The resulting values are shown in Figure 11 and range from (14.3 ± 0.6) h−1 for the model of Laakkonen et al. [84] to (17.3 ± 1.0) h−1 for the model of Lehr et al. [32]. Based on post-hoc analysis according to Conover, it can be concluded that there is no statistically significant difference between the values calculated using the model of Laakkonen et al. [84] and the model of Luo and Svendsen [85] (). There was, however, a statistically significant difference in terms of the value from the other models. The computation time for the models of Lehr et al. [32] and Luo and Svendsen [85] are close to each other and are over twice as high as the computation times of the other models. The model of Lehr et al. [32] behaves like their coalescence [32], both in terms of overestimating the value and the long computing time. In addition to the economic aspect, another argument against the model is that it is not designed for high values, which are of decisive importance in microbial processes. There was no statistically significant difference in values calculated using the Luo and Svendsen [85] model or the Laakkonen et al. [84] model, but the computing time for the Luo and Svendsen model was more than twice as long, therefore this model is less interesting. The exponential kernel requires the shortest computing time, but it is questionable whether more complex systems can be modeled realistically using it. The most promising results in terms of value and computation time were obtained using the model of Laakkonen et al. [84] with binary bubble breakup and modeled daughter gas bubble size distribution. This model was developed for stirred reactors and is accordingly widely used, which can be confirmed in this study [84]. Despite the promising model of Laakkonen et al. [84], a difference between simulation ( = (14.3 ± 0.6) h−1) and experiment ( = (11.1 ± 0.2) h−1) remains. It is not clearly identifiable how the remaining difference is composed; it could be due to a systematic measurement error in the experiments, the discretisation error described in Section 3.1 or the large number of different models leading to an accumulation of small errors [7].
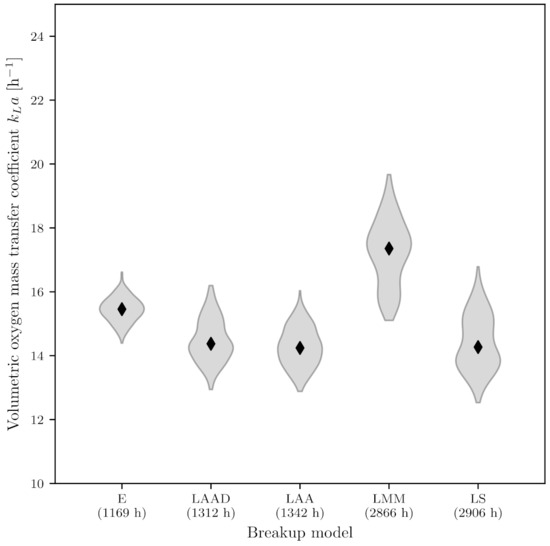
Figure 11.
Influence of different breakup models on the value. The mean values and the corresponding probability density function are shown in violin form. The time corresponds to the CPU time required for the simulation of 20 s (E = Exponential kernel, LAAD = Laakkonen, Alopaeus and Aittamaa with daughter size distribution [84], LAA = Laakkonen, Alopaeus and Aittamaa [84], LMM = Lehr, Millies and Mewes [32], LS = Luo and Svendsen [85]).
4. Conclusions
This work aimed to investigate the influence of different interfacial force models and PBM on the calculation of the volumetric oxygen mass transfer coefficient in stirred and aerated bioreactors using CFD. Using the Euler–Euler model, it was shown that the selected bubble diameter has a significant influence on the calculated value. Furthermore, modeling of the mass transfer coefficient also has a significant influence. The model of Brüning [114] showed the best agreement with the experimental data for the examined system. The analysis of the interfacial force models showed that the majority of the models calculate statistically significantly different values. The studies also considered economy in terms of computing time. For an economic calculation of the value using the Euler–Euler model in a stirred and aerated 2 bioreactor with turbulent flow, it was shown that the values agree best with the experimental values when the following interfacial models are used: the model of Schiller and Naumann [76] for the calculation of drag force, the model of Tomiyama et al. [81] for lift force and the model of Lamb [83], for virtual mass force. The turbulent dispersion force can be neglected. Although statistically significant different values could be described by the models, they are insignificant for practical applications. The often unknown mean gas bubble diameter should be estimated according to Garcia-Ochoa and Gómez [23]. The calculated values are comparable to those calculated by semi-empirical formulae like those of Van’t Riet [138]. It was found that the calculated values are about 50% higher than those in the experiments. One reason for this could be the lack of consideration of gas bubble breakup and coalescence. For this reason, various simulations were carried out with a PBM-coupled Euler–Euler model. All models examined resulted in better agreement with the experimentally determined values. The best agreement was obtained with the breakup model of Laakkonen et al. [84] and with the coalescence model of Luo [87]. However, the additional time should be accepted if the value is of interest. As a next step, further validation work should be carried out in the form of measurements and Shadowgraphy. The CFD model should also be optimized using the sliding mesh approach and other recent interfacial force models. Using the established PBM-coupled CFD model, it is possible to calculate the value for stirred and aerated bioreactors using OpenFOAM. This makes it possible to design new bioreactors for the biopharmaceutical industry in such a way that the oxygen supply is already optimal and adapted to process requirements. It also offers the possibility to determine optimal operating parameters, such as stirrer speed and aeration rate in advance in silico. By optimizing the bioprocesses with regard to the value, it should be possible to achieve a higher cell density, and with the same specific product formation rate, this would lead to a total increase in product and thus to higher profits. Although a good agreement between simulation and experiments could be achieved using the proposed models (measured of (11.1 ± 0.2) h−1 and simulated (14.3 ± 0.6) h−1 for the base simulation), success depends on many factors and it is questionable how useful it is to couple exact equations such as the Navier-Stokes equation with empirical approximations (e.g., models).
Author Contributions
Conceptualization, S.S. and D.E.; methodology, S.S.; software, S.S.; validation, S.S.; formal analysis, S.S. and D.E.; investigation, S.S.; resources, S.S.; data curation, S.S.; writing—original draft preparation, S.S.; writing—review and editing, D.E.; visualization, S.S.; supervision, D.E.; project administration, D.E. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by Zurich University of Applied Sciences.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We thank our colleagues Rüdiger W. Maschke, Valentin Jossen and Regine Eibl for their valuable feedback.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANOVA | Analysis Of Variance |
| CFD | Computational Fluid Dynamics |
| CFL | Courant-Friedrichs-Lewy |
| CPU | Central Processing Unit |
| DSD | Daughter Size Distribution |
| HPC | High Performance Computer |
| MOM | Method Of Moments |
| MRF | Moving Reference Frame |
| NDF | Number Density Function |
| OTR | Oxygen Transfer Rate |
| OUR | Oxygen Uptake Rate |
| PBE | Population Balance Equation |
| PBM | Population Balance Modelling |
| RANS | Reynolds-averaged Navier–Stokes |
| VOF | Volume of Fluid |
Nomenclature
| Latin symbols | ||
| A | Area | [] |
| a | Specific interfacial area | [m−1] |
| B | Birth rate | [m−3 s−1] |
| c | Constant value | [-] |
| Drag force coefficient | [-] | |
| Lift force coefficient | [-] | |
| Dissolved oxygen concentration at the gas liquid interphase | [mol m−3] | |
| Dissolved oxygen concentration in the liquid bulk | [mol m−3] | |
| Specific heat capacity | [J kg−1 K−1] | |
| Turbulent dispersion force coefficient | [-] | |
| Coefficient of variation | [-] | |
| Virtual mass force coefficient | [-] | |
| Wall lubrication force coefficient | [-] | |
| Biomass concentration | [cells L−1] | |
| Sauter mean diameter | [] | |
| D | Death rate | [m−3 s−1] |
| D | Dimensions | [-] |
| Bubble diameter | [] | |
| E | Error | [-] |
| F | Force | [] |
| Sum of volume-related interfacial forces [ | [] | |
| Drag force | [] | |
| Lift force | [] | |
| Turbulent dispersion force | [] | |
| Virtual mass force | [] | |
| Wall lubrication force | [] | |
| g | Gravitational acceleration | [m s−2] |
| Null hypothesis | [-] | |
| k | Turbulent kinetic energy | [m2 s−2] |
| Liquid side mass transfer coefficient | [m2 s−1] | |
| Volumetric oxygen mass transfer coefficient | [h−1] | |
| m | Molecular weight | [] |
| N | Total number of particles | [-] |
| N | Total number of cells | [-] |
| n | Number of particles per unit volume | [m−3] |
| Unit normal pointing away from the wall | [-] | |
| OTR | Oxygen transfer rate | [mol L−1 h−1] |
| OUR | Oxygen uptake rate | [mol L−1 h−1] |
| P | Power | [] |
| p | Pressure | [] |
| p | Exponent of error reduction | [-] |
| p | p-value | [-] |
| Q | Aggregation frequency | [s−1] |
| Cell specific oxygen uptake rate | [mol cells−1 h−1] | |
| r | Refinement factor | [-] |
| T | Temperature | [] |
| t | Time | [] |
| Velocity | [m s−1] | |
| V | Volume | [m3] |
| Representative volume for the ith size range | [m3] | |
| Data to be transformed | [-] | |
| Greek symbols | ||
| Volume fraction | [-] | |
| Significance level | [-] | |
| Dimensionless daughter size distribution | [-] | |
| Breakup frequency | [m3 s−1] | |
| Turbulent energy dissipation rate | [m2 s−3] | |
| Estimated discretisation error | [-] | |
| Factor defined by eq. 10 | [-] | |
| Cell specific constant | [-] | |
| Power parameter | [-] | |
| Dynamic viscosity | [] | |
| Kinematic viscosity | [m2 s−1] | |
| Density | [kg m−3] | |
| Surface tension | [N m−1] | |
| Reynolds stress tensor | [] | |
| Sub- and Superscripts | ||
| a | Air | |
| atm | Atmospheric | |
| b | Bubble | |
| br | Breakup | |
| coal | Coalescence | |
| g | Gas | |
| i | Index | |
| l | Liquid | |
| t | Turbulent | |
| w | Water | |
Appendix A

Table A1.
Boundary conditions.
Table A1.
Boundary conditions.
| Field | Fixed Walls (Vessel, Sparger) | Moving Walls (Stirrer, Shaft) | Inlet | Outlet |
|---|---|---|---|---|
| alpha.air | zeroGradient | zeroGradient | fixedValue (uniform 1) | inletOutlet |
| alphat. | compressible:: alphatWallFunction | compressible:: alphatWallFunction | calculated | calculated |
| epsilon | epsilonWall-Function | epsilonWall-Function | fixedValue (uniform 0.00015) | zeroGradient |
| k | kqRWallFunction | kqRWallFunction | fixedValue (uniform 3.75 · 10−5) | zeroGradient |
| nut. | nutkWallFunction | nutkWallFunction | fixedValue (uniform 1 · 10−8) | inletOutlet |
| p | calculated | calculated | calculated | calculated |
| p_rgh | fixedFluxPressure (uniform 1 · 105) | fixedFluxPressure (uniform 1 · 105) | fixedFlux-Pressure | prghPressure |
| Theta | zeroGradient | zeroGradient | fixedValue (uniform 1.0 · 10−7) | inletOutlet |
| T. | zeroGradient | zeroGradient | fixedValue (uniform 298.15) | inletOutlet |
| U.air | fixedValue | movingWall-Velocity | fixedValue uniform (x 0 0) | pressureInlet-OutletVelocity |
| U.water | fixedValue | movingWall-Velocity | fixedValue uniform (0 0 0) | pressureInlet-OutletVelocity |
x for both air and water. In U.air x represents the gas input velocity.
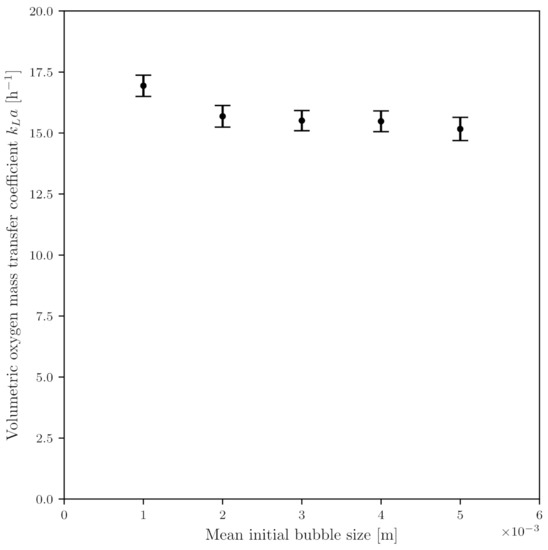
Figure A1.
Influence of initial bubble diameter on the computed value with the PBM coupled Euler–Euler model.
Short Biography of Authors
 | Stefan Seidel holds a Bachelor’s degree in biotechnology and a Master’s degree in applied computational life sciences from Zurich University of Applied Sciences. His focus is on the classical process engineering characterization of bioreactors as well as on multiphase CFD simulations and their validation using shadowgraphy and particle image velocimetry. Since 2017, he has been a research assistant in the Competence Center for Biochemical Engineering and Cell Cultivation Techniques at ZHAW and since 2020, a Ph.D. student at the Technical University of Berlin. |
 | Dieter Eibl has held an engineering degree in food technology since 1981 and a Ph.D. in biotechnology from the Technical University in Köthen since 1986. Since 1991, Prof. Eibl has been working at the University of Applied Sciences in Wädenswil as a lecturer. He is the head of the Competence Center for Biochemical Engineering and Cell Cultivation Techniques and working group leader for biochemical engineering. Prof. Eibl brings more than 25 years of professional expertise in upstream process development, scaling-up, project, and team management. |
References
- Langer, E.S.; Gillespie, D.E.; Rader, R. 17th Annual Report and Survey on Biopharmaceutical Manufacturing Capacity and Production, 17th ed.; BioPlan Associates, Inc.: Rockville, MD, USA, 2020; p. 555. [Google Scholar]
- Schirmer, C.; Maschke, R.W.; Pörtner, R.; Eibl, D. An overview of drive systems and sealing types in stirred bioreactors used in biotechnological processes. Appl. Microbiol. Biotechnol. 2021, 105, 2225–2242. [Google Scholar] [CrossRef] [PubMed]
- Paschedag, A.R. CFD in der Verfahrenstechnik; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Scully, J.; Considine, L.B.; Smith, M.T.; McAlea, E.; Jones, N.; O’Connell, E.; Madsen, E.; Power, M.; Mellors, P.; Crowley, J.; et al. Beyond heuristics: CFD-based novel multiparameter scale-up for geometrically disparate bioreactors demonstrated at industrial 2kL–10kL scales. Biotechnol. Bioeng 2020, 117, 1710–1723. [Google Scholar] [CrossRef]
- Mishra, S.; Kumar, V.; Sarkar, J.; Rathore, A.S. CFD based mass transfer modeling of a single use bioreactor for production ofmonoclonal antibody biotherapeutics. Chem. Eng. J. 2021, 412, 128592. [Google Scholar] [CrossRef]
- Cappello, V.; Plais, C.; Vial, C.; Augier, F. Scale-up of aerated bioreactors: CFD validation and application to the enzyme production by Trichoderma reesei. Chem. Eng. Sci. 2021, 229, 116033. [Google Scholar] [CrossRef]
- Seidel, S.; Maschke, R.W.; Werner, S.; Jossen, V.; Eibl, D. Oxygen Mass Transfer in Biopharmaceutical Processes: Numerical and Experimental Approaches. Chem. Ing. Tech. 2021, 93, 42–61. [Google Scholar] [CrossRef]
- Kocabaş, P.; Çalik, P.; Özdamar, T.H. Fermentation characteristics of l-tryptophan production by thermoacidophilic Bacillus acidocaldarius in a defined medium. Enzym. Microb. Technol. 2006, 39, 1077–1088. [Google Scholar] [CrossRef]
- Losen, M.; Frölich, B.; Pohl, M.; Büchs, J. Effect of oxygen limitation and medium composition on Escherichia coli fermentation in shake-flask cultures. Biotechnol. Prog. 2004, 20, 1062–1068. [Google Scholar] [CrossRef]
- Wagner, B.A.; Venkataraman, S.; Buettner, G.R. The rate of oxygen utilization by cells. Free. Radic. Biol. Med. 2011, 51, 700–712. [Google Scholar] [CrossRef] [Green Version]
- García-Ochoa, F.; Castro, E.G.; Santos, V.E. Oxygen transfer and uptake rates during xanthan gum production. Enzym. Microb. Technol. 2000, 27, 680–690. [Google Scholar] [CrossRef]
- Gotoh, T.; Chiba, K.; Kikuchi, K.I. Oxygen consumption profiles of Sf-9 insect cells and their culture at low temperature to circumvent oxygen starvation. Biochem. Eng. J. 2004, 17, 71–78. [Google Scholar] [CrossRef]
- Çalik, P.; Yilgör, P.; Ayhan, P.; Demir, A.S. Oxygen transfer effects on recombinant benzaldehyde lyase production. Chem. Eng. Sci. 2004, 59, 5075–5083. [Google Scholar] [CrossRef]
- Feng, Q.; Mi, L.; Li, L.; Liu, R.; Xie, L.; Tang, H.; Chen, Z. Application of “oxygen uptake rate-amino acids” associated mode in controlled-fed perfusion culture. J. Biotechnol. 2006, 122, 422–430. [Google Scholar] [CrossRef]
- Garcia-Ochoa, F.; Gomez, E.; Santos, V.E.; Merchuk, J.C. Oxygen uptake rate in microbial processes: An overview. Biochem. Eng. J. 2010, 49, 289–307. [Google Scholar] [CrossRef]
- Nienow, A.W. Reactor Engineering in Large Scale Animal Cell Culture. Cytotechnology 2006, 50, 9–33. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chmiel, H. Bioprozesstechnik; Spektrum Akademischer Verlag: Heidelberg, Germany, 2011; pp. 295–372. [Google Scholar] [CrossRef]
- Kraume, M. Transportvorgänge in der Verfahrenstechnik, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2020; p. 646. [Google Scholar] [CrossRef]
- Freed, L.E.; Guilak, F. Engineering Functional Tissues. In Principles of Tissue Engineering, 3rd ed.; Lanza, R., Langer, R., Vacanti, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 137–153. [Google Scholar] [CrossRef]
- Eibl, R.; Werner, S.; Eibl, D. Bag Bioreactor Based on Wave-Induced Motion: Characteristics and Applications. In Disposable Bioreactors; Springer: Berlin/Heidelberg, Germany, 2009; pp. 55–87. [Google Scholar] [CrossRef]
- Aunins, J.G.; Henzler, H.J. Aeration in Cell Culture Bioreactors. In Biotechnology: Bioprocessing; Rehm, H., Reed, G., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2008; Volume 3, pp. 219–281. [Google Scholar] [CrossRef]
- Werner, S.; Kaiser, S.C.; Kraume, M.; Eibl, D. Computational fluid dynamics as a modern tool for engineering characterization of bioreactors. Pharm. Bioprocess. 2014, 2, 85–99. [Google Scholar] [CrossRef]
- Garcia-Ochoa, F.; Gomez, E. Bioreactor scale-up and oxygen transfer rate in microbial processes: An overview. Biotechnol. Adv. 2009, 27, 153–176. [Google Scholar] [CrossRef] [PubMed]
- Karimi, A.; Golbabaei, F.; Mehrnia, M.R.; Neghab, M.; Mohammad, K.; Nikpey, A.; Pourmand, M.R. Oxygen mass transfer in a stirred tank bioreactor using different impeller configurations for environmental purposes. Iran. J. Environ. Health Sci. Eng. 2013, 10, 6. [Google Scholar] [CrossRef] [Green Version]
- Gill, N.K.; Appleton, M.; Baganz, F.; Lye, G.J. Quantification of power consumption and oxygen transfer characteristics of a stirred miniature bioreactor for predictive fermentation scale-up. Biotechnol. Bioeng. 2008, 100, 1144–1155. [Google Scholar] [CrossRef]
- Gestrich, W.; Krauss, W. Die spezifische Phasengrenzfläche in Blasenschichten. Chem. Ing. Tech. 1975, 47, 360–367. [Google Scholar] [CrossRef]
- Gestrich, W.; Esenwein, H.; Krauss, W. Der flüssigkeitsseitige Stoffübergangskoeffizient in Blasenschichten. Chem. Ing. Tech. 1976, 48, 399–407. [Google Scholar] [CrossRef]
- Yawalkar, A.A.; Heesink, A.B.M.; Versteeg, G.F.; Pangarkar, V.G. Gas-Liquid Mass Transfer Coefficient in Stirred Tank Reactors. Can. J. Chem. Eng. 2008, 80, 840–848. [Google Scholar] [CrossRef] [Green Version]
- Chu, P.; Finch, J.; Bournival, G.; Ata, S.; Hamlett, C.; Pugh, R.J. A review of bubble break-up. Adv. Colloid Interface Sci. 2019, 270, 108–122. [Google Scholar] [CrossRef] [PubMed]
- Liao, Y.; Lucas, D. A literature review of theoretical models for drop and bubble breakup in turbulent dispersions. Chem. Eng. Sci. 2009, 64, 3389–3406. [Google Scholar] [CrossRef]
- Chesters, A.K. Modelling of coalescence processes in fluid-liquid dispersions. A review of current understanding. Chem. Eng. Res. Des. 1991, 69, 227–259. [Google Scholar]
- Lehr, F.; Millies, M.; Mewes, D. Bubble-Size distributions and flow fields in bubble columns. AIChE J. 2002, 48, 2426–2443. [Google Scholar] [CrossRef]
- Shinnar, R.; Church, J.M. Statistical Theories of Turbulence in… Predicting Particle Size in Agitated Dispersions. Ind. Eng. Chem. 1960, 52, 253–256. [Google Scholar] [CrossRef]
- Howarth, W.J. Coalescence of drops in a turbulent flow field. Chem. Eng. Sci. 1964, 19, 33–38. [Google Scholar] [CrossRef]
- Liao, Y.; Lucas, D. A literature review on mechanisms and models for the coalescence process of fluid particles. Chem. Eng. Sci. 2010, 65, 2851–2864. [Google Scholar] [CrossRef]
- Ramkrishna, D. Population Balances; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar] [CrossRef]
- Hulburt, H.; Katz, S. Some problems in particle technology. Chem. Eng. Sci. 1964, 19, 555–574. [Google Scholar] [CrossRef]
- Randolph, A.D. A population balance for countable entities. Can. J. Chem. Eng. 1964, 42, 280–281. [Google Scholar] [CrossRef]
- Li, D.; Li, Z.; Gao, Z. Quadrature-based moment methods for the population balance equation: An algorithm review. Chin. J. Chem. Eng. 2019, 27, 483–500. [Google Scholar] [CrossRef]
- Jakobsen, H.A. Chemical Reactor Modeling; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–1244. [Google Scholar] [CrossRef]
- Wang, T.; Wang, J.; Jin, Y. A novel theoretical breakup kernel function for bubbles/droplets in a turbulent flow. Chem. Eng. Sci. 2003, 58, 4629–4637. [Google Scholar] [CrossRef]
- Askari, E.; St-Pierre Lemieux, G.; Proulx, P. Application of extended quadrature method of moments for simulation of bubbly flow and mass transfer in gas-liquid stirred tanks. Can. J. Chem. Eng. 2019, 97, 2548–2564. [Google Scholar] [CrossRef]
- Liang, X.F.; Pan, H.; Su, Y.H.; Luo, Z.H. CFD-PBM approach with modified drag model for the gas–liquid flow in a bubble column. Chem. Eng. Res. Des. 2016, 112, 88–102. [Google Scholar] [CrossRef]
- Solsvik, J.; Jakobsen, H.A. The Foundation of the Population Balance Equation: A Review. J. Dispers. Sci. Technol. 2015, 36, 510–520. [Google Scholar] [CrossRef]
- Laakkonen, M.; Moilanen, P.; Alopaeus, V.; Aittamaa, J. Modelling local bubble size distributions in agitated vessels. Chem. Eng. Sci. 2007, 62, 721–740. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Laurent, F.; Fox, R.O.; Massot, M. Solution of population balance equations in applications with fine particles: Mathematical modeling and numerical schemes. J. Comput. Phys. 2016, 325, 129–156. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.; Ramkrishna, D. On the solution of population balance equations by discretization—I. A fixed pivot technique. Chem. Eng. Sci. 1996, 51, 1311–1332. [Google Scholar] [CrossRef]
- Morel, C. Mathematical Modeling of Disperse Two-Phase Flows; Springer: Berlin/Heidelberg, Germany, 2015; Volume 114, pp. 57–76. [Google Scholar] [CrossRef]
- Tabib, M.V.; Roy, S.A.; Joshi, J.B. CFD simulation of bubble column-An analysis of interphase forces and turbulence models. Chem. Eng. J. 2008, 139, 589–614. [Google Scholar] [CrossRef]
- Suh, J.W.; Kim, J.W.; Choi, Y.S.; Kim, J.H.; Joo, W.G.; Lee, K.Y. Development of numerical Eulerian-Eulerian models for simulating multiphase pumps. J. Pet. Sci. Eng. 2018, 162, 588–601. [Google Scholar] [CrossRef]
- Thakre, S.S.; Joshi, J.B. CFD simulation of bubble column reactors: Importance of drag force formulation. Chem. Eng. Sci. 1999, 54, 5055–5060. [Google Scholar] [CrossRef]
- Magnaudet, J.J. Forces acting on bubbles and rigid particles. In Proceedings of the American Society of Mechanical Engineers, Fluids Engineering Summer Meeting FEDSM’97, Vancouver, BC, Canada, 22–26 June 1997. [Google Scholar]
- Gradov, D.V.; Laari, A.; Turunen, I.; Koiranen, T. Experimentally Validated CFD Model for Gas-Liquid Flow in a Round-Bottom Stirred Tank Equipped with Rushton Turbine. Int. J. Chem. React. Eng. 2017, 15. [Google Scholar] [CrossRef]
- Lou, W.; Zhu, M. Numerical simulation of gas and liquid two-phase flow in gas-stirred systems based on Euler-Euler approach. Metall. Mater. Trans. B Process. Metall. Mater. Process. Sci. 2013, 44, 1251–1263. [Google Scholar] [CrossRef]
- Saffman, P.G. The lift on a small sphere in a slow shear flow. J. Fluid Mech. 1965, 22. [Google Scholar] [CrossRef] [Green Version]
- Kolev, N.I.; Kolev, N.I. Drag, lift, and virtual mass forces. Multiph. Flow Dyn. 2 2011, I, 31–85. [Google Scholar] [CrossRef]
- Auton, T.R.; Hunt, J.C.; Prud’Homme, M. The force exerted on a body in inviscid unsteady non-uniform rotational flow. J. Fluid Mech. 1988, 197, 241–257. [Google Scholar] [CrossRef]
- Deen, N.G.; Solberg, T.; Hjertager, B.H. Large eddy simulation of the gas-liquid flow in a square cross-sectioned bubble column. Chem. Eng. Sci. 2001, 56, 6341–6349. [Google Scholar] [CrossRef]
- Antal, S.P.; Lahey, R.T.; Flaherty, J.E. Analysis of phase distribution in fully developed laminar bubbly two-phase flow. Int. J. Multiph. Flow 1991, 17, 635–652. [Google Scholar] [CrossRef]
- Tomiyama, A.; Kataoka, I.; Zun, I.; Sakaguchi, T. Drag Coefficients of Single Bubbles under Normal and Micro Gravity Conditions. JSME Int. J. Ser. B 1998, 41, 472–479. [Google Scholar] [CrossRef]
- Frank, T. Advances in computational fluid dynamics (CFD) of 3-dimensional gas-liquid multiphase flows. In Proceedings of the NAFEMS Seminar “Simulation of Complex Flows (CFD)”, Wiesbaden, Germany, 25–26 April 2005; pp. 1–18. [Google Scholar] [CrossRef]
- Lahey, R.T.; Lopez de Bertodano, M.; Jones, O.C. Phase distribution in complex geometry conduits. Nucl. Eng. Des. 1993, 141, 177–201. [Google Scholar] [CrossRef] [Green Version]
- Lopez de Bertodano, M.; Lahey, R.T.; Jones, O.C. Turbulent bubbly two-phase flow data in a triangular duct. Nucl. Eng. Des. 1994, 146, 43–52. [Google Scholar] [CrossRef]
- Gosman, A.D.; Lekakou, C.; Politis, S.; Issa, R.I.; Looney, M.K. Multidimensional modeling of turbulent two-phase flows in stirred vessels. AIChE J. 1992, 38, 1946–1956. [Google Scholar] [CrossRef]
- Lucas, D.; Krepper, E.; Prasser, H.M. Use of models for lift, wall and turbulent dispersion forces acting on bubbles for poly-disperse flows. Chem. Eng. Sci. 2007, 62, 4146–4157. [Google Scholar] [CrossRef]
- Burns, A.D.; Frank, T.; Hamill, I.; Shi, J.M. The Favre averaged drag model for turbulent dispersion in Eulerian multi-phase flows. In Proceedings of the 5th International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004; pp. 1–17. [Google Scholar]
- Basset, A.B. Hydrodynamics; C. J. Clay, M. A. and Sons: Cambridge, UK, 1888. [Google Scholar]
- Brown, R. XXIV. Additional remarks on active molecules. Philos. Mag. 1829, 6. [Google Scholar] [CrossRef] [Green Version]
- Autodesk. Autodesk Inventor Professional 2020. 2020. Available online: https://www.autodesk.com/products/inventor/overview?term=1-YEAR (accessed on 4 July 2021).
- Jasak, H.; Papers, S. OpenFOAM®; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Holzmann, T. Mathematics, Numerics, Derivations and OpenFOAM; Holzmann CFD: Loeben, Germany, 2019. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. Über die partiellen Differenzengleichungen der mathematischen Physik. In Kurt Otto Friedrichs; Birkhäuser Boston: Boston, MA, USA, 1986; pp. 53–95. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Kelly, W. Using computational fluid dynamics to characterize and improve bioreactor performance. Biotechnol. Appl. Biochem. 2008, 49, 225. [Google Scholar] [CrossRef]
- VDI-Wärmeatlas; Springer: Berlin/Heidelberg, Germany, 2013. [CrossRef]
- Schiller, L.; Naumann, A. A Drag Coefficient Correlation. Z. Ver. Dtsch. Ing. 1935, 77, 318–320. [Google Scholar]
- Ergun, S. Fluid Flow Through Columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Ishii, M.; Zuber, N. Drag coefficient and relative velocity in bubbly, droplet or particulate flows. AIChE J. 1979, 25, 843–855. [Google Scholar] [CrossRef]
- Tomiyama, A.; Celata, G.P.; Hosokawa, S.; Yoshida, S. Terminal velocity of single bubbles in surface tension force dominant regime. Int. J. Multiph. Flow 2002, 28, 1497–1519. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiphase Flow and Fluidization; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar] [CrossRef]
- Tomiyama, A.; Tamai, H.; Zun, I.; Hosokawa, S. Transverse migration of single bubbles in simple shear flows. Chem. Eng. Sci. 2002, 57, 1849–1858. [Google Scholar] [CrossRef]
- Legendre, D.; Magnaudet, J. The lift force on a spherical bubble in a viscous linear shear flow. J. Fluid Mech. 1998, 368, 81–126. [Google Scholar] [CrossRef]
- Lamb, H. Hydrodynamics, 4th ed.; Cambridge University Press: Cambridge, UK, 1993; p. 728. [Google Scholar]
- Laakkonen, M.; Alopaeus, V.; Aittamaa, J. Validation of bubble breakage, coalescence and mass transfer models for gas–liquid dispersion in agitated vessel. Chem. Eng. Sci. 2006, 61, 218–228. [Google Scholar] [CrossRef]
- Luo, H.; Svendsen, H.F. Theoretical model for drop and bubble breakup in turbulent dispersions. AIChE J. 1996, 42, 1225–1233. [Google Scholar] [CrossRef]
- Coulaloglou, C.; Tavlarides, L. Description of interaction processes in agitated liquid-liquid dispersions. Chem. Eng. Sci. 1977, 32, 1289–1297. [Google Scholar] [CrossRef]
- Luo, H. Coalescence, Breakup and Liquid Circulation in Bubble Column Reactors. Ph.D. Thesis, University of Trondheim, Trondheim, Norway, 1993. [Google Scholar]
- Prince, M.J.; Blanch, H.W. Bubble coalescence and break-up in air-sparged bubble columns. AIChE J. 1990, 36, 1485–1499. [Google Scholar] [CrossRef]
- Graham, R.L.; Woodall, T.S.; Squyres, J.M. Open MPI. In Parallel Processing and Applied Mathematics. PPAM 2005. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3911, pp. 228–239. [Google Scholar] [CrossRef] [Green Version]
- Yoo, A.B.; Jette, M.A.; Grondona, M. SLURM: Simple Linux Utility for Resource Management. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2003; Volume 2862, pp. 44–60. [Google Scholar] [CrossRef] [Green Version]
- Ahrens, J.; Geveci, B.; Law, C. ParaView: An End-User Tool for Large Data Visualization, Visualization Handbook; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- van Rossum, G. Python 3.6.5. 2018. Available online: https://www.python.org/ (accessed on 6 July 2021).
- Richardson, L.F. The Approximate Arithmetical Solution by Finite Differences of Physical Problems Involving Differential Equations, with an Application to the Stresses in a Masonry Dam. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1911, 210, 307–357. [Google Scholar] [CrossRef] [Green Version]
- Engels, H. Zur Anwendung der Richardson-Extrapolation auf die numerische Differentiation. Computing 1971, 8, 255–271. [Google Scholar] [CrossRef]
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. Ph.D. Thesis, Imperial College of Science, Technology and Medicine, London, UK, 1996. [Google Scholar]
- Baker, T.J. Mesh generation: Art or science? Prog. Aerosp. Sci. 2005, 41, 29–63. [Google Scholar] [CrossRef]
- Zimmerman, D.W. A note on preliminary tests of equality of variances. Br. J. Math. Stat. Psychol. 2004, 57, 173–181. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (Complete Samples). Biometrika 1965, 52, 591. [Google Scholar] [CrossRef]
- Box, G.E.P.; Cox, D.R. An Analysis of Transformations. J. R. Stat. Soc. Ser. B Methodol. 1964, 26, 211–243. [Google Scholar] [CrossRef]
- Bartlett, M.S. Properties of sufficiency and statistical tests. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1937, 160, 268–282. [Google Scholar] [CrossRef]
- Levene, H. Robust tests for equality of variances. In Contributions to Probability and Statistics: Essays in Honor of Harold Hotelling; Olkin, I., Hotelling, H., Eds.; Stanford University Press: Palo Alto, CA, USA, 1960; pp. 278–292. [Google Scholar]
- Fligner, M.A.; Killeen, T.J. Distribution-Free Two-Sample Tests for Scale. J. Am. Stat. Assoc. 1976, 71, 210. [Google Scholar] [CrossRef]
- Kruskal, W.H.; Wallis, W.A. Use of Ranks in One-Criterion Variance Analysis. J. Am. Stat. Assoc. 1952, 47, 583. [Google Scholar] [CrossRef]
- Iman, R.L.; Conover, W.J. The Use of the Rank Transform in Regression. Technometrics 1979, 21, 499. [Google Scholar] [CrossRef]
- Holm, S. A Simple Sequentially Rejective Multiple Test Procedure. Scand. J. Stat. 1978, 6, 65–70. [Google Scholar]
- Meusel, W.; Löffelholz, C.; Husemann, U.; Dreher, T.; Greller, G.; Kauling, J.; Eibl, D.; Kleebank, S.; Bauer, I.; Glöckler, R.; et al. Recommendations for Process Engineering Characterisation of Single-Use Bioreactors and Mixing Systems by Using Experimental Methods; DECHEMA: Frankfurt am Main, Germany, 2020. [Google Scholar]
- Aubin, J.; Mavros, P.; Fletcher, D.F.; Bertrand, J.; Xuereb, C. Effect of axial agitator configuration (up-pumping, down-pumping, reverse rotation) on flow patterns generated in stirred vessels. Chem. Eng. Res. Des. 2001, 79, 845–856. [Google Scholar] [CrossRef] [Green Version]
- Fukuma, M.; Muroyama, K.; Yasunishi, A. Specific gas-liquid interfacial area and liquid-phase mass transfer coefficient in a slurry bubble column. J. Chem. Eng. Jpn. 1987, 20, 321–324. [Google Scholar] [CrossRef] [Green Version]
- Prasher, B.D.; Wills, G.B. Mass Transfer in an Agitated Vessel. Ind. Eng. Chem. Process. Des. Dev. 1973, 12, 351–354. [Google Scholar] [CrossRef]
- Perez, J.F.; Sandall, O.C. Gas absorption by non-Newtonian fluids in agitated vessels. AIChE J. 1974, 20, 770–775. [Google Scholar] [CrossRef]
- Garcia-Ochoa, F.; Gomez, E. Theoretical prediction of gas–liquid mass transfer coefficient, specific area and hold-up in sparged stirred tanks. Chem. Eng. Sci. 2004, 59, 2489–2501. [Google Scholar] [CrossRef]
- Akita, K.; Yoshida, F. Bubble Size, Interfacial Area, and Liquid-Phase Mass Transfer Coefficient in Bubble Columns. Ind. Eng. Chem. Process. Des. Dev. 1974, 13, 84–91. [Google Scholar] [CrossRef]
- Johnson, A.I.; Huang, C. Mass transfer studies in an agitated vessel. AIChE J. 1956, 2, 412–419. [Google Scholar] [CrossRef]
- Brüning, S. Strömungssimulation als Werkzeug zur Bioreaktorcharakterisierung. Ph.D. Thesis, Technischen Universität München, Munich, Germany, 2012. [Google Scholar]
- Kawase, Y.; Moo-Young, M. Mathematical models for design of bioreactors: Applications of. Kolmogoroff’s theory of isotropic turbulence. Chem. Eng. J. 1990, 43. [Google Scholar] [CrossRef]
- Laín, S.; Bröder, D.; Sommerfeld, M.; Göz, M.F. Modelling hydrodynamics and turbulence in a bubble column using the Euler-Lagrange procedure. Int. J. Multiph. Flow 2002, 28, 1381–1407. [Google Scholar] [CrossRef]
- Lote, D.A.; Vinod, V.; Patwardhan, A.W. Comparison of models for drag and non-drag forces for gas-liquid two-phase bubbly flow. Multiph. Sci. Technol. 2018, 30, 31–76. [Google Scholar] [CrossRef]
- Santos-Moreau, V.; Lopes, J.C.B.; Fonte, C.P. Estimation of kLa Values in Bench-Scale Stirred Tank Reactors with Self-Inducing Impeller by Multiphase CFD Simulations. Chem. Eng. Technol. 2019, 42, 1545–1554. [Google Scholar] [CrossRef]
- Karimi, M.; Akdogan, G. Comparison of different drag coefficient correlations in the CFD modelling of a Laboratory-Scale Rushton-Turbine Flotation Tank. In Proceedings of the Ninth International Conference on CFD in the Minerals and Process Industries, Melbourne, Australia, 10–12 December 2012; pp. 1–7. [Google Scholar]
- Halvorsen, B.M.; Du Plessis, J.P.; Woudberg, S. The performance of drag models on flow behaviour in the CFD simulation of a fluidized bed. WIT Trans. Eng. Sci. 2006, 52, 3–12. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Academic Press: Cambridge, MA, USA, 2012; pp. 1–467. [Google Scholar] [CrossRef]
- Dey, S.; Karmakar, M.; Chandra, P.; Chatterjee, P. Studies on various drag models in fluidized bed for abatement of environmental pollution. Int. J. Environ. Sci. 2015, 5, 1011–1021. [Google Scholar] [CrossRef]
- Colombo, M.; Fairweather, M.; Lo, S.; Splawski, A. Multiphase RANS simulation of turbulent bubbly flows. Int. Top. Meet. Nucl. React. Therm. Hydraul. 2015, 4, 2644–2657. [Google Scholar]
- Basavarajappa, M.; Miskovic, S. Investigation of gas dispersion characteristics in stirred tank and flotation cell using a corrected CFD-PBM quadrature-based moment method approach. Miner. Eng. 2016, 95, 161–184. [Google Scholar] [CrossRef]
- Zhang, Y.; Bai, Y.; Wang, H. CFD analysis of inter-phase forces in a bubble stirred vessel. Chem. Eng. Res. Des. 2013, 91, 29–35. [Google Scholar] [CrossRef]
- Kolev, N.I. Multiphase Flow Dynamics 2: Mechanical Interactions; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–363. [Google Scholar] [CrossRef]
- Zhang, D.; Deen, N.G.; Kuipers, J.A. Numerical simulation of the dynamic flow behavior in a bubble column: A study of closures for turbulence and interface forces. Chem. Eng. Sci. 2006, 61, 7593–7608. [Google Scholar] [CrossRef]
- Oertel, H., Jr. Prandtl—Führer durch die Strömungslehre; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2017. [Google Scholar] [CrossRef]
- Brennen, C.E. A Review of Added Mass and Fluid Internal Forces. Technical Report. 1982. Available online: https://resolver.caltech.edu/CaltechAUTHORS:BREncel82 (accessed on 6 July 2021).
- Pudasaini, S.P. A fully analytical model for virtual mass force in mixture flows. Int. J. Multiph. Flow 2019, 113, 142–152. [Google Scholar] [CrossRef]
- Ahmadi, W. Study of Turbulent Dispersion Modelling Effects on Dispersed Multiphase Flows. Properties. Dissertation, Technische Universität Darmstadt, Darmstadt, Germany, 2013. [Google Scholar]
- Peirano, E.; Chibbaro, S.; Pozorski, J.; Minier, J.P. Mean-field/PDF numerical approach for polydispersed turbulent two-phase flows. Prog. Energy Combust. Sci. 2006, 32, 315–371. [Google Scholar] [CrossRef] [Green Version]
- Sanyal, J.; Marchisio, D.L.; Fox, R.O.; Dhanasekharan, K. On the Comparison between Population Balance Models for CFD Simulation of Bubble Columns. Ind. Eng. Chem. Res. 2005, 44, 5063–5072. [Google Scholar] [CrossRef] [Green Version]
- Venneker, B.C.; Derksen, J.J.; Van den Akker, H.E. Population balance modeling of aerated stirred vessels based on CFD. AIChE J. 2002, 48, 673–685. [Google Scholar] [CrossRef]
- Mawson, R.A. Bubble Coalescence and Breakup Modeling for Computing Mass Transfer Coefficient. Ph.D. Thesis, Utah State Universty, Logan, UT, USA, 2012. [Google Scholar]
- Kaiser, S.C. Characterization and Optimization of Single-Use Bioreactors and Biopharmaceutical Production Processes Using Computational Fluid Dynamics. Ph.D. Thesis, Technischen Universität Berlin, Berlin, Germany, 2014. [Google Scholar]
- Marchisio, D.L.; Fox, R.O. Computational Models for Polydisperse Particulate and Multiphase Systems; Cambridge University Press: Cambridge, UK, 2013; Volume 39, p. 22. [Google Scholar] [CrossRef] [Green Version]
- Van’t Riet, K. Review of Measuring Methods and Results in Nonviscous Gas-Liquid Mass Transfer in Stirred Vessels. Ind. Eng. Chem. Process. Des. Dev. 1979, 18, 357–364. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).