Probabilistic Vulnerability Assessment of Transmission Lines Considering Cascading Failures

Abstract

The prevention of cascading failures and large-scale power outages of power grids by identifying weak links has become one of the key topics in power systems research. In this paper, a vulnerability radius index is proposed to identify the initial fault, and a fault chain model of cascading failure is developed with probabilistic attributes to identify the set of fault chains that have a significant impact on the safe and stable operation of power grids. On this basis, a method for evaluating the vulnerability of transmission lines based on a multi-criteria decision analysis is proposed, which can quickly identify critical transmission lines in the process of cascading failure. Finally, the proposed model and method for identifying vulnerable lines during the cascading failure process is demonstrated on the IEEE-118 bus system.

1. Introduction

Large-scale power outages around the world are often caused by cascading faults [1,2], and the propagation of cascading faults is closely related to weak links in the power grid [3,4]. In order to reveal weak links of the system, it is necessary to conduct a vulnerability assessment of the power grid.

A few power grid vulnerability assessment methods have been previously proposed for studying cascading failure, namely, structural analysis methods based on complex network theory [5,6,7], fault simulation methods based on self-organizing criticality theory [8,9,10], fault evolution methods based on cellular automata theory [11,12], and fault chain extraction methods based on Heinrich causal chain theory [13,14,15].

The structural vulnerability of a power grid is studied from the perspective of graph theory using structural analysis methods based on complex network theory, but the consideration of the physical process of the actual system is relatively simplified, so this method cannot analyze the operation state of the power grid. Fault simulation methods based on self-organized criticality theory reveal that the self-organized criticality of a power grid is the internal driving force of cascading blackouts, but it cannot describe the electrical characteristics of a power grid in detail. The principle of fault evolution methods based on cellular automata theory is to simulate component faults through cell rupture, and then simulate power grid cascading faults. However, because only the state combination of itself and neighborhood cells is considered in the change of cell state, the influence of electrical characteristics is ignored. Based on fault chain extraction methods, the relationship between cascading failure and components’ states is established on the premises of the power flow process and network structure of power grids. Not only can the phenomena of large-scale power outage be studied from the perspective of fault sequences, but also the causes of cascading failure can be identified from the various factors contributing to the fault sequences.

To perform vulnerability assessment using the fault chain model, the fault chain set must first be generated. When the power grid is very large, if all lines in the network are used as initial faults in turn [16,17], the workload of searching the fault chain is quite high. When predicting subsequent fault lines, if only one line is selected [18,19], the usefulness of the prediction result will be drastically limited and some of the riskier fault chains may remain unidentified. Moreover, if the lower-level fault line set is selected through index calculation, the results may also deviate from reality because of the uncertainty in the impact of the system’s load and the deterministic analysis of fault chains. Therefore, it is very important to select appropriate initial faults and subsequent fault lines to obtain the fault chain set.

After the fault chain set is obtained, the vulnerability of transmission lines can be evaluated from the perspective of topology, power flow, and vitality measures [20,21]. Regardless of the use of a topology or power flow perspective, (n-k) failure analyses [22,23] are required, and this poses computational concerns due to the large number of fault combinations and long calculation time. The vitality measures are mainly divided into probabilistic vitality [24,25] and deterministic vitality [26,27]. The probabilistic vitality is determined by the failure probability of each component in the power grid and the partial derivative of outage probability for each component, requiring a large amount of complex computation for large power grids. The deterministic vitality, on the other hand, only focuses on the position of lines in the fault chain of the fault tree, ignoring the importance of each fault chain itself and the difference between different lines in different fault chains, making the analysis result rather inaccurate.

In view of the above shortcomings, a probabilistic vulnerability assessment method based on the fault chain model is proposed in this paper to identify the weak lines. The major contributions of this article are as follows: (1) a cascading fault chain model with probabilistic attributes considering a variety of factors affecting cascading failure in the power system is proposed. This model can reasonably select initial faults and the subsequent lines, save the calculation of searching fault chain set, and predict the chain fault development mode with a more serious impact on the power grid. (2) A method for evaluating the vulnerability of transmission lines based on multi-criteria decision analysis is presented, which further avoids the faults combination problem and calculation time problem caused by n-k fault analysis and can evaluate the vulnerability of transmission lines from various aspects quickly and quantitatively. Simulation results from IEEE-118 bus system demonstrate the feasibility and effectiveness of the method proposed in this paper.

2. Cascading Failure Model

2.1. Probabilistic Load Flow

Cascading failure of the power system will cause power supply interruption, and load variation will lead to uncertain power flow distribution. Moreover, the propagation path of cascading failure is not unique. Considering the uncertainty of power flow and fault propagation, probabilistic load flow methods [28] have been applied to construct cascading failure models.

Power system is a high-order complex nonlinear network. In case of cascading failure, the repeated solution of complete nonlinear power flow equations is huge and time-consuming. The DC power flow model, commonly used in power system planning and security analysis, can simplify the nonlinear problem into a linear problem and obtain the approximate value of component overload in a short time. Therefore, it is also suitable for analyzing cascading faults.

Without considering the influence of reactive power distribution, DC power flow model is used to calculate the flow distribution of power grid, which can be expressed as

$$\{\begin{array}{l}\mathrm{P}=-\mathrm{B}\mathsf{\theta }\\ {\mathrm{P}}_{\mathrm{line}}=\mathrm{T}\mathsf{\theta }\end{array}$$

(1)

where P is the power vector injected to buses; B is the admittance matrix of the power system; θ is the bus voltage angle phase vector; P_line is the power flow vector of all transmission lines; T is the parameter representing that the line power flow can be linearly expressed by the bus voltage angle phase.

The uncertainty associated with load demand variation can be described by a normal distribution [29], i.e.,

$$\mathrm{f}\left({\mathrm{E}}_{\mathrm{L},\mathrm{i}}\right)=\frac{1}{\sqrt{2\pi {\mathsf{\sigma }}_i}}\exp [\frac{{({\mathrm{E}}_{\mathrm{L},\mathrm{i}}-{\mathsf{\mu }}_{\mathrm{i}})}^2}{2{\mathsf{\sigma }}_{\mathrm{i}}^2}]$$

(2)

where E_L,i is the load demand at bus i, μ_i is the mean value of the load, and σ_i is the standard deviation.

Using the probabilistic power load analysis, a cumulative distribution function of power flow under the influence of random disturbance and fault occurrence can be obtained, which can be integrated into a cascading fault index by using the Cumulant Method and Gram-Charlier expansion series.

2.2. Fault Chain

The propagation of cascading faults in a power system can be represented by a set of fault sequences [30,31]. Suppose a power grid has n fault chains. Fault chain set L and fault chain Li can be denoted as

$$\begin{array}{l}\mathrm{L}=\{{\overrightarrow{\mathrm{L}}}_1,{\overrightarrow{\mathrm{L}}}_2,\cdots ,{\overrightarrow{\mathrm{L}}}_{\mathrm{n}}\}\\ {\overrightarrow{\mathrm{L}}}_{\mathrm{i}}=\{{\mathrm{T}}_{\mathrm{i}1}{\mathrm{T}}_{\mathrm{i}2},\cdots ,{\mathrm{T}}_{\mathrm{im}}\}\end{array}$$

(3)

where T_ij is the j-th stage of fault chain i, which is the fault line in this paper.

To establish the cascading failure model based on fault chains, we first identify initial faults, and then determine subsequent fault lines.

2.3. Selection of Initial Faults

In theory, all the lines in the network can possibly be an initial fault in turn, but this will be a time-consuming and blind process. For some light-load lines, moreover, the fault has little impact on other components in the network. Therefore, in this paper, combining the overload probability distribution of transmission lines and the normalized directed electric betweenness, a vulnerability radius index is proposed to select the lines that are more likely to cause subsequent faults as the initial fault set, resulting in improved effectiveness of initial faults identification.

The overload probability index p_k is defined as the probability of overloading of line k calculated from probabilistic load flow taking into account load variations. Although the occurrence of the initial fault is random, the possibility of a fault in a heavy load line is greater [32]. Therefore, the index can be used to screen the initial fault lines in actual operating conditions.

The normalized directed electric betweenness b_k is defined as

$${\mathrm{B}}_{\mathrm{k}}={\displaystyle \sum _{\mathrm{i}\in \mathrm{G}, \mathrm{j}\in \mathrm{L}}\frac{{\mathrm{P}}_{\mathrm{Gi}}\cdot {\mathrm{P}}_{\mathrm{ij}}\left(\mathrm{k}\right)}{{\mathrm{P}}_{\mathrm{ij}}}}$$

(4)

$${\mathrm{b}}_{\mathrm{k}}{=\mathrm{B}}_{\mathrm{k}}{/\mathrm{B}}_{\max }$$

(5)

where G is the generator set, L is the load set, P_Gi is the active power of generator i, P_ij (k) is the active power transmitted from generator i to load j through line k, P_ij is the active power transmitted from generator i to load j, B_k is the directed electric betweenness of line k, B_max is the maximum value of the directed electric betweenness for all lines. The network topology has an important influence on whether the system can maintain stability after being disturbed [33]. A larger value of b_k means greater influence of line k on the network topology.

The overload probability values are all greater than or equal to 0, and less than or equal to 1. The greater the value, the higher the risk of branch failure. The normalized directed electric betweenness values are also between 0 and 1. The larger the value, the more important the line is in the system structure. Based on this, the vulnerability radius index VR_k is defined in this paper as follows:

$${\mathrm{VR}}_{\mathrm{K}}=\sqrt{{\mathrm{b}}_{\mathrm{k}}{}^2+{\mathrm{p}}_{\mathrm{k}}{}^2}$$

(6)

Thus, the vulnerability radius is essentially the distance from point (b_k, p_k) to the origin, as shown in Figure 1, and indicates the likelihood of line k causing subsequent cascading failures. For the same VR_k, there can be many possible (b_k, p_k), and thus lines with different values of b_k and p_k may have the same effect on subsequent cascading failures.

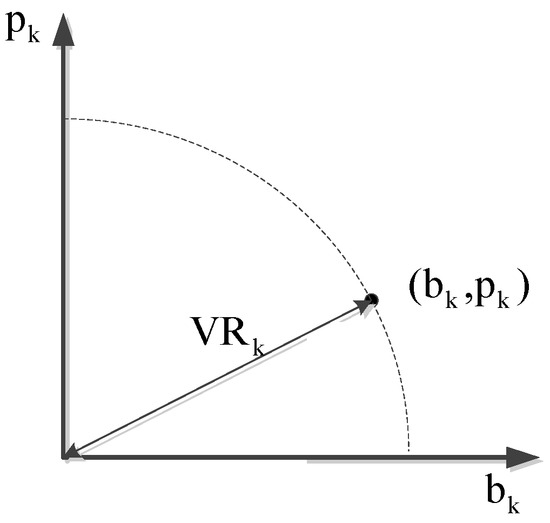
Figure 1. Vulnerability radius.

According to the vulnerability radius index, a reasonable threshold is set, and the line with the largest index value is selected to form the initial fault set. In large power systems, this can avoid listing all unexpected events that may cause system instability.

2.4. Subsequent Cascading Failures

Cascading failure in power systems is caused by the successive tripping of links. There is a correlation between the upper and lower-level faults along a fault line. In addition, component faults in a power grid can be divided into explicit faults and implicit faults. Explicit faults are related to the extent of loading of the lines [34], while implicit faults are related to fluctuation of power [35].

Based on the vulnerability analysis, an evaluation index for subsequent cascading failure lines is proposed by combining the line probability correlation, line overload probability and probabilistic load flow fluctuation.

Suppose line j fails at the T-th stage of a fault chain. For a normal (healthy) line i in the network, the expected values of transmitted power in the T-th stage and the (T − 1)-th stage are S_i^T and S_i^T−1, respectively. Then, the line probability correlation M_i is defined as

$${\mathrm{M}}_{\mathrm{i}}=\left|\frac{{\mathrm{S}}_{\mathrm{i}}^{\mathrm{T}}\cdot \mathrm{F}\left({\mathrm{S}}_{\mathrm{i}}^{\mathrm{T}}\right)-{\mathrm{S}}_{\mathrm{i}}^{\mathrm{T}-1}\cdot \mathrm{F}\left({\mathrm{S}}_{\mathrm{i}}^{\mathrm{T}-1}\right)}{{\mathrm{S}}_{\mathrm{j}}^{\mathrm{T}-1}\cdot \mathrm{F}\left({\mathrm{S}}_{\mathrm{j}}^{\mathrm{T}-1}\right)}\right|$$

(7)

where F(S_i^T) is the cumulative probability of line i corresponding to S_i^T in the T-th link, and F(S_i^T−1) is the cumulative probability of line i corresponding to S_i^T−1 in the (T − 1)-th stage of the fault chain. Thus, the ratio of power flow difference of line i at the T-th stage and the (T − 1)-th stage to the power flow of line j at the (T − 1)-th stage would reflect the relative impact of the failure/withdrawal of faulty line j on healthy line i. The larger the value of M_i, the greater the impact.

The line overload probability p_i is defined as the probability of line i to become overloaded as calculated from probabilistic load flow after faulty line j exits operation. The higher the value of p_i, the higher the probability of an explicit fault.

The removal of line j will affect the power flow in line i. Considering the power flow transfer on line i and the probability margin of line i, the probabilistic load flow fluctuation D_i is defined as follows:

$${\mathrm{D}}_{\mathrm{i}}=\frac{{\mathrm{LODF}}_{\mathrm{ij}}\cdot {\mathrm{P}}_{\mathrm{j}}\cdot \mathrm{F}\left({\mathrm{P}}_{\mathrm{j}}\right)}{{\mathrm{P}}_{\mathrm{i}.\max }-{\mathrm{P}}_{\mathrm{i}}\cdot \mathrm{F}\left({\mathrm{P}}_{\mathrm{i}}\right)}$$

(8)

where LODF is line outage distribution factor, P_j is the expected active power of line j, F(P_j) is the cumulative probability of line j at P_j, P_i,max is the power limit of line i, P_i is the expected active power of line i before line j is removed, and F(P_i) is the cumulative probability of line i at P_i. When D_i is large, power flow fluctuation has a greater influence, and the probability of implicit fault is higher.

Thus, an overall evaluation index for subsequent cascading failure lines G_i can be defined as follows:

$${\mathrm{G}}_{\mathrm{i}}={\mathrm{w}}_1{\mathrm{M}}_{\mathrm{i}}+{\mathrm{w}}_2{\mathrm{p}}_{\mathrm{i}}+{\mathrm{w}}_3{\mathrm{D}}_{\mathrm{i}}$$

(9)

where w₁, w₂ and w₃ are the corresponding weights. The value of G_i represents the extent to which non-faulty lines are affected by random factors such as power fluctuations and power flow shifts. Fault occurrence exhibits a probabilistic characteristic, and the subsequent line break based on this is a probabilistic property that reflects the likelihood of subsequent failure. In order to measure the complexity and uncertainty of the development process of cascading failure, a set of non-faulty lines with large G value is selected as the set of lower-level breaking lines.

2.5. Cascading Failure Process

In this paper, two criteria are used to end the cascading failure process: (1) The system has been judged as being transient unstable; (2) the predicted depth has reached a maximum of 8, because it is difficult to keep the power grid fully connected after N-8 failure events [23].

The flowchart of cascading failure is shown in Figure 2. From this, the fault chain set can be obtained.

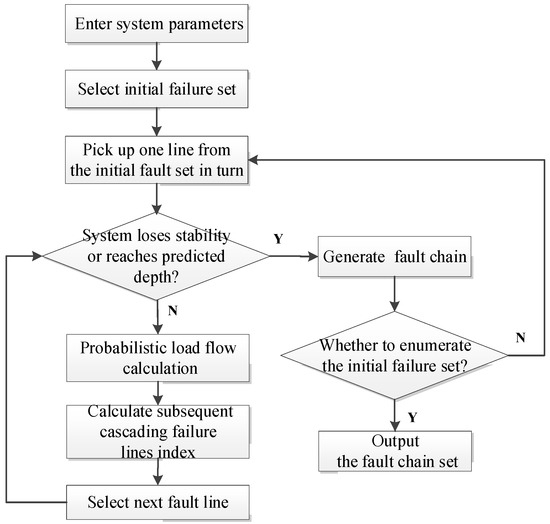
Figure 2. Flow chart of cascading failure.

3. Vulnerability Evaluation Method of Transmission Lines

The fault chain set gives different paths from the initial fault to the blackout. The purpose of the vulnerability assessment is to find the specific link (a particular stage) of the fault chain which is important to the stability of the power grid, combating the inaccurate prediction of a single fault chain.

Focusing on the fault chain set itself, a multi-criteria decision analysis model is proposed in this paper, which can evaluate the vulnerability of transmission lines without excessive and complex computational effort. The method involves four processes: selection of evaluation criteria, normalization of data, determination of criteria weights, and synthesis of data.

3.1. Selection of Evaluation Criteria

In assessing the vulnerability of transmission lines, the following considerations of the fault chain set should be noted. First, the intermediate fault link of a fault chain is the necessary step contributing to the occurrence of a system blackout. If more fault chains contain this fault link, the relative risk of the link is higher. Second, different intermediate links play different roles in the same fault chain. Furthermore, because different fault chains have varied levels of importance, the role of the same intermediate link in different fault chains can be different. Thus, a set of criteria should be used to evaluate the vulnerability of transmission lines, including the frequency, average location of lines in the fault chain set and the average depth of the fault chain to which the lines belong.

The frequency of line l in the fault chain set, denoted as α_l, is

$${\mathsf{\alpha }}_{\mathrm{l}}={\mathrm{n}}_{\mathrm{l}}$$

(10)

where n_l is the total number of occurrences of line l in the fault chain set. The average location of line l in the fault chain set β_l is

$${\mathsf{\beta }}_{\mathrm{l}}={\displaystyle \sum _{\mathrm{i}=1}^{{\mathrm{d}}_{\max }}\frac{{\mathrm{x}}_{\mathrm{i}}}{{\mathrm{n}}_{\mathrm{l}}}}\mathrm{i}$$

(11)

where x_i is the frequency of line l appearing on the fault chain at depth i, and d_max is the maximum depth of in the fault chain set. Thus, a smaller value of β_l means that line l is at the earlier position of the fault sequence, which will cause subsequent fault links to trigger one after another.

The average depth of fault chain to which line l belongs, denoted as γ_l, is defined as follows:

$${\mathsf{\gamma }}_{\mathrm{l}}=\frac{1}{{\mathrm{n}}_{\mathrm{l}}}{\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{f}}{\mathrm{d}}_{\mathrm{l},\mathrm{j}}}$$

(12)

where f is the total number of fault chains in the fault chain set, d_l,j is the depth of the j-th fault chain, where line l is located. If line l does not appear in the j-th fault chain, d_l,j = 0. A smaller value of γ_l means that the fault chain where line l is located is more likely to cause serious blackout in the power grid.

3.2. Normalization of Data

For ease of referencing and analysis, data should be normalized. However, the usual linear transformation method may not offer the needed comparability for high-optimal and low-optimal indices. Thus, it is more advantageous to use a non-linear transformation function [36] to normalize sample index value x to the (0, 1) interval. For simplicity, the logistic value function v(x) can be used, i.e.,

$$\mathrm{v}\left(\mathrm{x}\right)=\{\begin{array}{l}\frac{1}{{1+\mathrm{e}}^{-\left(\mathrm{x}-\mathsf{\mu }\right)/\mathsf{\sigma }}}, \mathrm{x}\in \mathrm{LB}\\ \frac{1}{{1+\mathrm{e}}^{+\left(\mathrm{x}-\mathsf{\mu }\right)/\mathsf{\sigma }}}, \mathrm{x}\in \mathrm{SB}\end{array}$$

(13)

where μ and σ are model parameters, LB (SB) is the range of values of x corresponding to indices that are larger (smaller) the better.

3.3. Determination of Criteria Weights

The variation coefficient method is an objective method of weighting by directly using the information contained in each index and calculating the weight. Suppose there are n transmission lines, and each transmission line has m evaluation criteria. The variation coefficient of criteria i, denoted as ρ_i, is given by

$${\mathsf{\rho }}_{\mathrm{i}}=\frac{{\mathsf{\sigma }}_{\mathrm{i}}}{{\mathsf{\mu }}_{\mathrm{i}}}, \mathrm{i}=1,2,\cdots ,\mathrm{m}$$

(14)

where σ_i is the standard deviation of criterion i, and μ_i is the mean value of criterion i.

If ρ_i is large, it means that criterion i requires a high standard score technically. Thus, it can be reasonably assumed that the weight of criterion is proportional to the variation coefficient. Then, the relative weight of criterion i, denoted as ω_i, is defined as follows:

$${\mathsf{\omega }}_{\mathrm{i}}=\frac{{\mathsf{\rho }}_{\mathrm{i}}}{{\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{m}}{\mathsf{\rho }}_{\mathrm{j}}}}$$

(15)

3.4. Synthesis of Data

The widely used data synthesis model is the weighted sum model. The disadvantage of this model lies in its mutual cancellation effect, that is, the low score of one criterion gets compensated by the high score of another criterion. In order to overcome this problem, the weighted geometric average model with relatively weak compensation [37] is adopted here, i.e.,

$$\mathrm{u}=\exp [{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{m}}{\mathsf{\omega }}_{\mathrm{i}}}\ln ({\mathrm{v}}_{\mathrm{i}})]$$

(16)

where u is the vulnerability of a transmission line, v_i is the normalized index value, w_i is the relative weight, and each transmission line has m evaluation indexes.

The vulnerability evaluation method of transmission lines proposed in this paper uses the logistic value function to normalize data, avoiding the loss of information in linear transformation. Then, the weighted geometric average model is used to aggregate each criterion into a comprehensive index, which avoids the problem where a high score index and a low score index cover up each other in the weighted sum model.

4. Case Study

To verify effectiveness of the method proposed in this paper, the IEEE118-bus system is used as an example for illustration. The schematic of the system is shown in Figure 3.

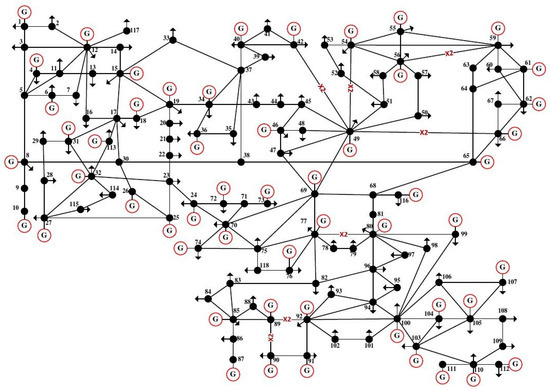
Figure 3. IEEE 118-bus system.

4.1. Initial Fault Set

An initial fault set is selected based on the vulnerability radius index, as shown in Figure 4. Each point in the figure represents a transmission line, and its distance from the origin is the vulnerability radius, which can be represented by the VR (Vulnerability Radius) line. The graph can be divided into three regions by setting a suitable threshold. The ability of lines in area 1 in causing subsequent cascading failures is weak. For lines in area 2, since their vulnerability radii exceed the threshold value but below 1, they are likely to cause subsequent cascading failures. Moreover, the vulnerability radii of lines in area 3 all exceed 1, which can be defined as generalized vulnerability radius. Lines with such characteristics are considered to have a high risk of causing subsequent cascading failures.

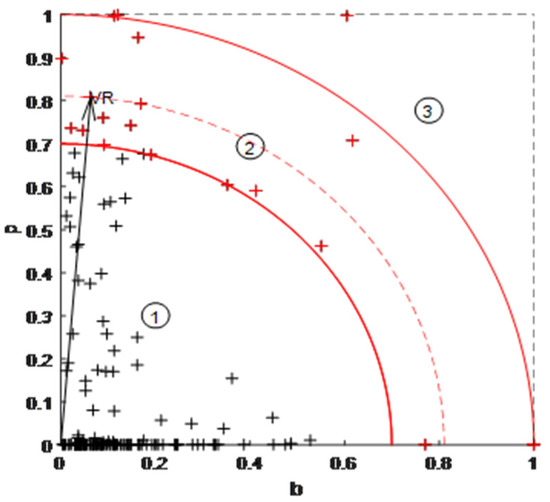
Figure 4. Vulnerability radius index.

In order to facilitate the analysis, the entropy weight method is applied to find the fault set and is compared with the method proposed in this paper. We rank the calculated values from high to low and select the top 20 lines as the initial fault set, as shown in Table 1.

Table 1. Initial Fault Set.

Sequence Number	Vulnerability Radius Method		Entropy Weight Method
	Line	Vulnerability Radius	Line	Weighted Index
1	L49–69	1.1664	L49–69	0.8955
2	L69–77	1.0073	L69–77	0.7722
3	L69–75	1.0029	L69–75	0.7675
4	L8–9	1	L24–70	0.7443
5	L9–10	1	L75–77	0.6837
6	L24–70	0.9615	L13–15	0.6650
7	L75–77	0.9383	L47–69	0.6313
8	L38–65	0.8971	L3–5	0.6147
9	L47–69	0.8109	L22–23	0.5877
10	L49–66	0.8102	L17–31	0.5856
11	L89–92	0.7705	L16–17	0.5528
12	L17–31	0.7646	L19–20	0.5503
13	L45–46	0.7563	L45–49	0.5492
14	L30–38	0.7361	L89–92	0.5460
15	L16–17	0.7315	L23–25	0.5436
16	L23–25	0.7195	L100–106	0.5400
17	L8–30	0.7191	L26–30	0.5387
18	L100–106	0.7031	L103–105	0.5256
19	L45–49	0.7012	L32–113	0.5101
20	L26–30	0.7002	L8–30	0.4847

It can be seen from Table 1 that some lines located near a generator bus or at important transmission and connection positions can be identified by both methods, but their ranking is different. In addition, lines 8–9 and lines 9–10 are in the initial fault set calculated by the vulnerability radius index, and are ranked higher, but lines 8–9 and lines 9–10 are not included in the set calculated by entropy weight method. Through qualitative analysis, it is found that removal of lines 8–9 and lines 9–10 will cause the system to be disconnected, creating isolated islands, leading to large fluctuations of power flow on other lines. It is thus reasonable for them to appear in the initial fault set. Lines 13–15 and lines 3–5 are ranked in the top positions by the entropy weight method, but they are neither heavy-load lines nor important connecting lines. In this comparison, we see that the vulnerability radius method can more accurately identify the lines which will more likely cause subsequent failures.

4.2. Fault Chains of Cascading Failure

The consequence of cascading failure is measured by the number of lines in the fault chain in this paper. The less number of lines in the fault chain, the more serious consequence it will have on the system, which shows that only a few line faults can lead to system instability.

Due to space limitation, we do not list all fault chains here. We take lines 26–30 as the initial fault as an example. After the failure of lines 26–30, the system maintains its stable operation, and the subsequent fault line indexes are calculated. The cascading failure sequence predicted by the fault chain model with probabilistic attributes is shown in Table 2. Moreover, without considering uncertainty factor associated with load demand variation, the cascading failure sequence based on a deterministic method is shown in Table 3.

Table 2. Fault Chains Obtained by Probabilistic Method.

Number	Fault Chain
1	L26–30	L69–75	L70–74	L70–75	L75–77	L76–77
2	L26–30	L69–75	L69–70	L24–70	L75–77	L76–77
3	L26–30	L69–75	L69–70	L24–70	L75–77	L23–32	L25–27
4	L26–30	L69–75	L69–70	L24–70	L75–77	L45–49	L23–32	L25–27

Table 3. Fault Chains Obtained by Deterministic Method.

Number	Fault Chain
1	L26–30	L24–70	L45–49	L49–54	L49–54	L42–49	L42–49	L75–77
2	L26–30	L24–70	L45–49	L49–54	L49–54	L42–49	L25–27	L38–65
3	L26–30	L24–70	L69–75	L69–70	L45–49	L75–77	L23–32	L25–27
4	L26–30	L24–70	L69–75	L70–74	L70–75	L75–77	L77–80	L79–80

Comparing Table 2 and Table 3, we see that the deterministic results deviate significantly from the results obtained by the proposed method. When the fault path develops according to the first and second scenarios given in Table 2, the system loses stability after the removal of 6 lines. However, the results in Table 3 show that the system will still operate stably after disconnecting 6 lines, and cascading failure will continue to develop until the maximum predicted depth is reached. Based on the above discussion, we see that the cascading failure model with probabilistic attributes proposed in this paper can predict fault chains with more serious consequences, with the uncertainty of line disconnection taken into consideration.

4.3. Line Vulnerability Assessment

As vulnerability assessment based on the fault chain set can quantify the vulnerability of each line in the set which poses serious threats to the safe and stable operation of a power grid; vulnerability assessment is practically important to power grid monitoring. The lines with outstanding vulnerability based on the method in this paper are listed in Table 4, and these important power lines are highlighted in Figure 5.

Table 4. Vulnerability of Transmission Lines.

Sequence Number	Line	Vulnerability
1	L47–69	0.8340
2	L38–65	0.8231
3	L92–100	0.7951
4	L69–75	0.7904
5	L49–69	0.7472
6	L26–30	0.7328
7	L69–77	0.7095
8	L42–49	0.7068
9	L89–92	0.7029
10	L8–30	0.6633
11	L30–38	0.6630
12	L49–54	0.6174
13	L69–70	0.6069
14	L49–66	0.6013
15	L100–106	0.6004
16	L23–24	0.5742
17	L16–17	0.5578
18	L24–70	0.5542
19	L45–49	0.5345
20	L34–43	0.5321

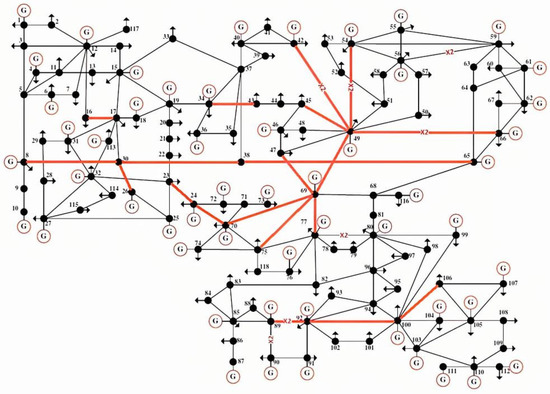
Figure 5. Vulnerable lines in IEEE 118-bus system.

For illustration purposes, we compare the results with those generated by other previously proposed methods.

The results of structural vulnerability lines obtained by risk theory [38] are shown as “method 1”, and those state vulnerability lines [38] are shown as “method 2”. The same fault chain model is adopted in method 1 and method 2. After the initial fault is randomly selected, the outage probability of each line is estimated based on the DC power flow model. With failure probability acknowledged, the roulette wheel selection is utilized to determine the next fault line until the system collapses or no failure happens consecutively, and the simulation runs for 300,000 times. In contrast, the initial fault is not randomly selected in this paper, and a more identifiable initial fault set is proposed, which can greatly reduce the workload of searching the fault chain set.

From the perspective of topology, the system and topology related changes caused by transmission lines are analyzed in method 1, and the line structure vulnerability is evaluated combined with risk theory. From the perspective of power flow, the system state changes caused by transmission lines are evaluated in method 2, and the line state vulnerability results are obtained. Based on the fault chain set proposed in this paper, the structural importance method of fault tree theory [21] is used to evaluate the vulnerability of transmission lines from the perspective of importance, and the results are shown as “method 3”.

The following points can be observed from Table 5:

Table 5. Comparison of Vulnerability Assessment Results.

Sequence Number	Proposed Method	Method 1 [38]	Method 2 [38]	Method 3 [21]
1	L47–69	L49–69	L38–65	L69–75
2	L38–65	L38–65	L92–94	49–54
3	L92–100	L24–70	L92–100	47–69
4	L69–75	L92–100	L68–69	26–30
5	L49–69	L47–69	L26–30	45–49
6	L26–30	L41–42	L47–69	75–77
7	L69–77	L80–99	L41–42	16–17
8	L42–49	L45–49	L85–89	38–65
9	L89–92	L24–72	L25–26	70–74
10	L8–30	L98–100	L59–63	42–49
11	L30–38	L99–100	L85–86	69–77
12	L49–54	L71–72	L63–64	76–77
13	L69–70	L77–82	L65–68	70–75
14	L49–66	L40–42	L69–75	49–54
15	L100–106	L92–94	L86–87	69–70
16	L23–24	L25–26	L49–54	19–34
17	L16–17	L34–43	L49–54	25–27
18	L24–70	L94–96	L69–70	49–51
19	L45–49	L49–54	L80–99	19–34
20	L34–43	L49–54	L40–42	45–46

(1)

Although the proposed model is different from those of methods 1 and 2, the results are partially similar, especially for the lines with the highest vulnerability, which show the effectiveness of the proposed model. However, method 1 only considers structural risks, while method 2 focuses on state risks. Moreover, both structural factors and state factors are considered in our proposed method, which thus avoids one-sided results. In addition, in methods 1 and 2, new line interruptions are selected based on the initial fault, without considering cascading failure. Since cascading failure does occur in practice, simulation without considering cascading failure may lose its relevance. Thus, critical lines identified in this paper will be more practically relevant.

(2)

Based on the same fault chain model, the similarity between the results of method 3 and ours is 50%. The difference is that only the frequency of the line in the fault chain set is considered in method 3, while the frequency of the line, the different roles of different lines in the fault chain and the importance of the fault chain itself are considered by the multi-criteria decision analysis model proposed here. In comparison, the evaluation results of this paper contain more information. If the probabilistic importance method is used to quantify the vulnerability of each line in the fault chain set, it is necessary to know the failure probability of each component in the power grid and the partial differential equation of outage probability for each component. For a large power grid, the calculation is very complex. The method given in this paper focuses on the fault chain set itself, which not only reduces computational complexity, but also evaluates the vulnerability of each line in the fault chain set from multiple aspects.

Referring to Figure 6, the IEEE 118-bus system can be divided into three parts, as shown on the upper left, upper right, and the lower half of the diagram. The three parts are connected by lines 23–24, 24–70, 8–30, 30–38, 38–65, 34–43, 47–69, 49–69, 69–75 and 69–77. These lines play an important role in the power exchange between regions. At the same time, high load-to-capacity ratio and regional power fluctuations increase the vulnerability of these lines. It can be seen that the method proposed in this paper can effectively identify the vulnerable transmission lines during the development of cascading failure. It is particularly necessary to pay attention to these lines in the prevention and control of cascading failure.

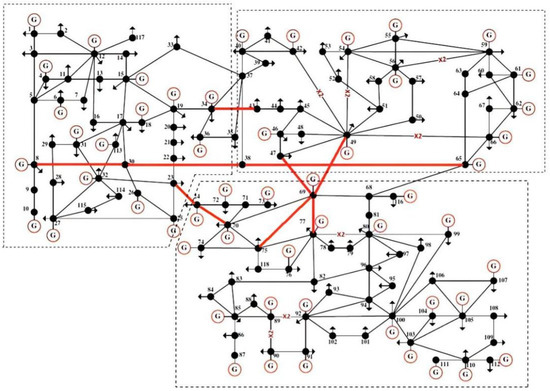
Figure 6. IEEE 118-bus system, with three partitions interconnected.

It can be seen from the vulnerability evaluation results that balancing heavy load nearby and avoiding long-distance power transmission are effective means to prevent and control cascading failure in a power grid. For example, the maximum load bus in the IEEE 118-bus system is bus 59 (277 MW). There is a generator on the bus, and only a small portion of the power required for the load is transmitted over a long distance. Thus, the vulnerability of lines connected to bus 59 is relatively low. On the contrary, although the load on bus 106 (43 MW) is lower than that on bus 59, the vulnerability of line 100–106 connected to bus 106 is higher due to the need for long-distance transmission of power. On this basis, qualitative analysis of buses can be further performed. For example, buses 69, 49 and 100, which are connected to multiple vulnerable lines, play an important role in the transmission network and are critical buses. These results are consistent with that reported earlier in the literature [39].

5. Conclusions

Identification of critical links in power systems is an effective procedure for predicting occurrences of serious faults and failure events. Such prediction is often complicated by uncertainty factors which deprive direct applications of deterministic methods. In this paper, a probabilistic vulnerability assessment method of transmission lines with consideration of cascading failure and uncertainties is proposed. Specifically, a fault chain model with probabilistic attributes is established, which can identify the fault chain set that has a serious impact on the operation of power grids. Based on this model, a multi-criteria decision analysis method is proposed to evaluate the vulnerability of transmission lines with considerations of structural, operational, and other uncertainty factors, making the evaluation results more comprehensive. The feasibility of the method proposed has been demonstrated with simulation experiments performed on the IEEE 118-bus system for the assessment of vulnerable lines in the cascading failure process. The proposed assessment method can be used to prevent large-scale power outages and provide reference for the operation, maintenance, and planning of power systems.