A New Perspective for Solving Manufacturing Scheduling Based Problems Respecting New Data Considerations

Abstract

In order to attain high manufacturing productivity, industry 4.0 merges all the available system and environment data that can empower the enabled-intelligent techniques. The use of data provokes the manufacturing self-awareness, reconfiguring the traditional manufacturing challenges. The current piece of research renders attention to new consideration in the Job Shop Scheduling (JSSP) based problems as a case study. In that field, a great number of previous research papers provided optimization solutions for JSSP, relying on heuristics based algorithms. The current study investigates the main elements of such algorithms to provide a concise anatomy and a review on the previous research papers. Going through the study, a new optimization scope is introduced relying on additional available data of a machine, by which the Flexible Job-Shop Scheduling Problem (FJSP) is converted to a dynamic machine state assignation problem. Deploying two-stages, the study utilizes a combination of discrete Particle Swarm Optimization (PSO) and a selection based algorithm followed by a modified local search algorithm to attain an optimized case solution. The selection based algorithm is imported to beat the ever-growing randomness combined with the increasing number of data-types.

1. Introduction

Industry 4.0 (I4.0) has accustomed manufacturing to the digital age via Cyber Physical Systems (CPS) and Digital Twins (DTs). CPS and DTs are two integrated approaches of several intelligent tools that facilitate the use of data-driven approach in industry. A system can have the ability to physically interact the environment and collect data to virtually represent a complete description along system states progress. Such description causes a state of awareness or smartness that empowers smart manufacturers to take the place of conventional manufacturers [1]. Accordingly, the progress of sensor devices, communication technologies and enabling intelligent techniques have evolved for the sake of big data analytics [2]. Enabling techniques have been used in industry for more than three decades. However, what makes a difference is the perspective of data that empowers the intelligent techniques [3]. In a dynamic collaboration, CPS allow information communication between systems/sub-systems aspects, where the real physical phase and cyber phase are associated to fulfill the system awareness gap through data analysis [4,5]. While, DTs support integration between the dual states of data: static state and dynamic state. Data states are beneficial in creating a virtual model or emphasizing interdependent instances of included sub-systems, approaching a model-based system [6,7]. Briefly, both the CPS and DTs are employed to achieve cyber-physical pervasive integration [5].

The motive behind the three previous industries is still applied in I4.0 but is influenced by sustainability and adaptability. Sustainability is a requirement for the future, being one of the pillars that accompanies value added activities [8,9]. The latter term, adaptability, is accomplished through three self-functionalities: self-configuration, self-organization and self-maintenance [3]. The system exploits the available data to achieve the parameters of self-configuration and self-organization. While, system life-cycle data can be operated to address self-maintenance. The three terms target higher levels of automation compatibilities, approaching what is meant by awareness which enables the progress in the new manufacturing era.

The research topics in smart manufacturing are being pinpointed recently by academics in a number of review papers [10,11], declaring the new horizon of challenges. As expected, the challenges are conventional manufacturing challenges in real-time. Such instances result in a complex dynamic-oriented challenge. Accordingly, the solution seeks optimization from a comprehensive view in respect to the interdependent data between the subs. The main contributions of this piece of research can be concluded as follows:

• A short review on the JSSP root problems and their evolution, outlined the elements of the heuristic based techniques (Section 1, Section 2 and Section 3).
• Regarding that, a projected literature review on a number of highlighted research studies are demonstrated (Section 4).
• A new perspective of FJSSP is outlined and tackled through a case study (Section 5).
• A proposed two stages approach is designed considering improved steps to enhance the neighborhoods shaking search (Section 6).
• Finally, the results and conclusion are present in Section 7, followed by the future discussion.

2. JSSP Evolution

In manufacturing systems, shop scheduling problems are initiated as a resources organization problem of a single or multiple identical machine(s) processing identical jobs of the same route. The problem was evolved quickly through the last decades to be a root of several distinct problems, differing in formation and complexity [12]. Three research problems have appeared the most often. The first is the Job Shop Scheduling Problem (JSSP), wherein each job follows its own predetermined route. Second, in a more general forum, the Flexible Job Shop Scheduling Problem (FJSP) discusses the alternative routes and assigned machines of each job to follow. Till that point, all studies focus on that field as a static approach. Third, the Dynamic Job Shop Scheduling Problem (DJSP) brings JSSP to real-time, in order to handle the disruptive events that happen in manufacturing, such as the arrival of new jobs and machines breaking down. Nevertheless, researchers during the recent decade urged that process planning and scheduling are two dependent processes that should be considered as a linked one [13,14,15,16]. In process planning, the machining process, tools and related configuration parameters are selected. The advances in CAD/CAM field has designed files that contain viable data for the scheduling problems [17]. The integration of the two processes is known as Integrated Process Planning and Scheduling (IPPS).

General speaking, JSSP related problems are crucial from more than one aspect and can stop the wasting of resources of a manufacturer. The new paradigm of manufacturing leverages technical devices to boost data that empowers knowledge of multiple aspects of a problem [18,19]. In such cases, future manufacturers will be able to adopt participating parts as an object-oriented entity that are completely describing the entity state. Regarding machines as an example, the enclosed life-time information is capable of drawing a detailed picture of the machining efficiency [20], the wearing that has occurred, and the expected maintenance time, etc. Such information paves the way for energy saving and predictive maintenance to be included in scheduling optimization considerations. Applying that upon a decision-making based problems [21], scheduling can be now considered as a multiple dynamic layers of optimization.

The JSSP complexity level is upgraded in conformity with variable insertion. In other words, FJSP and DJSP have higher complexity than the JSSP, following that sequence, additional integrations further increase the decision complexity, and hereafter, the cost of optimization increased.

3. Heuristics

Heuristics based algorithms are utilized heavily to find a solution for the JSSP based problems. In varied research topics, several heuristics and meta-heuristics taxonomies have been introduced for optimization an algorithms family [22,23,24,25,26,27], however, most of those taxonomies are influenced by relatively old anatomy. As an actively updated field, the recent years hold new discoveries in optimization techniques paired with a synchronous implementation in application based approaches. Hence, herein we produce a reshaped classification considering JSSP related spots respective to the inspired techniques, as in Table 1.

Table 1. Meta-heuristics observed taxonomy.

(Meta-) Heuristic Optimization	Evolutionary Inspired, i.e.,		Genetic Algorithms (GA) Differential Evolution (DE)
	Trace Trajectory Inspired, i.e.,		Tabu Search (TS)
	Food-Hunting Inspired	Swarm based, i.e.,	Artificial Colony Optimization (ACO) Particle Swarm Optimization (PSO) Pigeon based Optimization
		Predatory based, i.e.,	Wolf based Optimization Whale based Optimization Bats based optimization
	Breeding–Hunting Inspired, i.e.,		Honey-Bee Mating Algorithm (HBMO) Hybrid behavior
	Physical Behaviour Inspired, i.e.,		Big-Band optimization Expansion optimization Simulated Annealing (SA)

3.1. Heuristics

Classical heuristic algorithms can be briefly interpreted as an algorithm initiated by a suggested solution, chasing an optimal solution or near optimal through an iterative process of sharing information. The algorithm can be executed in parallel mode in order to expedite the running process, and disclose the search space, as well [28,29]. Parallel mode distils the considered problem into smaller sub-problems of the same scheme, causing diverse scenarios of pointed solutions. This heterogeneous enlarges the ability to discover the search space [30].

Discovering the solution is a process of intensifying and diversifying the search space, where the algorithm manipulates the data to generate a solution over number of iterations in one of two forms. A population form lists several suggested solutions as a pool of solutions upgraded from parents’ generation to a children’s generation. A single solution form discovers the neighbors of a given initial solution. The rapid upgrade of Computing Processing Units (CPU) and Graphic Processing Units (GPU), plus the need for more hands to analyses data, attract both the evolutionary- and the mathematical model-based algorithms [31,32]. Hereby, both algorithms are capable of sharing information within multiple levels; the straightforward level as in mono-pool execution, and the plane level between the sub-populations—recognized as migration. Several topologies draw traces for the migration process such as: chain topology, ring topology, tours topology, etc., [33].

3.2. Common Components of Heuristic Based Algorithms

Being either population based or neighborhoods/single based, the study begins with a potential representation of individual(s) coded as genes. Multiple genes ensemble the assigned problem solution—known as chromosome or individual Thus, the first step is to introduce the code process.

3.2.1. Problem Encoding and Decoding

Encoding encrypts the concerned information of a problem in a handler format directly or indirectly, wherein the imported analyses model/method effectively able to operate it. In heuristic based, it is the process of representing the suggested solution of the performed problem as a chromosome of genes. The chromosome intra structure acclaimed as trees/graph, arrays/strings, lists, or any other objects. The inter representation, the gene, is coded as an element of binary or decimal numbers or in any other suitable representation. At this end, JSSP and its relatives concern arrays/strings and directed graph encoding, composed of bits, numbers, or rather values [22,34,35,36].

In that respect, permutation encoding adopts a string of real numbers in sequence. Hence, permutation encoding is preferable in problems having violent ordering or precedence constraint(s). Instead of numbers, value encoding approves values in a suitable form regarding the represented problem.

As a still growing problem, job scheduling based problems have brought viable derivatives of the aforementioned encoding forms. Therefore, the performance of the implemented algorithm depends to a great extent on the encoding strategy. Job, operation and machine information, three terms mainly govern the FJSSP, but the FJSSP is not limited to them. Thus, researchers tried to represent the individual as a single string of tuples, of three or more elements accordingly. Others have carried double and triple strings for each. The presence of information may be found as an indication, for case of explanation, operation cell could refer to the used strategy of performed path not the operation itself. Figure 1, Figure 2 and Figure 3 represent varied examples of the chromosomes constructions.

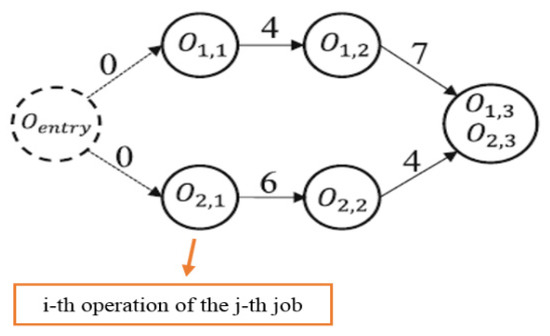
Figure 1. The Acyclic Directed Graph (DAG) depicts the precedence operations of two jobs, where O_1,1, O_1,2 and O_1,3 represent job 1 operations and O_2,1, O_2,2 and O_2,3 represent job 2 operations. O_1,3 and O_2,3 processed in combination, the corresponding setup time present as an edge number [37].

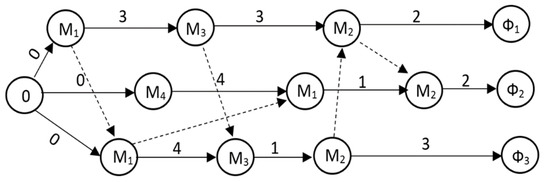
Figure 2. Disjunctive graph of three jobs: the nodes contain the processing machine, the conjunctive arc connects consecutive operations, Φ_i is a dummy node associated to the ith job completion time. Another disjunctive graph of the operation is created in pair with the machine graph [38].

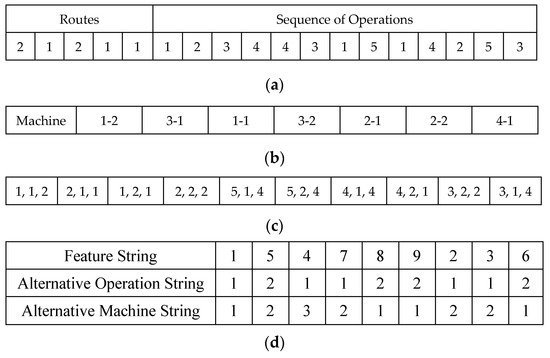
Figure 3. Examples of chromosome coding: (a) chromosome is a bi-part coding multiple routes of a job indexation and the corresponding operation sequence [39], (b) chromosome is a machine coded of job-operation number as a tuple, (c) chromosome cell is a triple tuple of job-operation-machine coding [40], and (d) three chromosomes of a single cell information represents job as a feature string followed by operation and machine strategy indexation.

3.2.2. Mating Procedures

In a more general construction, population based algorithms are rather a discrete nature or a continuous nature. As the JSSP approach is a discrete field, applying discrete heuristic based algorithms in such an approach is a forthright process. The process observes the evolution of chromosomes through a crossover and mutation procedures. Wherein, the evolution mostly follows a pattern of two-to-two mating that is two individuals—parents—produce corresponding two updated individuals—children—e.g., GA.

In different circumstances, continuous algorithms evolve, relying on adjustment of a point in a continuous solution space. Continuous based algorithms dominate the optimization race, since they achieve better results than the discrete based algorithms [41]. To make use of continues based algorithms in discrete approaches several suggestions have been contributed. The premise behind most of these suggestions is to project continuous variable parameters as a logical or a crossover method [17,42]. Through that, the related evolution pattern appeared as a multiple-to-one pattern, mostly two-to-one.

a. 

Crossover Procedure

In discrete space, crossover operation mimics the natural chromosomes mating process, aiming to recombine parents’ genes, in order to produce new chromosome(s). Crossover is the main engine that defines how children inherit genes from their parents, since crossover manipulates the genes and in turn the genes representation directs the used crossover method. As discussed previously, an array of indexes coding is frequently used, thus, correspondingly array based crossover forming the main cluster [43]. Additionally, it is worth mentioning that the number of individuals resulting from the crossover process varied depending on the way the evolution based algorithm implements the mating procedure.

Earlier discussions in crossover partitioned a single parent array of genes around a cut-point, creating two shortened arrays—sub-arrays. With parent I and parent II, either part of parent I, the sub-array attached to the opposite part of parent II sub-array generates a chromosome. The procedure is known as Single Point crossover (SPX). SPX expanded to Double cut-points crossover (DPX), and also multiple points—known as uniform crossover. In a wider scope, if it is a two-to-two mating process, the second chromosome will be generated by merging the unused complementary parts in the same positioned order. The inherited parts are similarly traversed in an opposite complementary manner. In the case of determining specified genes permutations, repeated genes appear while others are absence. For the sake of solution feasibility, Choi et al. [44] exchanged only a sub-array and rearrange the missing genes regarding to the opposite sub-array. The arrangement order derived additional types of crossovers, known as Ordered crossover (OX), Linear Ordered crossover (LOX), and Partially Mapped crossover (PMX) [43,45]. Besides, the generalized form of OX and PMX that taken into count permutation repetition demands had acronyms of GOX and GPMX respectively [46].

Selecting the crossover point(s) is where most of new trends in crossover studies have evolved. The simplest way is to select point(s) randomly. Recently, in a crossover sub-scale, methods such as local search neighborhood, distributed mathematical models mostly as a filter/mask and evolution based strategies have emerged to determine the selected cut-points. As a particular case, in FJSP wherein multiple combined-chromosomes represented a job-operation-machine, Xinyu et al. [47] presented two crossovers, which exhibits multiple points as masked points applied to the job chromosome and operation strategy chromosome shorted as JOX and POX, respectively. Figure 4 depicts some of the frequently mentioned strategies.

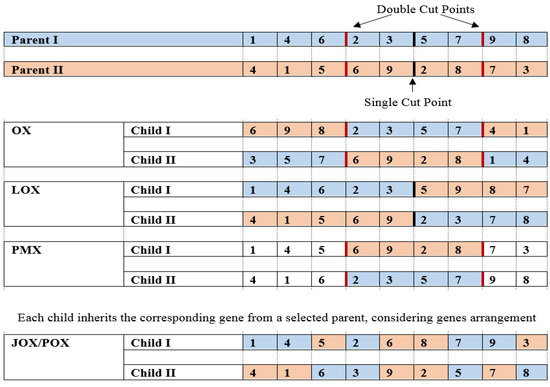
Figure 4. Frequently used crossover strategies based in JSSP.

b. 

Mutation Procedure

Mutation is a unary evolutionary operator that has a tendency to manipulate a single individual functioning in a probability factor to produce another version of it. Mutation diversifies the search space. The search space type and gene probability evoke varied types of mutation methods [48]. In discrete space, especially in a JSSP based instance, mutation is best represented as swapping operator, reversion operator and insertion operator, pictured in Figure 5. There is also, a fragment mutation, where the child inherits the exact gene(s) from a specified parent. Similar to the crossover operator, mutated genes/points are frequently selected randomly. Recently, uniform random mutation and normally distributed mutation have prevailed, as well as heuristics based in mutation sub-scales [34].

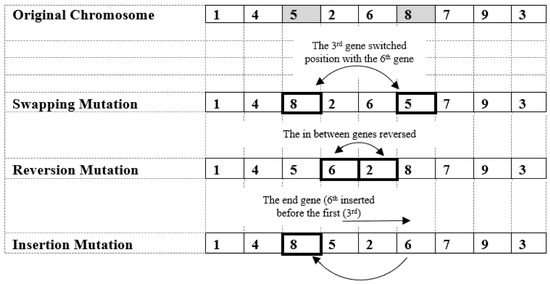
Figure 5. Famous mutation strategies.

c. 

Selection Procedure

Selection is a priority engine that defines the chance of a solution to be recommended over others regarding to the occupied strategy. The selected strategy defines a weight that supports the solution probability to be selected. To the best of our knowledge, there is no concise explanation supports a strategy over another in JSSP based fields. However, some strategies are utilized on a large scale through the population generating mechanism. Tournament selection strategy, a prescribed number of solutions are randomly selected and the fittest represented as a winner of a race. In tournament, a weight is responsible for the times the procedure implemented. Displaying a trade-off between intensification and diversification, Roulette Wheel Selection (RWS) yields a weight proportional to the relative fitness of a solution. Thus, as a role of thumb, the higher the fitness, the higher the probability of a solution to be picked. Rank Based Selection (RBS) normalizes the RWS, producing a weight corresponds to the solution rank [43].

d. 

Objective Function

A fitness function is used to evaluate the quality of a chromosome, also known as objective function. The comprehensive perspective of optimization problems disclose interdependency among diverse elements, either as a configuration set or a consequence results. In other words, multiple conflicts, wherein enhancing the objective of one aspect affects another, a manner that may be a cycle of deterioration in total. Such an instance—which is almost everywhere in real-world—triggers a multi-objective optimization algorithm. Multi-objective optimization is mainly discussed as: aggregation selection, criterion selection and Pareto selection.

Aggregation selection presses linearly a multi-objective case to a mono-objective. For that purpose, the multi-objectives is aggregated as a penalty cost in terms of weight, constraint, or as a goal with a priority, depending on the studied circumstance. Aggregation based is commonly functioned in large number of evolutionary based studies in both general perspectives and JSSP related perspectives. Criterion based methods paid attention to the fitness function one at a time. Late studies focused on Pareto selection based, wherein a representative set deploying a relation based dominance [49,50], as depicted in Table 2.

Table 2. Literature survey.

Publication	Method	Coding	Search/Mating Strategy		Objective Function	Problem Perspective
			Cross-Over	Mutation
Ahmadi et al. [51]	A Pareto based approach employing New version of non-dominated sorting genetic algorithm (NSGA-II) and non-dominated ranking genetic algorithm (NRGA)	Matrix permutation-based chromosome of three columns represented Gantt chart as (current job, operation, machine)	POX	modified Position Based Mutation (PBM) as well as Machine Based Mutation (MBM)	Multi-objective: make-span and stability measure	FJSSP/IPPS Multiple machines problem
Singh et al. [52]	Quantum behaved PSO	stochastic particle (operation, machine priority sequencing representation)	Particles updated based on masked procedure	Random position swapping mutation that happened governed by a condition	Minimize make-span	FJSSP Multiple machines problem
Li et al. [53]	Sequencing operation based Hybrid Artificial Bee Colony (ABC)	Two vectors of operation based coding: (position, operation, machine) combination	Random positioning	Multiple stage swapping based on random points	Minimize make-span	DFJSSP Multiple machines problem
Nouiri et al. [54]	Two stage of PSO	Two vector parts of process and corresponding assigned machine	Particles updated based on mathematical formulation		Multi-objective: Minimize make-span and stability measure simultaneously.	FJSSP, Generates predictive schedules insensitive to breakdowns [55].
Wu et al. [56]	Mathematical model and non-dominated sorting genetic algorithm (NSGA-II)	Row vector of positioned operations.	LOX	Random points swapping	Multi-objective: (i) Minimize energy consumption. (ii) Minimize make-span	FJSSP
Che et al. [57]	mixed-integer linear programming (MILP) model based on position assignment	Mathematical representation	Pareto front considering Stochastic calculation that paid attention to machine idle period		Multi-objective: (i) Minimizing total energy consumption, and (ii) Maximum tardiness	JSSP Single machine scheduling
García-León et al. [40]	General local neighbour search based on a disjunction graph model	Two disjunction graph; operation- and machine- sequencing graph	Pareto front employing four search strategies and two neighbourhood structures based on semi-random three variable selected criteria.		Multi-objective based on criteria	FJSSP
Mokhtari et al. [58]	Hybrid GA and SA	Matrix based mathematical model	Two cross-over: uniform- and position based- crossover are mixed as a masked crossover	Two mutations technique are mixed reverse sequence and swapping	Multi-objective: (i) Minimize completion time, (ii) Maximize total availability of the system, and (iii) Minimize energy consumption	FJSSP Considering different paths of each machine
Dai et al. [59]	Modified GA based on mathematical model	Multi-layer encoding strings composed horizontally of: alternative process plan strategy positioned in job sequenced order, and scheduling plan gene-string	Multiple Single point cross-over	SA-based mutation operator	Multiple objective: (i) Minimize energy consumption, and (ii) Minimize make span	IPPS
Li et al. [60]	Hybrid of HBMO and SA	Feature string	Single point cross-over	Adjacent swapping	Minimize energy through tool change time and travelling time (make-span)	JSSP Single job optimization, No precedence constraints
Defersha et al. [42]	Two stage GA	(job, operation) string in first stage and then Indirect (job, operation, machine) string	Three cross- over: (i) single-point randomly selected, (ii) job cross-over and (iii) assignment cross-over both are exchanged based on a probability	Operations swapping mutation, and assignment altering mutation	Minimize make-span	FJSSP
Meng et al. [61]	Mixed models of integer linear programming (MILP)	Mathematical representation	Sequenced stages of mathematical formulation of nine decision variables		Minimize energy consumption summation: idle, total and common	FJSSP Environmental awareness point of view
Luo et al. [31]	Heterogeneous parallel GA with developed event driven strategy with a two level of parallelization	Modified operation based encoding (two paired patterns)	Random chosen point cross over	Different arbitrary genes randomly chosen to exchange values	Muti-objective into single: (i) Minimize the total tardiness. (ii) Minimize the total energy cost. (iii) Minimize the schedule changes delay	DJSSP
Min et al. [62]	Enhanced heuristic based on combination of GA, PSO and SA	two-layer horizontally encodes machine gene string and operation gene string	Cross over design based on PSO	Based on SA	Multi-objective optimization model: (i) Minimize energy consumption. (ii) Minimize make-span.	DJSSP Energy efficient perspective
Mahmoodjanloo et al. [63]	Mathematical model relying on two Mixed Integer-Linear Programming (MILP)	Mathematical Representation	Modified masked crossover based on rate factor	Two main strategies of: (i) Based on differential evolution and (ii) Multiple self-adaptive strategies based on indices	Minimize completion time (make-span)	FJSSP Reconfigurable machine tool included
Ambrogio et al. [64]	Mathematical model	Mathematical formulation based on three main decision making variables			Minimize consumption time as energy saving indicator	FJSSP
Deng et al. [65]	Timetable method of a local search algorithm applied with Nawaz-Enscore-Ham based heuristic	Two square matrices, operation matrix and corresponding machine matrix	-	-	Minimize Total flow time	JSSP
Li et al. [47]	Hybrid based of a genetic algorithm and variable neighbourhood search	Three strings: Job-Feature string indexes feature appearance, operation string insert alternative operation strategy and machine alternative operation strategy string	JOX, POX, POX respecting t feature, operation, machine strings.	Two-points swapping	Minimize make-span	FJSSP Precedence constraint included with a correctness step
Li et al. [15]	Discrete PSO based algorithm	Three strings: Job-Feature string indexes feature appearance, operation string insert alternative operation strategy and machine alternative operation strategy string	JOX, POX, POX respecting t feature, operation, machine strings.	Two-points swapping	Minimize make-span	FJSSP Precedence constraint included with a correctness step
Jing et al. [66]	Integrated optimization GA	Operation string	Single cut-point	Random swapping mutation	Multi-objective: (i) Minimize completion time, and (ii) Minimize total load	FJSSP preventive maintenance scope
Cao et al. [39]	Heterogeneous earliest finish time (HEFT) adopting arbitrary directed acyclic graph (DAG) on Parallel CPU	DAG—Graph based	Two-cut points	Two-cut points	Minimize make-span	DJSSP Manipulate setup time
Lin et al. [67]	Developed GA based on incomplete Graph representation	Two-hand sides strings; process plan and sequence of operation, respectively.	Two crossover operators—one crossover per side; Process plan: random cut-points with orderbased generator.Operation sequence: masked	Two mutation operators: Random swapping based on two genes, and escalation based on random single gene.	Minimize Make-span	IPPS/DFJSSP
Zhang et al. [68]	Mathematical formulation included into a GA based	Array of layer-coded of (job, process plan strategy, assigned machine), and the gene position indicates the processing sequence	PMX based on job and process plan matching along the whole parent.	Two mutation strategies: Operation conditioned exchange Machine based on random selection	Minimize total energy consumption	IPPS Considered tool power profile of different machining parameters
Liu et al. [69]	Hybrid of mathematical model and GA based	Matrix of available machines by operation sequence	Random cut-point	Random swapping point	Minimize make-span/completion time respecting work load	DFJSSP Single machine—maintenance perspective
Yavari et al. [70]	Mixed-integer linear programming model (MILP Model) cooperated with GA based two local search windows.	Two strings; 1- jobs sequence string on a machines and 2- parts ordering string.	Single cut-point attached to the first string only	Random swapping point, attached to the first string only.	Minimize completion time, parts ordering and holding cost	JSSP Supply chain perspective
Zhou et al. [71]	A Pareto front explored by two multi-objective approached via three models of multi-agent structure: (i) NSGA II, and (ii) Strength Pareto searching algorithm.	Disjunction graph based	Single-cut point (node randomly selected)	Based on a probability, a selected root inherited from parents	Minimize three objectives: (i) Weighted tardiness, (ii) Max tardiness, and (iii) Mean wait time of operation tasks.	FJSSP Parallel computing
Lu et al. [72]	GA based	1D-to-3D representation based on a job string and operation-machine matrix	Single point cross-over	Two genes swapping	Minimize cell make-span	DFJSSP New order arrival with transportation time is considered
Caldeira et al. [55]	Backtracking search based on GA with directed old population	Two vector representation: operation sequence and machine assignation	A similarity based POX (SPOX)	Dynamic mutation relying on rate factor	Multi-objective: (i) Minimize make-span. (ii) Minimize energy consumption, and (iii) Instability	DFJSSP Considering new job arrival
Wu et al. [73]	A Self-deterioration model and energy consumption model are optimized through a hybrid pigeon inspired followed by SA.	String of two tuples genes: job number—operation number	LOX	Swapping mutation	Multi-objective: (i) Minimize make-span, and (ii) Minimize energy consumption.	DFJSSP Machine wearing included
Zheng et al. [41]	Integer programming model and Based on Non-dominated Sorting GA II (NSGA-II).	Chromosome of job routes and the corresponding sequence of operations	Exchange two selected operation gene between the parents	Two positions swapping	Bi-objective: (i) Minimize make-span, and (ii) Minimize cost of processing	FJSSP
Zhu et al. [74]	Multiple-independent micro-swarm of hierarch communication structure paired with constraints mathematical model	Two-vectors encode job sequence and process sequence	Multi-masked/conditioned cross-over	Three mutations techniques: insertion, swap and inversion.	Minimize interval grey make-span	FJSSP with job precedence constraints
Yang et al. [75]	Creating two phases of optimizations via prediction model and robustness model deploying learning machine and NSGA-II	Single long string of two parts; operation sequences of multiple jobs followed by machine assignment. [76]	Single point cross-over	Swapping mutation	Bi-objective: (i) Minimize make-span, and (ii) Maximize workload (robustness)	DFJSSP Machine breakdowns considered
Vela et al. [77]	Fuzzy uncertainty model combined with a schedule based a hybrid TS-GA	Disjunction graph model representation	JOX, GOX and GPMX	Insert, swap and partial inversion	Maximize due-date satisfaction	FJSSP
Zhang et al. [78]	Improved GA through enhancing the inter procedures behaviours, combined with a greedy operation.	Two arrays of machine selection and operation sequence. Each array is consisted of two parts, the chromosome length is the total number of operations	Machine selection chromosome had multiple point crossover, and operation sequence used POX cross-over	Machine selection used roulette-wheel, Operation sequence used adaptive neighbourhood search	Multi-objective: (i) Minimizing the make-span time, (ii) Minimizing total time, and (iii) Minimize setup time	FJSSP
Samarghandi et al. [79]	GA based on mixed integer programming model, a local search is added to enhance the pool chromosomes	Job routing matrix	Random selected jobs to be inherited from each parent with a corresponding order	Reorder position of multiple points regarding a threshold value	Minimize make-span	JSSP
Tang et al. [80]	Hybrid of discrete PSO and SA, implementing two neighbourhood structures.	Two vectors: Operation scheduling vector and resource assignment vector	POX and Rand-point Preservation Crossover	Conditioned two elements exchange	Multi-objective: (i) Minimize the tolerated overtime. (ii) Minimize the total tardiness, and (iii) Minimize make-span	FJSSP Workers are included as a resources
Sotskov et al. [81]	Five heuristic algorithms split between job sequencing and machine assignation	Mixed graph model function at resource and precedence constraints creating a train timetable for a railroad			Minimize the make-span.	FJSSP Concerning on the case where the number of jobs is less than the total number of the available machines
Fanjul-Peyro [82]	Mixed Integer linear programming developed along three phases of assignment, sequencing and timing.	Three graph for resources; presents resources, setup resources and shared resources			Minimize the make-span.	FJSSP

A typical JSSP based instance mostly uses make-span/completion time, labor cost and total profit as optimized targets. A few studies have paid marginal attention to dynamic JSSP throughout new job arrival cases. With the big data tool and industry 4.0 concepts, the JSSP objective is extended to cope with higher levels of real-time factors and resources enriched manufacture consensus. Energy sustainability directs the evaluation to attain machine-energy consumption. Material resources, predictive maintenance and workload, however, they are not common along the new trends studies, they present a salient and viable analysis tool.

4. Literature Review

Several studies have been introduced in JSSP fields. Notable here are the recent studies introduced in Table 2, as they show premises scopes and higher information manipulation that serve smart manufacturing best. The table introduces those studies respecting to the previous discussed elements for better comprehensive view. The review mostly focuses on the recent years to avoid redundant information and to be more integrated and process planning oriented.

5. Case Study Formulation

For flexibility terms, there are a large number of research papers in that field, however, a lot of them suffer from limited flexibility dimensions [15], as they ignore alternative machine/operation strategies [47], or rather discuss flexibility from a single machine point of view. A number of them do not examine precedence constraints. The studies are conflicted between suboptimal and optimal problems [83], where limited information about the environment or the time life cycle were eliminated. Furthermore, expanding the problem to adopt more information (i.e., inserted tool information, features location, machining speed, etc.) reflects upon the structure of the chromosomes, and hence the searching space. The more the available data types are increased the more the chromosomes total numbers—in vertical structural chromosomes or length in horizontal designed chromosomes—increased. As a consequence, the randomness exploration progressed between generations may result as exhausted diversification steps of the increased number of chromosomes.

The current case study is going to tackle the JSSP based problem as a FJSP problem with dynamic term that is being submitted as machine-tool state. In that, a path based assignation strategy is designed to explore the searching space with less randomness. The new perspective of the problem formulation is designed as the discussed following points:

(1)

Each work-piece has its job that is independent from others.

(2)

Each machine within the cell can process a single job per time, and each machining concurrent time slot can only has a job once.

(3)

No job pre-emption present.

(4)

A machine availability is governed by its efficiency.

(5)

An operation may be performed by multiple machines.

(6)

Processing a job along machines takes into count the transmission time, no immediate processing.

(7)

Tool insertion setup time is considered.

(8)

Supporting flexibility, alternative strategies for machining present in more than a level: feature level, process level and machine level.

(9)

Precedence constraints are considered during feature-operation level or operation machine level.

Depending on the aforementioned, this study urges that, no matter the number of variables to be considered during the machining process, the complexity of the new perspectives can be transferred to computational levels only. Meaning that, the valid suggested solutions through optimization levels are better differentiated and may lead to a specified solution, wherein, the data can be handled to a realistic optimized solution.

6. The Proposed Algorithm

Now, since the potential elements are identified, the modification on that elements can be introduced through the proposed method. This study tackles the problem in two sequential stages. The first stage is capable of producing earlier proper valid chromosomes that can be the near enough to the optimal solution. The second stage is where a neighbor search checks the near optimal solution, targeting the optimal individual. The two stages have a dual beneficial influence, the first stage enhances the quality of the second stage initial solution, where the second ensures escaping from a local optima, if the first step result stuck in it. The following steps are applied in compatible sequence with the flow chart indicated in Figure 6.

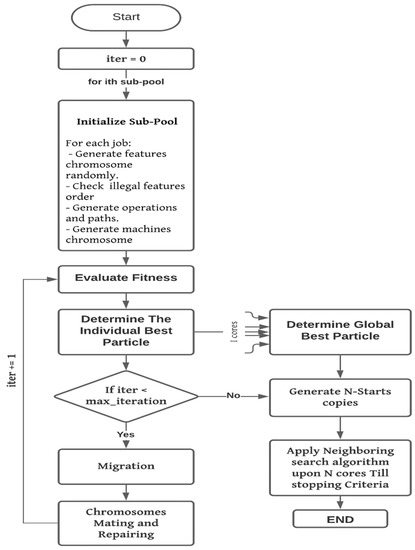
Figure 6. The proposed algorithm.

6.1. Coding Steps

The objective of this step is to represent the features, operations and assigned machines of the cell jobs as geno-types (machines encoded sequence). This piece of research adopts two strings upon two-steps, dealing with multiple alternative levels. A single gene of the first string codes a tuple of a selected feature paired with the assigned operation strategy, as shown in Figure 7. The second is a selection operation that produces an operation-machine that can accept any additional inserted data, i.e., tool, etc., the string refers to machine path. For either string, the position of each gene refers to the execution order. The occurrence pairs the feature-operation and machining data as a path enable feature-operation precedence check as an intra-check, and machines precedence check as inner-check.

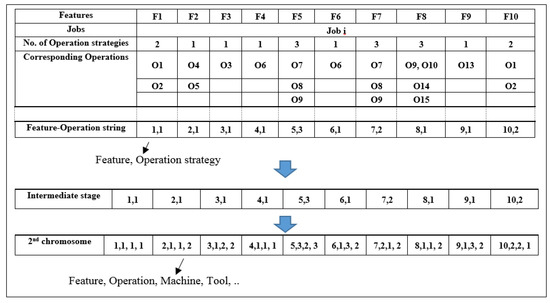
Figure 7. Coding procedure.

6.2. Path Creation Phase

Machining an operation on the ith machine requires additional data, such as inserted tool or feature position, which makes a list of collocations to choose between. Each collocation in that list is a machining path to be considered. A designed function is created to select a machining path, structured on a modified roulette-wheel selection. The roulette-wheel suffers from ignoring less occurred probability that may diminish appearance of available solutions over generation, and thus affects diversification. Therefore, the wheel gained score built on exponential mapping, as following:

$$P_i=\{\begin{array}{cc}{\exp }^{\raisebox{1ex}{${{\displaystyle \sum }}^{F_{MP}}$}\!\left/ \!\raisebox{-1ex}{${\mu MP}_i$}\right.}& ,\mathrm{all}\mathrm{path}\mathrm{machines}\mathrm{efficiency}>\mathrm{threshold}\\ 0& ,\mathrm{otherwise}\end{array}$$

(1)

Such that a single path probability $P_i$ increases exponentially respecting to the total number of feasible paths scored on the ith machine ${{\displaystyle \sum }}^{F_{MP}}$ over a single path$M{P}_i$. Considering only a tool as additional data, a single $M{P}_i$ presented as:

$$M{P}_i=M{T}_{ip}+T_i+M{C}_j$$

(2)

And,

$$M{C}_j=M{D}_j/Ef{f}_i$$

(3)

For a job, $M{T}_{ip}$ is the machine transmission cost between the ith machine and the previous recorded machine, $T_i$ is the tool changing cost, $M{C}_j$ is the duration cost regarding machine efficiency $Ef{f}_i$, and $M{D}_j$ is the ideal operation machining duration. Setup configuration duration can be added to the calculation as well. In cases where there are large differentiation between the scored paths cost, $\mu$ is used to save the computation resources. If the path has a machine with efficiency gain less than a specific threshold value, the path will be eliminated conditioned to the maintenance action.

6.3. Mating Phase

The algorithm uses a modified two-parents-to-single child mating as a discrete version of PSO to be implemented in parallel. A single PSO particle has a predefined feature-operation string to follow based on the crossover and mutation procedures, but, the machine chosen path has is selected by step. In other words, the particle own experience term in continuous algorithm discretized in path list selection step. The designed sub-pool attaches chromosomes respecting to the survival rate and the migration rate.

Survival rate: A rate that defines the number of candidate chromosomes to be transferred from generation to the next. The candidates follow score pattern, which categorizes the sub-pool into classes based on the fitness.

Migration rate: For the parallel computing, depending on the chosen migration topology, each sub-pool communicates with the adjacent one through sending and receiving candidate chromosomes.

Both rates are defined using a practical trial and error. Tracing back the PSO structure, a sub-population elects a lead/local-best chromosome respecting the best scored fitness, and a global best respecting the history of the best local. The global-best mates all other individuals to generate new off-springs.

6.3.1. Crossover

The applied crossover is a LOX on feature part of chromosome and POX upon operation strategy part, respectively.

6.3.2. Mutation Procedure

A random single point mutation is performed along a feature-operation strategy. In the case where one of the swapped results exceeds the chosen limitation, the strategy is randomly chosen from the operation available strategies.

6.3.3. Precedence Repairing Mechanism

The resulted off-spring undergoes a precedence repair mechanism to reconsider the precedence constraints, to avoid wasting resources upon illegal chromosomes Awad et al. [84]. The mechanism is performed before the machine assignment step (path creation), in order to correct any confliction happened after the crossover and mutation procedures. As a shifting based strategy, wherein a dependent gene is dropped out from the string and the must-be-preceded genes shifted back corresponds to the gap gene, then the dropped out gene placed at the end array gap, as depicted in Figure 8.

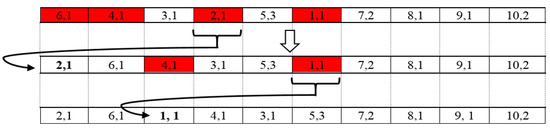
Figure 8. Features 4 and 6 are locked by features 1 and 2, respectively.

6.4. Objective Function

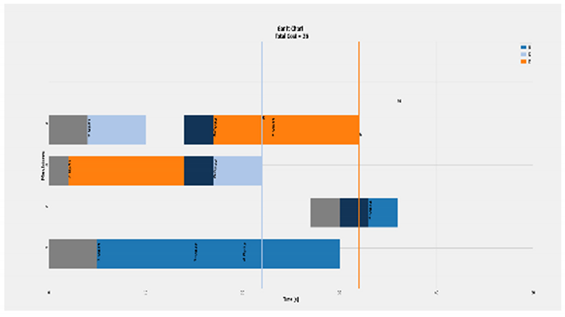
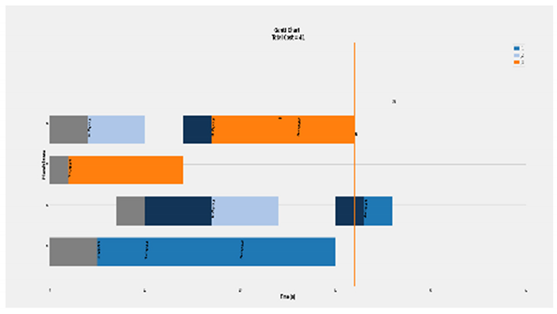
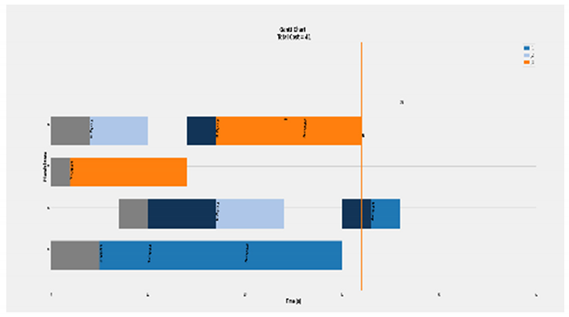
The objective function is a machine oriented programmed function. During each assignation step, the corresponding machine record the duration slots as in Figure 9, while Figure 10 indicates the difference between assigning tool change and machine transmission cost. The machine class has a history record that includes, the assigned job, feature, operation and the actual duration, plus the corresponding duration cost. During each new assignation the job-machine data is updated. Based on that the station cost is calculated regarding the completed working time of all machines, for machine ith, the machine ends at $M_{iend}$, and station cost is:

$$StationCost=\max \left(M_{iend}\right)$$

(4)

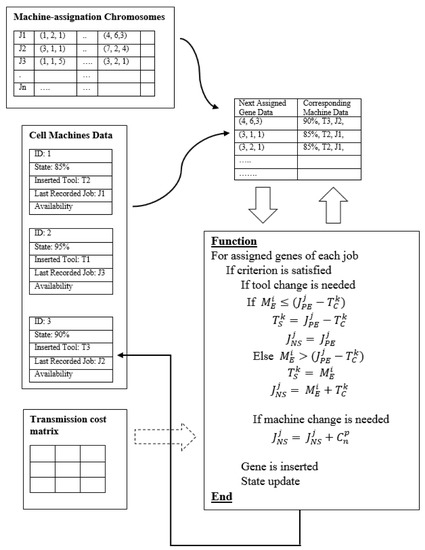
Figure 9. Objective function calculations, For the jth job and ith machine, the previous machining performed at $J_{PE}^j$ and next implementing machining starts at $J_{NS}^j$, while machine last assigned job ends at $M_E^i$. The considered setups machine transmission of an instant job from previous to next machines or kth tool change indicated as $C_n^p$ and $T_C^k$, respectively. Tool setup starts at $T_S^k$.

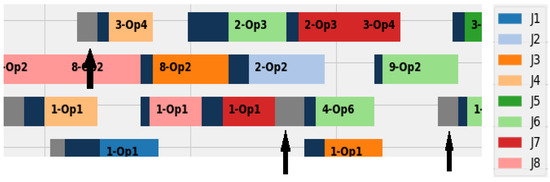
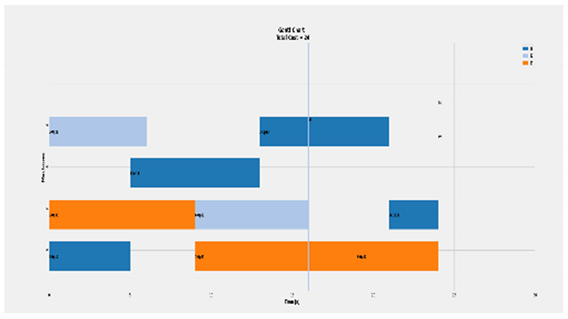
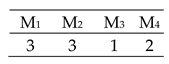
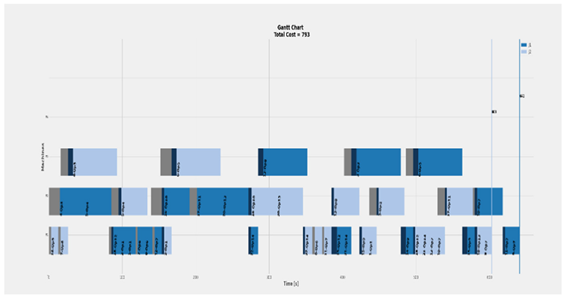
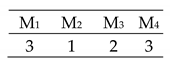
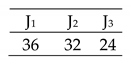
Figure 10. An example of the tool change calculation: Each job is represented by a different colour assigned to a feature-operation, the tool change duration is coloured in grey, where the three arrows pointed, and machine transmission duration is in navy blue. While job 4, feature 1 is assigned to operation, running on machine 3, machine 5 prepares the operation 4 selected tool that performs feature 3, of the same job. The same logic applied for job 6 and 8, as long as there is available time.

6.5. Neighborhood Searching Algorithm

As a starting point to evade from local optima repercussion, our problem-solving methodology employs a later stage of heuristic to ensure optimality in such complicated case. For that sake, a comparison is made between two modified single heuristics algorithms to find the best suitable next added stage. The considered modified single heuristics is an adaptive SA based and TS based as the following discussion. This section starts by stating the shared modified element that is shared through both modifications: the neighbors’ local search. In neighborhood searching techniques, the effectiveness of an algorithm depends on the strategy of the employed local search.

In general, single heuristics provide higher chances for near optimal solutions to escape local optima, which makes it more appropriate to be extensively utilized throughout a followed stage to the population based heuristics [68,85]. TS and SA used at JSSP are based as supplemented algorithms. The reason behind that can be deduced from two reciprocal inferences. One of them relates to the used single solution search itself. Applying upon the aforementioned techniques as the common used techniques. In SA, temperature behavior propels the early achieved solutions to better influence the individual progress, while in TS case, memory list length to ovoid repetitions [86,87,88]. On the same hand, in a discrete searching space with a single discovering step, available neighbor permutations run in O(n²) time, what is appeared as size-quality trade-off. Thus in order to satisfy near optimality in search space, the iterations gained extensive cost [43].

The local search improvements distilled to a parallel multi-start and a straightforward looping. The former enhancing step is wherein parallel multi-cores that can provide the advantage of emerging a Multi-Start (MS). While the straightforward step coordinates the variable neighbors search. Thus, instead of a large iterative local search, the adaptive single search algorithm is compressed into alleviated straightforward enhanced shake along each job upon a single-core and another horizontal shake up among cores at the same time.

6.5.1. Modified SA

The SA adaptability is entailed in three terms seeking improvements in neighbor local search as aforementioned and the move condition. The MS-SA shakes the best aforementioned chromosome resulted from the previous stage in random differently. Moreover, additional enhancement step is performed upon the rejection condition to avoid going through the same path of a deadlock progress. In that, where no progress happened in the inner phase of, the search back to the last scored best solution as a new initiated point. The adaptive SA for a single core is introduced in Table 3.

Table 3. Modified SA Procedure.

	Functions
1	SA Initialization
	current_solution ← initial solution
	best_solution ← initial_solution
	current_cost ← evaluate (current_solution)
	best_cost ← evaluate (best_solution)
2	Searching Progress
	T ← Tinit
	While (T > Tstopping)
	For i = 1 to iterations (T)
	new_solution ← Modified_Move (current_solution)
	new_cost ← evaluate (new_solution)
	Δcost ← new_cost—current_cost
	If (Δcost ≤ 0 or $e^{-\left(\frac{\Delta cost}{T}\right)}$ > random ())    /* accept new solution */      current_solution ← new_solution      current_cost ← new_cost
	If new_cost < best_cost      best_solution ← new_solution      best_cost ← new_cost
	Else    /* escape deadlock state */      current_solution ← best_solution      current_cost ← best_solution

6.5.2. Modified TS

Parallelization introduces a small memory for each core. As an accumulated case, the neighbors are explored in feature-of-job arrangement and feature-of-cell arrangement. The feature-of-job arrangement utilizes the variable neighbors’ structure adopted by Li et al. [15] to discover per job feature adjacent combinations amidst consistent adjacent jobs. The feature-of-cell arrangement switches the search between adjacent jobs as an intra-loop.

7. Results and Discussions

In the software context, all the models coding and formulation are executed in python upon a Spyder 4.1.4 environment. The codes are implemented on Lenovo PC with an Intel Core i7-4720HQ processor of 2.6GHZ. The result of this study is discussed considering a number of problems that were recorded as benchmarks from previous studies. The algorithm is carried out on python Spyder 4.1.4 environment, meanwhile, the parallel implementation is performed through the CPU using the encapsulated DEAP library. To further evaluate the proposed algorithm accurately, the benchmarks are tested as their original studies suggest with the same parameters mapped on the designed algorithm. Then, some of them are tested respecting to the new considerations. The desired fitness function is structured to obey the following criteria:

• Minimum transmission cost.
• Workload to maintenance balance based.
• Minimum make-span.

7.1. Experiments Set

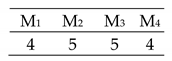
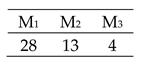
The first group of experiments are carried out through the original data sets taken from Kacem et al. [89,90], Chan et al. [91], Gao et al. [92], Teekeng et al. [93], Zhang et al. [94,95], as indicated in Table 4, in order to check the algorithm validity using varied configurations. The data sets have no precedence constraints, which make them sufficient to test only the first stage of the proposed method. GA algorithms the simple two-to-two mating termed as GA and the GA introduced by Li et al. [47], and two types of PSO, the designed PSO (DPSO) and the PSO mating according to Li et al. [15], all are implemented upon parallel CPU, and the parameters are tuned as in Table 4.

Table 4. Parallel implementation parameters.

Parameters	Value
No. of islands	8
Sub-pop size	70
No. of emigrant chroms	5
No. of history chroms	3
Crossover probability	0.6
Mutation Probability	0.2

The second set of data recorded by Naseri et al. [96], Li et al. [15], Shao et al. [97] and Leung et al. [98] display a precedence constraints and machine transmission is considered.

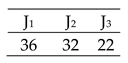
The second set of experiments are designed to trace the effect of first stage migration and history rates. Figure 11 concludes the rates effect by example upon 12 × 7 case included in Table 5, where the rates presented as a percentage of the total number of chromosomes of sub-pool size. Supplementing the sub-pool with around 10 % of its total number of chromosomes shows a stable improvement along the GA and the DPSO algorithms. This may be resulted as enhancement in the explored solution or the minimum hit fitness value. That progress encourages the experiments to follow the 10:15 % rate divided between the rates as indicated in Table 5.

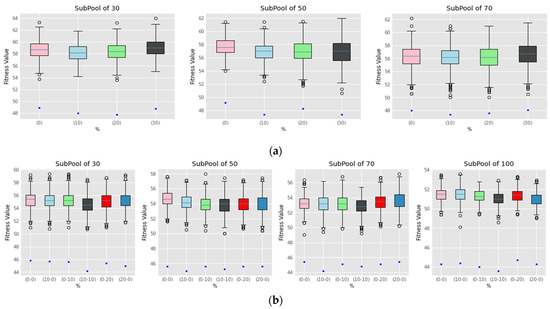
Figure 11. Migration - history rate effect upon: (a) GA sub-pool of sizes of 30, 50 and 70, respectively. (b) PSO sub-pool of sizes 30, 50, 70 and 100, respectively.

Table 5. Recorded results.

Case No.	Total No. of Jobs per Machines	E × Act Solution	GA			GA Li et al. [47]			PSO Li et al. [15]			DPSO			Adopted From
			Best	Average	Average Convergent Generation	Best	Average	Average Convergent Generation	Best	Average	Average Convergent Generation	Best	Average	Average Convergent Generation
1	3 × 4	5	5	5.2	18	5	5	10	5	5	12.1	5	5	5	Kacem et al. [89,90], and Zhang et al. [94]
2	4 × 5	11	11	11.5	23	11	11	12	11	11	12.6	11	11	8
3	8 × 8	14	14	14	27	14	14	12	14	14	11.6	14	14	9
4	10 × 10	7	7	7.1	29	7	7	12.4	7	7	13.1	7	7	9
5	15 × 10	11	11	13.1	39	11	11	19.1	11	11	20	11	11	15
6	10 × 7	11	11	13.2	41	11	11	25.1	11	11	26.8	11	11	13
7	6 × 8	148	152	154.6	68.1	148	149.7	24.4	148	150.9	31.4	148	149.1	18	Based on Shao et al. [97]
8	10 × 8	253	257	259.8	81.2	253	256.1	28.1	253	259.2	36.1	253	255.2	22.4
9	15 × 8	288	305	305.8	89.6	288	290	29	288	291.9	38.4	288	289.5	23.7
10	3 × 4	24	24	24.1	56.4	24	24.2	23.2	24	24.7	27.8	24	24.1	11.1	Based on Naseri et al. [96]
11	6 × 4	43	43	43.6	72.1	43	43.3	22.3	43	44.3	32.1	43	43.4	18.6
12	8 × 4	54	55	57.1	79.3	54	54.3	56.1	54	55.2	36.3	54	54.3	19.1
13	12 × 7	58	64	67.3	82.1	58	58.89	60.2	58	60.2	38.5	58	59.4	26.3
14	1 × 15	377	377	377.1	61	377	377	21	377	377	22.1	377	377	11	Based on Li et al. [15,47]
15	1 × 5	222	222	222.3	45.1	222	222	18	222	222	19.8	222	222	8
16	9 × 15	395	418	423.2	70.5	395	406.7	30.2	395	410.7	29.2	395	404.2	18.9
17	17 × 15	455	473	481.5	90.1	455	469.9	40.1	455	472.9	39.1	455	466.8	28.5

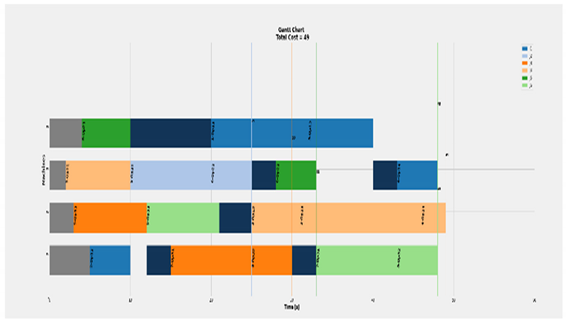
Till that point, the first stage is studied in strict scope, which moves the investigation to the second stage. The used neighbors searching algorithm is going to be the multi-start TS algorithm, since it produces the best followed progress across studied cases, some of them are used during the comparison. As declared by Figure 12, the multi-start adaptive SA (ASA) improves the SA results as expected, but multi-start TS is still obtaining the overall best scored values.

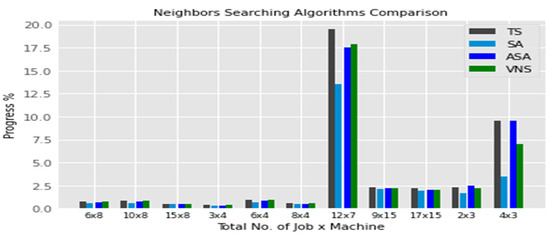
Figure 12. Neighbors searching algorithms comparisons.

7.2. Experiments Set 2

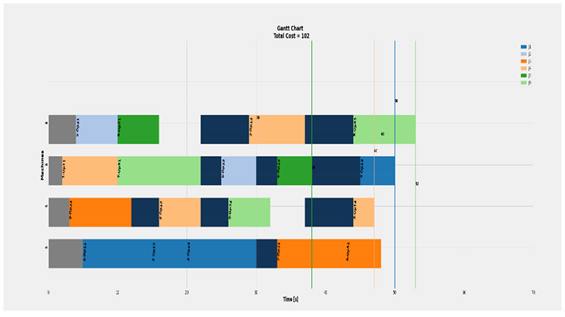
This set of experiments are performed upon the previous mentioned data sets, in addition to Falih et al’s [99] recorded benchmark, in addition to other extended problems. The corresponding solutions are presented in Table 6. The transmission cost, the tool change cost and the work-load effect are included later, where the Table 7 is referring to that case as a complete case. In Table 7, total cost exhibits the resulted final cost considering the penalties, where actual cost points the exact time duration of the executed jobs. A threshold value is set equal to 50%, since if a tool exceeds that point, a tool change is needed. During that set, the tool electricity profiles are recorded as an indicator referring to machine-tool efficiency. The recorded profiles are calibrated before applied to the cosine similarity measure. Furthermore, a deterioration factor is tuned roughly for the sake of a tool model life-cycle wearing. Here, a deterioration factor of 0.98 is included during the process, such that a deterioration penalty balances the workload with the operation duration O_d and machine-tool state M_s as:

Penalty = O_d * (−log(M_s))

(5)

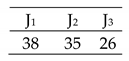
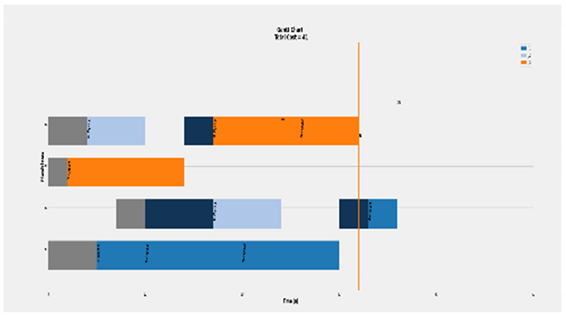
Table 6. Falih et al. [98] based problems best recorded solutions.

Case No.	Total No. of Jobs per Machines	Reported Solution	GA + TS	DPSO + TS
18	1 × 3	423	441	423
19	1 × 4	790	800	790
20	1 × 5	393	398	388
21	4 × 3	1089	1193	1089
22	2 × 3	510	522	510

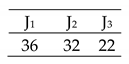
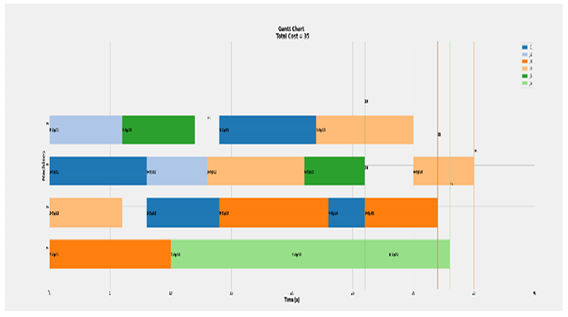
Table 7. Complete progress of different resulted scenarios.

Ideal scenario of 3 × 4		Total Cost = 24 Actual Cost = 24 Jobs completion cost: Machine usage as followed:
Transmission and Tool change included of 3 × 4		Efficiency = [100, 100, 100, 100]% Total Cost = 36 Actual Cost = 36 Jobs completion cost: Machine usage as followed:
Deterioration factor effect. Transmission and tool change cost included. (Complete Case) 3 × 4		Eff = [100, 100, 100, 100]% Total Cost = 41 Actual Cost = 36 Jobs completion cost: Machine usage as followed:
Complete Case of 3 × 4		Eff = [65, 92, 73, 68]% Total Cost = 61 Actual Cost = 38 Jobs completion cost: Machine usage as followed:
Complete Case of 3 × 4		Eff = [85, 55, 79, 78]% Total Cost = 56 Actual Cost = 36 Jobs completion cost: Machine usage as followed:
Ideal scenario of 6 × 4		Total Cost = 35 Actual Cost = 35 Jobs completion cost: Machine usage as followed:
Transmission and Tool change included of 6 × 4		Eff = [100, 100, 100, 100]% Total Cost = 49 Actual Cost = 49 Jobs completion cost: Machine usage as followed:
Complete Case of 6 × 4		Eff = [85, 55, 79, 78]% Total Cost = 102 Actual Cost = 53 Jobs completion cost: Machine usage as followed:
Deerioration snd tool change of 2 × 3		Total Cost = 510 Actual Cost = 510 Jobs completion cost: Machine usage as followed:
Complete Case of 2 × 4		Eff = [1, 1, 1, 1]% Total Cost = 793 Actual Cost = 641 Jobs completion cost: Machine usage as followed:

8. Conclusions and Future Work

This study discusses FJSP scheduling as a case that can benefit from the smart manufacturing big data in order to make scheduling more realistic and up to date with the machine life cycle. Via that available new data, the scheduling will be able to gain awareness as the other manufacturing terms. In that, the machine tool change and maintenance can be scheduled as a part of the FJSP scheduling cycle. The challenge is in how the inserted data will be handled to serve the diversification and the intensification terms of the heuristic based algorithms without fall only in the diversification terms.

The designed algorithm utilizes the PSO with a modified selection algorithm implement such a continuous algorithm in the discrete domain considering the machine/tool efficiency data. The suggested data can be extended to include the features position in future cases. Energy consumption and the tool cracking through an image processing based techniques can be added as well.

In terms of implementations, the advances in parallel computing have brought GPU techniques into the spotlight. These techniques may be inserted in a future work with the current tested CPU parallel implementation, especially when image processing comes into action. Therefore, the JSSP based problems will be capable of achieving fully dynamic environment.