Experimental and Statistical Validation of Data on Mesh-Coupled Annular Distributor Design for Swirling Fluidized Beds

Abstract

In this study, velocimetry and statistical analyses were conducted on a swirling fluidized bed. A bed of spherical particles (4 mm) was fluidized by using an annular distributor covered with mesh. The angles of rectangular blades in the distributor were set at 30°, 45°, 60°, 75° and 90°, and the cell size of the mesh cover was 2.5 × 2.5 mm². The weight was varied from 500 to 1250 g and the effect of each variable on bed velocity response was quantified through velocimetry and statistical analysis. The statistical analysis was conducted using NCSS statistical software. The blade angle, bed weight and superficial velocity for 4 mm particles were statistically optimized at 750 g, 58.26° and 1.45 m/s, respectively. On the experimental side, these parameters have been optimized at 750 g, 60° and 1.41 m/s, respectively. A small difference of 1.74° was noticed in experimental and statistical predictions for the blade angle. The bed weights and superficial velocities were found to be same in both cases. The confidence interval (95%) for bed velocity was proposed in the range of 0.513 to 0.519 m/s. The experimentally optimized bed velocity remained within the proposed range. The well-agreeing results indicate good practical value of distributor design and high precision of the experimental measurements.

1. Introduction

Though fluidized beds are in use in many industries, the stable regime of fluidization is lacking in many traditional fluidized beds [1]. Uniform fluidization of the materials under processing is needed in almost all practical applications of fluidized beds. The swirling fluidized bed (SFB) is the refined form of a conventional fluidized bed. SFBs can be used to perform industrial-scale processing of nano to micro-sized materials. The most reported SFBs are operated with different variants of air distribution plates. The workings, applications and efficiency of a SFB depend on distributor design. To date, scant information is available on distributor design-based workings and regimes of SFBs [2]. Owing to several geometries and a central role in the fluidization of bed material, the distributor designs should be investigated properly, as these designs explicitly affect the quality of the fluidization. In the processing industry, the fluidization phenomenon is used to produce and transport nano to macro-sized materials by suspending the precursors in an upward flowing fluid [3]. This fluid–solid interaction facilitates uniform processing of materials at relatively fast rates and with low processing costs.

The fluidization technology in implemented in various physical and chemical processes through many conventional and nonconventional designs of fluidized beds. The conventional designs are not versatile, as each design can only perform a specific physical or chemical process. An uneven distribution of fluid flow in conventional beds results in slugging and channeling in the bed and consequently the maldistribution of the material to be processed. These designs are also energy intensive and less efficient compared to the nonconventional or modern designs. The nonconventional designs are more versatile and can perform multiple tasks with high process efficiency [4,5]. The key stigmas associated with conventional beds can be resolved by incorporating new distributor concepts into their configurations. Ergun and Orning [6] studied the pressure drop in a conventional fluidized bed by changing the angles of fluid flow. Using this information, they established the hypothetical framework of fluidization process. Wen and Yu [7] tested different conventional fluidized beds and determined the minimum fluidization velocity required to fluidize the settled beds. Chitester et al. [8] studied the fluidized bed conditions for relatively larger and irregularly shaped materials. They determined the minimum fluidization velocity required to fluidize the coarse particles.

The knowledge of conventional fluidized beds help when developing their advanced versions. One such example is the swirling fluidized bed (SFB). TORBED is an early version of SFB, which was operated by changing the fluid flow from vertically upward mode to swirling flow mode [9]. Ouyang and Levenspiel [10] designed a spiral air distributor for producing swirling motion in the bed. Shu et al. [9] compared the workings of a conventional bed and TORBED. No significant difference between the workings of both designs was revealed during early stages of fluidization. However, both beds behave differently at higher superficial velocities. Sreenivasan and Raghavan [11] conducted pioneer work on SFBs by introducing an annular spiral distributor in the setup. Batcha and Raghavan [12] studied the influence of the inclination angle of the blades in an annular distributor on the flow response of a SFB. The effect of blade angle on bed velocity profiles was more pronounced compared to other bed design parameters. Kumar and Murthy [13] tested an air distributor with inclined blades assembled in a single row. This distributor design provided high proportion of opening area between blades compared to the previously reported distributor designs. The high opening area minimized the pressure drop across the bed and back pressure. Rasteh et al. [14] tested a centrifugal fluidized bed to dry the wet particles and to study the heat and mass transfer. The drying rate was increased with superficial velocity and particle size and decreased with increasing the swirling speed of the particles. It was concluded that the shape, dimensions, type of product and operating conditions show significant effects on the drying profiles.

Naz et al. [15] proposed a hybrid design of distributor for SFBs. They coupled a wire mesh with an annular distributor of a relatively larger percentage opening area between the blades. Using this design, different batches of spherical plastic beads were set into swirling motion at various blade angles. Particle image velocimetry (PIV) analysis was conducted on a quarter part of the fluidized bed. The Gaussian distribution of particles’ velocity was revealed along the radial line of the bed at lower superficial velocities. At higher superficial velocities, an almost uniform flow trend was observed throughout the bed. The bed velocity gradually increased with an increase in inclination angle of the blades. Roughly, the bed velocity exhibited a 6.35% increase for each 3° increase in inclination angle. Fang and Hong [16] tested a Laser diagnostic method for PIV analysis on tracer particles in a fluidized bed. They discussed the issues associated with drift area measurements by using PIV. Soto et al. [17] tested a plasma-assisted SFB reactor for production of nanoparticles. The silica-alumina particles were fluidized as a support material for growth of silver nanoparticles. Under suitable fluidization conditions, it was possible to produce nanoparticles of average size in the range of 3 to 50 nm. Since they tested a laboratory-scale SFB setup, it was revealed that the process can be scaled up to produce larger quantities of nanomaterials. However, they did not investigate the effect of input process parameters on bed parameters. A better insight into the bed dynamics may increase the product yield and process efficiency by lowering the process cost.

Naz et al. [18] conducted a PIV study on bed dynamics from the top and side of a SFB. Several layers of particles in the bed were swirling with relatively increasing velocities while moving along the bed column. These partial layers appear more when larger batches of materials are processed; that is, when chemical reactions are carried out at bulk scale. A detailed survey of the published literature showed that it would be important to investigate the effects of input parameters on the bed dynamics before testing SFB designs for different industrial applications. This study elaborates the bed dynamics of a SFB both experimentally and statistically by measuring the velocity profiles of particles along the radial lines in the bed.

2. Materials and Methods

2.1. Distributor Geometry

A set of annular distributors was fabricated by fixing rectangular blades between two concentric metal rings at inclination angles of 30°, 45°, 60°, 75° and 90°. Distributors had wire mesh coverings, which had an average cell size of 2.5 × 2.5 mm². Without having wire mesh, this distributor design was not suitable for processing the smaller particles due to large opening areas between the blades. The wire mesh worked as a platform for the settled bed and made the distributor design suitable for fluidization of smaller particles. After having mesh at the top, the distributor was suitable for fluidizing the particles larger than 2.5 mm. The detailed drawing of the distributor is shown in Figure 1. The inner ring was half the diameter of the outer ring (30 cm). A metal cylinder was placed on the inner ring to suppress the clogging of particles and dead zones in the middle of the bed. The distributor was placed on the top opening of a wind box of the same diameter as the outer ring. An acrylic cylinder was fitted over the distributor, as shown in Figure 2. A high-pressure blower supplied air at a required flowrate. The air blower was attached via an orifice plate to the wind box. The pressure drop across the orifice plate and the settled bed was measured using a pressure gauge. For measuring the pressure drop across the bed, two plastic pipes of 3 mm diameter were used to connect the pressure gauge to the cylindrical assembly just below the distributor and 10 cm above the wire mesh. The equation of pressure drop ($∆P$) due to turbulent air flow through the bed is:

$$∆P=g({\rho }_p-{\rho }_f)\left(1-\epsilon \right)h$$

(1)

where, g is a gravitational constant, ${\rho }_p$ is the density of the bed, ${\rho }_p$ is the density of air, h is bed height and $\epsilon$ is void size in the settled bed. $∆P$ is used to determine minimum air velocity (U_m) needed to initiate fluidization in the settled bed.

$$U_m=\frac{k}{\mu }({\rho }_p-{\rho }_f)\left(1-\epsilon \right)g$$

(2)

where $\mu$ is air viscosity and k is a constant. U_m depends on superficial velocity (U_s).

$$U_{sup}=\frac{Volumeflowrateofair}{Activecross-sectionalareaofbed}$$

(3)

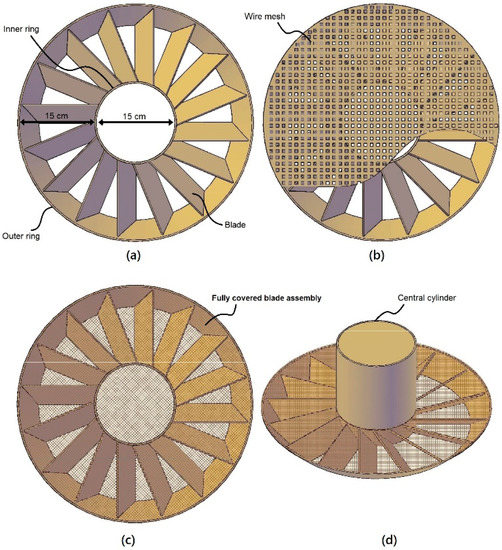
Figure 1. Geometry of mesh-coupled annular distributor: (a) fixing of rectangular blades between concentric rings, (b) cutaway view of the distributor with mesh cover, (c) complete distributor assembly, and (d) distributor with solid cylinder in the middle.

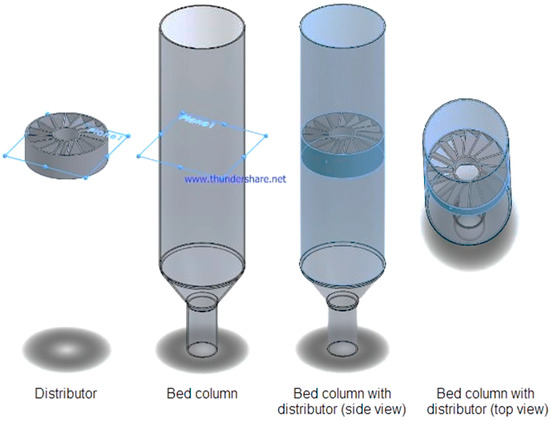
Figure 2. Complete design drawing of the bed column.

A graphical relationship was developed between $∆P$ and U_sup to determine U_m for initiation of fluidization.

2.2. Imaging and PIV Analysis

Spherical plastic beads of 4 mm size were used as a bed material. The particles were taken in two different colors. Black particles were utilized to develop the dark background for white tracers. The background and tracer particles were taken in 3:1 ratio. Initially, 500 g of bed material was distributed uniformly on the distributor. The blade angle for this test was fixed at 30°. The settled bed was set into fluidization by introducing tangential air flow into the bed. Although different fluidization regimes are possible from the settled bed to fast fluidization regime, the presented work only investigated the slugging swirling regime of fluidization. As shown in Table 1, some of the regimes may not occur during fluidization, depending on U_s, distributor design and shape of the bed material. The area under investigation was illuminated using surface mount device (SMD) lamps. These lamps offered a high-lumen output and low heat production for taking better quality images. A high-speed camera was mounted at the top of the bed column, as shown in Figure 3. The resolution of the camera was two mega pixels. The fluidized bed was photographed at a fixed framerate of 1000 fps. The images were translated into their binary form by using a binary imaging cross-correlation method. This method is preferred over other available methods due to its simple algorithm and high noise tolerance [18]. A similar procedure was repeated for 750, 1000 and 1250 g bed weights and 45°, 60°, 75° and 90° blade angles.

Table 1. Possible regimes of fluidization of a bed as air velocity increases.

Fluidizing Regime	Fluid Velocity	Features	Notes
Settled bed	0 < U < Um	Particles are quiescent. Air flows through interstices. Follows Darcy′s law.
Particulate regime	U < Um < Ub	Bed expends homogeneously. Surface is well-defined. Pressure drop is steady	This regime was missing in case of large particles.
Bubbling regime	Ub < U < Us	Voids form near the air distributor. The voids rise and grow in the form of bubbles. Pressure drop fluctuates by the passage of bubbles	Bubbling, slugging, turbulent and fast regimes are often collectively called aggregative fluidization.
Slugging regime	Us < U < Uu	Bubbles nearly fill the cross-section of the bed. Bed diameter and depth will affect the fluidization. Pressure drop fluctuates vigorously.	Amplitude of the pressure fluctuation can be as high as 80% of the average pressure drop; this regime may not exist for shallow beds.
Uniform swirling regime	Uu < U < Ut	Bubbles disappear and bed material start to swirl	Most of the industrial process with SFBs are carried out in this regime.
Turbulent regime	Ut < U < Ue	Small cavities and particle clusters move to and fro. It is difficult to distinguish the bed surface. Local mixing is intensive.
Elutriation regime	Ue < U	Particles are transported out of the bed	Used to separate particles of different sizes.

U = actual air velocity, U_m = minimum fluidization velocity, U_b = bubbling velocity, U_t = turbulent velocity, U_e = elutriation or terminal velocity.

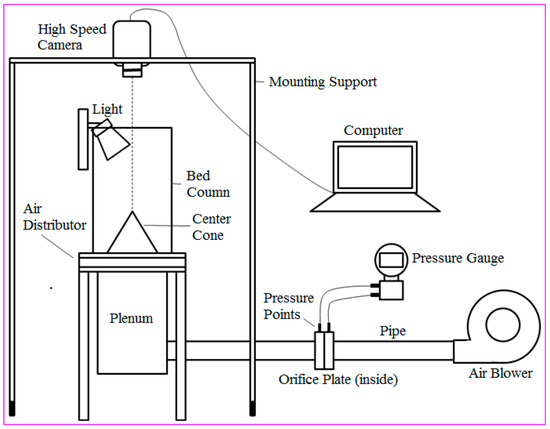
Figure 3. The experimental rig consisted of a swirling fluidized bed (SFB), a high-speed camera and a data acquisition setup.

A set of 20 sequential images from each group was exported to the PIV program. PIV analysis was conducted on quarters of images by masking the remaining areas. The masking of uninvestigated parts eliminated the shadow effect of the solid cylinder in the middle of the bed. The interrogation window was reduced from 128 to 32 pixels to generate the vector field. Although a large interrogation window results in a better signal to noise ratio, very few vectors per frame are obtained by setting up larger interrogation windows. Therefore, PIV analysis started with a relatively bigger interrogation window (128 pixels) and ended up at 32 pixels. The velocity vector fields were obtained for each bed weight and blade angle. The fields were processed to measure the average bed velocity along 5 radial lines on the surface of swirling bed. The accuracy in measurements was enhanced by removing the erroneous vectors in the field and by averaging the empty areas. The erroneous vectors appear either due to poor illumination of the bed or due to strong out-of-plane flow. On the statistical side, a response surface regression program was employed to predict the responses of bed velocity to the independent bed parameters. Once the bed entered the swirling regime of fluidization, the particle velocity and pressure drop across the distributor were about 0.43 m/s and 60 mm of H₂O, respectively.

2.3. Statistical Analysis

Regression analysis in statistics is a set of rules used to predict a suitable relationship among various quantities. Regression analysis usually predicts conditional expectation values of a dependent variable by fixing the independent variables. The response surface regression model is implemented by a program that fits the polynomial regression model with the cross-product terms of variables, which can take up to the third power. The polynomial approximation of the model is based on Taylor’s series. This approximation is well suited for studies of specified regions. If the specified area is made narrower and smaller, there is often a decrease in the number of significant variables or factors. A narrower region may require a linear or first order model, but if the region is broader, it may require a quadratic or second order model. Let us suppose there are some independent variables (Xs), which have at least three distinct values, and Y is the dependent or response variable. The polynomial model is one where Xs exist as multiples of one another. βs are called the regression coefficients or beta weights. A few examples of polynomial models are:

$$Yj=ß0+ß1X1j+\epsilon j°$$

(4)

$$Yj=ß0+ß1X1j+ß2X2j+ß3X1jX2j+\epsilon j$$

(5)

$$Yj=ß0+ß1X1j+ß2X2j2+ß3X1j2X2j3+\epsilon j$$

(6)

The unknown parameter, denoted by beta, represents a scalar or a vector quantity. The data are added in two or more columns. The first column contains the response or dependent variable, while the columns following the first column contain the independent variables or factors. The effects of independent variables on the response variable are investigated. The statistical program ignores the missing values. Although this program provides approximate values, it is easy to estimate even minor details of the process. The regression analysis process is run after the data are fed to the program in the form of dependent and independent variables. After the procedure is complete, the descriptive statistical section provides maximum, minimum and mean values of the variables. This section also illustrates whether the data come under the set criteria. The optimal solution section contains information on the optimization of the response variable, which in the given work is the bed velocity. Along with the dependent variable, the optimal values of all independent variables were also predicted. The normal probability plots were obtained for validation of the normality assumption.

3. Results and Discussion

3.1. Velocity Vector Field

Inside the settled bed, some voids occur as U_sup rises during the gas–solid interaction. These voids initially appear near the wire mesh and grow like bubbles, upward. The sizes of bubbles and $∆P$ increase with an increase in settled bed height. As U_sup increases, the bubbles burst and cause some fluctuations in $∆P$. The particles, which form the bubble walls, move upward by sending the bed into a particulate regime. This regime may be missing during the fluidization of larger particles because there is no velocity interval over which the bed material swells gradually before the formation of bubbles (i.e., U_b = U_f for large particle systems). At a certain velocity “U_s”, the bubbling process intensifies over time. The bed starts slugging and bubbles fill the whole column cross-section. Bubbles rise and fall during this process by moving up and down the bed surface over a considerable distance. $∆P$ fluctuates at higher amplitudes, and in some cases these variations are transformed into electrical signals for conventional beds to study the bubbling phenomenon [19]. The fluidization of relatively smaller particles is a complex phenomenon due to an increased cohesiveness between the particles and the container walls. In such situations, the cohesive force is larger than the gravitational force. This results in the particles binding to the walls allowing air to flow into the bed as channels blow through it. These channels are called “rat holes” in the bed. With a further increase in U_sup, these holes disappear and bed material undergoes a swirling motion due to tangential air entry into the bed via annular distributor. This swirling regime was investigated for the velocity vectors field and the bed velocity measurements.

Figure 4 shows the vector field of whole bed area. The inset provides a photographic view of the swirling bed. The bed weight and blade angle for this typical vector field were 750 g and 60°, respectively. The arrows show the trajectories of the individual particles, and yellow streamlines simulate a collective flow response of the bed. The blue sectors in the vector field show the particle slugging during fluidization. The sluggish flow was more noticeable in 1000 and 1250 g beds for larger blade angles. Particles showed lower velocities in these sectors compared to the yellow sectors, wherein particles had the highest velocities. Although some blue sectors were seen in the vector fields, the particles swirled smoothly overall, particularly for U_sup above 1.8 m/s.

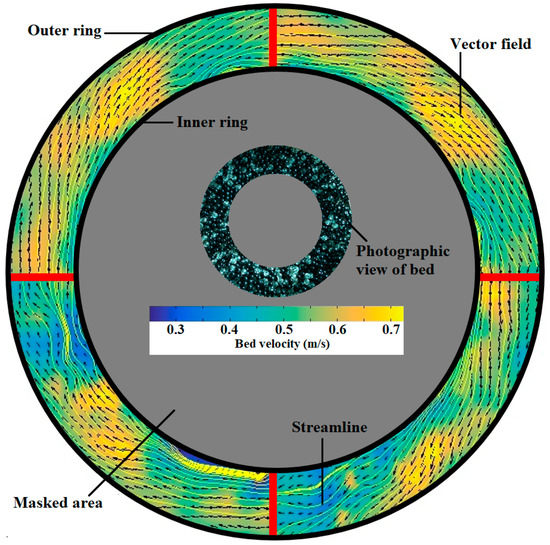
Figure 4. A vector field of a bed fluidized above U_m. Inset provides a photographic view of the swirling bed.

3.2. The Effect of Blade Angle on U_m

The minimum velocity at which fluidization starts in a settled bed is determined through a number of practical correlations available in the published literature [20,21]. Since no mathematical correlation has been developed so far for SFBs, U_m is estimated by plotting $∆P$ against U_sup. The intersection point of two tangent lines on the data plot provides rough estimate of U_m for each blade angle. For a 750 g bed, a change in $∆P$ with increasing U_sup is shown in Figure 5. The average U_m values for blade angles of 30°, 45°, 60° and 75° were estimated to be about 1.36, 1.41, 1.47 and 1.71 m/s, respectively. That shows that U_m increases slightly with an increase in blade angle from 30° to 60°. For a 75° blade angle, U_m changes significantly due to the relatively larger vertical component of U_sup. The vertical velocity component induces only bubbling or turbulence in the bed, whereas the horizontal component imparts a swirling motion to the bed material. Since the horizontal velocity component vanished at 90°, no swirling motion was observed for this blade angle. A ratio of superficial velocity and minimum velocity is also used to decide the air flowrate and power of the air blower.

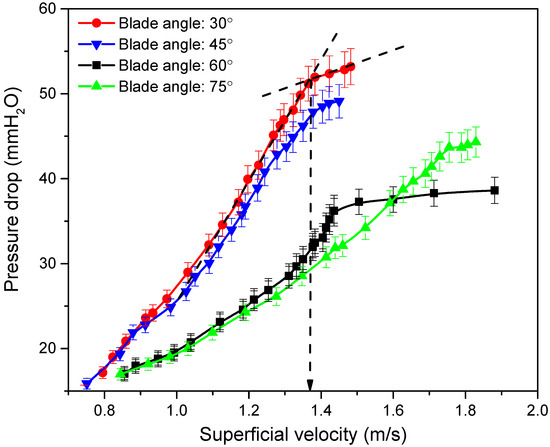
Figure 5. Estimation of U_m for different blade angles by plotting $∆P$ against U_sup for bed weight of 750 g.

The interplay of forces, which determine the bed hydrodynamical, can be comprehend from a free body diagram of forces being exerted on bed material. For a cylindrical system (r, θ, z) in mechanics, as shown in Figure 6, a tangential frictional force is produced due to forces normal to the surface. For example, resistance on a block which slides down an inclined plane. In a swirling bed, the reaction forces develop due to an outward centrifugal force which acts horizontally, normal to the column wall. The first force is the horizontal tangential force, which opposes the swirling of bed material by limiting the bed velocity. The second one is the orthogonal force acting downward, which resists the bed expansion. According to the second law of motion, this force should be zero for stable operation of the bed. The other forces are usually grown vertically (z-coordinate). Such forces in a bed provide downward friction at the wall and upward lift due to drop in air pressure. Similarly, in “θ” direction, the friction of particles against the wall reduces the angular momentum of particles. Along “r” coordinate, the centrifugal force of swirling particles is compensated by the centripetal force arising from the weight of the bed. Said force acts on the lower portion of the bed and creates an orthogonal force for the reaction. A balance between all forces along r, θ and z components exists once the bed operation gains stability.

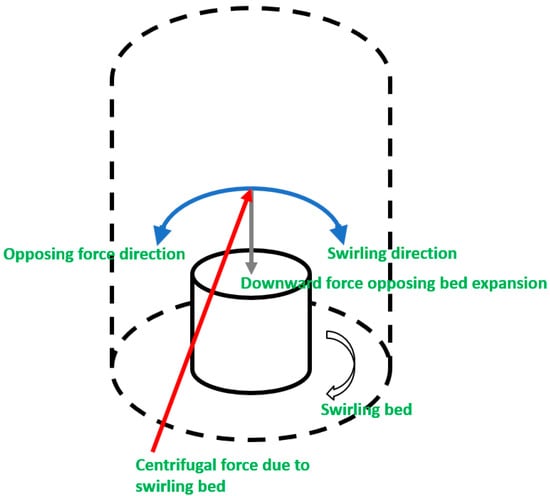
Figure 6. Free-body diagram of forces acting on swirling bed material.

Figure 7 Shows the estimation values of U_m for different bed weights by fixing the blade angle at 60°. U_m increases linearly with an increase in settled bed weight, since higher flowrates are required to balance the bed weight. U_m was increased from 1.32 to 1.6 m/s with an increase in bed weight from 500 to 1250 g. These findings were in line with the work of Shukrullah et al. [3]. They conducted a similar study on slightly heavier particles. A vector field of the fourth part of the swirling bed is shown in Figure 8. The velocity magnitude was measured on five lines and averaged to ensure high accuracy in the measurement.

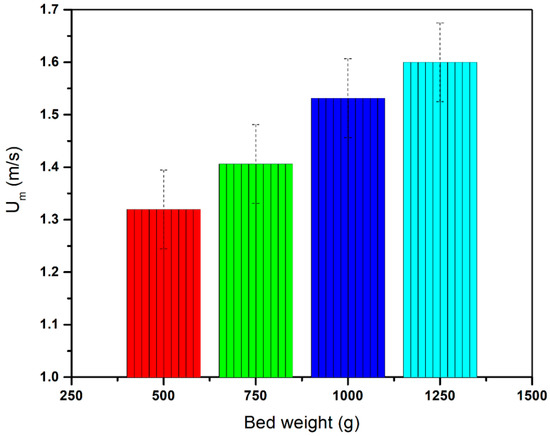
Figure 7. Estimation of U_m for different bed weights by fixing the blade angle at 60°.

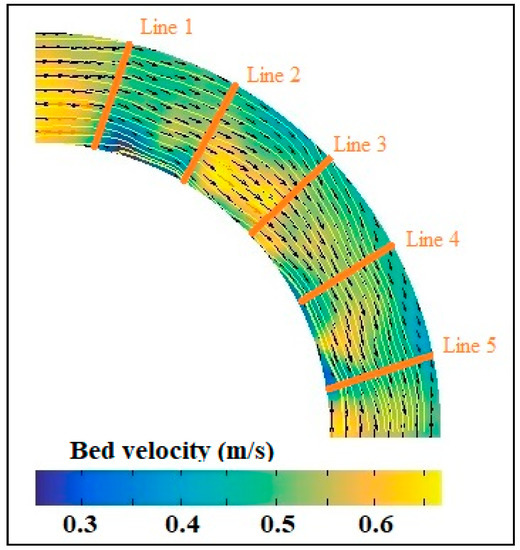
Figure 8. Marking of vector field for bed velocity measurements.

Figure 9 shows average velocity of the particles on radial line for 500, 750, 1000 and 1250 g beds. The velocity profiles of the 500 g batch showed a Gaussian distribution at all U_sup values. The bed velocity persisted near the inner ring between 0.31 and 0.38 m/s, and between 0.1 and 0.2 m/s at the outer ring. On the radial line, a maximum bed velocity of 0.9 m/s was estimated at a distance of 25 mm. Small bed velocities along the boundaries are believed due to frictional interaction between the column wall and the particles. For a 750 g sample, the bed velocity persisted near the inner ring between 0.15 and 0.2 m/s, and between 0.35 and 0.4 m/s at the outer ring. The highest velocity of 0.5 m/s was observed at a distance of 10–20 mm from the inner ring. An almost similar trend was observed for the 1000 g bed; however, the bed velocity was slightly lower than for the 750 g batch. This trend was changed with an increase in bed weight over 1000 g. For the 1250 g batch, the bed velocity near the outer ring was found to be higher than for the inner ring. That reveals that as the bed height increased, the centrifugal effect of the bed material was not as strong as in the case of smaller batches. This shows a uniform distribution of air near both ends of the bed, and therefore the bed velocity.

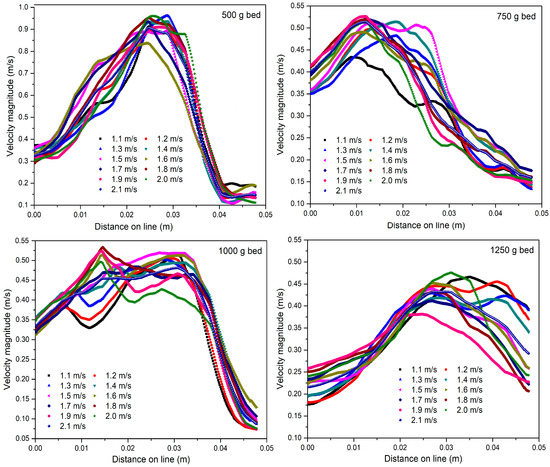
Figure 9. Trend of bed velocity magnitude on radial lines for different superficial velocities.

The velocity magnitudes of different bed weights at 60° are compared in Figure 10. All bed weights except 500 g showed almost similar velocity trends with peak velocities between 0.41 and 0.51 m/s. The velocity magnitude of the 500 g bed exhibited a sharp increase with distance and reached the peak value of 0.93 m/s in the center of the line. Thereafter, velocity started decreasing at the same rate by following a Gaussian distribution pattern. At 40 mm along the line, the bed attained a constant velocity of 0.15 m/s. That indicates that as the superficial velocity rises, the lighter bed materials migrate towards the outer wall. Owing to the packing effect near the wall, the particles travel at comparable velocities. Naz et al. [15] observed stable swirling of 6 mm spherical particles at U_sup of 2.12 m/s. Above this value, U_sup pushes the bed into slugging and or turbulence regime by reducing the process efficiency. Since the vertical component of U_sup at 60° slightly dominates the horizontal component, the bed expands gently and particles start gaining moderate velocities, except in the case of the 500 g bed.

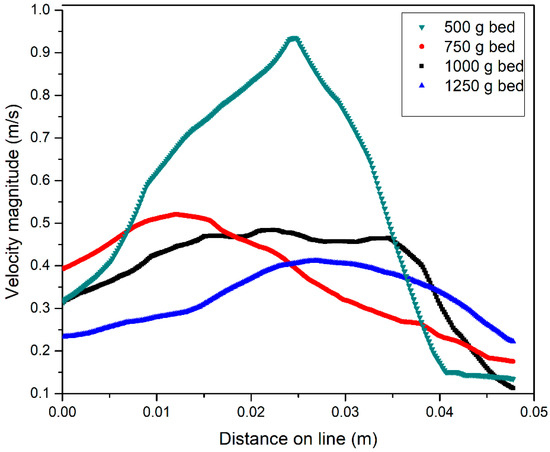
Figure 10. Comparison of average velocity profiles of different bed weights at 60°.

Figure 11 reveals vertical expansion in the 750 g bed with U_sup at different angles. The height of the settled bed is always lower than that of the fluidized bed. The bed starts to expand at the U_sup of 1.3 m/s and shows rapid expansion between 1.3 and 1.45 m/s. The bed swirls uniformly after 1.45 m/s and also reveals steady expansion over U_sup. After 1.9 m/s, the bed enters the elutriation regime and particles start moving out of the bed column. The settled bed height was around 55 mm, which increased to 75 mm just before entering the regime of complete fluidization. The bed height, in this regime, remained between 75 and 88 mm. As expected, the bed expansion increases with increasing blade angle. The vertical component of U_sup increases with an increase in blade angle, which contributes to expansion of the bed rather swirling motion.

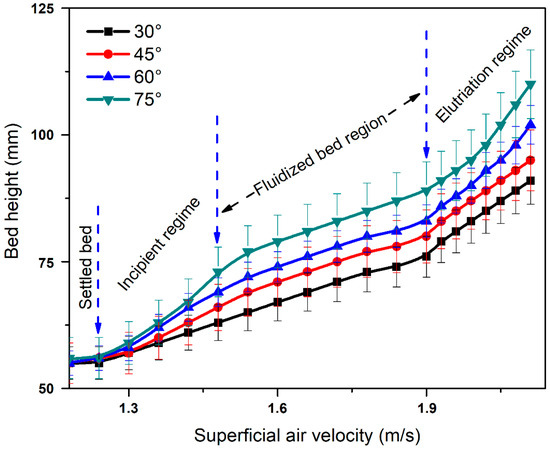
Figure 11. Illustration of bed height and flow response to superficial velocity at different blade angles.

3.3. Review of SFB Parameters

Batcha and Raghavan [12] tested an annular distributor for a swirling bed. They used two sizes of spherical particles; namely, 5.75 and 9.84 mm. The open area between the blades was found to be about 12.9% to 17.2% with an overlapping angle of 9° to 12°. Bed weight was varied from 500 to 2000 g while the U_sup was varied from 1 to 7 m/s. It was revealed that $∆P$ keeps on increasing with U_sup even after U_m. In conventional bed operations, $∆P$ does not change after U_sup surpasses U_m. The results of our study on pressure drop agreed with the trend reported by Batcha and Raghavan [12]. Since they used larger bed weights, the settled bed height increased with batch weight. They observed double-layered fluidization in deeper beds. Naz et al. [18] also revealed multilayered fluidization of the spherical particles. The layer speed increased while moving up along the bed column. These layers appeared in the bed when larger batches were subjected to swirling motion. Josephkunju [22] tested an annular blade distributor for fluidization of three sizes of spherical particles (3.2, 5.5 and 7.4 mm). The distributor designs had four rows of slits with inclination angles of 0°, 5°, 10° and 15°. For the fixed bed weight of 2.5 kg, $∆P$ decreased with an increase in blade angle. These measurements were carried out at different radial distances of between 60 and 150 mm. For 7.4 mm particles and 15° angled blades, the minimum velocity for fluidization was about 1.846 m/s. Swirling motion in the bed started at 1.898 m/s, and some vortices were also formed at U_sup of 2.951 m/s. U_sup increased by 0.029 m/s for each degree increment in blade angle from 0° to 5°. For 5°–10° and 10°–15° ranges, U_sup increases by 0.018 and 0.007 m/s, respectively.

Venkiteswaran et al. [23] constructed a distributor by fixing blades at 10° and studied the effect of particle shape on pressure drop. They fluidized 0.5, 0.75 and 1 kg batches of spherical, cylindrical and elliptical particles. $∆P$ showed a linearly increasing trend with bed weight regardless of shape of the particles. The highest $∆P$ was measured for spherical particles among the shapes tested. The lowest U_m of 1.0 m/s to 1.2 m/s was reported for elliptical particles. Kumar et al. [13] constructed an annular distributor by fixing 60 blades at an angle of 15°. This distributor was tested for fluidization of 1000, 1500 and 2500 g batches of spherical glass beads. The pressure drop for this distributor was lower than a perforated plate distributor having inclined holes and slightly higher than a three-row inclined blade distributor. The minimum velocity (U_m) was estimated to be about 1.2 m/s. Above this value, superficial velocity did not influence the pressure drop. Naz and Sulaiman [1] conducted a particle-tracking velocimetry study on the hydrodynamics of spherical particles in a SFB. They constructed a set of annular distributors by choosing blade angles of 10°, 15° and 20° and a particle size of 6 mm. The superficial velocity for uniform swirling motion was estimated in the range of 2–2.6 m/s, depending on the blade angle. Gaussian distribution of bed velocity was predicted along the radial line at lower superficial velocities.

Miin et al. [2] investigated the bed dynamics in a stable swirling regime. Particles of different sizes were fluidized by changing the blade angle in the annular distributor. They fixed 60 blades between two concentric rings to construct the annular distributor. The blade angles were set at 12°, 15° and 18°. They used 500, 750, 1000, 1250 and 1500 g bed weights of 2.9 and 3.9 mm particles. The highest bed velocity was measured at the center of the radial line. A 3° change in blade angle resulted in an 18% decrease in velocity. The minimum fluidization velocities for the 500 g beds of 2.9 and 3.9 mm particles were estimated to be about 1.4 and 1.6 m/s, respectively. Faizal et al. [24] reported an annular distributor to dry biomass using a SFB. Rigorous drying and mixing of stock were observed at moderate pressure drops when the blade angle was 15° and bed weight was 500 g. A summary of the past literature, relevant to the current study, is provided in Table 2.

Table 2. A summary of the published literature on annular designs.

Reference	Distributor	Parameters	Findings
Rahimpour et al. [19].	Perforated Plate	Time, frequency and space domains, superficial air velocity, pressure drop	Distributor underperforms in case of fine particles, especially at low superficial velocity. Low pressure fluctuations were observed.
Rees et al. [25]	Perforated Plate	Superficial air velocity, pressure drop	Voids or bubble streams were observed even at U < Um. Dead zones were formed between the orifices of distributor. Jet length was increased with an increase in U/Um ratio.
Akbari et al. [26]	Perforated Plate	Drag coefficient, time step, number of nodes and specularity coefficient in CFD	The distributor configuration affects the bed flow parameters. Fluidization starts with bubbles, which disturb the flow field. Better gas–solid mixing was observed above the entrance region due to jet formation. Some dead zones were also seen in the bed.
Rahimpour et al. [19].	Porous plate	Time, frequency and space domains, superficial air velocity, pressure drop	The bubble clustering rate was very large, although the pressure drop across porous plate was double than the pressure drop across a perforated distributor.
Yudin et al. [27]	Inclined slotted	Particulate mixing and uniform fluidization	swirling motion resulted in uniform mixing of particles. The swirling flow pattern was obvious for shallow beds while two-layers motion was observed in case of deep beds.
Sánchez-Prieto et al. [28]	Bubble cap	Temperature, pressure drop, air flow	The pressure drop was high due to small discharge coefficient. The bed hydrodynamics were affected by the operating temperature.
Aworinde et al. [4,5]	Nozzle	Superficial air velocity, pressure drop	The lateral dispersion promoted by the swirl of nozzle, which caused better gas–solid contact. Smaller and less frequent bubbles were produced in the bed. The pressure drop was higher due to swirl in the helix and secondary flow friction. The drawbacks included higher operating cost and energy consumption.
Akbari et al. [26]	Sparger	Entrance region hydrodynamics, time step, drag coefficient, number of node, and specularity coefficient	The flow structure significantly affected by the entrance configuration. The flow field was homogeneous with smaller bubble sizes through the bed. Dead zones were spotted at the corners of the sparger distributor due to particles clustering.
Kumar and Murthy [13]	Swirled fluidized bed	The inlet diameter, number of inlets, settled bed height, diameter of column, properties of bed material	A swirl flow in bed material was achieved by the tangential flow of air via multiple fluid inlets, located at the base of bed column. The minimum swirl velocities were measured about 1.2–1.3 times the Um of conventional fluidized beds. The pressure drop across the bed decreased due to larger opening areas between the blades.
Josephkunju [22]	Annular distributor	Particle size, particle density, blade inclination angle	Pressure drop increased along radial direction until 90 mm. Pressure drop decreased for larger blade angles. Pressure drop showed inverse relationship with diameter and size of particles.
Venkiteswaran et al. [23]	Annular distributor	Particle shape, pressure drop, bed weight, superficial air velocity	The pressure drop increase with bed weight. The highest pressure drop was measured for spherical shape. The pressure drop kept on increasing even after incipient fluidization due to centrifugal weight of bed material.
Naz et al. [15]	Annular distributor	Pressure drop, blade fin angle, superficial velocity, blade angle	Bed velocity exhibited Gaussian distribution on radial line. The optimized superficial velocity was 2.3 m/s. No bubbles were found in the bed due to swirling motion. Fall back of particles into the plenum chamber was a major drawback of the setup.
Sulaiman et al. [29]	Annular distributor	Distributor pressure, blade angle, superficial air velocity, particle shape, bed weight	The bed velocity increases with an superficial velocity and decreases with bed weight. Gaussian distribution of bed velocity was observed. A 3° increase in angle caused 18% decrease in particle velocity.
Batcha and Raghavan [12]	Annular distributor	Number of blades, blade angle, bed velocity, pressure drop	An annular assembly of 30 blades with inclination angle of 10° was found as an optimum configuration. Variations in pressure drop were nominal.
Current study	Mesh-coupled annular blade distributor	Bed weight, superficial velocity, blade angle, pressure drop, bed velocity	All the batches except 500 g showed almost similar velocity trends with peak velocities between 0.41 m/s and 0.51 m/s. The velocity magnitude of 500 g bed exhibited sharp increase with radial distance and reached peak value of 0.93 m/s. Thereafter, velocity started decreasing at the same rate by following a Gaussian distribution pattern. At 40 mm on the line, the bed attained constant velocity of 0.15 m/s. As the superficial velocity rises, the lighter bed materials migrate towards the outer wall. Owing to the packing effect near the wall, the particles travel at comparable velocities.

3.4. Comparison of Velocimetry and Statistical Data

Optimization of variables for fluidized beds is usually performed to increase the process efficiency. Since velocimetry data of the presented work provided a plethora of information, it was difficult to figure out the most significant and least significant variables. Since three independent variables and one response variable were involved in these investigations, the regression analyses were conducted on experimental data to determine the optimum values of these variables. NCSS statistical software was used to perform polynomial statistical regression analysis. The results of polynomial regression analysis are summarized in Table 3. A relation between response variable and independent variables was also established, as shown in Figure 12. The independent variables were bed weight, blade angle and superficial velocity. The optimum values of these variables were predicted as 750 g, 58.26° and 1.45 m/s, respectively. Experimentally optimized values of bed weight, blade angle and superficial velocity were 750 g, 60° and 1.41 m/s, respectively. Both statistical and velocimetry studies predicted the same optimum bed weight values. The blade angles and superficial velocities showed small differences of 1.74° and 0.04 m/s, respectively.

Table 3. Comparison of statistical findings of bed weight, blade angle and superficial velocity with experimental findings for 4 mm particles.

Analysis	Bed Weight (g)	Blade Angle (°)	Usup (m/s)	Response Parameter (Bed Velocity in m/s)
Statistical	750 g	58.26°	1.45 m/s	0.518 m/s
Experimental	750 g	60°	1.41 m/s	0.5 m/s

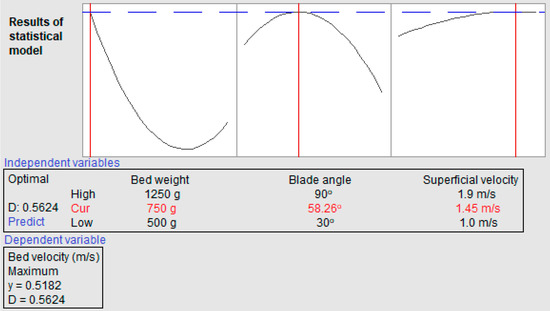
Figure 12. Statistical analysis of response and independent variables.

The confidence interval for the response variable was set at 95%. This interval suggested a number of possible values of bet velocity response. The optimum bed velocity must fall in the statistically proposed range. The statistical analysis of data proposed the confidence interval of 0.513–0.519 m/s. The statistical response of bed velocity was 0.518 m/s, which remains in the proposed range. In velocimetry analysis, the bed velocity was found to be about 0.5 m/s. The experimental measurements show good agreement with the results of statistical analysis. The well-agreeing results indicate good practical value of distributor design and high precision of the experimental measurements.

4. Conclusions

This study elaborated on the bed dynamics of a SFB both experimentally and statistically by measuring the velocity profiles of particles along the radial lines in the fluidized bed. A set of annular distributors was fabricated by fixing rectangular blades between concentric rings at inclination angles of 30°, 45°, 60°, 75° and 90°. These distributors were covered with wire mesh having average cell size of 2.5 × 2.5 mm². The average superficial velocities for blade angles of 30°, 45°, 60° and 75° were estimated to be about 1.36, 1.41, 1.47 and 1.71 m/s, respectively. A maximum bed velocity of 0.9 m/s was estimated at 25 mm on a radial line of the bed. For the 750 g batch, the bed velocity remained between 0.15 and 0.2 m/s near the inner ring and between 0.35 and 0.4 m/s near the outer ring. The highest velocity of 0.5 m/s was observed between 10 and 20 mm on the radial line. An almost similar trend was observed for 1000 g bed; however, bed velocity was slightly lower than for the 750 g batch. This trend was changed with an increase in bed weight over 1000 g. Both statistical and velocimetry studies predicted nearly the same optimum values of independent and response variables. The blade angles and superficial velocities showed small differences of 1.74° and 0.04 m/s, respectively. The statistical analysis of data proposed the confidence interval of 0.513–0.519 m/s. In velocimetry analysis, the bed velocity was about 0.5 m/s. The experimental measurements show good agreement with the results of statistical analysis.