On Molecular Descriptors of Face-Centered Cubic Lattice
Abstract
:1. Introduction
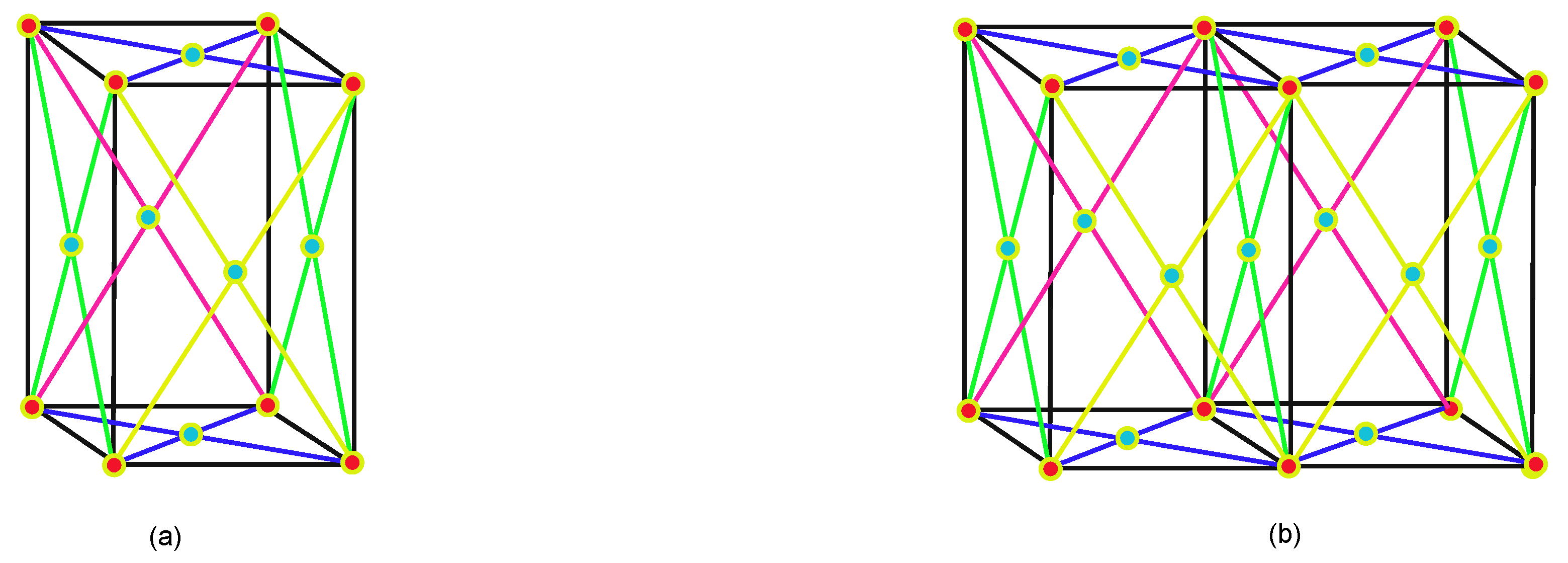
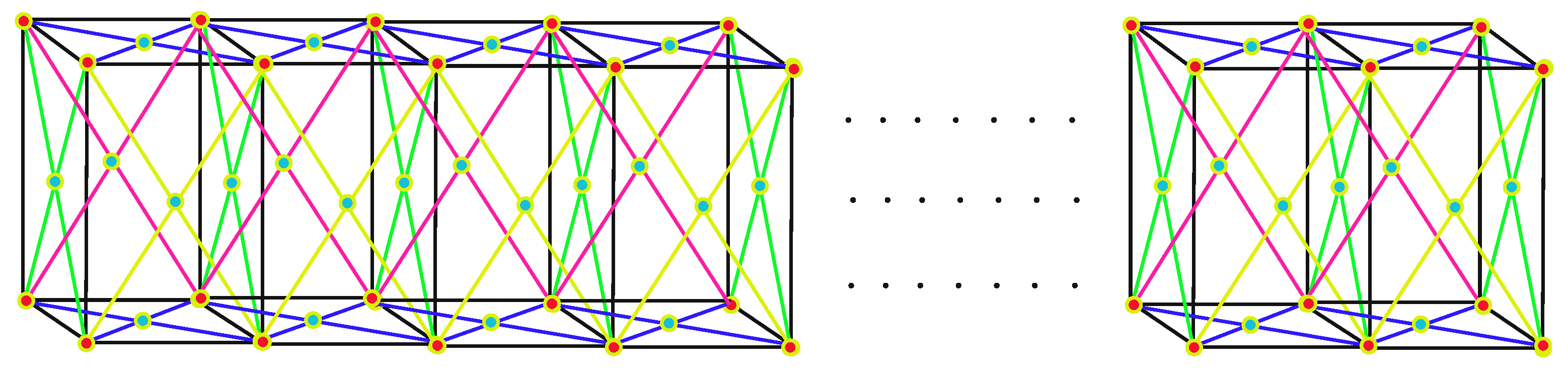
2. Face-Centered Cubic Lattice
Methodology of Face-Centered Cubic Lattice Formulas
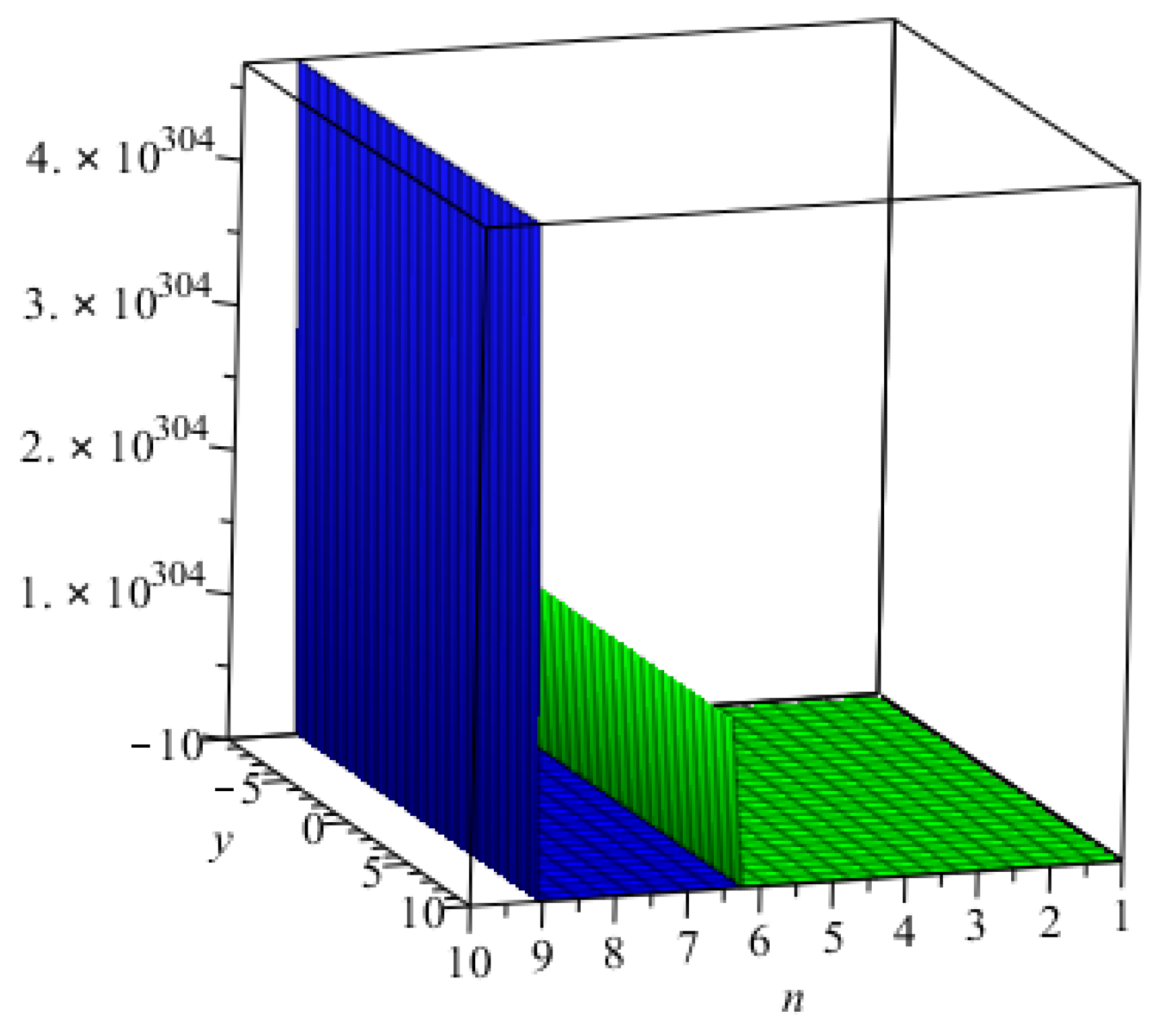
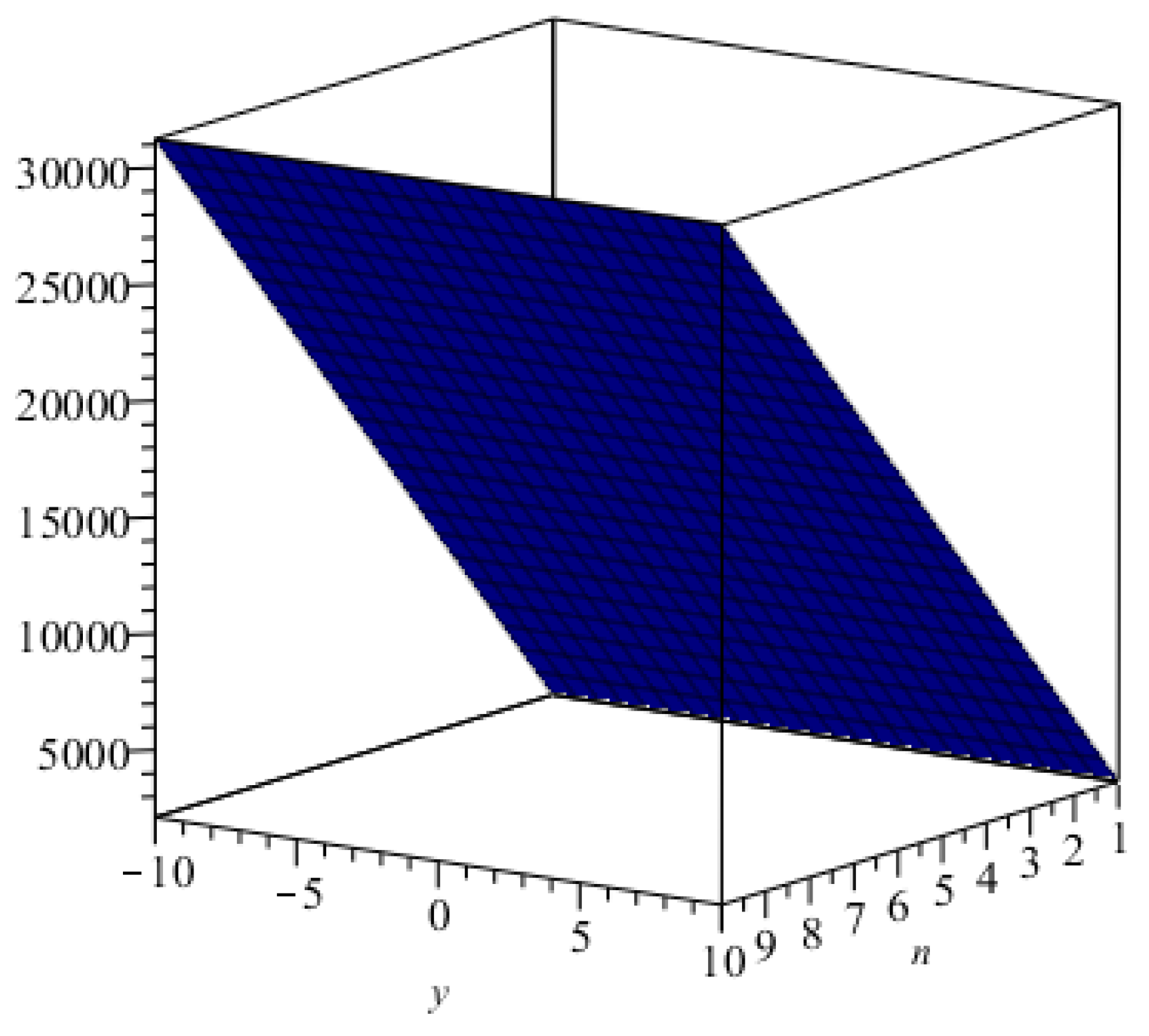
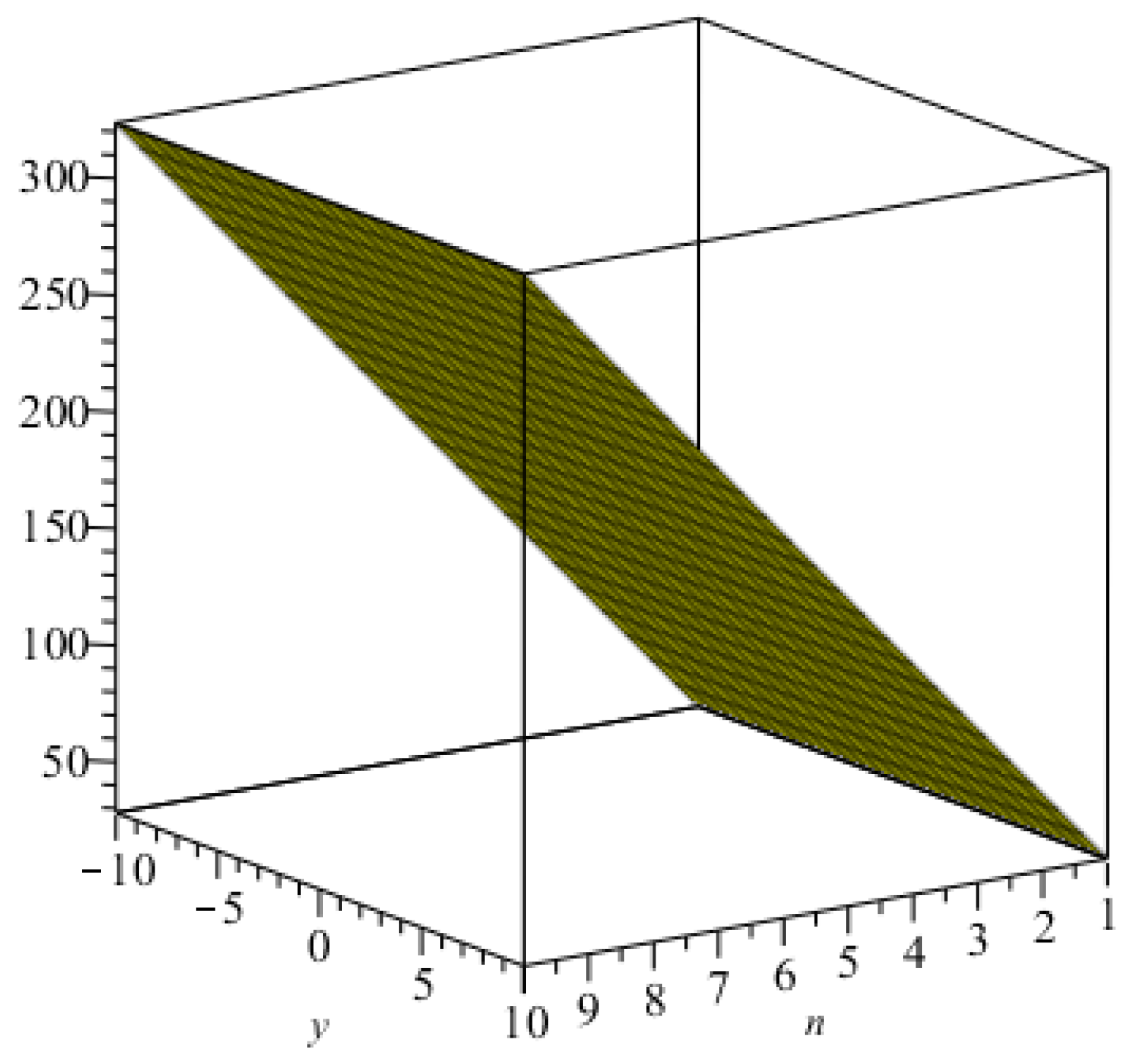
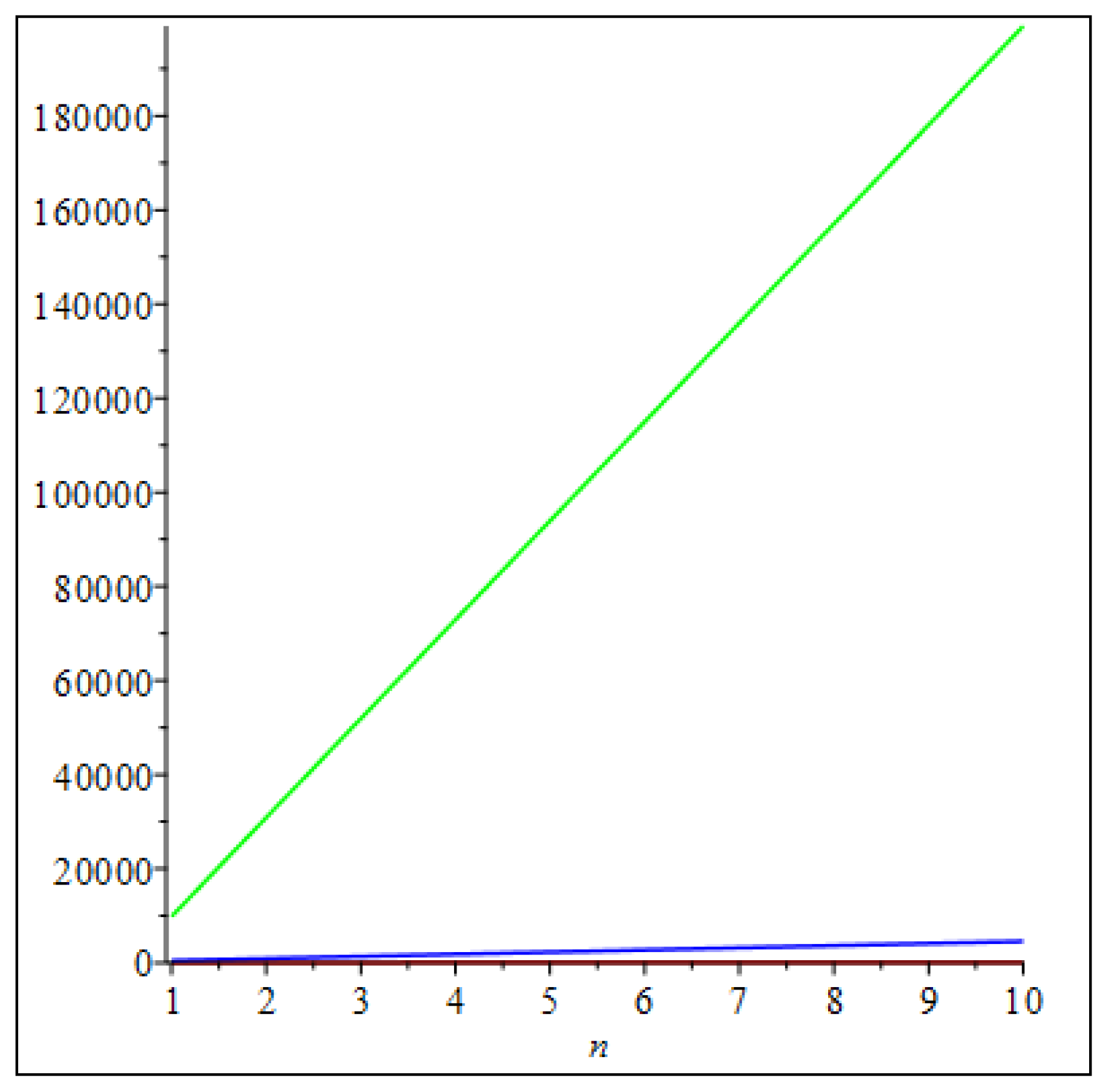
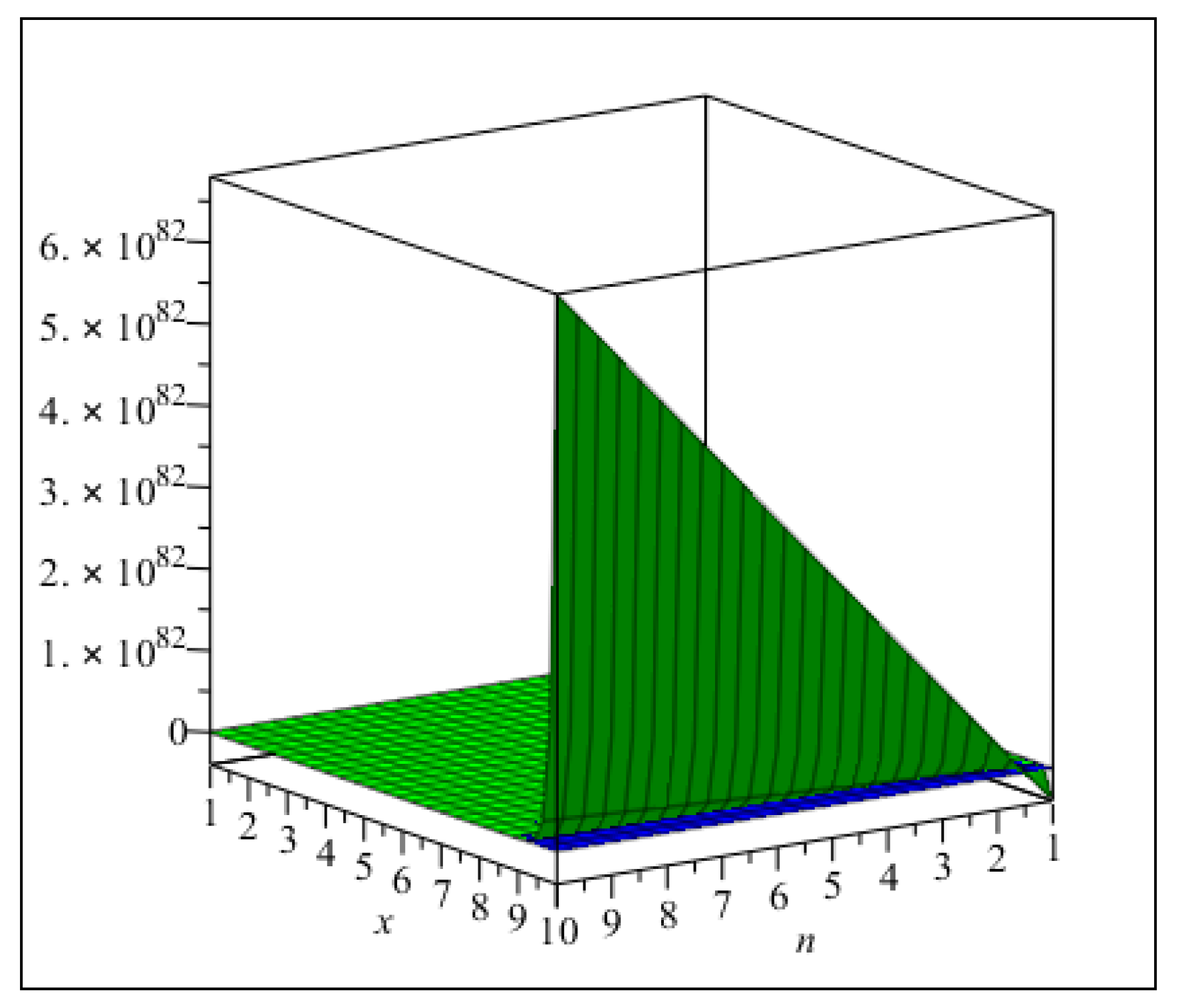
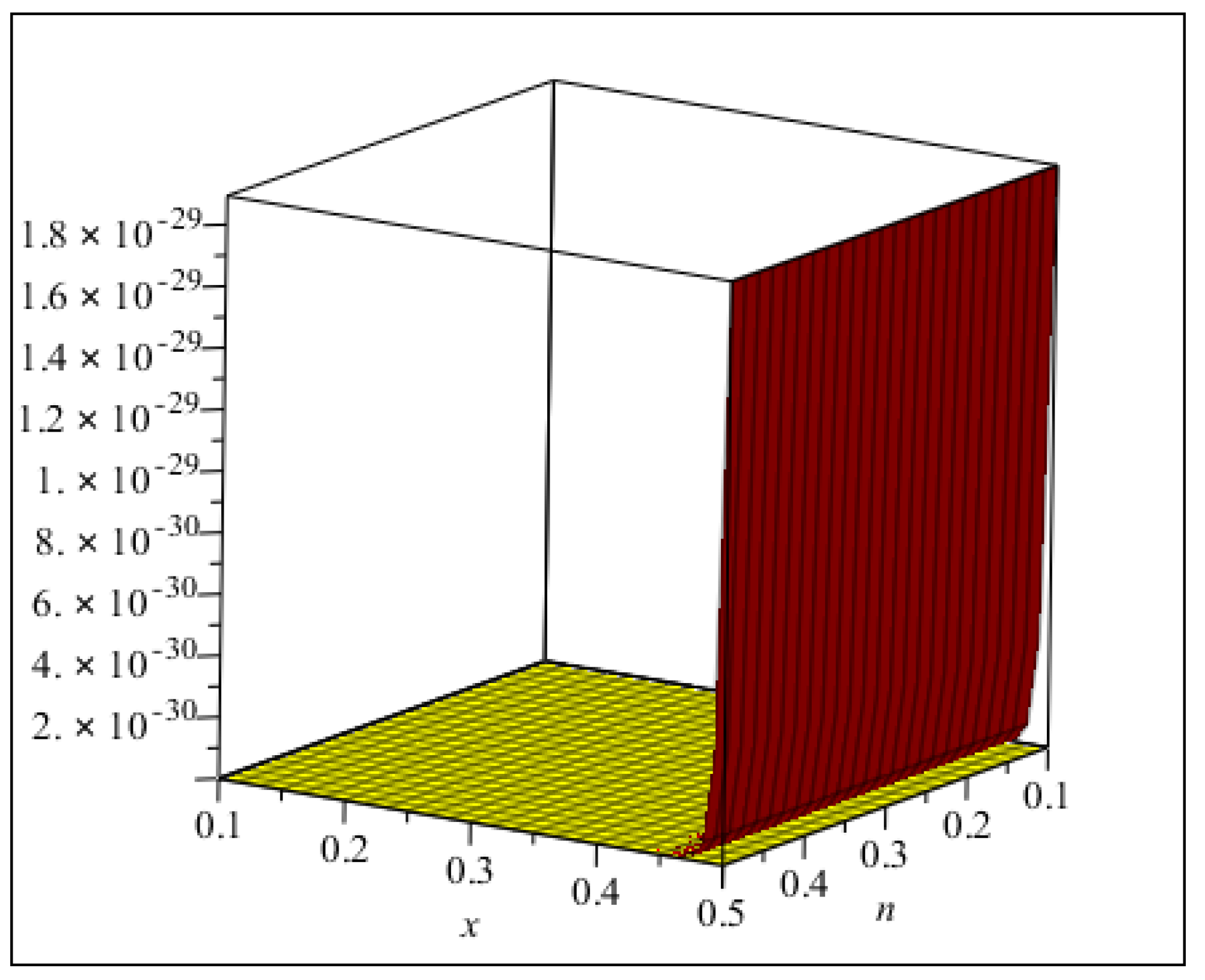
3. Main Results
4. Comparisons and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Catlow, C.R.A. Modelling and predicting crystal structures. Interdiscip. Sci. Rev. 2015, 40, 294–307. [Google Scholar] [CrossRef]
- Bača, M.; Horváthová, J.; Mokrišová, M.; Suhányiová, A. On topological indices of fullerenes. Appl. Math. Comput. 2015, 251, 154–161. [Google Scholar] [CrossRef]
- Bača, M.; Horváthová, J.; Mokrišová, M.; Semanicová-Fenovcíková, A.; Suhányiová, A. On topological indices of carbon nanotube network. Can. J. Chem. 2015, 93, 1–4. [Google Scholar] [CrossRef]
- Gao, W.; Siddiqui, M.K. Molecular Descriptors of Nanotube, Oxide, Silicate, and Triangulene Networks. J. Chem. 2017, 2017, 6540754. [Google Scholar] [CrossRef]
- Imran, M.; Siddiqui, M.K.; Naeem, M.; Iqbal, M.A. On Topological Properties of Symmetric Chemical Structures. Symmetry 2018, 10, 173. [Google Scholar] [CrossRef]
- Imran, M.; Ali, M.A.; Ahmad, S.; Siddiqui, M.K.; Baig, A.Q. Topological Characterization of the Symmetrical Structure of Bismuth Tri-Iodide. Symmetry 2018, 10, 201. [Google Scholar] [CrossRef]
- Gao, W.; Siddiqui, M.K.; Naeem, M.; Rehman, N.A. Topological Characterization of Carbon Graphite and Crystal Cubic Carbon Structures. Molecules 2017, 22, 1496. [Google Scholar] [CrossRef]
- Gharibi, W.; Ahmad, A.; Siddiqui, M.K. On Zagreb Indices, Zagreb Polynomials of Nanocone and Nanotubes. J. Comput. Theor. Nanosci. 2016, 13, 5086–5092. [Google Scholar] [CrossRef]
- Idrees, N.; Naeem, M.N.; Hussain, F.; Sadiq, A.; Siddiqui, M.K. Molecular descriptors of benzenoid system. Quimica Nova 2017, 40, 143–145. [Google Scholar] [CrossRef]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef]
- Dobrynin, A.A.; Entringer, R.; Gutman, I. Wiener index of trees: Theory and applications. Acta Appl. Math. 2001, 66, 211–249. [Google Scholar] [CrossRef]
- Ghorbani, M.; Azimi, N. Note on multiple zagreb indices. Iran. J. Math. Chem. 2012, 3, 137–143. [Google Scholar]
- Gutman, I.; Das, C.N. The first Zagreb index 30 years after. MATCH Commun. Math. Comput. Chem. 2004, 50, 83–92. [Google Scholar]
- Gutman, I.; Trinajst, N. Graph theory and molecular orbitals, Total π-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Furtula, B.; Gutman, I. A forgotten topological index. J. Math. Chem. 2015, 53, 1184–1190. [Google Scholar] [CrossRef]
- Gao, W.; Siddiqui, M.K.; Imran, M.; Jamil, M.K.; Farahani, M.R. Forgotten Topological Index of Chemical Structure in Drugs. Saudi Pharm. J. 2016, 24, 258–267. [Google Scholar] [CrossRef]
- Furtula, B.; Graovac, A.; Vukicevic, D. Augmented zagreb index. J. Math. Chem. 2010, 48, 370–380. [Google Scholar] [CrossRef]
- Balaban, A.T. Highly discriminating distance-based topological index. Chem. Phys. Lett. 1982, 89, 399–404. [Google Scholar] [CrossRef]
- Balaban, A.T.; Quintas, L.V. The smallest graphs, trees, and 4-trees with degenerate topological index. J. Math. Chem. 1983, 14, 213–233. [Google Scholar]
- Ranjini, P.S.; Lokesha, V.; Usha, A. Relation between phenylene and hexagonal squeez using harmonic index. Int. J. Graph. Theory 2013, 1, 116–121. [Google Scholar]
- Fath-Tabar, G.H. Zagreb Polynomial and Pi Indices of some Nano Structures. Dig. J. Nanomater. Biostruct. 2009, 4, 189–191. [Google Scholar]
- Chaluvaraju, B.; Boregowda, H.S.; Diwakar, S.A. Hyper-Zagreb indices and their polynomials of some special kinds of windmill graphs. Int. J. Adv. Math. 2017, 4, 21–32. [Google Scholar]
- Ghorbani, A.; Hosseinzadeh, M.A. Computing ABC4 index of nanostar dendrimers. Optoelectron. Adv. Mater. Rapid Commun. 2010, 4, 1419–1422. [Google Scholar]
- Graovac, A.; Ghorbani, M.; Hosseinzadeh, M.A. Computing fifth geometric–arithmetic index for nanostar dendrimers. J. Math. Nanosci. 2011, 1, 33–42. [Google Scholar]
- Siddiqui, M.K.; Imran, M.; Ahmad, A. On zagreb indices, zagreb polynomials of some nanostar dendrimers. Appl. Math. Comput. 2016, 280, 132–139. [Google Scholar] [CrossRef]
- Siddiqui, M.K.; Gharibi, W. On Zagreb Indices, Zagreb Polynomials of Mesh Derived Networks. J. Comput. Theor. Nanosci. 2016, 13, 8683–8688. [Google Scholar] [CrossRef]
- Siddiqui, M.K.; Naeem, M.; Rahman, N.A.; Imran, M. Computing topological indices of certain networks. J. Optoelectron. Adv. Mater. 2016, 18, 884–892. [Google Scholar]
- Kang, S.M.; Siddiqui, M.K.; Rehman, N.A.; Naeem, M.; Muhammad, M.H. Topological properties of 2-dimensional silicon-carbons. IEEE Access 2018, 6, 59362–59373. [Google Scholar] [CrossRef]
- Gao, W.; Siddiqui, M.K.; Naeem, M.; Imran, M. Computing multiple ABC index and multiple GA index of some grid graphs. Open Phys. 2018, 16, 588–598. [Google Scholar] [CrossRef]
- Conway, J.H.; Sloane, N.J.A. Sphere Packings, Lattices, and Groups, 2nd ed.; Springer: New York, NY, USA, 1993. [Google Scholar]
- Mujahed, H.; Nagy, B. Exact Formula for Computing the Hyper-Wiener Index on Rows of Unit Cells of the Face-Centred Cubic Lattice. An. Univ. Ovidius Constanta 2018, 26, 169–187. [Google Scholar] [CrossRef]

| Frequency | Edge Sets | |
|---|---|---|
| 24 | ||
| 8 | ||
| 8 | ||
| Number of Edges | Edge Sets | |
|---|---|---|
| (33, 33) | 8 | |
| (24, 33) | 8 | |
| (30, 33) | 16 | |
| (36, 53) | 24 | |
| (30, 53) | 16 | |
| (33, 53) | 8 | |
| (53, 53) | 8 | |
| (53, 56) | 8 | |
| (56, 56) | 8n-28 | |
| (36, 56) | 20n-60 |
| n | |||||
|---|---|---|---|---|---|
| 1 | 2112 | ||||
| 2 | 5348 | ||||
| 3 | 8548 | ||||
| 4 | 11820 | ||||
| 5 | 15056 | ||||
| 6 | 18292 |
| n | |||||
|---|---|---|---|---|---|
| 1 | 14 | 9864 | |||
| 2 | 23 | 30888 | |||
| 3 | 32 | 51912 | |||
| 4 | 41 | 72936 | |||
| 5 | 50 | 93960 | |||
| 6 | 59 | 114984 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Rashid, M.A.; Ahmad, S.; Khan, S.S.; Siddiqui, M.K. On Molecular Descriptors of Face-Centered Cubic Lattice. Processes 2019, 7, 280. https://doi.org/10.3390/pr7050280
Yang H, Rashid MA, Ahmad S, Khan SS, Siddiqui MK. On Molecular Descriptors of Face-Centered Cubic Lattice. Processes. 2019; 7(5):280. https://doi.org/10.3390/pr7050280
Chicago/Turabian StyleYang, Hong, Muhammad Aamer Rashid, Sarfraz Ahmad, Saima Sami Khan, and Muhammad Kamran Siddiqui. 2019. "On Molecular Descriptors of Face-Centered Cubic Lattice" Processes 7, no. 5: 280. https://doi.org/10.3390/pr7050280
APA StyleYang, H., Rashid, M. A., Ahmad, S., Khan, S. S., & Siddiqui, M. K. (2019). On Molecular Descriptors of Face-Centered Cubic Lattice. Processes, 7(5), 280. https://doi.org/10.3390/pr7050280





