Abstract
The compressor fuel cost minimization problem (FCMP) for natural gas pipelines is a relevant problem because of the substantial energy consumption of compressor stations transporting the large global demand for natural gas. The common method for modeling the FCMP is to assume key modeling parameters such as the friction factor, compressibility factor, isentropic exponent, and compressor efficiency to be constants, and their nonlinear relationships to the system operating conditions are ignored. Previous work has avoided the complexity associated with the nonlinear relationships inherent in the FCMP to avoid unreasonably long solution times for practical transportation systems. In this paper, a mixed-integer linear programming (MILP) based method is introduced to generate piecewise-linear functions that approximate the previously ignored nonlinear relationships. The MILP determines the optimal break-points and orientation of the linear segments so that approximation error is minimized. A novel FCMP model that includes the piecewise-linear approximations is applied in a case study on three simple gas networks. The case study shows that the novel FCMP model captures the nonlinear relationships with a high degree of accuracy and only marginally increases solution time compared to the common simplified FCMP model. The common simplified model is found to produce solutions with high error and infeasibility when applied on a rigorous simulation.
1. Introduction
Natural gas accounts for an estimated 21% of the current global energy demand, with this share expected to grow to 24% by 2040. The projected 1.5% annual growth in absolute natural gas demand makes it the fastest growing among the fossils fuels [1]. The large and growing natural gas demand puts a heightened importance on natural gas transportation systems, given the enormous quantities of gas being distributed globally. The magnitude of the issue means even marginal improvements in the efficiency of gas transportation can result in substantial energy and cost savings.
This paper addresses a particular area of natural gas transportation research which has been studied for decades, the fuel cost minimization problem (FCMP). The problem exists because pressure drives gas flow in pipelines, but friction between the gas and pipeline wall results in a drop in gas pressure along the length of the pipeline. To maintain gas flow, the gas pressure must be increased at points throughout the pipeline network, which is achieved by compressor stations. The FCMP is concerned with determining the natural gas pressure change at each compressor station in the pipeline network, and the amount of gas to flow through each pipeline segment of the network, to achieve the minimum compressor fuel costs. The system operation must obey gas supply and demand constraints and physical equipment limitations. With an estimated 3–5% of all natural gas transported by transmission pipelines consumed by the compressor stations responsible for maintaining gas flow, substantial energy and cost savings can be realized through optimizing the FCMP. It has been estimated that at least a reduction in compressor station fuel consumption can be obtained through global optimization of pipeline operation [2].
The FCMP is a difficult optimization problem because real pipeline systems have complex network topographies, integer variables are required to represent the pipeline binary operating states (bi-directional flow, ON/OFF compressor units), and gas and compressor physics are governed by highly nonlinear equations. The FCMP is most appropriately modeled as a nonlinear program (NLP) or mixed-integer nonlinear program (MINLP), depending on whether bi-directional flow or ON/OFF compressor units are considered [3]. Given the complexity of the FCMP model, current algorithms can only solve simplified versions for networks large enough to have practical importance. With this, there are numerous simplifications of model parameters that are broadly accepted across FCMP literature because of the computational savings they provide. However, upon inspection of the error such simplifications introduce to the model, the ability for the model to provide a useful representation of the real system is brought into question.
There has been virtually no previous work done on methods of approximating the nonlinear relationships inherent in the FCMP model that balances model accuracy and solution time. This paper introduces a systematic approach to approximating the nonlinear relationships of the parameters that are commonly simplified as constants. The approach is shown to introduce insignificant model error compared to a rigorous FCMP model formulation, and only marginally increases model solution time compared to a common simplified FCMP model. The approach can be summarized as identifying practically convex/concave relationships between model variables that can be approximated by simpler functions, such as piecewise-linear or quadratic functions. This allows the complex nonlinear equations required for rigorous calculation to be eliminated from the model. Here, a practically convex/concave function means a function that does not need be convex/concave according to the mathematical definition per se, but can be approximated well by a function that is mathematically convex/concave. The piecewise-linear approximations are not constructed manually by the modeler, but instead are generated by inputting the nonlinear relationship data into an mixed-integer linear programming (MILP) that optimally determines the piecewise-linear break-points and linear segment orientation so that approximation error is minimized. This MILP relies on the convexity/concavity of the relationship being approximated for its simple formulation. As stated above, the value of this systematic modeling approach is that a model is produced with insignificant error when compared with the most rigorous model. Further, the model is only marginally more difficult to solve by current global MINLP solvers when compared to the highly simplified model. The reason is that the produced model only differs from the simplified model in the additional piecewise-linear functions, which are easily handled by modern global MINLP solvers such as BARON [4,5] and SCIP [6].
Although we have applied this modeling approach to the FCMP, the techniques are transferable to many engineering problems that are difficult to optimize because of complex nonlinear relationships.
This introduction is followed by six main sections. Section 2 introduces the FCMP model that is most commonly used throughout gas transportation literature, and areas of the model that are simplified are discussed. Next, Section 3 presents the method of optimal piecewise-linear function generation for approximating practically convex/concave curves. Section 4 applies this technique to approximate the previously ignored nonlinear relationships. The novel FCMP model that incorporates the piecewise-linear approximations is then developed in Section 5. In Section 6, a case study is presented that compares the optimization results of the simplified, newly developed, and most rigorous FCMP optimization models to the results from a rigorous simulation. Section 7 reiterates the importance of these results and provides a discussion of future work.
2. Common Natural Gas Transportation Model
The model developed in this section is for application specifically to the FCMP, although many of the model components are used across all types of natural gas transportation models. A summary of the model parameters and variables introduced in the following sections can be seen in Table 1.

Table 1.
Parameters and variables describing gas transportation.
2.1. Network Topography
The gas transmission network is most commonly modeled as a directed graph with nodes N and arcs A [7,8,9,10]. The set of nodes is made up of entry nodes , exit nodes , and junctions , representing pipeline supply points, delivery points, and junctions,
Each node in the network is arbitrarily assigned a unique number from 1 to n, with n being the total number of nodes in the network. Nodes are denoted by .
The set of arcs is made up of passive arcs , and active arcs , representing pipeline sections that do not contain compressor stations, and sections that contain compressor stations,
Differing from nodes, arcs are not arbitrarily assigned numbers but are instead classified according to the nodes they connect. Arcs are denoted by , corresponding to a pipeline section running from node i to node j.
2.2. Gas Flow Model
The three non-isothermal Euler equations for compressible fluids govern gas dynamics in a pipeline [7], but in their complete form are too complex to be used in an optimization model that is solvable by modern NLP solvers. By making the common approximations of isothermality in pipeline segments and negligible slope in pipeline segments, the equations can be reduced to two manageable equations. These equations are the gas conservation equation (Equation (3)) and pipeline resistance equation (Equation (4)):
where is a model input that represents the mass flow rate of natural gas being supplied to node i (positive for a supply node, negative for a demand node), and and are the gas compressibility factor and friction factor for arc [7]. It is most common in natural gas transportation literature to assume both parameters to be constants [9,11,12,13,14,15]. In reality, these parameters have complex relationships with the pipeline operating conditions that cannot be ignored without introducing significant model error.
2.2.1. Compressibility Factor
The compressibility factor has a complex dependence on temperature, pressure, and gas composition, which is most accurately calculated implicitly through:
where are constants, and are functions of temperature and gas composition [16]. The complexity of Equation (5) is clear, and its avoidance by FCMP researchers is justifiable. Although it is most common to remove this source of complexity by assuming the compressibility factor is constant with both temperature and pressure, on occasion the empirical formulas of the American Gas Association (Equation (6)) or Papay (Equation (7)) are used [7].
Despite these formulas partially capturing the relationship between the compressibility factor and temperature–pressure, Figure 1 shows that over typical pipeline operating conditions they deviate significantly from the rigorous compressibility factor as calculated through Equation (5). The 0.1–10 MPa pressure range used for comparison encompasses the typical operating range of both natural gas distribution and transmission pipelines [3,17].
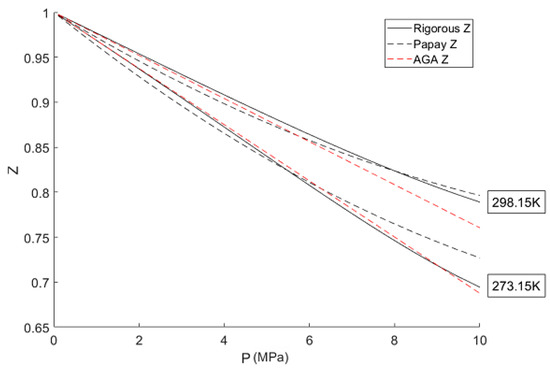
Figure 1.
Comparison of the rigorously calculated gas compressibility factor with the American Gas Association and Papay empirical models for natural gas with a composition of: 85% methane, 14% ethane, and 1% nitrogen.
2.2.2. Friction Factor
It is most common in FCMP literature to assume the friction factor to be a constant that depends only on the length, diameter, and roughness of the pipe. The Nikuradse equation is most commonly used to calculate a constant friction factor that has no dependance on the operating condition of the pipeline [18]:
However, it is widely accepted that in natural gas transmission pipelines the Colebrook–White friction factor (Equation (9)) is more accurate as it captures the dependance of the friction factor on the natural gas mass flow rate [7,18]. Despite this, it is often omitted in favor of the Nikuradse equation because of the complexity required to capture the dependence on mass flow rate through the Reynolds number in Equation (10) [7].
Figure 2 shows how the Nikurasde and Colebrook–White friction factors compare over the typical range of transmission pipeline mass flow rates. The range of typical transmission flow rates was determined from data publicly available on all U.S. interstate natural gas pipeline capacities through the U.S. Energy Information Administration [19].
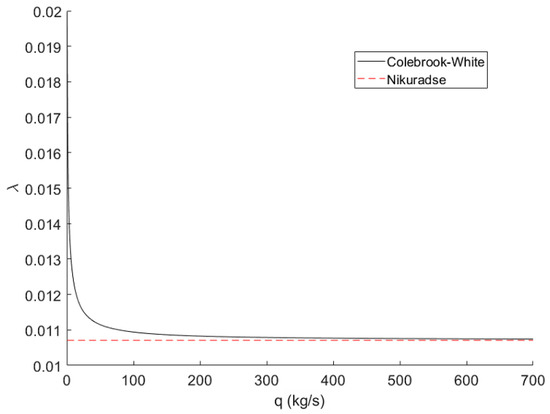
Figure 2.
Comparison of the Colebrook–White and Nikuradse friction factor on a pipeline with a diameter of m, and roughness of mm.
It can be seen in Figure 2 that for mass flow rates on the low range of those typically seen in transmission networks there is a substantial difference between the Nikurasde and Colebrook–White friction factors. The Colebrook–White friction factor approaches the Nikurasde friction factor from above, corresponding to the pressure drop calculated using the Colebrook–White friction factor always being greater than that of the Nikurasde friction factor. As a result, solutions to the FCMP that are deemed feasible when using the Nikurasde friction factor could be infeasible in practice from underestimating the pressure drop throughout the transmission network.
2.3. Compressor Equations
The compressor adiabatic head equation is standard across virtually all FCMP literature, as it is derived from thermodynamic first principles with reasonable assumptions and is not overly complex [20]:
2.3.1. Isentropic Exponent
The isentropic exponent () is the ratio of specific heat at constant pressure to specific heat at constant volume, and is needed to calculate the energy required for compressing a gas [20]. The rigorous calculation of the isentropic exponent is extremely computationally difficult, so in virtually all natural gas transportation literature it is assumed to be constant. At best, the following simplified relationship with temperature is used:
where T is defined to be the average of the compressor inlet and outlet temperatures [7].
Similar to the compressibility factor, the isentropic exponent has a complex dependence on temperature, pressure, and gas composition. The rigorous calculation of the isentropic exponent requires over 50 equations, most of which are nonlinear and several are implicitly defined [21]. Figure 3 shows that over typical natural gas pipeline operating conditions significant model error is introduced using the simplifiied Equation (12).
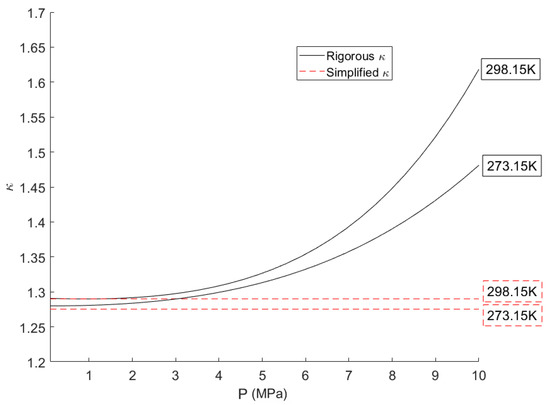
Figure 3.
Comparison of the rigorously calculated isentropic exponent with a common simplification for natural gas with a composition of: 85%methane, 14% ethane, and 1% nitrogen.
2.3.2. Compressor Operating Envelop
A restriction on the feasible operating region of the compressor station is necessary to reflect physical equipment limitations. FCMP models typically consider compressor stations made up of centrifugal compressors given their prevalence in natural gas transmission systems. The operating region of a centrifugal compressor is limited by the maximum allowable speed, minimum allowable speed, maximum allowable gas flow rate (surge limit), and minimum allowable gas flow rate (stonewall limit) [22]. The combination of the four limits gives a non-convex operating envelop such as that in Figure 4. The operating envelop in Figure 4 was simulated using the compressor parameters found in Wu et al. [23].
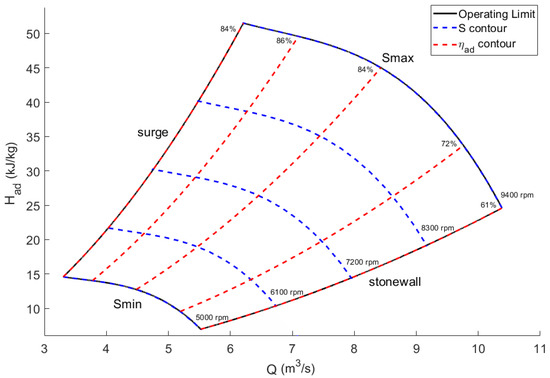
Figure 4.
Typical operating envelop of a centrifugal compressor unit, with compressor speed and efficiency contours shown.
There is some variation in how the compressor operating envelop is modeled across FCMP literature. The method that is widely accepted as the most rigorous can be seen in Equations (13)–(15), which capture the highly nonlinear relationship among compressor head, compressor speed, and volumetric gas flow rate [7,9,15,23]. The coefficients and are constants that are typically estimated by fitting Equation (13) to compressor data of the quantities and [23]. The complexity that is introduced to the FCMP model by using the rigorous compressor model has given rise to numerous simplified operating envelops. These simplifications involve replacing Equations (13)–(15) with simpler bounds that ignore compressor speed altogether. Some simplifications include reducing the operating window to just an upper limit on the compressor exit gas pressure [12], putting an upper and lower limit on compressor head or power [24,25], or approximating the operating window by a linearly bounded convex region [23].
2.3.3. Compressor Efficiency
A compressor efficiency parameter () is required to relate the ideal adiabatic quantity of energy required to achieve a given pressure change, and the actual quantity required by real compressors that are subject to deviations from ideal conditions [20]. The rigorous method of calculating compressor efficiency is through Equation (16), which requires the use of Equation (13) to calculate the compressor speed at a given compressor head and volumetric flow rate [7,23]. As with the coefficients in Equation (13), and are constants that are estimated by fitting Equation (16) to compressor data.
Given that many FCMP models use a simplification of the compressor operating envelop that ignores compressor speed, the method of calculating compressor efficiency often must be simplified as well. Such simplifications include capturing the compressor efficiency dynamics using a simpler polynomial function of compressor mass flow rate, inlet pressure, and outlet pressure [23], or assuming the compressor efficiency to be constant [8,25,26,27]. The compressor efficiency contour lines in Figure 4 show that there is a large variation in efficiency across the operating envelop which is lost by assuming a constant efficiency. Any error introduced through these simplifications contributes directly to error in the model’s objective function (see Problem (17)) because of the dependance of fuel cost on compressor efficiency.
2.4. Common FCMP Model
Combining the above formulas and simplification gives the complete FCMP model that is most common across FCMP literature:
where represents the compressor operating envelop as defined through one of the previously discussed methods. The compressibility factor (Z), friction factor (), isentropic exponent (), and compressor efficiency () are all assumed to be constant in this model.
3. Optimal Piecewise-Linear Function Generation
Linearization of nonlinear relationships is often an effective method for reducing the complexity of an optimization model to increase solution efficiency [28,29,30]. Many of the common linearization techniques manually determine the break-points of the linear segments and the orientation of the linear segments follow, or they manually determine the orientation of the linear segments and the position of the break-points follow. The drawback of these methods is that they offer no guarantee of producing an optimal approximation. When the nonlinear relationships are complex, and especially when they are more than two-dimensional, the manual linearization approach is likely to produce significantly suboptimal approximations.
The linearization technique suggested here is Piecewise-Linear Function Generation (PLFG) that offers the guarantee that for a given number of line segments the approximation is optimal, and can be applied to data for which no analytical function exists. The technique simultaneously determines the break-points and positioning of the linear segments such that they fit the curve with the minimal error. The approximation produced from this method is a convex/concave piecewise-linear function, so must be applied to data that can be approximated closely by a convex/concave curve. This does not restrict the technique to relationships that are mathematically convex/concave.
The technique is a mixed-integer linear program (MILP) that requires data points of the relationship being approximated, and the number of linear segments to approximate the relationship with, as model inputs. The problem is to determine , which defines a set of continuous piecewise-linear functions, for a finite set of n-dimensional data points [31], that solves:
A solution to this problem produces the piecewise-linear function that has the minimum maximum relative difference between the generated function and the data points being approximated.
In MILP PLFG, it is customary to introduce a binary variable for each linear segment , and each data point . The binary variable is used to represent if the linear segment is “active” at the data point , where active means the line segment is used for approximation at that part of the domain. The following MILP model is used for PLFG of convex curves:
where and are the coefficients being determined for the k n-dimensional linear segments, and is some large constant. This model is a variation of the well-known model seen in Toriello and Vielma [31].
Figure 5 helps to demonstrate the importance of each constraint in Problem (19). The constraint ensures that the approximation of point i is somewhere in the shaded gray region of Figure 5a, that is, above or equal to all of the line segments. Without any additional constraints, any number of line segments could yield an objective function equal to zero by having the line segments below all of the data points, allowing every approximation point to equal every data point exactly. The constraint has no effect unless the binary variable is equal to one, in which case the approximation point must be below or equal to the line k at point . Combining these two constants with yields the approximation shown in Figure 5b, as it ensures the approximation point is equal to the greatest line segment at point . An optimal solution that is subject to all of these constraints is one that minimizes the maximum relative error between the points along the line segments and the data points.
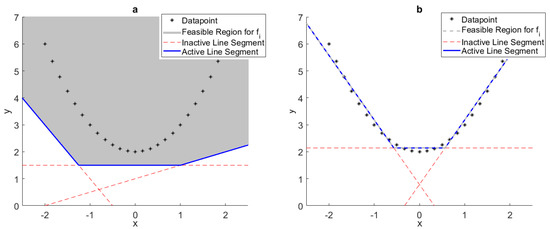
Figure 5.
(a) Example of potential approximation produced when only the constraint is used in the PLFG MILP; (b) Example of potential approximation produced when all of the constraints are used in the PLFG MILP (PLFG: Piecewise-Linear Function Generation; MILP: mixed-integer linear program).
The MILP in Equation (19) can be easily adapted for fitting concave curves:
These versions of the MILP produce a piecewise-linear approximation that has the freedom to cross-over the curve being approximated, as shown in Figure 6a. However, in certain applications, it may be desirable to produce an approximation that is entirely above the curve being approximated (Figure 6b), and in other applications for the approximation to be entirely below the curve being approximated (Figure 6c). The MILP can be modified to generate such approximations by adding the constraint in Equation (21) for the approximation always above, and Equation (22) for the approximation always below.
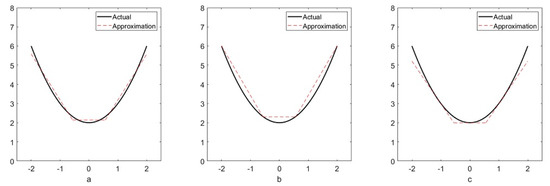
Figure 6.
(a) Example of approximation produced when curve cross-over is allowed; (b) Example of approximation when restricted to entirely above the curve; (c) Example of approximation when restricted to entirely below the curve.
The number of data points and linear segments are user inputs to the PLFG MILP, so it is necessary to be deliberate about how these inputs are decided by the modeler. A higher number of data points and linear segments will always yield a more accurate approximation. However, the tractability of the PLFG MILP is worsened as these inputs increase because of the additional constraints and variables in the model. Additionally, the more linear segments used for approximating the relationship the worse the tractability of the optimization model where the approximation is being implemented. A procedure is required for determining the number of data points and linear segments that gives a desirable balance between model tractability and approximation accuracy.
The suggested procedure is as follows:
- Decide what is an acceptable amount of maximum relative error between the piecewise-linear function being generated and the relationship being approximated, this is the stopping criteria . Typically, 1% is appropriate.
- Start with and , where M is some relatively small number of data points equally dispersed over the approximation domain. Solve the MILP for the piecewise-linear function, .
- Calculate the maximum error between and the entire dataset of the relationship being approximated, .
- Increase m to , and solve the MILP for .
- Calculate .
- Iterate Steps 4 and 5 until the change in is less than 1% for two consecutive iterations, then move to Step 7. If the MILP becomes intractable before this, move to Step 7.
- If the smallest is less than , or has changed less than 1% for two consecutive increases in p, terminate, the corresponding is either an acceptable approximation or as good as the PLFG method is likely to yield. Else, increase p to , reinitialize , and return to Step 4. If the MILP becomes intractable before meeting the stopping criteria, terminate and consider breaking up the domain of approximation.
This procedure can be summarized as an inner loop that increases the number of data points used for PLFG until the maximum approximating error plateaus, and an outer loop that increases the number of line-segments in the piecewise function until the approximation error is smaller than an acceptable tolerance or plateaus.
4. Relationship Approximation
Section 2 shows how key parameters in the FCMP model are commonly simplified to reduce model complexity. In this section, we develop accurate approximations for these commonly ignored nonlinear relationships. The approximations are developed based on the PLFG method introduced in Section 3. The relationships approximated are the compressibility factor, friction factor, isentropic exponent, compressor operating envelop, and compressor efficiency. Two approaches are used to apply the PLFG method to approximate nonlinear parameter relationships. The first method is to approximate the relationship between the parameter and the pipeline operating condition directly. This method is valid whenever the relationship between the parameter and pipeline operating condition is practically convex/concave, as the PLFG MILP can only produce accurate approximation for such relationships. When the rigorous relationship between the parameter and pipeline operating condition does not fit this criteria, there is still the possibility that the PLFG method can be used to approximate the relationship, but a different approach is needed. The alternative approach is to identify a relationship that is practically convex/concave between a particular lumped term of variables and the pipeline operating condition, of which the parameter is one of the variables in the lumped term, and it is the only instance where the parameter is required in the formulation. The lumped term is then approximated by the piecewise-linear approximation, and the term along with the parameter is removed from the formulation entirely. This approach can help reduce the complexity of the formulation by both eliminating the complexity of the lumped term and capturing the rigorous parameter relationship by the piecewise-linear function. The additional complexity that this approach has the potential to remove makes it desirable to be applied even in cases where it is not strictly needed. However, such a lumped term is not always possible to identify so this method is not always valid. The first method is only applied to the compressibility factor, all other parameters are approximated using the alternative method.
4.1. Compressibility Factor
Figure 7a shows the three-dimensional relationship between the compressibility factor and temperature–pressure calculated using Equation (5). It can be seen that the relationship exhibits regions of convexity and concavity, and therefore the PLFG method would not be able to produce a good approximation. However, Figure 7b shows that two-dimensional compressibility factor isotherms are all practically convex and so are well suited to be approximated by the PLFG method. Further, because the isothermal assumption is accepted as necessary across virtually all natural gas transportation literature, the two-dimensional isothermal contours can be used as the basis of approximation without introducing additional model error. The suggested method is then to discritize the compressibility factor along the temperature domain and to approximate the compressibility factor relationship as a function of only pressure. Practitioners implementing the model can then simply choose the isothermal approximation that is closest to their pipeline operating temperature. The 12 isotherms in Figure 7b were chosen so that there is no more than a error range between each contour. By choosing the isotherm closest to a given operating temperature at most 1% error plus any approximation error is introduced to the model, compared to the rigorous calculation.
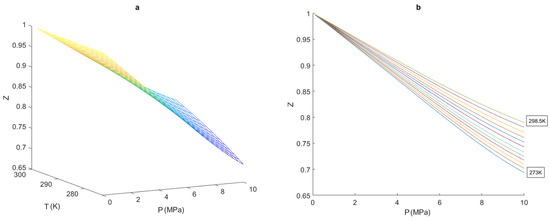
Figure 7.
(a) Three-dimensional compressibility factor relationship with temperature–pressure; and (b) two-dimensional compressibility factor isothermal relationship with pressure for natural gas with a composition of: 85% methane, 14% ethane, and 1% nitrogen.
Figure 8 shows the approximation output from the PLFG method for the 289.5 K compressibility factor isotherm, where approximation cross-over is allowed. The procedure discussed in Section 3 produced an optimal piecewise-linear function comprised of two line segments. The maximum approximation error from the generated approximation is 0.06%.
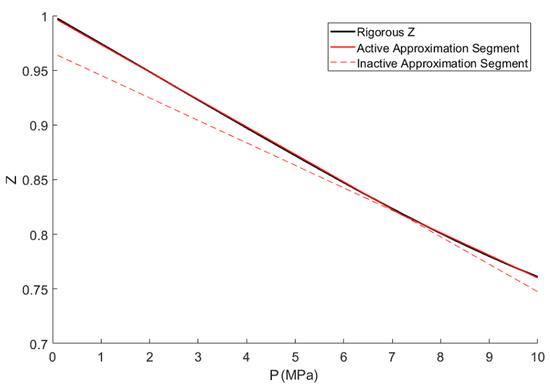
Figure 8.
Piecewise-linear function generated for approximating 289.5 K compressibility factor isotherm, consisting of two line segments.
4.2. Friction Factor
The friction factor appears only once in the FCMP model through the pipeline resistance equation (Equation (4)). Although the relationship between the Colebrook–White friction factor and mass flow rate in Figure 2 could be approximated directly, an approximation that removes further model complexity can be made. The friction factor is multiplied by the squared mass flow rate in the pipeline resistance equation. By lumping these terms together, a single function of mass flow rate can be produced:
The plot of in Figure 9a, where the friction factor is calculated using the Colebrook–White equation (Equation (9)), shows that it has a quadratic relationship with mass flow rate. This relationship is approximated well by performing a nonlinear regression that fits a quadratic function to the curve. No y-intercept coefficient is used in the regression function because at zero mass flow rate anything other than zero for is not physically realistic. The resulting quadratic regression function can be seen to approximate closely in Figure 9a. Figure 9b compares the error of the quadratic regression function with a that uses the constant Nikurasde friction factor. The quadratic regression function contains less error over the entire range of typical natural gas transmission mass flow rates. It is important to note that the regression is specific to pipeline diameter and absolute roughness.
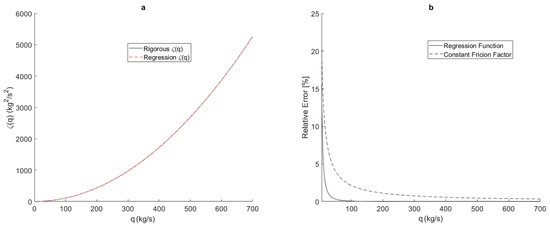
Figure 9.
(a) Relationship between and mass flow rate, and quadratic regression approximation; (b) Comparison of error for from the quadratic regression and constant friction factor. All for a pipeline with a diameter of 0.9144 m and absolute roughness of 0.05 mm.
4.3. Isentropic Exponent
The isentropic exponent only appears in the compressor head equation (Equation (11)) in the FCMP model. Additionally, by making the substitution the isentropic exponent is removed from the formulation entirely:
By approximating the relationship of m with temperature and pressure, the complexity of the compressor head equation is reduced. More importantly, if the relationship between the isentropic exponent and temperature–pressure were to be used then any approximation error would be magnified in the formulation through the ratio . By approximating the ratio directly, the magnification of error is avoided.
Figure 10a shows that the rigorously calculated three-dimensional relationship between m and temperature–pressure is practically convex, and so the PLFG method can produce a good approximation. A valid approach would be to discritize m in the temperature domain like the compressibility factor, but because the three-dimensional relationship is practically convex it is unnecessary. Figure 10b shows the approximation produced using the procedure described in Section 3, where approximation cross-over is allowed. The optimal piecewise-linear function generated consists of four planes, and has a maximum error from the rigorous relationship of 0.92%.
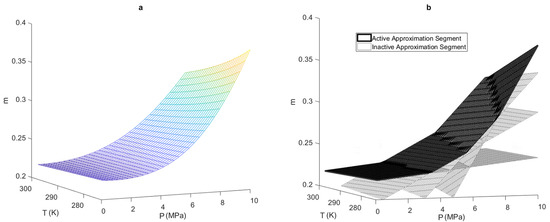
Figure 10.
(a) Rigorous three-dimensional relationship between m and temperature–pressure; and (b) piecewise- linear approximation of m using four planes for natural gas with a composition of: 85% methane, 14% ethane, and 1% nitrogen.
4.4. Compressor Model
4.4.1. Compressor Operating Envelop
Equations (13)–(15) combine to form the compressor operating envelop, which introduce considerable complexity to the FCMP model. It is possible to remove these equations from the formulation by using four piecewise-linear approximations that are functions of volumetric flow rate. This corresponds to one approximation for each of the four curves that bound the operating envelop. By removing these equation from the formulation, the relationship of compressor speed with compressor head and volumetric flow rate is removed, which is important for calculating the compressor efficiency through Equation (16). This issue will be dealt with in the next section.
Figure 4 shows that the surge and stonewall bounds are convex curves, whereas the Smin and Smax bounds are concave curves. Given that the operating envelop bounds the feasible operation of a compressor unit, it is desirable to produce an inner approximation of the envelop so that approximation error does not allow regions of operation to be feasible in the FCMP model that are not feasible in reality. To achieve this, Equation (21) or (22) is used in the PLFG MILP so that approximation cross-over is not allowed. The surge and Smax bounds are approximated by piecewise-linear functions that must be below the actual bounds, and the stonewall and Smin bounds are approximated by piecewise-linear functions that must be above the actual bounds.
Figure 11 shows the inner approximation of the compressor envelop after applying the procedure discussed in Section 3 to each of the four operating bounds, where a stopping criteria of 1% maximum error was used for each bound. The resulting piecewise-linear approximations has three line segments for the surge and stonewall bounds, and four line segments for the Smin and Smax bounds.
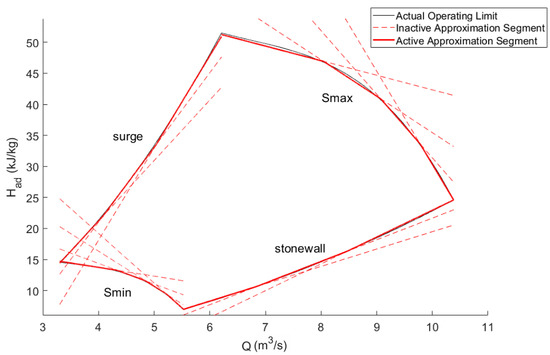
Figure 11.
Approximation of the compressor operating envelop shown in Figure 4.
4.4.2. Compressor Efficiency
By removing Equations (13)–(15) from the FCMP model, the compressor speed is meaningless in the compressor efficiency equation (Equation (16)). This is fine because it is desirable to remove Equation (16) from the formulation because of its complexity. Equations (11) and (16) determine that the compressor efficiency is specified for any combination of compressor head and volumetric flow rate, which can be seen in Figure 12. Although the compressor speed is necessary for defining this relationship through an analytical expression, the relationship in Figure 12 can be approximated using a piecewise-linear function of compressor head and volumetric flow rate. This allows compressor speed to be removed from the formulation entirely, as the analytical expression is no longer necessary.
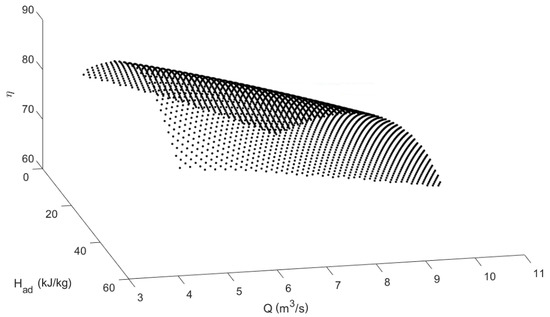
Figure 12.
Rigorous relationship of compressor efficiency with compressor head and volumetric flow rate.
While the relationship in Figure 12 is well suited to be approximated using the PLFG method given its concavity, an approximation that removes further model complexity can be made. Aside from in the equation used to calculate compressor efficiency, the compressor efficiency only appears in the FCMP model through the objective function (see Problem (17)). Therefore the compressor efficiency can be removed from the formulation with no effect if its influence on the objective function is still captured. The term appears in the FCMP model objective function, and the relationship of this term with compressor head and volumetric flow rate can be seen in Figure 13a. The relationship is a simple convex curve that can be approximated well by the PLFG method, and by doing so removes compressor efficiency from the formulation entirely. Using the procedure discussed in Section 3, the approximation shown in Figure 13 is generated, which consists of four planes and has a maximum approximation error of 1.12%.
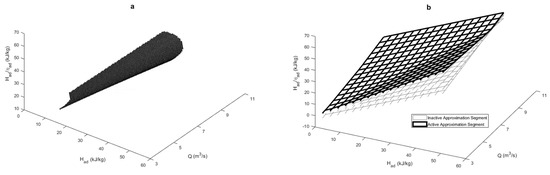
Figure 13.
(a) Rigorous relationship of with compressor head and volumetric flow rate. (b) Approximation of rigorous relationship of with a maximum relative error of 1.12%.
5. FCMP Model with Novel Relationship Approximations
There are two distinct methods for implementing the piecewise-linear function approximations developed in Section 4 into the FCMP model. The first method is to simply allow the parameter or term being approximated to be the convex region bounded by the piecewise-linear function. Equation (25) is the expression used by this method for convex piecewise-linear approximations, and Equation (26) is the expression used for concave piecewise-linear approximations.
Equation (25) restricts the parameter or term to be above the maximum of the set of convex line segments, and it corresponds to the epigraph of , as illustrated in Figure 14a. Equation (26) restricts the parameter or term to be below the minimum of the set of concave line segments, and is the hypograph of , as illustrated in Figure 14b. The benefit of this method is that the piecewise-linear function can be implemented without using integer variables. This method is valid only when replacing the function curve with its epigraph or hypograph does not change the optimal solution. For example, if the function in Figure 14a is the objective function to be minimized, then minimizing its upper bound is same to minimizing itself, and therefore Equation (25) is sufficient for implementing the piecewise-linear approximation.
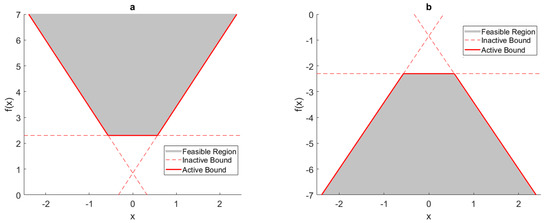
Figure 14.
(a) Convex feasible region produced by bounding a parameter to be greater than a set of convex line segments. (b) Concave feasible region produced by bounding a parameter to be less than a set of concave line segments.
When it is not valid to represent the function curve by its epigraph or hypograph, the use of integer variables is necessary to select which linear segment is active for a given section of the approximation domain. The method for implementing this form of piecewise-linear function follows directly from the PLFG MILP:
Table 2 describes the parameters and variables used to implement the approximations into the novel FCMP model.

Table 2.
Parameters and variables for implementing the approximations into the Fuel Cost Minimization Problem (FCMP) model.
5.1. Compressibility Factor
The two-dimensional piecewise-linear approximation for the compressibility factor must be implemented in the FCMP model using integer variables. This is because the compressibility factor must be equal to a specific value for each temperature–pressure combination. The following constraints are used in the FCMP model to implement the compressibility factor approximation:
where is the average pressure between nodes i and j.
5.2. Friction Factor
The friction factor is approximated through the fitting of a quadratic equation to the lumped friction factor-squared mass flow term in the pipeline resistance equation. Thus, a straightforward substitution of this term for the regressed quadratic function with no y-intercept term is made in the pipeline resistance equation:
5.3. Isentropic Exponent
The three-dimensional piecewise-linear approximation for the function of the isentropic exponent must be implemented using the integer based method. Similar to the compressibility factor, m must be equal to a specific value for each temperature–pressure combination and so cannot be defined by a convex region. The following constraints are used in the FCMP model to implement the isentropic exponent approximation:
5.4. Compressor Operating Envelop
The two-dimensional piecewise-linear approximations of the compressor operating envelop bounds are implemented using both the convex region method and integer-based method. The stonewall and Smax bounds are able to be approximated using the convex region method, as the stonewall limit is a convex curve that bounds the envelop from below, and the Smax limit is a concave curve that bounds the envelop from above. The surge and Smin limits do not bound a convex region, and thereby need to be implemented using integer variables. Accordingly, only seven binary variables are added to the FCMP model for the 14 lines that approximate the operating envelop. The complete operating envelop approximation is implemented in the FCMP model through the following constraints:
5.5. Compressor Efficiency
The compressor efficiency parameter is eliminated from the FCMP formulation by approximating the term , which appears in the objective function. For any combination of compressor head and volumetric flow rate, a specific must be calculated for the approximation to be accurate. Implementing the piecewise-linear approximation of would require an integer method if it were not for the approximation being a convex set of planes, and appearing in the objective function that is being minimized. That is to say, the convex region method for implementing the approximation can be used because the minimum of a convex region is equivalent to the boundary of the convex region. The approximation of is implemented into the FCMP as follows:
The full FCMP model that includes all of the novel approximations can be found in Appendix A.
6. Case Study
Three simple gas networks are used in the case study to investigate the performance of the novel FCMP model. The first two networks investigated are identical to the networks studied in Wu et al. [23]. The Example 3 network is an extension of Example 2 intended to increase complexity. In each network, the compressor stations are comprised of five centrifugal compressor units operated in parallel that can each be switched ON or OFF, and the fitted coefficients of Equations (13) and (16) are the same as in Wu et al. The integer variable represents the number of compressor units ON in station . For each network, the operating temperature is 288.7 K, however the 289.5 K compressibility factor contour (Figure 8) was used for the piecewise-linear approximation to investigate the error introduced by discritizing the temperature domain into sufficiently small intervals.
The three case study gas networks are made up of at most 17 arcs and so are much simpler versions of typical gas networks encountered in practice. In practice, it is common to encounter networks that contain hundreds of arcs, such as those provided in the publicly available gas network test instances library GasLib, which are comparable to real-world networks of Open Grid Europe GmbH [32]. It is important to be able to solve the FCMP on these networks within minutes as the FCMP is an operational problem that needs to be solved in real-time to respond to changing network conditions. When the FCMP is being solved for long-term planning purposes it is often solved numerous times for a large batch of scenarios so solution times within minutes are still needed to be useful for practitioners.
The optimization software used for the case study was GAMS version 25.1.1 [33], and the MINLP solver used was SCIP version 5.0 [6]. GAMS was ran on the Ubuntu 16.04 operating system, with a CPU frequency of 3592 MHz and 4 GB of RAM. The simulation software used to investigate the optimization results was Matlab version 2018a [34].
6.1. FCMP Models
Three different FCMP models were applied to each of the simple case study gas networks to investigate how the novel FCMP model balances accuracy and solution time. Figure 15 describes the components of the FCMP model with common simplifications (), the novel FCMP model which includes the approximations developed here (), and a partially rigorous FCMP model (). The model found in Appendix B includes all of the common simplifications and so is included to benchmark the lowest reasonable solution time for an FCMP model. Given that the model’s components are commonly found throughout FCMP literature, it is also useful for making comparisons to what is currently accepted as a standard FCMP model. The model found in Appendix C is included to benchmark model accuracy, as it is made up of the most rigorous calculations for its components, except for the compressibility factor and isentropic exponent. The model uses the novel approximations for the compressibility factor and isentropic exponent as their rigorous calculations cannot be feasibly implemented in an optimization model, and the novel approximations are the most accurate alternative.
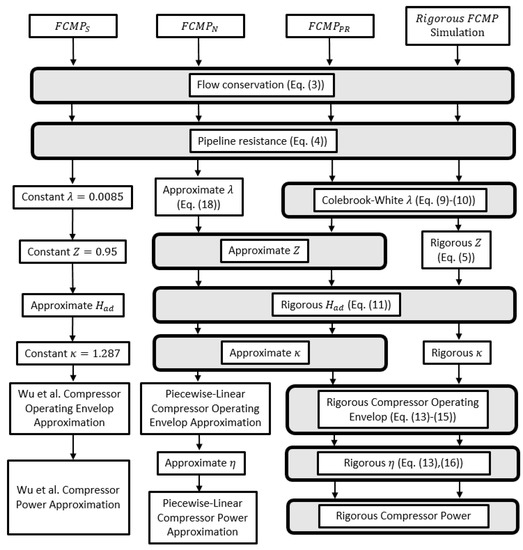
Figure 15.
Flow chart detailing the components of each FCMP model applied in the case study, and the rigorous simulation model.
The optimal solutions from the three optimization models are applied on a rigorous simulation model that is composed of the most rigorous modeling components known. The rigorous simulation is ran to assess the accuracy and feasibility of a given optimal solution as follows:
- The pressure of the first node is set as the first node pressure from the optimal solution.
- If the next arc is a pipe section, then the pressure of the next node is calculated using the pipeline resistance equation, where Z and are calculated using their rigorous relations. Else, move to Step 3.
- The next arc is a compressor station, so the outlet pressure is set as the outlet pressure from the optimal solution. The simulated compressor fuel cost is then calculated using the rigorous calculations for Z, , , and so that a theoretically exact fuel cost is obtained.
- Return to Step 2 and iterate until all node pressures and compressor station fuel costs are calculated.
The optimal solutions obtained from the three FCMP optimization models are all feasible with respect to their individual simplifications and constraints, but when applied on a rigorous simulation that calculates the pressure drop and compressor physics rigorously certain constraints may be violated. It is important to note that the simulation will complete its calculation of node pressures and compressor station fuel costs even if constraints are violated. In the case of the simulation finding physical constraint violations, the optimal solution is noted as infeasible, but the simulated fuel cost is still computed so that the error in the optimal solution can be quantified.
6.2. Example 1
The Example 1 gas network in Figure 16 is a simple gun-and-barrel network with two compressor stations. The optimization and simulation results in Table 3 show that the and models are highly accurate, with their optimal fuel cost differing by less than 1% compared to the fuel cost obtained from the simulation. The model had the quickest solution time, but the optimal solution differed by 11.41% compared to the fuel cost obtained from the simulation. Further, the optimal solution obtained from the model was proven to be infeasible by the rigorous simulation, whereas both the and models produced optimal solutions that were feasible in the simulation. The reason for the infeasibility obtained in the simulation is that the model underestimated the pressure drop in pipe sections due to error introduced in both Z and . This resulted in the simulation pressure at the end of the pipeline being below the lower pressure limit, and the simulation compressor stations operating outside the operating envelop due to the larger pressure increase required. The 0.09% difference between the simulated fuel costs of the and models demonstrates that the compressor model and friction factor approximations developed introduce an insignificant amount of model error compared to their rigorous calculations.

Figure 16.
Example 1 gas network consisting of three pipes and two compressor stations. 4.14 MPa, and 5.52 MPa for all . 0.9144 m and 80.47 km for all .

Table 3.
Example 1 case study results. Both compressor stations only have one unit active in all three model solutions. Lines in bold represent outlet pressures from compressor stations.
For this gas network, the model produced an optimal fuel cost that deviates from its solution’s simulated fuel cost less than the optimal fuel cost produced by the model deviates from its solution’s simulated fuel cost. This gives the false impression that the model is more accurate than the model, and, given that the model contains fewer approximations than the model, this is an unexpected result. The reason for this unexpected result is that in this particular case the error introduced by approximating some parameters in the model cancels out with the error introduced by approximating some other parameters. Both and models contain approximation error that produces an overestimation of pressure drop compared to the simulated pressure drop, so this results in an overestimation of the compressor fuel cost compared to the simulated fuel cost. However, the model contains approximation error in the objective function while the model does not, and, depending on where the optimal solution of the places the operation of the compressor stations, the objective function approximation error can result in an underestimation of the compressor fuel costs. For the model, the overestimation of compressor fuel cost through overestimating pressure drop, and the underestimation of compressor fuel costs introduced by approximating the objective function can result in a cancellation of model error that results in the optimal fuel cost being closer to the simulated fuel cost compared to that of the model. It is important to note that the model will not always benefit from the cancellation of model errors. There will be cases where the optimal solution is on a part of the compressor operating domain where the objective function approximation error results in fuel cost being overestimated, and therefore the pressure drop error is compounded with the objective function error.
6.3. Example 2
The Example 2 gas network shown in Figure 17 is a tree network with three compressor stations. Table 4 shows that the optimal solutions obtained from the and models are both highly accurate, differing from their simulated fuel costs by 1.02% and 0.78%, respectively. Both optimal solutions produced by these models were found to be feasible in the rigorous simulation. The model was found to be infeasible in the simulation due to the compressor stations on arcs and operating outside the feasible operating envelop. Further, the optimal fuel cost of the model was found to be different than the fuel cost obtained from the simulation. As in Example 1, this difference can largely be attributed to underestimating the pressure drop in pipeline segments. The solution times of the and models are comparable, both being under 2 s. The solution time is much higher, at 54.26 s. Given that the simulated fuel cost is only 0.28% lower than that of the model, the drastically higher solution time of the model shows the value of the model.
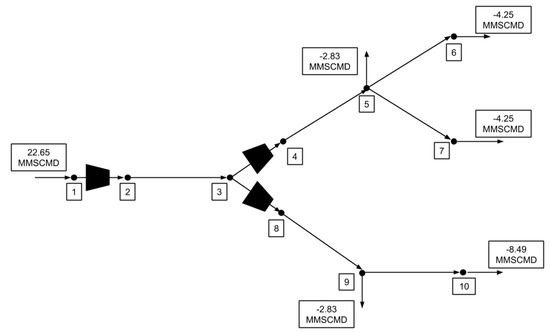
Figure 17.
Example 2 gas network consisting of six pipes and three compressor stations. 4.14 MPa, 3.10 MPa, 3.45 MPa, 3.79 MPa, 2.76 MPa. 4.83 MPa, 5.52 MPa for all . 0.9144 m and 80.47 km for all .

Table 4.
Example 2 case study results. All three compressor stations only have one unit active in all three model solutions. Lines in bold represent outlet pressures from compressor stations.
6.4. Example 3
The Example 3 network shown in Figure 18 is an extension of the Example 2 network, with two additional compressor stations and six additional pipes. Table 5 shows that the accuracy of the and models was unaffected by the additional complexity of the Example 3 network, with the error between the optimal and simulated fuel costs being less than 1% for both models. The accuracy of the model did suffer from the extension of the network, with the fuel cost error increasing to 47.50% compared to the simulation. Again, the simulation showed that the model solution is infeasible and the and model solutions are feasible. The solution time of the model increased drastically, going from 54.26 s in Example 2 to 994.98 s in Example 3. The model solution time also increased, but only to 8.21 s from 1.88 s in Example 2. The increased solution efficiency of the model over the model does not come at a loss of model accuracy, with the simulated fuel costs differing by only 0.41% between the models. As in Example 1, the optimal solution is observed to have slightly less model error than the model. The explanation for this unexpected result is the same as was given for Example 1.
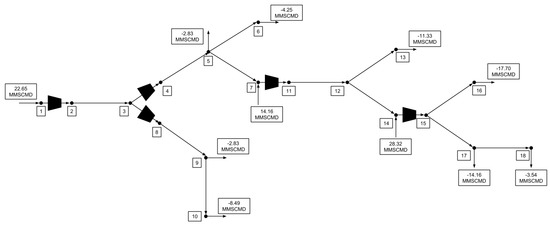
Figure 18.
Example 3 gas network consisting of 12 pipes and five compressor stations. 4.14 MPa, 3.10 MPa, 3.45 MPa, 3.79 MPa, 2.76 MPa, 0.69 MPa. 4.83 MPa, 5.52 MPa for all . 0.9144 m and 80.47 km for all .

Table 5.
Example 3 case study results. Lines in bold represent outlet pressures from compressor stations.
A final note on the three examples is that the the solution time for the model grows much more quickly than that for the model. It can be seen that, between each of the case study examples, the problem size is roughly doubled while the solution time for is increased an order of magnitude. Following the observed exponential time complexity, one could imagine that, for a real industrial gas network (10–100 times larger than Example 3), the solution time for would be several hours to days which is too slow for real-time operation or even off-line analysis. On the other hand, the solution time for the model is much less for each example and it does not increase with problem size dramatically. The computational advantage of the proposed MILP modeling approach makes it more appealing for real-world problems.
7. Conclusions and Future Work
The common way of modeling the FCMP has been to assume key modeling parameters as constant to avoid the complexity involved with their rigorous calculation. We have shown that, even for three simple gas networks, the model error that is introduced by making these simplifications are significant and often cause the optimal solution obtained from these models to be infeasible in reality. A method for approximating the complex relationships that have typically been avoided has been demonstrated. The method is to apply an optimal piecewise-linear function generating MILP to the rigorously simulated data points of the relationship being approximated. An optimal solution to the MILP determines the orientation and break-points of a specified number of linear segments so that the maximum relative error between the approximation and the actual data points is minimized. For the MILP to be applicable, the relationship being approximated must be practically convex or concave, meaning that it is a relationship that can be approximated by a convex or concave function without significant error.
The piecewise-linear approximations developed have been implemented in a novel FCMP model and applied to three simple gas networks. The novel FCMP model was shown to marginally increase the solution time compared to the common simplified model, but significantly reduce model error. When compared to a theoretically exact simulation, the optimal solutions produced by the novel FCMP model had a maximum error of 1.02%. A comparison was also made to a rigorous FCMP model and the novel FCMP model was found to have a much great solution efficiency, and a similar model accuracy.
The proposed piecewise linearization approach is believed to be more advantageous than classical piecewise linearization approaches in that it determines the break-points in an optimal way. Since there has been no other work that linearizes the nonlinear relationships considered in this paper, it will be an interesting future work to apply the classical piecewise linearization approaches to FCMP and compare their performance to that of the proposed piecewise linearization approach. Given that the proposed method cannot be applied to clearly non-convex functions, future work will also seek to formulate a piecewise-linear function generating MILP that can be applied to non-convex relationships. This MILP will also aim to have the property of determining the optimal orientation and break-points of linear segments so that approximation error is minimized. This will allow the piecewise-linear method of linearization to be applied to any type of relationship and to benefit a wide variety of NLPs and MINLPs which are difficult to solve.
Author Contributions
Data curation, K.K.; Formal analysis, K.K.; Funding acquisition, X.L.; Investigation, K.K.; Methodology, K.K. and X.L.; Project administration, X.L.; Resources, X.L.; Software, K.K.; Supervision, X.L.; Validation, X.L.; Visualization, K.K.; Writing—original draft, K.K.; and Writing—review and editing, X.L.
Funding
This research was funded by Natural Sciences and Engineering Research Council of Canada through the the Discovery Grant (RGPIN 418411-13) and the Collaborative Research and Development Grant (CRDPJ 485798-15).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FCMP | Fuel Cost Minimization Problem |
| NLP | Nonlinear Program |
| MINLP | Mixed-Integer Nonlinear Program |
| PLFG | Piecewise-Linear Function Generation |
| MILP | Mixed-Integer Linear Program |
Appendix A. Novel FCMP Model (FCMPN)
Appendix B. Simplified FCMP Model (FCMPS)
Appendix C. Rigorous FCMP Model (FCMPR)
References
- IEA. World Energy Outlook 2016; International Energy Agency: Paris, France, 2016; p. 684. [Google Scholar]
- Schroeder, D. Hydraulic analysis in the natural gas industry. In Advances in Industrial Engineering Applications and Practice I; International Journal of Industrial Engineering: Houston, TX, USA, 1996; pp. 960–965. [Google Scholar]
- Ríos-Mercado, R.Z.; Borraz-Sánchez, C. Optimization problems in natural gas transportation systems: A state-of-the-art review. Appl. Energy 2015, 147, 536–555. [Google Scholar] [CrossRef]
- Tawarmalani, M.; Sahinidis, N.V. A polyhedral branch-and-cut approach to global optimization. Math. Program. 2005, 103, 225–249. [Google Scholar] [CrossRef]
- Sahinidis, N.V. BARON 17.8.9: Global Optimization of Mixed-Integer Nonlinear Programs, User’s Manual; BARON Software: Pittsburgh, PA, USA, 2017. [Google Scholar]
- Gleixner, A.; Eifler, L.; Gally, T.; Gamrath, G.; Gemander, P.; Gottwald, R.L.; Hendel, G.; Hojny, C.; Koch, T.; Miltenberger, M.; et al. The SCIP Optimization Suite 5.0; ZIB-Report 17-61; Zuse Institute: Berlin, Germany, 2017. [Google Scholar]
- Schmidt, M.; Steinbach, M.C.; Willert, B.M. High detail stationary optimization models for gas networks. Optim. Eng. 2015, 16, 131–164. [Google Scholar] [CrossRef]
- Misra, S.; Fisher, M.W.; Backhaus, S.; Bent, R.; Chertkov, M. Optimal Compression in Natural Gas Networks: A Geometric Programming Approach. IEEE Trans. Control Netw. Syst. 2015, 2, 47–56. [Google Scholar] [CrossRef]
- Borraz-Sánchez, C.; Haugland, D. Minimizing fuel cost in gas transmission networks by dynamic programming and adaptive discretization. Comput. Ind. Eng. 2011, 61, 364–372. [Google Scholar] [CrossRef]
- Martin, A.; Moller, M.; Moritz, S. Mixed Integer Models for the Stationary Case of Gas Network Optimization. Math. Program. 2006, 105, 563–582. [Google Scholar] [CrossRef]
- Wong, P.; Larson, R. Optimization of Natural-Gas Pipeline Systems Via Dynamic Programming. IEEE Trans. Autom. Control 1968, 13, 475–481. [Google Scholar] [CrossRef]
- Wolf, D.D.; Smeers, Y. The Gas Transmission Problem Solved by an Extension of the Simplex Algorithm. Manag. Sci. 2000, 46, 1454–1465. [Google Scholar] [CrossRef]
- Borraz-Sanchez, C.; Rios-Mercado, R.Z. Improving the Operation of Pipeline Systems on Cyclic Structures by Tabu Search. Comput. Chem. Eng. 2009, 33, 58–64. [Google Scholar] [CrossRef]
- Flores-Villarreal, H.; Rios-Mercado, R. Computational Experience With a GRG Method for Minimizing Fuel Consumption on Cyclic Natural Gas Networks. In Computational Methods in Circuits System Applications; World Scientific and Engineering Academy and Society Press: Cambridge, UK, 2003; pp. 90–94. [Google Scholar]
- Chebouha, A.; Yalaoui, F.; Smati, A.; Younsi, K.; Tairi, A. Optimization of Natural Gas Pipeline Transportation Using Ant Colony Optimization. Comput. Oper. Res. 2009, 36, 1916–1923. [Google Scholar] [CrossRef]
- ISO-12213-2. Natural Gas—Calculation of Compression Factor—Part 2: Calculation Using Molar-Composition Analysis; Technical Report; International Organization for Standardization: Geneva, Switzerland, 2006. [Google Scholar]
- Westhoff, M.A. Using Operating Data at Natural Gas Pipelines; Technical Report; Colorado Interstate Gas Company: Houston, TX, USA, 2004. [Google Scholar]
- Coelho, P.; Pinho, C. Considerations About Equations for Steady State Flow in Natural Gas Pipelines. J. Braz. Soc. Mech. Sci. Eng. 2007, 29, 262–273. [Google Scholar] [CrossRef]
- About U.S. Natural Gas Pipelines—Transporting Natural Gas. Available online: https://www.eia.gov/naturalgas/archive/analysis_publications/ngpipeline/interstate.html (accessed on 27 March 2018).
- Kelkar, M. Natural Gas Production Engineering; PennWell Books: Tulsa, OK, USA, 2008; Chapter Gas Compression; pp. 445–464. [Google Scholar]
- Maric, I.; Galovic, A.; Smuc, T. Calculation of natural gas isentropic exponent. Flow Measur. Instrum. 2005, 16, 13–20. [Google Scholar] [CrossRef]
- Mokhatab, S.; Poe, W.A.; Speight, J.G. (Eds.) Handbook of Natural Gas Transmission and Processing; Elsevier: Amsterdam, The Netherlands, 2006; Chapter Natural Gas Compression; pp. 295–322. [Google Scholar]
- Wu, S.; Rios-Mercado, R.; Boyd, E.; Scott, L. Model Relaxations for the Fuel Cost Minimization of Steady-State Gas Pipeline Networks. Math. Comput. Model. 2000, 31, 197–220. [Google Scholar] [CrossRef]
- Wu, X.; Li, C.; Jia, W.; He, Y. Optimal Operation of Trunk Natural Gas Pipelines Via an Inertia-Adaptive Particle Swarm Optimization Algorithm. J. Nat. Gas Sci. Eng. 2014, 21, 10–18. [Google Scholar] [CrossRef]
- Nørstebø, V.S.; Rømo, F.; Hellemo, L. Using operations research to optimise operation of the Norwegian natural gas system. J. Nat. Gas Sci. Eng. 2010, 2, 153–162. [Google Scholar] [CrossRef]
- Tabkhi, F.; Pibouleau, L.; Hernandez-Rodriguez, G.; Azzaro-Pantel, C.; Domenech, S. Improving the Performance of Natural Gas Pipeline Networks Fuel Consumption Minimization Problems; Wiley Interscience: Hoboken, NJ, USA, 2009. [Google Scholar]
- Rios-Mercado, R.Z.; Kim, S.; Boyd, E.A. Efficient operation of natural gas transmission systems: A network-based heuristic for cyclic structures. Comput. Oper. Res. 2006, 33, 2323–2351. [Google Scholar] [CrossRef]
- Camponogara, E.; Nazari, L. Models and Algorithms for Optimal Piecewise-Linear Function Approximation. Math. Probl. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Codas, A.; Camponogara, E. Mixed-integer linear optimization for optimal lift-gas allocation with well-separator routing. Eur. J. Oper. Res. 2011, 217, 222–231. [Google Scholar] [CrossRef]
- Carrión, M.; Arroyo, J.M. A Computationally Efficient Mixed-Integer Linear Formulation for the Thermal Unit Commitment Problem. IEEE Trans. Power Syst. 2006, 21, 1371–1378. [Google Scholar] [CrossRef]
- Toriello, A.; Vielma, J. Fitting piecewise linear continuous functions. Eur. J. Oper. Res. 2012, 219, 86–95. [Google Scholar] [CrossRef]
- GasLib. Available online: http://gaslib.zib.de/ (accessed on 25 September 2018).
- GAMS Development Corporation. General Algebraic Modeling System (GAMS) Release 25.1.1; GAMS Development Corporation: Washington, DC, USA, 2018. [Google Scholar]
- The MathWorks Inc. MATLAB and Statistics Toolbox Release 2018a; The MathWorks Inc.: Natick, MA, USA, 2018. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).